Economic Record
Volume 100, Issue 329 pp. 137-159
Original Research
Open Access

Alternative Monetary Policy Commitments and the Yield Curve*

Prasanna Gai, 

Prasanna Gai

University of Auckland, Auckland, New Zealand

Search for more papers by this author
Cameron Haworth, 

Corresponding Author

Cameron Haworth

University of Auckland, Auckland, New Zealand

Correspondence: Cameron Haworth, University of Auckland, 12 Grafton Road, Auckland 1010, New Zealand. Email: [email protected]Search for more papers by this author
First published: 19 March 2024
https://doi.org/10.1111/1475-4932.12794
*

We thank two anonymous referees, the editor, James Morley, and seminar participants at the Deutsche Bundesbank, Reserve Bank of Australia, Reserve Bank of New Zealand, the 57th Canadian Economics Association Conference, the 17th Western Economic Association International Conference, the 25th Anniversary of the Central Bank Modelling Workshop and the January 2023 Central Bank Macroeconomic Modeling Workshop for their helpful comments. All remaining errors are our own. Open access publishing facilitated by The University of Auckland, as part of the Wiley - The University of Auckland agreement via the Council of Australian University Librarians.

Abstract

We present a simple model to characterise central bank forward guidance, large-scale asset purchases and yield curve control. Endogenous yield curve reactions to policy shocks are a key determinant of monetary conditions and can support or offset policy intentions. Alternative monetary policy tools allow the central bank to signal central bank private information to investors when the policy rate is at the effective lower bound, shaping yield curve reactions. Commitments to these tools offer policy certainty but can become time-inconsistent if the economy recovers sooner than expected. If commitments become time-inconsistent, endogenous yield curve tightening can offset excess stimulus. The strength of this offset, and the optimality of monetary conditions, improves with the precision of investor inferences of central bank private information.

I Introduction

Central banks use alternative monetary policy tools to influence monetary conditions when policy rates are constrained by the effective lower bound. These tools, namely forward guidance, large-scale asset purchases (LSAPs) and yield curve control, loosen monetary conditions by reducing long-term bond yields (Fig. 1). Because bond yields are determined in financial markets, the central bank can only influence them. Understanding how investors respond to the use of such tools is therefore key to their implementation. Moreover, alternative monetary policy tools are implemented as state-contingent policies or unconditional commitments. This choice may influence the effectiveness of the tools in reducing bond yields. However, there are few real world examples of unconditional commitments to forward guidance or yield curve control (Potter & Smets, 2019; Sutherland, 2023).

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Stylised Yield Curve with Intended Alternative Monetary Policy Effects

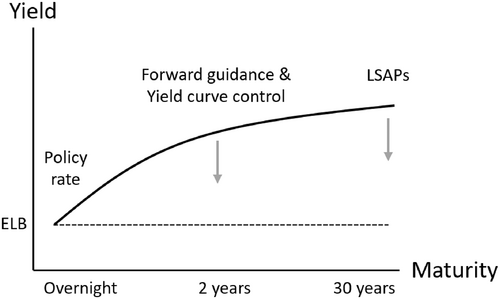
In this paper, we present a simple analytical framework to articulate the channels by which alternative monetary policy tools influence activity and understand the implications of alternative monetary policy commitment. Our framework offers an alternative yield curve model from Ellingsen and Söderström (2001), allowing bond yields with endogenous term premia to influence monetary conditions and, hence, the real economy. We assume the central bank has private information regarding the central bank's own preferences which rational bond investors infer from policy decisions.

When bond yields influence monetary conditions, imprecise investor inference of central bank information can create sub-optimal yield curve responses to policy shocks. Yield curve responses are also state-dependent, varying with the size of output and inflation deviations from target. In particular, long-term yields tighten following a faster-than-expected economic recovery when policy is unexpectedly loose. This has implications for the time-inconsistency of policy commitments: even if monetary policy becomes unmoored from market expectations, endogenous yield curve reactions can keep overall monetary conditions close to their optimal level. The central bank's lack of sole discretion over monetary conditions therefore enables it to take greater risks in providing stimulus, knowing the risks of over-stimulation can be partially offset by the market. This mechanism is weakened under yield curve control, which restricts yield curve reactions and is, hence, more prone to time-inconsistency.

We identify several alternative monetary policy transmission channels across the expected policy path and term premium components of the yield curve. The expected policy path responds directly to the forward guidance path (direct channel), signals of central bank private information (signalling channel) and an implied sequencing that the policy rate will not rise until LSAPs or yield curve control end (sequencing channel). The term premium responds to unconditional forward guidance commitments, reducing interest rate volatility (certainty channel), as well as to central bank asset purchases that reduce net bond supply (bond scarcity channel).

Commitments to forward guidance may reduce term premia relative to conditional guidance through the certainty channel, providing greater stimulus. This can hasten economic recovery at the expense of less frequent information signalling and a risk of time-inconsistency. Commitments to LSAP and yield curve control provide no additional stimulus over their conditional form and suffer from weaker signalling and time-inconsistency risks. These results suggest that central bank aversion to LSAP commitments and yield curve control may be justified, but forward guidance commitments merit consideration when responding to large negative shocks.

Our model sheds light on the experiences of the Reserve Bank of New Zealand (RBNZ) and Reserve Bank of Australia (RBA) over the period 2020–2022. The New Zealand example highlights the potential benefits of an unconditional forward guidance commitment combined with a state-contingent LSAP programme in providing initial stimulus, and shows the benefits of state-contingent policy when pivoting. However, it also illustrates the difficulties in accurately signalling central bank preferences through conditional LSAPs. The Australian case illustrates how endogenous yield curve reactions can reduce the time-inconsistency of alternative monetary policy commitments – even in the extreme case of yield curve control. It also highlights important differences between the various forms of explicit versus implicit forward guidance.

The rest of the paper is as follows. Section II reviews our contribution to the literature. Section III outlines the model. Sections V and VI consider alternative monetary policy tools in the context of the model. Section VII discusses the experiences with these tools in New Zealand and Australia, and the final section concludes.

II Literature Review

There is a vast empirical literature studying the effects of alternative monetary policy tools on the yield curve. The consensus finding is that forward guidance and LSAPs have significant announcement effects and work through both the expected forward path and term premium components of the yield curve. However, there are few cases of alternative monetary policy commitments (Potter & Smets, 2019; Sutherland, 2023), with only two modern uses of yield curve control and one instance of an explicit, unconditional commitment to forward guidance being fulfilled. This makes empirical evaluation difficult.

In the theoretical literature, Angeletos and Sastry (2021) find that unconditional (calendar-based) and state-contingent guidance are isomorphic under rational expectations, making commitment irrelevant. Similarly, Bassetto (2019) concludes that under perfect information commitments may offer no additional stimulus to conditional guidance, but risks time-inconsistency. Jones and Kulish (2022) examine how unconditional forward guidance and yield curve control can extend the duration of zero interest rate policies in a manner which deviates from the monetary policy rule if economic shocks occur, risking time-inconsistency. Goy et al. (2020) explore commitments and belief frictions, finding that commitments provide stronger signalling effects, but can grow time-inconsistent. These studies do not model term premia or how bond market responses to shocks affect monetary conditions. This can disable important channels for distinguishing between policy designs, such as the certainty effect offered by commitments, identified empirically in Hattori et al. (2016), Bundick et al. (2017) and Hansen et al. (2019), or how endogenous yield curve reactions can offset time-inconsistent central bank commitments – a major contribution of this paper.

Ellingsen and Söderström (2001) provide a tractable model for how the yield curve responds to changes in the central bank policy rate. This involves extending the Svensson (1997) macro model with private central bank information to add a yield curve consisting of (i) an expected forward path of the policy rate that abides by the strict expectations hypothesis and (ii) an exogenous term premium. This yield curve cannot model alternative monetary policy at the lower bound because (i) through the strict expectations hypothesis, long-term rates automatically fall towards the lower bound given sufficiently large shocks without the need for additional policy actions, (ii) there is no term premium through which alternative tools – particularly LSAPs – can affect monetary conditions and (iii) long-term rates do not affect monetary conditions, so there is no effect in the model from the central bank reducing them.

We offer an alternative yield curve extension to Svensson (1997) that differs from Ellingsen and Söderström (2001). We relax the assumption of the strict expectations hypothesis and develop a model in line with the liquidity-preference theory of the yield curve, with endogenous term premium that responds to bond liquidity and policy uncertainty. Relaxing the strict expectations hypothesis, long-term movements in the expected forward path of the yield curve become conditional on the state of the economy: with yield curve reactions amplifying or offsetting policy shocks based on the signs and deviations of output and inflation from their target (rather than following an expected forward path of rates explicitly). This both allows investors to consider the effects of a broader suite of tools to affect economic conditions and restricts central bank control over long-term rates in a more realistic manner.

III Model

(i) Monetary Conditions

Let i t be the deviation of the short-term nominal interest rate from its long-run equilibrium level, subject to an effective lower bound
i t = Max ι t i ¯ , (1)
where ι t is the unconstrained policy rate and i ¯ is the effective lower bound.
Let i t n be the interest rate on an n -maturity bond at time t , derived in Section (iii), which prices in the expected policy path and term premium. We define monetary conditions as
θ 1 i t + θ 2 i t n , (2)
where θ 1 + θ 2 = 1 and θ 1 , θ 2 ∈ 0 , 1 represent the relative influence of short- and long-term interest rates on the macroeconomy.

We examine the implications of an effective lower bound in Section IV.

(ii) Aggregate Supply and Demand

Let π t be the deviation of inflation from target at time t and let y t be the output gap. Inflation dynamics are governed by a standard Phillips Curve
π t + 1 = π t + α y t + ε t + 1 , (3)
where α > 0 and ε t is an i.i.d. supply shock with zero mean. The output gap is negatively related to ex-ante real monetary conditions, namely
y t + 1 = β y t − γ θ 1 i t + θ 2 i t n − E t π t + 1 + η t + 1 , (4)
where 0 < β < 1 , γ > 0 and η t is an i.i.d. demand shock with zero mean.
Taking expectations of (3) at time t and substituting into (4) yield the output gap in terms of ex-post real monetary conditions, namely
y t + 1 = β + αγ y t − γ θ 1 i t + θ 2 i t n − π t + η t + 1 . (5)

Monetary policy acts with a two-period lag, meaning that agents are forward-looking with respect to policy despite the backwards-looking Phillips curve.

(iii) Bond Market

A mass of rational long-term bond investors maximise exponential utility
u W = E − e − ρ ⋅ W , (6)
from a portfolio of risk-free cash and interest-risk bearing bonds, with constant absolute risk aversion, ρ > 0 . The expected return on an n -maturity bond at time t is
r t n + z t n , (7)
where r t n = 1 / 1 n Σ s = 0 n − 1 E t i t + s is the return given the expected path of interest rates from time t until n , and z t n ∼ N 0 , n ⋅ σ 2 reflects the expected volatility from the sum of inflation and output shocks on interest rates over the next n periods.
Under Gaussian uncertainty, investor demand for government bonds of maturity n at time t is given by
D t n = r t n − P t n ρ ⋅ n ⋅ σ 2 , (8)
where P t n is the market price for a given residual bond supply, S t n ,
P t n = r t n − ρ ⋅ n ⋅ σ 2 ⋅ S t n , (9)
such that risk averse investors receive a mark-up of ρ ⋅ n ⋅ σ 2 ⋅ S t n over the expected value of the investment, r t n , to compensate for their interest rate risk. This reflects the liquidity preference theory of bond yields and implies a time-varying term premium.
Residual bond supply at time t is given by
S t n = ψ t n − E t Σ s = 0 t + n Q s n , (10)
where ψ t n is gross bond supply and E t Σ s = 0 t + n Q s n is the expected stock of central bank asset holdings of maturity n bonds at time t .
Bond yields are equal to the inverse of the market price for the n -period security and to the average of future short-term rates plus a term premium
i t n = 1 P t n , i t n = 1 n Σ s = 0 n − 1 E t i t + s + T t n . (11)
Combining (9) and (11) with r t n = 1 / 1 n Σ s = 0 n − 1 E t i t + s yields the term premium, i.e.
T t n = 1 r t n − ρ ⋅ n ⋅ σ 2 ⋅ S t n − 1 r t n , (12)
which is a maturity-varying, percentage mark-up for risk averse investors over the expected path of interest rates.
From (12), long-term bond yields can be expressed as
i t n = 1 r t n − τ t n , (13)
where τ t n ≡ ρ ⋅ n ⋅ σ 2 ⋅ S t n is the mark-up for bearing interest rate risk.

(iv) Central Bank

The monetary authority chooses i t to minimise the intertemporal loss function
L t = E t Σ s = 0 ∞ δ s ℓ π t + s y t + s , (14)
where δ is a discount factor and ℓ ⋅ takes the quadratic form
ℓ π t + s y t + s = 1 2 π t 2 + λ t y t 2 . (15)

Inflation and output gap targets are normalised to zero and λ t ≥ 0 is the relative weight the central bank places on output stabilisation.

Optimal monetary conditions are an increasing function of the current inflation rate and output gap (derived in the Appendix):
θ 1 i t + θ 2 i t n = 1 + A π t + By t , (16)
where
A ≡ αδk γ λ t + α 2 δk > 0 ,   and   B ≡ β + αγ γ + αA > 0 , (17)
and
k = 1 2 1 − λ t 1 − δ α 2 δ + 1 + λ t 1 − δ α 2 δ 2 + 4 λ t α 2 ≥ 1 . (18)

The form of optimal monetary conditions in (16) resembles Ellingsen and Söderström (2001), but the make-up and behaviour of long-term yields, i t n , differ markedly.

(v) Information and Timing

If the central bank's preference for output stabilisation is time-invariant λ t = λ , and common knowledge, investors perfectly anticipate policy and price i t n accordingly. There is little need for alternative monetary policy tools because long-term yields adjust with perfect knowledge of the policy path required to optimise monetary conditions.

In reality, central bank preferences are constantly evolving as the members of decision-making committees shift and economic thinking changes. Policy-makers can struggle to communicate this. We therefore suppose that λ t is private information to the central bank and follows a random walk conditioned to remain positive, λ t = Max λ t − 1 + ξ t 0 , where ξ t ∼ N 0 , 1 and λ t ≥ 0 for all t . Bond market investors must infer the weight on output stabilisation λ ̂ t each period based on the central bank's actions and use this to forecast the policy path.

With imperfect inference, λ ̂ t ≠ λ t , long-term yields fail to adjust optimally. This problem becomes significantly worse at the effective lower bound when the central bank cannot move the policy rate at will to correct misinterpretations seen in the yield curve, allowing for potential belief drift. This means that the central bank cannot control long-term yields and must look for other tools to influence long-term yields.

The central bank can attempt to forecast the investors' imperfect inference and account for this when setting policy. But doing so requires the use of forward guidance (which we treat as a separate tool) to avoid a signal extraction problem. We explore this fully in the next subsection.

Table 1 summarises the timing within each period of the model.

Table 1. Timing Within Each Period with Private Central Bank Preferences
Stage Action
1 Shocks hit the economy, observable to all
2 Market predicts i t * and the yield curve adjusts to i t ′ n given inferred λ ̂ t − 1
3 Central bank responds to shock, setting i t *
4 Market infers λ ̂ t and adjusts its response; yield curve shifts to i t n *

(vi) Optimal Responses

Investors predict the central bank's response to economic shocks using last period's yield curve, i t − 1 n , and the estimate of λ ̂ t − 1 to find
i ̂ t * = 1 θ 1 1 + A ̂ t − 1 π t + B ̂ t − 1 y t + θ 2 i t − 1 n , (19)
where A ̂ t ≡ αδk γ λ ̂ t + α 2 δk > 0 , and B ̂ t ≡ β + αγ γ + α A ̂ t > 0 . They then price bonds using (19) for the current period policy rate
i t n ′ = 1 θ 2 1 + A ̂ t − 1 π t + B ̂ t − 1 y t − θ 1 i ̂ t * . (20)
The central bank responds to shocks, taking the i t n ′ yield curve as given (explained shortly) and setting the optimal policy rate
i t * = 1 θ 1 1 + A π t + By t + θ 2 i t n ′ . (21)
Investors infer λ ̂ t from (21)
λ ̂ t = αδk π t + α y t γ θ 1 i t * + θ 2 i t n ′ − π t − y t β + αγ γ − α , (22)
and, if λ ̂ t ≠ λ ̂ t − 1 , the expected forward path adjusts to create the yield curve that affects economic activity for the period
i t n * = 1 θ 2 1 + A ̂ t π t + B ̂ t y t − θ 1 i t * . (23)

When realised monetary conditions from θ 1 i t * + θ 2 i t n * deviate from the optimal level, the central bank realises welfare losses as per its loss function, (14). Because the central bank sets the i t * each period to achieve optimal monetary conditions, deviations from optimal monetary conditions depend entirely on deviations of i t n * from the i t n ′ yield the central bank assumed when it set policy. Therefore, deviations from optimal monetary conditions depend on the precision of market inference of central bank preferences, λ t − λ ̂ t 2 .

Why does the central bank not forecast the change in the yield curve from its policy decision? Doing so requires it to make a choice: to keep the yield curve forecast private, or to publish it. Doing the latter is an act of forward guidance, which we explore in Section V. Keeping the yield curve private creates a signal extraction problem as investors now need to infer two pieces of private information from one data point; from (22), investors' inference of λ ̂ t depends on the yield curve the central bank used when it set i t * . In this case, investors fail to interpret whether a policy surprise is due to a change in the central bank's preferences or due to the central bank forecast of the yield curve, and the resulting yield curve reaction cannot perfectly align with the central bank's forecast. Because the central bank cannot forecast yield curve reactions without publishing forward guidance, it takes the yield curve as given for regular policy rate adjustments.

(vii) Comparative Statics

We next summarise how the yield curve responds to shocks and changes in model parameters (Propositions 1 and 2), and how the central bank policy rate and yield curve shape monetary conditions (Propositions 3 and 4). Proofs of the propositions are contained in the Appendix.

Proposition 1.Bond yields, i t n , are influenced by the expected forward path of policy, 1 n Σ s = 0 n − 1 E t i t + s , and are increasing with inflation and output shocks ε t η t . The strength of the relationship is diminishing with maturity, n .

Proposition 2.The term premium, T t n , increases with investor risk aversion, ρ , the volatility of real economy supply and demand shocks, σ 2 , the maturity of the bond, n , and the supply of bonds, S n .

Proposition 3.The optimal central bank policy rate, i t * , increases with inflation and output gaps ( π t , y t ), and decreases with the term premium and the expected forward path.

Proposition 4.The response of market rates to central bank surprises varies with the state of the economy. If π t + y t is positive (negative), market rates decrease (increase) with the innovation in the central bank policy rate. When π t + y t = 0 , market rates do not respond.

The behaviour of the yield curve contrasts with that of Ellingsen and Söderström (2001) in two key ways. Firstly, the expected forward path in Proposition 4 has state-dependent reactions to central bank policy surprises. In Ellingsen and Söderström (2001), when the central bank has private information, all central bank policy surprises result in long-term yields moving in the opposite direction to the shock. In particular, agents react to surprisingly loose policy by expecting central bank policy to be tighter in the future, resulting in a higher expected forward path for policy. In our model, this occurs only when output and inflation are above target; when they are below target, agents respond to surprisingly loose policy by pricing in looser policy for longer. This distinction is particularly important as the latter case will apply at the effective lower bound. Secondly, our term premium is endogenously determined by several bond market variables, rather than exogenous as in Ellingsen and Söderström (2001), which is critical for the analysis of alternative monetary policy tools.

IV Effective Lower Bound Implications for Monetary Conditions

Optimal monetary conditions at the effective lower bound are given by
θ 1 i ¯ + θ 2 i t n = 1 + A π t + By t . (24)

If a large shock hits the economy, long-term yields fall on the expectation of lower future short-term rates. However, this reduction in long-term yields is also constrained, because the expected path of short-term rates cannot fall below the sum of bounded short rates. It is therefore possible that constrained monetary conditions may be unable to ease by a sufficient degree to satisfy the optimal monetary conditions in (24).

We can identify the maximum possible easing in monetary conditions obtainable via an endogenous easing in long-term rates at the effective lower bound. Let i ¯ n ≡ E t 0 − 1 i t 0 − 1 n + T t 0 − 1 n before a shock hits at t 0 . Then let i ¯ n ≡ n − 1 n i ¯ + T t 0 n be the sum of short-term interest rates fixed at the effective lower bound for the next n periods, plus a term premium. Then, i ¯ n − i ¯ n is the largest possible change in yields for any given yield curve i t n in response to a supply or demand shock at the effective lower bound. It follows that the easing generated by this adjustment in yields is θ 2 i ¯ n − i ¯ n , and therefore the largest negative supply and demand shocks that can be offset from endogenous yield curve responses at the effective lower bound are
ε t + 1 ¯ = θ 2 1 + A i ¯ n − i ¯ n , (25)
and
η t + 1 ¯ = θ 2 B i ¯ n − i ¯ n . (26)

Negative shocks ε t + 1 < ε t + 1 ¯ and η t + 1 < η t + 1 ¯ reduce output and inflation by too large a degree to be offset by endogenous yield curve reactions – even if investors perfectly infer central bank preferences to achieve maximum possible easing.

When investors have imperfect inference of central bank preferences, long-term yields do not adjust perfectly in response to shocks. While they cannot over-adjust beyond the limits imposed by the effective lower bound, they can under-react, dampening economic activity further. Because the central bank loses the ability to further loosen the policy rate at the effective lower bound, the central bank cannot continually signal its preferences to investors to correct any belief drift between λ t and λ ̂ t . The ultimate threat to the central bank achieving optimal monetary conditions is therefore not simply the constraint of the effective lower bound on the policy rate, but rather, constraints to the expected forward path of the policy rate, and the alignment of investor expectations with central bank preferences, as these factors prevent endogenous yield curve responses from sufficiently easing monetary conditions when the policy rate is constrained.

Alternative monetary policy tools therefore have two motivations in this setting. The first is to signal λ t to investors to reduce belief drift and ensure long-term yields loosen appropriately at the effective lower bound. The second is to reduce term premia – which do not necessarily fall in response to economic shocks and are not constrained by the effective lower bound.

In the following sections, which analyse alternative monetary policy, we assume that short-term interest rates are initially at the effective lower bound, so that additional monetary easing must come through longer-term interest rates.

V Forward Guidance

Forward guidance is the publication of a policy rate path that can be state-contingent and conditional on economic developments, or unconditional and committed to without deviation. We consider the implication of each type of guidance in turn.

(i) State-Contingent Guidance

Under state-contingent forward guidance, the central bank publishes the probable policy path without committing to it. The central bank follows the path on average (in expectation) but deviates in response to shocks so that the path remains optimal.

Definition 1.State-contingent guidance, i s SC s = t 0 m SC , is a sequence of policy rates that the central bank believes is necessary to achieve optimal monetary conditions, set first at t 0 and then adjusted every period for the next m SC periods.

State-contingent guidance affects monetary conditions by influencing the expected forward path of the yield curve through two channels: a direct effect and a signalling effect. The expected forward path under state-contingent guidance is given by
1 / r t n = 1 m SC Σ t = t 0 m SC i t SC , for t 0 ≤ t ≤ m SC , 1 n Σ s = 0 n − 1 E t i t + s , for t > m SC . (27)

State-contingent guidance directly influences investor policy rate expectations over the m SC period guidance horizon, with investors' expected forward path adjusting to match the central bank's guidance. State-contingent guidance also signals central bank's output stabilisation preferences, λ t . As with signals of λ t stemming from policy rate adjustments, surprisingly loose state-contingent guidance – indicating lower rates for longer – signals a higher λ t , and vice versa for tight guidance. Long-term rates move in the same (opposite) direction to the λ t shock if π t + y t < > 0 . Low-for-long guidance therefore reduces long-term yields when the economy is sufficiently weak.

Under state-contingent guidance, central banks retain flexibility with their policy rate, adjusting the probable path of policy in response to economic shocks. This means state-contingent guidance can never become time-inconsistent.

(ii) Unconditional Guidance

We define unconditional forward guidance as a commitment to the published path for the policy rate.

Definition 2.Unconditional guidance, i s U s = t 0 m U , is a commitment at t 0 to set a given sequence of policy rates for the next m U periods.

Under unconditional guidance, the expected forward path of interest rates is as given in (27), with m U replacing m SC , but now interest rate volatility is given by
z t n ∼ N 0 , 0 , for t ≤ m U , N 0 , n − m U ⋅ σ 2 , for t > m U . (28)

Unconditional guidance therefore provides a direct m U -period path of rates with zero interest rate risk and hence a zero term premium for bonds of m U maturity or below. In addition to the direct and signalling channels provided by state-contingent guidance, unconditional commitments therefore provide a certainty effect. By restricting central bank policy rate responses to economic shocks, unconditional guidance reduces the volatility of the policy rate. This reduces the mark-up required by risk-averse investors over the expected value of a bond, reducing the term premia out to the m U maturity date.

Figure 2 illustrates the effects of unconditional guidance. The direct and certainty effects directly reduce the expected forward path and term premium, respectively, over the m U guidance horizon, flattening the front-end of the yield curve. These effects are determined by the central bank. The signalling channel mostly affects long-term yields, and its effects are determined by investors' inferences of central bank policy preferences and the state of the economy. In particular, if the central bank commits to a surprisingly loose policy path when the economy is relatively strong, long-term yields rise, partially offsetting the stimulus offered by the guidance (Fig. 2a). When the economy is relatively weak, surprisingly loose unconditional guidance induces long-term yields to fall, reinforcing central bank stimulus (Fig. 2b).

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Effects of Unconditional Guidance on the Yield Curve

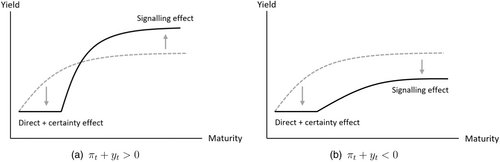
The central bank can benefit when investors offset excessive stimulus. If positive shocks arrive over the commitment period, tighter monetary conditions become optimal, and unconditional commitments can become time-inconsistent. Rational investors respond to such shocks by expecting a higher path of future policy rates when the guidance ends; the expected ‘liftoff’ from the effective lower bound is increased in magnitude and potentially brought forward in time (provided that it arrives no earlier than the end of the commitment window). This immediately tightens monetary conditions and reduces central bank losses from over-stimulation. Endogenous investor responses can therefore reduce the severity of time-inconsistent commitments. The degree to which these reactions benefit the central bank depends on the deviation of λ − λ ̂ 2 , with smaller deviations implying investor reactions that align with central bank interests.

(iii) Trade-Offs in Forward Guidance Design

A commitment to unconditional forward guidance provides an additional channel of stimulus, through term premia, at the cost of reduced flexibility and the risk of time-inconsistency. Because state-contingent guidance provides lower per-period stimulus than unconditional guidance, state-contingent guidance must be maintained for longer to achieve the same monetary impact, if there are no additional shocks over the guidance horizon.

Proposition 5 describes the impact of shocks on the realised duration of unconditional versus state-contingent forward guidance.

Proposition 5.If the net sum of supply and demand shocks hitting the economy between t 0 and min m U m SC is negative in nature, the policy rate, i t , will stay fixed for longer than the initial estimates of m U and m SC , and rise sooner under unconditional guidance. If the net sum of supply and demand shocks hitting the economy between t 0 and min m U m SC is positive in nature, the policy rate can rise sooner than the initial estimates of m U and m SC , and rises sooner under state-contingent guidance, m SC ≤ m U .

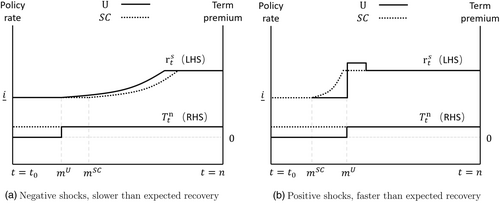
Proposition 5 shows that unconditional guidance offers better protection against negative shocks and state-contingent guidance offers better protection against positive shocks.

Figure 3 illustrates these points. In Figure 3a, the reduction in term premia under unconditional guidance accelerates the delivery of stimulus relative to state-contingent guidance, allowing for the policy rate and expected forward path to rise above the effective lower bound sooner. In Figure 3b, unconditional guidance keeps conditions too loose for too long; the duration of the stay at the effective lower bound is extended (as in Jones & Kulish, 2022). Policy must then tighten rapidly when the guidance ends. Investors price in the need for future tightening into the expected forward path. If investors cannot accurately infer the required tightening to maintain optimal monetary conditions, the tightening priced in may be insufficient or excessive – yielding sub-optimal monetary conditions.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Yield Curve Decomposition of State-Contingent (SC) Guidance and Unconditional (U) Guidance Under Different Shocks

VI LSAPs and Yield Curve Control

We treat an LSAP programme as the volume of central bank bond purchases over a given horizon that can either be committed to or kept conditional on economic developments. We follow Bernanke (2020) and define yield curve control as an LSAP commitment where a given yield is targeted (rather than a purchase volume) and purchase volumes are determined endogenously (rather than yields).

(i) State-Contingent LSAPs

Definition 3.The central bank may publish a state-contingent schedule at t 0 to purchase Σ s = t 0 m L , SC Q s n n -maturity bonds at the market price over the next m L , o periods, where the value of cumulative purchases is limited by an exogenous budget constraint Ω ¯ , Σ s = 0 n Q s n ⋅ P s n ≤ Ω ¯ and total bond issuance Σ s = 0 n Q s n ≤ ψ t n . The purchase schedule is revised each period.

LSAPs affect monetary conditions through three channels: a direct effect on bond scarcity, a signalling effect and an implied sequencing effect.

LSAPs reduce the residual supply of marketable bonds. This increases the price and hence decreases the yield on the purchased bond tenor. This bond scarcity channel works through the term premium, as per (10). The expected accumulated stock of LSAP bonds determines the magnitude of the effect, as investors are forward-looking and price in anticipated central bank purchases. The volatility of such expectations do not have an effect in our model.

The LSAP signalling channel follows the same mechanisms as forward guidance. Larger volumes of LSAP purchases signal greater intended stimulus and, hence, a higher λ t . This works exclusively through the expected forward interest rate path.

LSAPs also imply a form of one-off state-contingent guidance indicating that the central bank does not intend to raise the policy rate for at least the next m L , SC periods while it loosens conditions through asset purchases. This works exclusively through the expected forward path of interest rates. The length of the purchase period determines the sequencing effect, with longer purchase windows implying longer one-off state-contingent guidance that the policy rate is expected to remain flat until at least the end of the purchase window. This has less information content than explicit state-contingent guidance, because the sequencing effect only implies the soonest possible hike intended at t 0 , rather than the expected hiking date, which formal state-contingent guidance provides.

(ii) Unconditional LSAP Commitment

Definition 4.The central bank may commit at t 0 to purchase Σ s = t 0 m L , U Q s n n -maturity bonds at the market price over the next m L , U periods, where the value of cumulative purchases is limited by the budget constraint Σ s = 0 n Q s n ⋅ P s n ≤ Ω ¯ and total issuance Σ s = 0 n Q s n ≤ ψ t n .

An unconditional commitment to an LSAP programme has three consequences. Firstly, a commitment provides certainty regarding the expected value of purchases under the programme. However, this certainty does not provide additional stimulus in the model, as the volatility of asset purchase expectations does not affect bond term premia. Secondly, LSAP commitments can become time-inconsistent as the central bank may need to continue purchases at a time when they wish to tighten monetary conditions. However, because the central bank can raise the policy rate without an upper bound, they do not have to rely on bond investors to keep monetary conditions time-consistent, so long as no co-commitment to unconditional guidance is also made. Thirdly, the signalling and sequencing effects of LSAPs are less frequent under a one-off commitment and cannot be adjusted to correct investor belief drift if λ − λ ̂ 2 rises over time.

(iii) Yield Curve Control

Definition 5.Yield curve control is a central bank commitment at t 0 to purchase m YCC maturity bonds in the volume required to maintain m YCC bond yields at a target rate, i ¯ , for all periods t ≤ m YCC subject to budget and bond issuance constraints ( Σ s = 0 n Q s n ⋅ P s n ≤ Ω ¯ , and Σ s = 0 n Q s n ≤ ψ t n ).

Yield curve control works through the same channels as LSAPs. However, the two tools differ markedly over periods with positive economic shocks. Yield curve control naturally inhibits endogenous yield curve reactions to such shocks. Longer-maturity N > m YCC yields can still rise, tightening monetary conditions, but a significantly larger increase in long-term yields may be needed to offset the time-inconsistency of a yield curve control commitment relative to forward guidance and LSAPs, as part of the curve is fixed. Furthermore, if the central bank has not committed to unconditional guidance alongside yield curve control, the market will price time-consistent policy rate responses to any over-stimulation involving yield curve control. This can raise the expected policy path, with hikes priced in before the end of yield curve control. This puts upwards pressure on bond yields. An offsetting reduction in term premia is therefore needed for the central bank to maintain the yield target, increasing the required volumes of bond purchases. This raises a unique risk to yield curve control: the central bank budget constraint or bond issuance constraint may bind before the central bank completes the purchases required to offset the pressure from the rising expected forward path. When this occurs, the yield curve control commitment cannot be fulfilled.

Definition 6.If Σ s = 0 n Q s n P s n = Ω ¯ or Σ s = 0 n Q s n ≥ ψ t n , yield curve control commitments are abandoned.

Investors' endogenous purchase responses to a rapid economic recovery under yield curve control can therefore still restore time-consistency to overall monetary conditions. However, the purchase response, forcing the central bank to abandon their policy, is far blunter than the yield curve response to other alternative monetary policy commitments. While LSAPs are subject to the same bond purchase constraints as yield curve control, the central bank chooses its LSAP commitment subject to the limitation, and need not violate it.

The likelihood of abandoning a yield curve control policy at some time t > t 0 due to positive economic shocks is increasing with the sum of positive economic shocks because the t 0 commitment was made Σ s = t 0 m YCC η s + ε s , decreasing with the influence of longer N -maturity bond yields (where N > m YCC ) on monetary conditions, and decreasing with the upper limit of the central bank's budget constraint Ω ¯ and bond issuance constraint Σ n = t 0 m YCC Q t n . Central banks with limited purchase capacity operating in economies where short-term lending is dominant will therefore struggle to maintain yield curve control in the face of rapid recoveries.

VII Policy Implications

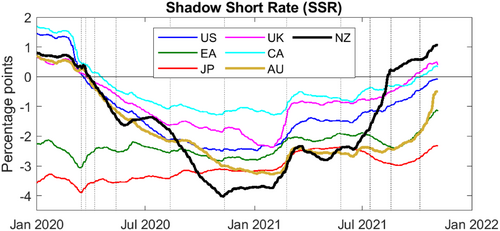
We next explore the experience of alternative monetary policy commitments made by the RBNZ and RBA. These two cases reflect some of the most aggressive use of alternative monetary policy as crisis response tools, as measured by shadow short rates of government bond curves (Fig. 4).

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Shadow Short Rate Estimates of Selected Central Banks from Krippner (2021)

(i) Case Study: RBNZ, 2020–2021

The RBNZ responded to the COVID-19 pandemic in March 2020 by announcing an unconditional commitment to keep their policy rate at the effective lower bound ‘for at least the next 12 months’, accompanied by a state-contingent LSAP programme of purchases ‘up to $ NZ 30 billion’ (10 per cent of GDP; RBNZ, 2020a,b). The unconditional guidance was implemented to ‘provide clarity to financial market participants’ regarding the path of the policy rate.

Over the next 12 months, the New Zealand economy stabilised. However, with inflation at 1.5 per cent in March 2021, the RBNZ continued to increase stimulus. The LSAP programme was expanded to purchase ‘up to $ NZ 100 billion’ (30 per cent of GDP). While the upper limits on purchases were communicated by the monetary policy committee, staff were delegated responsibility for weekly purchases, with the RBNZ stating that changes in the weekly purchase rate ‘were not signals of monetary policy stance’, RBNZ (2022). Unconditional guidance was maintained to maturity and followed by ongoing state-contingent guidance with a published expected path for the policy rate.

The RBNZ's combined alternative monetary policy response contributed in part to an over-stimulation of the New Zealand economy, with inflation eventually rising to 7.3 per cent by mid-2022, far above the 2 per cent target. With conditional forward guidance and LSAPs in use in 2021, the RBNZ was able to pause stimulus and then reverse asset purchases while raising the policy rate. Asset purchases peaked at $ NZ 56 billion in July 2021, far short of the $ NZ 100 billion state-contingent limit, with aggressive asset sales planned to reduce holdings to zero by 2027 (RBNZ, 2022).

The experience with alternative monetary policy tools has been reviewed by RBNZ (2022), McKibbin (2022) and Schembri (2022). The RBNZ and Schembri describe a trade-off existing between the flexibility and effectiveness of alternative monetary policy tools. Schembri argues that the state-contingent nature of the RBNZ's LSAPs may have been less effective, and that by communicating an upper limit on purchase volumes rather than a target may have further reduced effectiveness. Additionally, both RBNZ and Schembri raise the possibility that the decision to (i) publish weekly LSAP purchase updates but (ii) claim they were not monetary policy signals may have confused market participants.

Both the RBNZ and Schembri question the value of the initial 12-month unconditional commitment to forward guidance. Schembri argues that the ‘effectiveness [of unconditional guidance] in providing additional monetary stimulus depends on the extent to which it influences expectations of the path of the policy rate and thus the yield curve’, and that if the policy rate was already expected to be low for 12 months, the commitment's effect ‘would have been minimal’.

Our model argues that a trade-off exists between flexibility and certainty offered by alternative monetary policy tools – and that certainty only influences effectiveness to the extent that it influences bond pricing. In the case of LSAPs, this certainty does not directly affect yields if the expected purchase volume can still be inferred. In fact, state-contingent LSAPs have the potential to be more effective than commitments due to the increased frequency of the signalling and sequencing effects they can achieve. However, in the RBNZ's case, (i) the decision not to announce an explicit LSAP target volume left the expected value to be inferred by the market and (ii) inference was disrupted by the noisy messaging of information which was released and discredited by the RBNZ. In our model's terms, this relates to an increase in the variation of ξ in the formation of RBNZ preferences λ t = λ t − 1 + ξ , increasing the chance of belief drift between the market and RBNZ. Therefore, while conditional LSAPs may have provided frequent signals, they may have even increased λ − λ ̂ 2 , rather than closing the gap, creating suboptimal monetary conditions.

Our model is more optimistic than both the RBNZ's and Schembri's analysis of unconditional commitments to forward guidance. In contrast to Schembri's description, our model suggests that by reducing interest rate risk through the certainty channel, unconditional guidance can reduce term premia even when the expected path of policy is perfectly priced by bond investors. Furthermore, because unconditional commitments have little chance of becoming time inconsistent in the early stages of recovery from large negative shocks, there is little risk to making such commitments – especially when conditional LSAPs can be used to continue signalling central bank information and investors can offset residual potential time-inconsistency. Our model therefore suggests that unconditional guidance of this form may be valuable and a low-risk stimulus enhancement in the early stages of such recoveries.

(ii) Case Study: RBA, 2020–2021

The RBA responded to the COVID-19 pandemic by announcing a yield curve control target on 3-year government bonds equal to the policy rate in March 2020. The purpose of the programme was to ‘directly anchor the short end of the yield curve so that funding costs were low across the economy’ (Lowe, 2021), and to reinforce state-contingent guidance that the board would ‘not increase the cash rate from its current level until progress was made towards full employment and that we were confident that inflation will be sustainably within the 2–3 per cent range’ (Lowe, 2020). The RBA was also prepared to purchase bonds ‘in whatever quantities are necessary to achieve this objective’ (Lowe, 2020), supported by small-scale bond purchases across the curve to restore market functioning.

The RBA's response was initially successful. The target was achieved with $ A 36 billion of asset purchases (2 per cent of GDP) and maintained until June 2021 with minimal intervention. Upon announcement, short-tenor bond yield fell significantly, while long-term yields rose (Fig. 5). This significantly eased monetary conditions, as the local market was dominated by lending at short tenors. Long-term yields drifted lower as investors understood the nature of small-scale bond purchase across the curve, but 6 months later, the RBA implemented a series of LSAP commitments to buy $ A 280 billion of bonds (15 per cent of GDP) to more aggressively reduce term premia along the longer-term tenors of the curve (and lean against currency appreciation – influenced by a relatively high 10-year yield).

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Change in Australian Government Bond Yields Over 16 and 19 March 2020 from Finlay et al. (2022)

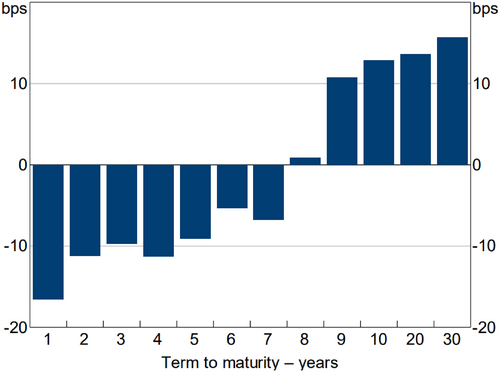
By June 2021, economic data had rapidly improved and investors priced in policy rate hikes within the 3-year window of the yield curve control commitment. The RBA verbally rebuffed this pricing, but did not strengthen their state-contingent guidance with an explicit unconditional commitment that they would not hike before the end date of yield curve control. With a rising expected forward path, the yield curve control target came under pressure. The RBA purchased large quantities of bonds. When purchases stopped in November 2021 and the RBA did not defend the target rate, yields rose around 75 basis points and the RBA abandoned yield curve control, stating ‘its effectiveness as a monetary policy tool declined as expectations about future interest rates shifted due to the run of data and the forecast progress towards our goals’ (Lowe, 2021). However, the RBA continued its LSAP commitments to completion in February 2022.

The RBA's experience with alternative monetary policy tools has been reviewed by RBA (2022), de Brouwer et al. (2023) and Orphanides (2023), and yield curve responses have been analysed by Finlay et al. (2022).

These papers note the value of the yield curve target in ‘reinforcing’ the RBA's forward guidance, with the RBA observing that this effectiveness diminished ‘as market participants reassessed their views of the outlook for the cash rate’ (RBA, 2022). de Brouwer et al. and Orphanides focus on the time-inconsistency associated with the use of ‘a “calendar-based” component to their forward guidance’ used intermittently in 2020 and 2021 to indicate the timing implied by the RBA's forecasts of when the economy would return to target (de Brouwer et al., 2023). The state-contingent nature of this guidance was ‘not well understood by the public’ and ultimately ‘damaged the credibility of the RBA’ when the timings proved wrong (de Brouwer et al., 2023). The length of this guidance – 3 years – has been noted by de Brouwer et al. as being an outlier internationally for its length. de Brouwer et al. noted that the RBA's response indicates preferences to ‘provide more support and for longer, rather than risk not doing enough’.

The addition of successive LSAP commitments to purchase bonds beyond the tenor of the yield target, while effective in reducing long-term bond yields (Finlay et al., 2022), was questioned by de Brouwer et al. and Orphanides, noting that ‘bank funding in Australia (unlike in some other countries) largely occurs at the short end of the term structure’ (de Brouwer et al., 2023) while Orphanides suggests the asset purchase programme caused the ‘demise’ of the yield curve target by creating concerns of over-stimulation, because after it was announced ‘markets expected an earlier lift-off and larger hikes following lift-off’ (Orphanides, 2023). The RBA noted that the desire to reduce 10-year government bond rates stemmed from concerns about a high exchange rate (Finlay et al., 2022; RBA, 2022).

Our model suggests that yield curve control does not ‘reinforce’ forward guidance, but rather provides a one-off issuance of state-contingent forward guidance upon announcement, implying a lower bound on when the policy rate can be hiked. This naturally falls out of date as shocks arrive and therefore cannot be relied upon to continually ‘reinforce’ state-contingent guidance, which should itself adapt to changing conditions. The ‘calendar-based’ component of the RBA's guidance was not an unconditional commitment as described in our model, but describes the probable path of policy and therefore subject to shocks. Our model suggests that if policy certainty was desired, then the RBA could have made a clearer unconditional commitment to the policy path to bond investors to benefit from the forward guidance certainty channel – decreasing the need for a yield curve control programme to reduce term premia over the guidance horizon. If not, the state-contingent nature of the forecasts could have been emphasised to help signal the RBA's intent and align household and investor expectations.

De Brouwer et al.'s comments regarding the RBA's preferences for a speedy recovery suggest a high λ t value. Our model suggests that investors inferring a high λ t price in a faster and sharper tightening in the expected forward path of the policy rate. This may explain part of the steepening observed by Orphanides (2023) and Finlay et al. (2022).

By using both yield curve control to inhibit short-term yield curve reactions and LSAP commitments to reduce long-term term premia, investors were unable to endogenously offset the excessive stimulus supplied by the RBA's time-inconsistent policies through a rising expected forward path until heavy selloffs forced the abandonment of the yield target. Our closed-economy model concurs with the questions raised by de Brouwer et al. and Orphanides regarding the addition of general LSAPs to complement yield curve control (noting that we cannot capture exchange rate effects). When long-term interest rates have little relative effect on the economy ( θ 2 is low), the stimulus from reducing these yields is minimal.

Overall, the RBA's response favoured commitments that restrained yield curve reactions. Our model suggests that commitments benefit from endogenous market reactions for reducing time-inconsistency risks, making this a dangerous approach. The final abandonment of the yield curve target reflects this. If the yield target had been maintained for longer, the resulting stimulus would have been excessive; the market aided the RBA by counteracting its commitment. However, the nature of yield curve controls makes this process difficult. Our model suggests rather than restricting yield curve reactions, central banks should seek to signal their private information to investors to make yield curve reactions work in their favour. Policy commitments are best undertaken if accompanied by other tools which frequently signal central bank preferences and intentions, to reduce divergence between investor and central bank information.

VIII Conclusion

We study endogenous yield curve reactions to the deployment of alternative monetary policy. Crucially, we assume that bond yields affect the real economy through monetary conditions and that the central bank has private information that investors continually infer.

We identify several alternative monetary policy transmission channels across our decomposed yield curve. The expected interest rate path responds directly to the forward guidance path (direct channel) as well as central bank signals regarding the economy and central bank preferences (signalling channel) and implied sequencing that the policy rate will not rise until LSAPs or yield curve control end (sequencing channel). The term premia responds to unconditional forward guidance, reducing interest rate volatility (certainty channel), as well as to central bank asset purchases that reduce net bond supply (bond scarcity channel).

The experiences of the RBNZ and RBA highlight the importance of aligning investor inference of policy-maker private information with its actual value; endogenous yield curve reactions can reinforce or work against the central bank's policy intentions. They also emphasise how financial market responses can tighten monetary conditions in the face of over-stimulation, and that inhibiting these responses for long intervals increases the risks of commitments becoming time-inconsistent.

Our results are sensitive to assumptions of rational investors and credible central bank commitments. Bounded rationality can hinder investor inference of central bank private information, reducing the ability of endogenous yield curve reactions to offset time-inconsistent commitments. If commitments are not fully credible, investors may price in the risk of the central bank reneging. These frictions suggest our model may overestimate the benefits and underestimate the risks of unconditional guidance in particular, and alternative monetary policy commitments more generally, although this is mostly a question of magnitude. Future research may look to explore endogenous central bank credibility where central banks over- and under-shoot objectives, to better determine commitment risks. The heuristic switching framework in Goy et al. (2020) provides one direction, and the methods for determining the endogenous probability of a central bank reneging in Haberis et al. (2019) provide another.

CONFLICT OF INTEREST STATEMENT

There are no conflicts of interest to disclose.

Appendix

A Derivation of Optimal Monetary Conditions

We use the recursive structure of the model and treat E t y t + 1 as the control variable to write the optimisation problem as a control problem with
V E t π t + 1 = min E t y t + 1 1 2 E t π t + 1 2 + E t λ t + 1 y t + 1 2 + δ E t V E t + 1 π t + 2 , (A.1)
subject to
E t + 1 π t + 2 = π t + 1 + α y t + 1 = E t π t + 1 + ε t + 1 + α E t y t + 1 + η t + 1 , (A.2)
λ t + 1 = Max λ t + ξ t + 1 , 0 where ξ t + 1 ∼ N 0 , 1 , (A.3)
i t n = 1 r t n − τ t n , (A.4)
with the first-order condition and value function
λ t + 1 E t y t + 1 + αδ E t V π E t + 1 π t + 2 = 0 , (A.5)
V E t + 1 π t + 2 = k 0 + k 2 E t π t + 1 2 , (A.6)
where k is determined shortly and the central bank optimises y t + 1 by controlling the constrained overnight rate i t given in (1), but has imperfect control over y t + 1 due to the presence of the long-term rate, i t n , set by investors. Without the use of alternative monetary policy tools, the central bank takes the current long-term rate as given when setting the short-term policy rate, as attempts to forecast the investor response results in a signal extraction problem described in Section (vi).
Using the law of iterated expectations, we express the optimal expected output gap as
E t y t + 1 = − αδk λ t + 1 E t π t + 2 , (A.7)
with the unique solution for k derived as follows.
We can write (A.7) in terms of y t and E t π t + 1 , using expectations in (3)
y t = − αδk λ t E t π t + 1 = − αδk λ t + δα 2 k π t . (A.8)
Then the equilibrium inflation forecast satisfies
E t π t + 1 = 1 − αδk λ t + δα 2 k π t = λ t λ t + δα 2 k π t . (A.9)
Using the envelope theorem in (A.1) and (A.6) and using (A.9), we find
V π π t = 1 + δλ t k λ t + δα 2 k π t . (A.10)
Identification of the coefficient for π t gives
k = 1 + δλ t k λ t + δα 2 k , (A.11)
where the RHS is equal to 1 when k = 0 and increases towards 1 + λ t / α 2 as k → ∞ . There is therefore a unique positive solution fulfilling k ≥ 1 .
k = 1 + δλ t k λ t + δα 2 k k λ t + δα 2 k = λ t + δα 2 k + δλ t k k 2 δα 2 − k δα 2 + δλ t − λ t − λ t = 0 k 2 − k 1 − λ t 1 − δ δα 2 − λ t δα 2 = 0 , (A.12)
which yields the quadratic solution
k = 1 2 1 − λ t 1 − δ α 2 δ + 1 + λ t 1 − δ α 2 δ 2 + 4 λ t α 2 ≥ 1 . (A.13)
We now back out the optimal real monetary conditions from (A.7) and (5) as
θ 1 i t + θ 2 i t n − π t = αδk γλ t E t π t + 2 + β + αγ γ y t , (A.14)
which indicates that monetary policy can only affect inflation through a two-period lag. We derive an expression for this future inflation rate by leading (3) two periods ahead and taking expectations
E t π t + 2 = π t + α 1 + β + αγ y t − αγ θ 1 i t + θ 2 i t n − π t . (A.15)
Combining (A.14) with (A.15) yields an expression for optimal real monetary conditions with respect to current period inflation and output
θ 1 i t + θ 2 i t n − π t = αδk γλ t π t + λ t β + αγ + α 2 δk 1 + β + αγ λγ y t − α 2 δk λ t θ 1 i t + θ 2 i t n − π t = A π t + By t , (A.16)
where
A ≡ αδk γ λ t + α 2 δk > 0 , and B ≡ β + αγ γ + αA > 0 , (A.17)
and the optimal nominal monetary conditions are therefore given by the rule
θ 1 i t + θ 2 i t n = 1 + A π t + By t . (A.18)

B Proofs of Propositions

Proposition 1. Yield Curve Response to Economic Shocks

Proof. The result follows from partial derivatives of 1 n Σ s = 0 n − 1 E t i t + s * with respect to ε and η , and then taking further partial derivatives with respect to n .
∂ 1 n Σ s = 0 n − 1 E t i t + s * ∂ ε = 1 + A τ t n τ t n 1 + A π t + By t − θ 1 i t + 1 2 > 0 , ∂ 1 n Σ s = 0 n − 1 E t i t + s * ∂ η = B τ t n τ t n 1 + A π t + By t − θ 1 i t + 1 2 > 0 .
Then
∂ ∂ n ∂ 1 n Σ s = 0 n − 1 E t i t + s * ∂ ε = − 2 n 2 B ⋅ ρ ⋅ σ 2 ⋅ S t n ⋅ y t + 2 A + 1 π t ⋅ ρ ⋅ σ 2 ⋅ S t n − θ 1 i t + 1 n 3 ⋅ ρ ⋅ σ 2 ⋅ S t n 2 B ⋅ ρ ⋅ σ 2 ⋅ S t n ⋅ y t + A + 1 π t ⋅ ρ ⋅ σ 2 ⋅ S t n − θ 1 i t + 1 3 ,
which is greater than 0 ∀ n ≥ 1 and implies ∂ ∂ n ∂ 1 n Σ s = 0 n − 1 E t i t + s * ∂ η > 0 , because B = 1 + A α + β / γ . □

Proposition 2.Term Premium Statics

Proof. The result follows from partial derivatives of (12).

First note that
∂ T t n ∂ ρ = − − n ⋅ n ⋅ σ 2 ⋅ S t n * − E t Σ s = 0 t Q s n r t n − ρ ⋅ n ⋅ n ⋅ σ 2 ⋅ S t n * − E t Σ s = 0 t Q s n > 0 ,
and so the term premium is increasing with market risk aversion.

It follows similarly that ∂ T t n ∂ n > 0 , ∂ T t n ∂ σ > 0 , ∂ T t n ∂ S t n * > 0 and ∂ T t n ∂ E t Σ s = 0 t Q s n < 0 . □

Proposition 3.Policy Rate and Bond Yields Are Substitutes for Monetary Easing

Proof. The result follows from partial derivatives of i t * with respect to π t , y t , τ t n , and 1 n Σ s = 0 n − 1 E t i t + s .
∂ i t * ∂ π t = 1 θ 1 1 + A > 0 ,
∂ i t * ∂ y t = 1 θ 1 B > 0 ,
∂ i t * ∂ τ t n = − θ 2 θ 1 ⋅ 1 n Σ s = 0 n − 1 E t i t + s τ t n ⋅ 1 n Σ s = 0 n − 1 E t i t + s − 1 2 < 0 ,
∂ i t * ∂ 1 n Σ s = 0 n − 1 E t i t + s = − θ 2 θ 1 ⋅ 1 τ t n ⋅ 1 n Σ s = 0 n − 1 E t i t + s − 1 2 < 0 .

□

Proposition 4.Yield Curve Response to Central Bank Preference Shocks

Proof. The result follows from the partial derivative of 1 n Σ s = 0 n − 1 E t i t + s * with respect to λ .
∂ 1 n Σ s = 0 n − 1 E t i t + s * ∂ η = π t + y t θ 1 i t − τ t n ⋅ π t − 1 λ − τ t n ⋅ y t − τ t n ⋅ π t 2 .

□

Proposition 5.Comparison of Unconditional Versus State-Contingent Guidance

Proof. This follows from Propositions 1 and 4 and the following note regarding the length of forward guidance intervals.

Let the certainty effect of unconditional guidance via the term premium be given by Δ T n and the net effect of the direct and signalling channels under unconditional guidance and outcome-guidance to be Δ 1 / r t n unconditionalguidance and Δ 1 / r t n state − contingentguidance , respectively.

If the two policies are used to achieve the same net easing in monetary conditions, then Δ T n + Δ 1 / r t n unconditionalguidance = Δ 1 / r t n state − contingentguidance . Then if Δ T n > 0 ,
Δ 1 / r t n unconditional guidance < Δ 1 / r t n state − contingent guidance .

This implies m U < m SC .

It follows that when the sum of economic shocks over a guidance period is less than or equal to zero, that interest rates can rise sooner under unconditional guidance. However, if the sum of shocks is positive, unconditional guidance keeps rates lower for longer than necessary. □

  • 1 This approach complements the literature of preferred habitat yield curve models such as Chen et al. (2012); Hamilton and Wu (2012); Greenwood and Vayanos (2014) and Vayanos and Vila (2021).
  • 2 See Gagnon et al. (2011a,b); Joyce et al. (2011); Campbell et al. (2012); Eser and Schwaab (2016); Carvalho et al. (2016); Arrata and Nguyen (2017); Bundick et al. (2017); Nakamura and Steinsson (2018); Andrade et al. (2019); Sutherland (2023); Andrade and Ferroni (2021); Breitenlechner et al. (2021); Galati and Moessner (2021); Swanson (2021); Rebucci et al. (2022); Finlay et al. (2022); Hattori and Yoshida (2022).
  • 3 Long-term inflation expectations, E t π n , do not directly enter the output gap. This is because n -maturity inflation expectations should converge to the central bank's target, which means E t π n = 0 . While there may be exceptions to this treatment, it greatly simplifies the model. Inflation risk – reflecting deviations from expectations – are captured in the term premium, which reacts to economic volatility.
  • 4 A higher σ 2 reflects a volatile economy that requires more active central bank stabilisation.
  • 5 The empirical literature finds a ‘bond market functioning effect’ where LSAPs are found to have their strongest impact on yields while offsetting poor liquidity in bond markets (e.g. Gagnon et al., 2011b; Christensen & Gillan, 2022; Finlay et al., 2022). This can be explored in the model by considering an exogenous market dynamic shock, such as a flight to cash, which LSAPs offset by filling the demand gap.
  • 6 This process of investor reaction differs significantly from Ellingsen and Söderström (2001), where investors predict the expected forward path of rates by explicitly applying the strict expectations hypothesis to forecast every overnight interest rate until period n . Here, investors focus on forecasting what optimal monetary conditions currently are, and, taking into account the overnight policy rate, back-out an expected forward path of policy with term premium mark-up that is consistent with this.
  • 7 Term premia have been estimated at negative values in many economies, particularly following the advent of LSAPs (e.g. Krippner, 2015).
  • 8 The periodic flow rate of purchases is a residual, determined by the expected purchase stock divided by the purchase window. Should central banks announce their policy as a flow rate over a purchase window, it is still the implied expected stock that drives monetary conditions. This treatment aligns with the general view among central bankers, for example, Lane (2019).
  • 9 We call this a ‘sequencing’ channel to distinguish it from the signalling channel, but this aligns with the ‘policy signalling’ effects discussed in the literature, for example, Bhattarai et al. (2015) and Sutherland (2023).

The full text of this article hosted at iucr.org is unavailable due to technical difficulties.