Risk Aversion and the Elasticity of Intertemporal Substitution among Australian Households*
Abstract
This paper explores the degree of risk aversion amonsg Australian households using panel data from the Household Income and Labour Dynamics in Australia (HILDA) Survey. Using households' share of risky assets, we test whether relative risk aversion is constant in wealth. After accounting for measurement error, we cannot reject the constant relative risk aversion (CRRA) assumption. Using a CRRA utility function, we estimate the elasticity of intertemporal substitution and infer a coefficient of relative risk aversion of 1.2 to 1.4. These findings can provide guidance for calibrating household preferences in macroeconomic models of the Australian economy.
1 Introduction
Risk aversion and the willingness of people to substitute consumption tomorrow for consumption today are central to the theory of individual decision-making under uncertainty underpinning models of intertemporal consumption and saving behaviour, portfolio choice and labour supply. Risk aversion has also been identified as an important empirical factor in a broad range of economic and social choices.1 The household's degree of risk aversion is also a crucial input in large-scale macroeconomic models, where it plays a large part in determining the economy's steady-state and dynamic response to changes in interest rates, taxes, and the economic environment.2
While a range of international studies, mostly from the USA, have estimated the key parameter which determines risk aversion, there is no evidence, to our knowledge, for Australia. It seems plausible that Australian households might differ substantially from their S counterparts in their attitude towards risk and the degree to which they substitute consumption across time. Australia-specific estimates will thus be particularly useful for researchers who build large-scale models of the Australian economy. This is our main contribution in this paper.
We provide Euler equation-based estimates of the risk aversion parameter (
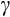 ) from the constant relative risk aversion (CRRA) utility function for Australia using longitudinal consumption data from the Household Income and Labour Dynamics in Australia (HILDA) Survey and data on aggregate interest rates. We exploit the relationship between consumption growth and expected interest rates to identify risk aversion. In the CRRA framework, the elasticity of intertemporal substitution (EIS) is equal to the inverse of the coefficient of relative risk aversion. Under the CRRA framework, we are thus able to identify
) from the constant relative risk aversion (CRRA) utility function for Australia using longitudinal consumption data from the Household Income and Labour Dynamics in Australia (HILDA) Survey and data on aggregate interest rates. We exploit the relationship between consumption growth and expected interest rates to identify risk aversion. In the CRRA framework, the elasticity of intertemporal substitution (EIS) is equal to the inverse of the coefficient of relative risk aversion. Under the CRRA framework, we are thus able to identify
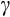 through substitution responses to the intertemporal price of consumption. These are the first Euler equation estimates using microdata in Australia, as far as we are aware.
through substitution responses to the intertemporal price of consumption. These are the first Euler equation estimates using microdata in Australia, as far as we are aware.
To preview the results, our preferred nonlinear specifications that allow for the well-known and substantial problem of measurement error suggest
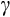 is in the range of 1.2 to 1.4. This implies a relatively modest degree of risk aversion for the mean household, similar to the 1.5 found in Alan et al. (2009), a recent comparable US study.
is in the range of 1.2 to 1.4. This implies a relatively modest degree of risk aversion for the mean household, similar to the 1.5 found in Alan et al. (2009), a recent comparable US study.
The CRRA utility function and our estimation approach also embed the assumption that relative risk aversion is constant with respect to a household's level of wealth. Previous Australian studies have found mixed evidence regarding this assumption. We also test this assumption and we are unable to reject the CRRA assumption. We also attempt to explain the variety of findings from previous Australian studies.
Section 2 provides background about the research agenda around estimating risk aversion. Section 3 describes our data, while Section 4 details our tests of the assumption that relative risk aversion is constant in wealth. Having established some empirical support for the CRRA assumption, Section 5 presents our estimates from various Euler equation models derived from the CRRA assumption. Section 6 provides some conclusions and areas where further research would be useful in the Australian context.
2 Background
Given the fundamental interest around risk aversion and its importance in economic modelling, an extensive body of empirical research attempts to quantify the degree of risk aversion among households. Although there are a number of possible ways to proceed,3 this paper follows the `Euler equation' approach pioneered in Hall (1978). In basic terms, this approach exploits the relationship between consumption and interest rates derived from the household's intertemporal optimisation problem to uncover the risk aversion parameter in the household's underlying utility function.
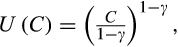 where
where
 is consumption and
is consumption and
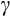 is the coefficient of relative risk aversion. A particular advantage of CRRA preferences is that they imply an empirically tractable Euler equation,
is the coefficient of relative risk aversion. A particular advantage of CRRA preferences is that they imply an empirically tractable Euler equation,
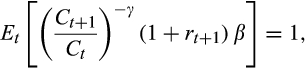 (1)
(1)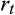 is the return on a generic asset at time
is the return on a generic asset at time
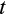 ,
,
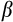 is the household's discount factor, and the expectation operator
is the household's discount factor, and the expectation operator
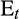 indicates that the household's consumption decision takes place in an environment where the value of future variables (such as earnings) is uncertain.
indicates that the household's consumption decision takes place in an environment where the value of future variables (such as earnings) is uncertain.CRRA preferences have a number of other desirable properties, which have made them a popular specification in models of intertemporal consumption decisions under uncertainty. This includes the convenient feature that the standard (Arrow–Pratt) measure of relative risk aversion is constant in wealth and given directly by
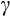 ,4 while the EIS is also constant and equal to 1/
,4 while the EIS is also constant and equal to 1/
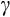 .5 CRRA preferences also have a number of economically appealing aspects, including the presence of `prudence', which gives rise to a precautionary (or `buffer stock') savings motive when households face future income uncertainty.6
.5 CRRA preferences also have a number of economically appealing aspects, including the presence of `prudence', which gives rise to a precautionary (or `buffer stock') savings motive when households face future income uncertainty.6
The Euler equation approach that we use was initially discredited in the early 2000s in the US literature because it generally failed to deliver consistent and reliable estimates of
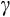 and
and
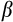 despite the large number of studies (Carroll, 2001a). This disappointing performance was attributed to a number of factors including measurement error in consumption data and difficulty in finding suitable instruments for the endogenous variables, especially in the case of the log-linearised Euler equation as explained below.
despite the large number of studies (Carroll, 2001a). This disappointing performance was attributed to a number of factors including measurement error in consumption data and difficulty in finding suitable instruments for the endogenous variables, especially in the case of the log-linearised Euler equation as explained below.
More recently, lengthening panel data sets, improved availability of consumption data, and analytical refinements have allowed estimation of
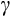 and
and
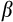 , using the Euler equation approach, in a more precise way. For example, Alan et al. (2009) derive a generalised method of moments (GMM) panel estimator that explicitly allows for measurement error in consumption data, while Alan et al. (2018) show that synthetic panel data based on repeated cross-sections can overcome the endogeneity problems given a long enough time dimension.7
, using the Euler equation approach, in a more precise way. For example, Alan et al. (2009) derive a generalised method of moments (GMM) panel estimator that explicitly allows for measurement error in consumption data, while Alan et al. (2018) show that synthetic panel data based on repeated cross-sections can overcome the endogeneity problems given a long enough time dimension.7
Following these recent refinements in the international literature, we provide Euler equation-based estimates of
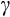 for Australia using data from the HILDA Survey. Based upon empirical research and simulation studies from other countries, the HILDA data are only now becoming long enough to support this kind of analysis, with around 14 years considered to be the minimum required panel length se Attanasio and Low (2004) and Alan et al. (2009).
for Australia using data from the HILDA Survey. Based upon empirical research and simulation studies from other countries, the HILDA data are only now becoming long enough to support this kind of analysis, with around 14 years considered to be the minimum required panel length se Attanasio and Low (2004) and Alan et al. (2009).
While CRRA preferences are a convenient assumption, they impose a restriction on the relationship between risk aversion and wealth, namely that relative risk aversion is constant with respect to a household's level of wealth. In fact, the empirical support for this form of preferences is not overwhelming, in part because there are relatively few studies that have formally tested the CRRA assumption.8, Chiappori and Paiella (2011) and Tsigos and Daly (2016) Therefore, we undertake an initial test of whether the CRRA assumption is in fact a good one for Australian households, using an approach based on a household's share of risky assets, similar to that in Chiappori and Paiella (2011) and Tsigos and Daly (2016) (the latter being a recent Australian study). Once we account for endogeneity in risk aversion and wealth as well as measurement error (which we show is crucial in such regressions), we cannot reject the CRRA assumption.9 While constant for a particular household over time, our analysis reveals considerable variation in relative risk aversion between households, with a median
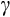 of 1.8.10 As a cross-check, we find that the distribution of this `objective' measure of risk aversion is significantly correlated with the two subjective measures of risk aversion contained in the HILDA Survey.
of 1.8.10 As a cross-check, we find that the distribution of this `objective' measure of risk aversion is significantly correlated with the two subjective measures of risk aversion contained in the HILDA Survey.
We next turn to a detailed description of our data and sample selection.
3 Data
The HILDA Survey began in 2001 and provides annual data on a broad range of economic and social topics. The samples used in all components of our analysis comprise household heads of working age. A head is defined as the oldest male member of a household, or the oldest female in households without a male adult.
Our definition of household head is not important for the results presented below. We identify a `household head' so that we can follow individuals over time using the xwaveid variable in HILDA. The analysis is based upon household-level data, so choice of head is rather arbitrary. In our Euler equation estimates below we only use couples who stay together, so choosing the female as the head of household does not alter the results. We have verified this using alternative definitions of household head and the results presented below are unchanged.
We use the sum of expenditure on groceries and meals out as a proxy for household consumption.11 Unlike other components of household expenditure, information on these components has been collected in almost all years of the survey.12 Just as importantly, the data quality of these items is probably higher than other components of expenditure in the HILDA Survey (Wilkins & Sun, 2010), although they still contain significant measurement error, as we quantify in Appendix IV. These nominal series are deflated using state-specific consumer price indices for food.
Because of differing data requirements, the samples used in our risky asset share and Euler equation estimates differ in a number of key respects, as we now describe.13 Table A3 in Appendix I provides descriptive statistics for the sample that we use for the risky asset regression. These descriptive statistics are pooled across the four waves that contain information from the wealth module. In the second part of Table A4, we consider the sample of those who have positive risky assets who also have a university education. While those with a university education hold more risky assets, the ratio of risky assets to financial assets is not very different for those with and without a university education.14
3.1 Risky Asset Share Regressions
The risky asset share regressions rely on HILDA's wealth module, which is included in only four survey years: 2002, 2006, 2010 and 2014. The sample is based on an unbalanced panel of these four years consisting of all responding household heads between ages 23 and 59 inclusive.
In the base model, risky assets are defined narrowly as equities, to allow comparability with the two existing Australian studies, although we consider broader definitions of risky assets in extended models. The regressions only include households with positive risky assets (however defined), and those with information on household size and age of household head.15 The mean value of the risky asset share is 16 per cent, based on the narrow definition of risky assets. The instrumental variable (IV) regressions also require non-missing data on the instruments, that is, household disposable income and household consumption (which we again proxy using expenditure on groceries and meals out).
3.2 Consumption Euler Equations
Again, our Euler equation analysis uses grocery and meals out expenditure as a proxy for overall household consumption, an approach also adopted in most overseas studies.16 The panel encompasses the period 2001–16 inclusive, except for 2002 when information on expenditure was not collected in HILDA.
Our sample selection choices closely follow Alan et al. (2009) to aid comparability with that study. We restrict the sample to households consisting of couples who were in a stable relationship over the period in which they feature in the survey. To restrict the sample to working-age households, we exclude households with heads aged under 22 in the first year of the survey and households with heads aged over 60 in the last year of the survey (2016). Also, because the Euler equation only holds for an interior solution, we exclude households who are liquidity constrained, which we define as having zero financial assets in any of the years they feature in the panel. In other words, if they ever report having zero financial assets in one of the wealth module years, they are dropped from all years of the analysis. The latter restriction removes only 36 observations. The real interest rate series is calculated as the annual average nominal 3-month bank accepted bill rate less inflation expectations pertaining to that period.17
4 Testing the CRRA Assumption Using Share of Risky Assets
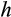 's relative risk aversion,
's relative risk aversion,
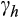 ,
,
 (2)
(2)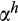 is the risky asset share,
is the risky asset share,
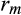 is the return on the risky asset,
is the return on the risky asset,
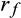 is the risk free rate and
is the risk free rate and
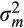 is the variance of the return on the risky asset.
is the variance of the return on the risky asset.However, they also formally demonstrate that cross-sectional wealth data alone are insufficient to test whether relative risk aversion is constant. This is because the distribution of risky asset share in the population depends on the joint distribution of wealth and risk aversion, not just the form of preferences (Chiappori & Paiella, 2011). For example, if risk aversion is heterogeneous across the population, it is reasonable to expect that less risk-averse people will earn, on average, higher returns and accumulate greater wealth over time. This would lead to a negative correlation between relative risk aversion (measured by risky asset share) and wealth cross-sectionally, even when the underlying preferences were CRRA. Chiappori and Paiella (2011) show that panel data can overcome this problem, by allowing one to test whether relative risk aversion varies with wealth for a particular household.
In Australia, Tsigos and Daly (2016) test the relative risk aversion assumption using HILDA wealth data. Using a different measure of relative risk aversion (based on observed portfolio weights for each household), Tsigos and Daly find a negative correlation between risk aversion and wealth. However, they find no relationship between relative risk aversion and wealth when they instead use risky asset share as their measure of risk as in Chiappori and Paiella (2011). In contrast, Cardak and Wilkins (2009) find a small positive relationship between risky asset share and wealth. Their study was also based on the HILDA Survey, but they only had access to a single cross-section of wealth data (for 2002) that was available at the time.
Given the mixed findings in Australia, we retest the question of whether relative risk aversion varies with wealth. Compared to the previous Australian studies by Cardak and Wilkins and Tsigos and Daly, we benefit from an additional three waves and one wave of data, respectively. In particular, this allows us to use the panel dimension of the HILDA Survey, which was unavailable to Cardak and Wilkins. We follow the measure of risk aversion used in Chiappori and Paiella and Cardak and Wilkins based on risky asset shares. Strictly, we could have a set of households that are infinitely risk averse and others that have finite risk aversion. Our test is whether risk aversion varies with wealth across those households with finite risk aversion (see footnote 15).
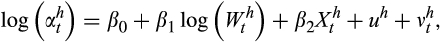 (3)
(3)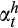 is the share of risky assets for household
is the share of risky assets for household
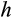 at time
at time
 ,
,
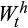 is total financial wealth,
is total financial wealth,
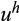 is a fixed effect and
is a fixed effect and
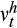 is a random error term. To control for the likely endogeneity between risky asset share and wealth, we also estimate the equation in first differences (FD) which eliminates the possible bias from
is a random error term. To control for the likely endogeneity between risky asset share and wealth, we also estimate the equation in first differences (FD) which eliminates the possible bias from
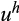 :
:
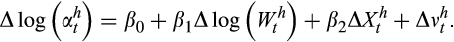 (4)
(4)As pointed out in Chiappori and Paiella, measurement error in the wealth data can also result in biased estimates of the relationship between risk aversion and wealth if not adequately dealt with. This is because total financial wealth is the denominator of the dependent variable and therefore appears on both sides of Equation (4). We show in Appendix III that for a mean risky asset share of <50 per cent, standard multiplicative measurement error in the wealth data will result in moderate to severe downward bias in estimates of
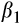 , given plausible values for the variance of the measurement error.18 To address the problem of measurement error, we instrument wealth with disposable household income and food consumption in the levels equation. Similarly, we use growth in disposable income and growth in consumption as instruments for wealth in the FD equation. Our final specification also includes year dummies (to control for macroeconomic effects) and controls for household composition and age.
, given plausible values for the variance of the measurement error.18 To address the problem of measurement error, we instrument wealth with disposable household income and food consumption in the levels equation. Similarly, we use growth in disposable income and growth in consumption as instruments for wealth in the FD equation. Our final specification also includes year dummies (to control for macroeconomic effects) and controls for household composition and age.
4.1 Results
As suspected, the estimated relationship between risky asset share and wealth is sensitive both to whether we use IVs to adjust for the impact of measurement error and to whether the model is estimated in levels or FDs (Table 1). The basic ordinary least squares (OLS) regression in levels (column 1) shows a strong and highly significant negative relationship (
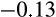 ) between risky asset share and wealth. However, once we adjust for the impact of measurement error by instrumenting for wealth, the coefficient on wealth falls in magnitude and becomes insignificant (column 2). As we argued above, there are good reasons to think that measurement error would contribute to a negative cross-sectional relationship even when none truly exists when the mean risky asset share is <50 per cent.19 Column 3 re-estimates the basic model in FDs. The coefficient on wealth is again negative, but is very imprecisely estimated and not significantly different from zero at standard confidence levels.
) between risky asset share and wealth. However, once we adjust for the impact of measurement error by instrumenting for wealth, the coefficient on wealth falls in magnitude and becomes insignificant (column 2). As we argued above, there are good reasons to think that measurement error would contribute to a negative cross-sectional relationship even when none truly exists when the mean risky asset share is <50 per cent.19 Column 3 re-estimates the basic model in FDs. The coefficient on wealth is again negative, but is very imprecisely estimated and not significantly different from zero at standard confidence levels.
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| OLS Level | IV Level | OLS FD | IV FD | IV FD | IV FD | |
| Risky assets: numerator denominator | E | E | E | E | E + C+T | E + C+T + BE+S |
| FA | FA | FA | FA | FA | FA + BE+S | |
| Total Financial Assets† | −0.128 (0.0122) | −0.047 (0.0452) | −0.313 (0.0191) | −0.173 (0.139) | −0.226 (0.1355) | −0.033 (0.0222) |
| Year dummies | ||||||
| 2006 | −0.056 (0.0405) | −0.08 (0.042) | ||||
| 2010 | −0.229 (0.0437) | −0.248 (0.0451) | −0.157 (0.0642) | −0.136 (0.0664) | −0.099 (0.0658) | −0.012 (0.0138) |
| 2014 | −0.363 (0.0463) | −0.391 (0.0481) | −0.168 (0.0677) | −0.161 (0.069) | −0.166 (0.0684) | −0.024 (0.0135) |
| HH size | −0.205 (0.0409) | −0.218 (0.0418) | −0.258 (0.0759) | −0.342 (0.1018) | −0.211 (0.0965) | 0.035 (0.0195) |
| Age | 0.076 (0.0186) | 0.077 (0.0189) | 0.015 (0.0303) | 0.012 (0.0319) | 0.008 (0.0312) | 0.007 (0.0056) |
| Age squared | −0.081 (0.0215) | −0.085 (0.0219) | −0.025 (0.0371) | −0.022 (0.0388) | −0.018 (0.0381) | −0.01 (0.0071) |
| Constant | −1.415 (0.3946) | −2.199 (0.5738) | −0.16 (0.6024) | −0.127 (0.6331) | 0.029 (0.6161) | −0.055 (0.1064) |
| N | 6,952 | 6,849 | 3,111 | 3,070 | 3,245 | 10,408 |
- Standard errors, clustered at the household level, in parentheses.
- E = Equities; C = Cash investments; T = Trusts; BE = Business equity; S = Superannuation; FA = Financial assets = E+C + T+ Bank accounts.
- † Equal to denominator used to calculate risky asset share.
Columns 4 and 5 experiment with expanded definitions of risky assets. Column 4 adds cash investments (bonds and the like) and trusts to the measure of risky assets, while the regression in column 5 additionally includes business equity and superannuation. In the latter regression, the denominator is also adjusted to include business equity and superannuation. The coefficient on wealth remains insignificant, although it continues to be negative.
Given the difference between the OLS and IV estimates, we explore whether the results are robust to alternative instruments for wealth. One obvious alternative instrument for change in wealth is the cumulative difference between disposable income and consumption in the intervening periods between observations on wealth. In other words, this utilises income and consumption data in years that did not contain a wealth module in HILDA. For example, for 2006 we subtract cumulative food consumption from cumulative disposable income for each household over the period 2002–6, which yields a `flow' measure of change in wealth. When we use this variable as the instrument in models 3–5, the key results are unaffected.
We also conduct a weak instruments test, and find that our chosen instruments are well correlated with financial wealth and change in financial wealth.20 A test of overidentifying restrictions fails to reject the null hypothesis that the chosen instruments are exogenous for models 3–5, but does reject the null for model 2.21 We also try including labour force participation as a component of
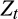 , and use its lag as an instrument. This addition does not affect the main results in Table 1.
, and use its lag as an instrument. This addition does not affect the main results in Table 1.
4.2 Comparison with Tsigos and Daly's Results
In finding no significant relationship between risky asset share and wealth, our results confirm the results from Tsigos and Daly 's sensitivity analysis but contradict their main result. However, their main result (that relative risk aversion falls with wealth) is based on a different measure of risk that uses portfolio weights calculated using external information on asset returns. Tsigos and Daly do not attempt to explain why the two approaches yield different results in their paper. It is also worth noting that, compared with Tsigos and Daly, our test of the relationship between risk aversion and wealth benefits from an extra year of wealth data, giving our test additional power.
While we are unable to reject the CRRA assumption, the estimated coefficient on wealth is negative in all six specifications, albeit insignificant in four cases. We therefore view our results as providing tentative support for the CRRA, particularly given that the insignificant estimates only arise in the IV regressions. Additional years of HILDA data going forward will help us to work out whether risk aversion really is constant with respect to wealth or not.
4.3 Distribution of Implied Relative Risk Aversion Parameter
Equation (2) can be used to calculate the distribution of
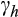 across the population. However, as Chiappori and Paiella (2011) note, this distribution is only identified up to a scale factor, given by the ratio of the excess return to the variance of the risky portfolio,
across the population. However, as Chiappori and Paiella (2011) note, this distribution is only identified up to a scale factor, given by the ratio of the excess return to the variance of the risky portfolio,
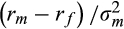 . Taking the case where this ratio is equal to
. Taking the case where this ratio is equal to
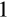 , as in Chiappori and Paiella (2011), the value of
, as in Chiappori and Paiella (2011), the value of
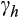 is just the inverse of the risky asset ratio for investor h. Clearly, the derived value of
is just the inverse of the risky asset ratio for investor h. Clearly, the derived value of
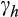 will depend inversely on the definition of ‘risky asset', and will be higher or lower for narrower and broader definitions, respectively. Additionally, very small values of
will depend inversely on the definition of ‘risky asset', and will be higher or lower for narrower and broader definitions, respectively. Additionally, very small values of
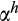 will result in very large values of
will result in very large values of
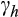 . Following Chiappori and Paiella, we therefore truncate the distribution of risky asset shares to exclude values <6 per cent and compute the median rather than mean value. The median estimates of
. Following Chiappori and Paiella, we therefore truncate the distribution of risky asset shares to exclude values <6 per cent and compute the median rather than mean value. The median estimates of
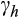 are 1.1, 2.2 and 2.4 across the three definitions of risky assets used in our regressions. We also find little evidence that
are 1.1, 2.2 and 2.4 across the three definitions of risky assets used in our regressions. We also find little evidence that
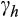 varies by wealth. Table B1 in Appendix II contains further details.
varies by wealth. Table B1 in Appendix II contains further details.
4.4 Correlation with Subjective Data on Risk Aversion
An interesting question is whether the risk aversion measure derived from risky asset shares correlates with subjective measures of risk aversion contained in the HILDA Survey. In particular, the two separate survey questions ask respondents to indicate the degree of financial risk they are prepared to take.22 The risky asset share is significantly correlated with both subjective measures, with a correlation coefficient of
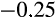 for one subjective measure (which measures risk aversion) and
for one subjective measure (which measures risk aversion) and
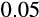 . for the second measure (which measures risk appetite). Both are statistically significant.
. for the second measure (which measures risk appetite). Both are statistically significant.
5 Estimates of Risk Aversion Using a Consumption Euler Equation
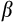 and an interest rate
and an interest rate
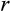 , the Euler equation linking consumption in period
, the Euler equation linking consumption in period
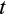 to consumption in period
to consumption in period
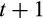 for household
for household
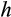 is
is
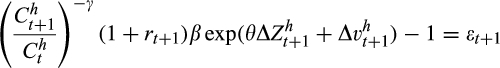 (5)
(5)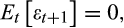 (6)
(6)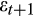 , is equal to 0 for a given household over time rather than for the cross-section.
, is equal to 0 for a given household over time rather than for the cross-section.Two other points about Equation (5) are worth making. First, this condition holds only for an interior solution for consumption, and will generally not hold for households subject to binding borrowing constraints. Second, Equation (5) is derived on the assumption that consumption and leisure are additively separable in the hsousehold's utility function. As a sensitivity test of our main results, we also consider the case where consumption and leisure are non-separable.
5.1 Exact Nonlinear Equation Versus the Linearised Version
Previous studies have typically proceeded in one of two ways: estimating the exact, nonlinear Euler equation as it appears in Equation (5) using GMM; or taking a first- or higher-order linear approximation of the Euler equation and using OLS or linear IV estimation. Both approaches have drawbacks.
To begin with, both approaches require instruments for the model's endogenous variables: consumption growth and the interest rate. In the nonlinear case, economic theory implies that any variables in the consumer's information set at time
 are valid instruments, including lags of consumption growth and the interest rate. However, Carroll (2001a) and Alan et al. (2009)) show that estimates based on the exact nonlinear equation are biased when the consumption data contain measurement error, which is almost certainly the case in practice. These studies suggest that estimates of
are valid instruments, including lags of consumption growth and the interest rate. However, Carroll (2001a) and Alan et al. (2009)) show that estimates based on the exact nonlinear equation are biased when the consumption data contain measurement error, which is almost certainly the case in practice. These studies suggest that estimates of
 will be particularly biased in the presence of measurement error, and this bias does not improve with a longer panel length Attanasio and Low (2004);Alan et al. (2009)).
will be particularly biased in the presence of measurement error, and this bias does not improve with a longer panel length Attanasio and Low (2004);Alan et al. (2009)).
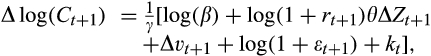 (7)
(7)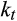 includes higher-order terms remaining from the approximation process.
includes higher-order terms remaining from the approximation process.The problem is that the composite error term is now likely to be correlated with consumption growth and interest rates via the higher-order terms in
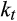 . Carroll (2001a) shows that these high-order terms are inherently endogenous in a standard model of life-cycle consumption behaviour with wage uncertainty, and that estimates of
. Carroll (2001a) shows that these high-order terms are inherently endogenous in a standard model of life-cycle consumption behaviour with wage uncertainty, and that estimates of
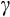 will be severely biased. A further disadvantage of using Equation (7) is that
will be severely biased. A further disadvantage of using Equation (7) is that
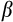 can no longer be recovered as it is subsumed into the constant along with the mean values of the measurement error and approximation errors.
can no longer be recovered as it is subsumed into the constant along with the mean values of the measurement error and approximation errors.
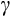 and
and
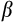 even in panels of only moderate length (that is, around 15 years of data). Each of these studies essentially proceeds by assuming that true consumption (
even in panels of only moderate length (that is, around 15 years of data). Each of these studies essentially proceeds by assuming that true consumption (
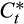 ) is subject to independent and identically log-normally distributed measurement error
) is subject to independent and identically log-normally distributed measurement error
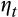 with equal variance
with equal variance
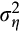 across households, such that
across households, such that
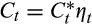 . The modified Euler equation is
. The modified Euler equation is
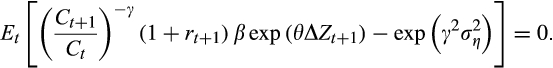 (8)
(8)While this single moment equation does not allow
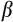 and
and
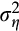 to be separately identified, Alan et al. (2009) show that an analogous moment condition for two-period-apart consumption
to be separately identified, Alan et al. (2009) show that an analogous moment condition for two-period-apart consumption
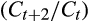 can be used to identify
can be used to identify
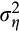 (and therefore
(and therefore
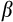 ).
).
Alternatively, Alan et al. (2018) show that relatively precise estimates of
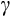 can be obtained using the linearised model if a long enough time series on consumption is available. However, their paper suggests that `long enough' equates to perhaps 40 years of data, a requirement that few if any panel surveys satisfy. As a practical alternative, they show that a synthetic panel formed from repeated cross-sectional surveys over a long enough period can deliver reliable estimates of
can be obtained using the linearised model if a long enough time series on consumption is available. However, their paper suggests that `long enough' equates to perhaps 40 years of data, a requirement that few if any panel surveys satisfy. As a practical alternative, they show that a synthetic panel formed from repeated cross-sectional surveys over a long enough period can deliver reliable estimates of
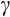 using the linearised Euler equation.
using the linearised Euler equation.
5.2 Our Approach
With (at most) 15 years of available consumption data in the HILDA Survey, we opt for GMM on the exact nonlinear Euler equation, allowing for measurement error in our preferred specifications. For reference, we also obtain an estimate of
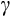 from a linearised version of the model, noting the caveats above in relation to biased estimates in small panels such as ours.
from a linearised version of the model, noting the caveats above in relation to biased estimates in small panels such as ours.
In dealing with measurement error, we consider two approaches. As we use a single moment equation, neither approach allows us to separately identify the discount rate
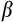 and the variance of the measurement error
and the variance of the measurement error
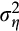 without further moment conditions or an `external' estimate of
without further moment conditions or an `external' estimate of
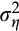 .24 In the first approach, we estimate a single parameter, which is some unknown combination of
.24 In the first approach, we estimate a single parameter, which is some unknown combination of
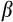 and
and
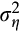 . In the second approach, we use separate estimates of the variance of the measurement error
. In the second approach, we use separate estimates of the variance of the measurement error
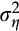 , which enables us to recover an estimate of
, which enables us to recover an estimate of
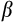 . This analysis is reported in Appendix IV.
. This analysis is reported in Appendix IV.
The vector
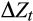 can in principle consist of any variables that may affect the marginal utility of consumption, including endogenous variables such as labour supply choices (Attanasio & Low, 2004). While we experiment with other variables, our final specification for
can in principle consist of any variables that may affect the marginal utility of consumption, including endogenous variables such as labour supply choices (Attanasio & Low, 2004). While we experiment with other variables, our final specification for
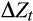 only includes change in household size as in Alan et al. (2009). Changes in household size should have a large and direct effect on marginal utility, and this has been confirmed empirically (Attanasio & Low, 2004. We also include a 2008 year dummy in some specifications. This dummy would capture a possible structural break in the relationship between consumption growth and interest rates that may have occurred with the onset of the global financial crisis (GFC).
only includes change in household size as in Alan et al. (2009). Changes in household size should have a large and direct effect on marginal utility, and this has been confirmed empirically (Attanasio & Low, 2004. We also include a 2008 year dummy in some specifications. This dummy would capture a possible structural break in the relationship between consumption growth and interest rates that may have occurred with the onset of the global financial crisis (GFC).
5.3 Empirical Model
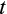 (where the household superscript has been suppressed) whose sample counterparts are used in GMM estimation:
(where the household superscript has been suppressed) whose sample counterparts are used in GMM estimation:
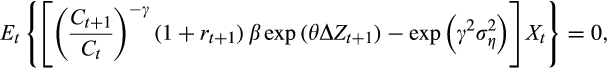 (9)
(9)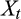 is the set of instruments at time
is the set of instruments at time
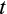 , as described in the next section.
, as described in the next section.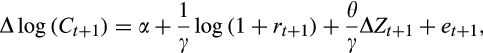 (10)
(10)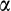 now includes
now includes
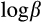 as well as the means of the higher-order approximation errors, and
as well as the means of the higher-order approximation errors, and
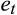 now includes the household's expectational error, the measurement error and the time-varying components of the approximation error.
now includes the household's expectational error, the measurement error and the time-varying components of the approximation error.5.4 Choice of Instruments
We follow many previous studies in using lags of the interest rate (in addition to a constant) and consumption growth as instruments in our nonlinear GMM estimation. There are a number of reasons why these are likely to be good instruments. First, rational expectations suggests that lagged variables, which are known to the household at time
 , will be uncorrelated with their forecast error the following period. Second, consumption and interest rates tend to be adequately correlated with lags of themselves, avoiding the problem of `weak instruments'. Finally, simulation exercises have shown that they are valid in a standard life-cycle model environment (Alan et al., 2009). We also use change in household size as an instrument for itself, and do likewise with the 2008 year dummy where present. We also experiment with dropping lagged consumption growth from our instrument list (see column 4 in Table D1). This leaves the lagged interest rate and a constant to identify the two parameters of interest,
, will be uncorrelated with their forecast error the following period. Second, consumption and interest rates tend to be adequately correlated with lags of themselves, avoiding the problem of `weak instruments'. Finally, simulation exercises have shown that they are valid in a standard life-cycle model environment (Alan et al., 2009). We also use change in household size as an instrument for itself, and do likewise with the 2008 year dummy where present. We also experiment with dropping lagged consumption growth from our instrument list (see column 4 in Table D1). This leaves the lagged interest rate and a constant to identify the two parameters of interest,
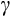 and
and
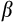 , which is essentially the just-identified model applied in (Alan et al., 2009). Because the linearised model is a log transformation of the true model, we substitute log versions of the instruments used in the nonlinear equation.25
, which is essentially the just-identified model applied in (Alan et al., 2009). Because the linearised model is a log transformation of the true model, we substitute log versions of the instruments used in the nonlinear equation.25
All estimates of the nonlinear model are based on a standard two-step GMM with robust weight matrix. Estimation based on an alternative weight matrix, such as iterative GMM, had very little impact on the results. The linearised model is also estimated using (linear) GMM.
5.5 Allowing for Non-separable Consumption and Leisure
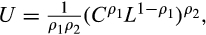 where
where
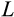 is leisure. Here, the coefficient of relative risk aversion is a combination of both utility parameters and is given by
is leisure. Here, the coefficient of relative risk aversion is a combination of both utility parameters and is given by
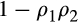 . The resulting Euler equation is
. The resulting Euler equation is
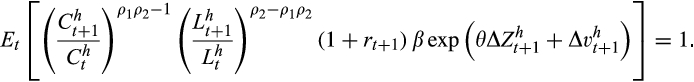 (11)
(11)5.6 Results
The GMM point estimates of
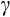 range from 1.19 to 1.39 across the four separable specifications tested; see Table 2. This equates to an estimated EIS of between 0.74 and 0.84. In the context of Euler equation-based studies, the GMM estimates are relatively precise, with standard errors between around 0.17 and 0.24.27 The estimate for
range from 1.19 to 1.39 across the four separable specifications tested; see Table 2. This equates to an estimated EIS of between 0.74 and 0.84. In the context of Euler equation-based studies, the GMM estimates are relatively precise, with standard errors between around 0.17 and 0.24.27 The estimate for
 of 2.38 from the linearised Euler equation is quite a bit higher than the GMM estimates, but is very imprecise. This specific finding is very similar to that in (Alan et al., 2009) using PSID data. Their simulation exercise in the same study highlights that estimates of
of 2.38 from the linearised Euler equation is quite a bit higher than the GMM estimates, but is very imprecise. This specific finding is very similar to that in (Alan et al., 2009) using PSID data. Their simulation exercise in the same study highlights that estimates of
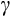 based on linearised models are prone to severe biases in cases where the time dimension is <3s 0 years or so (see also Attanasio and Low (2004)).
based on linearised models are prone to severe biases in cases where the time dimension is <3s 0 years or so (see also Attanasio and Low (2004)).
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Log. Lin. | EGMM | EGMM | EGMM | EGMM | EGMMn | |
Coeff. of relative risk aversion (
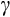 ) ) |
2.381 (1.097) | 1.368 (0.166) | 1.289 (0.202) | 1.392 (0.236) | 1.186 (0.199) | 2.251 (0.73) |
| Discount factor (β) | 0.92 (0.062) | 0.961 (0.023) | ||||
| β/Meas'nt error in consumption† | 0.759 (0.065) | 0.804 (0.082) | 0.737 (0.228) | |||
Household size (
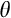 ) ) |
0.529 (0.246) | 0.362 (0.07) | 0.334 (0.077) | 0.381 (0.094) | 0.298 (0.069) | 1.455 (1.112) |
| 2008 dummy | −0.075 (0.011) | −0.070 (0.051) | ||||
| Constant | 0.007 (0.003) | |||||
| Inflation measure for real interest rate instruments‡ | Survey | Survey | Survey | Survey | Bond M. | Survey |
| Lagged interest rate | Yes | Yes | Yes | Yes | Yes | Yes |
| Lagged consumption growth | No | Yes | Yes | No | Yes | Yes |
- EGMM = exact GMM; EGMMn = exact GMM with non-separable preferences.
- Standard errors in parentheses.
- † Measurement error variance set to 80 per cent of variance in consumption growth, consistent with our findings in Appendix IV.
- ‡ The set of instruments also includes a constant in all equations, as well change in HH size and the GFC dummy where present for columns (1) to (5). Lagged changes in household leisure time, and age and age-squared of the household head are also included for the model in column (6).
As noted above,
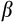 and
and
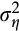 are not separately identifiable without further assumptions (or additional moment conditions). In models 4 and 5, we assume that measurement error accounts for 80 per cent of the overall variance in consumption growth, a proportion guided by our separate estimates in Table D1. Given the variance in the Australian consumption data, this implies a measurement error variance of around 0.095 and yields estimates for
are not separately identifiable without further assumptions (or additional moment conditions). In models 4 and 5, we assume that measurement error accounts for 80 per cent of the overall variance in consumption growth, a proportion guided by our separate estimates in Table D1. Given the variance in the Australian consumption data, this implies a measurement error variance of around 0.095 and yields estimates for
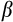 between 0.92 and 0.96 across two specifications.
between 0.92 and 0.96 across two specifications.
The coefficient on change in household size ranges from 0.3 to 0.4 for the exact GMM estimation based on separable preferences and is statistically significant across all four specifications. This suggests that family size has an important effect on consumption growth, a standard finding in the life-cycle consumption literature (see Attanasio (1999)).
In the non-separable model, we estimate a coefficient of relative risk aversion of 2.25 (column 6). While somewhat higher than the separable model estimates, the much larger standard error indicates no statistically significant difference from the separable estimates at standard confidence levels.
We run a series of tests to check the sensitivity of our results to sample selection. We find that the exclusion of consumption growth outliers has very little impact on the results, as does introducing a requirement that a respondent appears in at least five consecutive waves (as per Alan et al., 2009)). However, we find that including households whose head has begun or ended a marriage or de facto relationship during their time in the panel leads to implausibly low estimates of
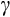 (well below 1) and instability in the GMM estimation procedure. In column 5, we experiment with an alternative real interest rate series, which is calculated using the inflation rate derived from market pricing of inflation-linked bonds. This leads to an only slightly lower estimate of
(well below 1) and instability in the GMM estimation procedure. In column 5, we experiment with an alternative real interest rate series, which is calculated using the inflation rate derived from market pricing of inflation-linked bonds. This leads to an only slightly lower estimate of
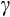 .
.
Food consumption measurement was changed in HILDA from 2006 (see footnote 3). Therefore, as an additional robustness check we re-estimated Table 1 using data from 2006 onwards. A major problem with this is that the shorter time period makes estimation more difficult. Estimates for the coefficient of relative risk aversion (
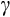 ) in columns 2–5 are slightly larger but statistically identical: 1.47, 1.45, 1.39 and 1.29. The estimation algorithm failed to converge for column 6, demonstrating the difficulty of estimating with a shorter panel. The estimate for column 1 was somewhat larger, at 2.77, but would be unreliable for the reasons already discussed.
) in columns 2–5 are slightly larger but statistically identical: 1.47, 1.45, 1.39 and 1.29. The estimation algorithm failed to converge for column 6, demonstrating the difficulty of estimating with a shorter panel. The estimate for column 1 was somewhat larger, at 2.77, but would be unreliable for the reasons already discussed.
We removed households that were liquidity constrained on the basis of having no financial assets as described in Section 3 above. Another option would be to remove households who report difficulty in raising funds for an emergency. We use a question from HILDA about how difficult it would be to raise $2,000 ($3,000 after 2008) in an emergency. We drop households who indicate that they ‘couldn’t raise the funds’ or that it would require ‘something drastic’. This definition of `liquidity constrained' results in our dropping 4,831 households, many more than what we presented above in our preferred approach. However, our results are not materially affected. The estimates for columns 2–6 of Table 1 are 1.36, 1.27, 1.37, 1.16 and 2.03, none of which are statistically different than what is reported in our main estimation.
5.7 Comparison with International Estimates
Overall, our point estimates of
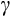 for Australia based on the nonlinear Euler equation are within the range of recent estimates obtained in the USA.28 In the most comparable US study, Alan et al. (2009) shows GMM estimates of
for Australia based on the nonlinear Euler equation are within the range of recent estimates obtained in the USA.28 In the most comparable US study, Alan et al. (2009) shows GMM estimates of
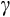 ranging from 1.15 to 1.53 using data from the PSID, with a preferred point estimate of 1.45.29 Our estimates of
ranging from 1.15 to 1.53 using data from the PSID, with a preferred point estimate of 1.45.29 Our estimates of
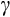 are also within the range of estimates found in Gourinchas and Parker (2002), who use the quite different approach of simulated method of moments. However, as noted earlier, these moderate estimates of
are also within the range of estimates found in Gourinchas and Parker (2002), who use the quite different approach of simulated method of moments. However, as noted earlier, these moderate estimates of
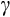 contrast with the very high values needed to explain the large equity premium in the USA (Kocherlakota, 1996).
contrast with the very high values needed to explain the large equity premium in the USA (Kocherlakota, 1996).
5.8 Caveats
We use the combination of food purchased at home, non-food grocery items and meals eaten out as a proxy for overall consumption. We then calculate the EIS with respect to food expenditure. This will only be an unbiased estimate of the overall EIS if within-period preferences are homothetic Browning and Crossley (2000).
As a necessity, food consumption has an income elasticity below
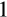 , violating the homotheticity requirement. We have tried to mitigate this somewhat through the combination of food purchased for consumption at home (which definitely has an income elasticity below
, violating the homotheticity requirement. We have tried to mitigate this somewhat through the combination of food purchased for consumption at home (which definitely has an income elasticity below
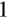 ) with non-food grocery items purchased at grocery stores and meals eaten out which are usually found to have an income elasticity greater than
) with non-food grocery items purchased at grocery stores and meals eaten out which are usually found to have an income elasticity greater than
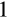 .
.
We ran a few simple regressions in our data and found an income elasticity of 0.72 for our combined measure. So, although it is less than unity, it is much closer to unity than standard income elasticity estimates for food consumption purchased to be eaten at home.
When we looked at the relationship between wealth and the share of risky assets, we found some heterogeneity in the distribution of
 across the population. This does pose some challenge for our GMM estimation of the Euler equation, where
across the population. This does pose some challenge for our GMM estimation of the Euler equation, where
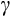 is assumed to be common across households. While pooled estimates are often conducted in economics across sub-populations with different parameter values, it is will known (going back at least DuMouchel and Duncan (1983)) that such pooled regressions do not produce population- or sample-weighted averages of parameters.
is assumed to be common across households. While pooled estimates are often conducted in economics across sub-populations with different parameter values, it is will known (going back at least DuMouchel and Duncan (1983)) that such pooled regressions do not produce population- or sample-weighted averages of parameters.
Alan et al. (2012) look at the performance of linearised Euler equation estimates when
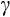 takes two different values across households. They find that the estimated value of
takes two different values across households. They find that the estimated value of
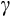 is roughly the mean of the two values. Theirs is a very stylised situation.
is roughly the mean of the two values. Theirs is a very stylised situation.
All that we can conclude is that potential heterogeneity in
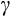 is an additional source of uncertainty for our estimates.
is an additional source of uncertainty for our estimates.
This also raises some questions about the instruments used in our risky assets regression. Looking back at Equation (2), if the returns process is common across households, then heterogeneity in shares must be driven by heterogeneity in
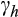 . That heterogeneity will end up in the error term in Equation (3), but this invalidates the instrument in the levels equation since the growth rate of consumption and the error term will both depend upon
. That heterogeneity will end up in the error term in Equation (3), but this invalidates the instrument in the levels equation since the growth rate of consumption and the error term will both depend upon
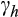 . So despite the result from the overidentification test for column 3 of Table 1, we prefer the first-difference IV estimators of columns 4 and 5 where this influence of
. So despite the result from the overidentification test for column 3 of Table 1, we prefer the first-difference IV estimators of columns 4 and 5 where this influence of
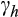 will be differenced away.
will be differenced away.
6 Conclusion
Testing the CRRA assumption empirically is crucial as it underpins many theoretical and applied models of decision-making under uncertainty, and our paper provides some qualified empirical support for the CRRA assumption for Australia. That said, given the difficulties associated with measurement error in the wealth data as well as the deeply endogenous relationship between risky asset share and wealth, further studies are needed to increase the level of confidence in this result. Such future studies will benefit from additional waves of panel data and may be able to approach the question from a different angle than ours, perhaps relying also on the subjective data in HILDA.
While informative, our Euler estimates of the coefficient of relative risk aversion
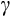 are also subject to uncertainty. Other approaches, such as the more structural simulated method of moments technique established by Gourinchas and Parker (2002), should be used to confront our results, given the heavy reliance on this parameter in applied policy analysis.
are also subject to uncertainty. Other approaches, such as the more structural simulated method of moments technique established by Gourinchas and Parker (2002), should be used to confront our results, given the heavy reliance on this parameter in applied policy analysis.
A recent working paper by Iskhakov and Keane (2018) estimates a value of 0.8 for
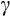 using the simulated method of moments combined with HILDA data. This implies a much lower degree of relative risk aversion than we find.
using the simulated method of moments combined with HILDA data. This implies a much lower degree of relative risk aversion than we find.
Our estimates of
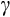 also have interesting implications for precautionary saving that could be explored further.30 In particular, Kimball (1990) shows that for consumers who face income (or other) uncertainty, the strength of the precautionary saving motive depends directly on their degree of prudence.31 With CRRA preferences, our preferred estimates of
also have interesting implications for precautionary saving that could be explored further.30 In particular, Kimball (1990) shows that for consumers who face income (or other) uncertainty, the strength of the precautionary saving motive depends directly on their degree of prudence.31 With CRRA preferences, our preferred estimates of
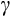 imply a coefficient of relative prudence (given by
imply a coefficient of relative prudence (given by
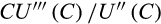 ) between 2.2 and 2.4.32 A structural life-cycle model could be used to explore what this implies for the proportion of household wealth attributable to precautionary saving. We are unaware of any Australian studies that have looked at this question.33
) between 2.2 and 2.4.32 A structural life-cycle model could be used to explore what this implies for the proportion of household wealth attributable to precautionary saving. We are unaware of any Australian studies that have looked at this question.33
Appendix I
Sample Selection
| Dropped | Remaining | |
|---|---|---|
| Unbalanced panel of respondents | 317,738 | |
| Keep years for which there are wealth data | 241,025 | 76,713 |
| Keep working age | 38,730 | 37,983 |
| Keep household heads | 17,280 | 20,703 |
| Keep positive risky assets | 1,250 | 19,453 |
- Additional observations were lost in first differencing; instrumental variables contained some missing values.
- Risky assets use broadest definition.
| Dropped | Remaining | |
|---|---|---|
| Unbalanced panel of respondents | 317,738 | |
| Keep couples who did not split up | 36,423 | 281,315 |
| Keep partners | 151,319 | 129,996 |
| Keep household heads | 54,311 | 75,685 |
| Keep non credit constrained households | 36 | 75,649 |
| Keep working age during panel | 1,600 | 74,049 |
- Additional observations were lost because of the presence of lagged variables in the equation and the instruments.
| Mean | SD | p25 | p50 | p75 | |
|---|---|---|---|---|---|
| Disposable income ($‘000 p.a.) | 88.4 | 69.7 | 49.0 | 76.2 | 110.5 |
| Expenditure on groceries and meals out ($‘000 p.a.) | 13.2 | 6.8 | 8.5 | 12.2 | 16.4 |
| Net worth ($‘000) | 569.4 | 952.1 | 61.1 | 289.5 | 710.0 |
| Age (Years) | 41.8 | ||||
| Proportion of household heads | |||||
| In relationship (%) | 63.0 | ||||
| With dependent children (%) | 40.0 | ||||
| University educated (%) | 26.0 | ||||
| From non-English speaking background (%) | 9.0 | ||||
| Employed (%) | 81.0 | ||||
| Paying off a mortgage (%) | 41.0 | ||||
| All household heads (including with zero risky assets) | |||||
| Risky assets: E ($‘000) | 27.6 | 166.6 | 0.0 | 0.0 | 3.6 |
| Risky assets: E + C + T ($‘000) | 39.1 | 222.7 | 0.0 | 0.0 | 4.7 |
| Risky assets: E + C+T + BE + S ($‘000) | 227.0 | 561.0 | 21.9 | 72.7 | 209.5 |
| RA ratio: E/FA (%) | 16.0 | 29.0 | 0.0 | 0.0 | 16.0 |
| RA ratio: (E + C+T)/FA (%) | 18.0 | 31.0 | 0.0 | 0.0 | 24.0 |
| RA ratio: (E + C+T + BE+S)/(FA + BE+S) (%) | 78.0 | 29.0 | 70.0 | 91.0 | 98.0 |
| Heads with positive holdings of equities | |||||
| Risky assets: E ($‘000) | 82.3 | 279.4 | 3.3 | 11.8 | 52.8 |
| Risky assets: E + C + T ($‘000) | 102.1 | 341.0 | 3.6 | 13.2 | 61.8 |
| Risky assets: E + C+T + BE + S ($‘000) | 424.7 | 793.8 | 78.8 | 188.8 | 449.3 |
| RA ratio: E/FA (%) | 45.0 | 33.0 | 13.0 | 42.0 | 77.0 |
| RA ratio: (E + C + T)/FA (%) | 48.0 | 34.0 | 16.0 | 47.0 | 81.0 |
| RA ratio: (E + C+T + BE + S)/(FA + BE + S) (%) | 84.0 | 20.0 | 77.0 | 92.0 | 97.0 |
| Heads with positive equities & university education: | |||||
| Risky assets: E ($‘000) | 106.7 | 313.0 | 4.4 | 19.0 | 79.3 |
| Risky assets: E + C + T ($‘000) | 136.1 | 388.3 | 4.7 | 20.0 | 95.2 |
| Risky assets: E + C+T + BE + S ($‘000) | 498.7 | 889.4 | 94.3 | 241.1 | 547.6 |
| RA ratio: E/FA (%) | 47.0 | 33.0 | 15.0 | 45.0 | 80.0 |
| RA ratio: (E + C + T)/FA (%) | 51.0 | 34.0 | 18.0 | 52.0 | 84.0 |
| RA ratio: (E + C+T + BE + S)/(FA + BE + S) (%) | 83.0 | 20.0 | 75.0 | 92.0 | 97.0 |
- N = 20,703.
- Dollar values are deflated using the ABS Consumer Price Index (reference year = 2012–13).
- E = Equities; C = Cash investments; T = Trusts; BE = Business equity; S = Superannuation; FA = Financial assets = E+C + T + Bank accounts.
Appendix II
Relative risk aversion estimates by net worth
| Net worth quartile | Equities and shares | +Bond-like assets | +Bus. Equity and Super |
|---|---|---|---|
| Bottom | 2.24 | 2.15 | 1.1 |
| Second | 2.6 | 2.44 | 1.1 |
| Third | 2.47 | 2.28 | 1.09 |
| Top | 2.43 | 2.01 | 1.08 |
| Overall | 2.47 | 2.18 | 1.09 |
Appendix III
Impact of Measurement Error in Wealth on Risky Asset Regressions
Research on the impact of measurement error in household panel data has mainly focused on income and expenditure data (Bound, Brown & Mathiowetz, 2001), but it is likely that wealth data also suffer from substantial measurement error. This appendix explores the impact on the estimated relationship between risky asset share and wealth.
We begin by assuming that the logarithm of household wealth,
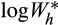 , is normally distributed with mean
, is normally distributed with mean
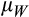 and variance
and variance
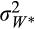 , where the star denotes the true value of the variable.34 Each household invests a share
, where the star denotes the true value of the variable.34 Each household invests a share
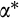 in risky assets
in risky assets
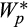 , and
, and
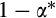 in risk-free assets
in risk-free assets
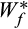 .
.
Observed assets are subject to multiplicative measurement errors
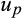 and
and
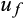 , so that
, so that
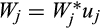 for
for
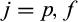 . We also assume that
. We also assume that
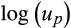 and
and
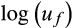 are normally distributed with mean zero and variances
are normally distributed with mean zero and variances
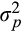 and
and
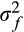 , respectively. We further assume zero correlation between the two measurement errors.
, respectively. We further assume zero correlation between the two measurement errors.
 . In this setting, cross-sectional variation in
. In this setting, cross-sectional variation in
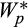 and
and
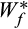 is driven solely by a household's wealth level. Observed wealth,
is driven solely by a household's wealth level. Observed wealth,
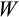 , and the observed risky asset share,
, and the observed risky asset share,
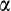 , are then given by
, are then given by
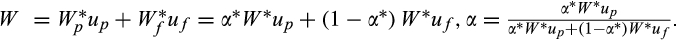 (12)
(12)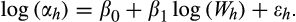 (13)
(13)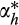 and
and
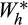 is zero by construction. However, in the presence of measurement error, the covariance between
is zero by construction. However, in the presence of measurement error, the covariance between
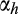 and
and
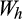 becomes
becomes
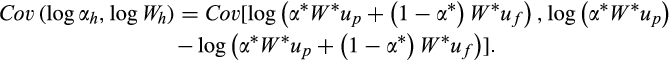 (14)
(14)This will not be equal to zero as measurement error affects both the dependent and independent variables. This fact also makes the direction of the bias ambiguous, as it will depend on the precise values of
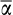 as well as the relative variances of the measurement errors. While there is no way of analytically quantifying this covariance expression, and therefore the direction and size of the bias, we can evaluate it numerically by simulating a large number of draws of
as well as the relative variances of the measurement errors. While there is no way of analytically quantifying this covariance expression, and therefore the direction and size of the bias, we can evaluate it numerically by simulating a large number of draws of
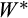 ,
,
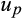 and
and
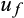 .35
.35
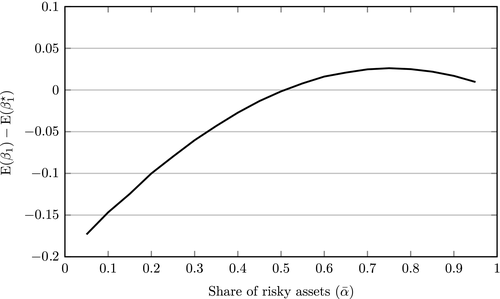
Figure C1 shows how the bias in OLS estimates of
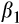 varies with different values of
varies with different values of
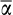 based on the numerical evaluation of Equation (14). The simulations assume that the variances of
based on the numerical evaluation of Equation (14). The simulations assume that the variances of
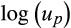 and
and
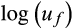 are equal to each other and imposes a signal-to-noise ratio of
are equal to each other and imposes a signal-to-noise ratio of
 (that is,
(that is,
 and
and
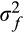 are a quarter of the variance in
are a quarter of the variance in
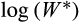 ). (The simulations involved 1 million random draws of W*,
). (The simulations involved 1 million random draws of W*,
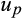 and
and
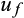 for each value of
for each value of
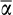 .) For values of
.) For values of
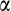 at or below 0.5, OLS estimates of β1 have a negative bias that becomes more severe as
at or below 0.5, OLS estimates of β1 have a negative bias that becomes more severe as
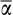 gets smaller. For values of
gets smaller. For values of
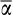 above 0.5, the bias in s β1 is positive but of relatively small magnitude. In short, the most severe (negative) bias in estimates of β1 is likely to occur when the average risky share is <0.5, which is the situation we face in the main text.
above 0.5, the bias in s β1 is positive but of relatively small magnitude. In short, the most severe (negative) bias in estimates of β1 is likely to occur when the average risky share is <0.5, which is the situation we face in the main text.
Appendix IV
Estimates of Measurement Error in Grocery Data
This appendix estimates the variance of measurement error in grocery expenditure data, which is an input into our Euler equation analysis in the main text.
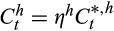 , where
, where
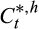 is the true (unobserved) consumption for each household h.36 We further assume that the measurement error
is the true (unobserved) consumption for each household h.36 We further assume that the measurement error
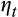 is an MA(1) process such that
is an MA(1) process such that
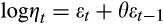 , where
, where
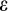 is an independent and identically normally distributed error with constant variance
is an independent and identically normally distributed error with constant variance
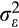 . Consumption growth is then given by
. Consumption growth is then given by
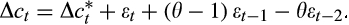 (15)
(15)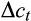 :
:
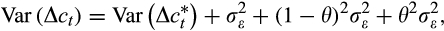 (16)
(16)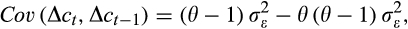 (17)
(17)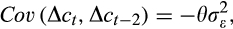 (18)
(18)We fit this model using data on self-reported grocery expenditure from HILDA's self-completion questionnaire (SCQ) for the response of the household head and separately for the head's partner.38 We also provide estimates of the model based on the spliced grocery and meals out series used in the main text, which covers a slightly longer period, from 2004 to 2016. In the latter case, the data are averaged across multiple responses from a single household where applicable.39 Our GMM estimation is based on the identity weight matrix.40
| (1) | (2) | (3) | |
|---|---|---|---|
| Expenditure measure | Groceries | Groceries | Groc. & meals out |
| Data source | Head SCQ | Partner SCQ | Av. SCQ & HQ |
| Period | 2006–2016 | 2006–2016 | 2004–2016 |
Var. of true cons. growth (Var (
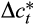 )) )) |
0.0483 (0.0158) | 0.0593 (0.0172) | 0.0205 (0.0018) |
Variance of meas’nt error (
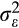 ) ) |
0.1001 (0.0142) | 0.0911 (0.0158) | 0.0699 (0.0025) |
| MA(1) coefficient (θ) | 0.0969 (0.048) | 0.0356 (0.0889) | 0.0454 (0.015) |
Proportion of var (
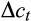 ) due to Msmt. Error (%) ) due to Msmt. Error (%) |
79 | 76 | 87 |
| Num. of obs. | 5502 | 5502 | 55554 |
- Standard errors in parentheses.
- The estimates in Table D1 imply that measurement error accounts for somewhere between 76 and 87 per cent of the variance in observed growth in grocery expenditure. This is within the range of international estimates, albeit towards the upper end. Interestingly, the process of averaging grocery responses across multiple household members, while reducing the noise, appears to reduce the signal even more so. This results in a higher estimated proportion of measurement error in this case (see column 3). The estimate of the MA(1) coefficient is significant in the first and last cases.
Appendix V
This paper uses unit record data from Release 16 of the Household, Income and Labour Dynamics in Australia (HILDA) Survey. The HILDA Project was initiated and is funded by the Australian Government Department of Social Services (DSS) and is managed by the Melbourne Institute of Applied Economic and Social Research (Melbourne Institute). The findings and views reported in this paper, however, are those of the authors and should not be attributed to either DSS or the Melbourne Institute.
References
- 1 While too numerous to list here, an interesting example is an individual's occupational choice, where more risk-averse individuals have been found to choose careers in occupations that involve lower earnings risk (Bonin et al., 2007).
- 2 The related concept of `prudence' is also an important factor in decision-making under uncertainty. See Kimball (1990) on this point.
- 3 A more structural approach would be to estimate the degree of risk aversion via simulated method of moments, as done in Gourinchas and Parker (2002). Alternatively, stock returns can be used to infer the degree of risk aversion, which is the approach underlying the `equity premium puzzle' literature [see Kocherlakota (1996) for example). A completely different approach to estimating individual risk aversion is employed in experimental studies such as Levy (1994).
- 4 For a generic utility function
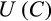 , the Arrow--Pratt measure of relative risk aversion is given by -
, the Arrow--Pratt measure of relative risk aversion is given by -
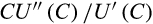 . For other preference specifications, the degree of relative risk aversion and the EIS are not simple mappings from preference parameters, and instead depend on the current values of consumption (or wealth).
. For other preference specifications, the degree of relative risk aversion and the EIS are not simple mappings from preference parameters, and instead depend on the current values of consumption (or wealth). - 5 This simple inverse relationship for CRRA preferences is what allows the Euler equation to identify the agent's degree of risk aversion. However, there are more general forms of preferences in which risk aversion and the EIS are governed by separate parameters. These more complicated models arose in response to some strong empirical puzzles that cannot be reconciled in the simple model. However, the one study to test this inverse relationship empirically found in favour of it (Yagihashi & Juan 2015).
- 6 For CRRA preferences, relative prudence is equal to
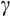 + 1. In general, a utility function exhibits prudence when its third derivative with respect to consumption is positive (Kimball, 1990).
+ 1. In general, a utility function exhibits prudence when its third derivative with respect to consumption is positive (Kimball, 1990). - 7 Both studies use evidence from Monte Carlo simulations to demonstrate the reliability of their proposed estimators using plausible data-generating processes and based on realistic features of the data with regard to panel length and the extent of measurement error in consumption.
- 8 Some examples include Ogaki and Zhang (2001); Chiappori and Paiella (2011); Tsigos and Daly (2016); Conlin et al. (2016).
- 9 In Appendix III, we show that failing to take account of measurement error in wealth in a regression of risky asset share on wealth can result in a negative estimated coefficient on wealth even when the true coefficient is known to be zero.
- 10 While the median value of 1.8 is somewhat above our Euler equation estimates, we note below that estimates of
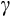 using risky asset shares are very sensitive to the definition of risky asset (see Appendix II) and assumptions about the market portfolio. For this reason, we consider the point estimates from our Euler equation analysis to be a better indicator of
using risky asset shares are very sensitive to the definition of risky asset (see Appendix II) and assumptions about the market portfolio. For this reason, we consider the point estimates from our Euler equation analysis to be a better indicator of
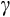 for the `average' or `typical' household.
for the `average' or `typical' household. - 11 The EIS with respect to food consumption will not equal the overall EIS except under certain circumstances; see the discussion in the Results section.
- 12 The expenditure information is taken from the household questionnaire for the years 2001 and 2003–2005, and from the self-completion questionnaire for subsequent years. In 2005 only, food expenditure was collected in both the household questionnaire and the self-completion questionnaire. This increased the mean and variance of the series,but the change in collection method does not appear to change the validity of the survey instrument see Barrett and Brzozowski (2012).
- 13 Further details are provided in Appendix I.
- 14 At the request of a referee, we estimated the model separately for those with university education and find results that are not statistically different from what we report. Details are available from the authors upon request.
- 15 In the baseline model, households who hold zero risky assets are dropped from the estimation sample. For the narrowest definition, based only upon shareholding, we drop 34 per cent of households. For the broadest definition, including superannuation and business equity, we drop 6 per cent of households. Households would hold zero risky assets if they had infinitely large relative risk aversion (see equation (2)). Our estimation over the subsample of those with risky assets is akin to estimating over those households with finite relative risk aversion.
- 16 This includes the recent US study by Alan et al. (2009). The use of food (and meals out) expenditure as a proxy for consumption in most US studies is because food was the only component of household expenditure covered in the US Panel Survey of Income Dynamics (PSID) from the survey's inception in 1968 until 1999.
- 17 We experiment with two different measures of inflation expectations: the Reserve Bank of Australia's survey of market economists and the inflation rate implied by inflation-indexed bond prices. The key results are not greatly affected by this choice.
- 18 In Appendix III we assume that 20 per cent of the variance in observed wealth is measurement error. While there is very little evidence on the extent of measurement error in wealth survey data, studies that have examined measurement error in food consumption suggest that this assumption is conservative [see, for example Ahmed et al. (2006); Brzozowski et al. (2017)). Further, the bias caused by measurement error is likely to be exacerbated in the FD regression, because the process of differencing data magnifies the noise-to-signal ratio.
- 19 The mean share of risky assets in the data is well below 50 per cent unless superannuation is included. Including superannuation as a risky asset results in a mean risky asset share of 73 per cent. If the model in column 1 is re-estimated using this broader measure of risky assets, the estimated coefficient becomes close to zero, which is what we would expect based on our simulation graph in Appendix III.
- 20 The correlation between financial assets and income is 0.44 in levels and 0.18 in growth terms, while the correlation between wealth and consumption is 0.26 in levels and 0.08 in growth terms.
- 21 Notwithstanding the result from the overidentifying restriction test, the heterogeneity in
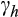 that we report on below would lead to the instrument in column 3 being invalid; see our discussion under `Caveats' in Section 5.6. Our preferred results are thus those of columns 4 and 5.
that we report on below would lead to the instrument in column 3 being invalid; see our discussion under `Caveats' in Section 5.6. Our preferred results are thus those of columns 4 and 5. - 22 The HILDA codes are _firisk and _pntrisk, respectively. For the former variable, higher values indicate higher risk aversion, while for the latter, higher values imply lower risk aversion.
- 23 With multiplicative measurement error, log-linearising renders the measurement error additive, meaning that measurement error would no longer affect the consistency of parameter estimates.
- 24 We also consider adding a second two-period-apart moment condition, which would allow
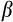 and
and
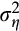 to be disentangled (Alan et al., 2009). However, we have found that the addition of two-period-apart moments greatly reduced the precision of the parameter estimates, resulted in implausible values for
to be disentangled (Alan et al., 2009). However, we have found that the addition of two-period-apart moments greatly reduced the precision of the parameter estimates, resulted in implausible values for
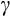 and often led to non-convergence in our GMM estimation routine.
and often led to non-convergence in our GMM estimation routine. - 25 In fact, by subsuming the measurement error into the error term, the error term becomes an MA(1) process. While this means that the first lag of the interest rate is no longer a valid instrument, we find that using the second lag of the interest rate results in implausible (negative) estimates of
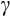 .
. - 26 We are not aware of any Australian studies that have examined this question.
- 27 Our standard errors are probably underestimates as we are using an aggregate variable--interest rates--on the right-hand side; see Moulton (1986) and Alan et al. (2018). The short, unbalanced structure of our panel makes clustering at the time period impractical.
- 28 We found very few recent studies outside the USA.
- 29 For comparison, their estimates of
 ranged from 0.87 (which the authors considered implausibly low) to 0.99.
ranged from 0.87 (which the authors considered implausibly low) to 0.99. - 30 There is a large empirical literature devoted to measuring the proportion of household wealth attributable to precautionary saving. Somewhat frustratingly, this literature has produced a very broad range of estimates. See Lusardi (1998) and Carroll and Samwick (1998) for examples at either extreme.
- 31 Deaton (1991) and Carroll (2001b), among others, point out that the prospect of borrowing constraints can cause households to engage in precautionary saving even when the utility function does not exhibit prudence.
- 32 As explained above, under CRRA preferences, the degree of relative prudence is simply equal to
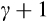 .
. - 33 Hanel and Haisken-DeNew (2017), using HILDA data, find a large effect of uncertainty on savings (that is, a strong precautionary saving motive), but do not quantify its contribution to overall household wealth.
- 34 From now on we suppress the subscript
 unless it is needed to remove ambiguity.
unless it is needed to remove ambiguity. - 35 The covariance depends on nonlinear transformations involving the sum of two log-normal random variables, which itself has no closed form.
- 36 To avoid notational clutter, we suppress the h superscript from now on.
- 37 This key identification assumption is equivalent to assuming that consumption is a martingale with drift, which is a common assumption in dynamic models of household consumption (see, for example Blundell et al. (2008)).
- 38 We restrict the sample to couple households where both members provide a unique response.
- 39 The expenditure section of the SCQ can be completed by anyone in the household with `any responsibility for the payment of household bills'. Wilkins and Sun (2010) show that around a quarter of households provide more than one response each year.
- 40 Altonji and Segal (1996) show that the identity weight matrix is superior to the `optimal' weight matrix (the variance of the sample moment conditions) when estimating models of covariance structures in short panels. Also, with unbalanced panel data, there is no guarantee that the variance of the sample moment conditions will be a positive semi-definite matrix, a problem that we encountered occasionally.




