Pay Referents and Satisfaction with Pay: Does Occupational Proximity Matter?
Abstract
We explore whether employees compare their pay to the pay of others in a similarly prestigious occupation and, if so, whether this comparison has a negative impact on pay satisfaction. Using an experimental vignette methodology, Study 1 found that people are more inclined to compare with others from a similar or identical occupation and that comparison negatively impacts pay satisfaction. This comparison and its negative effect is particularly strong in high-prestige occupations. Based on survey data, Study 2 also showed that the average pay of others in occupations of similar prestige is negatively correlated with employees’ pay satisfaction. This negative correlation was also stronger in higher-prestige occupations. Our analysis highlights the importance of occupational prestige as a main factor influencing pay comparison.
Introduction
Social comparisons are prevalent in both the work and life domains. As interdependence theorists posit, it is in our human nature to use others’ achievements as a benchmark to evaluate our own (Buunk and Gibbons, 2007; De Botton, 2005). This desire to keep up with our peers influences many daily and longer-term decisions, including what to consume, where to live or whom to select as our partner (Burleigh and Meegan, 2013; Luttmer, 2005; Watson and McLanahan, 2011; Wu, Garcia and Kopelman, 2017). Our innate desire to compare our pay or status to that of our peers also influences our workplace attitudes, performance and well-being (Duffy et al., 2012; Gartenberg and Wulf, 2017; Obloj and Zenger, 2017). In the present analysis, we explore how social comparison influences pay satisfaction and, more specifically, how the impact of social comparison on pay satisfaction is stronger among occupations of similar standing than dissimilar ones. By using the occupational code index that is based on social standing in society – the Cambridge Social Interaction and Stratification Scale, or ‘CAMSIS’ (Prandy and Lambert, 2003) – we are able to probe for the effects of occupational similarity as well as explore whether the effect of social comparison on pay satisfaction is greater among higher-tier occupations than lower-tier occupations.
The present analysis also makes interdisciplinary contributions to the management literature at several different levels. First, our analysis contributes to the pay-satisfaction literature by showing that occupational proximity influences pay comparison, thus adding a macro-level dimension to pay comparison research. Second, whereas economists perennially debate how to construe the reference group to understand pay satisfaction (e.g. Bordia and Blau, 1998; Luna-Arocas and Tang, 2015), the present analysis contributes to this economic debate by establishing occupational similarity as an important factor. Third, the present analysis offers a strong empirical contribution to the social comparison literature, which is principally based on social psychological research that is typically limited to laboratory settings or artificial contexts. Finally, because pay satisfaction is associated with employee performance, turnover intentions, absenteeism and workplace deviance (Bhave, Kramer and Glomb, 2013; Georgellis and Lange, 2012; Kish-Gephart, Harrison and Trevino, 2010; Pacheco et al., 2016; Ridge, Hill and Aime, 2017; Schreurs et al., 2013; Tekleab, Bartol and Liu, 2005), the present analysis offers important implications for human resource management by highlighting specific circumstances under which social comparison has the potential to impact pay satisfaction.
In the course of this analysis, we will discuss whether social comparison has a positive or negative impact on pay satisfaction (Card et al., 2012; Godechot and Senik, 2015), review the literature that suggests that occupational similarity matters (e.g. Festinger, 1954; Kulik and Ambrose, 1992), and extrapolate rankings and social comparison findings (Garcia, Tor and Schiff, 2013) to understand why we might expect that the level of prestige of an occupation will moderate social comparison's impact on pay satisfaction. To test our hypotheses, Study 1 uses an experimental decision-making methodology to establish the links between social comparison, pay satisfaction and occupational similarity. Study 2 empirically probes for these linkages in a dataset from the British Household Panel Survey (BHPS) to show how the average pay of others in a similar occupation is correlated with pay satisfaction and controlling for one's own pay.
Comparison effects on pay satisfaction: Positive or negative?
Whether pay comparison has a positive or a negative effect on individual well-being, or pay satisfaction in particular, has been widely debated in the management and organizational behaviour literature. Overwhelmingly, the empirical evidence suggests that pay comparison has a negative effect on individual well-being (Caporale et al., 2009). Still, there is some evidence suggesting that comparison pay has a potentially positive impact on well-being because it provides information about an individual's future prospects (Godechot and Senik, 2015). We will next consider when pay comparison has positive versus negative effects on well-being.
Pay comparison can yield positive effects on well-being when the social comparison coincides with a self-enhancement motive, which manifests when people make a downward comparison with those who are less fortunate than themselves so that they can feel better about themselves (Wills, 1981). For example, employees with a self-enhancement motive will make comparisons with those who earn a lower salary than themselves so that they can feel better about their own salary. On the flip side, positive effects can also occur with a self-improvement motive which manifests when someone makes upward comparisons with those who have higher salaries (Lockwood and Kunda, 1997; Pavlova, Lechner and Silbereisen, 2017; Wood, 1989). Employees who are making these upward comparisons become potentially pleased with the pay comparison, not because they discover that they make less than the comparison target, but because the comparison target motivates them to earn a potentially higher salary for themselves. These positive effects in the face of an upward comparison can also reflect what Carol Dweck (2007) calls a ‘growth mindset’; the optimistic outlook that one has the potential to grow and excel on any given dimension such as pay.
Despite some positive effects of pay comparison, more often than not, pay comparison can lead to negative effects on well-being. It is generally known, for example, that upward comparisons – when people are exposed to others more fortunate than themselves – can induce a negative effect on well-being, such as envy (Salovey and Rodin, 1984). Likewise, Dweck (2007) argues that most of us do not possess a ‘growth mindset’ but rather a ‘fixed mindset’ in which people see their own performance in any given domain as being fixed or immutable. As a result, upward comparisons can trigger a host of negative consequences such as desperation, stress, discouragement and more. Research on pay comparisons in particular has indeed found an effect of others’ pay upon an individual's own pay satisfaction (Shaw, 2014; Trevor and Wazeter, 2006), and this effect is broadly negative. For example, although Card et al. (2012) showed that the effect of pay comparisons did not negatively or positively impact those above the pay median in a large public organization, it did in fact lead to less pay satisfaction among those who were below the median. In this organizational context, the effect of comparison was negative, on balance. Large multinational analyses of happiness in Europe also corroborate this general pattern (e.g. Caporale et al., 2009). Across Europe, comparison with others’ income generally leads to lower happiness, although this effect seems to be stronger in Western Europe than Eastern Europe. Thus, on balance, it seems likely that pay comparison would have a negative effect on pay satisfaction.
Occupational similarity
We know from social comparison theory that people compare themselves with others who are similar to them in terms of performance (Festinger, 1954) or related attributes (Bartolini, Bilancini and Sarracino, 2013; Clark and Senik, 2010; Danzer et al., 2014; Garcia, Tor and Schiff, 2013; Goodman, 1974; Kulik and Ambrose, 1992). While the above literature has operationalized similarity in several ways, as we will review next, it has yet to probe for patterns of pay comparison as a function of occupational prestige similarity. Given the fact that our societies are fundamentally based on status hierarchies (De Botton, 2005), probing for similarity in occupational prestige as a factor that affects social comparison and pay satisfaction is important.
Accordingly, we argue that pay comparisons are more prevalent within the same or closely related occupations in terms of occupational prestige. According to social comparison theory (Festinger, 1954), we should expect that pay comparisons intensify within the same profession or a closely related occupational group. As Festinger notes, ‘Given a range of possible persons for comparison, someone close to one's own ability or opinion will be chosen for comparison’ (p. 121). Although Festinger was not speaking about occupational similarity per se, this notion of similarity was subsequently applied to the management literature by Kulik and Ambrose (1992), who theorized two important aspects of pay referent selection: the availability of information and the relevance of the referent. Factors that influence the availability of information include situational characteristics (i.e. job facet, change in procedures, physical proximity) as well as personal characteristics (i.e. gender, race, age, position), which is also consistent with the related attributes account of similarity (Goethals and Darley, 1977).
Where empirical studies that examine some form of similarity exist, they typically define reference group similarity using a variety of personal (i.e. gender, race, age) or situational characteristics (i.e. physical proximity, change in procedures). For example, McBride's (2001) measure is based on the average pay of individuals of similar age, similar educational attainment and proximal geographical area. Blau's (1994) study of pay-level satisfaction uses five different pay referents (financial, historical, organization, market and social). Using Australian data, Brown (2001) defines the market referent as the earnings of employees doing similar work in other organizations and identifies this to be the strongest predictor of pay satisfaction. Berkowitz et al. (1987) use other people's earnings in a broader sense as one of four potential factors affecting pay satisfaction. Law and Wong (1998) identify colleagues with the same qualifications as the most important referents. In their study of social comparisons and redistributive justice in East Asia, Kim, Edwards and Shapiro (2014) define the ‘referent other’ to be someone with similar job responsibilities, similar education and similar experience.
However, in the present analysis, we are interested in not just any personal or situational characteristic, but rather occupational similarity that takes into account the similarity of the prestige of the occupation. In other words, we are interested in how the occupations at different tiers of society themselves can become the basis of pay comparison and thus have an effect on pay satisfaction. To this end, a commonly used measure of occupational prestige (CAMSIS) was first introduced in the literature by Stewart, Prandy and Blackburn (1973) and later revised by Prandy and Lambert (2003) to conform with the 1990 Standard Occupational Classification (SOC). Research on CAMSIS suggests that occupations are more than just mere classification codes, but rather indicators of relative status within any given country. For example, although doctors and lawyers represent different professions and different industrial classification codes, the CAMSIS scale classifies them as being similar professions in terms of relative prestige. For this reason, we seek to probe for the first time how similarity in terms of occupational prestige affects pay comparison and pay satisfaction.
Accordingly, and in light of the weight of existing evidence on the negative association between social comparison and well-being, we argue that the negative influence of pay comparison on pay satisfaction is more prevalent within the same or similarly prestigious occupations. Thus, we propose the following hypotheses.
-
- H1a:
-
- The more similar or identical the prestige of others’ occupation, the greater an individual's tendency to compare pay.
-
- H1b:
-
- The more similar or identical the prestige of others’ occupation, the stronger the negative impact of pay comparison on pay satisfaction.
Moderating influence of higher occupational prestige
While we hypothesize that employees will be inclined to make comparison with occupational groups of similar prestige, research suggests that this tendency for employees to compare themselves with others of similar rank (Garcia, Tor and Gonzales, 2006) intensifies as occupational prestige increases. Thus, we argue that an employee's relative position in the occupational prestige distribution moderates the effect of pay referents on pay satisfaction. Experimental evidence supports the notion that social comparison intensifies with proximity to the #1 rank and most prestigious rank (Garcia and Tor, 2007; Garcia, Tor and Gonzales, 2006). For example, rivals who are commensurately ranked #2 and #3 in the organization are more likely to be concerned about how their outcomes compare with each other, in contrast to rivals who are commensurately but intermediately ranked #202 and #203 in the organization. Relatedly, Brown et al. (2008) provide evidence that employees’ well-being at work depends on the ordinal rank of an individual's earnings within a comparison group, not simply on relative earnings. The aforementioned negative effect of referent pay on one's attitudes is often stronger amongst high earners and CEOs, as pay comparisons and the selection of peer groups to benchmark performance become more salient (Skovoroda and Bruce, 2017). Against this background, we test whether being in a higher-prestige occupation moderates the effect of pay referents on pay-level satisfaction. Hence, we propose the following hypothesis.
-
- H2:
-
- The negative correlation between the pay of others in the same or a similarly prestigious occupation and pay satisfaction is stronger for employees in higher-prestige occupations.
Study 1: Experimental approach
Study 1 uses an experimental decision-making methodology to find evidence that (Hypothesis 1a) comparisons are greater as similarity intensifies (i.e. the same versus a different occupation) and that (Hypothesis 1b) the pay of others in similarly prestigious occupations has a negative impact on pay satisfaction. This study additionally probes for evidence of Hypothesis 2 – that the negative effect of comparison is stronger in higher-prestige occupations than it is in lower-prestige occupations.
Participants
A total of 200 participants (41% female, average age 32.19, 65% full-time employees) were recruited from Amazon Mechanical Turks in the USA to complete a short online survey.
Procedure
Imagine that you are a physician who makes about $170,000 a year. To what extent would you be inclined to compare your salary to another [physician/lawyer] across the street? (0 = not at all, 7 = very much)
If you learned that the [physician/lawyer] across the street made 15% more money than you, to what extent would that affect your pay satisfaction? (0 = not at all, 7 = very much)
How satisfied would you be with your pay of $170,000? (0 = not at all, 7 = very much)
The low-prestige version was identical, except that the participants were asked to imagine being a file clerk with a $30,000 salary and the referent person was either (a) another file clerk or (b) a plaster and stucco mason. We also collected information on their gender, age, employment status, ethnicity and region in the USA.
Results
Consistent with Hypotheses 1a and 1b, a multivariate analysis of variance reveals a significant main effect of occupational proximity on the following three outcomes.1 First, the tendency to compare one's salary with the reference person was greater when the professions were identical (M = 4.54, SD = 1.95) rather than different (M = 2.51, SD = 2.07; F(1,198) = 50.5, p < 0.001). Second, participants felt that learning the referent's salary was higher than their own would affect their own pay satisfaction more when the professions were identical (M = 4.55, SD = 1.96) rather than different (M = 2.47, SD = 1.93; F(1,198) = 57.0, p < 0.001). Finally, participants reported that they would feel significantly less satisfied with their pay when the referent had an identical profession (M = 3.79, SD = 2.05) rather than a different one (M = 4.75, SD = 1.98; F(1,198) = 11.4, p <0.01). This pattern of results is consistent with Hypothesis 1a as it provides evidence that comparison is greater as occupational proximity increases. It is also consistent with Hypothesis 1b by providing evidence that the negative impact on pay satisfaction is greater as occupational proximity increases.
The pattern of results remains significant, even when we analyse the high-prestige and low-prestige versions separately. In the high-prestige version, the reported tendency to compare (Hypothesis 1a) and the negative impact on pay satisfaction (Hypothesis 1b) was greater when the referent was a fellow physician (compare: M = 4.20, SD = 2.10; impact: M = 3.84, SD = 1.99; pay satisfaction: M = 5.06, SD = 1.59) rather than a lawyer (compare: M = 2.46, SD = 1.98; impact: M = 2.27, SD = 1.81; pay satisfaction: M = 5.77, SD = 1.40; all p < 0.05). The same pattern emerges in the low-prestige version when the referent was a fellow file clerk (compare: M = 4.86, SD = 1.75; impact: M = 5.24, SD = 1.67; pay satisfaction: M = 2.54, SD = 1.66) versus a plaster and stucco mason (compare: M = 2.57, SD = 2.18; impact: M = 2.67, SD = 2.07; pay satisfaction: M = 3.67, SD = 1.96; all p < 0.01). Thus, together these results suggest that the tendency to compare and its negative impact on pay satisfaction increase as the occupations become identical versus not identical, even when the level of prestige is commensurate. These results are also in accordance with Hypotheses 1a and 1b.
We can also probe this experimental dataset for evidence of Hypothesis 2 – that the tendency to compare is stronger among those in high-prestige occupations rather than low-prestige occupations. To do this, we conduct simple correlations by the prestige of the occupations. In high-prestige conditions, the tendency to compare and pay satisfaction are negatively correlated (r = −0.381, p < 0.001, n = 101). In low-prestige conditions, however, the correlation is slightly negative yet not significant (r = −0.114, p = 0.26, n = 99). A test between the two correlation coefficients shows that r = −0.381 is a significantly larger negative coefficient than r = −0.114. Thus, consistent with Hypothesis 2, it appears that the relationship between pay satisfaction and the tendency to compare is greater among high-prestige occupations than low-prestige occupations.
Study 2: Empirical approach
Sample and procedure
The data are from 18 waves of the BHPS covering the period 1991–2008. The BHPS is a longitudinal survey, which started in 1991, surveying 10,300 individuals in about 5500 households across 250 geographical areas of the UK. In wave 9, the sample includes an additional 1500 households from Wales and Scotland, while in wave 11, it also includes 2000 households from Northern Ireland. We restrict our sample to employees between 18 and 65 years of age, who work full time. We define full-time employees to be those who report usual weekly hours of 35 or more. In order to minimize the influence of outliers, we exclude from the sample those who report usual weekly hours of more than 65.
Measures
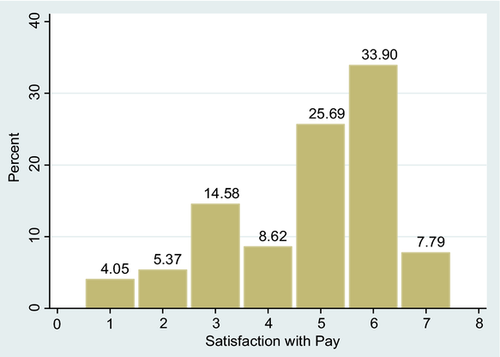
The dependent variable is satisfaction with pay. Respondents were asked a question on satisfaction with their pay. The responses were reported on an ordinal scale of 1 to 7, where a value of 1 corresponds to ‘not satisfied at all’ whilst a value of 7 corresponds to ‘completely satisfied’. Because the response categories in the first wave of the BHPS data are different from those in all later waves (Conti and Pudney, 2011), we exclude the 1991 survey from the analysis. Figure 1 displays a bar chart of these pay-satisfaction responses, with the vertical axis showing the percentage of responses in each pay-satisfaction category. The distribution of pay satisfaction is skewed, with 7.79% of respondents being completely satisfied with their pay (reporting a score of 7), while 33.90% reported a score of 6. A small proportion, about 4.05%, of respondents are completely dissatisfied with their pay.
To probe for evidence in support of our hypotheses, we need to construct an operational measure of referent pay. Our approach in constructing such a measure relies on the underpinning assumption that employees compare their pay with the average pay of others in the same occupational-prestige sub-category. Hence, we create a measure of referent pay using the average pay of others in the same or a similarly prestigious occupation. Occupational prestige is captured by the CAMSIS scale, which is based on data from the Office of National Statistics (ONS) longitudinal survey to assign a prestige-scale score to all three-digit occupational unit groups. The underpinning principle behind the CAMSIS scale is that the prestige of an individual's occupation is usually similar to that of the occupation of their spouse or cohabiting partner. Occupational assortative mating in marriage is indeed common, as individuals tend to marry others with occupations of similar prestige; a lawyer is likely to marry a doctor but unlikely to marry a manual worker (Prandy and Lambert, 2003). CAMSIS is scaled so that the national distribution of scores has a range from 0 for the lowest-prestige to 100 for the highest-prestige occupation, with a mean of 50 and a standard deviation of 15 (see Prandy and Jones, 2001 for a more detailed description of how the scale is constructed). Empirical evidence shows that higher CAMSIS scores are associated with higher income, higher job satisfaction and lower mortality rates (Feinstein and Hammond, 2004).
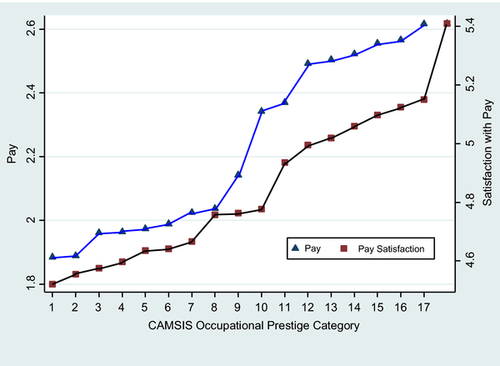
A difficulty in calculating referent pay using the average pay for each CAMSIS score separately is that we run into a small cell size problem because of the continuous and very refined nature of the CAMSIS scores. While for the majority of CAMSIS scores there is a sufficiently large number of observations, there are scores for which a very small number of observations are available. For example, for an occupation with a CAMSIS score of 83.69, there is only one observation in the sample. Similarly, there is one observation for a score of 83.78 and six observations for a score of 84.73. To mitigate this problem of small cell sizes, we split the CAMSIS scale into 17 sub-categories, as shown in Appendix Table A1. Accordingly, we define a proximal, similar-prestige occupation as one within the same sub-category of the recoded CAMSIS scale. At the lower end of the scale, we aggregate occupations with a CAMSIS score of less than 10, while at the upper end, we aggregate those with a score higher than 85. Table A1 displays the distribution of the recoded 17-sub-category CAMSIS scale, whereas Figure 2 depicts the average pay and satisfaction with pay for each sub-category. Average pay and satisfaction with pay are positively correlated, and they increase monotonically with occupational prestige.
As explained, the above approach to calculate referent pay is based on the assumption that employees compare their pay with the average pay of others in the same occupational-prestige sub-category. Nevertheless, it is important to consider also the moderating influence of career stage and location in pay comparisons. While we hypothesize that the reference group consists of other employees in similar-prestige occupations, we cannot ignore the fact that pay differs considerably by age and geographical location. Young employees compare their pay with starting salaries in similar-prestige occupations. They are unlikely to compare their pay with that of older employees who have accumulated seniority and work experience. By the same token, although the referent group consists of other employees in similar-prestige occupations, the influence of pay differences across geographical locations needs also to be controlled for. Differences in earnings and living costs, especially housing costs, are salient across UK regions, with particularly stark differences being evident when comparing London and the South East with the North (Cribb et al., 2013). Thus, to account for the moderating role of age and for regional variations in pay, we factor age categories and UK regions into the calculation of referent pay. More specifically, we consider three geographical regions: (i) London and the South East; (ii) the Midlands, Wales and the South West; and (iii) the North, Scotland and Northern Ireland and five age categories: (i) 18–25; (ii) 26–35; (iii) 36–45; (iv) 46–55; and (v) 56–65. We assume, for example, that employees in the 18–25 age group, living in London and the South East, compare their pay with that of others in similar-prestige occupations who are also in the 18–25 age group and live in London and the South East. Hence, referent pay ( ) is equal to the logarithm of the average pay of other employees in the same occupational-prestige category, within the same age group who live in the same region. When calculating the average pay, we exclude the individual's own earnings from the calculation and use the cross-sectional respondent sampling weights (XRWGHT), which are available in the BHPS.
) is equal to the logarithm of the average pay of other employees in the same occupational-prestige category, within the same age group who live in the same region. When calculating the average pay, we exclude the individual's own earnings from the calculation and use the cross-sectional respondent sampling weights (XRWGHT), which are available in the BHPS.
Analysis
 (1)
(1) on satisfaction with pay. Zit is a vector of control variables that includes age, education, marital status, number of children, education, health, job sector, firm size and managerial responsibilities (definitions and sample means are shown in Appendix Table A2). Other controls in the vector Zit include time and occupation dummy variables. The inclusion of time (year) dummies controls for inflation in pay, increased inequality and other factors that may have affected pay over the years. The purpose in including occupational dummies is to ensure that the effect of pay and comparison pay on satisfaction is net of the potential influence of permanent occupational-specific attributes. Occupational dummies would pick up, for example, observed as well as unobserved workplace characteristics such as organizational culture, perceived managerial support, inherent occupation-related stress and other pecuniary and non-pecuniary occupational characteristics. We estimate model (1) by treating the data as a repeated cross-section, clustering the standard errors to account for within-person variation in pay satisfaction.
on satisfaction with pay. Zit is a vector of control variables that includes age, education, marital status, number of children, education, health, job sector, firm size and managerial responsibilities (definitions and sample means are shown in Appendix Table A2). Other controls in the vector Zit include time and occupation dummy variables. The inclusion of time (year) dummies controls for inflation in pay, increased inequality and other factors that may have affected pay over the years. The purpose in including occupational dummies is to ensure that the effect of pay and comparison pay on satisfaction is net of the potential influence of permanent occupational-specific attributes. Occupational dummies would pick up, for example, observed as well as unobserved workplace characteristics such as organizational culture, perceived managerial support, inherent occupation-related stress and other pecuniary and non-pecuniary occupational characteristics. We estimate model (1) by treating the data as a repeated cross-section, clustering the standard errors to account for within-person variation in pay satisfaction.Results
To shed some initial light on whether referent pay matters for pay satisfaction, a calculation of simple partial correlation coefficients (r) reveals that pay satisfaction is positively correlated with own pay (r = 0.259), whereas it is negatively correlated with referent pay (r = −0.036). Table 1 presents additional preliminary evidence on the effect of own pay and referent pay on satisfaction. The top panel of Table 1 shows that individuals enjoy a higher level of pay satisfaction as they move up to higher-pay quintiles. The bottom panel of Table 1 examines the influence of referent pay. More specifically, it displays how relative pay (i.e. the ratio of own pay (Yit) and referent pay ( )) is correlated with pay satisfaction. It emerges that when relative pay increases, average satisfaction with pay also increases in a monotonic fashion, from 3.930 for the lowest quintile to 5.734 for the highest quintile. Therefore, for any given level of own pay, an increase in the pay of others in the same or a similarly prestigious occupation (
)) is correlated with pay satisfaction. It emerges that when relative pay increases, average satisfaction with pay also increases in a monotonic fashion, from 3.930 for the lowest quintile to 5.734 for the highest quintile. Therefore, for any given level of own pay, an increase in the pay of others in the same or a similarly prestigious occupation ( ) has a negative effect on satisfaction with pay.
) has a negative effect on satisfaction with pay.
| Mean | Standard error | |
|---|---|---|
| Own pay Yit: lowest quintile | 4.182** | 0.008 |
| Own pay Yit: second quintile | 4.506** | 0.008 |
| Own pay Yit: third quintile | 4.811** | 0.009 |
| Own pay Yit: fourth quintile | 5.028** | 0.009 |
| Own pay Yit: highest quintile | 5.444** | 0.008 |
Relative pay (Yit/ ): lowest quintile ): lowest quintile |
3.930** | 0.017 |
Relative pay (Yit/ ): second quintile ): second quintile |
4.438** | 0.017 |
Relative pay (Yit/ ): third quintile ): third quintile |
4.963** | 0.017 |
Relative pay (Yit/ ): fourth quintile ): fourth quintile |
5.073** | 0.017 |
Relative pay (Yit/ ): highest quintile ): highest quintile |
5.734** | 0.017 |
- Notes: +p < 0.1; *p < 0.05; **p < 0.01. The F-statistic for the equality of means is significant at the 1% level. All figures refer to weighted data.
A more systematic analysis is shown in Table 2. Table 2 reports the results of estimating the ordered probit regression model of pay satisfaction for the full sample in columns 1–2 and separately by gender in columns 3–4 and in columns 5–6 for men and women, respectively. The pooled sample comprises 67,110 person-year observations for 12,813 individuals. The standard errors are adjusted for clustering on individuals (i.e. 12,813 clusters). The chi-square p-values imply that the estimated models are statistically significant compared with the null models with no predictors. The McFadden pseudo-R2 values convey a similar message about the full model, with the likelihood ratio in the McFadden pseudo-R2 indicating an improvement over the intercept model.
| All | Males | Females | ||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Yit | 0.818** | 0.824** | 0.831** | 0.837** | 0.874** | 0.887** |
 |
−0.143** | −0.139+ | −0.236** | |||
| Male | −0.241** | −0.241** | — | — | — | — |
| Age | −0.053** | −0.045** | −0.061** | −0.054** | −0.054** | −0.039** |
| (Age)2/1000 | 0.634** | 0.546** | 0.714** | 0.645** | 0.676** | 0.497** |
| Number of children | −0.007 | −0.007 | −0.015 | −0.014 | 0.047** | 0.047** |
| Marital status | ||||||
| Married | −0.043 | −0.043 | 0.038 | 0.039 | −0.167** | −0.169** |
| Separated | −0.072** | −0.073** | 0.016 | 0.016 | −0.188** | −0.190** |
| Divorced | 0.073 | 0.073 | 0.015 | 0.018 | 0.036 | 0.034 |
| Widowed | −0.081** | −0.082** | −0.022 | −0.022 | −0.164** | −0.165** |
| Education | ||||||
| Higher degree | −0.360** | −0.360** | −0.298** | −0.298** | −0.468** | −0.468** |
| First degree | −0.253** | −0.254** | −0.213** | −0.213** | −0.289** | −0.293** |
| Teaching qualification | −0.265** | −0.263** | −0.302** | −0.302** | −0.268** | −0.264** |
| Other higher qualification | −0.162** | −0.162** | −0.165** | −0.164** | −0.136** | −0.136** |
| Nursing qualification | −0.275** | −0.273** | −0.401* | −0.398* | −0.248** | −0.247** |
| GCSE A-level | −0.156** | −0.156** | −0.175** | −0.175** | −0.105* | −0.104* |
| GCSE O-level | −0.060* | −0.059* | −0.081* | −0.081* | −0.030 | −0.027 |
| Health | ||||||
| Excellent | 0.295** | 0.294** | 0.341** | 0.342** | 0.250** | 0.248** |
| Good | 0.175** | 0.175** | 0.230** | 0.230** | 0.116** | 0.116** |
| Fair | 0.045+ | 0.045+ | 0.088** | 0.088** | 0.000 | −0.000 |
| Job tenure | −0.005** | −0.005** | −0.005** | −0.005** | −0.005* | −0.005* |
| Private-sector employee | 0.021 | 0.021 | 0.044 | 0.044 | 0.003 | 0.004 |
| Manager | 0.032+ | 0.037+ | 0.049* | 0.055* | −0.005 | −0.000 |
| Firm size | ||||||
| 100–199 employees | −0.075** | −0.075** | −0.067** | −0.067** | −0.083** | −0.084** |
| 200–499 employees | −0.073** | −0.074** | −0.064** | −0.065** | −0.076* | −0.078* |
| 500–999 employees | −0.060* | −0.061** | −0.050+ | −0.051+ | −0.075* | −0.077* |
| > 1000 employees | −0.090** | −0.091** | −0.062* | −0.063* | −0.122** | −0.126** |
| Year dummies | Yes | Yes | Yes | Yes | Yes | Yes |
| Occupational dummies | Yes | Yes | Yes | Yes | Yes | Yes |
| Pseudo-R2 | 0.041 | 0.041 | 0.047 | 0.047 | 0.041 | 0.042 |
| p-Value | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Log-likelihood | −108,954 | −108,947 | −67,404 | −67,401 | −41,039 | −41,030 |
| Restricted log-likelihood | −113,663 | −113,663 | −70,751 | −70,751 | −42,812 | −42,812 |
| Number of clusters | 12,813 | 7,258 | 5,555 | |||
| Person-year observations | 67,110 | 41,745 | 25,365 | |||
- Notes: +p < 0.1; *p < 0.05; **p < 0.01. Reference categories: Health, poor or very poor; Marital status, single/never married; Education, vocational qualification, no O-level; Firm size, less than 100 employees;
- McFadden pseudo-R2 = 1− (log-likelihood/restricted log-likelihood).
Column 1 displays the estimated coefficients of a baseline model of pay satisfaction, which includes individuals’ own pay Yit. Most of the sociodemographic controls have the expected effect on pay-level satisfaction. Briefly, men are less satisfied with their pay than women are. Consistent with previous findings (Clark, Oswald and Warr, 1996), there is a U-shaped relationship between age and satisfaction with pay, reflecting individuals’ changing personal circumstances and changing expectations over time. Compared with those who are single/never married (the reference category), separated employees are less satisfied with their pay. Widowhood has a similar, negative effect on satisfaction with pay. In general, education is negatively associated with pay satisfaction. Employees with a higher degree are less satisfied with their pay compared with those with no O-level or vocational qualifications (the reference category). The same is true for employees with a university degree, a teaching qualification, other higher qualifications and those with a nursing qualification. Notably, the results suggest that more education is negatively correlated with pay satisfaction in an almost monotonic fashion, with the dissatisfaction of teachers and nurses being particularly strong. Health has a positive influence on pay satisfaction. Employees in excellent health report higher pay satisfaction than those in poor or very poor health (the reference category). Similarly, those in good health or in fair health are more satisfied with their pay. Pay satisfaction decreases with job tenure. It is also generally lower for employees in medium or large firms. As the estimated coefficients for firm size suggest, pay satisfaction among employees in smaller firms (less than 100 employees) is generally higher than among employees in medium and large firms. Finally, managers are generally more satisfied with their pay than employees with no managerial responsibilities.
Turning attention to the effect of own pay on satisfaction, higher pay exerts a strong positive effect on pay satisfaction (β = 0.818, p < 0.01), even after controlling for demographic and firm characteristics. In column 2, we augment the baseline model to include referent pay,  , which is negatively associated with satisfaction with pay (β = −0.143, p < 0.01). Columns 3 and 4 display the results of estimating pay-satisfaction-ordered probit regressions based on the sample of male employees. Own earnings attract a positive and significant coefficient (β = 0.837, p < 0.01), whereas referent pay is negatively associated with pay-level satisfaction (β = −0.139, p < 0.1) at the 10% level of significance. Among the female employees sample, the estimated coefficients in columns 5 and 6 paint a similar picture. Although own earnings is positively associated with pay satisfaction (β = 0.887, p < 0.01), referent pay is negatively associated with pay satisfaction (β = −0.236, p < 0.01).
, which is negatively associated with satisfaction with pay (β = −0.143, p < 0.01). Columns 3 and 4 display the results of estimating pay-satisfaction-ordered probit regressions based on the sample of male employees. Own earnings attract a positive and significant coefficient (β = 0.837, p < 0.01), whereas referent pay is negatively associated with pay-level satisfaction (β = −0.139, p < 0.1) at the 10% level of significance. Among the female employees sample, the estimated coefficients in columns 5 and 6 paint a similar picture. Although own earnings is positively associated with pay satisfaction (β = 0.887, p < 0.01), referent pay is negatively associated with pay satisfaction (β = −0.236, p < 0.01).
To gain a greater appreciation of the quantitative importance of these effects, it is necessary to estimate marginal effects. Table 3 shows the estimated marginal effects for the probability that employees are very satisfied with their pay (i.e. reporting pay-satisfaction scores of 6 or 7). The marginal effects indicate that a 1% increase in own pay (Yit) increases the probability of employees reporting a pay satisfaction score of 6 by 18.7%, while it increases the probability of a pay-satisfaction score of 7 by 11.1%. In the bottom panel of Table 3, a 1% increase in referent pay reduces the probability of a pay-satisfaction score of 6 by 3.2% and the probability of a score of 7 by 1.9%. The marginal effects for male and female employees in columns 2 and 3 are similar, although the effect of referent pay for females is slightly stronger than that for males. A 1% increase in referent pay reduces pay satisfaction for females by 5.1% and 3.5% for satisfaction scores of 6 and 7, respectively. In sum, the marginal effects in Table 3 and the estimated coefficients in Table 2 confirm that employees’ pay satisfaction is negatively correlated with the earnings of others in occupations of similar prestige, thus lending support for Hypothesis 1b.
| All | Males | Females | |
|---|---|---|---|
| Yit | |||
| Prob(PAYSAT = 6) | 0.187** | 0.193** | 0.191** |
| Prob(PAYSAT = 7) | 0.111** | 0.104** | 0.133** |
 |
|||
| Prob(PAYSAT = 6) | −0.032** | −0.032* | −0.051** |
| Prob(PAYSAT = 7) | −0.019** | −0.017* | −0.035** |
| N | 67,110 | 41,745 | 25,365 |
- Notes: +p < 0.1; *p < 0.05; **p < 0.01; other controls as in Table 2.
In Tables 4 and 5, we explore whether there is support for Hypothesis 2, namely whether the negative correlation between pay referents and pay satisfaction is stronger in higher-prestige occupations. Table 4 reveals that when splitting the sample into low- and high-prestige occupations, referent pay does not affect pay satisfaction for those in occupations with a prestige score of less than 8. The same is true when we repeat the analysis for the sub-group with a prestige score of less than or equal to 10. In contrast, referent pay does matter, having a statistically significant negative effect on pay satisfaction for both male and female employees in occupations with a prestige score higher than 10. Finally, when limiting the sample to those in the most prestigious occupations, with a score greater than 14, the negative effect of comparison pay intensifies for female employees. In Table 5, the estimated marginal effects further support Hypothesis 2. In high-prestige occupations, a 1% increase in referent pay reduces the probability of female employees reporting a pay satisfaction score of 6 by about 14% and the probability of a score of 7 by about 10%. For occupations with a prestige score greater than 10, the reduction in the probability of high satisfaction (score 6 or 7) is about 5–6%. As Table 5 confirms, referent pay has no effect on the pay satisfaction of employees in low-prestige occupations.
| CAMSIS < 8 | CAMSIS < = 10 | CAMSIS > 10 | CAMSIS > 14 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All | Females | Males | All | Females | Males | All | Females | Males | All | Females | Males | |
| Yit | 0.762** | 0.839** | 0.741** | 0.872** | 0.857** | 0.785** | 0.940** | 0.824** | 0.796** | 0.836** | 0.865** | 0.895** |
 |
−0.052 | −0.179 | −0.111 | −0.165 | −0.099 | −0.081 | −0.272* | −0.306* | −0.263** | −0.041 | −0.718* | −0.263 |
- Notes: +p < 0.1; *p < 0.05; **p < 0.01; other controls as in Table 2.
| CAMSIS < 8 | CAMSIS < = 10 | CAMSIS > 10 | CAMSIS > 14 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All | Females | Males | All | Females | Males | All | Females | Males | All | Females | Males | |
| Yit | ||||||||||||
| Prob(PAYSAT = 6) | 0.171** | 0.194** | 0.165** | 0.183** | 0.201** | 0.195** | 0.161** | 0.172** | 0.178** | 0.177** | 0.170** | 0.170** |
| Prob(PAYSAT = 7) | 0.091** | 0.095** | 0.108** | 0.099** | 0.099** | 0.121** | 0.133** | 0.128** | 0.167** | 0.144** | 0.129** | 0.134** |
 |
||||||||||||
| Prob(PAYSAT = 6) | −0.026 | −0.041 | 0.011 | −0.019 | −0.023 | −0.037 | −0.053** | −0.064* | −0.052* | −0.052 | −0.141* | −0.008 |
| Prob(PAYSAT = 7) | −0.014 | −0.020 | 0.007 | −0.010 | −0.011 | −0.023 | −0.044** | −0.048* | −0.048* | −0.042 | −0.107* | −0.007 |
- Notes: +p < 0.1; *p < 0.05; **p < 0.01; other controls as in Table 2.
Discussion and conclusion
Using an experimental decision-making methodology, Study 1 found that pay comparison and its negative impact on pay satisfaction are more prevalent among individuals in the same or similar-prestigious occupations (Hypotheses 1a and 1b), in support of the view that occupational proximity matters. In addition, the negative correlation between pay comparison and pay satisfaction is stronger among high-prestige occupations than low-prestige occupations (Hypothesis 2). Probing a dataset comprising full-time employees, Study 2 empirically found the same pattern of results among survey participants of the BHPS.
Such findings add weight to previous studies suggesting that awareness of others’ pay in similar occupations spurs a negative emotional response, which is detrimental to employee morale. The study by Card et al. (2012), which explores the effects of pay disclosure on pay satisfaction at three campuses of the University of California, confirms that such disclosure had a negative impact on pay satisfaction among lower-paid workers and prompted them to seek new employment. Such findings have direct implications for the design of compensation structures within organizations, calling for a re-evaluation of the relative merits of compressed versus dispersed earnings distributions.
Furthermore, the present analysis has potential implications for whether pay secrecy practices are justified in terms of promoting workforce cohesion. There has been renewed interest in exploring the relative merits of pay secrecy in recent years, following President Obama's executive order in April 2014 to strengthen pay openness and disclosure practices. Similar measures were announced in 2015 by UK Prime Minister Cameron to make it compulsory for companies with more than 250 employees to disclose male and female employees’ pay. The benefit of pay openness is that it improves informational, procedural and distributive justice, with a positive effect on organizational citizenship behaviours (Marasi and Bennett, 2016). However, as Marasi and Bennett (2016) also argue, pay openness could have a damaging effect for organizational outcomes by spurring workplace deviance or unethical conduct. In a similar vein, Bamberger and Belogolovsky (2017) find that pay transparency has a negative effect on employees’ willingness to help their co-workers. To the extent that employees are affected by the pay of others, pay disclosure could cause lower pay satisfaction, especially in higher-prestige occupations. More specifically, while a general knowledge of others’ pay in the same or similar occupations is often demoralizing, triggering negative emotions, this effect may be less prevalent in lower-prestige occupations.
That said, the findings need to be evaluated in light of the following limitations. First, there is an implicit assumption that employees have access to pay information about others at the level of their occupational code. Although we cannot verify which individuals had access to such information, one can still foster a sense of pay information through a variety of news outlets (i.e. Chronicle of Higher Education), trade magazines and websites (i.e. payscale.com) that publish average salary information for a variety of industries. Thus, most individuals should have some sense of the variation of pay across industries. A second limitation is that we assume all participants have the same level of equity sensitivity. Clearly, such sensitivity is likely to vary from person to person, although we cannot control for these individual differences in our BHPS analyses. However, the experimental decision methodology used in Study 1 helps to mitigate this individual difference concern by randomly assigning participants to conditions. While this experimental approach additionally helps to uncover the comparison process, we acknowledge that it is based on a hypothetical vignette and lacks the realism of the BHPS. However, we are reminded of the benefits of this experimental decision-making methodology by economics Nobel Prize winner Daniel Kahneman (2000): ‘Choice … is the fruit fly of decision theory. It is a very simple case, which contains many essential elements of much larger problems. As with the fruit fly, we … hope that the principles that govern the simple case will extend in recognizable form to complex situations’ (p. xi). Thus, the experimental approach in Study 1 and the empirical approach in Study 2 complement each other well.
As for future directions, one path is to explore whether the results are replicated in an analysis of household data from other countries or cultures. While we would assume that British household data would closely resemble data from other western cultures such as the USA or Germany, perhaps the dynamics we observe would differ from those of eastern cultures such as Korea, China or Japan, where the construal of self is based on an interdependent versus independent self (Kim, Edwards and Shapiro, 2014; Oshio, Nozaki and Kobayashi, 2011).
Finally, although our discussion has focused on how pay comparisons affect pay satisfaction, it would be interesting to explore possible solutions and remedies to mitigate the negative effects of pay comparison. Because employees develop affective feelings not only towards their level of pay but also towards the system used to deliver pay (Heneman and Schwab, 1985), we believe that such remedies need to include measures to improve the fairness of rewards and pay disclosure systems. As one would expect, any initiatives to mitigate the impact of pay comparison need to be part of a comprehensive human resource strategy to boost employee well-being, beyond measures of pay satisfaction.
Appendix
Table A1. The distribution of recoded CAMSIS
| Males | Females | ||||
|---|---|---|---|---|---|
| Cambridge scale value | Recoded Cambridge scale | No. | % | No. | % |
| 0/9.99 | 1 | 1229 | 2.9 | 95 | 0.4 |
| 10/14.99 | 2 | 2193 | 5.2 | 296 | 1.2 |
| 15/19.99 | 3 | 4708 | 11.2 | 881 | 3.5 |
| 20/24.99 | 4 | 4761 | 11.3 | 1627 | 6.4 |
| 25/29.99 | 5 | 4074 | 9.7 | 859 | 3.4 |
| 30/34.99 | 6 | 2093 | 5 | 1316 | 5.2 |
| 35/39.99 | 7 | 2611 | 6.2 | 2173 | 8.5 |
| 40/44.99 | 8 | 4153 | 9.9 | 6380 | 25 |
| 45/49.99 | 9 | 2747 | 6.5 | 2161 | 8.5 |
| 50/54.99 | 10 | 3644 | 8.7 | 2315 | 9.1 |
| 55/59.99 | 11 | 2110 | 5 | 1283 | 5 |
| 60/64.99 | 12 | 3677 | 8.8 | 2251 | 8.8 |
| 65/69.99 | 13 | 2119 | 5 | 1446 | 5.7 |
| 70/74.99 | 14 | 470 | 1.1 | 1224 | 4.8 |
| 75/79.99 | 15 | 593 | 1.4 | 395 | 1.5 |
| 80/84.99 | 16 | 443 | 1.1 | 554 | 2.2 |
| > = 85 | 17 | 351 | 0.9 | 239 | 0.9 |
| Total | 41,976 | 100 | 25,495 | 100 | |
Table A2. Definition of variables and summary statistics
| Variable | Definition | Mean | Std. dev. |
|---|---|---|---|
| Satisfaction with pay | Integer response on a 1–7 scale to the question: ‘How satisfied are you with your pay?’ | 4.79 | 1.55 |
| Male | Dummy variable: 1 for male; 0 otherwise | 0.62 | 0.48 |
| Age | Age in years | 37.46 | 11.48 |
| Marital status | |||
| Married | Dummy variable: 1 for married; 0 otherwise | 0.55 | 0.43 |
| Separated | Dummy variable: 1 for separated; 0 otherwise | 0.03 | 0.17 |
| Divorced | Dummy variable: 1 for divorced; 0 otherwise | 0.10 | 0.31 |
| Widowed | Dummy variable: 1 for widowed; 0 otherwise | 0.01 | 0.09 |
| Number of children | Number of own children in household | 0.53 | 0.89 |
| Education | |||
| Higher degree | Dummy variable: 1 for higher degree; 0 otherwise | 0.04 | 0.18 |
| First degree | Dummy variable: 1 for first degree; 0 otherwise | 0.15 | 0.36 |
| Teaching qualification | Dummy variable: 1 for teaching qualification; 0 otherwise | 0.02 | 0.13 |
| Other higher qualification | Dummy variable: 1 for other higher qualification; 0 otherwise | 0.29 | 0.45 |
| Nursing qualification | Dummy variable: 1 for nursing; 0 otherwise | 0.01 | 0.10 |
| GCSE A-level | Dummy variable: 1 for GCSE A-level; 0 otherwise | 0.14 | 0.34 |
| GCSE O-level | Dummy variable: 1 for GCSE O-level; 0 otherwise | 0.18 | 0.39 |
| Health | |||
| Excellent | Dummy variable: 1 for excellent health; 0 otherwise | 0.29 | 0.45 |
| Good | Dummy variable: 1 for good health; 0 otherwise | 0.49 | 0.50 |
| Fair | Dummy variable: 1 for fair health; 0 otherwise | 0.18 | 0.38 |
| Job tenure | Job tenure in years | 4.45 | 6.08 |
| Private sector | Dummy variable: 1 for private-sector employee; 0 otherwise | 0.72 | 0.45 |
| Manager | Dummy variable: 1 for having managerial duties; 0 otherwise | 0.25 | 0.44 |
| Firm size | |||
| 100–199 employees | Dummy variable: 1 for firm size between 100 and 199 employees; 0 otherwise | 0.11 | 0.32 |
| 200–499 employees | Dummy variable: 1 for firm size between 200 and 499 employees; 0 otherwise | 0.14 | 0.35 |
| 500–999 employees | Dummy variable: 1 for firm size between 500 and 999 employees; 0 otherwise | 0.08 | 0.27 |
| 1000 or more employees | Dummy variable: 1 for firm size larger than 1000 employees; 0 otherwise | 0.12 | 0.32 |
| Yit | Log of hourly wage Hourly wage = [(usual pay per month × 12)/52]/(usual weekly hours of work) | 2.15 | 0.52 |
| Number of clusters | 12,813 | ||
| Person-year observations | 67,110 | ||
Biographies
Yannis Georgellis is Professor of Management at the University of Kent. Professor Georgellis is known for his work on happiness, adaptation and employee well-being. Spanning several disciplines, his research explores the psychological aspects of decision-making processes within the general context of employee happiness, well-being and engagement, and their impact on organizational performance. Professor Georgellis has published numerous articles in the areas of human resource management, organizational behaviour, applied psychology and behavioural economics. His work has appeared in such journals as Human Resource Management, Journal of Vocational Behavior, Journal of Public Administration Research and Theory, Economic Journal, British Journal of Management, Psychological Science and Journal of Personality and Social Psychology, among others.
Stephen M. Garcia is an Associate Professor of Psychology and Organizational Studies at the University of Michigan. His research interests span the topics of competition, social comparison, and judgment and decision making.
Andros Gregoriou is Professor of Finance at Brighton's Business School, University of Brighton. He has published widely in finance and economics and is a regular consultant for the CFA and the London Stock Exchange.
Mustafa Ozbilgin is Professor of Human Resource Management and Organizational Behaviour at Brunel University and the Associate Dean for Equality and Diversity at the College of Arts, Business and Social Sciences (CBASS). He conducts research and publishes on equality, diversity and inclusion at work from comparative and international perspectives. He is Editor-in-Chief of the European Management Review, the official journal of the European Academy of Management, and serves on the Editorial Boards of journals such as Academy of Management Learning and Education, British Journal of Management and Gender, Work and Organization.




