Australian Economic Review
Volume 55, Issue 3 pp. 389-404
Data Article
Full Access

Nowcasting the Australian Labour Market at Disaggregated Levels

Samuel Shamiri, 

Samuel Shamiri

Search for more papers by this author
Leanne Ngai, 

Leanne Ngai

Search for more papers by this author
Peter Lake, 

Peter Lake

Search for more papers by this author
Yin Shan, 

Yin Shan

Search for more papers by this author
Amee McMillan, 

Amee McMillan

Search for more papers by this author
Therese Smith, 

Therese Smith

Search for more papers by this author
Kishor Sharma, 

Kishor Sharma

National Skills Commission, Australian Government Department of Education Skills and Employment, Canberra, ACT 2601, Australia. Corresponding author: Sharma, email <[email protected]>. The authors are grateful to Bjorn Jarvis of the Australian Bureau of Statistics and to Bilal Rafi and Adam Bialowas of the Department of Education, Skills and Employment for their support and useful insights. They are also grateful to Adam Boyton, David Turvey and Angela Hope of the National Skills Commission for useful comments on an earlier version of the article. Useful comments were also received from Jeff Borland and John P. de New of the University of Melbourne, all of which significantly improved the quality of the article. The participants of the Australian Conference of Economists 2021 also provided insightful comments. All remaining errors are ours. The opinions expressed in this paper are those of the authors and do not necessarily represent the position or policy of the National Skills Commission or the Australian Government.

Search for more papers by this author
First published: 14 September 2022
https://doi.org/10.1111/1467-8462.12464

Abstract

Detailed labour market and economic data are often released infrequently and with considerable time lags between collection and release, making it difficult for policy-makers to accurately assess current conditions. Nowcasting is an emerging technique in the field of economics that seeks to address this gap by ‘predicting the present’. While nowcasting has primarily been used to derive timely estimates of economy-wide indicators such as GDP and unemployment, this article extends this literature to show how big data and machine-learning techniques can be utilised to produce nowcasting estimates at detailed disaggregated levels. A range of traditional and real-time data sources were used to produce, for the first time, a useful and timely indicator—or nowcast—of employment by region and occupation. The resulting Nowcast of Employment by Region and Occupation (NERO) will complement existing sources of labour market information and improve Australia's capacity to understand labour market trends in a more timely and detailed manner.

1 Introduction

The impacts of COVID-19 on economies around the world have demonstrated the need for timely, detailed and accurate labour market data to support targeted monitoring and policy interventions. Existing Australian data on occupational employment by region lack the frequency and detail needed to properly assess skill needs across occupations and regions, particularly in times of uncertainty. With this in mind, we develop a methodology to create the Nowcast Employment by Region and Occupation (NERO) for the Australian labour market, providing up-to-date estimates of employment for 355 occupations across 88 regions from September 2015 to January 2022, updated monthly.

We demonstrate how traditional and real-time data sources can be combined using innovative machine-learning techniques to create an employment dataset that is produced frequently, is detailed and is reasonably robust, supporting more responsive labour market policy-making. For instance, NERO offers timely insights to registered training providers to identify and design programs in line with labour market needs. Similarly, access to regularly updated occupational data by region can assist policy-makers in designing targeted policy responses to structural adjustment issues within occupations and regions.

Existing labour force surveys (LFS) provide useful insights into the state of the Australian labour market, but their usefulness for understanding emerging labour market trends and designing targeted policy responses is limited due to coverage, methodology and timeliness issues. Detailed labour market data are often released with considerable time lags at low frequencies, making it difficult for policy-makers to accurately assess emerging labour market trends. Although robust estimates of employment by occupation and region are available from the Australian Bureau of Statistics (ABS) Census of Population and Housing, these data are collected only every five years and arrive with a relatively long time lag after collection. Similarly, LFS, which have a sample of around 50,000 people, also face sparseness and volatility issues when disaggregated by both occupation and region. Furthermore, the data are subject to significant volatility, large standard errors and a high number of missing values due to a relatively small sample size at the regional and occupational levels. Hence, publicly available data on the ABS website present regional data only by the eight major occupation groups and are smoothed using an annual average. Although employment data are also available from the Household, Income and Labour Dynamics in Australia (HILDA) Survey conducted by the Melbourne Institute, this only occurs on an annual basis and the data become available with a relatively long time lag after their collection. In addition, data are often very sparse at a detailed geographic level due to the survey's relatively small sample size of approximately 17,000 households. Although the HILDA Survey was never intended to provide a detailed update on nationally representative employment by region and occupation, it does provide valuable insights into labour market dynamics.

The three above-mentioned sources of labour data are all imperfect due to their infrequency, coverage or long time lag between collection and release; moreover, the underlying estimates also differ. For example, as shown in Figure 1, some series document similar employment estimates across the three sources, others record significant differences. This is expected, given the differences in level of disaggregation, coverage and sample size. However, the differences highlight challenges in understanding labour market activity at granular levels and hence the need for more timely and frequent estimates. Understanding labour market activity in a timely manner through nowcasting was the purpose of developing NERO, and resulted in the development of a rich dataset by statistical regions at the four-digit ANZSCO level. To develop this dataset, we relied on innovative machine-learning techniques, drawing on data from the Census of Population and Housing, LFS and other sources to provide frequent estimates of employment at disaggregated levels.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Comparison of Employment for Selected Occupations and Regions

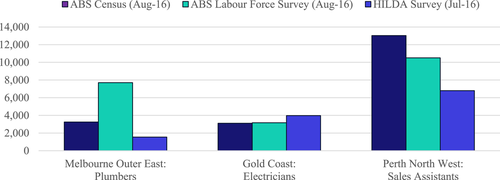
Source: Based on data from ABS (2016a, 2016b) and Melbourne Institute (2016).

Nowcasting is an emerging technique in the field of economics mainly used to derive data on economy-wide indicators such as GDP and unemployment. The goal of nowcasting is to produce a more frequent estimate of an economic series so as to support more responsive decision-making. Unlike forecasting, nowcasting does not attempt to predict or anticipate the future—its focus is understanding the now. This may be a timelier estimate of GDP (Higgins 2014), the unemployment rate (Moriwaki 2020) or current economic trends (Bok et al. 2017; OECD 2017; Kindberg-Hanlon and Sokol 2018; Nguyen and La Caga 2020). However, thus far, application of nowcasting to assess current labour market trends at the disaggregated level has been limited.

Traditionally, nowcasting has used time series econometric techniques and statistics, including vector autoregressions and mixed sampling methods. However, innovations on two fronts are transforming how nowcasting is done. One relates to the availability of novel datasets; the other is the emergence of machine-learning techniques in economic analysis (Varian 2014). These two innovations are extending the reach of nowcasting into new fields, including labour market analysis. As Dawson et al. (2020, p. 2) point out, ‘the confluence of more available labour market data facilitated by the internet (for example job ads), advances in computation and greater access to analytical tools (such as machine learning) are enabling more data-driven approaches for the labour prediction tasks’. This confluence of data provides a new way of examining labour market activity more frequently.

The methodology used to produce the NERO dataset involves both innovations. Information from numerous data sources was collected and transformed to be used as inputs in the modelling process. Machine-learning methods were then applied to ‘train’ or learn about patterns inherent in the data. The NERO database is updated every month for 355 occupations and 88 regions and goes back to September 2015.

The remainder of the article is structured as follows. Section 2 discusses the data issues and dataset used to develop the NERO model. The methodology and modelling process is discussed in Section 3. Section 4 presents key outputs. The article concludes in Section 5 with policy remarks and limitations.

2 Data

Australian labour market data at detailed levels are hard to find, especially if they need to be reasonably current. At more disaggregated levels—such as when examining regional and occupational components—the data are less readily available, particularly for investigating emerging labour market trends in uncertain times, for example, during the COVID-19 pandemic. For these reasons, we developed the NERO model, assembling data from nine different sources, including the ABS Census of Population and Housing, the LFS (including custom data provided by the ABS), the NSC's Internet Vacancy Index, Burning Glass Online job advertisements by region and occupation, Department of Education, Skills and Employment (DESE) jobactive program data, ABS weekly payroll jobs, ABS job vacancies, Department of Home Affairs visa holders by occupation and state/territory and ABS National Accounts. The selection of these sources was guided by their coverage and reliability.

A considerable amount of time was devoted to curating the datasets and ensuring they were of a consistent format as inputs for the NERO model. Treatments and transformations that were made to the datasets include:

  • cross-checking release dates and reference periods to ensure that any data being used to predict a date in the past were based only on data released prior to that prediction date.

  • mapping all regional data to Statistical Area 4 (SA4) boundaries (using geographical boundary concordances based on ABS 2016c).

  • aligning all industry-based data to the four-digit or unit-group level of the Australian and New Zealand Standard Classification of Occupations (ANZSCO) using a concordance of industry to occupational employment from the 2016 Census of Population and Housing, ABS 2016c).

  • excluding series that were considered out of scope (such as defence-related occupations, not-further-defined occupations and other territories).

  • imputing missing values in the data where necessary using various imputation techniques based on the mean/median of the series and the surrounding data values. Imputation was necessary as the data sources do not have full coverage across all the occupations and regions that are in scope. For example, online job advertisements tend to be for positions located in metropolitan areas.

  • smoothing the data using a Hodrick-Prescott filter (other smoothing techniques were tested, including Baxter King, Christiano Fitzgerald, Butterworth and several others).

Appendix 1 outlines data sources, series and levels of disaggregation. For all input data sources, numerous variables were created and tested as model inputs. This included using raw data, the change in raw data levels (weekly, fortnightly, monthly, quarterly and annual) and lagged values. The NERO model, which leads to the development of the NERO dataset, provides monthly up-to-date labour market information for 355 occupations and 88 regions, equating to around 31,240 series, by:

  • ANZSCO four-digit occupation (ABS 2013) and

  • SA4 region (ABS 2016b).

3 Methodology and Modelling Process

This section outlines the modelling process undertaken to develop the NERO database, including the use of machine-learning techniques and validation of the modelling outputs. The nowcasting approach followed in this study uses the Cross-Industry Standard Process (CRISP) (Shearer 2000; Studer et al. 2021), as outlined in Figure 2.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Cross-Industry Standard Process (CRISP) Methodology of the Modelling Cycle

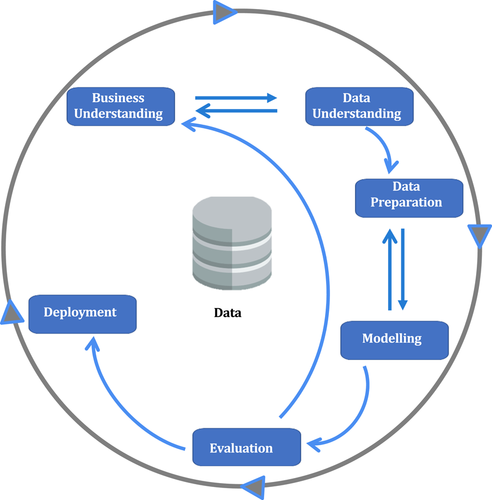
Source: Adopted from Shearer (2000).

3.1 Modelling Process to Generate Initial Estimates

Following the data-cleaning and enhancement process, a number of machine-learning techniques were used to develop predictions of employment by occupation and region. We follow the standard machine-learning practice for training, validation and testing by splitting the data into the following two categories:
  • (i)

    Training and validation dataset (covering period from August 2015 to February 2020, excluding August 2016).

  • (ii)

    Testing dataset (August 2016, to allow in-sample validation using the 2016 Census, and May 2020 to November 2020, to enable an out-of-sample validation).

The NERO model, which leads to the development of NERO database, was trained and tuned on the training and validation dataset. Testing of model performance was then conducted by running the built models on the testing dataset to examine how the resultant predictions performed.

Validation of the NERO model was challenging given the lack of timely data on regional employment by occupation in Australia. This was particularly true for the smaller series. To address this, several potential validation measures were developed, including:

  • Group 1—for larger series, the smoothed version of the ABS LFS custom data on occupational employment by region (quarterly) were used, and

  • Group 2—for smaller series, the outcomes of the 2016 ABS Census of Population and Housing were used.

Together, these two sources—although imperfect—provide an appropriate source of data with which to validate and test the predictions of the NERO model.

Three different but commonly utilised machine-learning approaches were used to construct the NERO model and generate predictions:

  • Random Forest (Breiman 2001): This model utilises a large number of ‘trees’ that are developed independently of each other to allow for uncorrelated errors to improve performance. Although some trees may be less accurate in some circumstances, many other trees will be more accurate—in effect, the trees protect each other from their individual errors. The final prediction is derived by taking the average prediction (or most common prediction) across all the ‘trees’.

  • Gradient Boosting (Friedman 2001): Similar to random forest, the gradient boosting model involves estimating ‘trees’ that seek to explain the target variable. However, while in random forest, each ‘tree’ is built independently, gradient boosting builds one ‘tree’ at a time, with each new ‘tree’ seeking to improve on the shortcomings of the previous version of the model. This iterative tree-building process continues until the learning algorithm is unable to develop new ‘trees’ to explain the residuals.

  • Elastic Net Regression (Zou and Hastie 2005): Elastic net regression is a common linear regression with an extra regularisation term. This penalises complex models and thus encourages smoother fitting.

These three methods are the main components of the machine-learning approach in developing NERO. Notably, each approach includes many sub-models.

With each iteration of the modelling process, the variables used as inputs were adjusted according to their relative importance. It should be noted that classical time series analysis tools such as correlogram can be useful for evaluating lag variables, but they do not help in selecting other types of variables, such as those derived from timestamps, moving averages or as change variables.

One of the key characteristics of machine learning is its ability to evaluate the joint importance of subsets of variables (Guyon and Elisseeff 2003). This is highly desirable when simultaneous changes in multiple measurements drive an outcome, such as job advertisements and job placements. Random forests use the out-of-bag samples to measure the prediction strength of each variable (Hastie, Tibshirani and Friedman 2009). Under this method, the random forest computes how much each variable decreases the variance. Variables that contribute to higher variance reduction are in general more important. Figures 3 and 4 summarise the relative variable importance of each data source from the last model iteration for Groups 1 and 2. Note that each dataset considers various lags, such as ∑ x t − i $\sum {x}_{t-i}$ , where i = 1,2,3,4 $i=\mathrm{1,2,3,4}$ .

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Variable Importance by Data Source for Group 1

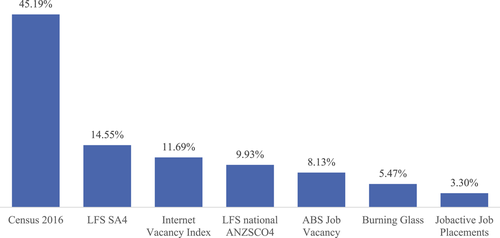
Source: Computed by the authors based on the NERO model, NSC.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Variable Importance by Data Source for Group 2

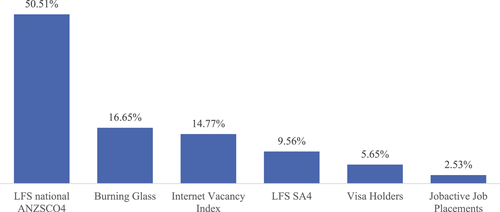
Source: Computed by the authors based on the NERO model, NSC.

3.2 Combining Multiple Models into a Single Estimate

Once the random forest, gradient boosting and elastic net models were run, initial estimates were combined or stacked, based on their hyper parameters, to produce a single optimal set of nowcasts.

Building the stacked ensemble model involved taking the final output from each model as input in a linear regression model. The linear regression model was then trained to optimally combine the inputs, again utilising the training and validation and testing datasets. Once the linear regression model was optimised, a single raw prediction of employment by region and occupation was produced.

Generally, a stacked ensemble framework achieves more accurate predictions and improves robustness and generalisability compared with the best individual model (Wolpert 1992; Opitz and Maclin 1999). This approach was adopted in developing the NERO estimates.

3.3 Adjusting Outliers, Smoothing and Scaling to Derive a Final Estimate

Once a single raw prediction was developed using the stacked ensemble model, an outlier adjustment, smoothing and scaling process was implemented to derive final estimates. Where the rate of change in the model's raw prediction deviated substantially from the national rate of change for Australia (estimated using the ABS LFS), an outlier adjustment process was completed. This ensures that the nowcasting estimates of smaller series, which are often volatile, remain broadly consistent with the national trends. A minimum of 10 people employed was also applied to all series to help ensure confidentiality.

Once the outlier adjustment process was completed, the estimates were smoothed using the Hodrick-Prescott filter to provide trend estimates. The estimates were then scaled to ensure broad consistency with the known trends identified through the publicly available ABS LFS data. This involved broadly scaling to ABS LFS estimates for total employment in each region, as well as the estimates for employment by occupation for Australia. This procedure ensures that the nowcasting estimates for each region and occupation are broadly consistent with existing estimates of total employment. Once this process was completed, a final, smoothed nowcasting estimate was derived.

3.4 Validation of the NERO Model

Model performance was evaluated with three different measures, namely, mean absolute percentage error (MAPE), weighted absolute percentage error (WAPE) and root mean square error (RMSE). For all three measures, the smaller the value, the better the model. These metrics can be derived as:

MAPE: a measure of how much each prediction has ‘missed’ by in percentage terms:
MAPE = 1 N ∑ i = 1 N x i − x ˆ i x i ${MAPE}=\frac{1}{N}\sum _{i=1}^{N}\left|\frac{{x}_{i}-{\hat{x}}_{i}}{{x}_{i}}\right|$
WAPE: a weighted measure that penalises errors for larger series:
WAPE = ∑ i = 1 N | x i − x ˆ i | ∑ i = 1 N | x i | ${WAPE}=\frac{\sum _{i=1}^{N}|{x}_{i}-{\hat{x}}_{i}|}{\sum _{i=1}^{N}|{x}_{i}|}$
RMSE: a measure that penalises larger errors:
RMSE = ∑ i = i N ( x i − x ˆ i ) 2 N ${RMSE}=\sqrt{\frac{\sum _{i=i}^{N}{({x}_{i}-{\hat{x}}_{i})}^{2}}{N}}$
where x i ${x}_{i}$ is the actual value, x ˆ i ${\hat{x}}_{i}$ is the predicted value and N $N$ is the number of data points.

While these measures and the above-mentioned data sources provide a method of measuring model performance, what should be considered adequate or sufficient performance is still less than clear. Since NERO is one of the first attempts to create new data at the disaggregated level using big data and machine-learning techniques, there is limited precedence for understanding performance. With this in mind, a simple model was constructed for benchmarking. This simple ‘benchmark’ model used a smoothed version of the ABS LFS data to predict the next value in the time series.

A quick overview of the performance metrics on Group 1 for the NERO model, including for each of the contributing models (i.e., random forest, gradient boosting and elastic net regression) and the benchmark model, is provided in Table 1. The performance is measured on the testing dataset.

Table 1. Performance Metrics for the NERO Model
Model MAPE (%) WAPE (%) RMSE
Benchmark 22 18 305
Random forest 16 13 231
Gradient boosting 19 13 237
Elastic net 20 13 219
NERO (stacked) 20 14 246
  • Notes: MAPE = mean absolute percentage error; NERO = Nowcast of Employment by Region and Occupation; RMSE = root mean square error; WAPE = weighted absolute percentage error.
Source: Computed by the authors based on the NERO dataset, NSC.

Table 1 shows that random forest, gradient boosting, elastic net and NERO (stacked) outperformed the benchmark. The performance of three individual model types and NERO (stacked) is comparable, with similar metrics recorded across all three models and performance measures (i.e., MAPE, WAPE and RMSE). Although the stacked final NERO model performs slightly worse than some of the individual models, it is still preferable at this stage as the existing evidence suggests that this model is likely to be more reliable and stable than a given single model in the medium to long term (Wolpert 1992; Opitz and Maclin 1999).

This level of performance was considered appropriate and usable, particularly given that two of the three periods the model is measured against include the impacts of COVID-19, which was extremely difficult to predict. As shown in Table 2, model performance declines slightly during 2020 at the height of COVID-19 in Australia.

Table 2. Performance Metrics for Pre-COVID, Post-COVID-19 and the Recovery Period
Period Description WAPE—benchmark (%) WAPE—random forest (%) WAPE—gradient boosting (%) WAPE—elastic net (%) WAPE—stacked model (%)
Aug 2016 Prior to COVID-19 15 11 11 11 11
May 2020 COVID-19 downturn 17 12 13 13 13
Aug 2020 COVID-19 recovery 21 15 16 15 17
Overall 18 13 13 13 14
  • Note: WAPE = weighted absolute percentage error.
Source: Computed by the authors based on the NERO dataset, NSC.

The model performance of various breakdowns of the series was investigated to find potential weak spots in the model that could be improved in the next iteration. As shown in Tables 3 and 4, the model performs consistently well across all states and territories and occupation categories.

Table 3. Summary of Model Performance by States and Territories
Series WAPE—benchmark (%) WAPE—random forest (%) WAPE—gradient boosting (%) WAPE—elastic net (%) WAPE—stacked model (%)
Australian Capital Territory 15 12 12 11 13
New South Wales 18 13 14 13 14
Northern Territory 17 14 16 15 15
Queensland 18 12 13 13 14
South Australia 17 12 13 13 13
Tasmania 17 13 14 14 13
Victoria 17 13 13 13 14
Western Australia 18 13 14 13 14
Overall 18 13 13 13 14
  • Note: WAPE = weighted absolute percentage error.
Source: Computed by the authors based on the NERO dataset, NSC.
Table 4. Model Performance by Occupation Categories (ANZSCO One-Digit Level)
Series WAPE—benchmark(%) WAPE—random forest (%) WAPE—gradient boosting (%) WAPE—elastic net (%) WAPE—stacked model (%)
Managers 18 13 14 13 14
Professionals 17 12 13 12 13
Technicians and trade workers 18 13 14 13 14
Community and personal service workers 19 14 14 14 15
Clerical and administrative workers 18 13 13 13 14
Sales workers 16 12 13 12 13
Machinery operators and drivers 17 12 13 13 13
Labourers 18 13 14 14 14
Overall 18 13 13 13 14
  • Note: WAPE = weighted absolute percentage error.
Source: Computed by the authors based on the NERO dataset, NSC.

Series that were stable or exhibited only small increases or decreases tended to have better performance. The series with the largest declines exhibited the largest errors (Table 5). The model performance by employment size demonstrates that models performed best for the largest series. As shown in Table 6, high errors are present in the smallest group (between 0 and 100 employed) due to a minimum value of 10 being applied to all predictions.

Table 5. Summary of Model Performance by Trend
Series Annual change of smoothed employment (%) WAPE—benchmark (%) WAPE—random forest (%) WAPE—gradient boosting (%) WAPE—elastic net (%) WAPE—stacked model (%)
Large increase Greater than 15 17 12 13 13 13
Small increase Between 2.5 and 15 13 10 10 10 10
Stable Between −2.5 and 2.5 7 6 8 8 8
Small decrease Between −10 and −2.5 13 10 10 10 11
Large decrease Less than −10 23 16 17 16 18
Overall 18 13 13 13 14
  • Note: WAPE = weighted absolute percentage error.
Source: Computed by the authors based on the NERO dataset, NSC.
Table 6. Summary of Model Performance by Employment Size of the Series
Employment size WAPE—benchmark (%) WAPE—random forest(%) WAPE—gradient boosting (%) WAPE—elastic net (%) WAPE—stacked model (%)
Between 0 and 100 98 75 90 89 88
Between 101 and 500 17 12 13 13 14
Between 501 and 1,000 18 12 13 13 13
Between 1,001 and 5,000 19 14 14 14 14
5,001 or more 12 11 11 9 11
Overall 18 13 13 13 14
  • Note: NERO = Nowcast of Employment by Region and Occupation; WAPE = weighted absolute percentage error.
Source: Computed by the authors based on the NERO dataset, NSC.

Model performance by employment size demonstrates that models performed best for the largest series. High errors are present in the smallest group (between 0 and 100 employed) due to a minimum value of 10 being applied to all predictions (see Table 6).

4 Overview of the Outputs

This section reports key outputs of the modelling exercise. A total of 31,240 series are provided covering 355 occupations and 88 statistical regions from September 2015 to January 2022; the dataset is updated monthly. The dataset is also capable of producing rankings, including the highest and lowest demanded occupations for each statistical area, either by month or as a comparison of changes over the last five years. Figures 5-7 provide some examples of NERO outputs.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Nowcasts of Motor Mechanics in Sydney—Blacktown

Source: Based on the NERO dataset, NSC.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Nowcasts of Software and Applications Programmers in Brisbane—South

Source: Based on the NERO dataset, NSC.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Nowcasts of Education Aides in Melbourne—North East

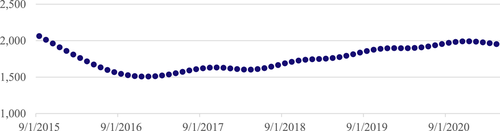
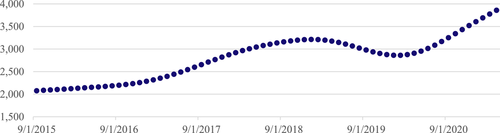
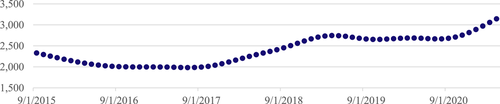
Source: Based on the NERO dataset, NSC.

The model also provides estimates for the largest employing regions for any of the 355 occupations. As an example, the 10 largest employing regions for Aged and Disabled Carers in April 2021 and a five-year percentage change are shown in Table 7. From a regional perspective, the model identifies the top occupations in each region, as well as the fastest growing occupations in the region. As an example, in Table 8 presents employment in Illawarra by occupation in April 2021 and a five-year percentage change.

Table 7. Ten Largest Employing Regions for Aged and Disabled Carers in April 2021 and a Five-Year Percentage Change
Employment of aged and disabled carers by region (SA4) Employment (NSC NERO)—April 2021 5-year change (%)
Gold Coast 9,043 63
Melbourne—West 8,373 63
Melbourne—South East 6,725 4
Perth—North West 6,711 41
Adelaide—North 6,596 45
Adelaide—South 6,578 39
Perth—South East 5,840 83
Melbourne—Outer East 5,701 22
Wide Bay QLD 5,208 80
Perth—South West 5,082 70
Sunshine Coast 4,868 73
Melbourne—North East 4,654 84
Capital Region NSW 4,027 41
  • Note: NERO = Nowcast of Employment by Region and Occupation.
Source: Computed by the authors based on the NERO dataset, NSC.
Table 8. Employment in Illawarra by Occupation in April 2021 and a Five-Year Percentage Change
Employment in Illawarra (NSW) by occupation Employment (NSC NERO —April 2021 5-year change (%)
Sales assistants (general) 6,623 2
General clerks 6,122 55
Registered nurses 4,762 32
Aged and disabled carers 3,325 25
Electricians 2,834 50
Primary school teachers 2,758 67
Metal fitters and machinists 2,613 18
Carpenters and joiners 2,592 13
Office managers 2,537 40
Retail managers 2,336 7
  • Note: NERO = Nowcast of Employment by Region and Occupation.
Source: Computed by the authors based on the NERO dataset, NSC.

Other outputs can be obtained via the data dashboard on the NSC's website where the data can also be downloaded, enabling stakeholders to conduct their own analysis of labour market trends.

5 Conclusion

This article outlines the methodology used to produce NERO—the Nowcast of Employment by Region and Occupation—a new monthly dataset that, starting from September 2015, provides detailed estimates of employment for 355 occupations across 88 regions, amounting to approximately 32,000 estimates in total. In providing detailed, reasonably robust estimates at regular monthly intervals, NERO enriches the evidence base for understanding the labour market, and is particularly useful in identifying emerging trends, which will provide useful insights to policy-makers and planners in the following ways:

  • assisting employment service providers and training providers to better target their service offerings to the jobs in demand in their region,

  • supporting students and job seekers to make more informed career decisions based on their local labour market,

  • targeting policy responses to local conditions, including policy responses that seek to address structural adjustment issues within industries and regions, and

  • accounting for regional differences when evaluating labour market programs and setting performance benchmarks for service providers.

The NERO data are downloadable free of charge via the publicly available portal. Researchers and policy planners using these data are requested to cite this article in their research. There are, however, two important caveats. First, the primary purpose of the NERO dataset is to complement existing data on employment by occupation and region. It should be used in conjunction with data from the ABS and other sources, rather than as a stand-alone resource. Second, its performance could be improved in the future by incorporating more sources of timely and disaggregated data (such as bank-transaction or accounting data) and through further model training and validation using data from future releases of the census (such as the 2021 Australian Census of Population and Housing).

Endnotes

  • 1 The NSC is grateful to the ABS for providing quarterly estimates of employment by region and occupation from the Labour Force Survey to support this project.
  • 2 It must be noted that the sample size of HILDA is insufficiently large to support the derivation of robust estimates at detailed levels of employment by region and occupation.
  • 3 ‘Not further defined’ is a code used by the ABS to process incomplete, non-specific or imprecise responses. For this reason, they were excluded as they were generally a low percentage of records. Defence-related occupations were also removed as it is a unique occupation series with poor data available.
  • 4 <https://www.abs.gov.au/ausstats/[email protected]/Lookup/1220.0Chapter22013,%20Version%201.3>.
  • 5 <https://www.abs.gov.au/ausstats/[email protected]/mf/1270.0.55.001>.
  • 6 Due to space constraints only a few examples are provided in this paper. Interested readers can view a total of 31,240 estimates, on a monthly basis from <https://www.nationalskillscommission.gov.au/our-work/nero>.
  • 7 See <https://www.nationalskillscommission.gov.au/our-work/nero/nero-dashboard> for the NERO data portal allowing immediate download of employment data.

    • Appendix 1

    (Table A1)

    Table A1. Data Sources, Level of Disaggregation and Frequency
    Source Series Level Regional level Start datea Frequency Access Comment
    ABS—Census Occupational employment by region 4-digit ANZSCO SA4 region TBC Every 5 years Via subscription The most reliable existing estimate of employment for smaller series that are not typically captured by the ABS LFS or HILDA Survey.b
    ABS Labour Force Survey Occupational employment nationally 4-digit ANZSCO National Aug 1986 Quarterly Publicly available
    Occupational employment by region 4-digit ANZSCO SA4 region Feb 2001 Quarterly Custom data request Subject to significant volatility, large standard errors and a high number of missing values.
    Total employment by region Total employment SA4 region Oct 1998 Monthly Publicly available
    NSC—Internet Vacancy Index Online job advertisements by region and occupation 4-digit ANZSCO IVI regions Mar 2010 Monthly Publicly available As the data are based on IVI regions, trends at the SA4 level will need to be inferred through a concordance process.
    Burning Glass Online job advertisements by region and occupation 4-digit ANZSCO SA4 region Jan 2013 Daily Via subscription Does not have the same breadth of coverage as the NSC IVI, although it is more timely/frequent.
    DESE—Jobactive program data Jobactive job placements by occupation and region 4-digit ANZSCO SA4 region Jul 2015 Fortnightly Government program data Remote areas are not captured in these data as the jobactive program does not operate in remote areas.c
    ABS—weekly payroll jobs Weekly payroll jobs by industry and region Total employment 1-digit and 2-digit ANZSIC SA4 region state and territory national Jan 2020 Weekly Publicly available As a relatively new series, caution must be exercised in utilising these data. A separate model that utilises these data may be required.
    ABS—Job Vacancies Job vacancies by state/territory Total vacancies State and territory Nov 1993 Quarterly Publicly available
    Home Affairs Visa holders by occupation and state/territory 4-digit ANZSCO State and territory Sept 2010 Quarterly Publicly available
    ABS—National Accounts Gross state product (GSP) 1-digit ANZSIC State and territory Jun 1990 Annual Publicly available The occupational impacts of economic activity by industry will need to be inferred through a concordance process.
    • (a) Start date indicates availability on a consistent time series basis.
    • (b) The ABS Jobs in Australia series has the potential to provide a detailed occupation by region picture using tax data on an annual basis.
    • (c) Placements are recorded by jobactive providers in the Employment Services System for job seekers in their caseload. Not all occupations where a jobseeker starts a new job are necessarily recorded as a placement, and placements are not recorded for participants in digital services. In response to the large increase to the jobactive caseload during the COVID-19 pandemic, Online Engagement Services was expanded, leading to a significant change in the percentage of the jobactive participants in digital services. This means there is a break in series from April 2020 onward.

    Appendix 2: Additional Information on the Modelling Methodologies

    This appendix provides further information regarding the machine-learning and modelling approaches utilised to produce the NERO estimates, consistent with the existing literature on these approaches.

    Gradient Boosting

    Gradient boosting was introduced by Friedman (2001). It is an ensemble method that can combine several weak learners into a strong learner as:
    y i ˆ = ∅ ( x i ) = ∑ k = 1 K f k ( x i ) $\hat{{y}_{i}}=\varnothing ({x}_{i})=\,\sum _{k=1}^{K}{f}_{k}({x}_{i})$
    where f k ( . ) ${f}_{k}(.)$ is a weak learner and K is the number of weak learners, combined to become a strong learner. Given a training dataset D = { ( y i , x i ) } ( | D | = n , x i ∈ R m , y i ∈ R ) $D=\{({y}_{i},{x}_{i})\}(|D|=n,{x}_{i}\in {{\mathbb{R}}}^{m},{y}_{i}\in {\mathbb{R}})$ , one would like to find a stronger learner, which finds the optimal parameters by minimising the loss function ∅ ${\rm{\varnothing }}$ , as shown in:
    L ( ∅ ) = ∑ i = 1 n l ( y i ˆ , y i ) + ∑ k = 1 K Ω ( f k ) ${\mathscr{L}}(\varnothing )=\sum _{i=1}^{n}l(\hat{{y}_{i}},{y}_{i})&#x0002B;\,\sum _{k=1}^{K}{\rm{\Omega }}({f}_{k})$

    Here, l $l$ is a differentiable convex loss function that measures the difference between the prediction y i ˆ $\hat{{y}_{i}}$ and the target y i ${y}_{i}$ . The second term Ω ${\rm{\Omega }}$ penalises the complexity of the model. The additional regularisation term helps smooth the final learned weights to avoid overfitting. The tree ensemble model used in XGBoost is trained in an additive manner until stopping criteria (e.g., the number of boosting iterations, early stopping rounds and etc.) are satisfied.

    The basic procedure of boosting is described in pseudocode below:

    Set uniform sample weights.

    for each base learner (weak learner) do

    Train base learner with weighted samples.

    Test base learner on all samples.

    Set learner weight proportional to weighted error.

    Set sample weights based on ensemble predictions.

    Weighted average all base learners as the final model

    Random Forest

    The random forest algorithm, proposed by Breiman (2001), has been extremely successful as a general purpose classification and regression method. The approach, which combines several randomised decision trees and aggregates their predictions by averaging, has shown excellent performance in many applications. The idea of the random forest algorithm is to improve the variance reduction of bagging by reducing the correlation between the trees without increasing the variance too much.

    The basic procedure of random forest is described in pseudocode below:

    for i = 1 to N do

    Randomly select k variables from total variables.

    Randomly select d samples from total learning samples.

    Build a tree with selected k variables and selected d samples.

    Average all N trees as the final model.

    Elastic Net

    The elastic net method is a recent development in regression and can be understood as a conventional regression with a penalty term. Given a training dataset with n $n$ observations and p $p$ predictors, let y = ( y 1 , … , y n ) T $y={({y}_{1},\ldots ,{y}_{n})}^{T}$ be the response and X = [ x 1 | … | x p ] $X=[{x}_{1}|\ldots |{x}_{p}]$ be the model matrix, where x j = ( x 1 j , … , x nj ) T , j = 1 , … , p ${x}_{j}={({x}_{1j},\ldots ,{x}_{{nj}})}^{T},{j}=1,\ldots ,p$ are the predictors. Elastic net regression attempts to minimise the residual sum of squares plus some penalty term.
    ∑ i = 1 n y i − β 0 − ∑ j = 1 p β j x ij 2 + λ ( 1 − α ) ‖ β ‖ 2 2 / 2 + α ‖ β ‖ 1 ${\sum }_{i=1}^{n}{\left({y}_{i}-{\beta }_{0}-\sum _{j=1}^{p}{\beta }_{j}{x}_{{ij}}\right)}^{2}&#x0002B;\lambda \left[(1-\alpha ){\Vert \beta \Vert }_{2}^{2}/2&#x0002B;\alpha {\Vert \beta \Vert }_{1}\right]$
    Here, ‖ β ‖ 1 ${\Vert \beta \Vert }_{1}$ is the Lasso penalty called the l 1 ${l}_{1}$ norm
    ‖ β ‖ 1 = ∑ j = 1 p | β j | ${\Vert \beta \Vert }_{1}=\sum _{j=1}^{p}|{\beta }_{j}|$
    Similarly, ‖ β ‖ 2 ${\Vert \beta \Vert }_{2}$ is the Ridge penalty called the l 2 ${l}_{2}$ or Euclidean norm
    ‖ β ‖ 2 = ∑ j = 1 p β j 2 ${\Vert \beta \Vert }_{2}=\sqrt{\sum _{j=1}^{p}{\beta }_{j}^{2}}$

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.