Slowness-domain kinematical characteristics for horizontally layered orthorhombic media. Part II: Pre-critical slowness match
ABSTRACT
Part II of this paper is a direct continuation of Part I, where we consider the same types of orthorhombic layered media and the same types of pure-mode and converted waves. Like in Part I, the approximations for the slowness-domain kinematical characteristics are obtained by combining power series coefficients in the vicinity of both the normal-incidence ray and an additional wide-angle ray. In Part I, the wide-angle ray was set to be the critical ray (‘critical slowness match’), whereas in Part II we consider a finite long offset associated with a given pre-critical ray (‘pre-critical slowness match’). Unlike the critical slowness match, the approximations in the pre-critical slowness match are valid only within the bounded slowness range; however, the accuracy within the defined range is higher. Moreover, for the pre-critical slowness match, there is no need to distinguish between the high-velocity layer and the other, low-velocity layers. The form of the approximations in both critical and pre-critical slowness matches is the same, where only the wide-angle power series coefficients are different. Comparing the approximated kinematical characteristics with those obtained by exact numerical ray tracing, we demonstrate high accuracy. Furthermore, we show that for all wave types, the accuracy of the pre-critical slowness match is essentially higher than that of the critical slowness match, even for matching slowness values close to the critical slowness. Both approaches can be valuable for implementation, depending on the target offset range and the nature of the subsurface model. The pre-critical slowness match is more accurate for simulating reflection data with conventional offsets. The critical slowness match can be attractive for models with a dominant high-velocity layer, for simulating, for example, refraction events with very long offsets.
INTRODUCTION
A review of the existing studies about moveout approximations for homogeneous and layered orthorhombic models is provided in Part I of this work; therefore, we only mention here the most relevant works for the current study. For long offsets in azimuthally isotropic layered media (e.g. VTI), Fomel and Stovas (2010) and Stovas and Fomel (2012) proposed the ‘generalized moveout approximations’ in both offset and slowness domains, respectively. This method requires information from an additional long-offset (wide-angle) ray. Alternative formulae, which are valid for an extended offset/slowness range, up to the case of nearly horizontal rays in multi-layer VTI media, have been presented in the offset domain by Ravve and Koren (2017) and in the slowness domain by Koren and Ravve (2018). In Part I of this work, we have extended the theory presented by Koren and Ravve (2018) from VTI to orthorhombic layered models, where, for each slowness azimuth, the additional wide-angle ray was considered to be the critical ray (critical slowness match). It was assumed that the model includes a dominant high-velocity layer, and that for nearly critical rays, most of the contributions to the offset and traveltime are due to the propagation in the high-velocity layer. In this work, Part II, the assumption of a dominant high-velocity layer is removed, and instead of the critical ray, a long-offset pre-critical ray is used. We derive the azimuthally varying slowness-domain kinematical characteristics (radial and transverse offset components, intercept time and traveltime) for compressional and converted waves, where the detailed derivations are described within the appendices. In Appendices A and B, we derive all partial derivatives of the intercept time, needed for the pre-critical slowness match, including the mixed derivatives, and the higher derivatives. In Appendix C, we discuss the limit case of the pre-critical slowness match, and compare it with the critical slowness match.
Using the same synthetic models as in Part I, we demonstrated that the accuracy of the pre-critical slowness match is higher than the accuracy of the critical slowness match within the given bounded slowness range.
Although this two-part paper is devoted to the forward computation of the kinematical characteristics for layered orthorhombic media, we have added a section describing the main role of the kinematical characteristics and the corresponding set of effective parameters within the seismic inversion workflow.
APPROXIMATIONS FOR THE KINEMATICAL CHARACTERISTICS
 are different and will be derived in this work. The expressions for the slowness-domain kinematical characteristics presented in Part I are given as:
are different and will be derived in this work. The expressions for the slowness-domain kinematical characteristics presented in Part I are given as:
- For the radial offset,
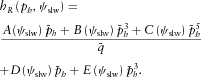 (1)
(1) - For the intercept time,
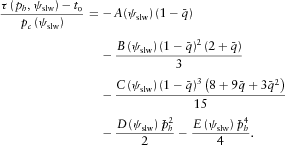 (2)
(2) - For the traveltime,
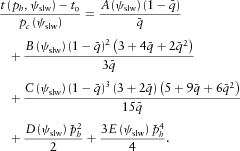 (3)
(3) - For the transverse offset,
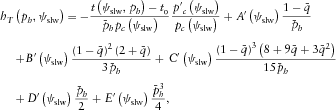 (4)
(4)
 are derivatives of coefficients
are derivatives of coefficients 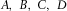 with respect to the slowness azimuth ψslw,
with respect to the slowness azimuth ψslw, 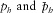 are the non-normalized and normalized horizontal slowness, respectively,
are the non-normalized and normalized horizontal slowness, respectively,  is the normalized complementary slowness,
is the normalized complementary slowness,
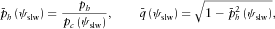 (5)
(5)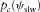 is the critical slowness at a given slowness azimuth ψslw.
is the critical slowness at a given slowness azimuth ψslw.COEFFICIENTS FOR THE PRE-CRITICAL SLOWNESS MATCH
 for the pre-critical slowness match differs from that for the critical slowness match. The first two equations are still related to the normal-incidence ray, whose second- and fourth-order normal moveout (NMO) velocities,
for the pre-critical slowness match differs from that for the critical slowness match. The first two equations are still related to the normal-incidence ray, whose second- and fourth-order normal moveout (NMO) velocities,  , can be computed for any pure-mode or converted wave type. Hence, like in Part I, the first two equations are given by
, can be computed for any pure-mode or converted wave type. Hence, like in Part I, the first two equations are given by
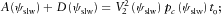 (6a)
(6a) (6b)
(6b)The three other equations are related to the pre-critical slowness match, and they are derived from the information given by the additional pre-critical traced ray. For 1D layered models, ray tracing actually means solving the vertical slowness equation A3 in Part I for the given horizontal slowness components,  . The vertical slowness in a given layer is used to compute the contribution of that layer into the intercept time. The partial derivatives,
. The vertical slowness in a given layer is used to compute the contribution of that layer into the intercept time. The partial derivatives,  , are then used to compute the contributions of that layer into the two offset components and the traveltime.
, are then used to compute the contributions of that layer into the two offset components and the traveltime.
 with respect to the normalized horizontal slowness
with respect to the normalized horizontal slowness  , the three additional conditions are
, the three additional conditions are
 (7a)
(7a) (7b)
(7b)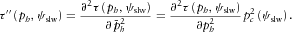 (7c)
(7c)Thus, for a given matching horizontal slowness magnitude  and azimuth ψslw, the values of the intercept time and its derivatives with respect to the normalized horizontal slowness are specified.
and azimuth ψslw, the values of the intercept time and its derivatives with respect to the normalized horizontal slowness are specified.
 is given by
is given by
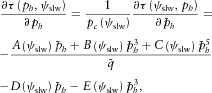 (8)
(8)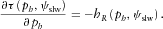 (9)
(9)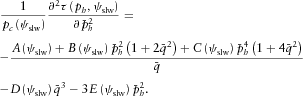 (10)
(10) and
and  for the normalized and non-normalized pre-critical matching horizontal slowness, respectively,
for the normalized and non-normalized pre-critical matching horizontal slowness, respectively,
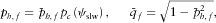 (11)
(11) is the normalized complementary matching slowness. Combining equations 2, (6), 8 and 10 and introducing the matching horizontal slowness instead of an arbitrary horizontal slowness,
is the normalized complementary matching slowness. Combining equations 2, (6), 8 and 10 and introducing the matching horizontal slowness instead of an arbitrary horizontal slowness,  we obtain the resolving linear set. The five equations can be arranged in the following matrix form:
we obtain the resolving linear set. The five equations can be arranged in the following matrix form:
 (12)
(12)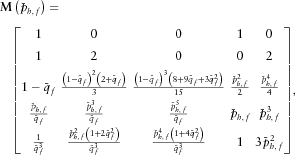 (13)
(13)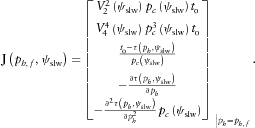 (14)
(14)The horizontal slowness  in equation 14 corresponds to the pre-critical matching horizontal slowness
in equation 14 corresponds to the pre-critical matching horizontal slowness  . Solving the linear set of five equations for the given fixed magnitude and azimuth of the horizontal slowness (pre-critical slowness match), we find the unknown azimuthally dependent coefficients
. Solving the linear set of five equations for the given fixed magnitude and azimuth of the horizontal slowness (pre-critical slowness match), we find the unknown azimuthally dependent coefficients 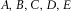 . We note that only the right-hand side vector J depends on the slowness azimuth. Its components have units of distance. The matrix components are independent of the azimuth. These components are normalized (unitless). The unknown variables also have units of distance. Once the approximation coefficients are obtained, the horizontal slowness in the approximation formulae (1)–(3) can accept any value, not to exceed the matching limit,
. We note that only the right-hand side vector J depends on the slowness azimuth. Its components have units of distance. The matrix components are independent of the azimuth. These components are normalized (unitless). The unknown variables also have units of distance. Once the approximation coefficients are obtained, the horizontal slowness in the approximation formulae (1)–(3) can accept any value, not to exceed the matching limit, 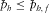 . For the normalized horizontal slowness
. For the normalized horizontal slowness  above the matching value, the errors of the approximations increase rapidly and catastrophically.
above the matching value, the errors of the approximations increase rapidly and catastrophically.
DERIVATIVES OF THE COEFFICIENTS FOR PRE-CRITICAL SLOWNESS MATCH
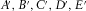 . First, azimuthal derivatives can be computed from the equations for the second- and fourth-order normal moveout (NMO) velocities,
. First, azimuthal derivatives can be computed from the equations for the second- and fourth-order normal moveout (NMO) velocities,
 (15)
(15)Next, we differentiate equations 2, 8 and 10 (for the intercept time τ and its derivatives 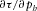 ,
,  ) with respect to the slowness azimuth ψslw, keeping the normalized horizontal slowness
) with respect to the slowness azimuth ψslw, keeping the normalized horizontal slowness  constant. Constant
constant. Constant  also means constant normalized complementary slowness
also means constant normalized complementary slowness  , because
, because  .
.
 (16)
(16)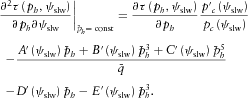 (17)
(17)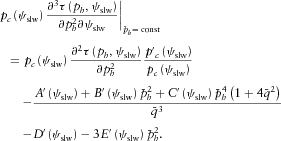 (18)
(18) (19)
(19) is the same as in equation 12, and its components are listed in equation 13. The right-hand side vector is different,
is the same as in equation 12, and its components are listed in equation 13. The right-hand side vector is different,
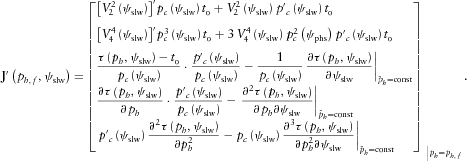 (20)
(20) . Once the approximation coefficients are obtained, the horizontal slowness in the approximation formula (4) can accept any value within the range of
. Once the approximation coefficients are obtained, the horizontal slowness in the approximation formula (4) can accept any value within the range of  . We emphasize that when computing the azimuthal derivatives, keeping the normalized horizontal slowness
. We emphasize that when computing the azimuthal derivatives, keeping the normalized horizontal slowness  constant is not the same as keeping the horizontal slowness
constant is not the same as keeping the horizontal slowness  constant, because the normalizing factor – the critical slowness
constant, because the normalizing factor – the critical slowness 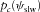 – depends on the slowness azimuth. It follows from equation 20 that three such derivatives are needed,
– depends on the slowness azimuth. It follows from equation 20 that three such derivatives are needed,
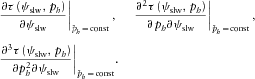 (21)
(21)Note that the notation for the constant  is related to the derivative with respect to the slowness azimuth only. The relationships between the azimuthal derivatives keeping
is related to the derivative with respect to the slowness azimuth only. The relationships between the azimuthal derivatives keeping  constant and those keeping
constant and those keeping  constant are given in Appendix A. Thus, we first compute regular partial derivatives of the intercept time (either with respect to the horizontal slowness magnitude, keeping the slowness azimuth constant, or vice versa). Next, we apply the relationships of Appendix A to establish the values for equation 21.
constant are given in Appendix A. Thus, we first compute regular partial derivatives of the intercept time (either with respect to the horizontal slowness magnitude, keeping the slowness azimuth constant, or vice versa). Next, we apply the relationships of Appendix A to establish the values for equation 21.
DERIVATIVES OF THE INTERCEPT TIME
 (23)
(23)where i is the layer index,  is the two-way intercept time of layer i,
is the two-way intercept time of layer i,  is the layer thickness and n is the number of layers in the model. Parameters
is the layer thickness and n is the number of layers in the model. Parameters 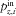 and
and  represent the vertical slowness of the ith layer for the incident and reflected waves (both are positive values). They depend on the wave mode, and, therefore, they are identical for pure-mode waves and different for converted waves. Thus, to obtain the derivatives of the intercept time, we just compute the derivatives of the slowness surface (the derivatives of the vertical slowness with respect to the magnitude and azimuth of the horizontal slowness), and stack these derivatives with the corresponding weights; each weight is the layer thickness
represent the vertical slowness of the ith layer for the incident and reflected waves (both are positive values). They depend on the wave mode, and, therefore, they are identical for pure-mode waves and different for converted waves. Thus, to obtain the derivatives of the intercept time, we just compute the derivatives of the slowness surface (the derivatives of the vertical slowness with respect to the magnitude and azimuth of the horizontal slowness), and stack these derivatives with the corresponding weights; each weight is the layer thickness  . The derivatives of the slowness surface, for all wave types propagating within the layered orthorhombic media, are obtained analytically by implicit differentiation of the Christoffel polynomial equation, as described in Appendix B.
. The derivatives of the slowness surface, for all wave types propagating within the layered orthorhombic media, are obtained analytically by implicit differentiation of the Christoffel polynomial equation, as described in Appendix B.
SYNTHETIC EXAMPLES
To test the accuracy of the pre-critical slowness match for the kinematical characteristics (the radial and transverse offset, intercept time and traveltime), we compute the relative errors of the approximations comparing them with the values computed by numerical ray tracing. We consider the same homogeneous and layered orthorhombic models as used in Part I, studying compressional waves and two types of converted waves, P–S1 and P–S2. The elastic and geometric properties of the layers for the two models are listed in Tables 1 and 2 in Part I. The error plots and maximum error tables demonstrate higher accuracy of the pre-critical slowness match that decreases as the matching slowness increases.
 |
Wave Type |
 |
Radial Offset | Transverse | Intercept Time | Traveltime |
|---|---|---|---|---|---|---|
| 0.86 | P–P | 3.905 |
 |
 |
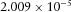 |
 |
| P–S1 | 2.554 |
 |
 |
 |
 |
|
| P–S2 | 2.572 |
 |
 |
 |
 |
|
| 0.90 | P–P | 4.887 |
 |
 |
 |
 |
| P–S1 | 3.070 |
 |
 |
 |
 |
|
| P–S2 | 3.092 |
 |
 |
 |
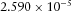 |
|
| 0.92 | P–P | 5.617 |
 |
 |
 |
 |
| P–S1 | 3.447 |
 |
 |
 |
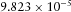 |
|
| P–S2 | 3.470 |
 |
 |
 |
 |
|
| 0.95 | P–P | 7.399 |
 |
 |
 |
 |
| P–S1 | 4.356 |
 |
 |
 |
 |
|
| P–S2 | 4.382 |
 |
 |
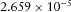 |
 |
|
| 0.97 | P–P | 9.808 |
 |
 |
 |
 |
| P–S1 | 5.573 |
 |
 |
 |
 |
|
| P–S2 | 5.600 |
 |
 |
 |
 |
|
| 1 | P–P | ∞ | 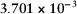 |
 |
 |
 |
| P–S1 | ∞ |
 |
 |
 |
 |
|
| P–S2 | ∞ |
 |
 |
 |
 |
 |
Wave Type |  |
Radial Offset | Transverse | Intercept Time | Traveltime |
|---|---|---|---|---|---|---|
| 0.90 | P–P | 2.202 |  |
 |
 |
 |
| P–S1 | 1.438 |  |
 |
 |
 |
|
| P–S2 | 1.509 |  |
 |
 |
 |
|
| 0.92 | P–P | 2.373 |  |
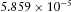 |
 |
 |
| P–S1 | 1.532 |  |
 |
 |
 |
|
| P–S2 | 1.603 |  |
 |
 |
 |
|
| 0.95 | P–P | 2.743 |  |
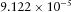 |
 |
 |
| P–S1 | 1.729 |  |
 |
 |
 |
|
| P–S2 | 1.802 |  |
 |
 |
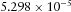 |
|
| 0.98 | P–P | 3.589 |  |
 |
 |
 |
| P–S1 | 2.164 |  |
 |
 |
 |
|
| P–S2 | 2.238 |  |
 |
 |
 |
|
| 0.99 | P–P | 4.448 |  |
 |
 |
 |
| P–S1 | 2.598 |  |
 |
 |
 |
|
| P–S2 | 2.672 |  |
 |
 |
 |
|
| 0.995 | P–P | 5.620 | 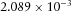 |
 |
 |
 |
| P–S1 | 3.186 |  |
 |
 |
 |
|
| P–S2 | 3.261 |  |
 |
 |
 |
|
| 0.998 | P–P | 7.910 |  |
 |
 |
 |
| P–S1 | 4.332 |  |
 |
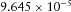 |
 |
|
| P–S2 | 4.407 | 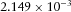 |
 |
 |
 |
|
| 0.999 | P–P | 10.48 |  |
 |
 |
 |
| P–S1 | 5.615 | 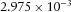 |
 |
 |
 |
|
| P–S2 | 5.691 |  |
 |
 |
 |
|
| 1 | P–P | ∞ | 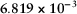 |
 |
 |
 |
| P–S1 | ∞ |  |
 |
 |
 |
|
| P–S2 | ∞ |  |
 |
 |
 |
Accuracy of the homogeneous model
Figures 1, 2 and 3 demonstrate the accuracy of the approximations for compressional waves, for the normalized matching horizontal slowness values  , respectively. Figures 4, 5 and 6 demonstrate the accuracy for P–S1 converted waves for the same matching horizontal slowness, and Figs 7, 8 and 9 for P–S2 converted waves. The relative errors are plotted for all slowness azimuths and for all magnitudes of the horizontal slowness, up to the matching values.
, respectively. Figures 4, 5 and 6 demonstrate the accuracy for P–S1 converted waves for the same matching horizontal slowness, and Figs 7, 8 and 9 for P–S2 converted waves. The relative errors are plotted for all slowness azimuths and for all magnitudes of the horizontal slowness, up to the matching values.
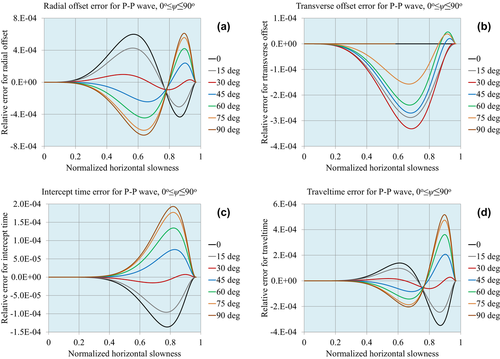
 : (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.
: (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.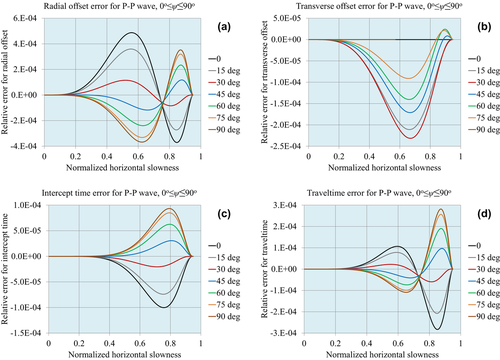
 : (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.
: (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.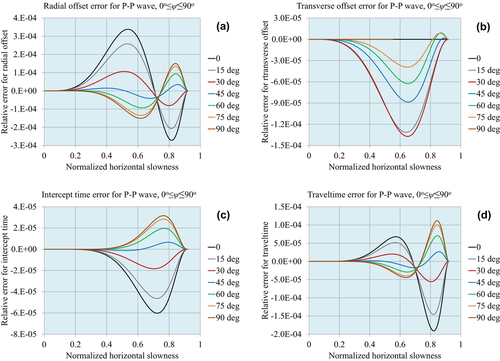
 : (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.
: (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.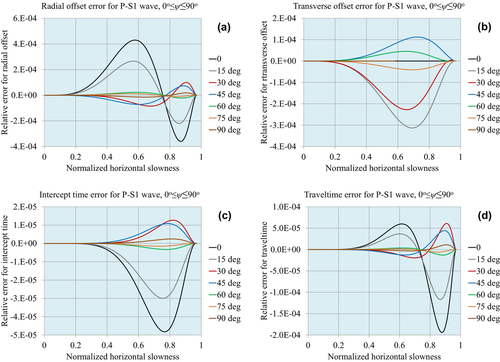
 : (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.
: (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.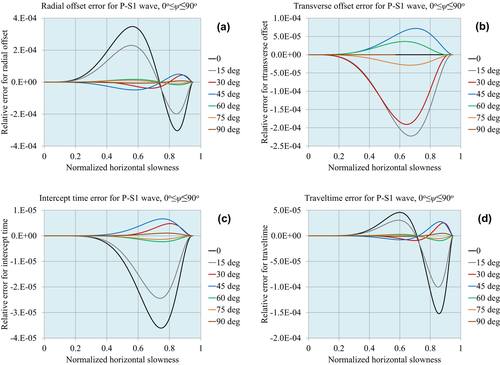
 : (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.
: (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.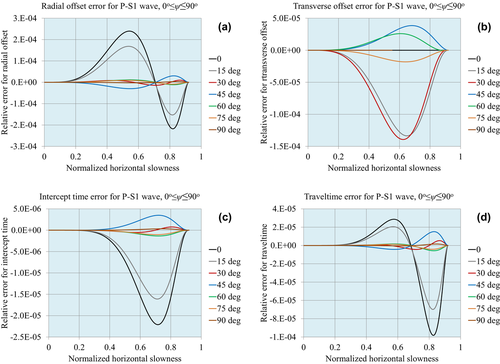
 : (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.
: (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.
 : (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.
: (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.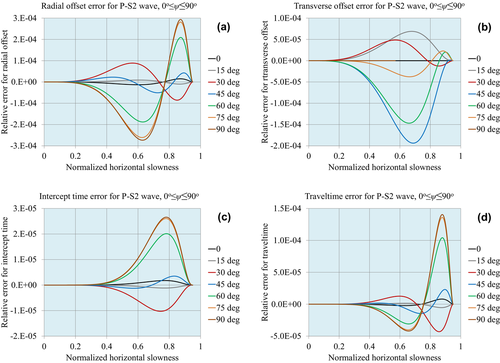
 : (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.
: (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.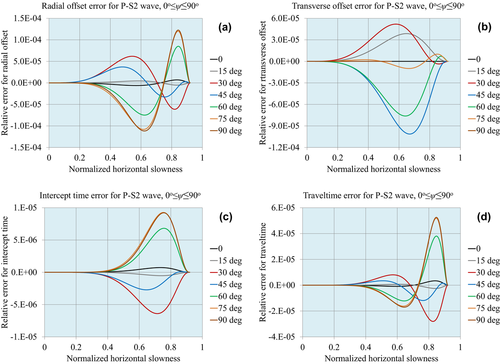
 : (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.
: (a) radial offset, (b) transverse offset, (c) intercept time and (d) traveltime.Accuracy of the layered model
Figures 10, 11 and 12 demonstrate the accuracy of the approximations for compressional waves, for the normalized matching horizontal slowness values 
 , respectively. Figures 13, 14 and 15 demonstrate the accuracy for P–S1 converted waves for the same matching horizontal slowness, and Figs 16, 17 and 18 for P–S2 converted waves. For the pre-critical slowness match, the same tendency holds as for the critical slowness match. The intercept time approximation is more accurate than the approximations for the radial offset and the traveltime, because the integration operator smoothens off the errors/inaccuracies of the function under the integral operator.
, respectively. Figures 13, 14 and 15 demonstrate the accuracy for P–S1 converted waves for the same matching horizontal slowness, and Figs 16, 17 and 18 for P–S2 converted waves. For the pre-critical slowness match, the same tendency holds as for the critical slowness match. The intercept time approximation is more accurate than the approximations for the radial offset and the traveltime, because the integration operator smoothens off the errors/inaccuracies of the function under the integral operator.
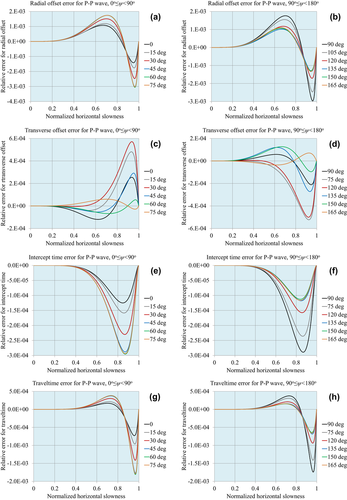
 : (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.
: (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.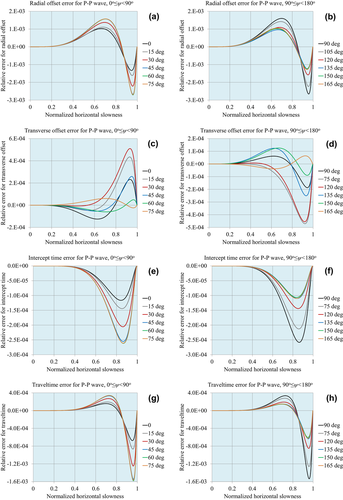
 : (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.
: (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.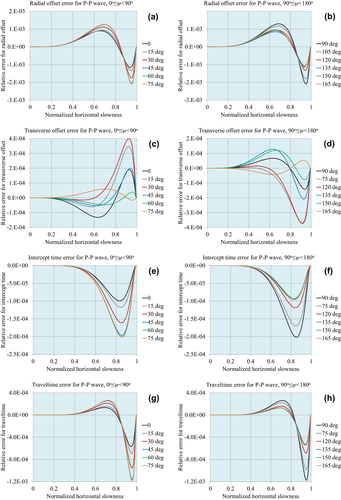
 : (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.
: (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.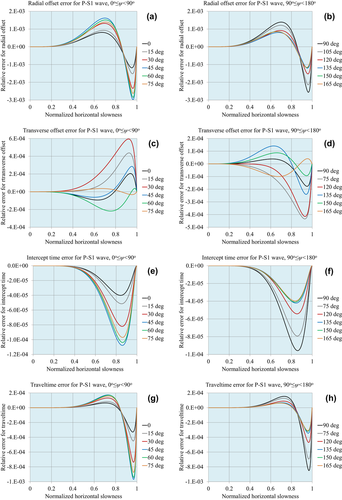
 : (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.
: (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.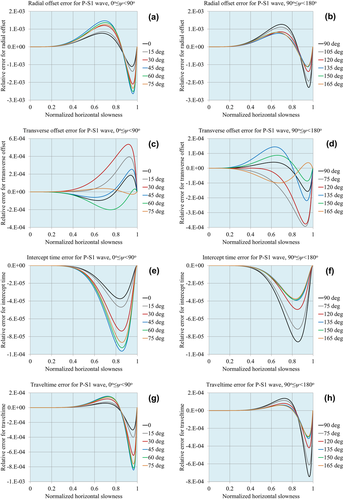
 : (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.
: (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.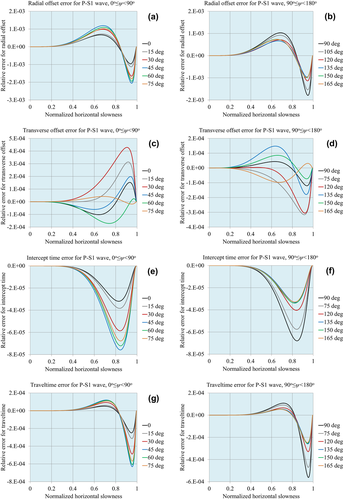
 : (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.
: (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.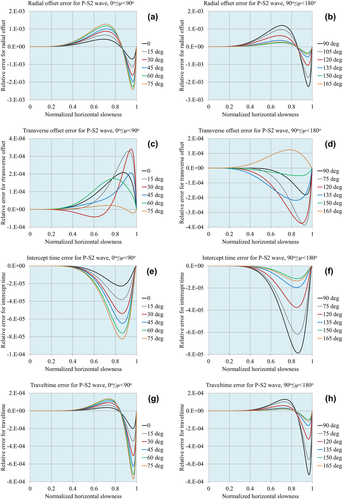
 : (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.
: (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.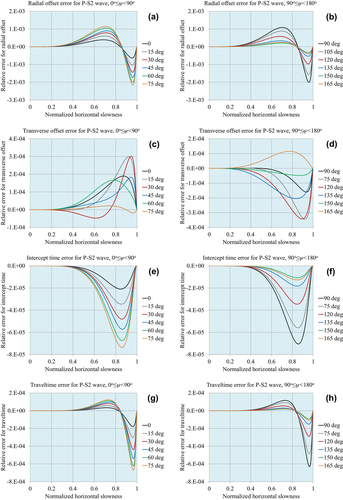
 : (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.
: (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.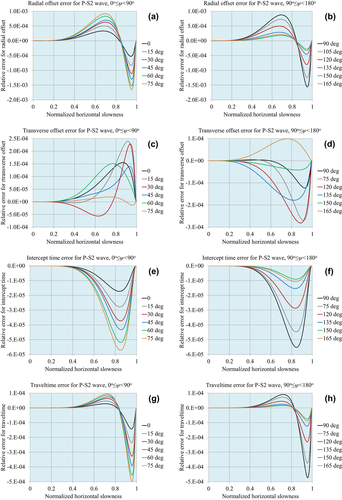
 : (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.
: (a) radial offset in the first azimuthal quadrant, (b) radial offset in the second quadrant, (c) transverse offset in the first quadrant, (d) transverse offset in the second quadrant, (e) intercept time in the first quadrant, (f) intercept time in the second quadrant, (g) traveltime in the first quadrant and (h) traveltime in the second quadrant.Tables 1 and 2 summarize the maximum relative errors for all magnitudes and azimuths of the horizontal slowness for the homogeneous and layered orthorhombic models, respectively. The first column in these tables shows the matching pre-critical slowness. Critical slowness match is considered a particular case. The second column is the wave type.
The normalized matching horizontal slowness  is a suitable computational parameter; however, the offset-to-depth ratio is more informative. Given a fixed normalized or non-normalized horizontal slowness (
is a suitable computational parameter; however, the offset-to-depth ratio is more informative. Given a fixed normalized or non-normalized horizontal slowness ( or
or  ), the offset-to-depth ratio in an orthorhombic model becomes azimuthally dependent. However, the exact value for each azimuth is not that essential, and therefore, we computed the average value for all slowness azimuths (column 3). The incidence and reflection angles are also azimuthally dependent for constant
), the offset-to-depth ratio in an orthorhombic model becomes azimuthally dependent. However, the exact value for each azimuth is not that essential, and therefore, we computed the average value for all slowness azimuths (column 3). The incidence and reflection angles are also azimuthally dependent for constant  .
.
Note that the normalized slowness matching values (0.999, 0.998 and 0.995) applied for the layered model were intentionally chosen much closer to the critical slowness than the matching values that we used for the homogeneous model (0.97, 0.95 and 0.92). For a multi-layer model, when  approaches 1, the offset-to-depth ratio increases with a smaller rate than for a single layer. The reason is the low-velocity layers, whose contribution to the offset (and traveltime) remains finite as the normalized slowness approaches 1. Columns 4–7 show the maximum relative errors for the four kinematical characteristics. The greatest errors are indicated in bold font and correspond to the critical slowness match.
approaches 1, the offset-to-depth ratio increases with a smaller rate than for a single layer. The reason is the low-velocity layers, whose contribution to the offset (and traveltime) remains finite as the normalized slowness approaches 1. Columns 4–7 show the maximum relative errors for the four kinematical characteristics. The greatest errors are indicated in bold font and correspond to the critical slowness match.
The accuracy of the approximations for the pre-critical slowness match is much higher than that for the critical slowness match, even in the cases when the matching slowness differs from the critical value by a couple of per cent (single-layer model) or even a small fraction of a per cent (multi-layer model).
DISCUSSION: THE ROLE OF KINEMATIC CHARACTERISTICS IN SEISMIC INVERSION
- Forward computation of the azimuthally varying effective parameters, or the five coefficients,
 plus the critical slowness
plus the critical slowness  , described in this two-part paper, for the background (migration-based) orthorhombic model. The superscript ‘bg’ indicates that the computation is performed on the ‘background’ model.
, described in this two-part paper, for the background (migration-based) orthorhombic model. The superscript ‘bg’ indicates that the computation is performed on the ‘background’ model.
- Analysing the RMOs: This stage requires first obtaining an explicit RMO formula for each normal-incidence (vertical) time and a given slowness azimuth. The explicit formula for the vertical time-scaled RMO,
 , is beyond the scope of this study. Although not essential, for simplicity, during the derivation of the RMO formula we assume that the critical slowness
, is beyond the scope of this study. Although not essential, for simplicity, during the derivation of the RMO formula we assume that the critical slowness 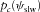 does not change and it corresponds to the background model.
does not change and it corresponds to the background model.  are the small perturbations of the effective parameters,
are the small perturbations of the effective parameters,  (and so forth all other parameters), where the superscript ‘up’ indicates ‘updated’ parameters. The explicit RMO formula is derived by setting to zero the full differential of the traveltime expression (preservation of the invariant traveltime of the seismic events) with respect to the normal-incidence (vertical) traveltime to, and all other, azimuthally dependent, effective parameters,
(and so forth all other parameters), where the superscript ‘up’ indicates ‘updated’ parameters. The explicit RMO formula is derived by setting to zero the full differential of the traveltime expression (preservation of the invariant traveltime of the seismic events) with respect to the normal-incidence (vertical) traveltime to, and all other, azimuthally dependent, effective parameters,  .
.
- The updated parameters,
 , make it possible to obtain the azimuthally dependent effective velocity parameters, for example, in the case of the ‘critical slowness match’,
, make it possible to obtain the azimuthally dependent effective velocity parameters, for example, in the case of the ‘critical slowness match’, 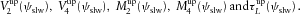
- A constrained generalized Dix-type approach can then be applied to obtain the local effective parameters between any two successive depth (vertical time) values. The azimuthally dependent local second- and fourth-order normal moveout (NMO) velocities
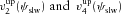 can then be inverted to provide the high and the low local NMO velocities at each layer, and the local azimuth of the high NMO velocity. A further constrained inversion can be applied to obtain the actual interval orthorhombic parameters and the azimuth of the local vertical symmetry planes.
can then be inverted to provide the high and the low local NMO velocities at each layer, and the local azimuth of the high NMO velocity. A further constrained inversion can be applied to obtain the actual interval orthorhombic parameters and the azimuth of the local vertical symmetry planes.
We believe that one should not underestimate the importance of the derived global and local effective parameters that provide explicit approximation formulae for the kinematical characteristics. Even within the frame of waveform- or ray-based inversions, the effective parameters provide valuable information (e.g. Zhang and Alkhalifah 2017). The seismic method, with all the available data, still cannot uniquely determine the complexity of the subsurface model, especially in areas characterized by considerable heterogeneity and anisotropy effects. The average nature of the effective parameters plays an important role in setting the framework of the model to be derived and the corresponding physical constraints to be applied.
CONCLUSIONS
Considering compressional and converted waves, we propose accurate, azimuthally dependent slowness-domain approximations for the kinematical characteristics: the radial and transverse offset components, intercept time and traveltime for horizontally layered orthorhombic models. The approximations are valid up to a given wide angle range. The approximations are based on merging the series expansion coefficients of the intercept time for two (virtual) rays: the normal-incidence ray and an additional azimuthally dependent wide-angle ray. In Part I, the wide-angle ray was considered the azimuthally varying critical ray, where we showed the effectiveness of this method in cases where the subsurface models include dominant high-velocity layers. In Part II, the requirement for a dominant high-velocity layer is removed, and the azimuthally varying wide-angle ray is associated with a finite long offset related to a given pre-critical slowness. The general form of the approximated formulae is the same; however, the coefficients are different. Within the given pre-critical slowness range, the accuracy of the pre-critical slowness match presented in Part II is higher than the accuracy obtained by the critical slowness match presented in Part I.
ACKNOWLEDGEMENTS
The authors are grateful to Emerson for the financial and technical support of this study and for the permission to publish its results. Gratitude is extended to reviewers Yanadet Sripanich and Alexey Stovas and to the associate editor of Geophysical Prospecting Tariq Alkhalifah for valuable comments and suggestions that helped to improve the content and style of this paper.
APPENDIX A: AZIMUTHAL DERIVATIVES FOR CONSTANT NORMALIZED SLOWNESS
 constant. This is not the same as the regular partial derivative
constant. This is not the same as the regular partial derivative  , where the non-normalized horizontal slowness
, where the non-normalized horizontal slowness  is kept constant. The reason is that the normalizing factor (the critical slowness) is azimuthally dependent,
is kept constant. The reason is that the normalizing factor (the critical slowness) is azimuthally dependent,  ,
,
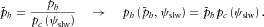 (A1)
(A1) , which may be in particular, but not necessarily, the intercept time . The azimuthal derivative for constant
, which may be in particular, but not necessarily, the intercept time . The azimuthal derivative for constant  reads
reads
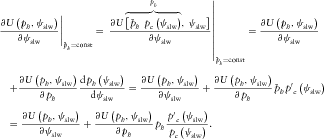 (A2)
(A2)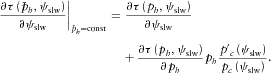 (A3)
(A3)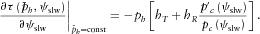 (A4)
(A4) , we obtain
, we obtain
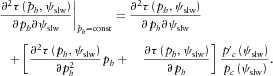 (A5)
(A5) (A6)
(A6)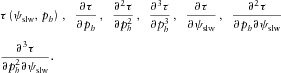 (A7)
(A7)Equation 23 relates the global two-way intercept time τ to the slowness surfaces of individual layers  and
and  , corresponding to the wave types of the incidence and reflection rays. Thus, to compute the derivatives of the intercept time, we need the corresponding derivatives of the slowness surfaces. The latter can be computed analytically for any wave type by implicit differentiation of the Christoffel polynomial equation for an orthorhombic medium, as explained in Appendix B.
, corresponding to the wave types of the incidence and reflection rays. Thus, to compute the derivatives of the intercept time, we need the corresponding derivatives of the slowness surfaces. The latter can be computed analytically for any wave type by implicit differentiation of the Christoffel polynomial equation for an orthorhombic medium, as explained in Appendix B.
 does not matter, we obtain one more useful relationship,
does not matter, we obtain one more useful relationship,
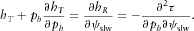 (A8)
(A8)APPENDIX B: DERIVATIVES OF THE SLOWNESS SURFACE
 of the slowness surface equation are functions of the horizontal slowness magnitude
of the slowness surface equation are functions of the horizontal slowness magnitude  and the azimuth ψslw (equations A4 and A8 of Part I). Computing successively the derivatives of the cubic polynomial, we obtain the derivatives of the slowness surface,
and the azimuth ψslw (equations A4 and A8 of Part I). Computing successively the derivatives of the cubic polynomial, we obtain the derivatives of the slowness surface,
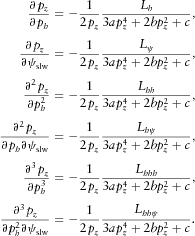 (B1)
(B1) in the numerators are auxiliary functions related to corresponding derivatives. Subscript h means ‘related to the derivative of the slowness surface with respect to the horizontal slowness magnitude’, while subscript ψ means ‘…with respect to the slowness azimuth’. The auxiliary functions are
in the numerators are auxiliary functions related to corresponding derivatives. Subscript h means ‘related to the derivative of the slowness surface with respect to the horizontal slowness magnitude’, while subscript ψ means ‘…with respect to the slowness azimuth’. The auxiliary functions are
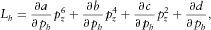 (B2)
(B2)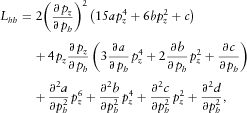 (B3)
(B3) (B4)
(B4)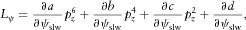 (B5)
(B5)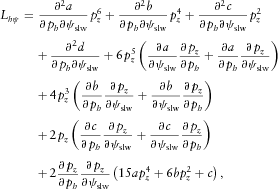 (B6)
(B6) (B7)
(B7) . These coefficients are listed in equation A8 in Part 1, and their derivatives read
. These coefficients are listed in equation A8 in Part 1, and their derivatives read
 (B8)
(B8)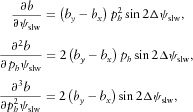 (B9)
(B9)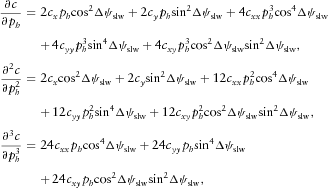 (B10)
(B10)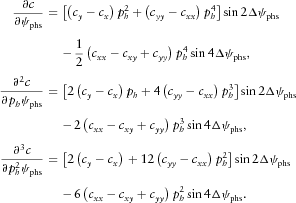 (B11)
(B11)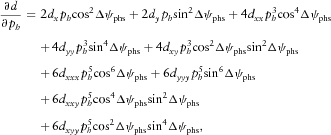 (B12a)
(B12a)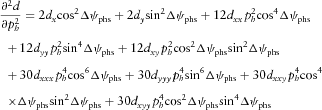 (B12b)
(B12b)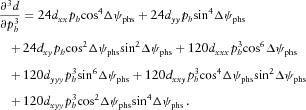 (B12c)
(B12c)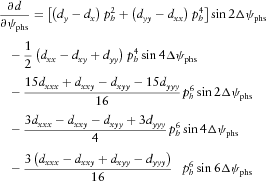 (B13a)
(B13a)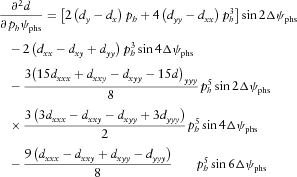 (B13b)
(B13b)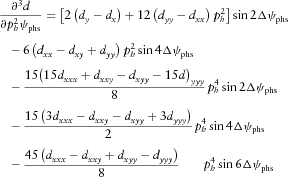 (B13c)
(B13c)Coefficients  depend on the material stiffness tensor components. They are listed in equations A4–A8 of Part I.
depend on the material stiffness tensor components. They are listed in equations A4–A8 of Part I.
APPENDIX C: A LIMIT CASE FOR THE PRE-CRITICAL SLOWNESS MATCH
 or
or  . The five azimuthally dependent coefficients governing the approximations of the kinematical characteristics
. The five azimuthally dependent coefficients governing the approximations of the kinematical characteristics  result from the linear equation set (12). The corresponding matrix M depends on the normalized horizontal slowness
result from the linear equation set (12). The corresponding matrix M depends on the normalized horizontal slowness  (equation 13), and the right-hand side depends on both the horizontal slowness and the slowness azimuth ψslw (equation 14). For the transverse offset component
(equation 13), and the right-hand side depends on both the horizontal slowness and the slowness azimuth ψslw (equation 14). For the transverse offset component  , we also need the azimuthal derivatives of the governing coefficients, which can be obtained from the linear set 19 with the same matrix and different right-hand side (equation 20). The critical slowness match cannot be considered a particular case of the pre-critical slowness match by assuming
, we also need the azimuthal derivatives of the governing coefficients, which can be obtained from the linear set 19 with the same matrix and different right-hand side (equation 20). The critical slowness match cannot be considered a particular case of the pre-critical slowness match by assuming  , because the matrix components include the normalized matching complementary slowness
, because the matrix components include the normalized matching complementary slowness 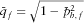 in the denominator. The right-hand side includes unbounded values as well. Recall that the first two equations, for the second- and fourth-order NMO velocities, correspond to the normal-incidence ray. These equations are the same for the pre-critical and critical slowness matches. Thus, the limit operator has to be applied to the last three equations of the set: for the intercept time and its first and second derivatives with respect to the normalized horizontal slowness. Note that as we approach the critical matching slowness, only low-velocity layers contribute to the intercept time, because the vertical slowness in the high-velocity layer vanishes. However, only the high-velocity layer contributes to the derivatives of the intercept time with respect to the horizontal slowness, because the first derivative of the intercept time is the radial offset. At the critical point, the contribution of the low-velocity layers to the offset is bounded, while that of the high-velocity layer is unbounded and prevails. The two equations of the linear set for the coefficients of the critical slowness match, responsible for M2 and M4, are (see equation set (2) of Part I),
in the denominator. The right-hand side includes unbounded values as well. Recall that the first two equations, for the second- and fourth-order NMO velocities, correspond to the normal-incidence ray. These equations are the same for the pre-critical and critical slowness matches. Thus, the limit operator has to be applied to the last three equations of the set: for the intercept time and its first and second derivatives with respect to the normalized horizontal slowness. Note that as we approach the critical matching slowness, only low-velocity layers contribute to the intercept time, because the vertical slowness in the high-velocity layer vanishes. However, only the high-velocity layer contributes to the derivatives of the intercept time with respect to the horizontal slowness, because the first derivative of the intercept time is the radial offset. At the critical point, the contribution of the low-velocity layers to the offset is bounded, while that of the high-velocity layer is unbounded and prevails. The two equations of the linear set for the coefficients of the critical slowness match, responsible for M2 and M4, are (see equation set (2) of Part I),
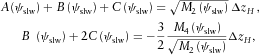 (C1)
(C1) is the thickness of the high-velocity layer. However, we do not obtain both of them in the limit case of the pre-critical slowness match from the equations responsible for the first and second derivatives of the intercept time with respect to the horizontal slowness. Instead, we obtain the first equation of set (C1) twice.
is the thickness of the high-velocity layer. However, we do not obtain both of them in the limit case of the pre-critical slowness match from the equations responsible for the first and second derivatives of the intercept time with respect to the horizontal slowness. Instead, we obtain the first equation of set (C1) twice. , responsible for M2 and M4, are (see equation set (29) of Part I),
, responsible for M2 and M4, are (see equation set (29) of Part I),
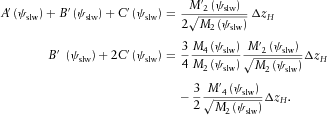 (C2)
(C2)Again, we do not obtain both of them in the limit case of the pre-critical slowness match. Instead, we obtain the first equation of set (C2) twice.
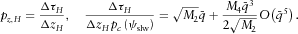 (C3)
(C3)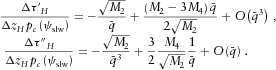 (C4)
(C4) , a smaller term containing
, a smaller term containing  (or a combination of both M2 and M4), and negligible high-order terms. As we approach the critical slowness
(or a combination of both M2 and M4), and negligible high-order terms. As we approach the critical slowness  , the first term with M2 prevails in both equations, for the first and second derivatives. In the limit case, the contribution of the second term with M4 vanishes as compared with the contribution of the first term with M2,
, the first term with M2 prevails in both equations, for the first and second derivatives. In the limit case, the contribution of the second term with M4 vanishes as compared with the contribution of the first term with M2,
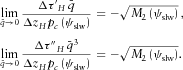 (C5)
(C5)As a result, in the limit case of the pre-critical slowness match, two equations of the set for either governing coefficients or their azimuthal derivatives become identical. Actually, in the limit case there are only four equations for five unknown variables, and the set becomes irresolvable. Thus, the limit case of the pre-critical slowness match does not converge to the critical slowness match. The reason is that the ‘pre-critical approach’ is based on matching the intercept time and its derivatives, while the ‘critical approach’ is based on the power series coefficients in the vicinity of the critical slowness. For the series with negative powers (normalized complementary slowness  in the denominator), these two approaches are not identical.
in the denominator), these two approaches are not identical.
As we demonstrated in the numerical example for the multi-layer orthorhombic model,  still leads to excellent results, exceeding the accuracy of the critical slowness match.
still leads to excellent results, exceeding the accuracy of the critical slowness match.
The resolving matrix of the pre-critical slowness match becomes non-invertible at the singular case  . In the critical slowness match approach, we directly study the case of the critical slowness,
. In the critical slowness match approach, we directly study the case of the critical slowness,  . The resolving matrix in this case is invertible, and the solutions for both approximation coefficients and their azimuthal derivatives are unique.
. The resolving matrix in this case is invertible, and the solutions for both approximation coefficients and their azimuthal derivatives are unique.
REFERENCES
| NOTATIONS | |
| Offset vector | |
| h | horizontal offset vector |
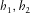 |
Cartesian offset components |
 |
radial offset component |
 |
contribution of the high-velocity layer into the radial offset |
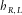 |
contribution of the low-velocity layers into the radial offset |
 |
transverse offset component |
 |
contribution of the high-velocity layer into the transverse offset |
 |
contribution of the low-velocity layers into the transverse offset |
| h | offset magnitude |
| ψoff | offset azimuth |
| Slowness vector | |
| p | slowness vector |
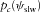 |
azimuthally dependent critical slowness |
 |
auxiliary coefficients needed to compute the critical slowness |
 |
horizontal slowness components in Cartesian frame |
 |
depth-dependent vertical slowness component (slowness surface) |
 |
depth-dependent slowness surface of the incidence ray |
 |
depth-dependent slowness surface of the reflection ray |
 |
slowness surface of the high-velocity layer |
 |
auxiliary parameters needed to compute derivatives of the slowness surface |
 |
horizontal slowness (magnitude) |
 |
pre-critical matching horizontal slowness |
 |
normalized horizontal slowness |
 |
normalized pre-critical matching horizontal slowness |
| q | complementary slowness |
 |
normalized complementary slowness |
 |
normalized complementary pre-critical matching slowness |
| ψslw | global slowness azimuth |
 |
local slowness azimuth, for a specific layer |
| Traveltime (two-way if not specified otherwise) | |
| t | reflection traveltime |
| to | vertical (normal-incidence) time |
 |
contribution of the high-velocity layer into the reflection traveltime |
 |
contribution of the low-velocity layers into the reflection traveltime |
| Intercept time (two-way if not specified otherwise) | |
| τ | intercept time |
 |
contribution of the high-velocity layer into the intercept time |
 |
contribution of the low-velocity layers into the intercept time |
| Global effective parameters (related to the entire multi-layer model) | |
 |
azimuthally dependent approximation coefficients (units of distance); in the case of pre-critical slowness match, the coefficients also depend on the matching slowness 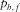 |
 |
derivatives of these coefficients with respect to the slowness azimuth ψslw |
| V1 | two-way average vertical velocity (azimuthally independent) |
 |
azimuthally dependent global second-order NMO velocity |
 |
azimuthally dependent global fourth-order NMO velocity |
 |
unitless azimuthally dependent second-order critical ray parameter |
 |
unitless azimuthally dependent fourth-order critical ray parameter |
 |
numerator of M2 |
 |
numerator of M4 |
 |
common denominator of M2 and M4 |
 |
second-order effective parameters of the normal-incidence ray |
 |
fourth-order effective parameters of the normal-incidence ray |
| M | resolving matrix of dimensions 5 × 5 for the critical slowness match |
 |
resolving matrix of dimensions 5 × 5 for the pre-critical slowness match |
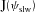 |
resolving vector of length 5 for the approximation coefficients (critical slowness match) |
 |
resolving vector of length 5 for the derivatives of the approximation coefficients (critical slowness match) |
 |
resolving vector of length 5 for the approximation coefficients (pre-critical slowness match) |
 |
resolving vector of length 5 for the derivatives of the approximation coefficients (pre-critical slowness match) |
| z | depth of reflection point |
 |
global frame of reference for multi-layer model; axis X1 corresponds to the zero (reference) azimuth. |
| Interval (layer) parameters (may have layer index) | |
| C | fourth-order stiffness tensor |
 |
components of the stiffness tensor in Voigt notation |
 |
Christoffel matrix (tensor) |
| I | second-order identity tensor |
 |
layer thickness |
 |
thickness of the high-velocity layer |
 |
contribution of an individual layer into the two-way intercept time |
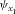 |
azimuth of the orthorhombic vertical symmetry plane  |
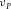 |
vertical compressional velocity |
 |
velocity of shear waves, propagating in x3 and polarized in x1 |
| f | factor relating vertical compressional and shear wave velocities |
 |
the normalized Tsvankin anisotropic coefficients for orthorhombic media |
 |
local second-order NMO velocity related to an individual layer |
 |
local fourth-order NMO velocity related to an individual layer |
 |
local slowness azimuth |
 |
coefficients of the Christoffel slowness-surface polynomial equation, depending on the horizontal slowness components |
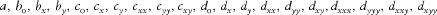 |
coefficients of the slowness-surface polynomial equation, depending on the material properties only |
 |
local frame of an orthorhombic layer whose axes are intersections of the corresponding symmetry planes |
| Approximation errors | |
 |
normalized (unitless) absolute error of the approximations |
 |
relative error of the approximations |
 |
parameter used to stabilize relative error of the intercept time (to avoid zero-divide) |



 in equation
in equation 
 and
and  ,
,  , are components of the right-hand side vectors in equation sets (12) and (19), respectively (listed in equations
, are components of the right-hand side vectors in equation sets (12) and (19), respectively (listed in equations 
