Normal moveout velocity for pure-mode and converted waves in layered orthorhombic medium
ABSTRACT
We study the azimuthally dependent hyperbolic moveout approximation for small angles (or offsets) for quasi-compressional, quasi-shear, and converted waves in one-dimensional multi-layer orthorhombic media. The vertical orthorhombic axis is the same for all layers, but the azimuthal orientation of the horizontal orthorhombic axes at each layer may be different. By starting with the known equation for normal moveout velocity with respect to the surface-offset azimuth and applying our derived relationship between the surface-offset azimuth and phase-velocity azimuth, we obtain the normal moveout velocity versus the phase-velocity azimuth. As the surface offset/azimuth moveout dependence is required for analysing azimuthally dependent moveout parameters directly from time-domain rich azimuth gathers, our phase angle/azimuth formulas are required for analysing azimuthally dependent residual moveout along the migrated local-angle-domain common image gathers. The angle and azimuth parameters of the local-angle-domain gathers represent the opening angle between the incidence and reflection slowness vectors and the azimuth of the phase velocity ψphs at the image points in the specular direction. Our derivation of the effective velocity parameters for a multi-layer structure is based on the fact that, for a one-dimensional model assumption, the horizontal slowness 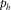 and the azimuth of the phase velocity ψphs remain constant along the entire ray (wave) path. We introduce a special set of auxiliary parameters that allow us to establish equivalent effective model parameters in a simple summation manner. We then transform this set of parameters into three widely used effective parameters: fast and slow normal moveout velocities and azimuth of the slow one. For completeness, we show that these three effective normal moveout velocity parameters can be equivalently obtained in both surface-offset azimuth and phase-velocity azimuth domains.
and the azimuth of the phase velocity ψphs remain constant along the entire ray (wave) path. We introduce a special set of auxiliary parameters that allow us to establish equivalent effective model parameters in a simple summation manner. We then transform this set of parameters into three widely used effective parameters: fast and slow normal moveout velocities and azimuth of the slow one. For completeness, we show that these three effective normal moveout velocity parameters can be equivalently obtained in both surface-offset azimuth and phase-velocity azimuth domains.
INTRODUCTION
In this work, we derive phase-domain azimuthally dependent normal moveout (NMO) velocities for quasi-compressional (qP-qP), quasi-shear (qS1-qS1, qS2-qS2), and converted (qP-qS1, qP-qS2, qS1-qS2) waves in 1D multi-layer orthorhombic media. For simplicity, from now on, we drop the term “quasi” and the prefix “q”, which refer to compressional and shear waves. It is assumed that the vertical orthorhombic axis is the same for all layers, but the elastic properties, the thickness, and the azimuthal orientation of the horizontal orthorhombic axes at each layer may be different. The phase-azimuth-domain moveout approximations are required for analysing azimuthally dependent residual moveout parameters from depth migrated gathers generated in the local angle domain (LAD) by full-azimuth angle domain imaging techniques (e.g., Koren and Ravve 2011 and the references within). The residual moveout curves result from the inaccuracy of the background orthorhombic model parameters used in the migration. For simple to moderate subsurface models, it is common practice to assume laterally varying local 1D models, where, although the model parameters change from location to location, for the residual moveout approximation, it is assumed that, locally, there are no lateral variations. Our derivation is then based on preserving the magnitude and azimuth of the horizontal slowness vector (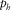 and ψphs) along the entire ray path in 1D models. It provides the NMO velocity and the NMO as a function of small offsets for each phase azimuth.
and ψphs) along the entire ray path in 1D models. It provides the NMO velocity and the NMO as a function of small offsets for each phase azimuth.
Small offset hyperbolic moveout approximations versus surface-offset azimuth for compressional, shear, and converted waves in 1D layered orthorhombic media have been presented by Grechka and Tsvankin (1998, 1999) and Grechka et al. (1999a,b). Thomsen (1999) analyzed the surface-offset-dependent moveout approximations for converted waves in a general inhomogeneous anisotropic medium. Bakulin et al. (2000, 2002) discussed modelling and inversion of the effective parameters for orthorhombic models formed by one or two orthogonal vertical fracture sets embedded in a vertical transverse isotropy (VTI) background, considering reflection moveout of P-P and P-S waves. Parameter estimation in orthorhombic layered media from P-P and P-S data was further explored by Grechka et al. (2005). A detailed discussion about the polarization of the fast and slow shear waves and the computation of their phase and ray velocity surfaces for media with symmetries lower than polar anisotropy has been presented in a recent paper by Grechka (2015). Overall, the offset-domain azimuthally dependent NMO approximations have been intensively explored and used for analysing azimuthal anisotropic parameters, such as intensity and orientation of aligned stress/fracture systems, from time or time-migrated gathers.
It has been shown (e.g., Koren and Ravve, 2011) that full-azimuth imaging in the LAD provides amplitude-preserved angle/azimuth-dependent reflectivity with higher accuracy and higher resolution. Our main aim in this work is to derive the phase-domain NMO velocities to establish explicit approximations for azimuthally dependent second-order residual moveout analysis in this domain, for all types of pure-mode and converted waves. Indeed, for compressional waves in layered orthorhombic media, higher order moveout approximations for longer offsets (wider angles) and for surface-offset azimuths have already been derived (Al-Dajani, Tsvankin, and Toksoz 1998; Grechka and Tsvankin 1998; Pech and Tsvankin 2004), and for phase azimuth by Ravve and Koren (2014) and Koren and Ravve (2015). However, in this work, in addition to compressional waves, we mainly concentrate on shear-wave propagation and converted P-S waves. The use of P-S methods in seismic exploration has been considered in the tutorial by Stewart et al. for isotropic (2002) and anisotropic (2003) media. It has been shown that converted waves experience more severe anisotropy than pure waves (e.g., Cary and Zhang 2010), where the azimuthal anisotropy causes shear-wave splitting of the converted waves into separate P-S1 and P-S2 waves (e.g., Wang, Hollis, and Nowry 2013). We therefore focus on studying the small offset moveout versus phase-velocity azimuth for the different pure-mode and converted waves.
Each layer is characterized by its thickness 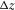 , azimuthal orientation of its local axis x1 (local azimuth
, azimuthal orientation of its local axis x1 (local azimuth 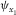 ), vertical compressional velocity vP, parameter f (explained in equation (2a) in the following) that depends on the ratio between the vertical shear velocity polarized in x1 and the vertical compressional velocity, and seven Thomsen-style parameters
), vertical compressional velocity vP, parameter f (explained in equation (2a) in the following) that depends on the ratio between the vertical shear velocity polarized in x1 and the vertical compressional velocity, and seven Thomsen-style parameters 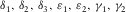 suggested by Tsvankin (1997); these parameters follow a similar anisotropic discretization for VTI (Thomsen 1986).
suggested by Tsvankin (1997); these parameters follow a similar anisotropic discretization for VTI (Thomsen 1986).
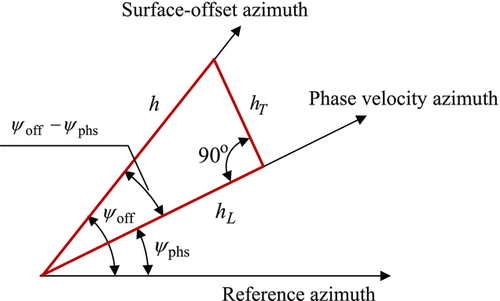
In a general anisotropic 1D medium, the horizontal slowness and azimuth of the phase velocity are constant through all layers. This statement follows from Snell's law, and it holds for both pure-mode and converted waves. In our previous study (Koren and Ravve 2014), we derived an analytic relationship for the azimuthal deviation between the phase and ray velocities in each individual layer. This azimuthal lag 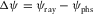 depends on the local fast and slow NMO velocities and the local “slow azimuth” (azimuth of the slow NMO velocity). With this relationship, we show that the ray-angle- and phase-angle-based approaches yield equivalent effective parameters for a layered azimuthally anisotropic 1D structure. We split the lateral propagation distance (offset) h into two horizontal components: lengthwise
depends on the local fast and slow NMO velocities and the local “slow azimuth” (azimuth of the slow NMO velocity). With this relationship, we show that the ray-angle- and phase-angle-based approaches yield equivalent effective parameters for a layered azimuthally anisotropic 1D structure. We split the lateral propagation distance (offset) h into two horizontal components: lengthwise 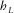 , along the phase-velocity azimuth ψphs, and transverse
, along the phase-velocity azimuth ψphs, and transverse 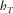 , in the normal direction
, in the normal direction 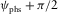 , as shown in the scheme in Fig. 1, where
, as shown in the scheme in Fig. 1, where 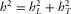 . A right triangle is shown in red, whose legs are
. A right triangle is shown in red, whose legs are 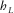 and
and 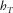 . Leg
. Leg 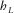 is in line with the phase-velocity azimuth ψphs, and the hypotenuse h is in line with the surface-offset azimuth ψoff. The acute angle adjacent to leg
is in line with the phase-velocity azimuth ψphs, and the hypotenuse h is in line with the surface-offset azimuth ψoff. The acute angle adjacent to leg 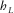 is
is 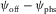 .
.
We establish the local NMO velocities and the lags between the ray and phase-velocity azimuths for individual layers, and we then generalize our findings from pure compressional and shear waves into the three types of converted waves, i.e., P-S1, P-S2, and S1-S2, and from a single layer to multi-layer media. We consider two numerical examples, one with weak anisotropy and the other with strong anisotropic parameters, where the hyperbolic approximations of the travel times are compared with travel times obtained through exact raytracing, studying all types of pure-mode and converted waves, for a multi-layer package. It is clearly seen, especially with strong anisotropy, that the accuracy of the hyperbolic approximations are acceptable only for short offsets, where the ratio between the maximum half-offset to the target depth is not larger than one half (∼27o half-opening angle). We define the opening angle as the angle between the incidence and reflection slowness vectors, assuming that the two rays emerge from the image point. Note that for compressional waves, the hyperbolic approximation loses its accuracy for strong anellipticities 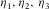 , and for shear waves, the loss of accuracy occurs even for relatively small anellipticity values, in particular for negative anellipticity. However, we show that even with the short offset (small angle) traces of the common image gathers, there is sufficient sensitivity to analyze the azimuthally varying moveout.
, and for shear waves, the loss of accuracy occurs even for relatively small anellipticity values, in particular for negative anellipticity. However, we show that even with the short offset (small angle) traces of the common image gathers, there is sufficient sensitivity to analyze the azimuthally varying moveout.
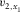 and
and 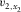 ), for both individual layers and the entire multi-layer structure. In Appendix C, we apply these relationships to establish the effective parameters of a layered structure, given the elastic properties of the layers, their thickness and azimuthal orientation, and the wave type. In Appendix D, we demonstrate that the three effective parameters (fast and slow NMO velocities and slow azimuth) can be equivalently calculated in both surface-offset azimuth and phase-velocity azimuth domains. We define S1 as the fast shear wave and S2 as the slow one.
), for both individual layers and the entire multi-layer structure. In Appendix C, we apply these relationships to establish the effective parameters of a layered structure, given the elastic properties of the layers, their thickness and azimuthal orientation, and the wave type. In Appendix D, we demonstrate that the three effective parameters (fast and slow NMO velocities and slow azimuth) can be equivalently calculated in both surface-offset azimuth and phase-velocity azimuth domains. We define S1 as the fast shear wave and S2 as the slow one. 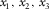 are local axes of a given orthorhombic layer, where the three planes of mirror symmetry intersect pairwise, whereas axis x3 is also the global vertical axis. Vertical shear waves are polarized along the orthorhombic axes x1 or x2. When studying the moveout approximations, we consider nearly vertical rays with an infinitesimal horizontal slowness
are local axes of a given orthorhombic layer, where the three planes of mirror symmetry intersect pairwise, whereas axis x3 is also the global vertical axis. Vertical shear waves are polarized along the orthorhombic axes x1 or x2. When studying the moveout approximations, we consider nearly vertical rays with an infinitesimal horizontal slowness 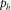 . One nearly vertical shear wave is polarized in the direction close to x1, notated in this study as Sx1. For the other shear wave, which is polarized in the direction close to x2, we use notation Sx2. The analysis of converted and shear waves in this study is performed on the assumption that the two differently polarized vertical shear wave velocities are different,
. One nearly vertical shear wave is polarized in the direction close to x1, notated in this study as Sx1. For the other shear wave, which is polarized in the direction close to x2, we use notation Sx2. The analysis of converted and shear waves in this study is performed on the assumption that the two differently polarized vertical shear wave velocities are different, 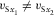 (or
(or 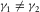 ). For a single orthorhombic layer, should we assume that
). For a single orthorhombic layer, should we assume that 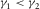 , then the x1 polarized wave is S1 (fast), and the x2 polarized wave is S2 (slow), i.e.,
, then the x1 polarized wave is S1 (fast), and the x2 polarized wave is S2 (slow), i.e.,
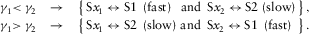 (1)
(1)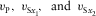 are vertical velocities of the compressional wave, shear wave polarized in x1, and shear wave polarized in x2, respectively. We use an auxiliary parameter f, which is related to the ratio between the vertical velocity of x1-polarized shear Sx1 and the vertical compressional velocity, i.e.,
are vertical velocities of the compressional wave, shear wave polarized in x1, and shear wave polarized in x2, respectively. We use an auxiliary parameter f, which is related to the ratio between the vertical velocity of x1-polarized shear Sx1 and the vertical compressional velocity, i.e.,
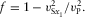 (2a)
(2a)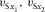 can be written as
can be written as
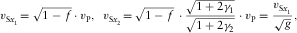 (2b)
(2b)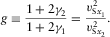 (2c)
(2c)For rays with an arbitrary direction of propagation, S1 and S2 are shear waves with larger and smaller shear phase velocities, respectively (rather than waves with larger and smaller vertical shear velocities for nearly vertical rays). We emphasize that fast shear means a higher velocity of the wave front propagation (and not necessarily a higher NMO velocity) as compared with the slow shear.
This work deals with a forward calculation of effective NMO velocity parameters for multi-layer orthorhombic models, which can then be used to compute phase-domain azimuthally varying NMO velocity to approximate the moveout. We reemphasize that the proposed moveout approximation in the phase-velocity azimuth domain is particularly important for analysing residual moveouts measured along full-azimuth common image reflection angle gathers. The use of the approximation formulas for the inversion of interval anisotropic velocity parameters is beyond the scope of this paper.
NORMAL MOVEOUT VELOCITY FOR A SINGLE ORTHORHOMBIC LAYER
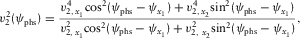 (3a)
(3a)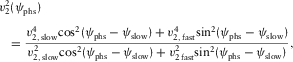 (3b)
(3b)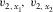 are the local axial NMO velocities in the directions of the local orthorhombic axes x1 and x2, respectively, and
are the local axial NMO velocities in the directions of the local orthorhombic axes x1 and x2, respectively, and 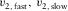 are the local fast and slow NMO velocities, respectively. These relationships can be compared with the well-known formulas derived by Grechka and Tsvankin (1998), where the local NMO velocity for a single layer is presented versus the ray-velocity azimuth, i.e.,
are the local fast and slow NMO velocities, respectively. These relationships can be compared with the well-known formulas derived by Grechka and Tsvankin (1998), where the local NMO velocity for a single layer is presented versus the ray-velocity azimuth, i.e.,
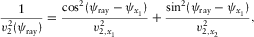 (3c)
(3c)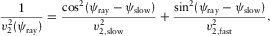 (3d)
(3d)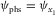 and
and 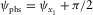 , respectively, where
, respectively, where 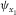 is the azimuth of the local orthorhombic axis x1. The axial NMO velocities are listed in Table 1, where the vertical shear velocities
is the azimuth of the local orthorhombic axis x1. The axial NMO velocities are listed in Table 1, where the vertical shear velocities 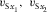 and parameter g are defined in equation (2), whereas σ1 and σ2 are
and parameter g are defined in equation (2), whereas σ1 and σ2 are
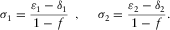 (4)
(4)| Wave type | Axial NMO velocity 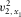 |
Axial NMO velocity 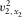 |
|---|---|---|
| pure-mode P |
 |
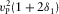 |
| pure-mode Sx1 |
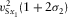 |
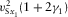 |
| pure-mode Sx2 |
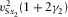 |
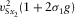 |
converted 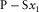 |
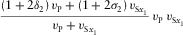 |
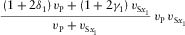 |
converted 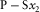 |
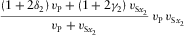 |
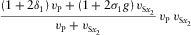 |
converted  |
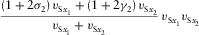 |
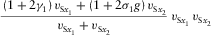 |
Our relationships for the axial NMO velocities for pure-mode compressional and shear waves, summarized in Table 1, match the results first published by Grechka et al. (1999a), which are based on the analysis of the ray-velocity azimuth. Note that, in the orthorhombic axial directions, the azimuths of the ray and phase velocities coincide. It is also important to note that the NMO velocity of shear wave Sx1 (polarized mainly in x1) in the azimuthal direction of axis x2 coincides with the NMO velocity of shear wave Sx2 (polarized mainly in x2) in the azimuthal direction of axis x1, i.e., the constraint 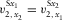 holds for any homogeneous orthorhombic layer. Note, however, that this is not true for multi-layer media where the two analogous global effective shear velocities are different, as we will see in a numerical example in the following. Grechka et al. (1999a, 1999b) emphasized that such constraint of shear velocities in the symmetry planes indicates a possible redundancy in the moveout measurements that can be used as a constraint to increase the accuracy of the inversion procedure.
holds for any homogeneous orthorhombic layer. Note, however, that this is not true for multi-layer media where the two analogous global effective shear velocities are different, as we will see in a numerical example in the following. Grechka et al. (1999a, 1999b) emphasized that such constraint of shear velocities in the symmetry planes indicates a possible redundancy in the moveout measurements that can be used as a constraint to increase the accuracy of the inversion procedure.
 (5a)
(5a)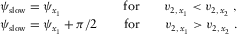 (5b)
(5b)The full derivation of the NMO velocity functions for pure-mode and converted waves for a single orthorhombic layer and a multi-layer structure is given in Appendix A. We note that the two-way offset is not equal to the algebraic sum of the one-way offsets (lateral propagations) in the case of converted waves in orthorhombic layered media, due to the varying azimuthal deviations between the phase and ray velocities for the incident and reflected rays. The incident and reflected phase-velocity azimuths are the same due to Snell's law. The incident and reflected ray-velocity azimuths are different in the case of P-S1, P-S2, or S1-S2 converted waves in the orthorhombic medium, as shown in Fig. 2. For a single layer, the lateral propagations of the incident and reflected rays should be added geometrically, i.e., we can add separately the lengthwise components  of the lateral propagation along the phase-velocity azimuth ψphs, and the transverse components
of the lateral propagation along the phase-velocity azimuth ψphs, and the transverse components 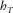 along the normal azimuth
along the normal azimuth 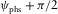 . The scheme in Fig. 2 shows a lateral projection of the two-way ray path. The surface offset is shown in the scheme by a red line. Angles
. The scheme in Fig. 2 shows a lateral projection of the two-way ray path. The surface offset is shown in the scheme by a red line. Angles 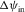 and
and 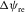 are azimuthal differences between the ray velocity and phase velocity for the incident and reflected waves, respectively. Both azimuthal deviations are known values or known functions of the Thomsen-like parameters and the azimuth of the phase velocity. For converted waves, these angles in the orthorhombic medium are unbalanced, i.e.,
are azimuthal differences between the ray velocity and phase velocity for the incident and reflected waves, respectively. Both azimuthal deviations are known values or known functions of the Thomsen-like parameters and the azimuth of the phase velocity. For converted waves, these angles in the orthorhombic medium are unbalanced, i.e., 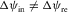 .
.
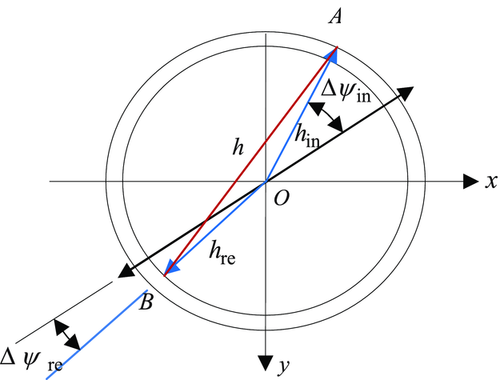
 are their magnitudes. Points A and B are locations of the source and receiver, respectively, and O is the projection of the reflection point onto the surface. Angles
are their magnitudes. Points A and B are locations of the source and receiver, respectively, and O is the projection of the reflection point onto the surface. Angles 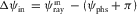 and
and 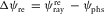 are the azimuthal lags between the incidence/reflection ray velocities and the phase velocity.
are the azimuthal lags between the incidence/reflection ray velocities and the phase velocity.AZIMUTHAL LAG AND NMO VELOCITY FOR A MULTI-LAYER PACKAGE
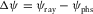 is the difference between the ray-velocity azimuth in a given layer and the phase-velocity azimuth. The global lag
is the difference between the ray-velocity azimuth in a given layer and the phase-velocity azimuth. The global lag 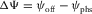 is the difference between the surface-offset azimuth (acquisition azimuth) and the phase-velocity azimuth. The local lag is related to one-way propagation within a given layer, whereas the global lag is related to two-way propagation along the multi-layer model. The global lag between the surface-offset azimuth ψoff and the phase-velocity azimuth ψphs, as shown in the scheme in Fig. 1, i.e.,
is the difference between the surface-offset azimuth (acquisition azimuth) and the phase-velocity azimuth. The local lag is related to one-way propagation within a given layer, whereas the global lag is related to two-way propagation along the multi-layer model. The global lag between the surface-offset azimuth ψoff and the phase-velocity azimuth ψphs, as shown in the scheme in Fig. 1, i.e.,
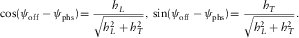 (6)
(6)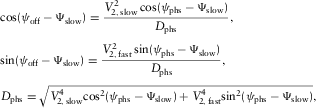 (7a)
(7a)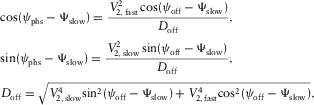 (7b)
(7b)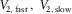 , and Ψslow are the global fast and slow NMO velocities and the azimuth of the global slow NMO velocity, respectively.
, and Ψslow are the global fast and slow NMO velocities and the azimuth of the global slow NMO velocity, respectively.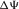 may also be expressed through the fast and slow global NMO velocities, the global slow azimuth, and either phase-velocity azimuth or surface-offset azimuth. It follows from equation (A-5) (written originally for the local lag) that
may also be expressed through the fast and slow global NMO velocities, the global slow azimuth, and either phase-velocity azimuth or surface-offset azimuth. It follows from equation (A-5) (written originally for the local lag) that
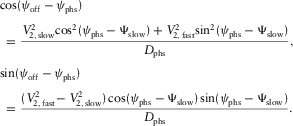 (7c)
(7c)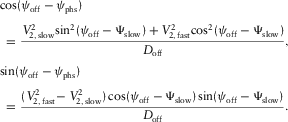 (7d)
(7d)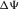 either through the phase-velocity azimuth or through the surface-offset azimuth. The global effective NMO velocity versus the phase azimuth and versus the offset azimuth, respectively, reads,
either through the phase-velocity azimuth or through the surface-offset azimuth. The global effective NMO velocity versus the phase azimuth and versus the offset azimuth, respectively, reads,
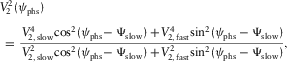 (8a)
(8a) (8b)
(8b)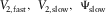 , respectively. With equation (8a) or (8b), we can use the standard hyperbolic moveout approximation
, respectively. With equation (8a) or (8b), we can use the standard hyperbolic moveout approximation
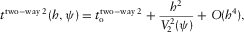 (9)
(9)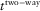 is the global two-way time,
is the global two-way time, 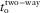 is the global two-way vertical time, and the azimuth ψ may be either the phase-velocity azimuth ψphs or the surface-offset azimuth ψoff. Estimation of the global effective NMO velocity parameters is explained in the following section.
is the global two-way vertical time, and the azimuth ψ may be either the phase-velocity azimuth ψphs or the surface-offset azimuth ψoff. Estimation of the global effective NMO velocity parameters is explained in the following section.PARAMETERS OF THE EFFECTIVE MODEL
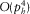 , and the errors of the offset components are
, and the errors of the offset components are 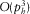 ; this accuracy is sufficient to establish the three exact global effective parameters for the normal moveout (NMO) velocity. For all types of pure-mode and converted waves, the governing equations for the effective models look alike, but the computed effective parameters are different. According to the formulas in Table 1, we first compute the two axial NMO velocities,
; this accuracy is sufficient to establish the three exact global effective parameters for the normal moveout (NMO) velocity. For all types of pure-mode and converted waves, the governing equations for the effective models look alike, but the computed effective parameters are different. According to the formulas in Table 1, we first compute the two axial NMO velocities, 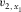 and
and 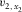 , related to the local orthorhombic axes x1 and x2. They depend on the given type of wave. We emphasize that all further equations in this section are generic and may be related to any type of conversion. The full derivation for the global effective parameters is presented in Appendices B and C. After the local axial NMO velocities for the pure-mode waves have been established, we introduce and compute the following local auxiliary parameters (
, related to the local orthorhombic axes x1 and x2. They depend on the given type of wave. We emphasize that all further equations in this section are generic and may be related to any type of conversion. The full derivation for the global effective parameters is presented in Appendices B and C. After the local axial NMO velocities for the pure-mode waves have been established, we introduce and compute the following local auxiliary parameters (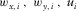 ) and global auxiliary parameters (
) and global auxiliary parameters (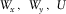 ),
),
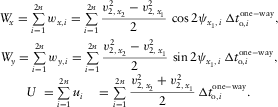 (10)
(10)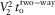 for azimuthally isotropic layered medium (e.g., isotropy or vertical transverse isotropy). Parameter
for azimuthally isotropic layered medium (e.g., isotropy or vertical transverse isotropy). Parameter 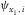 is the local azimuth of the orthorhombic axis x1 for a given layer i. Parameter
is the local azimuth of the orthorhombic axis x1 for a given layer i. Parameter 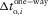 in equation 10 is the one-way local vertical time for the corresponding type of wave, and all layer auxiliary parameters are summed twice. The local one-way vertical time reads as follows:
in equation 10 is the one-way local vertical time for the corresponding type of wave, and all layer auxiliary parameters are summed twice. The local one-way vertical time reads as follows:
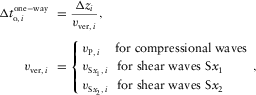 (11)
(11)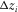 is the layer thickness, and
is the layer thickness, and 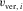 is the vertical velocity for the given type of wave. Next, we compute the slow azimuth of the global effective model (see Appendix C), i.e.,
is the vertical velocity for the given type of wave. Next, we compute the slow azimuth of the global effective model (see Appendix C), i.e.,
 (12a)
(12a)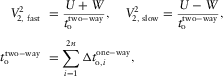 (12b)
(12b)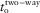 is the total two-way vertical time of the multi-layer package for the given type of pure-mode or converted wave.
is the total two-way vertical time of the multi-layer package for the given type of pure-mode or converted wave.DISCUSSION: RESIDUAL MOVEOUT
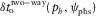 , and these errors can be associated with the azimuthally dependent variations of the effective NMO velocity
, and these errors can be associated with the azimuthally dependent variations of the effective NMO velocity 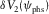 . Within the accuracy of the hyperbolic approximation, the travel time is delivered by equation 9. Assuming that the travel time and the offset components are preserved in the background and the updated (true) models, the change in vertical time is the result of the NMO velocity variation, i.e.,
. Within the accuracy of the hyperbolic approximation, the travel time is delivered by equation 9. Assuming that the travel time and the offset components are preserved in the background and the updated (true) models, the change in vertical time is the result of the NMO velocity variation, i.e.,
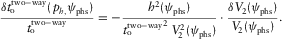 (13)
(13)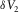 compensates the RMO
compensates the RMO 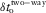 . According to equations (B-13) and (7b), the offset approximation versus the phase-velocity azimuth and versus the surface-offset azimuth reads as follows:
. According to equations (B-13) and (7b), the offset approximation versus the phase-velocity azimuth and versus the surface-offset azimuth reads as follows:
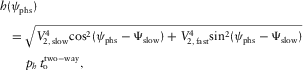 (14a)
(14a) (14b)
(14b)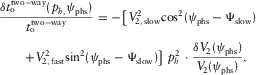 (15a)
(15a)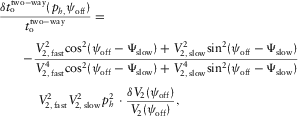 (15b)
(15b)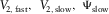 , the function for the NMO velocity
, the function for the NMO velocity 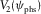 or
or 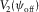 , and the vertical time
, and the vertical time 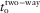 are related to the background model. In case of an azimuthally isotropic background effective model (with all layers isotropic or VTI), the relationship simplifies to the following:
are related to the background model. In case of an azimuthally isotropic background effective model (with all layers isotropic or VTI), the relationship simplifies to the following:
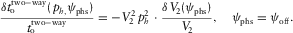 (15c)
(15c)As a result, we obtain the residual NMO velocity 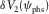 that makes it possible to update the effective fast and slow NMO velocities and the effective slow azimuth, related to the given top and bottom horizons. One can then use a generalized Dix-type inversion (e.g., Koren and Ravve 2014, for compressional waves) to obtain the local fast and slow NMO velocities of the layer and the orientation of its lateral orthorhombic axes. Alternatively, the residual moveout can be used as input for global tomography.
that makes it possible to update the effective fast and slow NMO velocities and the effective slow azimuth, related to the given top and bottom horizons. One can then use a generalized Dix-type inversion (e.g., Koren and Ravve 2014, for compressional waves) to obtain the local fast and slow NMO velocities of the layer and the orientation of its lateral orthorhombic axes. Alternatively, the residual moveout can be used as input for global tomography.
NUMERICAL EXAMPLES
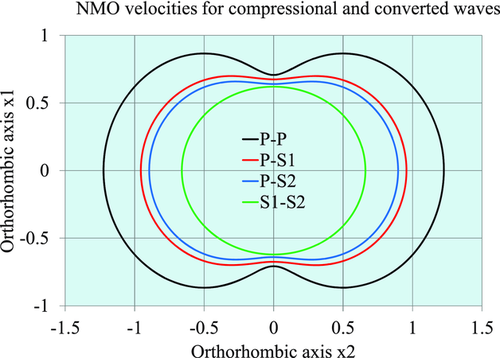
In Fig. 3, the normal moveout (NMO) velocities (divided by the vertical compressional velocity vP) are plotted versus the phase-velocity azimuth for the pure-mode compressional wave and for the three types of converted waves, with the corresponding shear polarizations, for an orthorhombic medium. The following parameters are used: 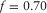 ,
, 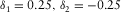 ,
, 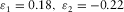 , and
, and 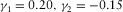 . In this example,
. In this example, 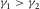 , and the fast shear wave S1 is polarized as Sx2, whereas the slow shear wave S2 is polarized as Sx1. The black line is a pure-mode compressional wave P-P, the red and blue lines are converted waves “compressional to fast shear” and “compressional to slow shear” (P-S1 and P-S2, respectively), and the green line is “shear to shear” converted wave S1-S2. In the phase-azimuth domain, in the case of strong azimuthal anisotropy, the NMO velocity plots may be essentially non-elliptic, as we see, for example for pure compressional wave in Fig. 3.
, and the fast shear wave S1 is polarized as Sx2, whereas the slow shear wave S2 is polarized as Sx1. The black line is a pure-mode compressional wave P-P, the red and blue lines are converted waves “compressional to fast shear” and “compressional to slow shear” (P-S1 and P-S2, respectively), and the green line is “shear to shear” converted wave S1-S2. In the phase-azimuth domain, in the case of strong azimuthal anisotropy, the NMO velocity plots may be essentially non-elliptic, as we see, for example for pure compressional wave in Fig. 3.
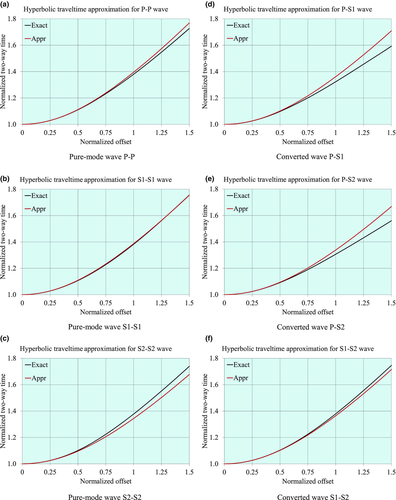
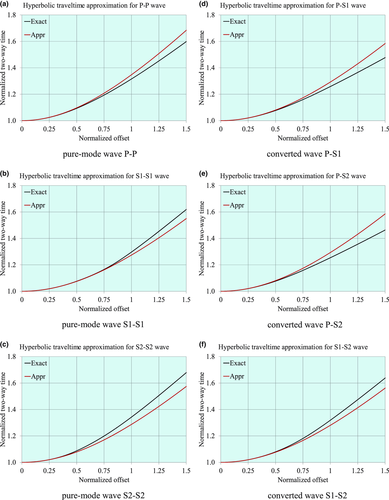
To evaluate the accuracy of the hyperbolic travel-time approximation versus phase-velocity azimuth 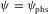 , for pure-mode and converted waves, we consider two multi-layer orthorhombic structures, with weak and strong anisotropy. The layer properties for the weak and strong anisotropy structures are listed in Tables 2 and 3, respectively. In Figs. 4 and 5, we compare the travel-time approximation with the exact raytracing solution, and we plot the global lag
, for pure-mode and converted waves, we consider two multi-layer orthorhombic structures, with weak and strong anisotropy. The layer properties for the weak and strong anisotropy structures are listed in Tables 2 and 3, respectively. In Figs. 4 and 5, we compare the travel-time approximation with the exact raytracing solution, and we plot the global lag 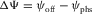 between the surface-offset azimuth and the phase-velocity azimuth for the weak anisotropy structure. In Figs. 6 and 7, the same analysis is performed for the strong anisotropy structure. The travel time is normalized by the two-way vertical time, and the offset is normalized by the doubled depth of the reflection point, i.e.,
between the surface-offset azimuth and the phase-velocity azimuth for the weak anisotropy structure. In Figs. 6 and 7, the same analysis is performed for the strong anisotropy structure. The travel time is normalized by the two-way vertical time, and the offset is normalized by the doubled depth of the reflection point, i.e., 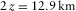 . In Figs. 4 and 6, we compare the hyperbolic approximation with the travel time obtained as a result of exact numerical raytracing for a package of orthorhombic layers, for all types of pure-mode and converted waves, for weak and strong anisotropy, respectively. In Figs. 4 and 6, the phase-velocity azimuth is kept constant, i.e.,
. In Figs. 4 and 6, we compare the hyperbolic approximation with the travel time obtained as a result of exact numerical raytracing for a package of orthorhombic layers, for all types of pure-mode and converted waves, for weak and strong anisotropy, respectively. In Figs. 4 and 6, the phase-velocity azimuth is kept constant, i.e., 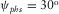 (and thus, the global NMO velocity V2 is also a constant value), whereas the offset h varies. The hyperbolic approximation of the travel time is given in equation 9, where the NMO velocity versus phase azimuth is computed with equation (8a).
(and thus, the global NMO velocity V2 is also a constant value), whereas the offset h varies. The hyperbolic approximation of the travel time is given in equation 9, where the NMO velocity versus phase azimuth is computed with equation (8a).
| Layer | δ1 | δ2 | δ3 | ε1 | ε2 | γ1 | γ2 | f |
 |
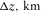 |
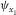 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.04 | −0.05 | 0.03 | 0.05 | 0.06 | −0.03 | −0.02 | 0.72 | 2.6 | 0.65 | 100.8o |
| 2 | 0.04 | −0.06 | −0.02 | 0.04 | 0.05 | −0.04 | 0.02 | 0.74 | 2.8 | 0.70 | 50.4o |
| 3 | 0.03 | −0.04 | 0.05 | 0.04 | 0.03 | 0.05 | −0.06 | 0.75 | 3.0 | 1.80 | 129.6o |
| 4 | 0.03 | −0.05 | 0.04 | 0.07 | 0.06 | 0.06 | −0.04 | 0.76 | 3.5 | 1.40 | 63.0o |
| 5 | 0.06 | −0.05 | 0.03 | 0.05 | 0.02 | 0.04 | −0.07 | 0.78 | 3.8 | 1.90 | 117.0o |
| Layer | δ1 | δ2 | δ3 | ε1 | ε2 | γ1 | γ2 | f |
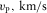 |
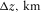 |
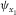 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.05 | −0.12 | 0.03 | 0.15 | 0.08 | −0.03 | −0.02 | 0.72 | 2.0 | 0.65 | 100.8o |
| 2 | 0.15 | −0.08 | −0.02 | 0.20 | 0.12 | −0.04 | 0.02 | 0.74 | 2.8 | 0.70 | 50.4o |
| 3 | 0.12 | −0.06 | 0.05 | 0.25 | 0.09 | 0.05 | −0.06 | 0.75 | 3.5 | 1.80 | 129.6o |
| 4 | 0.20 | −0.10 | 0.04 | 0.30 | 0.10 | 0.06 | −0.04 | 0.76 | 4.5 | 1.40 | 63.0o |
| 5 | 0.17 | −0.08 | 0.03 | 0.23 | 0.14 | 0.04 | −0.07 | 0.78 | 3.8 | 1.90 | 117.0o |
 , and for pure-mode and converted waves.
, and for pure-mode and converted waves.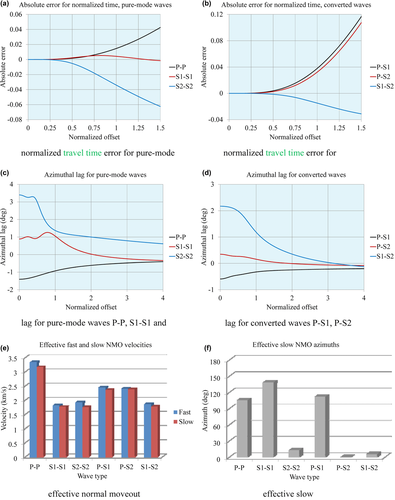
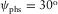 , and for pure-mode and converted waves.
, and for pure-mode and converted waves.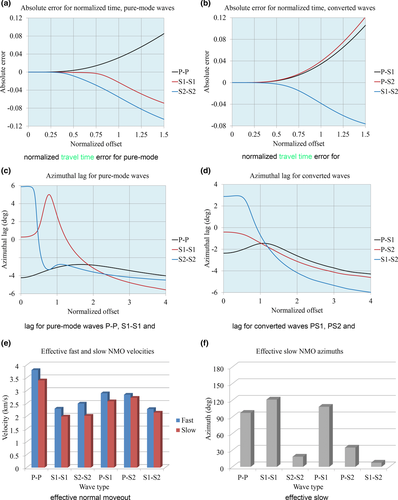
To establish the exact numerical value of the travel time, for each value of the opening angle we compute the two-way travel time and the offset 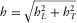 between the source and receiver. For this, we first obtain the incidence and reflection angles separately, applying Snell's law at the reflection point, and we then trace each of the two rays independently. For the lowermost layer, the direction of the phase velocity is known, and applying the Christoffel matrix, we can find the absolute value of the phase velocity (taking the root of the cubic equation corresponding to a given type of wave) and therefore the slowness components. For all other layers, lateral slowness components
between the source and receiver. For this, we first obtain the incidence and reflection angles separately, applying Snell's law at the reflection point, and we then trace each of the two rays independently. For the lowermost layer, the direction of the phase velocity is known, and applying the Christoffel matrix, we can find the absolute value of the phase velocity (taking the root of the cubic equation corresponding to a given type of wave) and therefore the slowness components. For all other layers, lateral slowness components  are kept constant, whereas the vertical slowness component p3 is obtained from the Christoffel equation. We assume that the smallest vertical slowness corresponds to the compressional wave, whereas two others correspond to shear waves (medium vertical slowness to S1 and large to S2). We then check our assumption, computing the three phase velocities vphs for fixed directions, in order to pick the proper root for p3. Thus, we know the magnitude and direction of the phase velocity for all layers. Next, we find the polarization, the ray velocity components, the two components of the offset, and the travel time (Vlaar 1968; Červený et al. 1977; Červený 2001). As we see, the hyperbolic approximation is accurate for small offsets and sometimes for moderate offsets. As expected, for the strong anisotropy structure, the error of the hyperbolic approximation grows much faster with the offset increase. In Tables 4 and 5, we present the effective models for the given multi-layer packages, considering all six types of pure-mode and converted waves. Recall that the fast shear S1 has a higher phase velocity (in this case – a higher vertical velocity and shorter vertical time) than the slow shear S2, but the NMO velocities of S1 are not necessarily higher than those of S2. In Figs. 5(a,b) and 7(a,b), we present the absolute error between the exact numerical result and the hyperbolic approximation of the normalized travel time versus normalized offset, for weak and strong anisotropy and for pure-mode and converted waves, respectively, for the fixed phase-velocity azimuth
are kept constant, whereas the vertical slowness component p3 is obtained from the Christoffel equation. We assume that the smallest vertical slowness corresponds to the compressional wave, whereas two others correspond to shear waves (medium vertical slowness to S1 and large to S2). We then check our assumption, computing the three phase velocities vphs for fixed directions, in order to pick the proper root for p3. Thus, we know the magnitude and direction of the phase velocity for all layers. Next, we find the polarization, the ray velocity components, the two components of the offset, and the travel time (Vlaar 1968; Červený et al. 1977; Červený 2001). As we see, the hyperbolic approximation is accurate for small offsets and sometimes for moderate offsets. As expected, for the strong anisotropy structure, the error of the hyperbolic approximation grows much faster with the offset increase. In Tables 4 and 5, we present the effective models for the given multi-layer packages, considering all six types of pure-mode and converted waves. Recall that the fast shear S1 has a higher phase velocity (in this case – a higher vertical velocity and shorter vertical time) than the slow shear S2, but the NMO velocities of S1 are not necessarily higher than those of S2. In Figs. 5(a,b) and 7(a,b), we present the absolute error between the exact numerical result and the hyperbolic approximation of the normalized travel time versus normalized offset, for weak and strong anisotropy and for pure-mode and converted waves, respectively, for the fixed phase-velocity azimuth 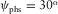 . The absolute error E of the normalized travel time is shown in the graphs, where the normalizing factor is the vertical time, which means that the two-way reflection travel time error is
. The absolute error E of the normalized travel time is shown in the graphs, where the normalizing factor is the vertical time, which means that the two-way reflection travel time error is 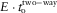 , where
, where 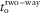 is the two-way vertical time. The error graphs in Fig. 5(a) are related to travel-time approximations in Fig. 4(a–c) (weak anisotropy, pure-mode waves), the error graphs in Fig. 5(b) are related to the approximations in Fig. 4(d–f) (weak anisotropy, converted waves), the error graphs in Fig. 7(a) are related to the approximations in Fig. 6(a–c) (strong anisotropy, pure-mode waves), and the error graphs in Fig. 7(b) are related to the approximations in Fig. 6(d–f) (strong anisotropy, converted waves).
is the two-way vertical time. The error graphs in Fig. 5(a) are related to travel-time approximations in Fig. 4(a–c) (weak anisotropy, pure-mode waves), the error graphs in Fig. 5(b) are related to the approximations in Fig. 4(d–f) (weak anisotropy, converted waves), the error graphs in Fig. 7(a) are related to the approximations in Fig. 6(a–c) (strong anisotropy, pure-mode waves), and the error graphs in Fig. 7(b) are related to the approximations in Fig. 6(d–f) (strong anisotropy, converted waves).
| Wave type |
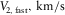 |
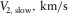 |
Ψslow |
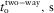 |
|---|---|---|---|---|
| P-P | 3.327 | 3.157 | 105.31o | 4.000 |
| S1-S1 | 1.805 | 1.758 | 138.23o | 7.455 |
| S2-S2 | 1.918 | 1.742 | 12.64o | 8.162 |
| P-S1 | 2.441 | 2.349 | 111.90o | 5.727 |
| P-S2 | 2.398 | 2.381 | 0.18o | 6.081 |
| S1-S2 | 1.852 | 1.763 | 5.74o | 7.809 |
| Wave type |
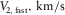 |
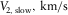 |
Ψslow |
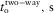 |
|---|---|---|---|---|
| P-P | 3.807 | 3.404 | 97.17o | 3.801 |
| S1-S1 | 2.301 | 1.993 | 121.15o | 7.103 |
| S2-S2 | 2.505 | 2.023 | 18.25o | 7.743 |
| P-S1 | 2.902 | 2.590 | 108.14o | 5.452 |
| P-S2 | 2.846 | 2.726 | 34.59o | 5.772 |
| S1-S2 | 2.286 | 2.146 | 5.07o | 7.423 |
In Figs. 5(c,d) and 7(c,d), we plot the corresponding graphs for the global lag 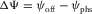 between the surface-offset azimuth and the phase-velocity azimuth, versus the normalized offset. In these plots, the phase-velocity azimuth is kept constant, i.e.,
between the surface-offset azimuth and the phase-velocity azimuth, versus the normalized offset. In these plots, the phase-velocity azimuth is kept constant, i.e., 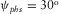 . These graphs are plotted by numerical raytracing because the hyperbolic approximation can predict this lag only for an infinitesimal offset and does not provide the dependence of this lag on the offset (note that a fourth-order moveout approximation is required to obtain second-order approximation of the azimuth lag). The graphs show that the global azimuthal lags may be essential. In these examples, for the chosen phase-velocity azimuth, the lags may reach 3.5o for weak anisotropy and 6o for strong anisotropy structures. The local azimuthal lags between the ray and phase velocity directions may be even greater, as the lags in different layers often compensate each other partially. The global lags vary in a wide range with the offset and may even change the sign, i.e., the surface-offset azimuth may actually lead or lag behind the phase-velocity azimuth. For very long offsets, the global lag converges to its asymptotic value, which is equal to the local lag between the ray and phase velocities of the layer with the fastest phase velocity in the horizontal symmetry plane, for the given azimuth.
. These graphs are plotted by numerical raytracing because the hyperbolic approximation can predict this lag only for an infinitesimal offset and does not provide the dependence of this lag on the offset (note that a fourth-order moveout approximation is required to obtain second-order approximation of the azimuth lag). The graphs show that the global azimuthal lags may be essential. In these examples, for the chosen phase-velocity azimuth, the lags may reach 3.5o for weak anisotropy and 6o for strong anisotropy structures. The local azimuthal lags between the ray and phase velocity directions may be even greater, as the lags in different layers often compensate each other partially. The global lags vary in a wide range with the offset and may even change the sign, i.e., the surface-offset azimuth may actually lead or lag behind the phase-velocity azimuth. For very long offsets, the global lag converges to its asymptotic value, which is equal to the local lag between the ray and phase velocities of the layer with the fastest phase velocity in the horizontal symmetry plane, for the given azimuth.
Figs. 5(e,f) and 7(e,f) show the effective fast and slow NMO velocities and effective slow azimuths for all types of waves and for weak and strong anisotropy models. As we see, for a multi-layer structure, the orientation of the effective slow azimuth Ψslow depends on the specific type of pure-mode or converted wave. Thus, for six wave types, we obtain six different values. This is not so for a single orthorhombic layer, where the slow azimuth coincides with one of the local axes 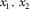 .
.
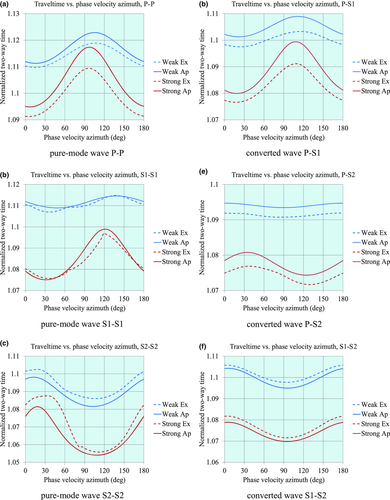
In Figs. 8 and 9, the normalized offset is kept fixed, i.e., 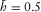 , whereas the azimuth of the phase velocity runs all values. Equation 9 is used to approximate the travel time, where
, whereas the azimuth of the phase velocity runs all values. Equation 9 is used to approximate the travel time, where 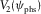 is now a varying function of the phase azimuth. Blue and red solid lines are approximations for weak and strong anisotropy, respectively. Blue and red dashed lines are the corresponding exact solutions. Label “Ex” means an exact numerical raytracing solution, and label “Ap” means the hyperbolic approximation. In Fig. 8, we compare the hyperbolic travel-time approximation with the exact solution, for all types of waves. In Fig. 9, we plot the lag (between the surface-offset azimuth and the phase-velocity azimuth) versus phase-velocity azimuth, for all types of waves. Within the entire range of the phase-velocity azimuth, the maximum global lag reaches 15o (Fig. 9c, strong anisotropy, pure-mode wave S2-S2,
is now a varying function of the phase azimuth. Blue and red solid lines are approximations for weak and strong anisotropy, respectively. Blue and red dashed lines are the corresponding exact solutions. Label “Ex” means an exact numerical raytracing solution, and label “Ap” means the hyperbolic approximation. In Fig. 8, we compare the hyperbolic travel-time approximation with the exact solution, for all types of waves. In Fig. 9, we plot the lag (between the surface-offset azimuth and the phase-velocity azimuth) versus phase-velocity azimuth, for all types of waves. Within the entire range of the phase-velocity azimuth, the maximum global lag reaches 15o (Fig. 9c, strong anisotropy, pure-mode wave S2-S2, 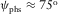 ). Note that in the case of strong anisotropy and pure-mode shear waves, the exact values of the travel time (versus phase-velocity azimuth) may be unsmooth (Fig. 8b), and the azimuthal lag may even be discontinuous (Fig. 9b), due to shear-wave cusps or close-to-cusp conditions. These points are candidates for the shear-wave singularities extensively studied by Crampin (1981, 1991), Brown, Crampin, and Gallant (1992), and Vavryčuk (1999).
). Note that in the case of strong anisotropy and pure-mode shear waves, the exact values of the travel time (versus phase-velocity azimuth) may be unsmooth (Fig. 8b), and the azimuthal lag may even be discontinuous (Fig. 9b), due to shear-wave cusps or close-to-cusp conditions. These points are candidates for the shear-wave singularities extensively studied by Crampin (1981, 1991), Brown, Crampin, and Gallant (1992), and Vavryčuk (1999).
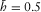 , for layered structures with weak and strong anisotropy.
, for layered structures with weak and strong anisotropy.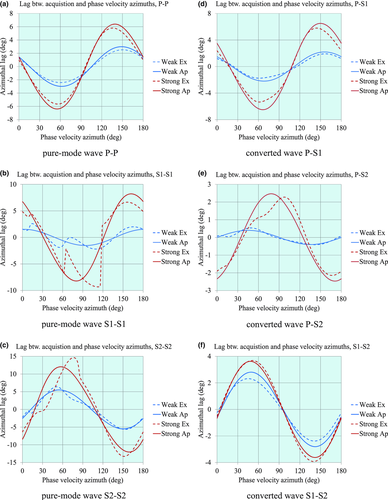
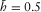 , and for layered structures with weak and strong anisotropy.
, and for layered structures with weak and strong anisotropy.The hyperbolic approximation is always smooth and continuous. However, even in these cases, the smooth continuous prediction of the travel time gives a reasonable quantitative insight (for short offsets), indicating the locations and values of minima and maxima, and the average rates.
CONCLUSIONS
We have derived the normal moveout (NMO) velocity formula for quasi-compressional, quasi-shear, and converted waves, considering two types of shear polarization, for a 1D package of orthorhombic layers versus their common phase-velocity azimuth. This phase-azimuth-domain NMO velocity is required for analysing residual moveouts along local-angle-domain (LAD) common image gathers. The azimuthally dependent NMO velocity formula consists of three independent global effective model parameters (fast and slow NMO velocities and the azimuth of the slow NMO velocity), defining a single layer that yields the same azimuthally dependent moveout as the whole package of layers. Note that the global effective “layer” is generic and not necessarily orthorhombic. To model the global effective NMO velocity for pure-mode and converted waves, we need the given azimuthal orientation 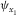 of the orthorhombic axis x1, the vertical compression velocity vP, the shear-to-compression ratio f (where shear is Sx1), and all Thomsen-like parameters of the orthorhombic medium, except δ3, which has no effect within the hyperbolic approximation. It has been demonstrated that when the ratio between the half-offset to the target depth is less than one half (about 25° half-opening angles), the comparison of the azimuthally dependent hyperbolic approximation of the moveout with the exact raytracing-based travel time still demonstrates satisfactory accuracy, even for strong anisotropy and converted waves.
of the orthorhombic axis x1, the vertical compression velocity vP, the shear-to-compression ratio f (where shear is Sx1), and all Thomsen-like parameters of the orthorhombic medium, except δ3, which has no effect within the hyperbolic approximation. It has been demonstrated that when the ratio between the half-offset to the target depth is less than one half (about 25° half-opening angles), the comparison of the azimuthally dependent hyperbolic approximation of the moveout with the exact raytracing-based travel time still demonstrates satisfactory accuracy, even for strong anisotropy and converted waves.
ACKNOWLEDGEMENT
The authors would like to thank Paradigm Geophysical for its financial and technical support of this study and for its permission to publish the results, and the anonymous reviewers and the Associate Editor of Geophysical Prospecting, Alexey Stovas, for valuable comments and suggestions that helped to improve the content and style of this paper.
APPENDIX A: LAG BETWEEN RAY AND PHASE VELOCITY AZIMUTHS AND LOCAL MNO VELOCITIES VS. RAY AND PHASE VELOCITY AZIMUTHS
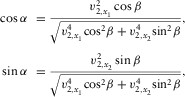 (A-1a)
(A-1a)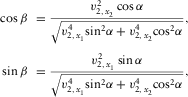 (A-1b)
(A-1b)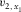 and
and 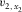 are local NMO velocities in the directions of the orthorhombic axes x1 and x2, respectively, α is the ray-velocity azimuth, and β is the phase-velocity azimuth. Both are measured from the azimuth
are local NMO velocities in the directions of the orthorhombic axes x1 and x2, respectively, α is the ray-velocity azimuth, and β is the phase-velocity azimuth. Both are measured from the azimuth 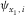 of the local axis x1,
of the local axis x1,
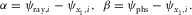 (A-2)
(A-2)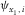 of the local axis x1 is replaced by the global azimuth of the slow NMO velocity Ψslow, and the local axial NMO velocities
of the local axis x1 is replaced by the global azimuth of the slow NMO velocity Ψslow, and the local axial NMO velocities 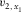 and
and 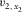 are replaced by the global slow and fast NMO velocities of the layered structure,
are replaced by the global slow and fast NMO velocities of the layered structure, 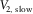 and
and 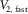 . Should we combine the two equations of either set A-1a or A-1b, we obtain the relationship between the local ray and phase-velocity azimuths, i.e.,
. Should we combine the two equations of either set A-1a or A-1b, we obtain the relationship between the local ray and phase-velocity azimuths, i.e.,
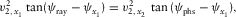 (A-3a)
(A-3a)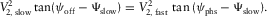 (A-3b)
(A-3b)It is clearly seen that the ray surface-offset azimuth is closer to the “fast azimuth”, whereas the phase-velocity azimuth is closer to the slow azimuth. Equations (A-1) and (A-3) are not exact and hold within the hyperbolic approximation. The trigonometric functions of the surface-offset azimuth versus phase-velocity azimuth (and vice versa) are series, and equations (A-1) and (A-3) present only the constant terms of these series, with the leading error term 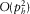 , where
, where 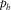 is the magnitude of the horizontal slowness vector. The proof of equation A-1 (Koren and Ravve 2014) was carried out for an elliptic front on the surface; however, the front is only approximately elliptic.
is the magnitude of the horizontal slowness vector. The proof of equation A-1 (Koren and Ravve 2014) was carried out for an elliptic front on the surface; however, the front is only approximately elliptic.
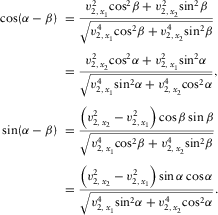 (A-4)
(A-4)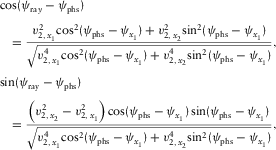 (A-5a)
(A-5a)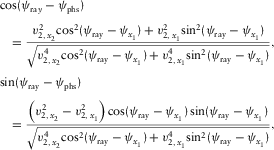 (A-5b)
(A-5b)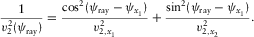 (A-6)
(A-6)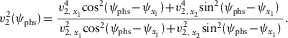 (A-7)
(A-7)We note also that introducing equation (A-1b) into equation (A-7) leads to equation (A-6). In other words, the relationship for the NMO velocity versus the phase-velocity azimuth can be obtained from the NMO velocity versus the ray (or surface-offset) azimuth, and vice versa.
APPENDIX B: HYPERBOLIC APPROXIMATIONS FOR OFFSET COMPONENTS AND TRAVELTIME VS. AXIAL VALUES OF NMO VELOCITY
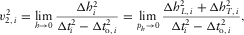 (B-1)
(B-1)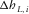 and
and 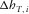 are lengthwise and transverse components of the contributions of the current layer with index i into the total offset,
are lengthwise and transverse components of the contributions of the current layer with index i into the total offset, 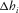 is the full horizontal propagation through the layer, and
is the full horizontal propagation through the layer, and 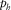 is the horizontal slowness. One-way propagation is studied in this appendix. Consider two neighbouring points on the upper interface of the layer, where one point belongs to the vertical ray and the other point to the tilted ray, with the local one-way travel times
is the horizontal slowness. One-way propagation is studied in this appendix. Consider two neighbouring points on the upper interface of the layer, where one point belongs to the vertical ray and the other point to the tilted ray, with the local one-way travel times 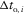 and
and 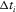 , respectively. We approximate the difference between the two one-way travel times, i.e.,
, respectively. We approximate the difference between the two one-way travel times, i.e.,
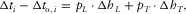 (B-2)
(B-2)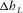 and
and 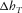 are lengthwise and transverse components of the distance between the two arrival points on the upper interface. On the lower interface, the two rays start at the same point. In our suggested frame of reference, the offset contribution has two components, i.e.,
are lengthwise and transverse components of the distance between the two arrival points on the upper interface. On the lower interface, the two rays start at the same point. In our suggested frame of reference, the offset contribution has two components, i.e., 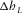 and
and 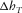 , but the horizontal slowness has only one component. The lengthwise direction coincides with the azimuth of the phase velocity, which is kept fixed. Thus, the transverse slowness component
, but the horizontal slowness has only one component. The lengthwise direction coincides with the azimuth of the phase velocity, which is kept fixed. Thus, the transverse slowness component 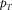 vanishes, whereas the lengthwise component represents (by definition) the entire horizontal slowness. The equation for the travel time increase simplifies to
vanishes, whereas the lengthwise component represents (by definition) the entire horizontal slowness. The equation for the travel time increase simplifies to
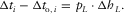 (B-3)
(B-3)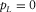 , whereas for the tilted ray,
, whereas for the tilted ray, 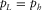 . The most accurate option is to take the average value of the horizontal slowness
. The most accurate option is to take the average value of the horizontal slowness 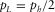 , i.e.,
, i.e.,
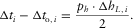 (B-4)
(B-4)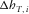 appears due to the azimuthal lag between the ray and phase velocities. Consequently, in the case of a layered structure, the transverse component appears due to the lag between the surface-offset and the phase azimuths. Therefore
appears due to the azimuthal lag between the ray and phase velocities. Consequently, in the case of a layered structure, the transverse component appears due to the lag between the surface-offset and the phase azimuths. Therefore
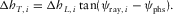 (B-5)
(B-5)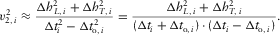 (B-6)
(B-6)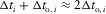 (B-7)
(B-7)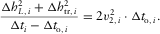 (B-8)
(B-8)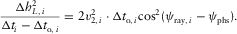 (B-9)
(B-9)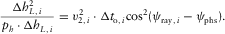 (B-10)
(B-10)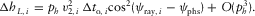 (B-11a)
(B-11a)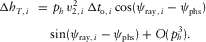 (B-11b)
(B-11b)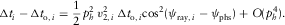 (B-11c)
(B-11c)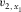 and
and 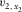 , i.e.,
, i.e.,
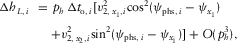 (B-12a)
(B-12a)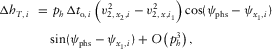 (B-12b)
(B-12b)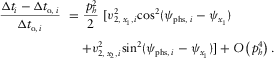 (B-12c)
(B-12c)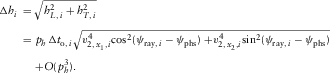 (B-13)
(B-13)Although the relationships in Appendices A and B are derived for individual layers, they are all valid for multi-layer structures as well. We only need to replace the local parameters by global.
APPENDIX C: PARAMETERS OF THE EFFECTIVE MODEL
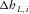 and
and 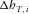 and the travel time
and the travel time 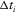 of each layer in terms of the horizontal slowness magnitude
of each layer in terms of the horizontal slowness magnitude 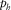 , which is constant for all layers of the package, thus making it possible to stack the travel time and horizontal propagation of all the layers. According to equation (B-4), the residual travel time
, which is constant for all layers of the package, thus making it possible to stack the travel time and horizontal propagation of all the layers. According to equation (B-4), the residual travel time 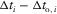 is proportional to the lengthwise offset component, i.e., it is a dependent value. We conclude that, in order to obtain the effective model that yields the same NMO velocity and the same surface-offset azimuth (within the hyperbolic approximation) computed for any azimuth of the phase velocity, the two offset components should be identical for the stacked package and the effective model, i.e.,
is proportional to the lengthwise offset component, i.e., it is a dependent value. We conclude that, in order to obtain the effective model that yields the same NMO velocity and the same surface-offset azimuth (within the hyperbolic approximation) computed for any azimuth of the phase velocity, the two offset components should be identical for the stacked package and the effective model, i.e.,
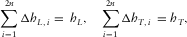 (C-1)
(C-1)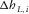 and
and 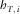 are one-way horizontal propagation components for the individual layers, and
are one-way horizontal propagation components for the individual layers, and 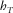 and
and 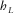 are the components of the full (two-way) surface offset in the direction of the phase-velocity azimuth and normal direction, respectively. Parameter n is the horizon index, and all layers above this horizon are passed twice: once for the incident wave and once for the reflected. Equations for the global offset components are similar to equation (B-12), where we replace the layer vertical time with the total vertical time, the local axial NMO velocities, and the azimuth of the local slow velocity with the corresponding effective parameters, i.e.,
are the components of the full (two-way) surface offset in the direction of the phase-velocity azimuth and normal direction, respectively. Parameter n is the horizon index, and all layers above this horizon are passed twice: once for the incident wave and once for the reflected. Equations for the global offset components are similar to equation (B-12), where we replace the layer vertical time with the total vertical time, the local axial NMO velocities, and the azimuth of the local slow velocity with the corresponding effective parameters, i.e.,
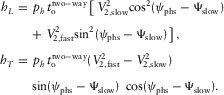 (C-2)
(C-2)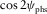
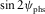 and the free terms separately. This results in a set of three equations, i.e.,
and the free terms separately. This results in a set of three equations, i.e.,
 (C-3)
(C-3)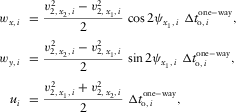 (C-4)
(C-4)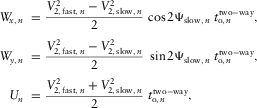 (C-5)
(C-5)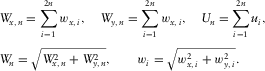 (C-6)
(C-6)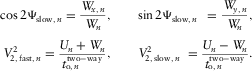 (C-7)
(C-7)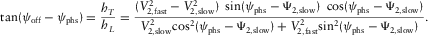 (C-8)
(C-8)
APPENDIX D: COMPARISON OF EFFECTIVE MODELS BASED ON PHASE AND SURFACE-OFFSET AZIMUTHS
- For each layer, create a 2 × 2 local matrix w,
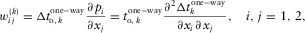 (D-1)
(D-1)
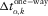 is the local one-way vertical time,
is the local one-way vertical time, 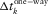 is the local one-way travel time,
is the local one-way travel time,  and
and 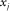 are components of the lateral propagation distance in the global frame,
are components of the lateral propagation distance in the global frame, 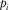 are components of the horizontal slowness in the global frame, and k is the layer number.
are components of the horizontal slowness in the global frame, and k is the layer number.
- Invert the matrix. Add the inverted matrices for all layers, and pass through the layers twice (for the incidence and reflection rays),
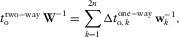 (D-2)
(D-2)
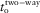 is the total two-way vertical time for the multi-layer structure, and n is the number of layers. The eigenvalues of the resulting matrix
is the total two-way vertical time for the multi-layer structure, and n is the number of layers. The eigenvalues of the resulting matrix 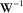 are the effective fast and slow NMO velocities, and the eigenvectors describe the azimuthal orientation of the effective axes.
are the effective fast and slow NMO velocities, and the eigenvectors describe the azimuthal orientation of the effective axes.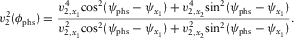 (D-3)
(D-3)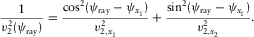 (D-4)
(D-4)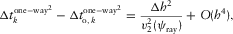 (D-5)
(D-5)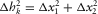 is the one-way horizontal propagation through that layer; and
is the one-way horizontal propagation through that layer; and 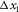 and
and 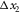 are components of the one-way horizontal propagation through that layer, in the global frame of reference. By combining equations (D-4) and (D-5), we obtain
are components of the one-way horizontal propagation through that layer, in the global frame of reference. By combining equations (D-4) and (D-5), we obtain
 (D-6)
(D-6)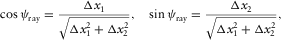 (D-7)
(D-7)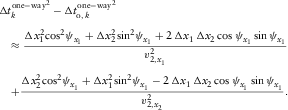 (D-8)
(D-8)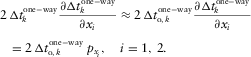 (D-9)
(D-9) (D-10)
(D-10)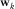 , i.e.,
, i.e.,
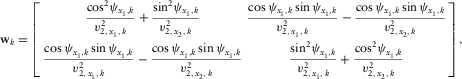 (D-11)
(D-11) (D-12)
(D-12)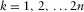 . The components of the resulting matrix are as follows:
. The components of the resulting matrix are as follows:
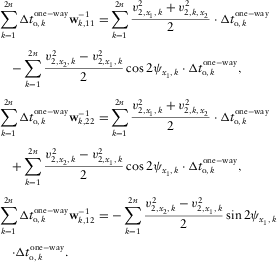 (D-13)
(D-13)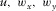 ,
,
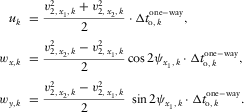 (D-14)
(D-14)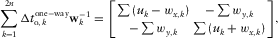 (D-15)
(D-15)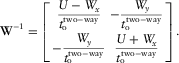 (D-16)
(D-16)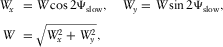 (D-17)
(D-17)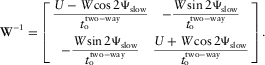 (D-18)
(D-18)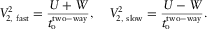 (D-19)
(D-19)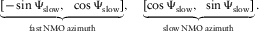 (D-20)
(D-20)Thus, the two methods lead to identical results.
REFERENCES
LIST OF SYMBOLS
Local Parameters
-
- vP
-
- Vertical compressional velocity.
-
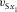
-
- Vertical velocity of shear polarized along axis x1.
-
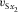
-
- Vertical velocity of shear polarized along axis x2.
-
- g
-
- Coefficient that depends on the ratio between two differently polarized vertical shear velocities.
-
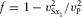
-
- Coefficient that depends on the ratio between the x1 polarized vertical shear velocity and the vertical compressional velocity.
-
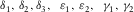
-
- Thomsen-style parameters for orthorhombic media.
-
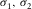
-
- Orthorhombic dependent parameters.
-
- vver
-
- Generic vertical phase velocity.
-
- vphs
-
- Magnitude of the phase velocity that depends on its direction.
-
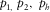
-
- Components and magnitude of the horizontal slowness vector, constant through all layers of the 1D model.
-
- p3
-
- Vertical lowness component varying with depth.
-
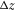
-
- Layer thickness.
-
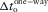
-
- Local one-way (unless otherwise specified) vertical time; for a given layer thickness
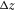 , it depends on the type of the wave.
, it depends on the type of the wave. - Local one-way (unless otherwise specified) vertical time; for a given layer thickness
-
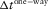
-
- Local one-way (unless otherwise specified) travel time.
-
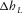
-
- One-way lateral propagation distance through a layer in the lengthwise direction (along the phase-velocity azimuth).
-
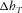
-
- One-way lateral propagation distance thorough a layer in the transverse direction.
-
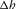
-
- Total one-way lateral propagation through a layer.
-
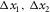
-
- Components of one-way lateral propagation through a layer in the global frame.
-
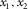
-
- Local horizontal orthorhombic axes with constant azimuthal directions within the layer.
-
- v2
-
- Local NMO velocity, which depends on the azimuth.
-
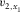
-
- Local NMO velocity along local orthorhombic axis x1.
-
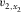
-
- Local NMO velocity along local orthorhombic axis x2.
-
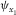
-
- Azimuth of local orthorhombic axis x1.
-
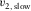
-
- Local slow NMO velocity.
-
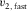
-
- Local fast NMO velocity.
-
- ψslow
-
- Azimuth of local slow NMO velocity.
-
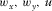
-
- Auxiliary local effective parameters.
-
- w
-
- 2 × 2 matrix with the second derivatives of local one-way travel time with respect to horizontal coordinates of global frame.
Global Parameters
-
- n
-
- Number of layers in a multi-layer structure, horizon index.
-
- z
-
- Depth of horizon or reflection point.
-
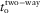
-
- Global two-way vertical time.
-
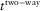
-
- Global two-way travel time.
-
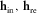
-
- One-way horizontal propagation vectors.
-
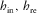
-
- One-way horizontal propagation distances.
-
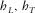
-
- Lengthwise and transverse components of the two-way lateral propagation (offset).
-
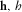
-
- Surface offset vector and its length (distance between the source and the receiver).
-
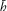
-
- Normalized surface offset,
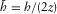 .
. - Normalized surface offset,
-
- V2
-
- Global NMO velocity, depends on the phase-velocity azimuth.
-
- Ψslow
-
- Azimuth of global slow NMO velocity of multi-layer structure.
-
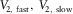
-
- Global fast and slow NMO velocities, respectively.
-
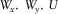
-
- Auxiliary global effective parameters.
-
- W
-
- 2 × 2 matrix with the second derivatives of global two-way travel time with respect to horizontal coordinates of global frame.
Azimuthal Parameters
-
- ψphs
-
- Azimuth of the phase velocity (constant along the whole package of layers).
-
- ψray
-
- Azimuth of the ray velocity for a given layer.
-
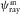
-
- Azimuth of the incidence ray velocity for a given layer.
-
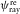
-
- Azimuth of the reflection ray velocity for a given layer.
-
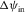
-
- Azimuthal lag between the incidence ray velocity and the phase velocity.
-
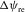
-
- Azimuthal lag between the reflection ray velocity and the phase velocity.
-
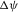
-
- Local lag between ray and phase-velocity azimuths.
-
- α
-
- Ray-velocity azimuth measured from the local orthorhombic axis x1.
-
- β
-
- Phase-velocity azimuth measured from the local orthorhombic axis x1.
-
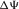
-
- Global lag between the surface-offset azimuth and the phase-velocity azimuth.
-
- ψoff
-
- Surface-offset azimuth (acquisition azimuth, CMP line azimuth).
Residual Velocities and Moveouts
-
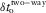
-
- Azimuthally dependent residual moveout (variation of global vertical time).
-
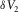
-
- Azimuthally dependent residual NMO velocity.
Subscripts and Superscripts
-
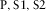
-
- Related to compressional, fast shear, and slow shear waves, respectively.
-
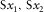
-
- Related to nearly vertical shear wave polarized in the direction close to x1 or x2, respectively.
-
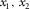
-
- Related to the azimuths of the corresponding local orthorhombic axes.
-
- in, re
-
- Related to incidence or reflection ray, respectively.
We call local orthorhombic axis  the intersecting line of two orthorhombic symmetry planes
the intersecting line of two orthorhombic symmetry planes 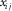 and
and 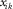 , where
, where 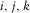 are all different and accept values of 1, 2, and 3.
are all different and accept values of 1, 2, and 3.




