The Induced Innovation Hypothesis and U.S. Public Agricultural Research
The authors gratefully acknowledge the helpful suggestions of Jonathan Yoder, Ray Batina, J.M.C. Santos Silva, and the anonymous reviewers on earlier drafts of this article, as well as the significant contributions of Katelyn Sellers, Eldon Ball, Wallace Huffman, and Daniel Johnson for the data used. This research was supported by the Washington Agricultural Research Center and by the USDA National Institute of Food and Agriculture, Hatch grant WPN000275.
Abstract
Applicability of the induced innovation hypothesis—that a change in relative input prices induces innovation to economize use of the increasingly expensive input (Hicks 1932)—is examined for U.S. public agricultural research. A reduced-form test is developed using input prices from the agricultural production sector, expenditures from the public research sector aimed at developing new technology to save specific agricultural inputs, and variables to control for innovation marginal cost differences and nonhomotheticity. Unlike recent demand-side studies that soundly reject the induced innovation hypothesis for agriculture, support for the hypothesis is found for several input pairings through these tests of public agricultural research using state-level panel data.
The induced innovation hypothesis (IIH)—that a change in relative input prices induces innovation to economize use of the increasingly expensive input (Hicks 1932)—has had a profound impact on both macroeconomic and microeconomic production literature. With the development of the microeconomic foundations of induced innovation theory (e.g., Ahmad 1966; Kamien and Schwartz 1968; Binswanger 1974a), empirical testing began with Hayami and Ruttan's (1970) examination of the contrasting paths of technological development in Japanese and U.S. agriculture. It was followed by Binswanger's (1974b) rigorous testing of the hypothesis for multiple inputs in U.S. agriculture using newly developed duality concepts. The hypothesis has since been tested extensively in many countries and industries. While it received nearly consistent support in the first two decades of empirical testing, tests conducted with improved methods and data sets during the last two decades have been far less supportive of the hypothesis.
Despite widespread testing, remarkably little attention has been given to the necessary conditions required for a valid test of the hypothesis.1 The most common test has been to determine whether input quantity shares (or ratios) in an innovation implementing industry are negatively related to own input prices (or ratios) lagged sufficiently to enable technology development and implementation to result and thus enable relatively expensive inputs to be saved. A variety of specific test procedures have been developed, including econometric (e.g., Armanville and Funk 2003), time series (e.g., Thirtle, Schimmelpfennig, and Townsend 2002), and nonparametric (e.g., Chavas, Aliber, and Cox 1997). Most assume (often implicitly) that production is homothetic and that shifts in the innovation possibility curve (IPC) that accounts for technical change (e.g., Ahmad 1966; Armanville and Funk 2003) are neutral.2 With homothetic production and neutral shifts in the innovation possibility curve (IPC), consistency with the IIH requires that input price changes influence movements along the isoquant and the IPC in the same direction.
Nonhomothetic production in the innovation implementing industry and nonneutral marginal costs in the innovation creating industry can each cause nonneutral shifts in the IPC in the innovation implementing industry in the opposite direction from those resulting from induced innovation. Consequently, they may also more than offset the induced innovation shifts resulting from changes in input prices in the implementing industry. In other words, an increase in the relative price of an input raises the marginal benefit of innovation that saves that input in production. However, the marginal cost of innovation also varies across inputs, a point that has been largely ignored in the literature.3 If these marginal costs are not accounted for, and particularly if innovation marginal costs are positively correlated with the prices of inputs they are intended to save, the induced innovation hypothesis could be valid even though some previous tests have failed to find evidence to support it.
Despite the large number of empirical tests of the IIH, nearly all have considered only the impact of relative price movements in the innovation implementing industry without regard to relative prices in the innovation creating industry. Thus, they are really only partial tests of the IIH based on demand side influences (Popp 2002). The only previous study to shed light on the role of prices in the innovation creating industry was Liu and Shumway (2009). However, their study did not test the hypothesis; rather, using nonparametric methods, it computed the rank order of the marginal costs of creating technology to save an equal percent of each of four inputs in order to be consistent with the induced innovation hypothesis.4 Although they also did not consider prices in the innovation creating industry, the studies by Popp (2002) and by Crabb and Johnson (2010) did include control variables to explicitly address supply side issues in their examination of the IIH in the energy sector.
It is important to recognize that Hicks’ statement of the induced innovation hypothesis did not imply that implemented technical change would actually substitute relatively cheap inputs for expensive ones but only that input prices would spur invention to economize the use of expensive inputs. Consequently, whether the failure to consider the endogeneity of the innovation possibilities function is attributed to a misinterpretation of Hicks’ theory of induced innovation or to relying on easily measured data, the upshot is that prior empirical tests of the innovation process are nearly all fundamentally flawed. Except for Popp (2002), Crabb and Johnson (2010) and a few others, “[a]ll tests of the induced innovation hypothesis have maintained the hypothesis that the marginal cost of developing and implementing technologies that save one input is the same as for saving an equal percent of another input” (Liu and Shumway 2009).5
We approach this problem by using a reduced-form approach analogous to Popp's (2002) and Crabb and Johnson's (2010). For theoretical consistency, we augment the Popp and Crabb-Johnson approaches by maintaining the hypothesis of a homothetic production function in the innovation creating industry. We test whether changes in relative prices in the innovation implementing industry induce changes in relative investments in the public innovation creating industry to develop technology to save inputs that become relatively more expensive. Popp (2002) and Crabb and Johnson (2010) focus on only one input (energy) and use time-series variation in energy prices to examine whether higher prices spur the development of patents on energy-saving technology. In contrast, our tests focus on four inputs (land, labor, energy, and fertilizer) used in U.S. agriculture (the innovation implementing industry). In addition, we use state-by-time variation in input prices to examine the applicability of the induced innovation hypothesis. In particular, our procedure utilizes a state-level panel data set on input prices in the innovation implementing industry (agriculture) and expenditures in the innovation creating industry (public agricultural research) to examine the effect of relative input price movements in the former on investments in the latter designed to save those inputs. Although we ignore resource allocation in private agricultural research, we expect public research allocations to be sensitive to relative prices in the agricultural production industry. This is consistent with the stated objectives of the U.S. Department of Agriculture and the State Agricultural Experiment Stations, which conduct most of the public research, to develop technology of value to production agriculture. It is also supported by the political economy expectation that farmers, when induced by changes in relative prices, press public research institutions to develop new technology to save the more expensive inputs (Hayami and Ruttan 1971).
By using a state-level panel data series of prices and public research expenditures along with appropriate estimation procedures, we are able to control for innovation marginal costs that have been overlooked by earlier research on induced innovation. Allowing for the possibility that such costs vary across states (perhaps because of differentiated past experience with research on particular topics), we control for the differences by including lagged public research expenditure ratios in the model. In addition to the advantages of panel data for dealing with the marginal cost of innovation in our research, our dependent variable (innovation effort) is less lumpy than patent realization data (which is positive only when highly stochastic research is successful), an additional advantage to our approach over Popp (2002) and Crabb and Johnson (2010).
In the next section we develop the empirical model and the control variables used to determine the applicability of the IIH in public research resource allocation decisions. We then describe the data used for estimation, including the procedure used to obtain expenditure data on research to develop technology to save each of four agricultural inputs. The results reported in the subsequent section indicate that relative input prices of some, but not all, inputs do affect research investments in ways that are consistent with the IIH and cannot be fully explained by pure randomness. We conclude in the final section.
Empirical Model
Our empirical testing procedure focuses on consistency of public research project funding decisions with the IIH. We construct tests to determine whether states with relatively higher prices of an input in the innovation implementing industry (agriculture) devote a relatively greater portion of the budget in the innovation creating industry (public research) to developing technology to save that input.
To ensure that scale of research does not affect the shape of the innovation possibility curves, we maintain homotheticity in “intended” outputs in the innovation creating industry by specifying a two-level constant elasticity of transformation (CET) decision model. This model is the output equivalent to the two-level constant elasticity of substitution (CES) production function often specified for the innovation implementing industry in the (potentially flawed) partial tests of the IIH. Although more restrictive than second-order Taylor expansions such as the translog and quadratic, it has the attractive features of “parsimony in parameter, ease of interpretation, computational ease, and interpolative and extrapolative robustness” (Kawagoe, Otsuka, and Hayami 1986, 529).
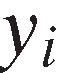 ,
,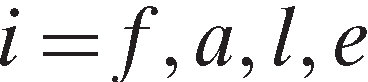 , represent the innovation creating industry's intended output quantities of fertilizer, land, labor, and energy saving innovation, respectively. Suppose input
, represent the innovation creating industry's intended output quantities of fertilizer, land, labor, and energy saving innovation, respectively. Suppose input (which can be thought of as an aggregate of scientist hours, scientist skill, scientific support, and research facilities) produces a biological innovation output index,
(which can be thought of as an aggregate of scientist hours, scientist skill, scientific support, and research facilities) produces a biological innovation output index,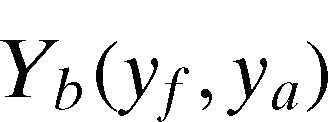 , and an energy innovation output index,
, and an energy innovation output index,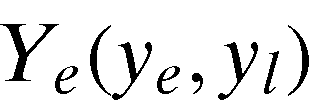 , according to a two-level production technology:6
, according to a two-level production technology:6
 (1)
(1)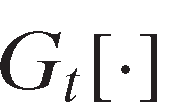 is permitted to vary across time
is permitted to vary across time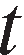 , and
, and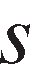 represents the state cross section. The two-level CET functional form approximates the innovation creation technology:
represents the state cross section. The two-level CET functional form approximates the innovation creation technology:
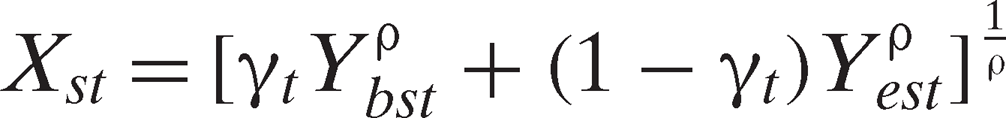 (2)
(2)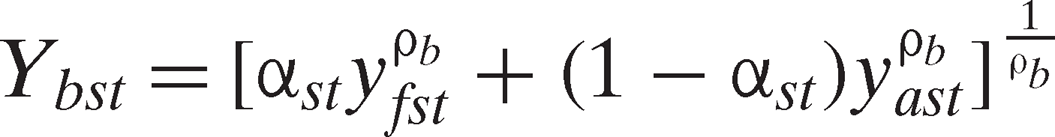 (3)
(3)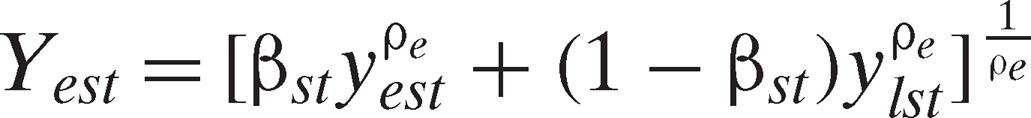 (4)
(4)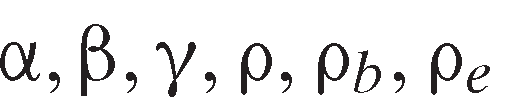 are parameters,
are parameters,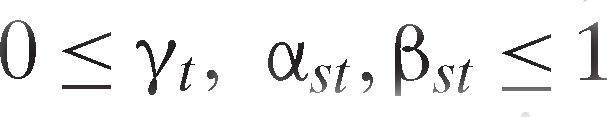 , and
, and in order to ensure concavity of the transformation function and each subtransformation function. While maintaining hypotheses of homotheticity (via homogeneity) and constant elasticity of transformation, the two-level structure allows for a different elasticity of substitution within each sublevel and between them. We allow
in order to ensure concavity of the transformation function and each subtransformation function. While maintaining hypotheses of homotheticity (via homogeneity) and constant elasticity of transformation, the two-level structure allows for a different elasticity of substitution within each sublevel and between them. We allow and
and to vary by state and time to reflect the fact that the input requirement necessary to generate innovation that saves an additional unit of
to vary by state and time to reflect the fact that the input requirement necessary to generate innovation that saves an additional unit of ,
, ,
, , or
, or may vary over these dimensions. When multiplied by prices of research inputs, input requirements determine marginal cost. With research, marginal cost is not known with precision because of the uncertainty surrounding its production function. Expected marginal cost is determined by both the cost of research inputs and also the probability of research success. It can be regarded as the cost of research inputs required to save an additional unit of
may vary over these dimensions. When multiplied by prices of research inputs, input requirements determine marginal cost. With research, marginal cost is not known with precision because of the uncertainty surrounding its production function. Expected marginal cost is determined by both the cost of research inputs and also the probability of research success. It can be regarded as the cost of research inputs required to save an additional unit of , or
, or divided by the probability of research success.
divided by the probability of research success.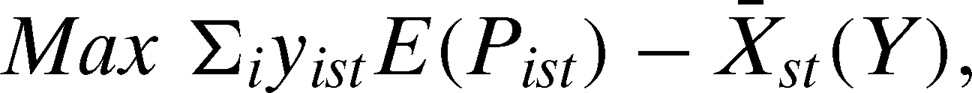 (5)
(5)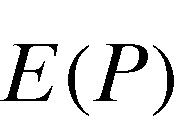 is expected output price,
is expected output price,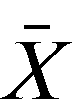 is the constrained aggregate input level, and
is the constrained aggregate input level, and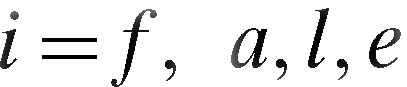 . The first-order conditions for constrained profit maximization can be rearranged to give:
. The first-order conditions for constrained profit maximization can be rearranged to give:
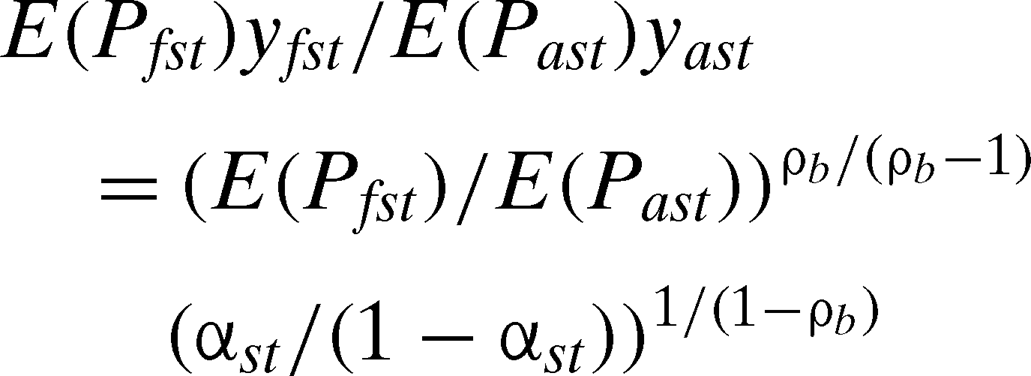 (6)
(6)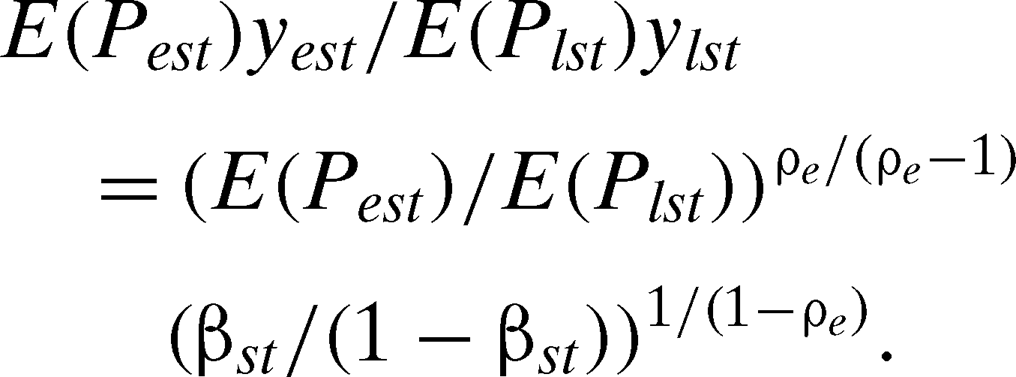 (7)
(7)Although public agricultural research is expected to respond to changing prices as would a competitive firm, there are also reasons why profit maximization in the implementing industry may not be the primary guide for project selection and funding decisions in the public sector. For example, public research can be expected to give more emphasis to research that may be more basic or risky than would be selected by the private-research sector. Also there is potential for increased public research to crowd out private research efforts and vice versa (David, Hall, and Toole 2000). Consequently, there are clear reasons why public agricultural research resource allocation decisions would not be driven as quickly by price signals nor to the same extent that the IIH would imply for a competitive innovation creating firm. Nevertheless, assuming profit maximization and competitive behavior as a primary guide might not be too farfetched. In recent literature, research and development has been regarded as a typical example of a mixed market where private firms and publicly owned firms compete with each other. When public sector R&D firms compete with private firms whose principal behavioral guide is profit maximization, the observed behavior of public firms can mimic private firms even though they pursue broader objectives (Ishibashi and Matsumura 2006).
Since we maintain the joint hypothesis of constant returns to scale in the public innovation creating industry with the industry behaving as a competitive firm, cost equals revenue in equilibrium. Consequently, we use public expenditures on research aimed to save each input as a proxy for the innovation creating industry's intended revenue in that category. We follow Popp (2002) in specifying an estimation model consistent with expected prices (the independent variables in equations (6) and (7)) following an adaptive expectations process. To deal with the possibility that expected marginal costs of innovating on particular inputs vary by state and time, we include three additional control variables. They are (a) a knowledge stock variable to account for overall differences in marginal costs of research across states, (b) the lagged dependent variable as a proxy for state of knowledge and differences in expected marginal costs across states in a specific innovation area as well as stickiness in adjusting research expenditures to a long-run equilibrium, and (c) year fixed effects to account for secular changes in the relative expected marginal cost of innovating in a specific innovation area in addition to exogenous factors that change innovation globally.
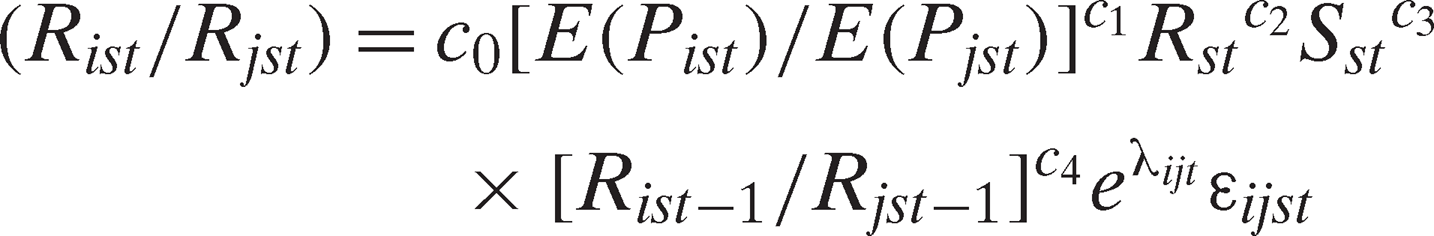 (8)
(8) is public research expenditure on input
is public research expenditure on input in state
in state in year
in year (
( and
and represent the pair
represent the pair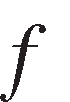 and
and or
or and
and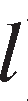 ),
),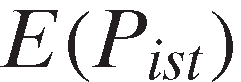 is expected price of input
is expected price of input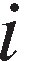 in state
in state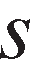 in year
in year in the agricultural (innovation implementing) industry and consequently expected output price in the public innovation creating industry,7
in the agricultural (innovation implementing) industry and consequently expected output price in the public innovation creating industry,7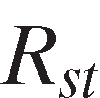 is total public research expenditures in state
is total public research expenditures in state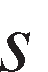 in year
in year ,
,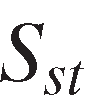 is the stock of patents issued for agriculture as the source of use industry in state
is the stock of patents issued for agriculture as the source of use industry in state in year
in year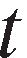 ,8
,8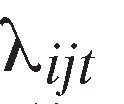 is year fixed effect, and
is year fixed effect, and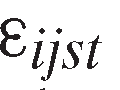 is the multiplicative regression error whose conditional expectation is assumed to be one. The variable
is the multiplicative regression error whose conditional expectation is assumed to be one. The variable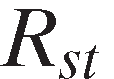 controls for scale and potential nonhomotheticity of the whole innovation creating industry of the state. Although we maintain linear homogeneity (which implies homotheticity) in the model structure, we include this control variable because our four outputs are not an exhaustive array of inputs in the innovation implementing industry and it permits us to treat homogeneity (and homotheticity) in the estimation model as a local rather than a global property. The patent stock variable
controls for scale and potential nonhomotheticity of the whole innovation creating industry of the state. Although we maintain linear homogeneity (which implies homotheticity) in the model structure, we include this control variable because our four outputs are not an exhaustive array of inputs in the innovation implementing industry and it permits us to treat homogeneity (and homotheticity) in the estimation model as a local rather than a global property. The patent stock variable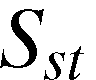 is included in the model as a proxy for the general state of agricultural innovation knowledge in state
is included in the model as a proxy for the general state of agricultural innovation knowledge in state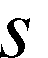 in year
in year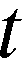 . Support for the IIH conditioned on a convex two-level CET innovation production function is provided if
. Support for the IIH conditioned on a convex two-level CET innovation production function is provided if is significantly positive.
is significantly positive.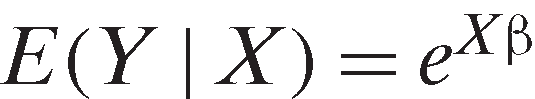 , where
, where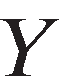 is the dependent variable,
is the dependent variable,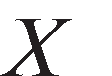 is a
is a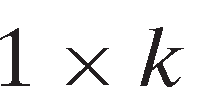 vector of independent variables, and
vector of independent variables, and is a
is a vector of parameters. This means:
vector of parameters. This means:
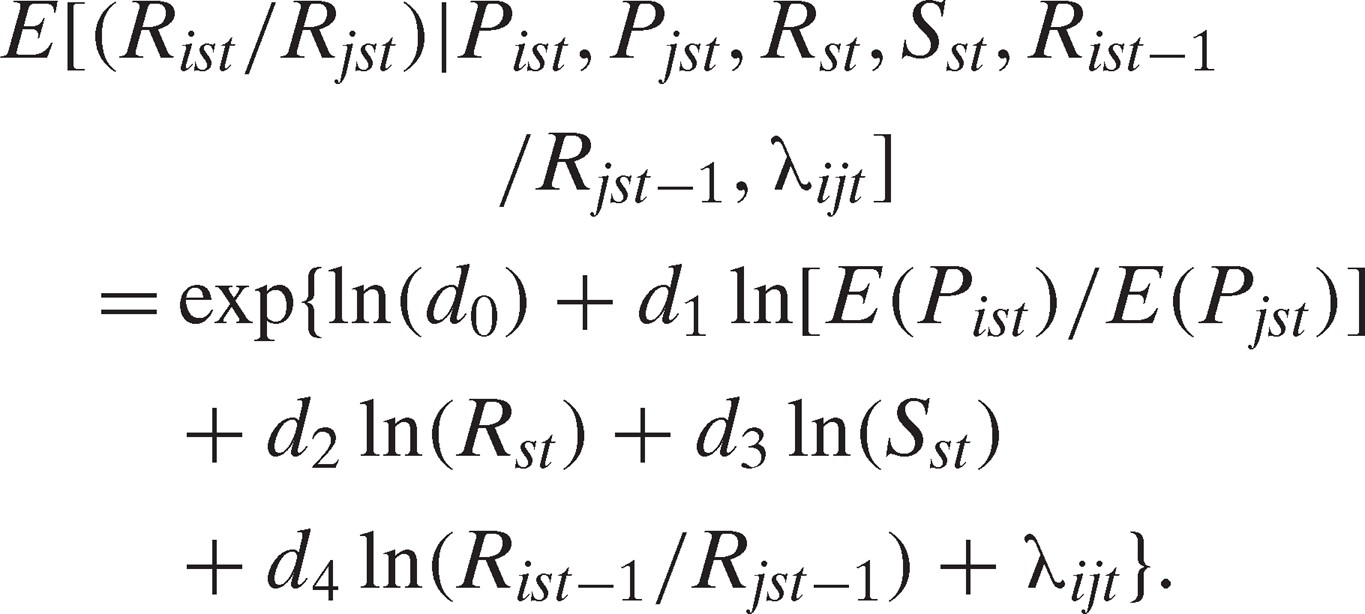 (9)
(9)As noted in Gourieroux, Monfort, and Trognon (1984), a consistent estimator of the parameters is obtained even if the data are not Poisson (indeed, the data do not even have to be integers). The advantage of PPML over ordinary least squares (OLS) in the log-linearized equation is twofold: first, since the dependent variable is not specified in logs, values of zero are permissible (in fact, PPML performs well even with a large number of zeros for the dependent variable; see Santos Silva and Tenreyro 2011).10 Second, under the assumption that the true conditional mean is as specified above, the OLS estimator associated with the log-linearized equation is biased in the presence of heteroskedasticity (Santos Silva and Tenreyro 2006). Furthermore, PPML is generally more efficient than other common nonlinear estimators such as nonlinear least squares (Santos Silva and Tenreyro 2006).
Zero values of the numerator of the dependent variable can be accommodated with the PPML estimator, but zero values of the denominator cannot. In the above specification we have deliberately chosen the denominators, land and labor, to ensure the largest number of observations in the estimation of each equation.11
While a significant negative coefficient on the price ratio is typically used to test the induced innovation hypothesis when input quantity ratios in the innovation implementing industry are used as the dependent variable, such a test is not critical unless innovation possibilities are neutral. In our case, assuming our controls sufficiently account for differences in marginal costs across states, a significant positive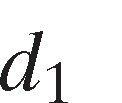 coefficient in the model constitutes an unambiguous critical test of the hypothesis for the public innovation creating industry regardless of whether innovation possibilities are neutral or nonneutral.
coefficient in the model constitutes an unambiguous critical test of the hypothesis for the public innovation creating industry regardless of whether innovation possibilities are neutral or nonneutral.
Expected price is defined as a geometrically lagged function of historical prices and is designed to capture expected input prices in the innovation implementing industry by giving more weight to recent than to earlier prices. Because of likely lags in the impact of any price changes, we begin the geometric lag with prices lagged one year and consider only the previous ten years of price data. Thus, expected price in is constructed as:
is constructed as: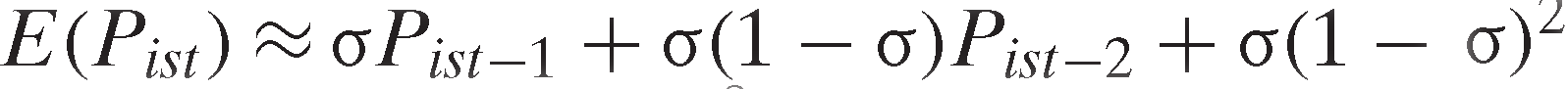
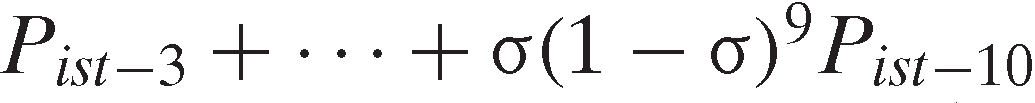 , (where
, (where is the geometric lag coefficient). The optimal lag is selected based on the Akaike information criterion from values of 0.1 to 0.9 in 0.1 intervals.
is the geometric lag coefficient). The optimal lag is selected based on the Akaike information criterion from values of 0.1 to 0.9 in 0.1 intervals.
Data
The data used for this study included total public research expenditures for agricultural productivity research, public research expenditures on technology aimed to save particular agricultural inputs, agricultural input prices for the same array of inputs, and patents issued for agriculture as the source of use industry.
Total annual public research expenditures for the period 1927–2009 were obtained for each state from Huffman (2012). They were compiled following the procedures in Huffman (2009). They included both federal (U.S. Department of Agriculture) and state (State Agricultural Experiment Stations and Veterinary Medicine Schools/Colleges of the Land Grant System) expenditures on agricultural research with a productivity focus.12 They excluded post-harvest research and research on households, families, and communities.
The number of patents issued for agriculture as the primary user of the patent was obtained for each state from Johnson (2013) for the period 1997–2008. The number of patents for earlier years was from Johnson's (2005) inventory of patents by state and U.S. patents by industry as the primary user of the patent for the period 1883–1996. The number of patents by state for agriculture as the primary user was prepared by multiplying the percent of patents granted by state each year by the number of patents granted in the U.S. for use in agriculture. Johnson's patent classification since 1976 follows the international protocol, and the Yale Technology Concordance (Johnson and Evenson 1997) was used to calculate industries of manufacture and sectors of use. Prior to 1976, the Wellesley Technology Concordance (Johnson 1999) was followed to classify patents. The knowledge stock was prepared following Wang et al.'s (2013) nineteen-year trapezoidal lag structure. Using weights based on the trapezoidal structure (with positive weights beginning in the second lagged year, peaking in years 7–10, and declining through year 18), patent knowledge stocks for agriculture were calculated for each state for the years 1998–2010.
Annual public expenditures on research aiming to save or more efficiently utilize specific agricultural inputs were obtained by keyword searches (with exclusions) of the U.S. Department of Agriculture's Current Research Information System (CRIS). This database inventories research projects supported by the U.S. Department of Agriculture, other federal agencies, and State Agricultural Experiment Stations. The inventory includes number of projects, scientist years working on each project, annual expenditures on each project, state where the research was conducted, detailed descriptions and outcomes of each project, and classification by knowledge area, subject of investigation, and field of science. The searches, conducted by Sellers (2012) in collaboration with the authors, began in February 2012, were refined during the subsequent months, and the final searches were conducted in July 2012.13 All projects reported in the system for the period 1998–2010 were searched.14 These include research projects supported by federal grant funds conducted both at land grant and non-land grant universities.
Following examination by the authors of project narratives from preliminary text searches, it was concluded that public research expenditures on projects seeking to save inputs could be reliably identified for only four input categories—labor, land, fertilizer, and energy. This is not an exhaustive array of inputs. It omits research that would save non-land capital as well as materials other than fertilizer and energy.
Additional preliminary text searches were conducted and the project narratives systematically reviewed by the authors to ensure that an objective of the selected research projects was to develop technology to save the specified category of inputs. The keywords used in the final search for each input category are reported in table 1.
| Labor Saving | Land Savinga | Fertilizer Saving | Energy Saving |
|---|---|---|---|
| labor cost | production efficiency | fertilizer placement | energy conservation |
| labor efficiency(ies) | production potential | fertilizer requirements | energy cost |
| labor productivity(ies) | yield potential | fertilizer response | energy demand |
| labor reduction | energy efficiency(ies) | ||
| labor saving | energy input | ||
| energy usage | |||
| energy use | |||
| energy utilization |
- a While the terms production efficiency and production potential might be associated with other types of research, examination of the project narratives revealed that the goal of such research was primarily land saving.
We began the searches with the same exclusions that Huffman imposed in his 2003 CRIS search of research focusing on agricultural production (Huffman 2009). This excluded projects that were clearly not related to agricultural productivity, that is, projects that addressed only the following subjects of investigation: recreation resources; trees, forests, and forest products; fish, shellfish, game and fur-bearing animals, and other wildlife and their habitats/wildlife and natural fisheries management, endangered species; food and manufactured resources (except for farm structures and related facilities, as well as drainage and irrigation facilities and systems); human resources, organization, and institutions (except the farm as a business enterprise); other technologies.15 We subsequently added the following subject of investigation exclusions to our searches for research projects aimed at saving particular agricultural inputs: watersheds and river basins; atmosphere; ornamentals, and turf; noncrop plant research; general plant research; horses, ponies, and mules; pets (companion animals); laboratory animals; other animals, general; cross-commodity research—multiple animal species; animal research, general; microorganisms. To avoid selection of energy projects aimed only at saving nutrient energy, the following keywords were also excluded from the energy saving project search: amino acid, body composition, calorimetry, diet, digestibility, digestion, feed, metabolism, nutrient, nutrition, pH, rumen.
Over the 1998–2010 period, the fraction of total research funds coming from “other nonfederal” (private) sources steadily increased from less than 10% in 1999 and 2000 to roughly a quarter in 2009 and 2010. The average percentage over the data period was just over 16%. Because we are analyzing ratios of research expenditures to save various inputs, this change in funding source should have little effect on our analysis unless private funds went predominantly to funding innovation to save some inputs but not others (the inclusion of year fixed effects further reduces the possibility that this change would cause bias in our results). However, because we expect that innovation funded through private means would be more sensitive to agricultural input prices (more likely to be subject to the IIH) than would publicly funded research, it is possible that there is more support for the IIH using CRIS data in later years than in earlier years. Unfortunately, our panel is extremely short and does not allow us to reliably test for differences in IIH support over time. We leave this question to future research.
The panel data of annual agricultural input prices for the forty-eight contiguous states came from the U.S. Department of Agriculture. See Ball, Hallahan, and Nehring (2004) and Ball et al. (1999) for the construction details. These data were compiled using theoretically and empirically sound procedures that preserve the economic integrity of national and state production accounts and are consistent with a gross output model of production. The state-level input price indices were constructed as multilateral chain-linked Elteto-Koves-Szulc (EKS) indexes of prices for exhaustive arrays of input types in each category in each state and year.
The land price index was computed from hedonic regressions of the price of land (implicit rental rates) in each county on a vector of land characteristics. For labor, the price index was computed from a gender, age, education, and employment class cross-classification of hours worked and average hourly compensation. Wage rates for self-employed workers were imputed as the wage of hired workers with the same demographics. The fertilizer price index was computed from hedonic regression results of prices of fertilizers on nutrients in the fertilizer materials. The energy price was computed from electricity, natural gas, and individual fuel prices. All intertemporal aggregations across individual inputs were computed as Tornqvist indexes.
Because of the limitations associated with obtaining accurate public research expenditure data for input saving research, we only utilize input prices that correspond to the research expenditure categories—land, labor, fertilizer, and energy. The price data for land and labor were available for the period 1960–2004, and the price data for fertilizer and energy were available for the period 1960–2008.
Annual data for each of the forty-eight states for the period 1999–2005 were used for the dependent variables, 1998–2004 for their lags, 1989–2004 for prices (because of the geometric lag structure), and 1999–2005 for total research expenditure and the knowledge stock. Additional data were used in a set of robustness checks. The extremes of the data periods used in robustness checks were 1998–2009 for the dependent variable, total research expenditures, and the knowledge stock and 1984–2008 for prices.16 Summary statistics for each variable for these data periods are reported in table 2.
| Variable | Unita | Observation Period | Mean Value | Minimum Valueb | Maximum Value | Standard Deviation | Number of Non-Zero Observations |
|---|---|---|---|---|---|---|---|
| Fertilizer research | $T | 1998–2005 | 284.9 | 3 | 2,698 | 497.3 | 196 |
| expenditure | $T | 1998–2009 | 255.3 | 3 | 2,698 | 450.8 | 284 |
| Land research | $T | 1998–2005 | 4,758 | 60 | 31,179 | 5,260 | 366 |
| expenditure | $T | 1998–2009 | 4,906 | 31 | 34,646 | 5,396 | 552 |
| Energy research | $T | 1998–2005 | 209.4 | 4 | 3,280 | 468.2 | 152 |
| expenditure | $T | 1998–2009 | 211.7 | 1 | 3,280 | 447.3 | 247 |
| Labor research | $T | 1998–2005 | 300.8 | 1 | 4,718 | 637.6 | 215 |
| expenditure | $T | 1998–2009 | 363.4 | 1 | 5,662 | 731.9 | 325 |
| Fertilizer price | index | 1989–2004 | 0.725 | 0.323 | 1.253 | 0.175 | 768 |
| index | 1984–2008 | 0.724 | 0.041 | 1.673 | 0.224 | 1,200 | |
| Land price | index | 1989–2004 | 1.044 | 0.195 | 3.632 | 0.543 | 768 |
| index | 1984–2004 | 1.019 | 0.195 | 3.632 | 0.516 | 1,008 | |
| Energy price | index | 1989–2004 | 1.141 | 0.825 | 1.883 | 0.195 | 768 |
| index | 1984–2008 | 1.303 | 0.787 | 3.496 | 0.488 | 1,200 | |
| Labor price | index | 1989–2004 | 0.801 | 0.280 | 2.111 | 0.294 | 768 |
| index | 1984–2004 | 0.707 | 0.211 | 2.111 | 0.310 | 1,008 | |
| Total research | $M | 1999–2005 | 21.16 | 0.490 | 106.4 | 18.30 | 336 |
| expenditure | $M | 1998–2009 | 21.19 | 0.175 | 127.6 | 19.26 | 576 |
| Knowledge stock | count | 1999–2005 | 37.18 | 1.216 | 290.5 | 48.61 | 336 |
| count | 1998–2009 | 37.36 | 1.185 | 292.2 | 48.17 | 576 |
- a The index is relative to the price in Alabama in 1996; $T is thousand dollars, $M is million dollars.
- b Minimum values for research expenditure are for cases where at least one project was funded.
The distribution of state-level average annual research funding for the 1998–2009 period to save each of the four agricultural inputs is presented in figure 1. For each of the inputs, the distribution is right-skewed with zero being the modal amount of funding, although the percentage of non-zero observations is always at least 40% (for energy) and as high as 96% (for land).
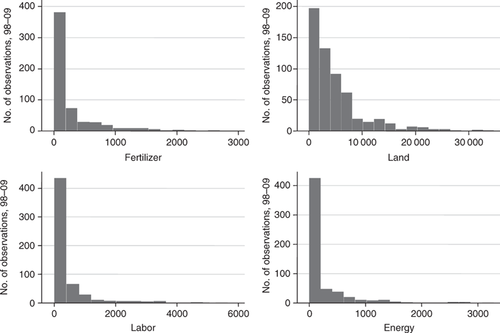
Distribution of state-level average annual research funding (thousand dollars)
Ratios of average state-level research funding are plotted over time along with price ratios in figure 2. Prices are lagged one year in the first row of graphs and five years in the second row. No obvious patterns were evident between the two series when prices were not lagged or lagged just one year. Patterns begin to emerge, however, when prices are lagged five years.
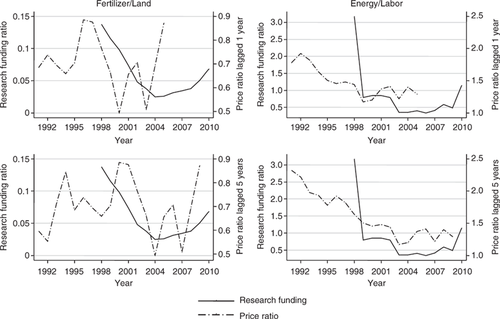
Ratios of average state-level research funding and lagged prices
Test Results
The PPML statistical estimates for the public agricultural research resource allocation decision model are reported in table 3. Estimates of the resource allocation decisions to save fertilizer relative to land and energy relative to labor are reported in the first two columns of the table. The remaining columns report estimates of the other input-saving resource allocation ratios, which we discuss below under robustness checks. With heteroskedasticity and autocorrelation likely to impact these models, we compute standard errors that are robust to both heteroskedasticity and autocorrelation for all estimated models. The robust standard errors are calculated using the clustered sandwich estimator using the state as the unit of cluster (Wooldridge 2002).17 All estimates of the effect of own-price ratio on the resource allocation ratios are equivalent to elasticities (for small changes in the independent variable). A 10% level of significance is used to judge statistically significant results.
| Variable | Fertilizer/Land | Energy/Labor | Labor/Land | Energy/Land | Fertilizer/Labor | Energy/Fertilizer |
|---|---|---|---|---|---|---|
| Own-price ratio | 0.468*** | -1.472 | 0.392 | 0.589*** | 2.477* | 3.563*** |
| (0.181) | (0.607) | (0.311) | (0.133) | (1.295) | (1.347) | |
| P-valueb | 0.00493 | 0.99231 | 0.10345 | 0.00001 | 0.02788 | 0.00408 |
| Lagged dependent variable | 0.883*** | 0.660*** | 0.584*** | 0.631*** | 0.434*** | 0.444*** |
| (0.098) | (0.135) | (0.100) | (0.074) | (0.105) | (0.134) | |
| Total research expenditure | 0.493* | 0.556 | -.068 | -.412* | 0.764* | -.751*** |
| (0.192) | (0.348) | (0.153) | (0.228) | (0.434) | (0.261) | |
| Knowledge stock | -.048 | 0.064 | 0.140* | 0.255* | -.402 | 0.596*** |
| (0.081) | (0.189) | (0.068) | (0.120) | (0.216) | (0.216) | |
| Intercept | 1.399 | 2.427 | 0.866 | -3.766*** | 5.336* | -5.707*** |
| (0.904) | (1.864) | (1.117) | (1.316) | (2.230) | (1.528) | |
| Geometric lag coefficient | 0.1 | 0.1 | 0.6 | 0.9 | 0.4 | 0.3 |
| R-square | 0.748 | 0.682 | 0.378 | 0.854 | 0.478 | 0.611 |
| Log-likelihood | -53.04 | -90.73 | -58.38 | -34.55 | -229.6 | -189.9 |
| Number of observations | 173 | 73 | 183 | 134 | 96 | 84 |
- a Robust standard errors are in parentheses. The t-tests conducted for the coefficients on own price ratio are one-tailed tests (with the null hypothesis being that the coefficient is less than or equal to zero). T-tests for coefficients on other regressors are two-tailed tests (null hypothesis that the coefficient is equal to zero). Asterisk codes:
 ,
, ,
, . Fixed time effects were also estimated in all models but are not reported.
. Fixed time effects were also estimated in all models but are not reported. - b P-value for one-sided hypothesis test.
The fertilizer/land resource allocation decision has a positive sign on expected price that is significant and is thus consistent with the IIH. The estimated coefficients on the lagged dependent variable and total research expenditure are also both positive and statistically significant in this equation. The estimated sign on the expected price variable is significantly negative in the energy/labor equation, which implies that an increase in energy price would induce reallocation of research resources to economize labor relative to energy. The lagged dependent variable is also significant in this equation. In both equations, the magnitude of the coefficient on the lagged dependent variable suggests that the resource allocation decision in any year is strongly dependent on the previous year's decision. In fact, they imply that the long-run effects of other explanatory variables, in other words, own-price, total research expenditure, and knowledge stock, is 2.9–8.5 times as great as the short-run effects in explaining resource allocation. In both equations, optimal expected price lag coefficients are 0.1, which imply very long lags in formation of price expectations (median 6.6 years).18 The regressors in these equations explain 68%–75% of the variance. Since all regressors (other than the time dummies) are specified in logarithmic form for PPML estimation, observations with a zero value of the lagged dependent variable are removed from the data set. This results in only 73 observations being used in the energy/labor equation and 173 observations in the fertilizer/land equation.
Robustness Checks
To examine the robustness of our initial results, we consider several plausible alternatives:
 values range from 0.48 to 0.85. For purposes of examining other robustness checks, we treat the initial two equations and the additional four equations in Alternative A as the base model since they represent the exhaustive output pairings.
values range from 0.48 to 0.85. For purposes of examining other robustness checks, we treat the initial two equations and the additional four equations in Alternative A as the base model since they represent the exhaustive output pairings.
-
Because the logic for output pairings in our specification of the two-level CET production function is not very strong, we also test for consistency with the IIH by considering the other possible pairings in the resource allocation decision stage of the estimation. Therefore, we test for consistency with the IIH using the exhaustive pairs of labor/land, energy/land, fertilizer/labor, and energy/labor.19
-
To generalize the two-level CET production function, we include all three price ratios in the resource allocation decision stage of estimation. The same denominator is used for all price ratios and is consistent with that of the dependent variable.
-
As already noted, our data periods do not match perfectly. Our most recent price data are 2008 for fertilizer and energy and 2004 for land and labor; we have research expenditure data to save individual inputs through 2010 and total research expenditure through 2009. To utilize more of the available data, we use four additional years of observations by starting the geometric lag of prices at five years.
-
Because we have more recent price data for fertilizer and energy, we also use all available data for the fertilizer and energy resource allocation decision with the geometric lag of prices starting at one year.
-
Imposing the assumption of global constant returns to scale (and consequently homotheticity), our final robustness check removes total research expenditure from the set of regressors in all models.
The IIH test results from the Robustness alternative specifications B–E are reported in table 4. With the exception of alternative D, six equations were estimated to provide all ratio combinations for each of these alternative specifications. Only one equation, the energy/fertilizer ratio, was estimated for alternative D.
| Specification | Number of Price Ratios | Geometric Lag Begins with Year | Total Research Expenditure | Own- Price Ratiob | Estimated Coefficient | Robust Standard Error | P-Valuec | R2 Value | Optimal Geometric Lag Coefficient | Number of observations |
|---|---|---|---|---|---|---|---|---|---|---|
| Alternative B – All price ratios | 3 | 1 | Yes | F/A | -.749 | 0.730 | 0.84774 | 0.787 | 0.3 | 173 |
| E/L | -4.025 | 1.002 | 0.99997 | 0.763 | 0.7 | 73 | ||||
| L/A | -.002 | 0.245 | 0.50340 | 0.407 | 0.9 | 183 | ||||
| E/A | 0.790 | 0.721 | 0.13678 | 0.879 | 0.8 | 134 | ||||
| F/L | 2.532*** | 0.974 | 0.00468 | 0.505 | 0.5 | 96 | ||||
| E/F | 4.545*** | 1.580 | 0.00201 | 0.680 | 0.4 | 84 | ||||
| Alternative C – Longer price lags | 1 | 5 | Yes | F/A | 0.454*** | 0.173 | 0.00430 | 0.645 | 0.2 | 259 |
| E/L | -.545 | 0.415 | 0.90559 | 0.601 | 0.9 | 130 | ||||
| L/A | 0.196 | 0.229 | 0.19699 | 0.376 | 0.1 | 297 | ||||
| E/A | 0.563*** | 0.147 | 0.00006 | 0.782 | 0.8 | 217 | ||||
| F/L | 1.171* | 0.885 | 0.09287 | 0.389 | 0.1 | 152 | ||||
| E/F | 2.282* | 1.526 | 0.06736 | 0.434 | 0.9 | 127 | ||||
| Alternative D – One-year price lags with price data through 2008 | 1 | 1 | Yes | E/F | 3.347*** | 1.204 | 0.00272 | 0.434 | 0.5 | 127 |
| Alternative E – No total research expenditure | 1 | 1 | No | F/A | 0.833*** | 0.086 | 0.00540 | 0.726 | 0.1 | 173 |
| E/L | -1.362 | 0.598 | 0.98868 | 0.690 | 0.1 | 73 | ||||
| L/A | 0.377 | 0.311 | 0.11265 | 0.387 | 0.6 | 183 | ||||
| E/A | 0.615*** | 0.163 | 0.00008 | 0.823 | 0.9 | 134 | ||||
| F/L | 2.227* | 1.384 | 0.05375 | 0.385 | 0.4 | 96 | ||||
| E/F | 3.434*** | 1.401 | 0.00713 | 0.559 | 0.3 | 84 |
- a All allocation decision models were estimated with time fixed effects. Asterisk codes:
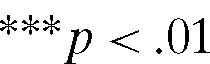 ,
, ,
, .
. - b Input codes: A is land, E is energy, F is fertilizer, L is labor.
- c P-value for 1-sided hypothesis test.
Considering all price ratios as explanatory variables in each equation (alternative B), the fertilizer/labor and energy/fertilizer equations again provide statistically significant support for consistency with the IIH, and the energy/labor equation again provides statistically significant support for the opposite. Considering longer price lags (alternative C), the fertilizer/land, energy/land, fertilizer/labor, and energy/fertilizer equations are consistent with the IIH, as they are in the base model. The energy/labor equation again has a negative statistically significant coefficient on the price ratio. When additional price data for energy and fertilizer are used with a one-year lag on initial price effects (alternative D), the price-ratio effect is positive and statistically significant (consistent with IIH). With total research expenditure removed from the set of regressors (alternative E), the results are qualitatively the same as for the base model.
For two output pairings, fertilizer/labor and energy/fertilizer, all robustness checks provide statistically significant support for the IIH. Three of four specifications of the fertilizer/land and the energy/land equations also support consistency with the IIH. No energy/labor or labor/land equations support the IIH. In fact, all energy/labor equations have significant negative coefficients on the price ratio. Thus, conclusions for the base model and all robustness checks are consistent for four of the six pairings. The fertilizer/labor and energy/fertilizer pairings provide unambiguously significant support for the IIH and the energy/labor and labor/land pairings provide no support. The other two pairings generally support the IIH.
Overall, fertilizer provides the greatest support (92% of its estimated equations) for consistency with the IIH. It is followed by energy with 62%, land with 50%, and labor with 33% of estimated equations supporting the IIH. If we were to subtract the number of significant negative responses (not noted by asterisks in the tables) from the number of significant positive responses, fertilizer would still provide the greatest net support with 92% of its equations. It would be followed by land with 50% and energy with 31%. Labor provides no net support.20
Counter to expectations based on the patterns exhibited in figure 2, no additional support for significant consistency with the IIH is demonstrated by the models based on a price expectation beginning with prices lagged five years than by those with prices lagged one year.21 The level of support was the same for all model specifications except alternative B (with all price ratios included as regressors).
Conclusions
We examine the applicability of the induced innovation hypothesis (IIH) to U.S. public agricultural research using the pseudo Poisson maximum likelihood estimator. In doing so, we report what could be referred to as the first direct test of the IIH for U.S. agriculture. It is the first time that a test has been conducted for this industry accounting for supply as well as demand for new technology aimed at saving inputs. However, our tests are really tests of congruence between the hypothesis and resource allocation in public research. Due to lack of data to estimate the expected marginal costs of developing new technology to save different inputs, we take a reduced-form approach to testing the hypothesis. We test whether relative input prices in the technology implementing industry (agriculture) affect resource allocation decisions by the public technology creating industry (federal government and state agricultural experiment stations) that increase relative research effort aimed at saving the relatively more expensive input across states and over time.
Considering several plausible specifications of the resource allocation decision, we find support for consistency between the IIH and public agricultural research funding decisions in four of six pairings. For two pairings, all specifications provide empirical results consistent with the IIH. For two more, three of four specifications do. Although not unambiguously supportive, the evidence collectively provides considerable evidence of consistency with the IIH in public research resource allocation decisions for four of six input pairings. The evidence is strongest for decisions to allocate research resources aimed at saving fertilizer relative to energy or labor. There is also substantial support for decisions to allocate research resources to save land relative to fertilizer or energy. There is no support in research funding decisions aimed at saving labor relative to land or energy. In fact, decisions regarding the last input pairing are significantly counter to the IIH.
We treat the public agricultural research (technology creating) industry in each state as though it were a perfectly competitive firm, motivated by changes in the prices of inputs in the technology implementing industry. While there is evidence that public sector organizations operating in a mixed market such as research and development can mimic private firms whose principal behavioral guide is profit maximization, there are also reasons not to expect profit maximization to be their primary guide. For example, more basic or risky research is typically selected by the public sector, and increased public (or private) research has potential to crowd out the other. Consequently, the degree of support found for the IIH in public agricultural research resource allocation decisions in this article represents a lower bound estimate of what could be expected from private research decisions that are clearly profit motivated.
The degree of support provided by this research for the IIH in U.S. public agricultural research funding decisions, which also provides support for its relevance in U.S. agricultural production, comes with several caveats. Although we included a control variable for homotheticity in the estimation model, we imposed the commonly maintained but strong assumption of a locally homothetic production function in the theoretical structure of public research underlying our tests. Because of data limitations, we were unable to examine private research decisions. Although we have defended our public research expenditure data as likely far less noisy than other data that might be used to proxy innovation discovery efforts to economize “the use of a factor which has become relatively expensive” (Hicks 1932), they are still very noisy. The search procedure for selecting relevant projects was far from perfect. The inclusion of a patent knowledge stock and lagged dependent variable to control for state differences in expected marginal cost of developing and implementing input-saving technologies is just one possible approach that might be taken to surmount data limitations. All of the shortcomings of the study suggest opportunities for further inquiry.
 and
and , respectively.
, respectively.


 Test Robust to Cluster Heterogeneity
Test Robust to Cluster Heterogeneity
