Behavioral Responses and the Impact of New Agricultural Technologies: Evidence from a Double-blind Field Experiment in Tanzania
The authors would like to thank editor Brian Roe and two anonymous referees for comments and suggestions that helped us to substantially improve the paper. The authors also thank Brad Barham, Jean-Paul Chavas, Valentino Dardanoni, Jeremy Foltz, Gunnar Köhlin, Razack Lokina, Vincenzo Provenzano, Laura Schechter, and seminar participants in Oxford Center for the Study of African Economies (CSAE) conference 2012, the University of Geneva, the University of Palermo, the University of Wisconsin, Madison, the University of Verona, and Wageningen University for their valuable comments. The authors are responsible for any remaining errors. Financial support offered by Swedish International Development Cooperation Agency (SIDA) via Environment for Development is gratefully acknowledged.
Abstract
Randomized controlled trials (RCTs) in the social sciences are typically not double-blind, so participants know they are “treated” and will adjust their behavior accordingly. Such effort responses complicate the assessment of impact. To gauge the potential magnitude of effort responses we implement a conventional RCT and double-blind trial in rural Tanzania, and randomly allocate modern and traditional cowpea seed varieties to a sample of farmers. Effort responses can be quantitatively important—for our case they explain the entire “treatment effect on the treated” as measured in a conventional economic RCT. Specifically, harvests are the same for people who know they received the modern seeds and for people who did not know what type of seeds they got; however, people who knew they had received the traditional seeds did much worse. Importantly, we also find that most of the behavioral response is unobserved by the analyst, or at least not readily captured using coarse, standard controls.
Compared to many parts of the world, agricultural productivity in sub-Saharan Africa has largely stagnated. The widespread adoption of new agricultural techniques has been identified as one possible way of addressing this concern (e.g., Evenson and Gollin 2003; Doss 2003).1 New technologies, including high-yielding varieties, drove the Green Revolution in Asia, and could provide increases in agricultural productivity across Africa as well, thereby stimulating economic growth and facilitating the transition from low productivity subsistence agriculture to a productive, agro-industrial economy (World Bank 2008). Understanding the productivity implications of new technologies is therefore of paramount importance. Randomized controlled trials (RCTs) have been identified as a crucial tool for evaluating yield impacts.2 Random assignment of units to treatment or control group ensures exogeneity of the variable of interest, potentially reducing the estimation of average treatment effects (ATE) to a simple comparison of sample means. Examples of RCTs in the domain of agricultural intensification—both in Kenya—include Duflo et al. (2008, 2011) on the profitability and adoption of fertilizers, and Ashraf et al. (2009) on the promotion of export crops.
A common element of (agricultural) interventions is that success often depends on a combination of the innovation provided by the experimenter and the response to the treatment provided by subjects. For example, the impact of new varieties depends on the use of complementary inputs such as fertilizer, labor, and land (Dorfman 1996). Further, Smale et al. (1995) modeled adoption as three simultaneous choices: whether to adopt components of the recommended technology; and the decision of how to allocate different technologies across the land area; the decision of how much of these inputs, such as fertilizer, to use (see also Khanna 2001). Not all dimensions of effort are observable, and effort expended and other behavioral responses will depend on the perceptions and beliefs of the subjects (Chassang et al. 2012a). This may threaten the internal validity of RCTs and, insofar as beliefs vary from one locality to the next, will also compromise the external validity of RCTs.
Such threats to validity have received some attention in the (medical) literature: it is common to distinguish between “efficacy trials” (evaluating under nearly ideal circumstances with high degrees of control, such as a laboratory) and “effectiveness trials” (evaluating in the field, with imperfect control and adjustment of effort in response to beliefs and perceptions). While the relevance of (unobservable) effort responses in the domain of impact assessment is widely accepted in economics, the difference between efficacy and effectiveness in development interventions has received scant (empirical) attention; Barrett and Carter (2010) discuss it under the general topic of “overlooked confounders in RCT data.” A few papers discuss the relevance of behavioral responses. For example, writing about field experiments more broadly, List (2011) remarks that “A plausible concern is that when subjects know they are participating in an experiment, whether as part of an experimental group or as part of a control group, they may react to that knowledge in a way that leads to bias in the results.” Moreover, “unobservable perceptions of … [an] intervention [will] vary among participants and in ways that are almost surely correlated with other relevant attributes and expected returns from the treatment” (Barrett and Carter 2010). The result is differential exposure to the intervention, or unobservable heterogeneity.3 The “muddy realities of field applications” imply that the attractive asymptotic properties of RCTs disappear—an outcome Barrett and Carter refer to as “faux exogeneity.”
As mentioned, empirical work on the “faux exogeneity” problem is scarce in economics. An exception is Malani (2006), who writes that “For one thing, placebo effects may be a behavioral rather than a physiological phenomenon. More optimistic patients may modify their behavior—think of the ulcer patient who reduces his or her consumption of spicy food or the cholesterol patient who exercises more often—in a manner that complements their medical treatment. If an investigator does not measure these behavioral changes (as is commonly the case), the more optimistic patient will appear to have a better outcome, that is, to have experienced placebo effects.” Another noteworthy exception is Glewwe et al. (2004), who compare retrospective and prospective analyses of school inputs on educational attainment, and suggest that behavioral responses to the treatment may explain part of the differences between these two types of analysis.4
To the best of our knowledge, this paper is the first to empirically investigate how behavioral responses may impact the validity of RCTs in the context of agricultural technology adoption. More specifically, we ask to what extent is unobservable effort quantitatively important in a specific agricultural economic application. To probe this issue, we combine evidence from a conventional RCT where both implementers and subjects are informed about assignment status (henceforth referred to as open RCTs) and a double-blind experiment, akin to the type of experiment routinely used in medicine. We focus on an agricultural development intervention in central Tanzania, and distributed modern and traditional seed varieties among random subsamples of farmers. By comparing outcomes in the double-blind RCT with outcomes of the open RCT, we seek to gauge the importance of behavioral responses (see below). We are aware of only one other non-drug study that executes a double-blind trial: Boisson et al. (2010) test the effectiveness of a novel water filtration device using a double-blind trial (i.e., including placebo devices) in the Democratic Republic of Congo. These authors found that while the filter improved water quality, it did not achieve significantly more protection against diarrhea than the placebo treatment.
Our results strongly suggest that (unobservable) effort matters: harvests are the same for people who know they received modern seeds, and for people who did not know what type of seeds they got; however, people who knew they received the traditional seeds did much worse. Hence, the open RCT identified a large and significant effect of the modern seed treatment on harvest levels, and a naïve experimenter may routinely attribute this impact to the greater productivity of modern seed. Surprisingly, all impact in the open RCT appears due to a reallocation of effort. A small part of this behavioral response is captured in our data—farmers who were unsure about the quality of their seed (in the double-blind experiment) and farmers who knew they received the modern seed (in the open RCT) planted their seed on larger plots than farmers who knew they received the traditional seed (control group in the RCT). However, most of this response was not picked up by our data, and is “unobservable” to the analyst. In spite of our efforts to document the effort reallocation process, we cannot explain most of the harvest gap between the open RCT and double-blind trial.
This paper is organized as follows. In section 2 we discuss effort responses in relation to impact evaluation, and demonstrate how under specific circumstances open RCTs and double-blind trials produce upper and lower bounds, respectively, of the outcome variable of interest. In section 3 we describe our experiments, data, and identification strategy. Section 4 contains our results. We demonstrate that the difference between treatment and control group in an open RCT appears to be due entirely to an effort response, and we identify which part of this reallocation process is unobservable using standard survey instruments. In section 5 we speculate on implications for policy makers and analysts.
Effort Responses and the Measurement of Impact
The experimental literature identifies various types of effort responses, which may preclude unbiased causal inference when experiments are not double-blind. These responses include the Pygmalion effect (expectations placed upon respondents affecting outcomes) and the observer-expectancy effect (cognitive bias unconsciously influencing participants in the experiment). Behavioral responses may also originate at the respondent side. Well-known examples are the Hawthorne effect (i.e., capturing that respondents in the treatment group change their behavior in response to the fact that they are studied—see Levitt and List 2011) and the opposing John Henry effect (i.e., bias is introduced by reactive behavior of the control group). Similarly, Zwane et al. (2011) demonstrate the existence of so-called “survey effects” (i.e., being surveyed may change later behavior). In addition to these effects, and the focus of this paper, optimizing participants should adjust their behavior if an intervention affects the relative returns of effort. While random assignment ensures that the intervention is orthogonal to ex ante participant characteristics, treatment and control groups will be different ex post if treated individuals behave differently.
A stylized model helps to elucidate the underlying idea. Consider a population of smallholder farmers, who we assume to be rational optimizers responding to new opportunities (e.g., Schultz 1964). Assume that each farmer seeks to maximize income and combines effort and seed to produce a crop, Y.5 There are two varieties of seed, modern and traditional, and we use τ∈{0,1} to denote treatment status, so that τ=1 when modern seed is received. We denote subject effort, which captures a potentially broad vector of choices and behaviors, by b(p), where p is the probability of receiving the treatment. Following Chassang et al. (2012b), we assume b(p)∈[0,1], where b(p=0)=0 corresponds to default effort in the absence of treatment (or effort expended by the control group in an RCT), and b(p=1)=1 corresponds to fully adjusted effort in anticipation of certain treatment (or effort expended by the treated group in an RCT). Double-blind trials obviously have intermediate probabilities of treatment (i.e., 0<p<1). Thus, b(p) maps probabilities into a potentially broad range of effort variables (e.g., labor input, fertilizer use, plot size), and captures attitudes and beliefs of the respondent.6
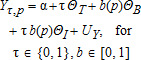 (1)
(1) (2)
(2)This treatment effect is the actual total derivative of the production function with respect to the intervention in the presence of potentially misguided expectations and beliefs. This measure picks up the direct treatment effect and the interaction effect—as it should, because these effects can only be obtained via the treatment. However, the measure also picks up the additional effort response, ΘB. The latter effect may be obtained in the absence of treatment and presumably comes at a cost (or else effort would presumably not vary across treatments, and we would have b(p=0)=b(p=1)). Including the ΘB effect implies that the standard RCT overestimates the production impact of treatment.8 Hence, for ΘB>0, equation (2) provides an upper bound of the effect that the policy maker is interested in (an RCT provides a lower bound when ΘB<0).
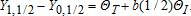 (3)
(3)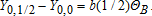 (4)
(4)Data and Identification
Two Experiments
We conducted two experiments with cowpea farmers in Mikese, Morogoro Region (Tanzania) from February–August 2011. Mikese is located along a road connecting Dar es Salaam to Zambia and the Democratic Republic of Congo. The livelihood activities of the households in our sample are agriculture and trade. As is common in Africa, farm households typically cultivate multiple plots. While all farm households grow cowpeas, none of them “specialize” in this crop—they grow a range of crops on their plots, often on a rotational basis.
We randomly selected 583 household representatives to participate in the experiment, and randomly allocated those to one of four treatment groups. Randomization was done at the level of individual households, and initially there were about 150 participants in each group.11 We organized two experiments: a conventional (open) economic RCT, and a “double-blind” RCT. Participants in both trials received cowpea seed of either a modern (improved) type or the traditional, local type. Farmers were free to combine the seeds they received with other farm inputs, but were instructed to plant all seeds. The name of the improved variety is TUMAINI. This variety was bred and released 5 years earlier by the National Variety Release Committee after being tested and approved by the Tanzania Official Seed Certification Institute (TOSCI). Earlier efficacy trials suggested this variety possesses some traits that are superior to local lines, such as being high yielding and early maturing, as well as exhibiting an erect growth habit. This was communicated to participants in all treatments.12
For the double-blind trial to “work,” it was important that the traditional and modern seed looked exactly the same—the seed types must be indistinguishable in terms of size and color. While information about seed type may be gradually revealed as the crop matures in the field, this does not invalidate our design because key inputs were already provided.13 Since the modern seed was treated with purple powder, we also dusted the traditional type, and clearly communicated this to the farmers—they knew that seed type could not be inferred from the color. The powder is a fungicide/insecticide treatment, APRON Star (42WS), and is intended to protect the seed from insect damage during storage. Our identification strategy rests on the assumption that fungicide dusting did not affect seed productivity (or else our estimates confound behavioral responses and the impact of dusting). The fungicide reduces seed damage prior to distribution, but should not matter for productivity in our experiment because we hand-selected unaffected seeds from the sets of undusted and dusted seed. Moreover, we distributed the seed just prior to the planting season, so losses during storage on the farm were minimal or absent.
Our concealing strategy appears to have been successful, as no less than 96% of the participants in the double-blind RCT indicated that they did not know which seed type they received at the time of seed distribution (of the remaining 4%, half guessed the seed type wrong). In contrast, nearly all participants in the conventional economic RCT knew which seed type they had received.
We informed participants in the open RCT about the type of cowpea seed they received. Subjects in group 1 received the modern seed, and subjects in group 2 received the traditional type. In contrast, subjects in the double-blind trial were not informed about the type of seed they received (nor were the enumerators interacting with the farmers informed about the seed type distributed). Subjects in group 3 received modern cowpeas, and subjects in group 4 received the traditional type. All participants in groups 3 and 4 were given the same information about the seeds. Farmers were not explicitly informed about the probability of receiving either seed type (which was 50%), but it was made clear that the seed they received could be either the traditional or modern variety.14 All seed was distributed in closed paper bags. Two enumerators participated in the experiment, and they were not assigned to specific treatments (so our results do not confound treatment and surveyor effects).
Participants from all groups were informed that they should plant all the seeds on one of their plots, and were not allowed to mix the seed with their own cowpeas (or sell the seed). The participants were also informed that the harvest fully belonged to them, and would not be “taxed” by the seed distributor. Each participant received a special bag to safely store the harvested cowpeas until an experimenter had visited to measure the whole harvest towards the end of the harvest season. Cowpeas are harvested on a continuous basis, and to avoid a bias in our results we collected information on both pods stored and sold or eaten between picking and measurement. Seed was planted during the onset of the rainy season (February–March), and harvested a few months later (June–July).
Data
Our dependent variable is the total harvest of cowpeas. As mentioned, cowpeas are harvested on a continuous basis towards the end of the growing season, so we asked farmers to store harvested pods in a special bag we provided. After completing the harvest, participants were visited at home by our enumerators. After removing the cowpeas from their pods, we weighed the seed. We have one main output variable: cowpeas available for measurement during the endline (where we implicitly assume that consumption rates or cowpea sales are similar for the modern and traditional cowpea varieties).15 We also consider how cowpea yields are affected (defined as harvest divided by plot size); we prefer the harvest over the yield measure, as it is not obvious how (information about) treatment status should affect yields. The reason is that the denominator of the yield variable may be affected by treatment. If farmers in the control group of the RCT (receiving traditional seed) respond by planting their seed on a small plot, we would unambiguously predict that harvest levels go down (because of inter-plant competition), but it is not obvious whether yields are higher or lower than in the treatment group. Yields may be higher (as crop density is higher when the plot is smaller) or lower (if complementary inputs are underprovided as well). That is, if farmers undersupply all inputs (including land, or plot size) to traditional seed in the RCT, then it is not obvious whether yields go up or down. In contrast, harvest levels should unambiguously decline, which makes them the preferred measure.
Explanatory variables were obtained during three waves of data collection. First, household survey data were collected during a baseline survey immediately after distributing the seed. This survey also included sections about demographic characteristics, welfare, land use, plot characteristics, cowpea planting techniques, labor allocation, income activities, and consumption. Second, we obtained field measurements when the crop was maturing in the field. This included measuring plot size, number of plants grown, number of pods per plant, and making observations on land quality (slope, erosion, weeding). Third, additional data were collected during a post-harvest endline survey, immediately after the weighting of the harvest. This endline survey included questions about updated beliefs regarding the type of seed, as well as about production effort (labor inputs, and the use of pesticides and fertilizer).
Attrition
Unfortunately, attrition in our sample is considerable. Specifically, a share of the participants chose not to plant the seed we provided (163 participants, or 28% of our total sample). We speculate that this is because we provided seeds just prior to the planting season (to avoid on-farm seed depreciation). Many farmers perhaps had different plans for their plots at the moment of seed distribution, and had already arranged inputs for alternative crops. We have no reason to believe that this cause of attrition is systematically linked to specific treatments (something that is confirmed by the data). Moreover, in a smaller number of cases (45 cases, or 8% of the total sample) we found that farmers had planted our seed but failed to harvest it. Possible reasons for crop failure include late rain or local flooding. Finally, our enumerators were unable to collect endline harvest data from some participants (52 cases, or 9% of the sample), as these farmers were absent when we tried to visit them for the endline measurement (twice). Among the households with harvest measurement, we managed to conduct the field measurement for a subsample (about 70%). The rest of the fields were not reachable due to their long distances to the village and/or bad condition of roads. Table 1 provides an overview of these numbers for each treatment group. Attrition rates are rather equal across the four groups.
| Open RCT | Double-blind Trial | ||||
|---|---|---|---|---|---|
| Improved seed | Traditional seed | Improved seed | Traditional seed | ||
| Group 1 | Group 2 | Group 3 | Group 4 | Total (%) | |
| Did not plant | 38 | 39 | 37 | 49 | 163 (28%) |
| Planted but failed to harvest | 6 | 13 | 13 | 13 | 45 (7%) |
| Planted and harvested, no endline measurement | 20 | 11 | 9 | 12 | 52 (9%) |
| Total missing, no harvest measurement | 64 | 63 | 59 | 74 | 260 (44%) |
| Missing, no field measurement | 26 | 21 | 27 | 31 | 105 (18%) |
| Total assigned | 141 | 147 | 142 | 153 | 583 |
High attrition is potentially problematic, as it could introduce selection bias in our randomized designs.16 We deal with attrition in several ways. First, we test whether our remaining sample is (still) balanced along key observable dimensions. We collected data on 44 household characteristics during the baseline, and ANOVA tests indicate that we cannot reject the null hypothesis of no difference between the four treatment groups for all but two variables. The exceptions to the rule are the dependency ratio and a variable measuring social group membership (both variables are slightly lower in group 3 compared to the other three groups). Table 2 reports a selection of these variables, and associated P-values of the ANOVA test.
| Open RCT | Double-blind | ||||
|---|---|---|---|---|---|
| Improved | Traditional | Improved | Traditional | ||
| Group 1 | Group 2 | Group 3 | Group 4 | ANOVA test | |
| Variables | (N = 77) | (N = 84) | (N = 83) | (N = 79) | (P-value) |
| Household size | 4.714 | 5.000 | 5.108 | 4.772 | 0.695 |
| (2.449) | (2.794) | (2.252) | (2.050) | ||
| Gender household head (1 = male) | 0.685 | 0.768 | 0.818 | 0.781 | 0.275 |
| (0.468) | (0.425) | (0.388) | (0.417) | ||
| Years of education household head | 2.681 | 2.580 | 2.618 | 2.534 | 0.994 |
| (2.731) | (3.169) | (2.894) | (3.644) | ||
| Age household head | 45 | 48 | 49 | 50 | 0.277 |
| (16) | (17) | (16) | (16) | ||
| Dependency ratio (percentage of household members older than 60 or younger than 16) | 0.525 | 0.569 | 0.485 | 0.581 | 0.091 |
| (0.268) | (0.289) | (0.239) | (0.273) | ||
| Literacy rate | 0.141 | 0.126 | 0.138 | 0.145 | 0.725 |
| (0.218) | (0.242) | (0.243) | (0.243) | ||
| % hh members secondary school | 0.071 | 0.076 | 0.068 | 0.083 | 0.034 |
| (0.121) | (0.159) | (0.122) | (0.145) | ||
| Village leaders' household and their relatives (1 = yes) | 0.182 | 0.202 | 0.229 | 0.177 | 0.839 |
| (0.388) | (0.404) | (0.423) | (0.384) | ||
| Members of economic groups (1 = yes) | 0.208 | 0.262 | 0.133 | 0.215 | 0.222 |
| (0.408) | (0.442) | (0.341) | (0.414) | ||
| Members of social groups (1 = yes) | 0.325 | 0.393 | 0.217 | 0.354 | 0.089 |
| (0.471) | (0.491) | (0.415) | (0.481) | ||
| Health (1 = somewhat good or good) | 0.533 | 0.470 | 0.524 | 0.494 | 0.848 |
| (0.502) | (0.502) | (0.502) | (0.503) | ||
| Economic situation compared to village average (1 = somewhat rich or rich) | 0.311 | 0.277 | 0.256 | 0.282 | 0.901 |
| (0.466) | (0.450) | (0.439) | (0.453) | ||
| Expectation of economic situation in future (1 = richer or somewhat richer) | 0.392 | 0.361 | 0.378 | 0.321 | 0.981 |
| (0.492) | (0.483) | (0.489) | (0.470) | ||
| Land owned (acre) | 4.670 | 5.520 | 4.197 | 3.793 | 0.285 |
| (7.012) | (7.243) | (4.275) | (3.325) | ||
| Has own or public tap | 0.740 | 0.786 | 0.711 | 0.785 | 0.600 |
| (0.441) | (0.413) | (0.456) | (0.414) | ||
| Own a cell phone | 0.221 | 0.286 | 0.337 | 0.354 | 0.756 |
| (0.417) | (0.454) | (0.476) | (0.481) | ||
| Own a bike (1 = yes) | 0.416 | 0.429 | 0.337 | 0.405 | 0.636 |
| (0.496) | (0.498) | (0.476) | (0.494) | ||
| Non-farm income (1,000 Tsh)* | 591 | 571 | 684 | 734 | 0.896 |
| (1534) | (1363) | (1576) | (1614) | {0.839}† | |
| Value of productive assets (1,000 Tsh)* | 6.810 | 6.165 | 6.400 | 6.405 | 0.936 |
| (6.398) | (5.892) | (6.066) | (6.298) | {0.420}† | |
| Value of other assets (1,000 Tsh)** | 129 | 123 | 124 | 113 | 0.947 |
| (196) | (183) | (160) | (135) | {0.641}† | |
| Food consumption 7 days (1,000 Tsh)** | 29.435 | 30.972 | 30.523 | 29.031 | 0.318 |
| (7.019) | (7.390) | (7.921) | (7.248) | {0.029}† | |
- a Notes: Asterisk * denotes Tsh = Tanzanian shilling; **denotes that observations in the top and bottom 5 percentiles of the variable are dropped when calculating the mean and the standard deviation; †denotes that an ANOVA test is likely to be affected by outliers for these variables; a P-value from a median test without dropping observations is reported in the curly brackets.
A second approach is to explain attrition with observable household characteristics. Table 3 presents the results of a probit regression where we regress attrition status on household characteristics; column 1 shows that group assignment is not correlated with attrition.17 We also report the result of a joint test of group dummy significance (p-value = 0.738) None of the other variables is correlated with our attrition-dummy, except for the participant's subjective health perception. Column 2 presents the results of a stepwise procedure, where insignificant variables are sequentially excluded from the regression. We now find that attrition is partially explained by health perception, education, and wealth indicators (including access to tap water, a positive expectation of future wealth, owning a cell phone, and non-farm income). None of these variables is significantly different across our four groups (table 2), but we cannot rule out that external validity of the impact analysis is compromised by non-random attrition. For example, when attrition is based on unobservables like entrepreneurship or farming skills, we could perhaps systematically over- or underestimate the productivity of cowpea seeds. This would happen, for example, if such unobservables are correlated with the disutility that respondents derive from participating in a double-blind experiment. In the follow-up analysis, we attempt to control for potential selection concerns by a weighting procedure as a robustness analysis (naturally we can only do this for observables). Specifically, each observation was weighted using the inverse of the likelihood of having a non-missing measure of the harvest of cowpea (calculated using the results of the probit regression reported in column (2) of table 3; see Wooldridge 2002).
| Total harvest in seeds is missing | Var. in Table 2 | Stepwise |
|---|---|---|
| Group 2 | −0.081 | |
| (0.156) | ||
| Group 3 | −0.095 | |
| (0.158) | ||
| Group 4 | 0.047 | |
| (0.156) | ||
| Household size | −0.031 | |
| (0.026) | ||
| Gender household head (1 = male) | −0.037 | |
| (0.139) | ||
| Years of education household head | −0.003 | |
| (0.021) | ||
| Age household head | −0.003 | |
| (0.004) | ||
| Dependency ratio | 0.170 | 0.288 |
| (0.221) | (0.201) | |
| Village leaders' household and their relatives (1 = yes) | 0.009 | |
| (0.148) | ||
| Members of economic groups (1 = yes) | −0.212 | |
| (0.181) | ||
| Members of social groups (1 = yes) | 0.150 | |
| (0.146) | ||
| Health (1 = somewhat good or good) | 0.324** | 0.374** |
| (0.123) | (0.115) | |
| Economic situation compared to village average (1 = somewhat rich or rich) | 0.041 | |
| (0.153) | ||
| Land owned (acre) | −0.006 | |
| (0.011) | ||
| Own a bike (1 = yes) | 0.004 | |
| (0.124) | ||
| Value of productive assets (1,000,000 Tsh)χψ | 0.465 | |
| (1.234) | ||
| Value of other assets (1,000,000 Tsh)χψ | 0.020 | |
| (0.053) | ||
| Food consumption 7 days (1,000 Tsh)χψ | 0.004 | |
| (0.006) | ||
| Has own or public water tap | −0.312** | −0.267** |
| (0.124) | (0.121) | |
| Expectation of economic situation in the future (1 = richer or somewhat richer) | −0.317** | −0.289** |
| (0.146) | (0.123) | |
| Own a cell phone (1 = yes) | 0.237* | 0.258** |
| (0.131) | (0.117) | |
| Percentage of household members with secondary school | −0.893* | -1.064** |
| (0.460) | (0.425) | |
| Non- farm income (1,000,000 Tsh) | 0.021 | 0.021* |
| (0.014) | (0.013) | |
| Constant | 0.102 | −0.260 |
| (0.358) | (0.165) | |
| P-value of test: Group 2+Group 3+ Group 4 = 0 | 0.738 | |
| Pseudo R-squared | 0.050 | 0.040 |
| N. of Obs. | 570 | 572 |
- a Notes: Standard errors are in parentheses; *p<0.10, **p<0.05, ***p<0.01; ψ Tsh = Tanzanian shilling; χ denotes that observations in the top and bottom 5 percentiles of the variable are dropped when calculating the mean and the standard deviation.
Identification
Our identification strategy is simple. First, we ignore attrition and restrict ourselves to the subsample of households that planted the seed and for which we have endline data. We compare sample means from groups 1 and 2 (groups in the open RCT) and compare sample means from groups 3 and 4 (groups participating in the double-blind experiment). We then compare harvest levels of the traditional seed variety across the open RCT and the double-blind trial (groups 2 and 4) to obtain a signal of the effort response. This enables us to gauge the relative importance of the seed effect vis-à-vis the effort response. To probe the robustness of our findings, we proceed along these same steps, but also weigh the observations to account for potential selection concerns due to non-random attrition, and also compute the average treatment effect (ATE) based on cowpea yields. When we compute ATEs, we use a “trimmed sample” from which we have omitted the top and bottom 5% of the observations (in terms of harvest). As an alternative method for dealing with outliers, we also report the results of a non-parametric Wilcoxon rank sum test to probe differences in harvest (and yield) levels.
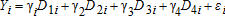 (5)
(5)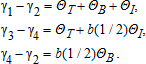
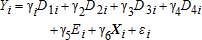 (6)
(6)Results
Treatment Effects
Table 4 contains our first result and summarizes harvest data for the 4 different groups. Columns 1 and 2 present the outcomes of the open RCT. For the un-weighted sample, the average modern seed harvest is 27% greater than the average harvest of the traditional seed type. A t-test confirms that this difference is statistically significant at the 5% level, and so does a Wilcoxon rank sum test (p-value 0.07). A naïve comparison would interpret these results as evidence that modern seed raises farm output. Based on such an interpretation, policy makers could consider implementing an intervention that consists of distributing modern seed to raise rural income or improve local food security (depending on the outcomes of a complementary cost-benefit analysis, one would hope).
| Open RCT | Double-blind | P-value of t-test | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Improved | Traditional | Improved | Traditional | Group | Group | Group | Group | Group | |
| Variables | Group 1 | Group 2 | Group 3 | Group 4 | 1 = 2 | 3 = 4 | 1 = 3 | 2 = 4 | 1 = 4 |
| Panel A: Average treatment effects (ATE) | |||||||||
| Total harvest in seeds (kg) | 9.865 | 7.238 | 9.912 | 9.400 | 0.05 | 0.72 | 0.97 | 0.06 | 0.77 |
| (10.809) | (6.175) | (10.012) | (8.614) | {0.07} | {0.89} | {0.98} | {0.11} | {0.95} | |
| [77] | [84] | [83] | [79] | ||||||
| Panel B: Attrition-weighted effects | |||||||||
| Total harvest in seeds (kg)† | 10.397 | 7.059 | 9.517 | 9.158 | 0.06 | 0.81 | 0.64 | 0.09 | 0.51 |
| (13.677) | (6.219) | (9.391) | (8.840) | ||||||
| [74] | [83] | [82] | [77] | ||||||
| Panel C: Average treatment effects (ATE) yield | |||||||||
| Yield in seeds (kg/m2) | 0.071 | 0.047 | 0.057 | 0.042 | 0.23 | 0.19 | 0.45 | 0.65 | 0.09 |
| (0.119) | (0.087) | (0.071) | (0.044) | ||||||
| [52] | [59] | [52] | [55] | {0.15} | {0.42} | {0.80} | {0.85} | {0.31} | |
- a Notes: Standard deviations, No. of observations and the P-values of the Wilcoxon rank-sum test are reported in brackets, square brackets and curly brackets, respectively; † denotes the attrition-weighted sample, using the inverse of the likelihood of having a non-missing measure of the harvest of cowpea. A few observations are lost after weighting because of the missing values in the variables used in calculating the weights.
A different picture emerges when we look at the outcomes of the double-blind experiment, summarized in columns 3 and 4. When farmers are unaware of the type of seed allocated to them, the modern seed type does not outperform the traditional type. All our tests suggest that the average treatment effect, according to the double-blind trial, is zero.19
Under the specific assumptions discussed above, we know that the ATE of the open RCT provides an upper bound of the “true” seed effect (defined as the sum of the direct effect of the intervention and the “optimal” subject's response to the new conditions), and that the ATE of the double-blind trial defines a lower bound. The former fails to account for the reallocation of (unobservable) complementary inputs, and the latter denies farmers the possibility of optimally adjusting their effort. Additional insights emerge when we combine the evidence from the RCT and double-blind experiment. In particular, comparing groups 2 and 4—output for the traditional seed-type with and without knowledge about treatment status—helps to assess whether the true effect is close to the upper or lower bound. A difference driven only by beliefs about treatment status reveals that the effort response must matter. For our data we find this is the case. The harvest of the traditional crop is larger when farmers are uninformed about treatment status (significant at the 5% level). In addition, since group 4 is not different from group 1, we infer that the complete harvest response is due to the reallocation of effort—not to inherent superiority of the modern seed.20 This interpretation is supported by the results of the non-parametric Wilcoxon rank-sum test (reported in curly brackets).
In panel B we probe the robustness of these findings and report the results for the attrition-weighted sample. The ATE is even greater after weighting, and the difference is now significant at the 6% level. In panel C we use our yield measure as an alternative outcome variable (for the sub-sample for which we have field measurements on plot size). As expected and discussed above, patterns in these data are qualitatively different, presumably reflecting that plot size is one of the variables used by farmers to respond to treatment status (ambiguously impacting on yield measures).21
Why are harvests lower when farmers are in the control group of the open RCT? We probe this question in table 5, which compares key inputs and conditioning variables across the three groups of farmers (groups 1 and 2, and the combination of groups 3 and 4, which are lumped together in light of their common information status—additional tests reveal that the distribution of the values of these variables are the same for groups 3 and 4). Data on inputs and conditional variables, except plot size, were collected during the endline survey. We measured the size of the plots ourselves in the field during an interim visit, and unfortunately this variable is only available for a subsample of the households (215). The ANOVA and MANOVA tests suggest differences in terms of soil quality and plot size. Pairwise comparisons of the groups reveals that (a) farmers in the RCT receiving the modern seed chose to plant this seed on good quality plots, and (b) farmers receiving traditional seed in the RCT chose to plant the seed on relatively small plots (inviting extra competition for space, lowering output). Of course differences in plot size could indicate that farmers in group 2 simply decided not to plant all their seed. This is not the case, however. Smaller plot size raises plant density, and the number of cowpea plants per plot does not vary statistically across groups.22
| Open RCT | Double-blind | ||||||
|---|---|---|---|---|---|---|---|
| Improved | Traditional | Combined | |||||
| P-value of t-test | |||||||
| ANOVA test | Group | Group | Group | ||||
| Variables | Group 1 | Group 2 | Group 3/4 | P-value | 1 = 2 | 1 = 3/4 | 2 = 3/4 |
| Household labor on cowpea | 9.273 | 10.354 | 9.654 | 0.59 | 0.33 | 0.67 | 0.47 |
| (5.789) | (8.039) | (6.749) | |||||
| Land is flat (1 = yes) | 0.319 | 0.421 | 0.369 | 0.44 | 0.20 | 0.48 | 0.46 |
| (0.469) | (0.497) | (0.484) | |||||
| Land erosion (1 = slight or heavy erosion) | 0.712 | 0.632 | 0.699 | 0.50 | 0.29 | 0.83 | 0.32 |
| (0.456) | (0.486) | (0.461) | |||||
| Improvement such as bounding, terrace (1 = yes) | 0.263 | 0.244 | 0.242 | 0.94 | 0.78 | 0.73 | 0.97 |
| (0.443) | (0.432) | (0.430) | |||||
| Intercropping (1 = yes) | 0.186 | 0.159 | 0.146 | 0.77 | 0.68 | 0.47 | 0.80 |
| (0.392) | (0.369) | (0.355) | |||||
| Weed between plants (1 = yes) | 0.819 | 0.681 | 0.746 | 0.15 | 0.05 | 0.23 | 0.32 |
| (0.387) | (0.470) | (0.437) | |||||
| Soil quality (1 = good) | 0.671 | 0.471 | 0.476 | 0.01 | 0.01 | 0.01 | 0.94 |
| (0.473) | (0.502) | (0.501) | |||||
| Used pesticide or fertilizer? | 0.097 | 0.069 | 0.063 | 0.676 | 0.550 | 0.391 | 0.872 |
| (0.035) | (0.030) | (0.022) | |||||
| Number of plants | 1054 | 874 | 995 | 0.439 | 0.198 | 0.664 | 0.330 |
| (112) | (86) | (81) | |||||
| Consult anybody on how to plant cowpea? (1 = yes) | 0.139 | 0.118 | 0.158 | 0.53 | 0.51 | 0.70 | 0.26 |
| (0.348) | (0.310) | (0.366) | |||||
| Plot size (square meter)* | 342 | 284 | 349 | 0.11 | 0.11 | 0.83 | 0.05 |
| (213) | (206) | (214) | {0.01}† | {0.13}†† | {0.91}†† | {0.06}†† | |
| MANOVA test (p-values) | |||||||
| Wilks' lambda: 0.660 | Pillai's trace: 0.660 | ||||||
| Lawley-Hotelling trace: 0.660 | Roy's largest root: 0.100 | ||||||
- a Notes: Asterisk * denotes that observations in the top and bottom 5 percentiles of the variable are dropped when calculating the mean and the standard deviation; † denotes P-value of the median test without dropping observations; †† denotes P-value of the Wilcoxon rank-sum test without dropping the observations.
Regression Analysis
Table 6 presents our regression results. Considering column (1) first, the significant difference between group 1 and group 2 confirms that a naïve experimenter may attribute considerable impact to the modern seed intervention. However, the difference between groups 1 and 2 may have two components: the effect we are interested in, ΘT+ΘI, and the effort effect, ΘB. The double-blind experiment provides an indication of the magnitude of these effects. Receiving traditional seed per se is not associated with lower harvests (group 3 does not significantly outperform group 4). In contrast, the effort effect is significant (group 4 outperforms group 2), and the size of this effect is very large. Column (1) reveals that the effort effect must exceed 0.254 (as b(1)>b(1/2)), but the total effect ΘT+ΘI+ΘB equals only 0.384. Two-thirds of all impact may be attributed to an effort response, and not to specific characteristics of the modern seed.
| Full sample | Restricted sample with field measures | |||
|---|---|---|---|---|
| Log total harvest in seeds (kg) | (1) | (2) | (3) | (4) |
| Improved seeds and know (group 1) γ1 | 1.969*** | 1.335*** | 2.092*** | 0.611* |
| (0.108) | (0.220) | (0.120) | (0.351) | |
| Traditional seeds and know (group 2) γ2 | 1.585*** | 1.025*** | 1.602*** | 0.152 |
| (0.103) | (0.219) | (0.108) | (0.347) | |
| Improved seeds and not know (group 3) γ3 | 1.937*** | 1.410*** | 1.973*** | 0.523 |
| (0.103) | (0.221) | (0.118) | (0.361) | |
| Traditional seeds and not know (group 4) γ4 | 1.839*** | 1.338*** | 2.131*** | 0.650* |
| (0.106) | (0.220) | (0.119) | (0.369) | |
| Log plot size | 0.140** | |||
| (0.051) | ||||
| Weed between plants (1 = yes) | −0.088 | |||
| (0.118) | ||||
| Log labor | 0.253*** | 0.320*** | ||
| (0.066) | (0.082) | |||
| Whether used pesticides or fertilizers | 0.299 | 0.319* | ||
| (0.192) | (0.191) | |||
| Soil quality (1 = good) | 0.356*** | 0.287** | ||
| (0.104) | (0.112) | |||
| Gender household head | -0.028 | 0.043 | ||
| (0.112) | (0.121) | |||
| Dependency ratio | −0.276 | −0.184 | ||
| (0.193) | (0.205) | |||
| Illiterate rate | -0.03 | -0.083 | ||
| (0.060) | (0.064) | |||
| Elected positions in the village | 0.078 | 0.108 | ||
| (0.128) | (0.147) | |||
| γ1−γ2=ΘT+ΘB+ΘI | 0.384*** | 0.310** | 0.490*** | 0.458*** |
| (0.149) | (0.145) | (0.161) | (0.152) | |
| γ3−γ4=ΘT+b(1/2)ΘI | 0.098 | 0.072 | -0.158 | -0.128 |
| (0.148) | (0.145) | (0.167) | (0.163) | |
| γ4−γ2=b(1/2)ΘB | 0.254* | 0.313** | 0.528*** | 0.498*** |
| (0.148) | (0.143) | (0.160) | (0.154) | |
| R-squared | 0.026 | 0.135 | 0.063 | 0.233 |
| Number of obs. | 321 | 317 | 215 | 215 |
- a Notes: Standard errors are in parentheses; *p<0.10, **p<0.05, ***p<0.01
This finding becomes stronger when we control for observable production factors. These results are reported in column (2).23 Not surprisingly, we also find that higher levels of production factors (labor and soil quality) are associated with greater harvests. Note that the coefficients for variables like soil quality, as reported in column (2), should not be interpreted as the causal effect of improved soil quality on harvests. Soil quality can be endogenous to treatment, and is therefore not a proper exogenous explanatory variable. Soil quality is only included in the model as a control (enabling us to verify how much of the measured variation in harvest levels is correlated with standard “observables,” and how much is determined by other factors).
As mentioned above, we observed that traditional seed farmers in the RCT chose to plant their crops on smaller plots. To examine the effect of plot size, we re-estimate the models in columns (1-2) on the subsample of households for which we have field measures. Results are reported in column (4). Column 3 is included to demonstrate that the reduction in sample size per se does not invalidate the insights from column (1). For our subsample with field measurements, the effort effect increases to 0.528, while the total effect is only 0.490, which is again not significantly different from the effort effect. Controlling for adjustments in plot size (and controlling for other inputs as well) hardly diminishes the effort effect, even though plot size is significant itself (note that the pesticide/fertilizer variable is now also significant). Specifically, the effort effect shrinks to 0.501, and remains significant at the 1% level.24
Hence, unobservable effort—that is, effort over and beyond the usual variables readily accommodated in surveys or field measurements such as plot size, “plot quality,” labor, and external inputs—is a key factor in determining harvests. Perhaps the vector of usual controls (including measures of labor, soil quality, and plot size) is too coarse, lumping together a variety of subtly different variables.25 For example, the timing of interventions might matter, or the quality of labor (household labor or hired labor), or characteristics of the plot may vary along multiple subtle dimensions. This result is consistent with agronomical evidence on smallholder farming in Africa, which emphasizes tremendous yet often subtle variability at the farm and plot level (Giller et al. 2011). It is difficult to capture all relevant adjustments in complementary inputs as farmers can optimize along multiple dimensions (some of these adjustments may be inter-temporal, involving changes in soil fertility and future productivity).26 Failing to control for all of them will result in biased estimates of impact in open RCTs.
Implications and Conclusions
Randomized controlled trials have changed the landscape of policy evaluation in recent years. There exists an important difference between such RCTs that are designed and implemented by economists and political scientists, and those that are designed as medical experiments. The so-called Gold Standard in medicine prescribes double-blind implementation of trials where patients in the control group receive a placebo, and neither researchers nor patients know the treatment status of individuals. Failing to control for placebo effects implies overestimating the impact of the intervention (Malani 2006). In policy and mechanism experiments (Ludwig et al. 2011), double-blind interventions are not the standard for many reasons. For example, we do not introduce sham microfinance groups or fake clinics as the “social science counterparts” of inert drugs when analyzing the impact of interventions in the credit or health domains (at least, not intentionally). One might argue that policy makers are not interested in the outcomes of double-blind experiments—-if an intervention affects the value marginal product of inputs, then ideally subjects should adjust their effort. If the experimental design precludes such effort responses, then it provides a biased estimate of the potential impact of the intervention.
Glewwe et al. (2004) argued that behavioral adjustments are relevant for impact measurement. These authors distinguished between so-called direct (structural) and indirect (behavioral) effects, which correspond to our direct treatment effect (ΘT) and the summation of our two behavioral effects (ΘB+ΘI), respectively. An RCT measures the so-called total derivative of an intervention—the sum of direct and indirect effects. This total derivative may be manipulated to obtain a measure of welfare. Specifically, to go from (total) impact to welfare, we should control for costs associated with the behavioral response—correct for changes in the allocation of other inputs multiplied by the value of those inputs. Our results extend those of Glewwe et al. (2004). First, for our case a large part of the total derivative should not be attributed to the intervention itself, but to (false) expectations raised by the prospect of receiving the intervention. Second, going from the total derivative to a measure of welfare by introducing “corrections” of inputs may be problematic in practice, as many adjustments are unobservable to the analyst. These findings support a claim by Barrett and Carter (2010) who critically discuss various pitfalls associated with the use of RCTs in development economics: “It is often unclear what varies beyond the variable the researcher is intentionally randomizing… As a result, impacts and behaviors elicited experimentally are commonly endogenous to environmental and structural conditions that vary in unknown ways within a necessarily highly stylized experimental design. This faux exogeneity undermines the claims of clean identification due to randomization.”
Recognizing the importance of (unobservable) effort responses, Chassang et al. (2012a) propose an alternative design for RCTs. They demonstrate that adopting a principal-agent approach to RCTs—designing so-called selective trials—enables the analyst to obtain unbiased estimates of impact. However, such designs are costly because they require large samples. An important question, therefore, is whether unobservable effort responses are quantitatively important to justify these extra costs. For our case, unobservable effort responses are of first-order importance, and virtually all impact measured in the open RCT appears to be due to the adjustment of effort. There may be many dimensions along which behavior can be adjusted, and future work could attempt to identify which dimensions matter most by using more finely-grained effort measures than the crude and standard ones we used. Future research should explore whether our findings hold up in larger samples (preferably with more tightly controlled attrition) and in other sectors. In particular, we analyze an extreme case—where the treatment seems to have nearly no effect—and it would be interesting to explore whether the quantitative assessment of the behavioral response extends to more “typical” contexts.
We believe these insights provide several implications for prospective interventions. For the (small) subsample of interventions where double-blind trials are feasible (because differences between treatment and control status are not easily discerned), data from open RCTs and double-blind trials may be combined to gauge whether or not (unobservable) effort responses are large. When double-blind trials are not feasible, analysts should be aware of challenges to internal and external validity following from behavioral responses (including unobserved heterogeneity due to heterogeneous responses). Data should be collected on as many components of the endogenous effort vector as possible, for both the treated and the control group, as this enables one to approximate the value of bi(p) for effort response i. This facilitates cost accounting to control for complementarities (or substitutions) in intervention and effort (as in Glewwe et al. 2004). While some “unobservable effort responses” will presumably remain, behavioral bias is reduced as more production factors are measured and entered in the vector of observables. Analysts may consider gauging certain non-standard behavioral factors via behavioral games, measuring risk preferences, entrepreneurial talents and so on (see Barrett and Carter 2010), or by including qualitative research methods to complement the “standard” open RCT. Insofar as theory enables the analyst to predict how observable and unobservable factors co-evolve in response to treatment status (i.e., the correlation between the various bi(p) for effort response i), observation of observables may also enable her to predict whether impact as measured by the RCT is an over- or underestimation of impact.
In addition, we found support for the idea that expectations matter. The behavioral response picks up subjective beliefs of participants, and many farmers in our sample were disappointed by the eventual harvests. No less than 58% of the farmers receiving the “modern variety” of seeds indicated that the present year's harvest was not better than the harvest in the previous year. If we would run the same experiment again with the same farmers, they would presumably allocate smaller quantities of their (unobservable and observable) inputs to this cowpea crop, thereby pushing harvest levels down. That is, behavioral responses can be short-lived and will almost certainly vary over time as farmers update their beliefs and expectations. Unfortunately we do not understand these dynamics, which implies that one cannot rely on stability of the parameters of interest.27
To avoid bias due to unobservable effort, one could measure impact at a higher level of aggregation. That is, rather than focusing on cowpea harvests, the analyst could explore how the provision of modern seed affects total household income (or profit). Many effort adjustments will have repercussions for earnings elsewhere, so it makes sense to measure impact at the level where all income flows (opportunity costs) come together. However, two considerations are pertinent. First, some of the adjustment costs do not materialize immediately, but will be felt over the course of years and are therefore easily missed by the analyst (e.g., altered investment patterns affecting various forms of capital, such as nutrient status of the soils). Second, moving to a higher level of aggregation implies summing various (volatile, on-farm and off-farm) income flows, and therefore lowers the signal to noise ratio.
Finally, we speculate that effort responses in experiments also matter for the external validity of experiments. A large body of literature examines this issue,28 and we have little to contribute. However, we observe that effort responses typically will be very context-specific (in accordance with local geographic, cultural, and social conditions). Hence, while the seed effect, as picked up in efficacy trials, may readily translate from one context to the other (provided growing conditions are not too dissimilar), it is not obvious whether estimates of the total harvest are valid beyond the local socio-economic system. Measuring the effort effect in RCTs enables the analyst to make predictions concerning impact elsewhere.




