Impact of a Two-Rate Property Tax on Residential Densities
Seong-Hoon Cho is a professor in the Department of Agricultural and Resource Economics, University of Tennessee Knoxville. Seung Gyu Kim is an assistant professor in the Department of Agricultural Economics, Kyungpook National University, Korea. Dayton M. Lambert is an associate professor in the Department of Agricultural and Resource Economics, University ofTennessee,Knoxville. Roland K. Roberts is a professor in the Department of Agricultural and Resource Economics, University of Tennessee, Knoxville.
Abstract
Municipalities sometimes reform property tax schedules in an effort to increase suboptimal residential densities. One such approach is to reduce the tax rate applied to building values and increase the tax rate applied to land, known as a two-rate property tax (TPT). This paper evaluates the impact of a TPT on residential density in Nashville-Davidson County, Tennessee where a conventional property tax schedule prevails during 2006–2007. When land taxes are proportionally higher than taxes on structures, 1.07 to 1 and 1.25 to 1 for general and urban service districts, respectively, ex ante simulations suggest that housing density increases by 18% in general services districts and 83% in urban services districts.
Most municipalities in the United States collect residential real estate property taxes based on a percentage of total assessed property value. These policies place equal value on land and structures, but the taxation of buildings or structures inflates the perceived cost of improvements, thereby discouraging site improvement and potentially reducing economic returns (26). Thus, the land owner can reduce their tax burden by developing projects that use relatively more land than structures. This behavior leads to lower than optimal residential densities (36)
In response to suboptimal residential densities, researchers have investigated reducing tax rates applied to structures and increasing tax rates on land using a “two-rate property tax” (TPT) as an alternative to placing equal weight on land and structure taxes14 demonstrated that TPTs might result in additional land improvements. Brueckner also showed that (1) land taxes, property improvement taxes, and property taxes had different effects on the speed and capital intensity of development and (2) that the precise effect depends on the complementarity or substitutability between capital and development time. 31 found that land tax increases accelerated commercial development in Pittsburgh, Pennsylvania, a city which had a TPT from 1913 to 2001. 33 revealed that 15 municipalities in Pennsylvania with TPTs between 1972 and 1994 had significantly higher levels of construction than 204 similar Pennsylvania municipalities with single-rate taxes. 24 concluded that a pre-development land tax also affected development density in Finland These retrospective analyses document the observed effects of municipal property taxes on residential development patterns, but ex-post analyses are context-specific which may limit their generality. Alternatively, ex ante analyses provide a framework for predicting the actions of agents in response to policies before policy implementation.
Our current research contribution applies a method for performing ex ante impact analyses of TPTs on residential density in municipalities. The methodology is theoretically consistent with the urban development literature related to the optimal residential location choice of consumers and the profitmaximizing behavior of housing service providers. We develop a conceptual framework for a housing market in spatial equilibrium following 13 and 16, among others. Based on this model we develop a method for quantifying the impacts of a TPT on residential density using a probabilistic two-step procedure to predict residential development patterns. We estimate the parcel development model/housing density model using individual parcel data collected in Nashville-Davidson County, Tennessee. The econometric method applies recent developments in estimating linear outcome equations with sample selection bias and spatial dependence. The two-step procedure first estimates development decisions using spatial probit regression. We use weighted least squares adjusted for spatial dependence to estimate the second-stage housing density equation.
Based on econometric estimates, ex ante in-sample and out-of-sample forecasts simulate changes in housing density to compare a “status quo” tax scheme (equal weight placed on land and structure values) to hypothetical TPT scenarios (different weights on land and structure values). The scenarios incrementally increase land tax rates relative to the tax rate on property improvements, holding total municipal property tax revenues unchanged from the observed, status quo aggregate revenue A non-parametric procedure compares the simulated distributions of development density, conditional on the hypothetical TPTs at different rates. The ex ante analysis finds that a TPT above a minimum level triggers an increase in residential density above suboptimal densities associated with the status quo property tax schedule.
Conceptual Framework for Modeling the Parcel Development Decision
We hypothesize that housing development is codetermined through neighborhood spillover effects based on findings from previous literature (e.g. 7; 8). The agent interaction models of 3 and 1 are useful for conceptualizing the transition of residential parcels from an undeveloped to a developed state. Two important assumptions are that the housing market is in equilibrium, yet the observed equilibrium may vary across the market (i.e. equilibrium may be local or neighborhoodspecific), and that the unobserved latent propensity to develop a parcel may be correlated with development decisions in nearby locations.
We extend 13 and 14 housing development models to represent local market equilibrium as the intersection between housing service providers (housing supply) and consumers (housing demand). For developers providing housing services, the indirect cost function is ci(qi,RHi,RH,−i,wi), where qi is a house built on parcel i, RHi is the cost of building a house on parcel i, and wi is a vector of other costs. We hypothesize that costs at location i are a function of costs at other locations (−i), so the development decision at parcel i is potentially influenced by development costs of neighboring parcels. The indirect utility that a house buyer receives at parcel i is vi(RHi,RH,−iyi,pi), where RHi and RH,−i are previously defined, yi is income, and pi is a price vector of other goods. Market clearing at location i occurs at cost 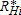 , where developers build houses at parcel i to meet consumer demand for houses at that location.
, where developers build houses at parcel i to meet consumer demand for houses at that location.
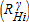 , the development decision depends on the difference between the reservation rent at parcel i and the market price of housing services, RHi:
, the development decision depends on the difference between the reservation rent at parcel i and the market price of housing services, RHi:
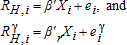 (1)
(1)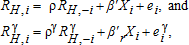 (2)
(2)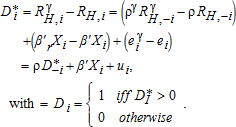 (3)
(3)Focusing on the reduced form system (the last term in equation (3)) is a common estimation strategy (25) because the reserved return is unobservable. In addition, the annual reservation rent is not observed for service providers who did not win development bids. However, because the development decisions are likely correlated, the usual maximum likelihood framework may not provide consistent estimates of the factors determining the parcel development outcome. We estimate the spatially-lagged latent variable development equation using a General Method of Moments (GMM) procedure suggested by 19, which is developed below. First, however, we provide a theoretical framework motivating an index for measuring the influence of a TPT on housing density, given the local factors determining parcel development.
Conceptual Framework for Modeling Residential Development Density
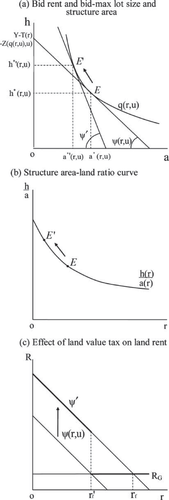
Our conceptual framework of demand for single family housing density extends 5, 13, and 16 respective interpretations of the Alonso-Mills-Muth residential location model. We modify the general model to demonstrate the potential role of a land value tax on housing density, and how such a tax operates through the consumer's housing bid rent function. The positive effect of the land value tax on development density is represented by the backward movement of the housing bid rent function which corresponds with more compact housing development. We develop the comparative statics of this system to illustrate the anticipated effects of a land value tax on housing density and to motivate the econometric model we use to evaluate a TPT on compact development We suppress the location-specific subscripts (i's) in what follows.
Consider a continuum of workers commuting distance r to work, earning income Y. Households consume an aggregate commodity called housing services, with the per unit price at distance r, RH(r) Housing services include the land parcel and the finished area of the structure built on the lot. The utility (U) of each consumer depends on the consumption of a composite good (z) that excludes housing services and the quantity consumed of household services q (13, p. 41). Utility is a twice continuously differentiable, quasi-concave function strictly increasing in each good. Both q and z are essential goods, and every indifference curve has each axis as an asymptote. The housing service bundle is a normal good. The consumer's budget constraint is z+q⋅RH(r)=Y −T(r), with Y −T(r) representing the net income remaining after commuting costs T(r).
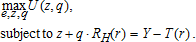 (4)
(4)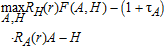 (5)
(5)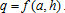 (6)
(6)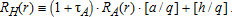 (7)
(7)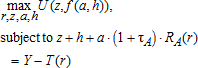 (8)
(8)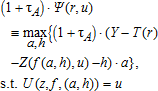 (9)
(9)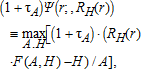 (10)
(10)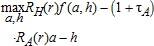 (11)
(11)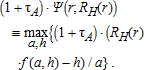 (12)
(12)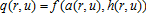 (13)
(13)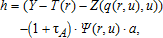 (14)
(14)
Relationship between housing-lot size density and a land value tax
 (15)
(15)In equilibrium then, land rent must adjust to correspond with the consumer's bid rent (14), Ψ(r,u)≡R(r). Because the housing service function has constant returns to scale, the ratio h(R′,q)/a(R′,q) is independent of output. This relationship defines the parcel-housing density equation as h(R′,q)/a(R′,q)=g(R′). First, it is apparent that as the land value tax increases, land rent and housing density also increase (i.e. ∂g(R′)/∂R′>0). Second, the bid rent function deceases moving outward from employment centers. By the envelope theorem and evaluating the bid rent function at equilibrium, ∂Ψ′/∂r<0.
It is evident in figure 1(a) that the house structure/lot size ratio increases as land rent becomes more expensive; dg(R′)/dR′>0 (development becomes more dense). Under the assumption that the same level of housing services must be maintained in equilibrium, the isocost line in figure 1(a) must also shift from Ψ(r,u) to Ψ′, with corresponding shifts in optimal tangency points from E to E′ and input demands (a′*(r,u),h′*(r,u)), which yields relatively smaller lots covered by more structure area. Thus, the structure area/land ratio increases as land value tax rates increase.
The correspondence between the reallocation of housing service inputs following an increase in land value and the location of this combination is nonlinear (figure 1(b)). This is a very general result of the Alonso-Muth-Mills model in that the equilibrium proportion of housing area/lot size decreases moving outward from a Central Business District (CBD), denoted by the shift from E to E′ in figure 1(b)). Overall, we expect that a higher tax on land value relative to a tax on improvements will increase the structure area/lot size ratio, thereby encouraging compact development.
In figure 1(c), rf represents the urban fringe that would result in the absence of a land value tax. The opportunity cost of land is the agricultural land rent, RG. The land value tax rate increases as the bid rent shifts from Ψ to Ψ′. The shift coincides with more compact housing development moving closer to the CBD, which corresponds with higher housing density inside the new urban fringe boundary r′f.
 (16)
(16)The econometric model assumes equation (15) can be linearized by applying a first order Taylor approximation, noting that housing density is restricted between the (0,1) interval, which eventually has implications for estimation. The following section provides details of the variables we hypothesize as influencing compact development. The details of the spatial process model we use to estimate equation (15) and the forecasting algorithm are also discussed.
Data and Study Area
The study area for this research is Nashville-Davidson County, Tennessee. We used four primary GIS data sets: individual parcel data, boundary data, census-block group data, and environmental feature data. We report definitions of the variables used in the regressions and their detailed statistics in table 1.
| Development (N=19,237) | Density (N=1,675) | ||||
|---|---|---|---|---|---|
| Variable (Unit) | Definition | Mean | Std. Dev. | Mean | Std. Dev. |
| Dependent variables | |||||
| Development | Dummy variable for parcel developed in 2006–2007 (1 if developed, 0 otherwise) | 0.087 | 0.282 | ||
| Density | Finished area divided by lot size | 0.276 | 0.133 | ||
| Structural variables | |||||
| Finished area (feet2) | Total finished square footage of house | 2,573.464 | 1,527.328 | ||
| Lot size (feet2) | Total parcel square footage | 152,972.805 | 643,314.239 | ||
| Pool | Dummy variable for swimming pool (1 if pool, 0 otherwise) | 0.014 | 0.116 | ||
| Garage | Dummy variable for garage (1 if garage, 0 otherwise) | 0.789 | 0.408 | ||
| Fireplace | Number of fireplaces in house | 0.553 | 0.545 | ||
| Bedroom | Number of bedrooms in house | 3.458 | 0.687 | ||
| Stories | Height of house in number of stories | 1.655 | 0.447 | ||
| Quality of construction | Dummy variable for quality of construction (1 if excellent, very good or good, 0 if average, fair, or poor, as rated by the tax assessors' office) | 0.340 | 0.474 | ||
| Census-block group variables | |||||
| Income ($) | Median household income for census-block group | 22,822.215 | 13,143.910 | 26,952.090 | 13,147.356 |
| Housing density(houses/acre) | Housing density for census-block group | 1.240 | 1.279 | 0.868 | 1.009 |
| Travel time to work (Min.) | Average travel time to work for census-block group in 2000 | 23.615 | 4.680 | 24.478 | 3.535 |
| Unemployment rate | Unemployment rate for census-block group in 2000 (ratio of unemployed to the labor force, age 16 or older) | 0.055 | 0.053 | 0.038 | 0.028 |
| Vacancy rate | Vacancy rate for census-block group in 2000 (ratio of vacant housing units to total housing units of any type) | 0.069 | 0.049 | 0.058 | 0.036 |
| Environmental variables | |||||
| Distance to park (feet) | Distance to nearest park among 42 municipal parks | 10,344.985 | 7,626.357 | 12,252.382 | 6,303.483 |
| Distance to golf course (feet) | Distance to nearest golf course | 30,990.470 | 17,809.148 | 36,579.291 | 16,313.498 |
| Distance to CBD (feet) | Distance to the central business district | 45,996.725 | 24,563.123 | 56,321.078 | 19,471.752 |
| Distance to greenway (feet) | Distance to nearest greenway (a mostly contiguous vegetated pathway developed for recreation, pedestrian, and bicycle uses) | 17,392.486 | 12,641.518 | 16,251.577 | 10,140.117 |
| Distance to railroad (feet) | Distance to nearest railroad track | 7,664.091 | 8,041.872 | 9,340.212 | 6,411.429 |
| Distance to highway (feet) | Distance to interstate highway | 11,636.207 | 9,207.390 | 14,392.173 | 8,494.841 |
| Water view | Dummy variable indicating viewable water body (1 if water body exists within 100m, 0 otherwise) | 0.020 | 0.140 | 0.009 | 0.094 |
| Slope (°) | Degree of slope at the parcel location | 5.346 | 5.018 | 4.403 | 3.325 |
| ACT score | Average composite score of American College Test by high school district | 17.330 | 1.450 | 18.152 | 1.199 |
| Tax variables | |||||
| Land value tax | Tax on land value | 823.319 | 2,638.781 | ||
| Property tax | Tax on property (land and structure) | 3,250.263 | 4,298.624 | ||
| Dummy variables | |||||
| MLA 3,750 (Reference) | Dummy variable indicating minimum lot area assigned by zoning regulation (1 if parcel located in 3,750 square feet minimum lot area zone, 0 otherwise) | 0.040 | 0.195 | 0.009 | 0.094 |
| MLA 5,000 | Dummy variable indicating minimum lot area assigned by zoning regulation (1 if parcel located in 5,000 square feet minimum lot area zone, 0 otherwise) | 0.087 | 0.282 | 0.065 | 0.247 |
| MLA 6,000 | Dummy variable indicating minimum lot area assigned by zoning regulation (1 if parcel located in 6,000 square feet minimum lot area zone, 0 otherwise) | 0.080 | 0.271 | 0.028 | 0.165 |
| MLA 7,500 | Dummy variable indicating minimum lot area assigned by zoning regulation (1 if parcel located in 7,500 square feet minimum lot area zone, 0 otherwise) | 0.070 | 0.254 | 0.102 | 0.303 |
| MLA 8,000 | Dummy variable indicating minimum lot area assigned by zoning regulation (1 if parcel located in 8,000 square feet minimum lot area zone, 0 otherwise) | 0.029 | 0.168 | 0.029 | 0.167 |
| MLA 10,000 | Dummy variable indicating minimum lot area assigned by zoning regulation (1 if parcel located in 10,000 square feet minimum lot area zone, 0 otherwise) | 0.149 | 0.356 | 0.330 | 0.470 |
| MLA 15,000 | Dummy variable indicating minimum lot area assigned by zoning regulation (1 if parcel located in 15,000 square feet minimum lot area zone, 0 otherwise) | 0.095 | 0.293 | 0.195 | 0.396 |
| MLA 20,000 | Dummy variable indicating minimum lot area assigned by zoning regulation (1 if parcel located in 20,000 square feet minimum lot area zone, 0 otherwise) | 0.055 | 0.229 | 0.051 | 0.220 |
| MLA 30,000 | Dummy variable indicating minimum lot area assigned by zoning regulation (1 if parcel located in 30,000 square feet minimum lot area zone, 0 otherwise) | 0.002 | 0.046 | 0.002 | 0.049 |
| MLA 40,000 | Dummy variable indicating minimum lot area assigned by zoning regulation (1 if parcel located in 40,000 square feet minimum lot area zone, 0 otherwise) | 0.042 | 0.201 | 0.021 | 0.143 |
| MLA 80,000 | Dummy variable indicating minimum lot area assigned by zoning regulation (1 if parcel located in 80,000 square feet minimum lot area zone, 0 otherwise) | 0.009 | 0.094 | 0.015 | 0.121 |
| MLA 87,120 | Dummy variable indicating minimum lot area assigned by zoning regulation (1 if parcel located in 2 acres minimum lot area zone, 0 otherwise) | 0.135 | 0.342 | 0.133 | 0.340 |
| Interaction variables | |||||
| Interaction 3,750 | MLA 3,750× land value tax (development equation) MLA 3,750× property tax (density equation) | 0.234 | 1.197 | 0.045 | 0.485 |
| Interaction 5,000 | MLA 5,000× land value tax (development equation) MLA 5,000× property tax (density equation) | 0.425 | 1.417 | 0.369 | 1.407 |
| Interaction 6,000 | MLA 6,000× land value tax (development equation) MLA 6,000× property tax (density equation) | 0.380 | 1.327 | 0.157 | 0.937 |
| Interaction 7,500 | MLA 7,500× land value tax (development equation) MLA 7,500× property tax (density equation) | 0.351 | 1.331 | 0.587 | 1.747 |
| Interaction 8,000 | MLA 8,000× land value tax (development equation) MLA 8,000× property tax (density equation) | 0.157 | 0.938 | 0.171 | 1.000 |
| Interaction 10,000 | MLA 10,000× land value tax (development equation) MLA 10,000× property tax (density equation) | 0.811 | 2.006 | 1.973 | 2.819 |
| Interaction 15,000 | MLA 15,000× land value tax (development equation) MLA 15,000× property tax (density equation) | 0.540 | 1.703 | 1.171 | 2.384 |
| Interaction 20,000 | MLA 20,000× land value tax (development equation) MLA 20,000× property tax (density equation) | 0.328 | 1.391 | 0.327 | 1.428 |
| Interaction 30,000 | MLA 30,000× land value tax (development equation) MLA 30,000× property tax (density equation) | 0.013 | 0.289 | 0.018 | 0.363 |
| Interaction 40,000 | MLA 40,000× land value tax (development equation) MLA 40,000× property tax (density equation) | 0.247 | 1.222 | 0.137 | 0.953 |
| Interaction 80,000 | MLA 80,000× land value tax (development equation) MLA 80,000× property tax (density equation) | 0.049 | 0.532 | 0.084 | 0.703 |
| Interaction 87,120 | MLA 87,120× land value tax (development equation) MLA 87,120× property tax (density equation) | 0.725 | 1.914 | 0.730 | 1.948 |
We obtained individual parcel data as polygon shape files (i.e. sales price, lot size, residential space, structural information, and property tax) from the Metro Planning Department (MPD), Nashville-Davidson County, and the Davidson County Tax Assessor's Office. We also obtained boundary data (i.e. high school district, jurisdiction boundary, taxing district, and zoning district including minimum lot size) from MPD. We assigned data from 2000 censusblock groups (i.e. income, housing density, travel time to work, unemployment rate, and vacancy rate) to parcels located inside the census-block boundaries, and we used them as time-lagged socioeconomic variables. We extracted environmental feature data (i.e. municipal parks, golf courses, greenways, railroads, interstate highways, and water bodies) from the Environmental Systems Research Institute (ESRI) Data and Maps 2008.
We collected parcel development data for 2006 through 2007. At the beginning of 2006, the number of vacant parcels in Nashville-Davidson County was 35,928. Among these, 1,675 parcels were developed from 2006–2007 for single-family detached houses and 16,691 parcels were developed for other uses such as single-family attached houses and commercial and industrial land uses. We removed the 16,961 parcels developed for other purposes from the combined data set of 35,928 vacant parcels, yielding 19,237 parcels for use modeling the residential development of single-family detached houses. Of these, we defined 1,675 parcels as “developed” leaving 17,562 parcels defined as “undeveloped” We calculated the land value tax and property tax used in the development and density equations based on the assessed value of property (i.e. assessed value of land and structures) and the tax rates of Nashville-Davidson County from 2006–2007. We assigned different tax rates based on the location of parcels inside the general services district (GSD) and urban service district (USD) boundaries.
Estimating the Parcel Development and Residential Development Density Equations
A challenging aspect of estimating the development density model is potential sample selection bias introduced into the subset of parcels converted to residential use from 2006–2007. A second challenge is attending to the spatial structure of the residential market. Conversion and residential location decisions in the housing market may also be codetermined through neighborhood spillover effects In the first case, well-established econometric methods can attend to sample selection bias (6). In particular, 17 two-step and bivariate maximum likelihood models are frequently used to address such problems. In the second case, the feasible estimation of limited dependent variables with spatially-lagged outcomes using large datasets is relatively recent.
Limited dependent variable models are relatively well developed in the spatial econometric literature (e.g. 9; 19), but sample selection models have only appeared recently, receiving relatively little attention in applied studies. Exceptions include Bayesian spatial tobit models (22), and 12 and 28 sample selection models. 28 approach is computationally attractive and thus we adopt it for our analysis. 19 use a linear approximation of the probit model, circumventing the need to repeatedly invert large n-by-n matrices, a feature especially attractive given the sample size of 19,237 parcels analyzed in the first stage selection (or “development”) equation. By linearizing the first-stage selection model, we avoid computational issues that could arise from the repeated inversion of a large matrix. We then estimate the second-stage outcome equation (or “housing-density equation”) using an appropriate least squares estimator. Nonetheless, while this two-step procedure has some computational advantages, the full 19,237-by-19,237 matrix had to be inverted using the Schur complement method (38). The Schur method partitions a matrix into submatrices inverts them separately, and then reconstructs the full matrix through matrix algebra rules. The procedure produces identical results to typical matrix inversion procedures.
Linear spatial probit model of the firststage development equation
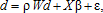 (17)
(17)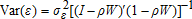 . The scale of d is unidentifiable in discrete choice models, so
. The scale of d is unidentifiable in discrete choice models, so 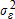 is restricted to be a constant. In the case of the probit specification,
is restricted to be a constant. In the case of the probit specification, 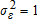 , with the variances
, with the variances 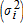 specified as the diagonal elements of Var(ε). Define S to be an n-by-n matrix with 1/σi on the diagonals, and let ωij be an element in the n-by-n matrix S(I−ρW)−1. This arrangement suggests rewriting the reduced-form version of the latent variable in (16) as:
specified as the diagonal elements of Var(ε). Define S to be an n-by-n matrix with 1/σi on the diagonals, and let ωij be an element in the n-by-n matrix S(I−ρW)−1. This arrangement suggests rewriting the reduced-form version of the latent variable in (16) as:
 (18)
(18)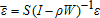 ,
, 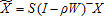 , and
, and 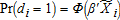 . The spatial probit model is estimated using the linearized general method of moments procedure suggested by 19.
. The spatial probit model is estimated using the linearized general method of moments procedure suggested by 19.Specification of the housing density equation
 (19)
(19)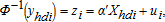 (20)
(20)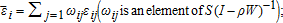 (ωij is an element of S(I−ρW)−1); cov(ui,uj)=0 for every i≠j. Moreover, assuming that the parcel was developed (d=1), the conditional expectation of the housing density equation is:
(ωij is an element of S(I−ρW)−1); cov(ui,uj)=0 for every i≠j. Moreover, assuming that the parcel was developed (d=1), the conditional expectation of the housing density equation is:
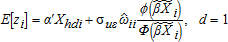 (21)
(21) ” denoting estimates from the first-stage development equation. The ratio of the probability mass function and the standard normal cumulative function is the inverse Mill's ratio (IMR), weighted by the diagonal elements of the n-by-n filter, S(I−ρW)−1. We evaluate the IMR using the spatial probit estimates with the transformed explanatory variables, with the spatial structure of the housing market relayed through ωii.
” denoting estimates from the first-stage development equation. The ratio of the probability mass function and the standard normal cumulative function is the inverse Mill's ratio (IMR), weighted by the diagonal elements of the n-by-n filter, S(I−ρW)−1. We evaluate the IMR using the spatial probit estimates with the transformed explanatory variables, with the spatial structure of the housing market relayed through ωii.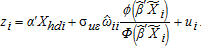 (22)
(22)Covariance estimation and inference
Inference for the first stage development equation was based on a heteroskedastic-robust covariance matrix of the GMM spatial probit model (19). For the housing density equation, we used a bootstrap procedure to estimate the probabilities associated with the tstatistics derived from the WLS covariance matrix (6). The Type I error rate was set to the 5% level. In this procedure, we matched the absolute value of the original t statistic with the bootstrap empirical distribution of the bootstrap replicate t tests. For example, if |tBg| lies between the 1,425th and 1,426th largest values of 1,499 bootstrap replicate t tests, then the bootstrapped p-value is 1−1,450/(1,499+1)=0.0333.
Specification of neighborhood structure
Defining spatial neighbors using Boolean or distance decay functions remains a challenge to practitioners (21). 10 discuss problems that may arise if spatial weight matrices are poorly selected. One approach guiding the weighting matrix selection is to test several types of weighting matrices to observe how they influence model estimates. We consider a variety of neighborhood specifications, including K-nearest neighbor (KNN) and Thiessen polygon (“queen” contiguity) arrays, as well as inverse distance matrices with the distance cut-off specified by the KNN or Thiessen polygon neighborhoods. For the KNN weights, we evaluated neighbors of the orders n1/5=7, n1/4=12, n1/3=27, and n1/2=139. Each contiguity or neighbor matrix was interacted with an inverse distance matrix to include decay effects between neighbors as defined by the KNN or contiguity criterion. All matrices were row standardized such that the sum over the columns of each row was one. Weighting matrix selection was based on overall model fit, including the log likelihood and McFadden's R2 (for the first-stage probit), in addition to an adjusted R2 (for the second-stage housing development equation).
Interaction between minimum lot size and land value tax
Compact development is often recommended or mandated by zoning laws and ordinances (2; Kopits, McConnell, and Miles 2009). Such regulations control the effects of minimum lot size (MLA) on development and housing density because MLA directly affects the compactness of individual lots and likely influences development decisions (23) Consequently, we hypothesize that development patterns and housing densities are different under different minimum lotsize requirements. To evaluate this hypothesis we included dummy variables indicating minimum lotsize zones in the development and housing density equations. The dummy variables were orthogonally restricted such that all dummy variables equal 1 for each mimimum lot size other than the reference group (the lowest minimum lot size category), and −1 where the reference group appears (the lowest mimimum lot size category), and 0 otherwise. (Such restrictions are commonly used in the boiometric literature to compare treatments using Analysis of Variance. See also Lambert, Lowenberg-DeBoer, and Malzer 2006.) Therefore, hypotheses about the coefficients of the dummy variables are made with respect to the overall average of the market and not to any particular MLA zone. In addition, interaction terms between various minimum lot sizes and the land value tax were included in both equations to capture the potentially different impacts of a TPT on development patterns and housing densities under different minimum lotsize zoning.
Determining Hypothetical TPT Rates and Forecasting Residential Development Density
We determine hypothetical tax rates on assessed land values using an optimization procedure. The key constraint in the mathematical program ensures that the sum of the tax revenue collected from all house locations following a hypothetical change in the tax rate is equal to the sum of the existing (“status quo”) property tax revenue. This constraint ensures that the hypothetical TPT scenario is tax revenueneutral compared to the existing property tax scheme. The justification for requiring tax revenue neutrality is that it may not be practical or politically feasible to raise or lower total municipal tax revenue.
Let 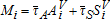 , where Mi is the municipal government's revenue from property taxes on the assessed value (V) of lot area (A) and structures (S) at location i, and
, where Mi is the municipal government's revenue from property taxes on the assessed value (V) of lot area (A) and structures (S) at location i, and  is the prevailing property tax rate. This equation depicts the existing property tax scheme (i.e. the baseline case) in which the tax rates on the assessed values of lot area and structures are identical (i.e
is the prevailing property tax rate. This equation depicts the existing property tax scheme (i.e. the baseline case) in which the tax rates on the assessed values of lot area and structures are identical (i.e 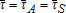 ). The annual aggregate tax revenue for the county from land and associated structures is
). The annual aggregate tax revenue for the county from land and associated structures is 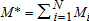 . Suppose a hypothetical TPT scenario placed more emphasis on the assessed value of land by decreasing the tax rate on structures by “α” percent. The revenue collected at property i is then
. Suppose a hypothetical TPT scenario placed more emphasis on the assessed value of land by decreasing the tax rate on structures by “α” percent. The revenue collected at property i is then 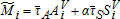 , where α∈[0,1], with lower levels of α reflecting greater emphasis on taxing the assessed value of lot area relative to structures. When α decreases and
, where α∈[0,1], with lower levels of α reflecting greater emphasis on taxing the assessed value of lot area relative to structures. When α decreases and 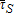 remains at the existing tax rate (
remains at the existing tax rate ( )
) 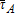 must increase for the hypothetical TPT to be revenueneutral.
must increase for the hypothetical TPT to be revenueneutral.
The amount that Mi changes is site-specific because 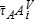 changes. We simulate the hypothetical TPT scenarios using four levels of α*=[0.25,0.50,0.75,0.95], using an optimization procedure to find parcel-specific values of
changes. We simulate the hypothetical TPT scenarios using four levels of α*=[0.25,0.50,0.75,0.95], using an optimization procedure to find parcel-specific values of 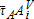 at a given α*. For each level of α, the optimization problem finds a new level of τA that satisfies the tax revenue neutrality constraint. Thus, the optimization problem is conditional on the selected values of α*.
at a given α*. For each level of α, the optimization problem finds a new level of τA that satisfies the tax revenue neutrality constraint. Thus, the optimization problem is conditional on the selected values of α*.
Nashville-Davidson County has two tax rates. In the GSD, the prevailing tax is 4.04% of the assessed value of land and structure, which is 25% of the appraised value of land and structure determined based on market value. In the USD the prevailing tax rate is 4.69%. Given equation (19), these levels generated assessed tax rates on land value of τA=[4.91%,4.62%,4.33%,4.10%] in the GSD In the USD, the simulated land value tax rates were τA=[5.70%,5.36%,5.03%,4.76%]. While the GSD covers the entire study area, the USD is an area originating from the old boundaries of the city extending into suburban areas that were annexed into the USD to receive urban services and includes those areas that incur another tax rate in addition to the basic GSD rate. The jurisdictions designate the boundaries of the USD as a means for phasing in capital improvements as determined by the location and density of allowed and existing development. Note that the ratios of the districts' τA relative to their respective base tax rates are identical, reflecting the neutrality of the TPT as expressed in the optimization problem.
To simulate the effect of a TPT on housing densities, we rescaled tax revenue at the ith location by the new tax rates on land (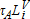 ) and structures
) and structures 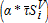 . Given the consistent parameter estimates of the first-stage development (equation (16)) and second-stage residential development density (equation (20)) equations, we forecasted deviations from the equilibrium (e.g. “status quo”) residential development density by replacing the observed tax rate at location iwith the simulated value holding other location factors constant.
. Given the consistent parameter estimates of the first-stage development (equation (16)) and second-stage residential development density (equation (20)) equations, we forecasted deviations from the equilibrium (e.g. “status quo”) residential development density by replacing the observed tax rate at location iwith the simulated value holding other location factors constant.
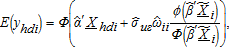 (23)
(23)Sensitivity analysis
As a sensitivity analysis, we performed an out-of-sample simulation to determine if the distribution rankings were similar to the baseline case. The expectation was that the density distributions would be similar to the calibrated results based on the original parcels that were actually developed. We made some assumptions, however, because the parcels that were not developed lacked information about finished area, pool, garage, fireplace, bedroom, stories, and construction quality. Therefore, we used the mean values of these variables for the undeveloped parcels to impute the unobserved data (e.g. pools, garage size) to matched pairs to forecast development density ratios.
Of the 17,562 undeveloped parcels, we matched 1,675 to the developed parcels. We matched undeveloped parcels to developed parcels using a Mahalanobis distance measure (18). Other matching routines are available, but this procedure requires relatively few assumptions. In addition, algorithms designed to match observations based on propensity scores estimated using spatial logit or probit models are uncommon in the empirical literature. For the nonparametric Mahalanobis distance matching procedure, we used all explanatory variables of the development density equation, including the spatiallyadjusted inverse Mill's ratios (equation 20) to match undeveloped parcels to 1,675 developed observations. We restricted eligible matches to the 27 parcels (empirically determined, see results below) closest to the parcel that had been developed. This matching approach ensured that each developed parcel was matched to an undeveloped parcel most similar with respect to the observable characteristics (i.e. hedonic, structural and environmental factors) and neighborhood proximity.
Implicit assumptions for the simulations
The simulations based on the parameters obtained from our empirical model rely on two important assumptions. First, we implicitly assumed that the parameters used for the simulations were obtained from residential development densities corresponding with the land use equilibrium conditions derived in the conceptual framework section. The forecasted deviation from the equilibrium residential development density is valid only if the land use equilibrium condition is assumed to be fulfilled under the baseline case. This critical assumption linking the conceptual and empirical frameworks allows the response function from our empirical model to be used for simulating counterfactual property tax rates based on the 2006–2007 dataset.
Second, we assumed that house buyers and developers reacted to changes in the tax-rate structure through changes in the total dollar amount of property taxes, as estimated in the secondstage development density model. Most municipal offices track changes in property tax schedules through total dollar amounts taxed, and home buyers typically make purchasing decisions based on annual lump sum taxes. Thus, it seems reasonable to model home buyer/developer reactions to changes in the property tax-rate structure through the effects of these changes on total dollar amounts taxed.
Results
The choice of a spatial weighting matrix had little effect on the overall measure of fit for the first stage probit and second stage WLS models (table 2). In some empirical applications and in certain experimental settings (11), the choice of a spatial weighting matrix may lead to identification problems (10). Our results are encouraging, suggesting that the definition of spatial neighborhood does not appear to be a critical factor in terms of model identification. About 24% of the variation observed across the developed parcels was explained (table 2). The null hypothesis that the spatial lag autoregressive coefficient was zero was rejected at the 5% level for each of the K-nearest neighbor configurations (table 2). In some cases the likelihood ratio test was negative, suggesting possible specification problems. Based on these results, we estimated the spatial lag probit using the (row standardized) KNN(27) specification. The spatial lag autoregressive coefficient was ρ=0.27 and significant at the 1% level, suggesting that parcel development was positively correlated and clustered. The second-stage model explained about 97% of the variation in housing density.
| First-stage probit regression Pr(Developed=1) | Second-stage weighted least squares regression house area/parcel area | ||
|---|---|---|---|
| Weighting Matrix | Log likelihood | McFadden's R2 | Adjusted R2 |
| K nearest neighbors of order q[KNN(q)]: | |||
| KNN(n1/5)=7 | −4340.10 | 0.2371 | 0.9737 |
| KNN(n1/4)=12 | −4339.70 | 0.2371 | 0.9732 |
| KNN(n1/3)=27 | −4338.90 | 0.2373 | 0.9734 |
| KNN(n1/2)=139 | −4338.90 | 0.2373 | 0.9734 |
| Queen Contiguity (Order 1): | −4348.70 | 0.2355 | 0.9710 |
| Inverse distance neighborhoods: | |||
| Queen Contiguity×inverse distance | −4352.60 | 0.2349 | 0.9653 |
| KNN(n1/5)=7×inverse distance | −4348.80 | 0.2355 | 0.9724 |
| KNN(n1/4)=12×inverse distance | −4349.70 | 0.2354 | 0.9719 |
| KNN(n1/3)=27×inverse distance | −4349.30 | 0.2354 | 0.9719 |
- a Notes: Aspatial probit log likelihood=−4348.90.
First-stage parcel development probit regression
Larger lots were less likely to be developed during the study period (table 3). Parcel development was more likely to occur in high income censusblock groups, and parcels in more densely populated censusblock groups where vacancy rates were higher were less likely to be developed. The farther away a parcel was from a city park or railroad line, the more likely it was developed. The former finding may suggest that most of the preferable lots near parks may have been developed before 2006. The latter result reflects the disamenities associated with being close to a railroad line. Preferences for water views appear to influence parcel development. The farther a parcel was from a water viewshed (i.e. an area of water that is visible), the less likely it was developed. Lots with views were more likely to be developed, as suggested by the negative coefficient associated with property slope. Parcels in censusblock groups with higher ACT scores (possibly reflecting higher quality schools) were less likely to be developed. The negative effect of ACT scores may be explained by prior development of parcels in high school districts with higher ACT scores. Thus, development occurrences from 2006–2007 were grouped in high school districts with lower ACT scores.
| Development | Density | |||
|---|---|---|---|---|
| Variables | Coefficient | P valuea | Coefficient | P valueb |
| Intercept | −3.713 | 0.000 | 4.250 | 0.000 |
| Structural variables | ||||
| ln (finished area) | 0.002 | 0.965 | ||
| ln (Lot size) | −0.200 | 0.000 | ||
| Pool | −0.861 | 0.000 | ||
| Garage | 0.064 | 0.289 | ||
| Fireplace | 0.012 | 0.775 | ||
| Bedroom | −0.015 | 0.687 | ||
| Stories | −0.005 | 0.900 | ||
| Quality of construction | 0.131 | 0.005 | ||
| Census-block group variables | ||||
| ln (Income) | 0.180 | 0.000 | −0.217 | 0.011 |
| Housing density | −0.063 | 0.000 | 0.073 | 0.001 |
| Travel time to work | 0.005 | 0.069 | −0.013 | 0.017 |
| Unemployment rate | −0.288 | 0.343 | −1.373 | 0.086 |
| Vacancy rate | −1.224 | 0.000 | 1.355 | 0.007 |
| Environmental variables | ||||
| ln (Dist. to park) | 0.082 | 0.000 | −0.148 | 0.001 |
| ln (Dist. to golf course) | 0.025 | 0.243 | −0.074 | 0.017 |
| ln (Dist. to CBD) | 0.009 | 0.807 | 0.193 | 0.123 |
| ln (Dist. to greenway) | −0.006 | 0.640 | 0.003 | 0.697 |
| ln (Dist. to railroad) | 0.094 | 0.000 | −0.191 | 0.000 |
| ln (Dist. to highway) | −0.023 | 0.128 | −0.037 | 0.027 |
| Water view | −0.345 | 0.000 | 0.840 | 0.001 |
| Slope | −0.017 | 0.000 | 0.017 | 0.011 |
| ACT score | −0.025 | 0.020 | 0.107 | 0.000 |
| Tax variables | ||||
| ln (Land value tax) | 0.234 | 0.000 | ||
| ln (Property tax) | 0.880 | 0.000 | ||
| Dummy variables | ||||
| MLA 5,000 | 1.161 | 0.000 | −3.577 | 0.007 |
| MLA 6,000 | 0.776 | 0.020 | −0.586 | 0.575 |
| MLA 7,500 | 0.405 | 0.203 | −0.329 | 0.741 |
| MLA 8,000 | 1.106 | 0.002 | −5.590 | 0.000 |
| MLA 10,000 | 0.293 | 0.329 | −2.156 | 0.000 |
| MLA 15,000 | 0.552 | 0.098 | −1.603 | 0.003 |
| MLA 20,000 | 0.082 | 0.845 | −0.525 | 0.235 |
| MLA 30,000 | −10.660 | 0.009 | 31.546 | 0.000 |
| MLA 40,000 | −0.941 | 0.233 | −0.082 | 0.904 |
| MLA 80,000 | 2.945 | 0.013 | −5.176 | 0.003 |
| MLA 87,120 | 0.082 | 0.808 | −2.993 | 0.003 |
| Interaction variables | ||||
| Interaction 5,000 | −0.127 | 0.007 | 0.457 | 0.010 |
| Interaction 6,000 | −0.055 | 0.289 | 0.092 | 0.470 |
| Interaction 7,500 | 0.082 | 0.079 | −0.141 | 0.351 |
| Interaction 8,000 | −0.111 | 0.043 | 0.662 | 0.000 |
| Interaction 10,000 | 0.077 | 0.064 | 0.142 | 0.015 |
| Interaction 15,000 | 0.039 | 0.411 | 0.055 | 0.419 |
| Interaction 20,000 | 0.054 | 0.378 | −0.017 | 0.739 |
| Interaction 30,000 | 1.391 | 0.013 | −3.625 | 0.001 |
| Interaction 40,000 | 0.180 | 0.107 | −0.043 | 0.578 |
| Interaction 80,000 | −0.725 | 0.000 | 0.859 | 0.001 |
| Interaction 87,120 | 0.016 | 0.733 | 0.290 | 0.024 |
| Spatial lag | 0.279 | 0.000 | ||
| Lambda | −1.413 | 0.000 | ||
| R2 | 0.235 | 0.960 | ||
| N | 19,237 | 1,675 | ||
- a Notes: a. P-values estimated from the probit GMM heteroskedastic-robust covariance matrix.
- b b. Bootstrapped p-values.
Of particular interest is the coefficient associated with the land value tax. Parcels with higher assessed land values were more likely to be developed, suggesting a premium that may be associated with a particular property. That the land value tax variable was significant in the first stage probit regression is important because this variable was incrementally changed during the simulations that follow. The MLA indicators and their interaction terms were jointly significant in view of the associated p-values, which were adjusted using Bonferroni's procedure (joint rejection level, p=0.0023) (30).
Second-stage housing density regression
The IMR coefficient (σuε) is negative and statistically significant at the 1% level, suggesting that the estimates would be upwardly biased if the development decision were not taken into account when estimating housing density. Zoning classification also influences land prices, implying a distinctive heterogeneity in the characteristics found across the zoning categories. The ratio of house size to parcel area was higher on parcels with high-quality houses (table 3). The density was lower on parcels located in censusblock groups with higher incomes and longer commuting distances. These lots may have been part of the “McMansion” boom that occurred during the study period. The higher the average housing density in a censusblock group, the higher was the ratio of residential structure-to-parcel area. House-to-parcel density was negatively correlated with distance to a city park, golf course, highway, and railroad, which could suggest some premium on having a larger house in suburban areas. The house-parcel area ratio was lower for properties developed on slopes and properties with water views. The MLA indicators and their interactions were jointly significant at the Bonferroni adjusted Type I error rate.
Of critical importance for the outcome equation is the sign and significance of the coefficient associated with the property tax variable. The property tax variable is positive and significant, suggesting that, holding other factors constant, increasing the assessed property value of a parcel would increase the house size-to-parcel area ratio.
Simulation of a land tax increase on housing density
A clear pattern emerged between the land value tax and the house-to-parcel density in the GSD and USD zones. In the GSD zone, a 0.06% point increase (land tax rate increase associated with α=0.25) in the land value tax rate from the base rate of 4.04% did not significantly increase the house-to-parcel ratio from the baseline scenario. Similarly, in the USD zone, a 0.07% point increase in the land value tax rate from the base rate of 4.69% did not significantly increase the house-to-parcel ratio from the baseline scenario (figure 2). However, at higher simulated land tax rates, the house-parcel area density significantly increased at all levels of the distribution. The average difference between the house-parcel ratios in the base case and highest simulated levels was about 20%. Thus, it appears that the expectations derived from the theoretical model developed above are consistent with the in-sample results; a TPT encourages higher house-to-parcel area ratios.
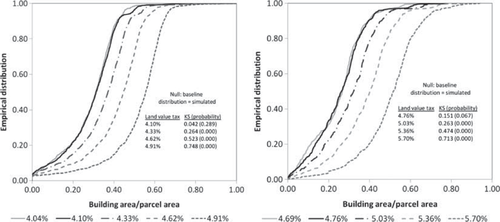
Empirical distributions of simulated and baseline developed housing density and corresponding Kolmogorov-Smirnov (KS) tests for the GSD (Left, Baseline=4.04%) and USD (Right, Baseline=4.69%) tax schedules
In general, the ordering of the out-of-sample simulated empirical ratios was consistent with the empirical densities associated with the observed house-to-parcel ratios, yet the shape of the distributions and the average difference between the housing-parcel ratios in the base case and the out-of-sample simulated case are remarkably different (figure 3). The KS tests demonstrate that the out-of-sample simulated empirical densities with a 0.06% point increase and a 0.07% point increase in the land value tax rate from the base rate for parcels in the GSD and USD zones, respectively, were not significantly different from those of baseline scenarios at the 5% level. As with the in-sample results, at higher simulated land tax rates, house-parcel area ratios significantly increased.
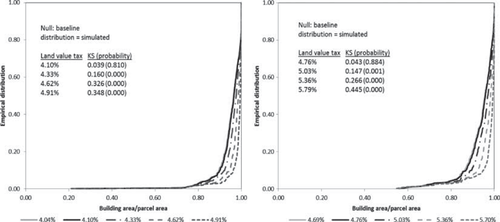
Empirical distributions of simulated and baseline developed housing density and corresponding Kolmogorov-Smirnov (KS) tests for the GSD (Left, Baseline=4.04%) and USD (Right, Baseline=4.69%) tax schedules
The consistent ordering of the out-of-sample simulated empirical densities passed the sensitivity test showing whether the TPT consistently increases house-to-parcel area ratios regardless of the parcels' development status. This finding suggests that with the higher TPT level, house buyers and developers of both undeveloped and developed parcels sharing similar observable characteristics and neighborhood proximity may prefer higher house-parcel area ratios. However, the different shapes of the distributions between the in-sample and out-of-sample results reflect differences in the degree of reaction with the same level of increases in the TPT between the developed and undeveloped parcels. Specifically, the average difference between the housing-parcel ratios in the base case and the highest simulated levels was about 3% for the out-of-sample result which is about 17% lower than the in-sample result.
In addition to differences between the developed and undeveloped parcels, other reasons may explain why the out-of-sample simulated distributions poorly fit the in-sample simulation results. The underestimated distributions may be an artifact of the imputed data used to proxy the unobserved attributes of the parcels. The relatively low predictive power of the first-stage probit could also affect the predictive power of the second-stage density equation through the spatially adjusted inverse Mill's ratio.
Despite the relatively poor correlation between the simulated out-of-sample and in-sample distributions, the findings of both simulations consistently suggest that the TPT is effective with respect to increasing housing density under the land value tax rates of 4.33%, 4.62%, and 4.91% in the GSD zone and 5.03%, 5.36%, and 5.79% in the USD zone (compared to the baseline distribution). This was not the case under the 4.10% and 4.69% rates in the GSD and USD zones, respectively. These findings imply that the increase in land value tax must be higher than a minimum level (i.e. minimums of between 4.10%–4.33% and 4.76%–5.03% in the GSD and USD zones, respectively) to increase house-parcel areas ratios.
Conclusions
Our research analyzed the impact of a two-rate property tax (TPT) on residential densities, measured by the finished house area-to-parcel size ratio using data from Nashville-Davidson County, Tennessee between 2006 and 2007. We applied recent developments in the spatial econometric modeling literature to attend to sample selection issues and define spatial neighborhoods using a data-driven procedure. Based on the empirical results, we conducted a counterfactual experiment to assess, ex ante, the impact of a TPT. We found that a TPT above a minimum level triggers increases in residential densities above the suboptimal densities associated with the conventional property tax system The empirical approach developed in this study may have broad implications for many U.S. municipalities because it can be used to evaluate the potential impacts of TPTs on residential densities in all but a few U.S. municipalities that currently have a conventional property tax structure (e.g. the same tax rate for land and structures). Our research extends TPT impact analyses by simulating development patterns, given the unique characteristics of a municipality's housing market under ex ante counterfactual property tax structures.
It is important to recognize two critical assumptions that condition the results: (i) the TPT simulations are valid only to the extent that the landuse equilibrium condition is fulfilled under the baseline case; and (ii) house buyers and developers react to the implementation of a TPT through changes in the total dollar amount of property tax owed. Other challenges remain in extending our methods. First, although the TPT is revenue-neutral, the distribution of winners and losers is undetermined. Changes in the tax burden caused by TPT implementation produce changes in net income after taxes; after-tax net income may increase, decrease, or remain the same depending on the site-specific weights on land and structures. These changes in after-tax net income may allow further evaluation of changes in consumer welfare following equilibrium shocks induced by a TPT, which could help determine winners and losers.
Second, this research focused on changes in housing density under a TPT at the site-specific level and dealt only with how individual decisionmaking was affected by a hypothetical tax scheme. We have not addressed the cumulative effects of those individual decisions on area-wide development patterns. Because an overall area-wide development pattern driven by individual choices across locations is important for land use planning, aspects that require further attention are the links between individual decision-making in response to a hypothetical TPT, and changes in spatial development patterns at the area-wide level.
Third, instead of using the mean values of developed parcels to proxy the unobserved attributes of undeveloped parcels, the poor out-of-sample estimates could be improved by using the attributes of the closest parcels developed prior to 2006 to proxy the unobserved attributes of the undeveloped parcels from 2006–2007. Bettermatching pairs may also result from using alternative matching procedures to generate out-of-sample observations for ex ante analysis. Although the Mahalanobis procedure is robust, a parameterized matching algorithm may be more efficient. Developing matching procedures that attend to spatially correlated observations would be a promising step in this direction.
Acknowledgements
Senior authorship is shared by the researchers. Authors are listed alphabetically. This research was funded by the Lincoln Institute of Land Policy. Views expressed are the authors' alone, and do not necessarily correspond to those of the University of Tennessee or Kyungpook National University.




