Trait-based Adoption Models Using Ex-Ante and Ex-Post Approaches
Pilar Useche is Assistant Professor of Food & Resource Economics at the University of Florida, Bradford Barham ([email protected]) is Vilas Professor and Jeremy Foltz ([email protected]) is Vilas Associate Professor of Agricultural & Applied Economics at University of Wisconsin-Madison. This article was presented in an invited paper session at the 2012 ASSA annual meeting in Chicago, IL. The articles in these sessions are not subjected to the journal's standard refereeing process.
The original version was incorrect. The bottom line of equation (4) now reads ∀j ≠ k).
Lancaster's (1966) model of characteristics has been considered a revolutionary approach to consumer theory, and is at the core of recent advances in marketing, finance, non-market valuation, transportation studies, and urban economics (Nevo 2011; Berry, Levinson, and Pakes 1995). This article develops the case for applying a characteristics or trait-based modeling approach to the analysis of a broad class of technology adoption issues; both for available technologies with traits that shape key utility outcomes (ex post situations) and new technologies that have similar traits to previous ones (in ex ante contexts).
Lancaster's advances are reflected in the pioneering econometrics work of McFadden (1973) and Train (2009). A key feature of their trait-based demand models is the tight integration of economic theory and econometrics. By specifying utilities associated with choice alternatives, based on choice characteristics and individual preferences, their discrete choice models achieve a direct correspondence between estimated demand parameters and behavioral microfoundations, thereby improving predictions and welfare evaluations. The structural integrity of their model specifications, particularly their capacity to account for heterogeneity, correlation of un-observables, and flexibility in substitution patterns explains why these discrete choice models are favored for the analysis of characteristics- or trait-based consumption behavior.
The relevance of combining the advances of Lancaster, McFadden, and Train for the study of agricultural technology adoption has been scarcely analyzed (Useche, Barham and Foltz 2009). This outcome is surprising, because it is easy to identify situations where individual traits of technologies could affect farm household utility through various channels in addition to profits. Consider these examples of seed traits shaping utility outcomes. Herbicide tolerant (Ht) corn or soy, one of the leading genetically modified (GM) seed innovations of the past fifteen years, reduces labor/management demands associated with weed management. Above and beyond profit effects, Ht seeds can contribute to reducing farmer effort and enhancing leisure or other pursuits. Second, some farmers may place lower value on innovations embedded in GM seeds because of environmental (or other) preferences, which in turn would shape adoption choices for essentially non-pecuniary reasons. Finally, especially in developing country contexts, seed innovations can affect the taste of food crops, which can then affect farmer utility and thus adoption through the consumption side. Whenever technology traits exhibit non-pecuniary effects or give rise to non-separability, it is essential to model the farm decision in terms of traits and utility.
This article shows how trait-based adoption models permit a deeper understanding of technological change processes. Next, we motivate that possibility with a brief literature review of standard farm technology adoption models, trait-based production models, and recent trait-based adoption models. Then we set forth the formal structure and basic econometric design of trait-based models. The next substantive section highlights the advantages and challenges of estimating trait-based models and the final section concludes.
Selective Literature Review of Adoption and Trait-based Models
For decades, standard models of agricultural technology adoption have examined how heterogeneity in farm and farmer characteristics shape decisions (Feder, Just, and Zilberman 1985; Rosenzweig and Foster 2010). They have also treated the adoption question as one of wholesale replacement of one technology with another. Conceptually and empirically, standard technology models feature a binary or multinomial reduced form comparison between profits or utility of distinct technology alternatives, which do not capture the explicit role of individual traits of the technology in farmer adoption decisions (Feder, Just and Zilberman 1985). Simply put, models of agricultural technology adoption typically ignore the explicit link between traits and technological choice behavior and focus only on the comparative choice in technology space.
These models have several shortcomings for technologies like seeds with multiple traits. They ignore the potential heterogeneity of demand for traits especially along broad utility lines. They submerge the substitution possibilities inherent in technologies with related traits. In contexts of uncertainty and learning, they gloss over the nuanced treatment of individual and social learning that might arise when the traits of a technology are explicitly considered. As a result, standard adoption models fail to capture important features of the trait differences that are likely to govern the adoption of differentiated technologies, and empirically may generate omitted variable biases.
Trait-based production models were introduced to the agricultural economics profession in the 1970s to analyze consumer demand for agricultural product characteristics and producer demand for input traits (Ladd and Martin 1976; Ladd and Suvannunt 1976). This approach led to subsequent trait-based work in the pricing dimension using hedonic pricing of input and product components (see e.g., Edmeades 2007). While these models have attractive properties for approximating the value of technological traits, they do not recover a full demand function, and they generally assume perfect competition, a continuum of products, and perfectly observable trait characteristics (Bajari and Benkard 2005). This approach becomes inappropriate when there are many traits, traits are not continuous, and/or traits are experienced or even perceived heterogeneously across users. These shortcomings, in turn undercut, the capacity of these models to provide reliable estimates of farmers’ willingness to pay for traits and producer and consumer surplus generated by new technologies. A structural-trait based framework exploits innovations in consumer demand analysis and puts formal structure on qualitative research by other social scientists, which documents the role of farmer assessments of the attributes of technologies on their adoption behavior (see, e.g., Rogers 1986).
Trait-based Adoption Models
Consistent with McFadden and Train, we next link trait-based theoretical models to appropriate discrete choice models of technological choice that allow for heterogeneity in traits and farmer preferences, substitution between traits, and correlation between this substitution and unobserved characteristics of the technology. This more nuanced approach to technology adoption allows recovery of estimates of the values of traits to farmers, such as labor or input savings associated with new seed technologies.
Adoption of an agricultural technology may diverge for two individuals who face the same prices of the technology and who earn the same income, because traits may differentially affect their utility functions. This may be due to technological traits related to quality, effects on the environment, location asymmetries or labor allocation issues, which are all naturally captured through trait-based models (Heckman and Scheinkman 1987). Similarly, trait valuation heterogeneity due to market imperfections, uncertainty or rigidities associated with trait-bundling can be readily captured with this approach. Trait-based models also address several operationalization problems associated with the specification of preferences directly on technologies as products, rather than on their characteristics. For example, demand systems in product space do not enable the researcher to analyze demand for new technologies prior to their introduction. Additionally, when technologies have a large number of substitutes, estimation of a demand system in product space faces basic dimensionality problems (Ackerberg et al. 2007). Explicit examination of the demand for traits requires a utility framework that compares the relative value of different combinations of traits to farmers and incorporates heterogeneity.
Assume a farmer maximizes her utility Vi and chooses among J alternative technologies. The farmer i divides her expenditures yi on one of the alternatives and one “outside good”: max Vi (xij,h) s.t. pj+phh=yi, where xij are characteristics of technology j, and pj the price, h is quantity of outside good, and ph its price. The conditional indirect utility function can be derived by substitution of the budget constraint: 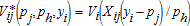 (pj,ph,yi)=Vi (xij(yi−pj)/ph). This reflects the fact that technological traits enter into the farmer's preference function in a dual way. Once directly affecting utility, and then, through the price traits’ effect on monetary expenditures.
(pj,ph,yi)=Vi (xij(yi−pj)/ph). This reflects the fact that technological traits enter into the farmer's preference function in a dual way. Once directly affecting utility, and then, through the price traits’ effect on monetary expenditures.
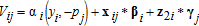 (1)
(1)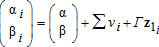 (2)
(2)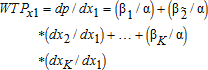 (3)
(3)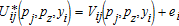 , where eij is observed by farmer i, but not by the researcher. The distributional assumptions on this term, for determine the form of farmer i's choice probabilities, such that the probability that farmer i buys technology alternative j is:5
, where eij is observed by farmer i, but not by the researcher. The distributional assumptions on this term, for determine the form of farmer i's choice probabilities, such that the probability that farmer i buys technology alternative j is:5
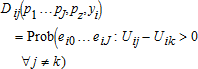 (4)
(4)The model represented by the above equations is more flexible than traditional adoption models in two primary aspects. First, it allows farmers’ tastes for a trait to deviate from average tastes.6 Farm and farmer characteristics, which are unobservable to the analyst, are allowed to influence a farmer's valuation for a trait, such that two different farmers facing the same levels of observed attributes for all alternatives might choose differently.7 Additionally allowing the preference parameters to vary with the observed individual characteristics presents the advantage of reducing the reliance on parametric assumptions and brings in additional information. This approach is also more flexible, because it allows for correlation in the unobservable components of the utility for different alternatives. A higher covariance between the unobservable components of two alternatives reflects the fact that two varieties with similar attribute levels are treated by a farmer as closer substitutes than two varieties with very different attribute levels.
In summary, we can express the farmer's maximization problem as a choice of the variety that gives her the highest utility, and which includes her knowledge of the traits of each variety, her expected profitability of each variety, her tastes for the traits, and her own characteristics. The chosen estimation procedure will estimate the preference parameters (αi,βi,γj) given information on the traits, xij, and farmer characteristics, zi.8
Dynamic Dimension
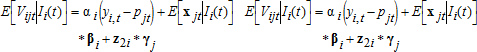 (5)
(5)While many recent studies have examined the dynamics of learning in the technology as product space (Foster and Rosenzweig 1995; Bandiera and Rasul 2006; Conley and Udry 2010), a trait-based approach to these issues has not been implemented yet in the agricultural economics literature. Doing so could open the door for a richer discussion of technology and learning in several ways. First, it places emphasis on the core objects of learning about technologies—their traits. Second, it focuses on learning the quality of the traits of the technology, which can vary and interact. Third, it allows users to learn about the qualities of different traits from multiple sources (right mix of inputs from sellers of inputs, right qualities for consumption from markets or neighbors, and the environmental damage from others besides the vendors). It also allows for differences in the mechanism and timing of learning about key traits. Fourth, the basic mechanics of the trait-based approach implies that what people have learned about traits from existing technologies can influence their preferences for new ones, and thus their adoption choices. All-in-all, a trait based approach can offer a deeper view of the social, temporal, and path-dependent nature of learning about technologies.
Advantages and Challenges of Estimating Trait-Based Models
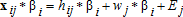 (6)
(6)Economists generally favor ex-post analyses that use revealed preference data, because they are based on technological choices made by farmers under real growing conditions and on a real-time basis. With this type of data, observability issues that create missing data problems mainly concern traits that vary at the individual level. For traits wj, the observation of w for a single individual in a specific market is the same for all other individuals in that market. But for hij, in the perfect information scenario, the researcher needs to observe the specific trait levels faced by each farmer for all available alternatives.
When information is a key constraint, the mechanism through which farmers learn about core technological traits can be specified to operationalize equation (1’). When technologies have already been commercialized, it is possible to collect information over time about technological traits and individuals’ adoption behavior. Thus, trait expectations can be assessed based on observed data and in dynamic frameworks of the type represented by (1’). Repeated observed technological choices then enable the identification of trait preferences at the individual level.9Ex-ante analyses also allow for repeated observations on individual behavior, by asking repeated questions to the same farmers about their demand for specific trait changes. However, these do not reflect adoption changes on a real time basis. Thus, while panel data econometric structures can be applied and individual level preferences for traits can be identified in both scenarios, they have different connotations.
In terms of variability, Equation (5) shows how some observed traits naturally attain less variability than others. Thus, the researcher has to be careful implementing ex-post models, in order to avoid potential multicollinearity (among w's) and/or endogeneity issues (if w and E are correlated).10 While ex-ante analyses rely mostly on hypothetical or stated technological choices, based on researcher-designed combinations of technological trait levels, the flexibility to design combinations overcomes observability concerns and allows for large data variability. In particular, attribute quantities that are not observed in real life (term Ej in (5)) can be specified in the ex-ante survey design.
Higher variability of data in ex-ante designs is especially useful for the estimation of WTP, which relies on the range and variability of the price variable (In equation (3) the price coefficient enters the WTP calculation). In trait- or technology space, correct WTP estimates in ex-post scenarios with revealed preference depend on having sufficient data on the demand for new products at prices that are high enough to enable the estimation of reservation prices of a large fraction of producers. This means that, the results are likely to be sensitive to a priori modeling assumptions; but less so in the trait-based analysis, since it uses the price variance for products with similar characteristics.
In ex-ante scenarios, the researcher also has the flexibility of eliciting preferences for trait changes in isolation, by specifying that no change in other traits will occur, holding constant the last terms of equation (3). This enables the use of standard contingent valuation methodologies and is very desirable for lines of technologies where changes are made continuously to single core traits. Concerns about hypothetical biases in ex-ante trait studies for agricultural technologies are likely to be minimized since farmers are familiar with valuation exercises for agronomical traits.
Recently, researchers have advocated the combination of hypothetical- and observed data sources (e.g., Hensher, Louviere and Swait 1999).11 Hypothetical data can be used to fill in the gaps in observed behavior, can be used when new technologies do not have any observed demand, when the quality of observed data is poor, or when valuation of quality change is beyond the range of historical experience. Observed data, in turn, can be used to complement or calibrate hypothetical information experience. In fact, one important advantage of trait-based models in ex-ante studies is the potential to use observed data on similar technologies to make inferences on the adoption behavior of individuals for technologies that are not in the market yet. New technologies can share main traits with existing ones, with innovations that change trait proportions, or add similar ones. Since farmers have specific preferences for these traits (e.g., herbicide use, yield stability), inferences can be drawn based on the degree of substitution with existing technologies. That said, even trait-based models will not be appropriate to predict demand for technologies whose traits are very different from previous technologies.
Manski (2004) proposes another way of combining sources of data: complement the information on the traits of a technology that a farmer observes with elicitation of probabilistic expectations for traits that a farmer has not experienced. In ex-antescenarios, where revealed data for closely related technologies are not available, survey-based hypothetical methods to elicit preferences can be calibrated with economic experiments where real choices can be presented, even when a technology is not commercialized. That is, the researcher can provide it on an experimental basis.
Conclusion
Trait-based adoption models provide opportunities to delve deeper into technological change processes. This article motivates that possibility, offers the formal structure and basic econometric design, and highlights links between this conceptual innovation and other methodological approaches. Trait-based models are better designed to analyze agricultural technology adoption in a context of increasing differentiation, where the introduction of specific traits via genetic modification is basic to innovation in cotton, corn, soy, and other seed varieties and the potential for close degrees of substitutability across traits in related seed technologies have become much more prominent. These make the direct effect of traits on technology choice of more central concern. Finally, because both input traits and consumer choices over quality characteristics can matter to farmers, traits can enter from both the supply and demand side to shape adoption patterns.




