Asymmetric Information and Profit Taking in Crop Insurance
Abstract
Excess returns to producers insured by the Federal Crop Insurance Corporation can arise due to asymmetric information or from the design of the insurance programs themselves. Using unique, unit-level crop insurance contract data for major crops such as corn, soybeans, and wheat in five growing regions, we find evidence that producers in most regions may profit by selecting optional units, buy-up coverage, or by using transitional yields to participate in the federal crop insurance program. We also find evidence that advantages increase with land resource heterogeneity. However, the results do not support hypotheses that producers profit by selecting revenue insurance, nor that high levels of government “incompetence” exist in the design and administration of the crop insurance system.
Agricultural policy has increasingly turned from direct counter-cyclical commodity programs toward social insurance and risk management programs. Prior to the mid 1990s, when the U.S. crop insurance program offered far fewer insurance options and lower premium subsidies, participation rates were extremely low. Through the Agricultural Reform Act of 1994 and the Agricultural Risk Protection Act (ARPA) of 2000, Congress attempted to entice producer participation in the crop insurance program by increasing premium subsidies and by introducing new insurance contracts (Agricultural Risk Protection Act, 2000).1 A key motive was the hope of reducing ad hoc disaster payments or emergency aid (Ker 2001). As desired, the higher subsidies and expanded contract options helped fuel a marked increase in insured acreage, which increased from 100 million to 265 million between 1994 and 2009 (USDA-RMA Bulletin, 2012). The latest U.S. farm bill legislation “upgrades” crop insurance as direct counter-cyclical payments are essentially eliminated. Hence, the lessons to be learned from experience to date are invaluable.
Subsidized and complex crop insurance programs may increase the likelihood that profit-maximizing producers can use information advantages to garner returns above what the government intends. Such excess returns would result in increased costs to taxpayers and potentially inefficient resource reallocations in agriculture.2
In this paper, we empirically examine some recent crop insurance financial experience. This analysis addresses several rating issues faced by insurance program designers and administrators. The deliberate subsidy presents a major challenge, and the widely varying production risks and market uncertainties make finding the actuarially correct design for the insurance contract exceedingly difficult.
In the absence of subsidies, one might investigate the relative profits of the insurer and the insured. If the industry is competitive and neither party is making excess profits, then empirically, the industry has found an efficient equilibrium (subject to the usual second best concerns). We hypothesize that in the case of a deliberate subsidy, if the program is poorly designed and/or has severe problems of moral hazard and/or adverse selection, these problems should show up as anomalies in returns to different program features and/or information settings.
We examine whether insurance contract characteristics stray from the neutral revenue impacts one would expect from actuarially neutral insurance (i.e., with premium rates set to cover expected costs under complete information) beyond the impact of subsidies and, if so, by how much. We look for evidence of such deviation by examining returns to particular features of insurance. If variation in unit-level crop insurance returns (other than the subsidy) is systematically associated with insurance contract characteristics or with geographic region for a representative time period, then either the insurance is not actuarially neutral or the subsidy is not implemented according to policy. Either case would permit participants to exploit opportunities within the insurance system to make profits, for example, by exploiting contracts that are too cheap relative to those that would emerge under neutral insurance.
We measure systematic evidence of opportunistic behavior exhibited in the examined historical crop insurance data. We conduct this analysis for a time period during which the subsidy policy changed abruptly. Further, we quantify the potential impact of any possible opportunism by examining the impact on producer revenue from the selection of alternative crop insurance contracts. We consider several characteristics of the contracts to determine which of them plays a role in providing producers with excess returns from crop insurance. We investigate whether producers using different insurance contracts (including buy-up coverage, unit type, revenue insurance, and T-yield) may have strategic advantages in their contract selection. Additionally, we examine whether regions with more heterogeneous growing conditions experience increased incidence of opportunistic behavior. While the aggregate data used in most related studies has the advantage of a wide view, use of aggregate data can “average out” potential program effects. The unique, very detailed, unit-level crop insurance contract and performance data we use provides a more precise and complementary window on crop insurance.
This paper proceeds as follows. We first couch our research within the context of the literature. We then model producer insurance decisions and discuss the possible relationships with opportunistic behavior. The empirical model and estimation procedures are then explained, followed by a description of the data and empirical analysis. We present and interpret findings in the results section, while our conclusions are provided in the final section.
Prior Literature
The root of inefficiency in insurance lies in asymmetric information, and these inefficiencies are generally subsumed under the categories of adverse selection or anti-selection (Akerlof 1970) or moral hazard (Arrow 1985), or both. An example of adverse selection would be the purchase of crop insurance (provision) where the insured has information that is unknown to the insurer, and so can obtain excess expected returns. Essentially, in such a case the insured is using loaded dice, and the insurer does not know it. Moral hazard occurs when participants change their (risky) actions when insured—for example by adopting more risky inputs or crop regimes. In agriculture the boundary between choosing to participate in insurance programs versus altering management practices because of participation can be ambiguous since often the insurance provision decision and the operational production decisions occur simultaneously. Hence, it is often difficult to distinguish empirically between adverse selection and moral hazard (Quiggin, Karagiannis, and Stanton 1993). In this study, we are not concerned about the category of behavior (i.e., adverse selection or moral hazard), but only whether and to what degree such actions occur. Hence, we will use the generic terms “opportunism” and “opportunistic behavior” to indicate either or both forms of (rational, profit-maximizing, but inefficient) behavior under information asymmetry.
A rich body of literature provides evidence both for and against opportunistic behavior in crop insurance (|Glauber 2004). Prior analyses have covered insurance contracts for a variety of crops in more than fifteen states. For example, Roberts, Key, and O'Donoghue (2006) found evidence of moral hazard in yield differences of insured wheat and soybean farms in Texas, but did not find moral hazard behavior in Iowa or North Dakota. Further, Coble et al. (1997) concluded that moral hazard affected the crop insurance decisions of Kansas wheat producers in poor production years but not in years with favorable growing conditions. Smith and Goodwin (1996) suggested that adopters of crop insurance exhibited moral hazard behavior by using fewer inputs than non-adopters. Horowitz and Lichtenberg (1993) described opportunistic behavior in the opposite form, with crop insurance participants using higher rates of inputs than non-participants, suggesting that both fertilizer and pesticides could be risk-increasing inputs.
Some of the literature has focused on specific contract features that may lead to opportunistic behavior. For example, Makki and Somwaru (2001) found evidence of adverse selection in both coverage-level and insurance-type decisions. That is, high-risk producers more often selected revenue insurance contracts and higher coverage levels. Skees and Reed (1986) concluded that adverse selection existed at that time because the selection of coverage level was not independent of expected yields and because trends were not used to establish expected yields. Although they did not quantify impacts, both Makki and Somwaru (2001) and Skees and Reed (1986) identified characteristics of insurance plans that may play a role in allowing opportunistic behavior. Very often such studies have had direct policy impacts by assisting policy implementers to design contracts and set premium rates to reduce the effects of opportunistic behavior within the crop insurance system.
One crop insurance feature of particular interest in this study is the transitional yield (T-yields) contract. Although they did not measure the actual impacts, Rejesus and Lovell (2003) found that informational asymmetries existed in contract characteristics such as T-yields and were vulnerable to abuse by producers growing cotton in Texas.3Knight and Coble (1999) also showed that using contract characteristics with limited actuarial experience could allow for artificially-inflated coverage, but the magnitude of such effects is unknown.
Additionally, the subsidization of insurance premiums may itself invoke opportunistic behavior. Just, Calvin, and Quiggin (1999) found that participation from the risk-aversion incentive was small and producers participated to receive the subsidy and/or because of adverse selection.
Insurance Decisions and Opportunistic Behavior
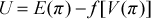 (1)
(1)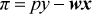 (2)
(2)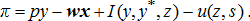 (3)
(3)In our examination of producer opportunism in subsidized crop insurance, we base our analysis on the principle that the provisions of actuarially neutral insurance should be neutral with regard to risk-related insurance options.4 In an unsubsidized neutral insurance system, there should be no systematic evidence that one contract provides higher expected utility to producers than another. If there is evidence that, on average, farmers can increase their expected utility by choosing a particular contract, opportunistic behavior would be implied and the hypothesis of neutral insurance would be rejected. With a subsidized neutral insurance system, departures should be consistent with the way the subsidy is implemented. Thus, our test for neutral insurance is subject to the maintained hypothesis that the subsidy is implemented according to legislated policy. This test is observationally equivalent to the test that the subsidy is implemented according to legislated policy subject to the maintained hypothesis that the insurance system is neutral. If the joint hypothesis is rejected, it could be due to a failure of either the neutral insurance hypothesis or the hypothesis that the subsidy is implemented consistent with policy, or both.
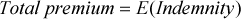 (4)
(4)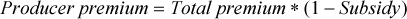 (5)
(5)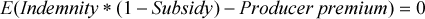 (6)
(6)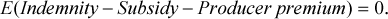 (7)
(7)The producer's indemnity and premium associated with insurance depend on the characteristics of the insurance contract. During the observation period, insurance could be purchased for different units representing a field (a section of land, i.e., 640 acres, west of the Mississippi and a farm serial number east of the Mississippi)7, share of ownership, enterprise, or whole farm (Edwards 2003a). Regarding unit types, we include only field (Risk Management Agency's [RMA] term is “optional units”) and share of ownership (RMA term is “basic units”) in our analysis because these were the dominant types selected by producers in the study regions during our data period of 1996–2009. Producers could select yield or revenue insurance to insure against low yield or revenue, respectively. We include one type of yield insurance (multiple peril) and one type of revenue insurance (crop revenue coverage) as choice options because these insurance types were the most frequently selected. Producers could select a coverage level between 50–85% coverage level in 5% increments.8 We include all coverage levels as options, except for the 55% level because so few producers selected this option.
Expected indemnities and producer premiums for yield and revenue insurance depend on the producer's actual production history and the selected yield coverage level.9 When producers do not have actual production histories, they can make use of the T-yield option.10 This option permits producers to enroll units in the crop insurance program that have not previously produced or have seldom produced the insured crop. The T-yields are based on the 10-year county average yield. If the producer cannot provide the minimum of four years of actual yields for a unit, a T-yield must be substituted for each missing year. Depending on the number of verifiable yield records and other circumstances, a producer may use one, two, three, or four T-yields, or special T-yields (new producer or a new practice/type/variety) when purchasing crop insurance. For a producer who is lacking only one of the required four years of verifiable yield records, that is, one T-yield, the producer uses 100% of the county average yield for the missing year in determining the “actual production history” (APH). When the producer needs to use two, three, or four T-yields, only 90%, 80%, and 65%, respectively, of the county average yield for the missing years is used to determine the APH. Presumably, the weights are actuarial adjustments for potential opportunism. For a new producer, s/he can obtain the new producer T-yield contract for which 110% of the county average yield is used in determining his/her APH. If the producer adds land where there is no existing unit to determine the APH, s/he may be able to obtain the new practice-type-variety T-yield contract for which 100% of the county average yield is used to determine APH.
Empirical Model and Estimation
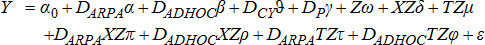 (8)
(8)We conduct several empirical tests of the joint hypothesis that crop insurance was neutral and that the subsidy was implemented consistent with policy during the observation period. Three of the tests are derived directly from the theory for producers who are risk-averse and seek to maximize expected utility. Such producers would not choose a contract that results in lower expected profit with risk levels that are at least as high. To test whether these producers face neutral insurance with a subsidy, we conduct one-sided tests for the joint hypothesis. These hypotheses focus on the selection decision of higher buy-up coverage, optional unit type, revenue insurance, or use of T-yields compared to a low buy-up, basic yield insurance contract during the 1996–2000 period.14 Since each of these options reduces risk to the producer, the joint hypothesis would be rejected by empirical evidence that one or more of these contracts systematically generates higher expected return from insurance (excluding the subsidy). The larger the number of contracts with higher returns than would be expected with random observations and a normal distribution, the stronger is the support for rejecting the joint hypothesis and concluding that producers systematically and successfully behave opportunistically.
Two of the tests focus on policy. Policy changes during the ADHOC period increased subsidy levels. Policy changes during the ARPA period changed the revenue insurance subsidy mechanism from dollars per acre to a percentage of premium and further increased overall subsidy rates above the ADHOC period. For both policy changes, the increase in subsidy rates lowers insurance cost to the producer while simultaneously reducing risk. For consistency with the joint hypothesis, the premium must decrease by the subsidy, less the value of risk reduction. The joint hypothesis would thus be rejected by empirical evidence that contracts in the ADHOC or ARPA periods systematically generated higher expected returns from insurance than in the pre-ARPA period.15
Land quality represents a particularly important determinant of land use and yields (Hardie and Parks 1997). Producer opportunism due to specific characteristics of the insurance contract may be greater in regions with greater within-county land resource heterogeneity. Land heterogeneity can increase the returns to selection of a higher coverage level, optional unit type, and/or revenue insurance because the correct premium rate is difficult to determine due to increased yield variance. This may increase the relative value of the asymmetric information held by farmers. This is particularly important when the insurance contract includes the use of T-yields. Because the Federal Crop Insurance Corporation (FCIC) calculates T-yields based on the county average yield (although discounted when multiple T-yields are used), regions with highly variable land resources may have greater variability of within-county yields, which would make it harder to accurately set premium rates to appropriately account for risks. The use of T-yields in locations with heterogeneous within-county resources could provide a yield guarantee well above some units' actual production ability and thereby inflate the yield guarantee to levels less likely to be achieved.
We estimate equation (8) separately for each region. However, before estimating the final model we need to address several econometric issues. First, because the data are reported for an insurance “unit” and one producer may operate multiple insurance units, the assumption of independent and identically distributed (IID) sampling errors is violated.16 Furthermore, all models showed evidence of heteroskedasticity, as is often the case with time series, cross sectional data. To account for the sampling error structure and the presence of heteroskedasticity, we estimated robust cluster standard errors by producer, which adjusts the variance for within-cluster correlation (Wooldridge 2002).
Second, contract selection and premium amounts are jointly determined, resulting in the possibility of endogeneity in the insurance contract decision.17 We instrumented the insurance contract decision using a combination of instruments that were found to be both strong and valid, and varied by state. We used a combination of yield lagged one and two years, acres lagged one and two years, coverage level lagged one year, unit type (optional or basic) lagged one year, insurance type (yield or revenue) lagged one year and all exogenous variables in equation (8).18 We chose these instruments because higher recent yields would increase APH and possibly alter incentives for higher coverage selection and/or insurance type.19 Contract choice, especially unit type, may not be neutral to production scale (which is proxied by lagged acres). Lagged coverage level and unit type would acquire stickiness in the decision process. Additional sources of endogeneity, for which we lack data, could be unit-level input use and soil quality, and it is possible that our instruments are correlated with them. However, while these are potential sources, there are also reasons they may not cause endogeneity. Year-to-year input use can change due to price and weather changes, as well as planting different fields within the unit. Unit-level soil quality can be highly variable within the unit (1 square mile area west of the Mississippi). A rotation would cause the location of the field inside the unit to change. Consequently, it is also possible that lagged acreage and yields are uncorrelated, or at least not highly correlated with these unobservables and so qualify as appropriate instruments.
Insurance contract decisions are represented by binary choice variables (coverage level, unit type, and insurance type) in X. Their predicted variables from the first stage of the instrumental variables approach yielded a continuous variable. We converted these continuous variables back to binary variables by sorting them from smallest to largest and assigning a value of zero to observations below the predicted mean and a value of one to observations above the mean.20
Third, we accounted for unobserved producer heterogeneity through producer fixed effects. Temporal and geographic heterogeneity is accounted for by including county-by-year fixed effects.
Fourth, not all producers participated in the crop insurance program every year. In addition, each producer could have multiple units but the individual units cannot be tracked over time in the RMA data. Consequently, we were unable to use a panel data estimator. Following estimation of the instrumental variables, equation (8) was estimated for each region using AREG (an OLS estimator) with the instrumental variables along with the absorb and cluster options in STATA (version11). The AREG is designed for data sets with one large categorical variable which, in our case, is producer.
Data
With three exceptions—Roberts, Key, and O'Donoghue (2006), Atwood, Robinson-Cox, and Shaik (2006), and Quiggin, Karagiannis, and Stanton (1993)—previous work related to opportunistic behavior and crop insurance relies on aggregate data. An important feature of the current research is the use of a rich, detailed, unit-level actuarial crop insurance data set obtained from the Risk Management Agency of the United States Department of Agriculture.21 Each crop on a farm contains one or more units, which are specified as separate insurable parcels of land for crop insurance purposes. This data set allows us to more precisely estimate the evidence regarding producer opportunistic behavior and, potentially, to provide more targeted policy recommendations.
The data include observations of crop insurance contract information and corresponding performance records for all insured units by the FCIC for each of 14 years—1996 through 2009; only insured units are included in the data set.22 Producers can change insurance contracts on each unit from year to year. The data set includes all information the FCIC has for each crop insurance contract: indemnity amount, premium paid by producer, amount of subsidy, crop type, number of acres, field practice, coverage level, unit type, insurance type, year, county location of unit, and type of APH (actual and/or T-yields).
We conduct our analysis using data for five different growing regions, two with relatively homogenous within-county land resources (Iowa and western Nebraska) and three with more heterogeneous land resources (Oklahoma, north-central Montana, and eastern Washington). To permit an examination of the effects of the heterogeneity of land resources, we limit our data sample to non-irrigated agricultural production. Even with the limited number of regions and considering only non-irrigated production, the data set includes 392,035 observations.
We analyze the returns to one yield-type insurance (MPCI) and one revenue-type insurance (crop revenue coverage).23 Buy-up coverage, unit type, revenue insurance, and T-yields can potentially vary by crop type and field practice. Thus, we distinguish these variables by several crop types: wheat, spring wheat, winter wheat, corn for grain (hereafter referred to as corn), soybeans, and “other crops.” We also distinguish between two field practices: summer fallow and continuously cropped.24 These three crops (corn, soybeans, and wheat) represent the highest-value insured crops grown in the United States. The “other crops” category represents other important insured crops grown in these regions.25
The constant in the estimated equations represents a producer who grew corn in Iowa, millet in Nebraska, cotton in Oklahoma, winter wheat in Montana, or barley in Washington on a continuously-cropped basic unit, who purchased yield insurance coverage at the 50% level using all actual yields for the unit's APH in a specific county in 1996 (during the pre-ARPA period). The constant captures the estimated returns in excess of neutral insurance with government subsidy implemented according to policy. Thus, we can directly interpret the marginal effect of insurance characteristics on the dependent variable by their estimated coefficients.
The five growing regions produce some of the same crops, but the crop mix differs by area. Soil organic matter represents an important indicator of soil quality and thus land resources (|Pulleman et al. 2000). Regions such as Oklahoma and north-central Montana generally have lower amounts of soil organic matter and vary much more across relatively small areas such as counties than regions such as Iowa and western Nebraska. Due largely to the geography of the region, which is prone to wind and water-caused erosion, eastern Washington has areas with high soil organic matter like Iowa and western Nebraska, but also exhibit high variability within counties similar to Oklahoma and north-central Montana.
Our data period is limited to 14 years between 1996 and 2009. This is an admittedly short time frame in which to provide conclusive evidence concerning opportunistic behavior in crop insurance. It is possible that some of our results could be due to differences between our data period and the longer historical period underlying crop insurance premiums. Accordingly, we plot density functions of the difference between actual yield and a 10-year moving average for the major crop in each state (corn in Iowa and Nebraska and wheat in the other states) for our data period, and superimpose it on the distribution for the 100-year period of 1913–2012. These graphs are presented in figure 1. It is the portion of the distribution below zero that is pertinent for crop insurance. Two states (Washington and Montana) have a larger cumulative distribution in the negative range for our data period but a smaller cumulative distribution for very large negative differences. Oklahoma is the counter example; it has a smaller cumulative distribution in the negative range but a larger cumulative distribution for very large negative differences. In contrast, Nebraska has a very small cumulative distribution in the negative range during our data periods and Iowa has none. Consequently, one should expect state differences in average annual indemnity and in average excess return during our data period for neutral insurance administered consistent with policy. We would expect Iowa to have the lowest indemnity and smallest excess return, followed in turn by Nebraska, Montana, and Washington. Expectations for Oklahoma are ambiguous; it should clearly have higher indemnity and higher excess return than Iowa and Nebraska, but it is unclear how it should rank relative to Montana and Washington. It is also unclear how the differences associated with our data period should impact other measures we examine. We will comment on some possibilities in the next section.

Yield distributions by region
Results
With 170 to 239 parameters (plus the producer fixed effects) estimated for each region, we present only summary marginal effect statistics pertinent to testing the hypotheses, four of which focus on opportunistic behavior and two on policy.26 Each of the hypotheses is a joint hypothesis focusing on specific evidence that crop insurance was neutral and that the subsidy was implemented consistent with policy.
The percentage of the sample using specific crop insurance contract choices are reported by state in table 1. We see large regional differences. For example, the percentage of producers using optional units (one insurable unit per section of ground) varies from a low of 49% in Washington to a high of 81% in Montana; the percentage selecting 75% and higher coverage levels ranged from 6% in Oklahoma to 70% in Washington; the percentage using any T-yields ranged from 7% in Nebraska and Montana to 50% in Iowa. Average annual indemnity per acre was highest in Oklahoma and lowest in Iowa, both of which would be consistent with evidence about the yield distribution during our data period compared to a longer data history. Average annual excess returns per acre were highest in Washington and lowest in Iowa, and again, both would be consistent with evidence about the yield distribution during our data period compared to a longer data history. The number of observations included and the R2 value obtained for each estimated equation are also reported in table 1. The number of observations used in the estimations range from 41,432 in Nebraska to 136,718 in Iowa. The R2 values range from 0.35 in Iowa to 0.45 in Washington, reflecting evidence of considerable noise in the estimated equations.
| Variable | Region | ||||
|---|---|---|---|---|---|
| Iowa | Nebraska | Oklahoma | Montana | Washington | |
| Percentage of sample using crop insurance contract choices: | |||||
| Crop revenue coverage | 52.90 | 68.61 | 35.98 | 53.63 | 36.13 |
| Optional units | 57.76 | 62.02 | 65.56 | 80.98 | 49.09 |
| 50% coverage level | 1.13 | 0.83 | 3.49 | 0.76 | 2.21 |
| 60% coverage level | 0.49 | 0.30 | 5.69 | 1.17 | 0.93 |
| 65% coverage level | 31.58 | 38.74 | 60.09 | 31.41 | 14.64 |
| 70% coverage level | 19.89 | 31.95 | 24.94 | 34.45 | 12.59 |
| 75% coverage level | 31.29 | 24.35 | 5.60 | 30.48 | 44.02 |
| 80% coverage level | 11.91 | 3.09 | 0.05 | 1.73 | 14.34 |
| 85% Coverage level | 3.72 | 0.74 | 0.00 | 0.00 | 11.27 |
| 4 T-yields | 0.25 | 0.40 | 0.26 | 0.51 | 0.42 |
| 3 T-yields | 0.52 | 0.69 | 0.56 | 0.66 | 0.44 |
| 2 T-yields | 0.95 | 0.92 | 1.27 | 0.56 | 0.40 |
| 1 T-yield | 47.70 | 3.83 | 46.10 | 4.86 | 37.49 |
| New producer T-yield | 0.79 | 0.32 | 1.31 | 0.26 | 0.43 |
New practice/type/variety T-yield |
0.27 | 0.55 | 0.40 | 0.52 | 0.39 |
| Average annual indemnity per acre: | 3.88 | 7.64 | 8.95 | 8.04 | 8.22 |
| 1996–1998 | 1.39 | 3.07 | 7.31 | 2.32 | 0.93 |
| 1999–2000 | 4.41 | 4.19 | 3.96 | 6.40 | 1.27 |
| 2001–2009 | 4.81 | 9.74 | 10.85 | 10.05 | 11.23 |
| Average annual excess return per acre: | −4.29 | −1.16 | 0.94 | 0.53 | 1.62 |
| 1996–1998 | −4.64 | −2.01 | 1.20 | −1.20 | −1.44 |
| 1999–2000 | −3.81 | −1.82 | −0.48 | 1.29 | −1.07 |
| 2001–2009 | −4.64 | −0.77 | 1.19 | 0.86 | 2.84 |
| Number of observations | 136,718 | 41,432 | 94,486 | 58,582 | 60,826 |
| Equation R2 value | 0.35 | 0.42 | 0.42 | 0.36 | 0.45 |
| Number of parameters estimated (excluding producer fixed effects) | 239 | 200 | 170 | 235 | 214 |
| Number of producer fixed effects | 17,039 | 5,250 | 8,296 | 5,177 | 8,676 |
Statistics to examine the null hypothesis that producer selection of higher coverage levels did not provide evidence of opportunistic behavior are presented in table 2. Significant positive marginal effects of coverage level by crop and practice provide evidence of the exercise of opportunistic behavior in an otherwise neutral insurance market with the subsidy implemented consistent with policy. The percentage of positive coverage level marginal effects that were significant at the 5% level ranged from a low of 6% in Montana to a high of 26% in Oklahoma. The percentage of significant variables that suggest opportunistic behavior in the selection of higher coverage levels was higher in all regions than would be expected with random observations and a normal distribution. The average magnitude of these significant marginal effects ranged from a low of $3 per acre in Washington to a high of $16 per acre in Nebraska, and two of the five regions exceeded the average indemnity per acre from crop insurance over the observation period. The lowest value of a significant positive marginal effect was $1 in Iowa, while the highest was $72 in Nebraska. In terms of average, maximum, and minimum magnitudes of positive significant coverage level marginal effects, Nebraska demonstrated most evidence of opportunistic behavior, while Washington demonstrated the least evidence in the average and maximum values. Iowa demonstrated the least in the minimum values.
| Significant Positive Marginal Effects (5% level) | Region | ||||
|---|---|---|---|---|---|
| Iowa | Nebraska | Oklahoma | Montana | Washington | |
| Number significant | 8 | 9 | 6 | 5 | 6 |
| Percentage of higher coverage level marginal effects significant | 17 | 15 | 26 | 6 | 14 |
| Average value ($/acre) | 6.33 | 15.54 | 8.85 | 4.81 | 2.64 |
| Maximum value ($/acre) | 13.86 | 71.66 | 18.41 | 6.36 | 5.86 |
| Minimum value ($/acre) | 1.45 | 3.82 | 2.09 | 1.87 | 1.50 |
| Pre ARPA average value ($/acre) | 7.86 | 20.90 | 13.23 | 5.81 | 0.67 |
| Post ARPA average value ($/acre) | 4.96 | 4.83 | 2.28 | 4.14 | 2.21 |
To gauge the performance of coverage level rate relativities, we compared average pre- and post-ARPA significant positive marginal effects (last two rows of table 2). These marginal effects were lower post-ARPA in four of the five regions and suggest that coverage level rate relativities are generally working as intended.
Producer selection of the optional unit type provided evidence of opportunistic behavior in three states (see table 3). The largest percentage of significant positive optional unit marginal effects was 17% in Oklahoma, but the value of the marginal effect was similar in all three states, ranging between $1–2. Our results lend modest support to Knight et. al. (2010), who found that unit aggregation changes the relationship between risks (i.e., expected indemnity) and premiums.
| Significant Positive Marginal Effects (5% level) | Region | ||||
|---|---|---|---|---|---|
| Iowa | Nebraska | Oklahoma | Montana | Washington | |
| Number significant | 0 | 0 | 1 | 1 | 1 |
| Percentage of optional unit marginal effects significant | 0 | 0 | 17 | 6 | 13 |
| Value ($/acre) | 0.00 | 0.00 | 2.04 | 2.12 | 1.40 |
There was no evidence of opportunistic behavior in the selection of revenue insurance in any region.
Evidence of opportunistic behavior in the use of T-yields, however, is reported in table 4. Evidence was found in all five regions, and in all five regions the evidence was greater than would be expected from a random, normally distributed sample. Oklahoma had the largest percentage of significant positive T-yield marginal effects at 19%. Only coverage level in Oklahoma had a larger percentage of violations than did T-yield. The average and maximum values of these marginal effects were highest in Montana, at $7 and $17 per acre, respectively. The highest average and maximum values of these marginal effects were lower than for the selection of higher coverage level.
| Significant Positive Marginal Effects (5% level) | Region | ||||
|---|---|---|---|---|---|
| Iowa | Nebraska | Oklahoma | Montana | Washington | |
| Number | 3 | 4 | 6 | 7 | 4 |
| Percentage of T-yield marginal effects significant | 7 | 7 | 19 | 8 | 9 |
| Average value ($/acre) | 2.37 | 2.70 | 4.29 | 7.48 | 5.41 |
| Maximum value ($/acre) | 4.86 | 6.73 | 7.76 | 17.33 | 8.85 |
| Minimum value ($/acre) | 0.92 | 1.32 | 0.75 | 1.90 | 3.21 |
As reported in table 5, there was evidence in only one region of significant violation of the joint hypothesis of a neutral insurance market with the subsidy implemented consistent with policy in each period. During the pre-ARPA period of 1996–1998, average indemnities were larger than premiums plus subsidies by $7 per acre in Oklahoma. During the ADHOC period of 1999–2000 the difference was $4 per acre in Montana, and during the ARPA period of 2001–2009 the difference was $8 per acre in Oklahoma. Only in Montana was there any evidence that the ADHOC period had a significant positive effect on producer returns after accounting for the change in subsidy implementation, while only in Oklahoma was there any evidence that ARPA had a similar effect.
| Significant Positive Marginal Effects (5% level) | Region | ||||
|---|---|---|---|---|---|
| Iowa | Nebraska | Oklahoma | Montana | Washington | |
| Constant ($/acre) | 0.00 | 0.00 | 7.04 | 0.00 | 0.00 |
| Positive effect of ADHOC subsidy increases ($/acre) | 0.00 | 0.00 | 0.00 | 4.00 | 0.00 |
| Positive effect of ARPA ($/acre) | 0.00 | 0.00 | 8.35 | 0.00 | 0.00 |
The effects of heterogeneity of land resources on evidence of inconsistency with the joint hypothesis of a neutral insurance market with the subsidy implemented consistent with policy are summarized in table 6. We have classified our five regions into two land resource categories—the relatively more homogeneous regions of Iowa and Nebraska and the more heterogeneous regions of Oklahoma, Montana, and Washington. For this comparison we report the percentage and average magnitudes of contract decision and policy marginal effects that are positive and significant. Evidence that regions with more heterogeneous growing conditions show more evidence of inconsistency with the joint hypothesis would be supported by larger percentages and/or larger absolute magnitudes of these marginal effects. Such evidence was observed using both criteria for optional unit type, T-yields, and for the ADHOC and ARPA policy changes. There was no difference between these groups for the revenue insurance decision, and there was less evidence for higher coverage levels. Consequently, we conclude that there is evidence of inconsistency with the joint hypothesis for regions with more heterogeneous growing conditions than for more homogeneous regions.
| Crop Insurance Contract | Significant Marginal Effects (5% level) |
Iowa and Nebraska | Oklahoma, Montana, and Washington |
|---|---|---|---|
| Higher coverage level | Average positive and significant ($/acre) | 10.93 | 0.92 |
| Percentage positive and significant | 16 | 15 | |
| Optional unit type | Average positive and significant ($/acre) | 0.00 | 1.85 |
| Percentage positive and significant | 0 | 12 | |
| Revenue insurance | Average positive and significant ($/acre) | 0.00 | 0.00 |
| Percentage positive and significant | 0 | 0 | |
| Use of T-yields | Average positive and significant ($/acre) | 2.53 | 5.73 |
| Average positive and significant ($/acre) | 7 | 12 | |
| Policy with higher subsidies | ADHOC, average positive and significant relative to pre-ARPA ($/acre) | 0.00 | 4.00 |
| ARPA, average positive and significant relative to pre-ARPA ($/acre) | 0.00 | 8.39 |
In addition to examining p-values for one-sided tests of individual marginal effects, we conducted two sets of joint hypothesis tests for opportunistic behavior. In the first, we tested the hypothesis that all the relevant marginal effects were jointly zero, that is, that insurance was neutral with respect to all the relevant characteristics. Unfortunately, there is no way to conduct a one-sided joint hypothesis test. Hence, significant negative marginal effects could also result in rejection of the hypothesis. In the second test, we removed all of the relevant marginal effects that were individually significantly negative and ran the joint hypothesis test on the remaining marginal effect estimates. This latter test is clearly only an approximation of a one-sided test since it could also be rejected by the cumulative effect of a large number of individually non-significant negative marginal effects.
The statistics for both sets of joint hypothesis tests are reported in table 7.27 Both sets of tests yield the same test conclusions for higher coverage level and T-yields. For the first test, except for the selection of optional units in Nebraska, all test statistics were significant at the 5% level. For the second test, all test statistics were significant except for optional units in Iowa, Nebraska, and Oklahoma. Thus, both sets of tests provide considerable support for rejection of the joint null hypothesis that producers exhibited no opportunistic behavior in a neutral insurance market with the subsidy implemented consistent with policy.
| Contract Decision | Region | ||||
|---|---|---|---|---|---|
| Iowa | Nebraska | Oklahoma | Montana | Washington | |
| Considering all marginal effects: | |||||
| Higher coverage level | 3.95* (46, 17038) | 6.14* (59, 5249) | 34.26* (23, 11551) | 10.06* (86, 5176) | 6.06* (44, 8650) |
| Optional unit type | 18.38* (7, 17038) | 0.89 (9, 5249) | 2.29* (6, 11551) | 5.06* (16, 5176) | 2.04* (8, 8650) |
| T-yields | 2.56* (41, 17038) | 2.41* (58, 5249) | 13.47* (29, 11551) | 21.84* (89, 5176) | 5.55* (47, 8650) |
| Excluding significantly negative marginal effects: | |||||
| Higher coverage level | 3.93* (41, 17038) | 5.24* (51, 5249) | 36.23* (21, 11551) | 7.95* (76, 5176) | 7.32* (38, 8650) |
| Optional unit type | 2.26 (2, 17038) | 0.39 (8, 5249) | 1.14 (5, 11551) | 2.67* (12, 5176) | 4.82* (2, 8650) |
| T-yields | 1.63* (28, 17038) | 1.66* (46, 5249) | 14.39* (22, 11551) | 4.73* (66, 5176) | 5.40* (43, 8650) |
- Note: Degrees of freedom are shown in parentheses. Single asterisk (*) represents significance at the 5% level.
It is unclear what effect our short data period might have on the likelihood of significant marginal effects and their magnitudes for coverage level, optional unit, or T-yield contract selection. If observation of an impact were an artifact of the data period used in this analysis, it would likely result in an order ranking with Iowa at one extreme and Washington or Oklahoma at the other, and with Washington, Montana, and Oklahoma on one side of the ranking and Iowa and Nebraska on the other. Such a ranking is evident in the optional unit and T-yield results tables but not in the coverage level table, nor in revenue insurance contract selection. Consequently, the findings relevant to the question of opportunistic behavior cannot be adequately explained by the uniqueness of the data period.
These findings suggest that the potential exists for producers in each region to profit by selecting higher coverage levels and/or by advantageous use of T-yields. Results also suggest that producers in a majority of regions might profit by strategic selection of optional unit types. These results, based on considerably more detailed unit-level data than earlier work, support the findings of opportunistic behavior in crop insurance choice noted by Roberts, Key, and O'Donoghue (2006), Makki and Somwaru (2001), Just, Calvin, and Quiggin (1999), Smith and Goodwin (1996), and Skees and Reed (1986). However, we found no evidence that producers profited by strategic selection of revenue insurance in any of the five regions over the data period.
Conclusions
We have investigated whether characteristics of crop insurance contracts create the potential for farmers to earn “excess profits” from crop insurance through the strategic use of asymmetric information. We take as given the government's decision to subsidize the insurance, and we assume the government has no purpose other than to induce greater participation—that is, government has no intention to (inefficiently) reallocate resources. We additionally assume a goal of least cost implementation. Under these assumptions our analysis is an implicit and indirect test of governmental competence in at least one arena: whether governmental agencies design an insurance program that creates no additional resource inefficiencies except for those that stem from the basic subsidy. Hence, our findings contribute to the debate about governmental competence as well as offer specific lessons to help crop insurance managers and policy makers “tune” the programs to provide the desired benefits at lower costs to the government.
We examined whether evidence of opportunistic producer behavior existed in unit-level crop insurance contract data for major crops in five different regions during 1996–2009 from the use of buy-up coverage, revenue insurance, optional units, and transitional yields (T-yields). Here, “opportunistic” and “opportunism” are strictly technical terms describing strategic behavior under asymmetric information (adverse or anti-selection and moral hazard). Our method is based solely on real-world behavior and empirical outcomes.
Reducing producer opportunism would create a more cost-efficient risk management program that would limit the ability of producers to extract net profits from participation beyond the intentional subsidy provided to induce higher rates of participation. In three of the four decision categories we found evidence of significant producer opportunism. The exception was the decision to purchase revenue insurance. Relative to average indemnities, the magnitudes were often quite large.
Opportunism was judged by assessing subsidy-adjusted net profits since actuarially neutral insurance with no asymmetric information should produce zero profits beyond the intentional subsidy used to induce participation. Given an efficiency goal, our findings suggest that an increase in rates for higher coverage levels and a restructuring of the T-yield system is warranted in most regions to decrease the effect of producer opportunism. Less evidence was found to support generally increased rates when the optional unit type is selected. Altered rates should be region-specific. Further investigation into the performance of rate relativity measures in different regions may be warranted.
In general, our findings provide support for the notion that the crop insurance program induces some inefficient allocation of resources that benefit producers who select certain crop insurance contract characteristics. However, some caution is necessary when interpreting the results. It is possible that some of the evidence of producer opportunism could be an artifact of the specific data period analyzed or could arise from differences in producer ability. However, we have minimized these issues as far as the data allow. We have checked our data against a longer history, and we have included a producer fixed effects variable. Still, if, for example, the ability of producers is inversely correlated with the use of T-yields, our estimates of producer opportunism in using T-yields would be biased downward. It is also possible that units that receive frequent indemnity payments are receiving larger expected returns from crop insurance than units that seldom receive an indemnity. If this is true, then increased premium amounts should focus on units with frequent indemnities.
Despite such caveats, our results provide three important implications relevant to policy makers. First, we have documented that optional units, buy-up coverage, and the use of T-yields can potentially increase the expected income of producers in excess of the deliberate subsidy. Second, our evidence suggests that producer opportunism exists in all five regions and that it is positively correlated with the heterogeneity of land resources. Third, information from this study provides the FCIC evidence that crop insurance contracts could be redesigned to reduce opportunistic possibilities and suggests some places to start.
Finally, we did not find extensive deviations from “neutrality”. Hence, the results do not suggest large levels of design and/or administration flaws in the system. Hypotheses about government inefficiency are usually informed more by ideology than by evidence. Our results provide some empirical evidence of modest government inefficiency, supporting neither perfect government nor incompetent government.
Acknowledgements
The authors express appreciation to the editor Spiro Stefanou, two anonymous reviewers, and to Lia Nogueira, Joshua Berning, and Adrienne Ohler for their helpful comments on earlier drafts of this paper. This project was supported by the Washington Agricultural Research Center and by the USDA Cooperative State Research, Education and Extension Service, Hatch Grant WPN000275. The crop insurance data was obtained from the Risk Management Agency.




