Influences of Experts' Personal Experiences in Fuzzy Logic Modeling of Atlantic Salmon Habitat
Abstract
The knowledge of scientific experts, which is regularly used in modeling, is acquired by training, education, and practical experiences that modify the experts' perceptions. Using a case study dealing with fish habitat modeling, we investigated the possible influences and potential biases imparted by some of these personal experiences. Thirty salmon experts with different backgrounds and nationalities defined fuzzy sets and fuzzy rules in a fuzzy habitat model of three Atlantic Salmon Salmo salar life stages. Weighted usable area (WUA) curves were calculated for each expert by coupling the fuzzy model with a hydraulic model applied to the Romaine River (Quebec, Canada). Experts were then split into subgroups, and three possible experiential biases were tested: the experts' main geographic region of expertise (Europe versus North America), their primary source of knowledge (fieldwork, scientific literature, or both), and their employment sector (public or private). A confidence interval was calculated around the median WUA curve for each subgroup by bootstrap resampling. A divergence in the confidence intervals (i.e., no overlap) indicated a significant influence of the tested experience. For all three considered life stages, we observed no significant impact of employment sector or knowledge source on modeled WUA. However, the experts' geographic region of expertise had a significant influence on the output of the spawning adult habitat model. Consequently, the use of local expert knowledge in modeling is recommended.
Received June 16, 2014; accepted December 1, 2014
Scientific expert knowledge in environmental management (e.g., from researchers, consultants, or field technicians) can be considered a huge and available database that is constantly improved by daily experience in the field and by familiarity with the published literature. Despite the difficulty in attaining tacit and implicit knowledge (i.e., inarticulate and hardly articulate knowledge; Nickols 2000; Raymond et al. 2010), solicitation of expert opinion is a valuable complement to experimental data because of its ability to synthesize and incorporate historical variability of environmental phenomena and to merge published, unpublished, and disparate sources of knowledge and experience (Fazey et al. 2006). Such knowledge is often used when a quick decision is required, when information must be extracted from complex environmental systems, or when formal theories are poorly developed (Cheung et al. 2005; Krueger et al. 2012).
In this work, an “expert” is defined as a person that has relevant and extended knowledge of the considered topic, with that knowledge having been acquired by training, education, and practical experience (Fazey et al. 2006; Krueger et al. 2012), all of which can influence personal, judgmental, analytical, and procedural behavior (Greenwell 1988, cited by Cornelissen et al. 2003). Consequently, each personal experience modifies the expert's perception, which is the basis for expert knowledge-based modeling and also a potential source of biases. Three types of biases inherent to the environmental sciences are known to have influences (Ford and Sterman 1997; Huesemann 2002): personal (e.g., convictions and ideologies, profit, or other personal motivations), institutional (e.g., direct or indirect pressure from the funding agency or employer), and sociocultural (e.g., western societies value the study of the environment for the benefit and profit of mankind). Biases and personal experiences explain some of the divergent opinions between experts in expert-based modeling, and these disagreements may provide valuable information about the studied process (Aspinall 2010; Knol et al. 2010). New approaches and methods to elicit and aggregate opinions with minimum bias are regularly proposed (Page et al. 2012; Vrana et al. 2012).
In ecology, several statistical models are based on expert knowledge (Pearce et al. 2001; Seoane et al. 2005), specifically Bayesian models (James et al. 2010; Kuhnert et al. 2010) and fuzzy logic systems (Zadeh 1965; Mamdani 1977; K. Jorde, M. Schneider, A. Peter, and F. Zoellner [paper presented at the Third International Symposium on Environmental Hydraulics, 2001]). Fuzzy logic uses linguistic variables, imitating the human expression and way of thinking, and allows a single data value to belong simultaneously to several categories with varying degrees of membership (Zadeh 1965). Such flexibility allows the fuzzy logic approach to deal with uncertainty and vagueness. This ability makes fuzzy logic particularly suitable in environmental sciences, where data can be scarce or plentiful (e.g., high-resolution spatial data or a long time series); can come from objective (e.g., measurements) and subjective (assessments or expert knowledge) information that is imprecise due to technical or budgetary constraints; or can be incomplete or inaccurate (Salski 1992, 1998). In the environmental sciences, fuzzy logic has been used in impact evaluation (Enea and Salemi 2001; Kampichler et al. 2010), population ecology (Daunicht et al. 1996; Bock and Salski 1998; Kampichler et al. 2000), hydrology and hydraulics (Bárdossy 1996; Legleiter and Goodchild 2005), and ecosystem modeling (Uhrmacher et al. 1997). Fuzzy models based on knowledge from multiple experts can be used to evaluate the sensitivity to one or more variables with the help of several experts who generally share the same goals and similar points of view modulated by their personal experiences (Ahmadi-Nedushan et al. 2008). Differences in points of view and perspective are known to exist in homogeneous groups of experts (Weisberg et al. 2008; Mocq et al. 2013), but can a group be considered homogeneous when experts have different backgrounds and experiences? Can the effects of these differences significantly influence model outcomes?
In the present study, we addressed the influence of some sources of bias and their consequences in expert-based fuzzy models. Fuzzy habitat models were built to evaluate the weighted usable area (WUA) for habitats of three Atlantic Salmon Salmo salar life stages (i.e., young-of-the-year [age-0] rearing habitat; parr rearing habitat; and adult spawning habitat, where the redds are built) in the Romaine River, Quebec (Canada), using the knowledge of several experts with different backgrounds, positions, and nationalities. The influence of three possible biases in multiple-expert fuzzy logic models were evaluated: the geographic region of experience (experts working in North America versus those working in Europe), the difference between practical and theoretical learning (reflected by the source of the experts' knowledge; i.e., mostly from the scientific literature, mostly from field experience, or some combination of these), and the sector of employment (private or public sector). Our objective was to highlight, within a pool of experts, a significant influence of a shared experience in the results of an expert-based model and then to emphasize the necessary precautions that should be taken when building a model with multiple experts who present potential personal biases.
METHODS
Fuzzy modeling and expert knowledge data collection.
A comprehensive presentation of the fuzzy method, fuzzy sets and rules, and model building is provided by Mocq et al. (2013).
To build the fuzzy models of Atlantic Salmon habitat, we chose depth, velocity, and mean substrate diameter—three of the most important variables defining salmon distribution and abundance (Heggenes 1990; Bardonnet and Baglinière 2000; Armstrong et al. 2003)—as input variables. These three variables form the physical template that determines whether spawning and rearing will occur at a given location in the river. To quantify the habitat potential of various combinations of the three variables, a habitat suitability index (HSI) was used as an output variable. The HSI is an index of habitat quality, with values ranging from 0 (poor habitat) to 1 (excellent habitat). For each life stage, each variable was divided into three categories (e.g., low, medium, and high substrate size, corresponding to fine, medium, and coarse substrate), and membership in each category was defined by combinations of piecewise linear (trapezoidal or triangular) functions that constituted the fuzzy sets. Described by four boundary values, a1, a2, a3, and a4 (Figure 1), the sets were easily defined by experts (rather than Gaussian functions) as membership functions in fuzzy logic applications (Kampichler et al. 2000; Mouton et al. 2008; Fukuda 2009). These boundaries have a central importance in the fuzzy logic model, as they determine the range of overlap between membership functions, consequently determining the frequency with which the different rules are used.
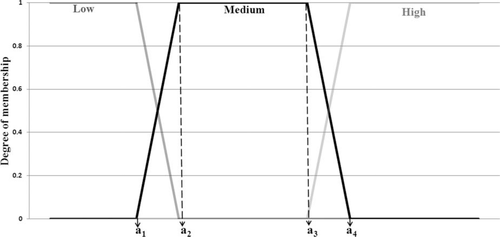
Example of fuzzy sets, with three linear membership functions (trapezoidal) describing the categories “low,” “medium,” and “high” and the four boundary values (a1, a2, a3, and a4) used by the experts to define the membership functions, as adapted from Adriaenssens et al. (2006).
To determine a consequence from the input variables, all combinations of habitat categories were considered to define fuzzy rules. These “IF…, THEN…” rules determine one HSI consequential category for each possible combination of categorical habitat variables. Premises (i.e., the first part of the rule, considering the environmental parameters and their categories) were linked with the operator “AND.” For k different habitat variables, the ith rule was defined with Ai,k as premises and Bi as the consequence (i.e., the HSI fuzzy value): “IF Ai,1 AND Ai,2 AND… AND Ai,k, THEN Bi.” For example, with k = 2 physical variables, a possible rule for Atlantic Salmon habitat could be “IF velocity is high AND IF substrate diameter is medium, THEN HSI is high.”
We elicited information from 30 experts: 9 experts from Europe (2 from the UK, 3 from France, and 4 from Norway) and 21 experts from Canada (16 from Quebec and 5 from New Brunswick). Thirteen of the experts were academics, 10 were environmental consultants, and 7 were government scientists. Twenty-two experts were surveyed alone or in small groups, while data from five experts were collected by mail surveys. Finally, three experts who participated in the study of Ahmadi-Nedushan et al. (2008) were unavailable for the present work. Ahmadi-Nedushan et al. (2008) developed the first methodology and models on which the present paper is based. Since the same expert knowledge collection method was used in the present study, the sets from those three experts were reused for parr rearing habitat and adult spawning habitat. Initial discussion with the experts were focused on requesting that they provide information based on all their experiences rather than focusing on a specific case study (i.e., the Romaine River); furthermore, we expected that the biases associated with their personal field and theoretical knowledge would be a source of uncertainty that would need to be quantified. Each expert had to define the fuzzy sets and rules alone; this was necessary to avoid any biasing of the marginal opinions toward that of the majority (Knol et al. 2010).
Because of changes in habitat preferences among Atlantic Salmon life stages, the experts had to define the fuzzy sets and fuzzy rules for three life stages: age 0, parr, and spawning adults. For this purpose, each expert had to complete an individual worksheet, which was kept confidential to prevent opinion convergence. For the considered life stage and the considered physical variable and based on the expert's knowledge, the expert had to (1) choose between the triangular and trapezoidal membership functions to define fuzzy sets for every category of the variable and then (2) determine the values of a1, a2, a3, and a4 (Figure 1) and the overlap width between two consecutive categories (see above). The expert determined his or her own preference curves for depth, substrate, and velocity according to his or her knowledge and appraisal without reference to a specific river—instead covering every condition in rivers the expert had encountered, thereby making our model as exportable as possible.
Subsequently, experts had to determine the consequences of the 27 fuzzy rules—that is, the suitability of habitat (low, medium, or high HSI)—for every possible combination of the physical variable (depth, velocity, and substrate size) categories. For each expert, three models were built to represent the three life stages of Atlantic Salmon: age-0 rearing habitat, parr rearing habitat, and adult spawning habitat.
Finally, experts had to answer three questions about the influence of their personal experiences: the region where they mostly worked (North America or Europe), the sector of employment (public or private), and the origin of their knowledge about Atlantic Salmon (primarily fieldwork experience; primarily the scientific literature; or a balanced combination of the two).
Data processing, inference, and defuzzification.
The integration and treatment of the fuzzy sets and rules formerly defined by the experts were performed with a fuzzy logic toolbox in Matlab (MathWorks 2006). In the application of fuzzy rules, habitat information in the form of fuzzy sets is combined. There are many ways to combine information from the fuzzy sets. We used the Mamdani inference method (Shepard 2005), which involves taking the minimum degree of membership reached by the categories of the variables involved in the rule during the implication phase (i.e., the determination of a rule conclusion). Thus, for a given habitat cell, if the degree of membership is 0.7 in the “small” category of velocity, 0.4 in the “medium” category of substrate, and 0.6 in the “large” category of depth, the application of a fuzzy rule combining this information would produce a degree of membership of 0.4 (the smallest input value) in the resulting fuzzy set describing the “poor” habitat category. This minimum degree puts an upper limit to the conclusion function (i.e., HSI). The fuzzy sets obtained for each rule are then aggregated by taking the maximum of the membership functions of the resulting HSI (Mamdani 1977).
At this stage, the conclusion is represented as a fuzzy set, but it can be further transformed into a final Boolean (“crisp”) number to be used in subsequent WUA calculations by the process of defuzzification. Defuzzification simply means that the final HSI fuzzy set is converted to a single HSI value. Among the existing methods, the center of gravity method was selected for application to the resulting fuzzy set output to determine the corresponding value of HSI (Jorde, Schneider, Peter, and Zoellner, unpublished). Although part of the fuzzy information is lost during this process, it is a necessary step for the HSI to be usable for calculating WUA with the hydraulic model outputs (described below), which cannot be done using fuzzy sets. See Mocq et al. (2013) for a graphic explanation of the process.
A case study: model of Atlantic Salmon habitat on the Romaine River.
The Romaine River, located in eastern Quebec, flows southward for 496 km and empties into the St. Lawrence River (Figure 2). It drains a catchment of 14,350 km2 and has a mean annual flow of 340 m3/s. Atlantic Salmon habitat is located 52 km above the confluence with the St. Lawrence River and is delimited by an impassable waterfall (Belles-Isles et al. 2004). An environmental consulting firm (Genivar) conducted surveys for spawning habitat and juvenile rearing habitat between 2001 and 2004 in the lower reaches of the river (Ahmadi-Nedushan et al. 2008); physical variables (velocity, depth, and substrate) quantifying spawning habitat and juvenile rearing habitat were measured in four reaches.
The Romaine River and its catchment area in eastern Quebec, Canada.
A hydraulic model, the Hydrologic Engineering Center's (HEC) River Analysis System (RAS; USACE 2002), was used for simulating depths and velocities in four reaches (20–40 km) in the lower part of the river as a function of discharge, which was varied between 50 and 1,200 m3/s in increments of 50 m3/s (i.e., 24 simulations). The HEC-RAS provides steady-state, one-dimensional simulations for gradually varied flows (Annear et al. 2004). A quasi-two-dimensional approximation was obtained by dividing transects in cells and distributing the flow along the subsections according to the cell areas while respecting the conservation of energy. Field measurements of velocities and depths were sampled to calibrate and validate the model (Hydro-Québec 2005; Ahmadi-Nedushan et al. 2008). Eight categories of substrate (i.e., silt, sand, small gravel, coarse gravel, cobble, rock, boulder, and bedrock) were used to evaluate the mean substrate diameter according to the percentage of coverage.
Fuzzy HSIs were calculated and defuzzified for each Atlantic Salmon life stage, each flow increment, and each expert. For each cell determined in the hydraulic simulations, the cell surface was weighted by the defuzzified HSI to provide a WUA for each expert and each flow increment. The WUA corresponds to a surface of habitat that is usable by the fish. Since cell areas are weighted by the associated HSI value, the WUA value for a large number of cell surfaces of poor habitat quality can be equivalent to the WUA value for a small number of cell surfaces of excellent quality. The WUA values were summed at the reach scale to obtain a total WUA. A mean value (µWUA) can be found by calculating the mean of the WUAs for the 1,200 discharge values (incremented by 1 m3/s).
Testing for the influence of expert experience.
Geographic region, employment sector, and knowledge source were hypothesized to influence this knowledge-based model. To evaluate these influences, experts were grouped into subcategories based on (1) whether they worked in North America or Europe, (2) the source of their knowledge (fieldwork, literature, or some combination), and (3) whether they were employed in the public sector (governmental offices or universities) or private sector (consulting firm).
For each subgroup, a standardized median WUA curve was constructed by interpolating between individual WUA values for each flow increment using a cubic spline, thus providing WUA estimates for any discharge value. The confidence interval (CI) around this curve was subsequently calculated by using a bootstrap resampling approach (Ayllón et al. 2012; Mocq et al. 2013). For each subgroup of experts, a pseudosample (same size as the initial sample) was created by random draw with replacement among the expert pool, from which a median value was calculated. The process was repeated 10,000 times. Values were sorted, and the 2.5th and 97.5th percentiles were calculated. A constant overlap of two subgroups' CIs implied that there was no statistically significant difference in the subgroups' median curves. Conversely, if the CIs of two subgroups did not overlap, the subgroups were inferred to have different perceptions of suitable habitat for a given life stage.
The frequencies of application of all 27 rules were calculated by summing all frequencies of use for every expert during the simulations and dividing that sum by the total number of rule applications. Thus, it was possible to determine the rules that were most frequently used and those that were less frequently used, consequently revealing the importance of a disagreement between experts for a given rule. Comparison of a rule's consensus (defined as the most frequently selected HSI category as a consequence for one rule) could help to detect different perceptions of suitable habitat, potentially biased by personal experiences. If a significant influence as explained above was observed, the consensuses of each subgroup were compared to highlight the difference.
RESULTS
Influence of Geographic Region
According to the broad study area where the experts mostly worked, 21 experts belonged to the North American group and 9 experts belonged to the European group. Regardless of the geographic group or the Atlantic Salmon life stage considered, the curves of median WUA followed a generally similar shape (Figure 3): a sharp initial increase followed by a leveling off or a decrease after reaching the plateau. The age-0 curve (Figure 3a) from the North American experts (mean of medians value µWUA ± SD = 0.33 ± 0.056, maximum = 0.39 at a discharge Q of 321 m3/s) was slightly lower than the curve from the European experts (µWUA= 0.46 ± 0.078, maximum = 0.52 at a Q of 339 m3/s). The CI for North American experts was narrower than that derived for European experts (mean difference between upper and lower confidence limits [CLs] = 0.16 and 0.21, respectively), but the two CIs overlapped over the entire discharge range.

Splines of standardized median weighted usable area (WUA) curves and confidence intervals (CIs) obtained by bootstrap, testing the influence of experts' geographic region of expertise (North America [AM] or Europe [EU]) on descriptions of habitat use by different life stages of Atlantic Salmon in the Romaine River: (a) age 0, (b) parr, and (c) spawning adults.
For the parr rearing habitat model (Figure 3b), the curve from North American experts (µWUA = 0.41 ± 0.096, maximum = 0.48 at a Q of 913 m3/s) was higher than the curve derived from the European experts (µWUA = 0.38 ± 0.096, maximum = 0.46 at a Q of 800 m3/s). Both CIs overlapped until the maximum possible discharge of 1,200 m3/s was reached; the large CI associated with the WUA curve for the European experts included almost the entire CI associated with the curve for the North American experts (mean difference between upper and lower CLs = 0.33 and 0.18, respectively).
The spawning habitat model was the only case that showed a significant difference between the two CIs (Figure 3c). The European experts' WUA curve (µWUA = 0.49 ± 0.11, maximum = 0.55 at a Q of 625 m3/s) was higher than the curve derived from North American experts (µWUA = 0.39 ± 0.081, maximum = 0.44 at a Q of 565 m3/s). The respective CIs (mean difference between upper and lower CLs = 0.16 and 0.10, respectively) overlapped for discharge values up to 567 m3/s and deviated thereafter, indicating a significant influence of the experts' geographic region.
During the definition of fuzzy rules, experts had to define the HSI resulting from the association of the different physical variable categories. The consensus (i.e., the most selected consequence for one rule) was determined for each subgroup and compared. Most of the rule consequences were similar between the two geographic groups, but for a minority of rules (8 rules) there were differences in which European experts tended to choose higher categories of HSI than North American experts (Table 1). Among the eight rules, five rules included the substrate category “high” (i.e., coarse substrate) for adult spawning habitat.
| Substrate size category | Velocity category | Depth category | Most frequent HSI consequence for: | |
|---|---|---|---|---|
| North American experts | European experts | |||
| M | L | H | L | M |
| M | M | L | M | M/L |
| M | M | H | M | H |
| H | L | M | L | M/L |
| H | M | H | L | M |
| H | H | L | L | L/M |
| H | H | M | L | M |
| H | H | H | L | M |
Influence of Knowledge Source
Eleven experts declared that they acquired their Atlantic Salmon knowledge mostly from fieldwork, and 14 experts specified that they acquired it almost equally from fieldwork and the scientific literature. The “literature only” group comprised only two experts and was excluded from the analysis.
For the age-0 model (Figure 4a), the median WUA curves diverged slightly before being superimposed as discharge increased (fieldwork group: µWUA = 0.35 ± 0.056, maximum = 0.43 at a Q of 311 m3/s; fieldwork + literature group: µWUA= 0.32 ± 0.062, maximum = 0.37 at a Q of 661 m3/s). The CI for the fieldwork + literature group was narrower than that for the fieldwork group (mean difference between upper and lower CLs = 0.18 and 0.25, respectively), and the CIs of the two groups were never fully separated. Thus, a significant influence of experts' knowledge source was not indicated for this model.
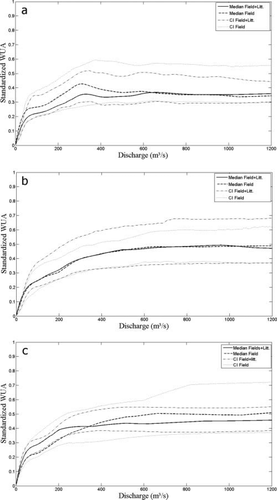
Splines of standardized median weighted usable area (WUA) curves and confidence intervals (CIs) obtained by bootstrap, testing the influence of experts' primary source of knowledge (fieldwork [field] or fieldwork + literature [field+lit]) on descriptions of habitat use by different life stages of Atlantic Salmon in the Romaine River: (a) age 0, (b) parr, and (c) spawning adults.
For the parr habitat model (Figure 4b), the two WUA curves were similar to each other (fieldwork group: µWUA = 0.42 ± 0.1, maximum = 0.49 at a Q of 1200 m3/s; fieldwork + literature group: µWUA = 0.42 ± 0.097, maximum = 0.49 at a Q of 800 m3/s). The CI for the fieldwork group was almost entirely enclosed within the larger CI from the fieldwork + literature group (mean difference between upper and lower CLs = 0.20 and 0.27, respectively) over the entire range of discharges. Again, no significant influence of knowledge source was apparent.
The median WUA curves associated with the two knowledge source categories were less similar for the adult spawning habitat model (Figure 4c) than for the two other life stages. The µWUA for the fieldwork group was 0.43 ± 0.11 (maximum = 0.51 at a Q of 1,200 m3/s), whereas the µWUA for the fieldwork + literature group was 0.41 ± 0.07 (maximum = 0.44 at a Q of 800 m3/s). The narrower CI for the fieldwork + literature group (mean difference between upper and lower CLs = 0.15) was completely included within the CI for the fieldwork group (mean difference = 0.27), thereby indicating that the source of experts' knowledge did not influence the spawning habitat model.
Influence of Public or Private Sector Employment
Among the 30 experts, 10 worked for the private sector and 20 had public sector positions. For the age-0 habitat model (Figure 5a), the median curves were similar to each other (private sector group: µWUA = 0.33 ± 0.05, maximum = 0.39 at a Q of 321 m3/s; public sector group: µWUA = 0.34 ± 0.06, maximum = 0.40 at a Q of 322 m3/s). The CIs were never fully separated; this result was attributable to the nearly identical median values and the large size of the CI from the private sector group (mean difference between upper and lower CLs = 0.35 and 0.20, respectively, for the private and public sector groups), likely a reflection of the small number of private experts (5 experts) used for this model.
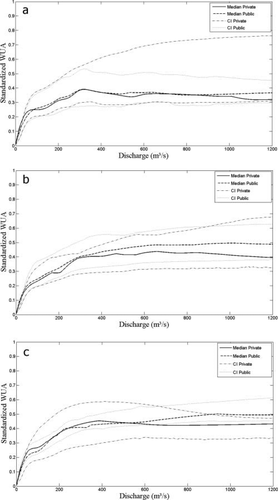
Splines of standardized median weighted usable area (WUA) curves and confidence intervals (CIs) obtained by bootstrap, testing the influence of experts' employment sector (private or public) on descriptions of habitat use by different life stages of Atlantic Salmon in the Romaine River: (a) age 0, (b) parr, and (c) spawning adults.
The median WUA curves from the parr model were less similar than those from the age-0 model, with the curve for the public sector group (µWUA = 0.424 ± 0.01, maximum = 0.5 at a Q of 1,004 m3/s) showing consistently higher WUA values than the curve for the private sector group (µWUA = 0.377 ± 0.08, maximum = 0.44 at a Q of 659 m3/s) over the entire discharge range (Figure 5b). The CIs were similar in size and shape (mean difference between upper and lower CLs = 0.21 and 0.23, respectively, for the public and private sector groups). No significant influence of employment sector was apparent for this model.
The median curves for adult spawning habitat were nearly superimposed several times and diverged slightly once discharge exceeded 530 m3/s (Figure 5c). The µWUA for the public sector group (µWUA = 0.423 ± 0.01, maximum = 0.5 at a Q of 942 m3/s) was higher than that of the private sector group (µWUA = 0.40 ± 0.07, maximum = 0.45 at a Q of 386 m3/s). The CIs were narrow (mean difference between upper and lower CLs = 0.12 and 0.21, respectively, for the public and private sector groups), and the two curves never became disjointed.
DISCUSSION
The number of experts involved in our project made it possible to study the influence of three possible experiential biases in a fuzzy-logic-based model applied to describe habitat use by three life stages of Atlantic Salmon. Our initial hypothesis was that the work environment and personal experiences would influence the experts' way of thinking and addressing the research problem (salmon habitat use) because of the differences in culture and/or perspectives related to research and management.
With respect to all three Atlantic Salmon life stages, we observed no significant effects for two of the three potential types of bias investigated (i.e., knowledge source and employment sector). The initial hypothesis was that the work environment can influence the expert due to differences in objectives and functioning. Ahmadi-Nedushan et al. (2008) built fuzzy models with four environmental consultants, one expert from the Quebec Ministry of Natural Resources, and one expert from a publicly owned hydroelectric company. The resulting six curves were practically superimposed, suggesting no effect of employment position on the expert's opinion. Our study seems to validate this finding. Despite our use of a much larger sample size of experts (6 versus 27 in the present study), the CIs of the curves from the private sector experts never diverged significantly from the CIs for the public sector experts.
The source of knowledge was another tested influence that could introduce bias in expert-based modeling, but our results showed very similar median curves and a large overlap between the CIs. However, for the two subgroups (fieldwork versus fieldwork + literature), all experts had some degree of field experience, which may be a confounding factor and could explain the similarity in results. It would be interesting to compare the knowledge acquired only by fieldwork with that acquired solely from the literature. Unfortunately, very few experts had strictly literature-based knowledge of Atlantic Salmon habitat preferences. Indeed, it can be argued that the majority of experts gained their expertise from some combination of theoretical and field knowledge.
No significant influences of geographic region were observed for the age-0 and parr habitat models, but when spawning habitat models were considered, the CIs for North American and European experts diverged significantly at discharge rates higher than 567 m3/s. Our results suggest a potential bias based on the geographic region of expertise, which could have an impact on policies and scientific reporting. Some hypotheses could explain this finding in our study. First, it could reflect the knowledge about Atlantic Salmon preferences from a specific geographic region. Indeed, Atlantic Salmon depth preferences for building redds were shown to differ among Scottish, Norwegian, and Canadian rivers (Armstrong et al. 2003). This local adaptation of the fish could modify the expert's perception and may have influenced the boundary values of the membership functions in the fuzzy sets or fuzzy rules in our experiment. In addition, the major divergences in expertise were for the most part associated with rules concerning coarse substrate (i.e., substrate size related with high discharge). North American experts thought that larger substrate sizes contributed to poor habitat quality, while the European experts considered larger substrate to represent better habitat quality (Table 1). An expert's knowledge took into consideration the whole range of environmental characteristics influencing Atlantic Salmon habitat in the rivers with which the expert was familiar; in this case, for rivers of similar size, some variables could be more important and influential in Europe (e.g., population density) than in Canada. Another explanation could be related to cultural differences in the appraisal of river size, paired with a possible divergent understanding of the reality represented by a word. According to their location, the Atlantic Salmon rivers considered by our experts may differ in size and discharge, from the short Breton coastal streams to the large Canadian rivers, thus modifying the expert's mental image of the river. Regarding the divergent understandings of a word's definition, for example, the word “river” could encompass streams with different sizes and discharges; this highlights the need to be cautious about the words used during interviews or in working documents, which could require a strict definition to avoid unwanted biases (Knol et al. 2010). In the model framework for a specific site, it could be wise to use only local scientific experts (e.g., Canadian expertise for Canadian rivers), especially in environmental modeling, where local adaptations of the considered organisms can exist. The selection of experts should be based upon specific knowledge or experience criteria (e.g., years of service, activity, knowledge reputation, etc.).
Some of the calculated CIs were particularly wide due to experts‘ extremely divergent WUA curves, but the number of involved experts in each subgroup helped to improve the reliability of results (Knol et al. 2010) and to limit the impact of the behavioral psychology aspects of the biases (Tversky and Kahneman 1974). This highlights the possible biases in models developed with few experts (e.g., Pearce et al. 2001; Seoane et al. 2005), which is usual in fuzzy logic applications where the experts are sometimes the authors with assistance from the scientific literature (Kampichler et al. 2000; Cheung et al. 2005; Adriaenssens et al. 2006). A description of the experts is generally missing, and little information about their position, experience, or knowledge origin is provided (Daunicht et al. 1996; Droesen 1996; Bock and Salski 1998). Information about the number of experts and their sectors of employment is given in some cases (Weisberg et al. 2008; Acosta et al. 2010; Page et al. 2012; Vrana et al. 2012), but the experts' geographic region of expertise is rarely specified (Cornelissen et al. 2003; Ahmadi-Nedushan et al. 2008). In this project, we tested three experiential biases among the many existing psychological and experiential biases of knowledge use in modeling that may have a significant influence. Model optimization (Mouton et al. 2008, 2009a) and involvement of a large number of experts (Knol et al. 2010) should improve model reliability.
Despite potential biases and uncertainties, expert knowledge is a valuable tool in environmental management, and the scientific literature still describes new approaches to make the use of this knowledge more reliable and precise. Although data-driven fuzzy models showed substantially better results than expert knowledge-based models (Mouton et al. 2009b), improvement of the method requires a good selection of experts, and the knowledge of experiences that may influence the experts' opinions is decisive. The results of the present work demonstrate that in a relatively homogeneous group of scientific experts working on a similar domain, expert opinions can be influenced significantly by personal experiences and backgrounds, such as the geographic region of expertise. According to our results, we recommend that for environmental models reserved for small-scale use, local experts should be selected whenever possible, and the selections should be based on objective criteria (e.g., experiences and reliability) to limit biases related to the choice of experts. However, careful selection of experts must balance the trade-off between the need to minimize uncertainty and the risk of imposing too much of a local bias in the model, as this bias may be further exacerbated by its propagation in the hydraulic model simulations, which are also tainted by uncertainty.
Much remains to be done in this field. The multiple-expert approach was used for Atlantic Salmon because there is a broad community of experts; the same approach should be attempted for other species. The need for postelicitation of experts is also recognized. It was not possible to reconvene all of the experts who were involved in the present study. Despite the potential risk of biasing some of the initial answers toward more consensual inputs, if the experts had been given the chance to compare their results, they might have been able to revisit and fine tune their inputs into the model.
ACKNOWLEDGMENTS
We wish to acknowledge every participating expert (and their respective organizations): K. Alfredsen, M. Belles-Isles, L. Belzile, N. Bergeron, M. Bérubé, A. Boivin, C. Breau, M. Buoro, F. Caron, M. Clément, D. Cuerrier, G. Dauphin, R. Dumont, C. Gauthier, N. Guérard, J. Heggenes, P. Johnston, A. Lapointe, F. Lesvesque, T. Linnansaari, N. Milner, D. Moore, M. Murdock, M. Noak, E. Prevost, B. Riley, M. Rodriguez, F. Sabourin, and S. J. Saltveit. We thank Genivar Consulting for hydraulic model outputs. This work was supported in part by the Natural Sciences and Engineering Research Council of Canada, Hydro-Québec, and the National Institute of Scientific Research. Additionally, we thank C. Gignac for his help in GIS data extraction and three anonymous reviewers for their valuable comments.




