Paternity success and the direction of sexual selection in a field population of a semelparous marsupial, Antechinus agilis
Abstract
Antechinus agilis is a small sexually size dimorphic marsupial with a brief annual mating period of 2–3 weeks. All males die after this period, and females give birth to up to 10 young. Mating is thought to be promiscuous, however, there is no field data to confirm this. Using microsatellites, we investigated paternity patterns over two seasons in a wild population. Male weight was significantly positively related to the number of females fertilized and with the number of offspring sired, in both years. Furthermore, selection gradients indicated selection for larger males. Both results suggest that size dimorphism in A. agilis can be explained by sexual selection for larger males. The proportion of offspring sired within litters, did not relate to male size. Therefore, larger males are more successful through higher mating access, not through their sperm outcompeting that of smaller males. As expected from their known ranging behaviour, the number of offspring within litters left unassigned to a father did not depend on the grid location of the mother. Female size did not differ between successful reproducing and unsuccessful females. However, females that weaned offspring had larger heads than females that did not wean offspring. Males did not ‘prefer’ mating with larger females, nor did assortative mating occur. From our results, the mating system of A. agilis is clearly promiscuous. Selection for larger males occurred in both years, even though in one year the operational sex ratio was highly female biased, suggesting that the potential reproductive rate is a better predictor of the direction of sexual selection in A. agilis.
Introduction
Sexual size dimorphism is common in vertebrate species. The three main hypotheses put forward to explain sexual dimorphism have as their main themes reproductive role division, intersexual food competition or sexual selection (Lande 1980; Hedrick & Temeles 1989). These mechanisms may operate simultaneously in the same species. Most studies focus on the sexual selection hypothesis, which proposes that sexual dimorphism arises from competition between males for access to females or from female preference for larger or more ornamented males (Darwin 1871; Ralls 1977; Clutton-Brock & Harvey 1978; Balmford & Read 1991; Andersson 1994). Males with particular traits may be more successful in siring offspring and, assuming these traits are heritable, their offspring are consequently more successful in the next generation. Several empirical studies confirm heritability of the fathers’ traits to their sons in a wide range of taxa (Hedrick 1988; Houde 1992; Horne & Ylonen 1998).
The intensity of sexual selection will strongly depend on the operational sex ratio (OSR; defined as the ratio of fertile females to sexually active males) during the mating season (Emlen & Oring 1977; Jann et al. 2000). If the sex ratio is strongly female biased, male–male competition will be reduced, and sexual selection will be less intense. The OSR is often difficult to determine in the field. An alternative measure that can be used to predict the direction of sexual selection is the potential reproductive rate (PRR). This is the offspring production per unit time for each sex, and takes into account the amount of time animals actually spent on mate searching and mating (‘time in’) and the amount of time spent on maintenance (‘time out’, Clutton-Brock & Parker 1992; Kvarnemo 1994; Kvarnemo & Ahnesjö 1996; Parker & Simmons 1996; Ahnesjöet al. 2001). If the difference in PRR between sexes is large, mating competition will be intense, and sexual selection can occur. The direction of sexual selection is also thought to depend on the cost of a single breeding event, sex differences in mortality patterns and mate quality (Kokko & Monaghan 2001).
In mammals, sexual size dimorphism is common and males are usually the larger sex (Ralls 1977). In most of these species, larger males have an advantage in gaining access to receptive females either through female choice or through dominance (Schwagmeyer & Brown 1983; Ryser 1992; McElligott et al. 2001). However, new molecular techniques have revealed that mating access does not necessarily reflect paternity success (Hughes 1998; Coltman et al. 1999). Therefore, behavioural observations alone are not sufficient to determine whether male size influences siring success. Especially in polyandrous mating systems, where sperm competition is prevalent, it is essential to determine paternity.
In the small carnivorous marsupial agile antechinus, Antechinus agilis, males (20–40 g) can be twice the size of females (16–23 g, Dickman 1998), and body mass varies considerably among males (Braithwaite 1979). Their mating system is thought to be lek promiscuity (Lazenby-Cohen & Cockburn 1988), however, there is no molecular evidence from field data to confirm this. The variation in male body mass cannot be explained by age differences, because all breeding males in any given season are from the same cohort, and are born within days of each other (Cockburn 1992). The males die after a synchronous two-week mating season that occurs once a year (usually in August), hence there is no paternal care (Braithwaite & Lee 1979). The potential for sperm competition is high because females mate several times with different males during the oestrus period, which can last up to 21 days, and store sperm in isthmic crypts in the oviduct (Selwood 1982; Selwood & McCallum 1987). Testis size in relation to body size is high (0.9%), again suggesting strong sperm competition (Rose et al. 1997; Taggart et al. 1998). Furthermore, females have up to 10 pouch young (Cockburn et al. 1983) that are usually sired by at least two males (Kraaijeveld-Smit et al. 2002a). The young stay attached to the mother's teats for up to 5 weeks. During late January, juveniles start to leave the nest, and most males leave their natal territory within two weeks, while females are philopatric (Cockburn et al. 1985). About 15% of females live to breed in a second season, but this proportion varies between populations and years (Lee & Cockburn 1985).
We examined whether size dimorphism in A. agilis can be explained by sexual selection for larger males. By genotyping all adults and pouch young caught in the population over two years using five microsatellite loci, we explored whether larger males sire a higher number of the offspring, possibly with a larger number of females, than smaller males. Furthermore, we determined whether larger males sire a larger proportion of the offspring within litters. Selection intensity differences between males and females and selection gradients at two different selection episodes for male and female body mass were calculated (Wade & Arnold 1980; Arnold & Wade 1984a,b). The considerable difference in the ratio of adult males to adult females between the two years of this study (46% males in 1999, 34% males in 2000, see Kraaijeveld-Smit et al. 2002a) provided us with the opportunity to investigate whether the OSR has an effect on paternity success and the intensity of selection.
We also compared the proportion of unassigned pouch young (young for which a father could not be determined) in litters from mothers located on the edge of the study site with litters from mothers located in the middle of the study area. Because Antechinus travel large distances to nest trees, presumably to mate (Lazenby-Cohen & Cockburn 1988, 1991), we expected no differences between these two groups.
In species where female survival during the lactation period is low, such as in Antechinus and Phascogale species (Lee & Cockburn 1985; Soderquist 1993), males may preferably mate with females that are more likely to breed successfully (‘high-quality females’). If males favoured high-quality females, these females may have young from more different fathers, and on average with heavier fathers, than low-quality females. In order to investigate male preferences we assessed whether female quality was related to any body parameters by comparing body parameters of females with differing breeding success. We also investigated whether females with higher body mass and condition had young from more and heavier fathers.
Materials and methods
Field methods
Antechinus agilis were trapped at least every two months over two years (1999 and 2000) in mountain ash, Eucalyptus regnans forest at Mt. Disappointment State Forest in Victoria, 70 km north of Melbourne, Australia. Each field trip consisted of four nights of trapping spread out over one week (twice for two consecutive nights). A night of trapping consisted of placing 196 Elliott small mammal live traps baited with oats, honey and peanut butter and spaced 20 m from each other on a 6-ha roughly square grid. Newly caught animals were individually marked with ear notches. Ear tissue (≈ 2 mm in diameter) from these notches was stored in 96% ethanol for subsequent DNA extractions. Body mass (g), head length (mm) and head–body length (mm) were recorded for each newly caught animal and for most recaptured animals. For males we also recorded scrotum width and scrotum length.
Females were classified as ‘second year’ if they weighed > 20 g and the pouch area and teats were clearly visible prior to the breeding season. Females weighing 20 g or less were classified as first-year females if their pouch area was furry and teats were barely visible at this time. As female growth is indeterminate, older females are heavier, and body mass is therefore a good indicator of female age (Cockburn & Johnson 1988). For a number of females the age was known as they were born in the study area and marked as pouch young. The body mass and pouch status of the animals of known age also provided us with evidence that the criteria we used to classify animals of unknown age were reliable. For all analyses of paternity or maternity in relation to body parameters, we used the last recorded measurements before the breeding seasons, as these increase in magnitude towards the breeding season (Kraaijeveld-Smit 2001).
To avoid interrupting the natural patterns of mating and paternity, trapping was not carried out during the two-week mating period. The breeding season of A. agilis in the study area is in August, so the number of animals known to be alive between late June and early August was used to determine the operational sex ratio. Tissue samples were collected from young between 18 and 23 October in both years when the young were 4–5 weeks old and still attached to the mothers’ teats. Pouch young size ranged from 9.5 to 15 mm crown to rump length between litters. One developing toe-bud (< 0.5 mm) was clipped per young and the toe tissue was stored in 96% ethanol for subsequent DNA extraction and analysis.
Genotyping methods
DNA was extracted from tissue samples using a ‘salting out’ method (Sunnucks & Hales 1996) and all animals were genotyped at five highly variable microsatellite loci (see Kraaijeveld-Smit et al. 2002b) to establish paternity. For a detailed description of the genotyping methods, heterozygosity levels and allele frequencies of the five microsatellites used in this study see Kraaijeveld-Smit et al. (2002a).
Paternity assignment
Because DNA samples from young were taken when they were still attached to the mother's teats, maternity was unambiguous. The computer package cervus (Marshall et al. 1998) was used to determine paternity, which allows for inclusion of the identity of the mother. Parameters required for paternity assignment and used in the simulation were set as follows: 1000 cycles, 27 (1999) or 33 (2000) candidate parents (number of males caught between June and early August), 0.7 as the proportion of fathers sampled, 0.99 as the proportion of loci typed, and 0.01 as the proportion of loci mistyped. In 1999 all males caught just before the breeding season (28 July to 6 August) were recaptures, whereas 17% of the males caught during this period in 2000 had not been trapped previously. Trapping on a grid can result in edge effects, where females with home ranges along the edge are likely to mate with males that have home ranges outside the trapping grid. Based on these two factors, we estimated that we had sampled 70% of all the candidate fathers.
Paternity was assigned under three different conditions: 80% confidence level, 95% confidence level (using cervus), and based on exclusion. Exclusion means that males that had any mismatches in microsatellite alleles with a pouch young were excluded from paternity. The exclusion power of the five microsatellite loci combined was 99.9% for both years.
Data analyses
Paternity. Measures of male breeding success (number of females fertilized, number of offspring sired and the proportion of offspring sired within litters) were investigated using general linear models (GLM) including body mass, head length, testis width × length and year as independent variables. A stepwise backward approach was used to simplify the models (P to enter or remove 0.1). Initially, we investigated whether correlations exist between male body mass and head length, testis width and testis length, pooling the data for the two years. All three measurements correlated significantly with body mass (Table 1), but a common correlation of ≈ 0.4 was not considered strong enough to cause multicollinearity problems in the GLM analysis. The proportion of females fertilized and the proportion of offspring sired was compared between years using contingency table tests.
| Mass | Head | Testis width | Testis length | |
|---|---|---|---|---|
| Mass | 0.018 | 0.011 | 0.014 | |
| Head | 0.419 | 1.000 | 1.000 | |
| Testis width | 0.439 | −0.02 | < 0.001 | |
| Testis length | 0.431 | 0.046 | 0.54 |
For the analysis on the number of offspring sired and the number of females fertilized, all males were included in the analyses. Only males that had sired offspring were used in the analysis on the proportion of offspring sired per litter.
Intensity of selection. Total selection intensities (I) were calculated for both sexes in each year following Wade & Arnold (1980). All animals present at the start of the breeding season were included. Total selection intensity I(m or f) was calculated by dividing the variance of the number of offspring by its squared mean. The balance in total selection intensity between males and females is Im/If. Wade & Arnold (1980) and Arnold & Wade (1984a,b) classify the number of mates as sexual selection, whereas the number of offspring (fertility success) is classified as natural selection. Because in our study species females mate with several males, sperm competition may play a role in fertility success, and may therefore by classified as sexual selection (Kraaijeveld-Smit et al. 2002b). To avoid ambiguous statements, we classify the two different selection episodes used in this study as follows: S1 = mating success (sexual selection 1, Is1) and S2 = fertility success (either natural or sexual selection 2). Is1/Im is the sexual selection 1 intensity as a proportion of the total selection intensity. For each episode we calculated the selection differential (Sk), selection intensity (ik) and univariate selection gradient (βk) for the natural logarithm of male body mass in each year (for calculations see Arnold & Wade 1984a,b). We were unable to include weaning success into the selection episodes, as juvenile males disperse within two weeks after they leave the nest and an accurate measure of the number of weaned offspring is therefore difficult to obtain.
Edge effects. Here we define ‘edge effect’ as the effect of living at the edge of the trapping grid on the proportion of a female's offspring sired by unknown males. Females were divided into two groups. One group contained females that were caught in the middle of the grid (never caught < 40 m from boundary), the other those that were caught on the edge of the grid. The proportion of unassigned offspring per litter was compared between years and between groups, using two-way anova.
Maternity. The relation between maternity and body size was only investigated in first-year females as sample sizes for second-year females were too small. First-year females were divided into two groups; those caught with pouch young, and therefore known to have bred, and those present at the start of the mating period but never caught with pouch young and not caught again at a later date. Because recapture rates throughout the season were generally high, we assumed that these later females had died without breeding successfully. We investigated whether larger females were more likely to breed, using logistic regression including year, body mass and head length as independent variables and breeding or nonbreeding as binary response variable. Subsequently, the females that were caught with pouch young were divided into two groups; those that successfully weaned offspring and those that did not wean offspring. Identical analyses were performed on these two groups of breeding first-year females.
We tested whether the number of sires per litter (dependent variable) was related to female size using a GLM, including year, body mass, head length and number of pouch young as independent variables. The number of pouch young (log transformed) was included as a continuous variable. In these analyses all unassigned offspring per female were assumed to be offspring from one unsampled male. Lastly, we calculated the average body mass of all males known to have fertilized a female and related that to her size using a GLM.
Means are given ± SE. Proportions were angularly transformed, and counts log-transformed to approach normality. All morphometric measurements approached a normal distribution, justifying the use of parametric tests. Power tests were performed in gpower Version 2.0 (Faul & Erdfelder 1992). t-Tests, anovas and GLMs were performed using systat (1999). Frequency distributions were tested using chi-square tests.
Results
Thirty adult males and 37 adult females were caught on the trapping grid during 1999 (early March to early August). In 2000, 56 adult males and 85 adult females were caught (late January to early August). In 1999, the proportion of males before the breeding season was 46.6% (ratio m/f = 0.87) and this did not deviate significantly from parity. However, in 2000 the sex ratio before the breeding season was highly female-biased with males comprising 34% (ratio m/f = 0.52) of the population (see Kraaijeveld-Smit et al. 2002a). Nineteen females were caught with a total of 143 pouch young in October 1999, and 28 females with 219 pouch young were captured in October 2000.
A total of 124 (88%) offspring were assigned a father at an 80% confidence level in 1999 and 161 (74%) in 2000. At a 95% confidence level, these numbers were 76 (53%) and 92 (42%) in 1999 and 2000, respectively. Paternity assignment based on exclusion resulted in 111 (78%) and 150 (69%) pouch young having an assigned father in 1999 and 2000, respectively.
Paternity
The ranges in the number of females fertilized, the number of offspring sired and the proportion of offspring sired within a litter are presented in Table 2.
| 1999 | 2000 | |||||
|---|---|---|---|---|---|---|
| No. females | No. offspring | Proportion | No. females | No. offspring | Proportion | |
| 80% | 0–7 | 0–17 | 0.118–0.498 | 0–8 | 0–34 | 0.111–0.527 |
| 95% | 0–5 | 0–13 | 0.125–0.435 | 0–8 | 0–20 | 0.111–0.667 |
| Exclusion | 0–7 | 0–18 | 0.106–0.500 | 0–9 | 0–35 | 0.111–0.604 |
The relationship between male body mass and paternity was comparable and gave similar significant outcomes at all three levels of assignment. Therefore, to aid clarity, figures and tables contain only data for assignments at a 95% confidence level. The proportion of females fertilized (Fig. 1a, χ2 = 8.33, df = 6, P > 0.05) and the number of offspring sired (Fig. 1b, χ2 = 8.58, df = 18, P > 0.05) per male in the sampled population showed a similar distribution for both years.
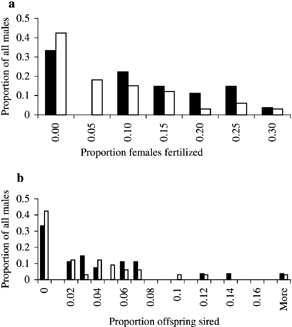
The proportion of all sampled females (n = 19 and 28 in 1999 and 2000, respectively) with which males (n = 27 and 33 in 1999 and 2000, respectively) sired offspring (a) and the proportion of assigned offspring sired (assigned 95% confidence, n = 76 and 92 in 1999 and 2000, respectively) (b). Black and white bars represent 1999 and 2000, respectively.
Males were significantly heavier in 1999 than in 2000 (1999: 34.0 ± 0.91 g, 2000: 28.5 ± 0.65 g, t = 5.02, P < 0.001, Fig. 2). Male body mass was significantly and positively correlated with the number of females fertilized (n = 60, R2 = 0.114), and the total number of offspring sired (n = 55, R2 = 0.142), but not with the proportion of offspring sired within litters (n = 34, R2 = 0.264, calculated only for males that were successful, Fig. 2a,b, Table 3). The interaction term in the GLM between year and male body mass was not significant, indicating that the relationship between male mass and overall siring success was similar between years (Table 3). However, the overall proportion sired was near significantly higher in 2000 than in 1999 (Tables 2 and 3). Furthermore, there were significant interactions between year and male body mass and male head length for the proportion of offspring sired within litters.
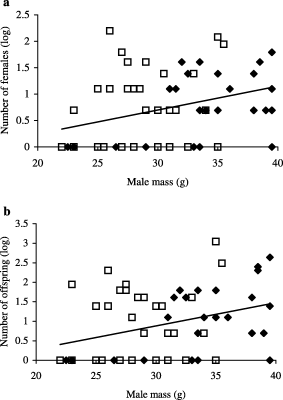
The number of females a male fertilized (a) and the number of offspring sired per male (b) in relation to male body mass. The filled diamonds represent 1999 and the open squares represent 2000. Assignment level is 95%. Data is log transformed to approach a normal distribution.
| Dependent | Source | Coefficient | anova df | F/t-ratio | P |
|---|---|---|---|---|---|
| Females | Constant | 0.30 | 1 | t = 0.46 | 0.65 |
| Mass | 0.05 | 1 | t = 2.69 | 0.01 | |
| Twtl | −0.01 | 52 | t = 2.12 | 0.04 | |
| Offspring | Constant | −0.91 | 1 | t = −1.33 | 0.19 |
| Mass | 0.06 | 58 | t = 2.73 | 0.01 | |
| Proportion | Constant | 0.43 | |||
| Year | 1.45 | 1 | F = 3.70 | 0.06 | |
| Year*Mass | 0.02 | 1 | F = 8.89 | 0.01 | |
| Year*Head | −0.07 | 1 | F = 6.67 | 0.02 |
Intensity of selection
The intensity of total selection was 1.83 and 1.59 times higher for males than for females in 1999 and 2000, respectively (Table 4). In 1999 and 2000, 69.6 and 74.7%, respectively, of the total selection intensity in males was caused by sexual selection 1 (mating success, Table 4). The positive values for the selection differentials and selection gradients indicate that there is selection for larger male body mass (Table 5). These values are higher for males than for females (female selection gradients range from −2.41 to 1.27).
| Year | Female | Male | Mean mates | σ2 | I s1 | I m/If | I s1/Im | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | Mean py | σ2 | I f | N | Mean py | σ2 | I m | ||||||
| 1999 | 31 | 4.65 | 16.28 | 0.75 | 27 | 2.85 | 11.21 | 1.38 | 1.63 | 2.55 | 0.96 | 1.83 | 0.696 |
| 2000 | 64 | 3.31 | 15.51 | 1.41 | 33 | 2.79 | 17.48 | 2.25 | 1.7 | 4.84 | 1.68 | 1.59 | 0.747 |
| Selection episode k | 1999 | 2000 | ||||
|---|---|---|---|---|---|---|
| Sk | i k | βk | Sk | i k | βk | |
| Mating success | 0.06 | 0.44 | 3.0 | 0.03 | 0.22 | 1.5 |
| Fertilization success | 0.01 | 0.10 | 0.5 | 0.01 | 0.07 | 0.5 |
| Total selection | 0.07 | 0.54 | 3.5 | 0.04 | 0.29 | 2.0 |
Edge effect
In 1999, at an 80% confidence level 11.8 ± 5.0% (n= 7 litters) of the offspring were unassigned in litters coming from mothers residing in the middle of the study site, whereas this proportion was 14.4 ± 3.6% (n = 12 litters) for litters produced by females from the edge of the study site. These proportions were 24.0 ± 6.0% (n= 8 litters) and 28.4 ± 4.9% (n = 20 litters), respectively, for 2000. An anova with year and location (middle or edge) of the mother as factors and the proportion of unassigned pouch young per litter as a dependent variable suggested a difference between years but not between locations (80% confidence level; year: F1,43 = 3.90, P = 0.06, location: F1,43 = 0.46, P = 0.54).
Maternity
In 2000 a lower percentage of females bred compared with 1999 (Table 6). No significant difference was observed in body size between first-year females with and without pouch young. However, females that successfully weaned offspring had larger heads than unsuccessful females (Table 6).
| Dependent variable | t-ratio | P-value | |
|---|---|---|---|
| Breeding/nonbreeding | Constant | −1.36 | 0.17 |
| Year | 2.00 | 0.05 | |
| Weaned/no weaned offspring | Constant | −2.11 | 0.04 |
| Head | 2.13 | 0.03 |
Paternity assignment at the 95% confidence level indicated that the number of sires per litter for first-year females did not differ significantly between years (1999: 3.60 ± 0.24, n = 16, 2000: 3.09 ± 0.24, n = 23, P = 0.148, t = 1.477, power = 0.45). The minimum number of males with which a first-year female produced offspring did not depend on female size, year or on the number of offspring per litter (data not shown). No relationship was observed between the average body mass of males with which a female produced offspring and female body size (data not shown).
Discussion
Larger males were more successful in siring offspring than smaller males in this population of Antechinus agilis, which together with the fact that total selection intensity and selection gradients are higher for males than for females, supports the theory that sexual selection drives sexual size dimorphism (Darwin 1871; Ralls 1977; Clutton-Brock & Harvey 1978; Lande 1980; Hedrick & Temeles 1989) in this species. Furthermore, larger males fertilized a higher number of females. This is in agreement with previous results on mating behaviour in A. agilis in the field, which showed a trend for larger males to mate with more females, using a radiotracer technique to establish mating success (Scott 1984). Larger males did not sire a larger proportion of offspring per litter, indicating that spermatozoa of larger males do not outcompete spermatozoa of smaller males in the female reproductive tract. Instead, our results suggest that larger males gain more matings than smaller males. This conclusion is supported by a sperm competition study in the laboratory on A. agilis, where mating order was a better predictor for paternity than male size (Kraaijeveld-Smit et al. 2002b).
Even though male size was positively and significantly related to paternity success, male size only explained 11.4–14.5% of the variation found. There are several likely explanations for this low percentage. Because this study was conducted in a wild population, some large males may have died just before the breeding season, resulting in zero paternity, and thus lowering the percentage. Furthermore, other factors that we did not (or could not reliably) measure, such as home-range size, familiarity with a female, and mating order may influence paternity success.
Emlen & Oring (1977) suggested that the variance in mating success of the limited sex (i.e. limited by the number of available mates) is greater than that of the limiting sex, and that this will increase selection pressure. This was not immediately apparent in our study species. We expected males in one year to be the limiting sex, which would result in a significant interaction between years and male body mass in relation to paternity success. However, a significant interaction between years was not observed. Furthermore, the intensity of total selection and selection gradients were higher for males than for females in both years. This indicates that males competed for mating access in both years. This is surprising as various aspects of the mating system of A. agilis would suggest an effect of the operational sex ratio on sexual selection pressure. First, the mating season is extremely synchronous, with all females being receptive to mating in approximately the same two weeks (oestrus duration per female can last up to 21 days). Second, mating duration is up to 18 h in captivity and on average 4–6 h (Shimmin 1998), with each male probably only able to mate successfully once a day. Third, the total number of spermatozoa available for the breeding season for each male is extremely limited due to spermatogenic failure before the breeding season. Each male has been estimated to have sufficient spermatozoa for only ≈ 10 normal matings (Taggart & Temple-Smith 1990). Furthermore, because of sperm depletion after mating and the time taken to recover, the amount of spermatozoa transferred by a male in the second mating is considerably less than that transferred in the first mating, particularly if these matings occur on consecutive days (Taggart & Temple-Smith 1991). Lastly, all males die soon after the two-week mating season, sometimes even before the females have ovulated (Braithwaite & Lee 1979; Selwood & McCallum 1987). All these factors suggest that females need to mate with several males to ensure fertilization (Kraaijeveld-Smit et al. 2002a). We would therefore have expected females to mate with small as well as large males in the year when fewer males were available.
Recently, it has become apparent that not only the operational sex ratio influences selection pressure. Another important factor is the time individuals spend searching for mates and to actually mate (‘time in’) compared with time spent on maintenance, such as searching for food or rearing young (‘time out’) (Clutton-Brock & Parker 1992; Kvarnemo 1994; Kvarnemo & Ahnesjö 1996; Ahnesjöet al. 2001). This is also part of the potential reproductive rate (PRR). Linked to the PRR is collateral investment (investment in more than one partner), which, for example, occurs when several males mate with the same female, and also influences the outcome of sexual selection (Parker & Simmons 1996). In A. agilis several males mate with the same female and males are likely to spend more ‘time in’ than females, both factors biasing the sex ratio towards males. It is known that males spend most of their time during the two-week breeding season searching for mates and mating, and do not spend much time maintaining themselves, which is reflected in the complete male die-off (Wood 1970; Braithwaite 1974; Braithwaite & Lee 1979; Lee & Cockburn 1985). Females, however, spend time maintaining themselves in order to survive the mating season and successfully produce offspring. The ‘time out’ for males will therefore be much lower than that for females. The difference in time out between males and females during the breeding period probably explains why the adult sex ratio does not influence sexual selection pressure. Although fewer males per female were available in 2000, they probably spent a much larger proportion of time on mate searching and mating compared with females, therefore biasing the reproductive adult sex ratio towards males.
For sexual selection to cause sexual dimorphism in this species, male mass needs to be heritable from fathers to sons (Hedrick 1988; Houde 1992; Horne & Ylonen 1998). In A. agilis however, all the juvenile males disperse far outside their natal territory within one to two weeks after weaning (Cockburn et al. 1985), and are difficult to recapture. Therefore, a captive programme is needed to study this question. Some evidence that certain size traits are heritable in A. agilis comes from the fact that head length is ‘heritable’ from mothers to daughters and fathers to daughters (Kraaijeveld-Smit 2001).
The average male body mass was higher in 1999 than 2000, however, the variance in male body mass in each year was high, and similar between years. This suggests that the difference in male mass between years depends on environmental factors (Gortazar et al. 2000) and that the variation between males within years is probably caused by genetic factors (Qvarnström & Price 2001). A. agilis densities were higher in the year when male mass was lower and competition for food may have played a role. Indeed in wild A. stuartii, a sister species to A. agilis (Dickman et al. 1998), body mass increased when their habitat was supplemented with food (Banks & Dickman 2000).
The mechanism underlying higher paternity success for larger males in field populations is unknown. This may happen because of female choice, as has been shown to occur in meadow voles, Microtus pennsylvanicus (Berteaux et al. 1999), or because of male–male competition and/or male dominance over females. Laboratory studies on A. agilis have shown that in mating trials in which two males and one female were housed in one cage, the larger male often gains mating access through male–male competition (Shimmin 1998). Another possibility is that spermatozoa of larger males out-compete spermatozoa of smaller males in the female's reproductive tract either by higher spermatozoa quantity or quality. However, this seems unlikely as mating order (last-male sperm precedence) has been shown to be more important than male size in siring success (Kraaijeveld-Smit et al. 2002b). Furthermore, larger males do not sire a larger proportion per litter, which also suggests that larger males have mating access to more females, rather than more competitive spermatozoa. Lazenby-Cohen & Cockburn (1988) proposed a lek mating system in A. agilis, and they suggested that paternity success may be higher for males that can stay in the ‘mating’ tree for long periods. It may well be that larger males can stay without food for longer than smaller males, and therefore gain higher paternity success. Alternatively, larger males may outlive smaller males, and gain mating access to females closer to ovulation, and therefore gaining higher paternity (Kraaijeveld-Smit et al. 2002b). However, Scott (1984) found that longevity was negatively correlated to male weight in one season.
In our study species, the proportion of pouch young in litters that remained unassigned to a father did not depend on the location of the mother on the grid. This may be explained by the known ranging behaviour. Outside, as well as during, the breeding season, males and females travel great distances (up to 400 m) to communal nests (Lazenby-Cohen & Cockburn 1988, 1991; Lazenby-Cohen 1991). Thus although our grid size (6 ha) covered many foraging home ranges, the social part of trapped individuals’ home ranges may often be located outside the trapping grid. In addition, males that have their foraging home ranges outside the grid probably visit nest trees inside the grid and these males might not be as easy to catch (Lazenby-Cohen & Cockburn 1988, 1991; Lazenby-Cohen 1991). This is in contrast to, for example, common shrews, Sorex araneus, and striped plateau lizards, Sceloporus virgatus, where males were most likely to sire offspring with females that had the closest spatial proximity (Stockley et al. 1996; Abell 1997).
Female survival during lactation is low in A. agilis (67% in 1999, and 56% in 2000). Limiting nesting space may explain the difference in the percentage of breeding females between years. Female densities were higher in 2000 and relative fewer may have found suitable nesting sites than in 1999. We may expect male choice for high-quality females to increase their fitness. Female quality is usually defined in terms of offspring size and the number of offspring produced (Hepp et al. 1987; Genoud & Perrin 1994). An indirect measure for female quality, such as female body mass, is often difficult to obtain (LeBas & Marshall 2000; Smiseth & Amundsen 2000). For example, in white-toothed shrews, Crocidura russula female reproductive success differs, but this difference is not related to the body mass of the female (Genoud & Perrin 1994). Furthermore, male choice may only operate under certain conditions. In the bushcricket, Kawanaphila nartee, male choice occurs only under conditions where food is limited and the OSR is female biased (Kvarnemo & Simmons 1999). We did not detect a difference in body size (measured just before the breeding season) between females that had pouch young and those that were not caught during the pouch young period, and were presumed to have died. When we compared females with pouch young that survived to the juvenile stage and those without, successful females had larger head lengths. Therefore, if male A. agilis show preferences for certain females, these may be based on female head length. Especially in 2000, the female-biased OSR should have increased potential for males to select larger females if female size was a good indicator for female quality (Kvarnemo & Simmons 1999). Yet, body size of successful females did not correlate with the minimum number of partners, or with the average mass of the known partners.
This study confirms promiscuous mating in A. agilis, with males and females mating with several partners. It also shows that larger males are more successful in siring offspring and supports the hypothesis that sexual selection promotes sexual size dimorphism in A. agilis. The operational sex ratio did not affect variance in paternity success, and this is likely to be caused by the much larger time spent on reproductive activities by males than females during the two-week breeding season. The potential reproductive rate may therefore be a better predictor of the direction of sexual selection than the operational sex ratio in A. agilis.
Acknowledgements
We thank all field assistants who helped collecting tissue samples, Andrea Taylor for assistance with molecular techniques, and Andrew Cockburn, Mariella Herberstein, Therésa Jones, Ken Kraaijeveld, David Lindenmayer, Juta Schneider and two anonymous referees for valuable comments on the manuscript. The Holsworth Wildlife Research Fund and Ethyl Mary Read Fund generously provided financial support to FJL Kraaijeveld-Smit. Research was conducted with ethics approval from the Faculty of Science Animal Experimentation Ethics Sub-Committee, University of Melbourne, reg. no. 99068 and 97071, and under Natural Resources and Environment permit numbers 10000899 and 10000954.
References
Femmie Kraaijeveld-Smit recently completed her PhD on sexual selection in Antechinus agilis. Simon Ward is a senior lecturer at the University of Melbourne, and his main research topics relate to life history of small marsupials. Peter Temple-Smith is the director of conservation at the Melbourne Zoo, and his research focuses on reproductive biology of marsupials.




