
Distribution of benthic diatoms in U.S. rivers in relation to conductivity and ionic composition
Summary
- 1
We quantified the relationships between diatom relative abundance and water conductivity and ionic composition, using a dataset of 3239 benthic diatom samples collected from 1109 river sites throughout the U.S.A. [U.S. Geological Survey National Water-Quality Assessment (NAWQA) Program dataset]. This dataset provided a unique opportunity to explore the autecology of freshwater diatoms over a broad range of environmental conditions.
- 2
Conductivity ranged from 10 to 14 500 μS cm−1, but most of the rivers had moderate conductivity (interquartile range 180–618 μS cm−1). Calcium and bicarbonate were the dominant ions. Ionic composition, however, varied greatly because of the influence of natural and anthropogenic factors.
- 3
Canonical correspondence analysis (CCA) and Monte Carlo permutation tests showed that conductivity and abundances of major ions (HCO
 + CO
+ CO , Cl−, SO
, Cl−, SO , Ca2+, Mg2+, Na+, K+) all explained a statistically significant amount of the variation in assemblage composition of benthic diatoms. Concentrations of HCO
, Ca2+, Mg2+, Na+, K+) all explained a statistically significant amount of the variation in assemblage composition of benthic diatoms. Concentrations of HCO + CO
+ CO and Ca2+ were the most significant sources of environmental variance.
and Ca2+ were the most significant sources of environmental variance. - 4
The CCA showed that the gradient of ionic composition explaining most variation in diatom assemblage structure ranged from waters dominated by Ca2+ and HCO
 + CO
+ CO to waters with higher proportions of Na+, K+, and Cl−. The CCA also revealed that the distributions of some diatoms correlated strongly with proportions of individual cations and anions, and with the ratio of monovalent to divalent cations.
to waters with higher proportions of Na+, K+, and Cl−. The CCA also revealed that the distributions of some diatoms correlated strongly with proportions of individual cations and anions, and with the ratio of monovalent to divalent cations. - 5
We present species indicator values (optima) for conductivity, major ions and proportions of those ions. We also identify diatom taxa characteristic of specific major-ion chemistries. These species optima may be useful in future interpretations of diatom ecology and as indicator values in water-quality assessment.
Introduction
Diatoms are the most common and diverse group of algae in many rivers and streams, and thus are important components of these ecosystems (Round, 1981). Although it is well known that salinity and concentrations of major ions have a strong influence on distributions of individual diatom taxa (Cholnoky, 1968), the relative importance of these factors has rarely been studied at large regional scales, and particularly not for the United States. Nor have ecological optima of taxa been quantified at these scales using large numbers of samples. This paper provides such information based on diatom data for samples collected by the USGS NAWQA Program. This information improves our understanding of how diatoms are distributed in U.S. rivers with respect to conductivity and major ions, and provides specific autecological data so that diatoms can be used more effectively in making assessments of ecological change.
Continental waters vary greatly in their mineral content and composition, mainly because of the variability in lithology, climate and vegetation. Anthropogenic factors are also important. Soil erosion, irrigation, or the direct input of industrial, municipal or agricultural wastes into rivers often increases total mineral content, or concentration of individual ions in river water (Meybeck & Helmer, 1989). For instance, the most noticeable environmental change in rivers of Massachusetts and New Jersey following development of their catchments was an increase in concentration of base cations (Dow & Zampella, 2000; Rhodes, Newton & Pufall, 2001), disrupting the natural communities of these rivers, which are adapted to low-alkalinity conditions. Agricultural land use often increases conductivity of river water and these changes are reflected in algal communities (Leland, 1995; Carpenter & Waite, 2000). Salt leaching from irrigated soils can further elevate the naturally high salinity of many rivers in arid and semi-arid zones. Mining operations can cause severe increases in the concentration of certain ions that not only dramatically alter natural communities, but also make water unsuitable for drinking, recreation and irrigation (Meybeck et al., 1992).
Diatoms are often used to monitor these environmental changes because of their range of response to ionic content and composition. Their use in monitoring would be enhanced significantly if species responses to the concentration of major ions in fresh waters were better quantified.
Most knowledge of the relationship of diatoms to salinity comes from studies of the composition of diatom assemblages collected across strong salinity gradients in salt-polluted continental waters, estuaries, inland seas and saline lakes (Kolbe, 1927, 1932; Hustedt, 1957; Cholnoky, 1968; Stoermer & Smol, 1999). The most widely used salinity classifications (Kolbe, 1927; Hustedt, 1957; van der Werff & Huls, 1957–1974as modified by van Dam, Mertens & Sinkeldam, 1994) assign diatoms to only a few salinity categories, based mostly on their occurrence in European inland and coastal waters. Consequently, these categories are most effective when used to determine whether observed assemblages are from fresh, brackish or saline waters. Strong responses of algal assemblages to the salinity or concentrations of certain ions are, however, not limited to major differences in salinity. A clear response to salinity is also often observed in sets of samples collected exclusively from fresh waters (e.g. Sabater, Sabater & Armengol, 1988; Sabater & Roca, 1992; Pipp 1997; Leland & Porter, 2000; de Almeida & Gil, 2001) and even for datasets limited to waters of very low concentration of dissolved salts (e.g. Potapova, 1996; Soininen, 2002).
Affinities of some freshwater diatoms towards certain ions can be found in widely used diatom floras (e.g. Patrick & Reimer, 1966, 1975). For instance, a number of taxa have been characterised as preferring calcium-rich or calcium-poor waters. It is difficult, however, to compile this information for water-quality monitoring purposes because it is scattered in floras and regional studies. Quantitative autecological characteristics derived from small-scale regional datasets are useful for regional monitoring programmes. However, as they are dependent on the restricted range and distribution of the environmental parameters in the dataset, they may not be appropriate for areas with different water chemistry characteristics. Reliable autecological data can be obtained only from a dataset with large numbers of observations representing the full range of environmental conditions. Here we characterise distributions of benthic diatoms along gradients of conductivity (as a measure of salinity) and ionic composition using data from samples collected as part of the National Water-Quality Assessment (NAWQA) programme from rivers throughout the U.S. Analysis of this dataset for samples collected in 1993–1998 showed that conductivity and ionic composition are among the most important determinants of diatom assemblage structure in U.S. rivers (Potapova & Charles, 2002). At the national scale the complex gradient of ionic strength and pH was the second most important after a so-called ‘downstream’ gradient, which combined gradients of river size, slope and nutrient concentration. Broad-scale differences in benthic diatom assemblages between rivers of the eastern coastal and western interior areas were largely because of a much higher mineral content in the arid western areas. In this study, we use an even larger NAWQA dataset, based on samples collected from 1993 to 1999, to study in more detail the relationship between these water chemistry properties and common diatom species. Our first objective was to investigate the influence of conductivity and ionic composition on diatom distributions in rivers of the U.S. The second objective was to calculate and present autecological data for use in environmental assessment.
Methods
Sample collection
Benthic algal samples were collected from 1993 to 1999 at 1109 sampling locations across the continental U.S., Alaska and Hawaii (Fig. 1). The USGS personnel collected benthic algal samples at each site once a year, during one to three consecutive years (Gurtz, 1993; Porter et al., 1993). At the majority of the sites, two types of quantitative samples were collected: one from erosional habitats (rocks, usually from riffles and snags) and another from depositional (soft sediment, typically from pools and stream margins) habitats. Both types of samples were used in the present study. Algal samples were collected most often during low-flow conditions, usually in summer or early autumn.
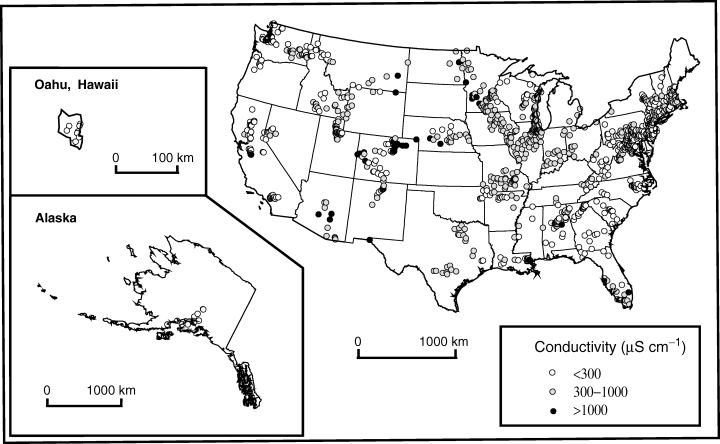
Location of the 1109 NAWQA sampling sites and corresponding average conductivity values.
Laboratory methods
Permanent diatom slides were prepared by oxidising organic material in samples with nitric acid and mounting cleaned diatoms in Naphrax. Diatom analysts at the Patrick Center of The Academy of Natural Sciences, Philadelphia (ANSP), the University of Louisville, Michigan State University, and independent contractors identified and counted diatoms. Analysts counted 600 diatom valves on each slide; fewer valves were counted on some slides when diatoms were scarce. Laboratory methods used at the ANSP are described in Charles, Knowles & Davis (2002). All slides were deposited in the ANSP Diatom Herbarium.
Taxonomy
The main diatom floras used for identification were those of Hustedt (1930a,b, 1959, 1961–1966), Patrick & Reimer (1966, 1975), Camburn, Kingston & Charles (1984–1986), Krammer & Lange-Bertalot (1986, 1988, 1991a,b), and Simonsen (1987). Other important works on diatom taxonomy were also consulted. A considerable effort was made to reach taxonomic consistency among analysts (Potapova & Charles, 2002). Some of the diatom taxa reported in this study have not yet been described in the literature; they are given temporary names that may include abbreviations of the name of the person making the determination and geographic location where the taxon was first collected. Images of these taxa are available at the ANSP Algae Image Database website (http://diatom.acnatsci.org).
Environmental data
Water chemistry samples were collected by the U.S. Geological Survey at least once a month. Conductivity, HCO , CO
, CO , Cl−, SO
, Cl−, SO , Ca2+, Mg2+, Na+, K+ were determined at the USGS National Water Quality Laboratory (Lakewood, CO, U.S.A.) (Fishman, 1993). For 70 sites where concentration of HCO
, Ca2+, Mg2+, Na+, K+ were determined at the USGS National Water Quality Laboratory (Lakewood, CO, U.S.A.) (Fishman, 1993). For 70 sites where concentration of HCO + CO
+ CO was not reported, we derived concentration of HCO
was not reported, we derived concentration of HCO + CO
+ CO from alkalinity values. We used chemical measurements closest to the date of algal sampling in our analyses. Concentration of major ions is reported here in milliequivalents per litre (meq L−1), and proportions of anions and cations are expressed as per cent equivalents of each ion of the sum of all anions or cations (% eq).
from alkalinity values. We used chemical measurements closest to the date of algal sampling in our analyses. Concentration of major ions is reported here in milliequivalents per litre (meq L−1), and proportions of anions and cations are expressed as per cent equivalents of each ion of the sum of all anions or cations (% eq).
Data analysis
Conductivity was determined at all 1109 sampling sites, whereas major ions were analysed at 807 sites only. We constructed two datasets: a ‘complete’ dataset, consisting of 3239 samples collected from all 1109 sites, and a second ‘limited’ dataset, which included only the 2674 samples collected at sites where major ions were measured. We excluded all planktonic species from the diatom counts, calculating relative abundance of the benthic diatoms only. Distinction between benthic and planktonic diatoms in inland waters is somewhat arbitrary. Therefore, we excluded only those diatoms (mostly centric species) that are known to spend most of their life in the water column, not considering them being a part of the benthic communities. For analyses, we retained only those species that reached relative abundance of at least 1% in at least two samples per dataset. The resulting ‘complete’ dataset contained 717 diatom taxa and the ‘limited’ dataset had 683 taxa.
For numerical analyses, conductivity and concentrations of individual ions (expressed in μeq L−1) were log-transformed to approximate a normal distribution.
To evaluate the strength of the relationship between composition of the diatom assemblages and conductivity, concentration, and proportion of each of the seven major ions, we used canonical correspondence analyses (CCA), with only one environmental variable at a time. A total of 15 CCAs corresponded to 15 tested variables (one for conductivity, seven for concentrations and seven for proportions of major ions). We evaluated the significance of the effect of each variable using Monte Carlo permutation tests with 199 unrestricted permutations, and used the ratio of the first to the second eigenvalue as a measure of the variable strength.
We ran another CCA to elucidate major coenclines and to estimate the relative importance of conductivity and proportions of the seven major ions in explaining variation among diatom assemblages. The eight parameters (conductivity and ion proportions) that were included in this CCA as constraining environmental variables were shown to explain a significant proportion of variation in species composition in previous CCAs and were not highly correlated (r < 0.8) with each other. Significance of the first four ordination axes was tested by permutation procedures in partial CCAs, as described by ter Braak & Šmilauer (1998). Significance of the second, third and fourth axes was checked in partial CCAs that used environment-derived sample scores for the first, second and third ordination axes, respectively, as covariables. The CCAs were performed with the canoco program (ter Braak & Šmilauer, 1998).
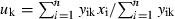 where yik is the relative abundance of species k in sample i; xi is the value of environmental parameter in sample i; n is the total number of samples in dataset. Tolerance or weighted standard deviation (tk) was calculated as
where yik is the relative abundance of species k in sample i; xi is the value of environmental parameter in sample i; n is the total number of samples in dataset. Tolerance or weighted standard deviation (tk) was calculated as
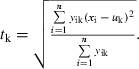
Results
Conductivity and ion concentrations
Conductivity varied from 10 μS cm−1, corresponding to waters extremely poor in electrolytes, to 14 500 μS cm−1, representing brackish water (Table 1). Median and interquartile range values for conductivity and concentration of individual ions indicated that most of the rivers had a moderate level of salt content (Meybeck & Helmer, 1989), and were of the calcium bicarbonate type. Highest conductivities were observed in rivers of south Florida and the Mississippi delta influenced by marine waters, rivers of the arid west, and some polluted rivers across the U.S. (black circles in Fig. 1).
| Parameter | Minimum | First quartile | Median | Third quartile | Maximum | Number of observations |
|---|---|---|---|---|---|---|
| Conductivity (μS cm−1) | 10 | 180 | 363 | 618 | 14500 | 3040 |
HCO +CO +CO (meq L−1) (meq L−1) |
0.016 | 0.819 | 2.278 | 3.671 | 9.288 | 2674 |
| Cl− (meq L−1) | 0.003 | 0.132 | 0.339 | 0.875 | 69.478 | 2674 |
SO (meq L−1) (meq L−1) |
0.002 | 0.135 | 0.413 | 1.083 | 47.886 | 2674 |
| Ca2+ (meq L−1) | 0.026 | 0.749 | 1.846 | 2.958 | 27.455 | 2674 |
| Mg2+ (meq L−1) | 0.017 | 0.288 | 0.775 | 1.613 | 18.104 | 2674 |
| Na+ (meq L−1) | 0.016 | 0.190 | 0.479 | 1.262 | 58.025 | 2674 |
| K+ (meq L−1) | 0.003 | 0.035 | 0.059 | 0.092 | 1.291 | 2674 |
Carbonate and bicarbonate were prevalent anions in samples from the majority of the 807 NAWQA sampling sites. Chloride and sulphate dominated only rarely (Fig. 2). Highest concentrations of chloride were found in the Mississippi delta and in some rivers of the arid west (Arizona Desert). The proportion of chloride was sometimes relatively high (up to 80% eq) in soft-water coastal rivers of North Carolina and Georgia. Highest concentrations of sulphate were recorded in some rivers of Colorado, Pennsylvania, Wyoming and Montana that receive coal-mining wastewater.
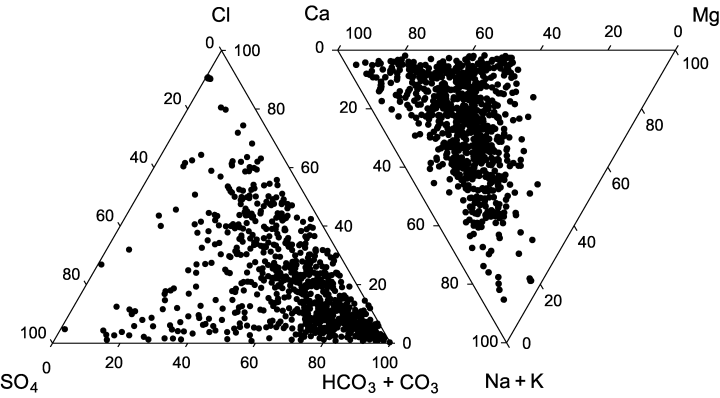
Ternary diagrams showing ion composition in 807 NAWQA sampling sites.
Alkaline earth metals, especially Ca2+, were usually the dominant cations in studied rivers, while the percentage of Na+ and K+ was rarely high (Fig. 2). The ratio of Ca2+ and Mg2+ was especially high in rivers of medium conductivity (160–380 μS cm−1) that drain carbonate bedrock (e.g. Ozark Plateaus and karst area in Georgia). The total concentration of Ca2+ and Mg2+ was, however, maximal in waters with the highest proportion of SO among anions, mostly in rivers draining mining areas.
among anions, mostly in rivers draining mining areas.
The highest concentrations of Na+ and K+ were observed in saline rivers of the Mississippi delta and western arid areas. A high proportion of Na+ was also sometimes observed in the low-conductivity rivers of the eastern U.S. coast. K+ was never a dominant cation – its ratio was highest in some dilute rivers of Washington, Alabama and Georgia.
There was no clear relationship between conductivity and dominant ions. Correlations between conductivity, [Na+], and [Cl−] are relatively high (indicating that highest values of conductivity were because of the increased concentration of these ions), but not much higher than between conductivity and other ions (Table 2). Relatively high correlation coefficients within sodium chloride and calcium carbonate/bicarbonate cation–anion pairs, combined with low correlation coefficients among them, indicate that the ratio of these salts forms a major gradient in ionic composition in the NAWQA dataset.
| Parameter | [HCO +CO +CO ] ] |
[Cl−] | [SO ] ] |
[Ca2+] | [Mg2+] | [Na+] | [K+] |
|---|---|---|---|---|---|---|---|
| Cl− | 0.16 | 1 | |||||
SO |
0.31 | 0.32 | 1 | ||||
| Ca2+ | 0.71 | 0.28 | 0.75 | 1 | |||
| Mg2+ | 0.67 | 0.52 | 0.74 | 0.74 | 1 | ||
| Na+ | 0.27 | 0.91 | 0.56 | 0.38 | 0.65 | 1 | |
| K+ | 0.32 | 0.63 | 0.39 | 0.32 | 0.48 | 0.72 | 1 |
| Conductivity | 0.58 | 0.76 | 0.68 | 0.70 | 0.84 | 0.88 | 0.65 |
Community analysis
[HCO + CO
+ CO ] and [Ca2+], followed by conductivity and [Mg2+], explained the highest proportion of variation in diatom data (Table 3). Ion percentages explained less variation than ion concentrations, but nevertheless had a significant relationship with diatom assemblages when tested by permutation procedures (P < 0.05). Eigenvalues in all analyses were relatively low, but a moderate to high ratio of the first to the second eigenvalue indicated the important role of conductivity and concentrations of major ions in structuring diatom assemblages (Table 3).
] and [Ca2+], followed by conductivity and [Mg2+], explained the highest proportion of variation in diatom data (Table 3). Ion percentages explained less variation than ion concentrations, but nevertheless had a significant relationship with diatom assemblages when tested by permutation procedures (P < 0.05). Eigenvalues in all analyses were relatively low, but a moderate to high ratio of the first to the second eigenvalue indicated the important role of conductivity and concentrations of major ions in structuring diatom assemblages (Table 3).
| Variable | λ 1 | λ 1/λ2 |
|---|---|---|
| Log10 conductivity (μS cm−1) | 0.189 | 0.47 |
| HCO3− + CO32− (% eq) | 0.089 | 0.23 |
| Cl− (% eq) | 0.122 | 0.32 |
| SO42− (% eq) | 0.049 | 0.12 |
| Ca2+ (% eq) | 0.086 | 0.22 |
| Mg2+ (% eq) | 0.054 | 0.13 |
| Na+ (% eq) | 0.092 | 0.23 |
| K+ (% eq) | 0.118 | 0.31 |
| Log10 [HCO3− + CO32−] (μeq L−1) | 0.236 | 0.60 |
| Log10 [Cl−] (μeq L−1) | 0.126 | 0.31 |
| Log10 [SO42−] (μeq L−1) | 0.130 | 0.33 |
| Log10 [Ca2+] (μeq L−1) | 0.201 | 0.51 |
| Log10 [Mg2+] (μeq L−1) | 0.180 | 0.45 |
| Log10 [Na+] (μeq L−1) | 0.144 | 0.36 |
| Log10 [K+] (μeq L−1) | 0.135 | 0.33 |
- λ 1, eigenvalue for axis 1; λ2, eigenvalue for axis 2
Another CCA was conducted to explore the simultaneous effects of various ions on diatom assemblages. It employed only conductivity and ion ratios as environmental variables, because concentrations of specific ions were highly correlated with each other and conductivity (Table 1). This CCA showed that conductivity and the ratio of Ca(HCO3)2 + CaCO3 to NaCl + KCl were major factors explaining the structure of diatom assemblages (Fig. 3). The first four ordination axes were all significant (P < 0.05) and had eigenvalues of 0.23, 0.11, 0.07 and 0.05, respectively, thus indicating that the first two axes explained most of the variation in diatom data.
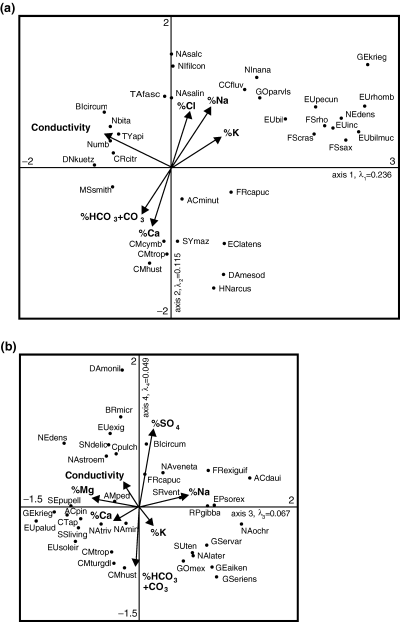
Canonical correspondence analysis (CCA) diagrams showing environmental variables and diatom taxa centroids in the ordination space of the 1st and 2nd (A) and 3rd and 4th (B) CCA axes. Environmental variables that had low correlations with ordination axes are not shown. Taxa shown in the diagrams were found in at least 1% of all samples and either had high influence on the corresponding axes (8 species with highest fit) or extreme scores along corresponding axes (8 taxa with highest and 8 taxa with lowest scores). Taxa codes correspond to those in Table 4.
Fig. 3a shows that conductivity and the proportions of Ca2+, HCO + CO
+ CO , Na+, Cl− and K+ were highly correlated with the first two axes. Diatom taxa placed in the right upper quadrant of the first and second axes ordination plot (Fig. 3a), mostly species of Eunotia, are found in water low in alkaline (Ca2+, Mg2+) cations. Taxa in the lower right quadrant favour low conductivity waters but with a higher proportion of alkaline cations. Calciphilous species of Cymbella are found in the lower left quadrant of the ordination diagram. Diatoms with higher affinity for total salt content are placed in the left upper quadrant.
, Na+, Cl− and K+ were highly correlated with the first two axes. Diatom taxa placed in the right upper quadrant of the first and second axes ordination plot (Fig. 3a), mostly species of Eunotia, are found in water low in alkaline (Ca2+, Mg2+) cations. Taxa in the lower right quadrant favour low conductivity waters but with a higher proportion of alkaline cations. Calciphilous species of Cymbella are found in the lower left quadrant of the ordination diagram. Diatoms with higher affinity for total salt content are placed in the left upper quadrant.
The third axis (Fig. 3b) can be interpreted as part of the variation in species composition along the gradient of monovalent–divalent cations (M : D) ratio. Another part of the variation along the M : D gradient was captured by the first, and especially, second axes, but that gradient also included the (HCO + CO
+ CO )/Cl−ratio. The M : D gradient expressed along the third axis is a residual remaining after extraction of the stronger conductivity and Ca(HCO3)2 + CaCO3 to NaCl + KCl gradients. In other words, species with high scores along the third axis can be found in waters with relatively high %Na+, even if the %Cl− is low, and species with low scores favour waters with high %Mg2+ and %Ca2+, even if the %(HCO
)/Cl−ratio. The M : D gradient expressed along the third axis is a residual remaining after extraction of the stronger conductivity and Ca(HCO3)2 + CaCO3 to NaCl + KCl gradients. In other words, species with high scores along the third axis can be found in waters with relatively high %Na+, even if the %Cl− is low, and species with low scores favour waters with high %Mg2+ and %Ca2+, even if the %(HCO + CO
+ CO ) is low. The fourth axis can be interpreted as a gradient in SO
) is low. The fourth axis can be interpreted as a gradient in SO /(HCO
/(HCO + CO
+ CO ) ratio (Fig. 3b). Species with high scores along this axis had high abundance in waters contaminated with mining discharge: they included halophilous (Diatoma moniliformis, Biremis circumtexta, Ctenophora pulchella) and acidophilous diatoms (Brachysira microcephala, Eunotia exigua, Stenopterobia delicatissima).
) ratio (Fig. 3b). Species with high scores along this axis had high abundance in waters contaminated with mining discharge: they included halophilous (Diatoma moniliformis, Biremis circumtexta, Ctenophora pulchella) and acidophilous diatoms (Brachysira microcephala, Eunotia exigua, Stenopterobia delicatissima).
Species indicator values
Apparent optima of the most frequently occurring diatoms (found in at least 500 samples) are presented in Table 4. Optima are also shown for diatoms that had extreme (highest 15 and lowest 15) optima along any of the examined variables (conductivity, concentration and per cent equivalent of the seven major ions) and occurred in at least 25 samples. Conductivity optima for these diatoms ranged from 40 to 902 μS cm−1. Most of the diatoms that exhibited highest affinity towards Ca(HCO3)2 water type had low (Hannaea arcus, Diatoma mesodon, Gomphonema olivaceoides) to moderate (Gomphonema mehleri, Nitzschia sinuata var. delognei) conductivity optima. Diatoms that had highest optima for the proportion of Na+ and Cl− either had very low (Psammothidium helveticum, Eunotia flexuosa) or relatively high conductivity optima (Navicula salinicola) thus reflecting two different types of rivers that had relatively high percentages of these ions: coastal soft-water rivers draining bedrock poor in alkaline cations and saline rivers of the arid zone. Many diatoms known as acidophilous taxa (Eunotia bilunaris var. mucophila, E. rhomboidea, Stauroneis livingstonii, Stenopterobia delicatissima, Eunotia paludosa) had relatively high optima for %Cl− and %K+ and very low conductivity optima.
| Taxon name | Code | Conductivity (μS cm−1) | Anion optima (meq L−1) | Cation optima (meq L−1) | Anion optima (% eq) | Cation optima (% eq) | N occ. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Opt. | Low | High | HCO3 +CO3 | Cl | SO4 | Ca | Mg | Na | K | HCO3 +CO3 | Cl | SO4 | Ca | Mg | Na | K | |||
| Brachysira brebissonii Ross | 40 | 21 | 76 | 0.16* | 0.05* | 0.05* | 0.13* | 0.08* | 0.07* | 0.01* | 54 | 24 | 21 | 44 | 24 | 27 | 4.7 | 48 | |
| Eunotia tenella (Grun.) A. Cl. | 48 | 23 | 100 | 0.17* | 0.09* | 0.04* | 0.17* | 0.08* | 0.12* | 0.02* | 53 | 33 | 15 | 41 | 21 | 32 | 5.8 | 74 | |
| Frustulia saxonica Rab. | FSsax | 50 | 26 | 97 | 0.17* | 0.12 | 0.04* | 0.12* | 0.09* | 0.15* | 0.02* | 50 | 38 | 13 | 32* | 23 | 38** | 6.7** | 39 |
| Eunotia bilunaris var. mucophila L.-B. & Nör. | EUbilmuc | 66 | 35 | 125 | 0.13* | 0.16 | 0.08 | 0.19* | 0.13* | 0.16 | 0.03 | 33* | 41** | 25 | 37* | 24 | 32 | 6.8** | 29 |
| Eunotia rhomboidea Hust. | EUrhomb | 66 | 34 | 127 | 0.11* | 0.17 | 0.07* | 0.18* | 0.12* | 0.16 | 0.04 | 32* | 44** | 24 | 36* | 24 | 33 | 7.8** | 75 |
| Stauroneis livingstonii Reimer | SSliving | 67 | 38 | 117 | 0.16* | 0.15 | 0.03* | 0.19* | 0.14* | 0.17 | 0.03 | 43 | 46** | 12 | 36* | 25 | 32 | 6.8** | 30 |
| Stenopterobia delicatissima (Lewis) Bréb. | SNdelic | 68 | 33 | 143 | 0.10* | 0.16 | 0.11 | 0.20* | 0.13* | 0.16 | 0.03 | 29* | 39** | 31** | 37* | 24 | 32 | 7.1** | 34 |
| Eunotia paludosa Grun. | EUpalud | 69 | 46 | 102 | 0.14* | 0.17 | 0.03* | 0.22* | 0.15 | 0.15 | 0.03 | 40* | 48** | 12 | 39* | 26 | 28 | 6.9** | 30 |
| Encyonema latens (Krass.) Mann | EClatens | 73 | 23 | 230 | 0.55 | 0.03* | 0.16 | 0.50 | 0.20 | 0.13* | 0.03* | 70 | 6* | 24 | 56 | 22 | 17 | 4.3 | 27 |
| Navicula lateropunctata Wallace | NAlater | 75 | 37 | 152 | 0.35 | 0.13 | 0.06* | 0.25* | 0.13* | 0.19 | 0.04 | 62 | 26 | 13 | 40 | 21 | 32 | 7.0** | 80 |
| Geissleria cf. kriegeri (Krass.) L.-B. & Metzeltin | GEkrieg | 76 | 45 | 130 | 0.12* | 0.22 | 0.05* | 0.22* | 0.14* | 0.19 | 0.05 | 31* | 51** | 18 | 35* | 23 | 32 | 8.7** | 53 |
| Frustulia crassinervia (Bréb.) L.-B. & Kram. | FScras | 79 | 42 | 147 | 0.23 | 0.16 | 0.06* | 0.26* | 0.13* | 0.18 | 0.04 | 49 | 35 | 16 | 41 | 21 | 31 | 6.7** | 157 |
| Fragilariforma bicapitata (Mayer) Round & Will. | 86 | 40 | 188 | 0.36 | 0.24 | 0.20 | 0.55 | 0.24 | 0.31 | 0.05 | 44 | 34 | 22 | 46 | 21 | 29 | 4.2 | 33 | |
| Eunotia naegelii Migula | 89 | 39 | 200 | 0.18* | 0.19 | 0.07* | 0.29 | 0.15* | 0.19 | 0.04 | 42 | 38 | 20 | 42 | 21 | 30 | 6.5** | 102 | |
| Cymbella‘sp.1 JCK’ | CM1JCK | 89 | 43 | 186 | 0.62 | 0.10* | 0.11 | 0.50 | 0.19 | 0.21 | 0.02* | 70 | 14 | 16 | 52 | 21 | 24 | 3.0 | 95 |
| Frustulia rhomboides (Ehr.) De Tony | FSrho | 90 | 39 | 208 | 0.22 | 0.20 | 0.08 | 0.27* | 0.15* | 0.21 | 0.03 | 42 | 41** | 17 | 39 | 21 | 33 | 6.0 | 165 |
| Psammothidium helveticum (Hust.) Bukht. & Round | 91 | 24 | 349 | 0.15* | 0.18 | 0.10 | 0.23* | 0.15 | 0.21 | 0.03 | 37* | 43** | 20 | 38* | 21 | 36** | 4.9 | 29 | |
| Eunotia flexuosa (Bréb.) Kütz. | 94 | 30 | 295 | 0.26 | 0.19 | 0.05* | 0.27* | 0.13* | 0.22 | 0.02* | 49 | 38** | 13 | 40 | 20 | 35** | 4.7 | 46 | |
| Eunotia exigua (Bréb. ex Kütz.) Rab. | EUexig | 94 | 39 | 229 | 0.15* | 0.16 | 0.16 | 0.34 | 0.17 | 0.18 | 0.04 | 33* | 33 | 34** | 45 | 23 | 27 | 6 | 158 |
| Eunotia incisa W. Sm. ex Greg. | EUinc | 95 | 40 | 226 | 0.19* | 0.21 | 0.09 | 0.27* | 0.15* | 0.22 | 0.03 | 37* | 43** | 20 | 38* | 21 | 35** | 5.5 | 143 |
| Tabellaria flocculosa (Roth) Kütz. | 95 | 36 | 248 | 0.25 | 0.09* | 0.10 | 0.32 | 0.14* | 0.15 | 0.02* | 49 | 27 | 25 | 47 | 21 | 27 | 3.8 | 170 | |
| Neidium densestriatum (Østrup) Kram. | NEdens | 97 | 58 | 164 | 0.12* | 0.24 | 0.13 | 0.31 | 0.20 | 0.21 | 0.04 | 28* | 42** | 30** | 40 | 25 | 28 | 6.5** | 27 |
| Hannaea arcus (Ehr.) Patrick | HNarcus | 100 | 42 | 236 | 0.69 | 0.02* | 0.12 | 0.59 | 0.18 | 0.11* | 0.01* | 77** | 5* | 18 | 63** | 20 | 15 | 2.0 | 169 |
| Neidium alpinum Hust. | 101 | 49 | 209 | 0.19* | 0.24 | 0.16 | 0.34 | 0.19 | 0.24 | 0.06 | 36* | 37 | 28** | 41 | 22 | 29 | 7.5** | 57 | |
| Eunotia monodon Ehr. | 102 | 51 | 203 | 0.31 | 0.22 | 0.07* | 0.36 | 0.16 | 0.22 | 0.04 | 51 | 35 | 14 | 45 | 21 | 29 | 5.9 | 91 | |
| Diatoma mesodon (Ehr.) Kütz. | DAmesod | 106 | 47 | 240 | 0.63 | 0.04* | 0.13 | 0.57 | 0.19 | 0.14* | 0.01* | 71 | 8* | 20 | 60** | 21 | 17 | 2.1 | 167 |
| Gomphonema olivaceiodes Hust. | 107 | 54 | 214 | 0.77 | 0.03* | 0.14 | 0.65 | 0.21 | 0.13* | 0.01* | 76** | 7* | 17 | 62** | 20 | 15 | 2.1 | 122 | |
| Eunotia soleirolii (Kütz.) Rab. | EUsoleir | 108 | 52 | 226 | 0.33 | 0.26 | 0.04* | 0.39 | 0.21 | 0.23 | 0.04 | 50 | 38 | 12 | 44 | 24 | 26 | 6.6** | 37 |
| Stauroneis smithii var. incisa Pant. | 109 | 53 | 226 | 0.28 | 0.18 | 0.14 | 0.39 | 0.19 | 0.20 | 0.05 | 47 | 28 | 25 | 46 | 22 | 25 | 6.6** | 40 | |
| Cymbella aspera (Ehr.) Perag. | 115 | 64 | 206 | 0.52 | 0.18 | 0.07* | 0.39 | 0.22 | 0.31 | 0.04 | 63 | 25 | 12 | 39 | 23 | 33 | 5.1 | 35 | |
| Eunotia pectinalis var. undulata (Ralfs) Rab. | 116 | 56 | 238 | 0.23 | 0.31 | 0.11 | 0.34 | 0.16 | 0.30 | 0.04 | 36* | 44** | 20 | 39* | 19 | 37** | 5.7 | 107 | |
| Geissleria aikenensis (Patr.) Torg. et Oliveira | GEaiken | 119 | 68 | 208 | 0.68 | 0.14 | 0.07* | 0.41 | 0.20 | 0.25 | 0.05 | 73 | 16 | 10* | 44 | 22 | 28 | 5.7 | 50 |
| Gomphonema rhombicum Fricke | 119 | 53 | 265 | 0.92 | 0.09* | 0.10 | 0.65 | 0.27 | 0.23 | 0.03* | 77** | 12 | 11* | 53 | 23 | 22 | 2.7 | 124 | |
| Navicula longicephala Hust. | 127 | 53 | 308 | 0.32 | 0.25 | 0.14 | 0.40 | 0.20 | 0.27 | 0.06 | 45 | 32 | 23 | 43 | 21 | 30 | 6.8** | 90 | |
| Pinnularia appendiculata (Ag.) Cl. | 129 | 41 | 398 | 0.33 | 0.31 | 0.22 | 0.48 | 0.27 | 0.36 | 0.07 | 39* | 33 | 28 | 40 | 23 | 31 | 6.3 | 52 | |
| Achnanthes stewartii Patr. | 134 | 40 | 451 | 0.48 | 0.26 | 0.15 | 0.42 | 0.26 | 0.33 | 0.04 | 53 | 29 | 18 | 39* | 25 | 31 | 5.3 | 28 | |
| Achnanthidium ‘sp. 10 NAWQA’ | 139 | 56 | 342 | 0.67 | 0.22 | 0.18 | 0.63 | 0.29 | 0.27 | 0.04 | 58 | 23 | 19 | 49 | 23 | 24 | 3.9 | 584 | |
| Achnanthes peragalli Brun & Heribaud | 141 | 69 | 287 | 0.63 | 0.12 | 0.11 | 0.61 | 0.27 | 0.15* | 0.03 | 68 | 18 | 14 | 54 | 25 | 17 | 3.1 | 34 | |
| Pinnularia intermedia (Lager.) Cl. | 157 | 65 | 380 | 0.56 | 0.40 | 0.16 | 0.58 | 0.27 | 0.46 | 0.06 | 48 | 34 | 18 | 40 | 20 | 34** | 5.4 | 61 | |
| Eunotia formica Ehr. | 163 | 79 | 336 | 0.53 | 0.38 | 0.11 | 0.52 | 0.21 | 0.42 | 0.05 | 49 | 38 | 13 | 42 | 18* | 36** | 4.7 | 82 | |
| Fragilaria capucina Desmazières | FRcapuc | 168 | 60 | 470 | 0.65 | 0.17 | 0.23 | 0.70 | 0.31 | 0.27 | 0.04 | 55 | 20 | 25 | 50 | 23 | 23 | 3.4 | 776 |
| Stauroneis phoenicentron (Nitzsch) Ehr. | 168 | 49 | 574 | 0.87 | 0.56 | 0.23 | 0.77 | 0.30 | 0.56 | 0.05 | 51 | 35 | 15 | 45 | 18* | 34 | 3.4 | 35 | |
| Eucocconeis flexella (Kütz.) Cl. | 185 | 88 | 389 | 0.81 | 0.11 | 0.22 | 0.89 | 0.30 | 0.21 | 0.02* | 63 | 20 | 18 | 59** | 20 | 19 | 1.7 | 37 | |
| Surirella tenera Greg. | SUten | 189 | 66 | 541 | 1.08 | 0.19 | 0.17 | 0.80 | 0.36 | 0.48 | 0.08 | 68 | 19 | 13 | 46 | 21 | 29 | 4.9 | 26 |
| Navicula viridula var. linearis Hust. | 191 | 85 | 429 | 1.08 | 0.21 | 0.13 | 0.81 | 0.33 | 0.28 | 0.04 | 70 | 19 | 11* | 51 | 22 | 24 | 3.8 | 147 | |
| Gomphoneis eriense (Grun.) Skv. & Meyer | GSeriens | 192 | 99 | 372 | 1.19 | 0.11 | 0.14 | 0.76 | 0.35 | 0.38 | 0.07 | 78** | 9.8 | 12 | 47 | 22 | 25 | 6.3 | 27 |
| Synedra mazamaensis Sovereign | SYmaz | 196 | 104 | 370 | 1.29 | 0.09* | 0.31 | 1.02 | 0.36 | 0.24 | 0.03* | 73 | 8* | 19 | 59 | 20 | 18 | 1.9 | 45 |
| Encyonema silesiacum (Bleisch) Mann | 197 | 83 | 468 | 1.23 | 0.13 | 0.26 | 1.05 | 0.42 | 0.29 | 0.03 | 68 | 13 | 19 | 55 | 23 | 19 | 2.6 | 564 | |
| Nitzschia nana Grun. | NInana | 201 | 60 | 676 | 0.44 | 0.50 | 0.22 | 0.61 | 0.34 | 0.55 | 0.08 | 40* | 37 | 23 | 39* | 21 | 34 | 6.3 | 61 |
| Gomphonema apuncto Wallace | 202 | 108 | 378 | 1.13 | 0.11 | 0.15 | 0.91 | 0.36 | 0.13* | 0.03 | 73 | 13 | 14 | 59 | 24 | 14 | 2.8 | 79 | |
| Cymbella cymbiformis Ag. | CMcymb | 204 | 112 | 369 | 1.58 | 0.06* | 0.10 | 1.17 | 0.42 | 0.08* | 0.02* | 86** | 6* | 8* | 66** | 26 | 6* | 1.7 | 55 |
| Fragilaria vaucheriae (Kütz.) Petersen | 209 | 79 | 555 | 1.07 | 0.18 | 0.28 | 0.97 | 0.44 | 0.35 | 0.04 | 62 | 17 | 21 | 51 | 24 | 22 | 3.0 | 1201 | |
| Encyonema minutum (Hilse) Mann | ECminu | 209 | 81 | 545 | 1.04 | 0.22 | 0.27 | 0.97 | 0.42 | 0.34 | 0.04 | 61 | 19 | 20 | 52 | 23 | 22 | 3.1 | 1476 |
| Gomphonema parvulum var. parvulius L.-B. & Reichardt | GOparvls | 209 | 109 | 401 | 0.58 | 0.61 | 0.19 | 0.67 | 0.25 | 0.59 | 0.05 | 41 | 46** | 13 | 39 | 15* | 43** | 3.4 | 26 |
| Achnanthidium deflexum (Reim.) Kingston | 211 | 97 | 456 | 1.42 | 0.12 | 0.17 | 1.11 | 0.48 | 0.16 | 0.03 | 75 | 9 | 16 | 57 | 27 | 13* | 2.4 | 526 | |
| Navicula minuscula Grun. | 212 | 85 | 526 | 1.29 | 0.09* | 0.25 | 1.13 | 0.39 | 0.25 | 0.03 | 68 | 12 | 20 | 59 | 20 | 18 | 2.3 | 75 | |
| Fragilaria pinnata var. lancettula (Schum.) Hust. | 216 | 89 | 528 | 1.52 | 0.13 | 0.22 | 1.02 | 0.53 | 0.35 | 0.05 | 76** | 10 | 14 | 49 | 27 | 21 | 3 | 216 | |
| Geissleria decussis (Hust.) L.-B. & Metzeltin | 220 | 83 | 583 | 1.29 | 0.28 | 0.23 | 1.06 | 0.46 | 0.38 | 0.05 | 66 | 18 | 16 | 51 | 23 | 22 | 3.7 | 654 | |
| Cymbella cf. tropica Kram. | CMtrop | 221 | 143 | 343 | 1.69 | 0.11 | 0.14 | 1.36 | 0.39 | 0.12* | 0.03 | 83** | 8* | 9* | 68** | 23 | 8* | 2 | 63 |
| Navicula cryptocephala Kütz. | 222 | 88 | 562 | 1.12 | 0.29 | 0.23 | 0.98 | 0.45 | 0.36 | 0.05 | 63 | 21 | 16 | 50 | 24 | 23 | 3.8 | 1048 | |
| Brachysira microcephala (Grun.) Compère | BRmicr | 225 | 61 | 832 | 0.57 | 0.17 | 0.34 | 0.91 | 0.44 | 0.26 | 0.03 | 48 | 17 | 35* | 53 | 25 | 19 | 2.5 | 185 |
| Surirella angusta Kütz. | 225 | 86 | 593 | 1.14 | 0.27 | 0.26 | 1.00 | 0.48 | 0.36 | 0.06 | 62 | 19 | 18 | 49 | 25 | 22 | 4.3 | 546 | |
| Epithemia turgida (Ehr.) Kütz. | 227 | 101 | 508 | 1.91 | 0.10* | 0.16 | 1.33 | 0.59 | 0.18 | 0.04 | 81** | 7* | 11 | 57 | 28 | 13* | 2.1 | 127 | |
| Achnanthidium minutissimum (Kütz.) Czarn. | ACminut | 229 | 81 | 652 | 1.31 | 0.20 | 0.31 | 1.22 | 0.51 | 0.32 | 0.04 | 64 | 15 | 21 | 55 | 24 | 19 | 2.4 | 2019 |
| Pinnularia acrosphaeria W. Sm. | 234 | 100 | 551 | 1.08 | 0.42 | 0.13 | 1.04 | 0.31 | 0.50 | 0.06 | 61 | 26 | 13 | 53 | 17* | 26 | 4.2 | 41 | |
| Navicula cf. ochridana Hust. | NAochr | 237 | 91 | 614 | 1.52 | 0.24 | 0.36 | 1.07 | 0.41 | 0.70 | 0.08 | 66 | 15 | 19 | 45 | 19 | 32 | 3.7 | 49 |
| Cymbella turgidula Grun. | CMturgdl | 243 | 144 | 410 | 1.93 | 0.13 | 0.11 | 1.46 | 0.41 | 0.13* | 0.04 | 86** | 7* | 7* | 67** | 24 | 8* | 1.8 | 57 |
| Reimeria sinuata (Greg.) Koc. & Stoermer | 251 | 107 | 587 | 1.47 | 0.22 | 0.33 | 1.28 | 0.53 | 0.40 | 0.04 | 65 | 16 | 19 | 54 | 23 | 21 | 2.4 | 1385 | |
| Synedra ulna (Nitzsch) Ehr. | 252 | 102 | 627 | 1.44 | 0.28 | 0.30 | 1.26 | 0.55 | 0.42 | 0.05 | 64 | 18 | 18 | 52 | 24 | 22 | 2.6 | 1311 | |
| Cymbella hustedti Krass. | CMhust | 254 | 189 | 340 | 1.94 | 0.08* | 0.11 | 1.69 | 0.35 | 0.09* | 0.03* | 88** | 5* | 7* | 77** | 17* | 5* | 1.3 | 48 |
| Achnanthes rostrataØstrup | 255 | 109 | 593 | 1.48 | 0.23 | 0.23 | 1.22 | 0.51 | 0.35 | 0.05 | 69 | 16 | 15 | 53 | 24 | 20 | 2.9 | 921 | |
| Gomphonema pumilum (Grun.) Reichardt | 260 | 108 | 627 | 1.58 | 0.24 | 0.28 | 1.25 | 0.53 | 0.45 | 0.06 | 68 | 15 | 16 | 51 | 23 | 23 | 3.0 | 863 | |
| Cocconeis fluviatilis Wallace | CCfluv | 261 | 98 | 692 | 0.59 | 0.63 | 0.30 | 0.63 | 0.39 | 0.71 | 0.08 | 39* | 39** | 22 | 35* | 21 | 40** | 4.5 | 83 |
| Gomphonema sphaerophorum Ehr. | 262 | 169 | 408 | 1.57 | 0.26 | 0.23 | 1.44 | 0.47 | 0.27 | 0.04 | 70 | 18 | 13 | 61** | 21 | 16 | 2 | 64 | |
| Gomphonema angustatum Kütz. | 264 | 106 | 659 | 1.31 | 0.20 | 0.28 | 1.21 | 0.54 | 0.30 | 0.04 | 65 | 16 | 19 | 54 | 25 | 18 | 2.9 | 637 | |
| Achnanthes exilis Kütz. | 266 | 97 | 731 | 1.44 | 0.19 | 0.24 | 1.21 | 0.56 | 0.21 | 0.03 | 71 | 12 | 17 | 58 | 27 | 13* | 2.2 | 47 | |
| Epithemia sorex Kütz. | EPsorex | 266 | 116 | 611 | 2.00 | 0.22 | 0.47 | 1.45 | 0.64 | 0.67 | 0.06 | 68 | 11 | 21 | 48 | 22 | 27 | 2.3 | 205 |
| Cymbella delicatula Kütz. | 269 | 135 | 533 | 1.75 | 0.10* | 0.20 | 1.48 | 0.60 | 0.13* | 0.03 | 78** | 6* | 16 | 63** | 28 | 8* | 1.6 | 204 | |
| Cocconeis placentula var. lineata (Ehr.) V.H. | 270 | 111 | 655 | 1.64 | 0.31 | 0.33 | 1.35 | 0.61 | 0.49 | 0.05 | 65 | 18 | 16 | 51 | 24 | 23 | 2.3 | 1340 | |
| Staurosirella pinnata (Ehr.) Will. & Round | 271 | 110 | 665 | 1.66 | 0.25 | 0.32 | 1.29 | 0.61 | 0.50 | 0.05 | 67 | 15 | 17 | 49 | 24 | 24 | 2.6 | 815 | |
| Epithemia adnata (Kütz.) Bréb. | 279 | 104 | 746 | 2.11 | 0.17 | 0.21 | 1.59 | 0.75 | 0.29 | 0.04 | 76 | 13 | 11* | 54 | 27 | 17 | 2 | 68 | |
| Gomphonema parvulum (Kütz.) Kütz. | 284 | 101 | 794 | 1.33 | 0.39 | 0.34 | 1.21 | 0.55 | 0.53 | 0.06 | 59 | 22 | 19 | 48 | 23 | 25 | 3.4 | 1898 | |
| Achnanthes lanceolata (Bréb.) Grun. | 286 | 114 | 719 | 1.52 | 0.30 | 0.32 | 1.27 | 0.60 | 0.47 | 0.05 | 65 | 17 | 17 | 50 | 24 | 22 | 2.9 | 1330 | |
| Nitzschia archibaldii L.-B. | 288 | 114 | 728 | 1.51 | 0.38 | 0.37 | 1.31 | 0.57 | 0.57 | 0.07 | 61 | 20 | 19 | 49 | 23 | 25 | 3.3 | 726 | |
| Navicula submuralis Hust. | 290 | 163 | 515 | 1.93 | 0.38 | 0.22 | 1.34 | 0.49 | 0.54 | 0.06 | 71 | 18 | 11* | 50 | 21 | 27 | 2.4 | 28 | |
| Nitzschia sinuata var. tabellaria (Grun.) Grun. | 294 | 155 | 557 | 1.87 | 0.21 | 0.32 | 1.69 | 0.52 | 0.24 | 0.05 | 72 | 11 | 17.4 | 64** | 22 | 13* | 2 | 164 | |
| Fragilaria exiguiformis L.-B. | FRexiguif | 296 | 95 | 920 | 1.18 | 0.44 | 0.59 | 1.17 | 0.46 | 0.86 | 0.06 | 50 | 23 | 27 | 44.5 | 18 | 35** | 2.6 | 61 |
| Staurosira construens var. venter (Ehr.) Ham. | SRvent | 300 | 109 | 822 | 1.60 | 0.31 | 0.44 | 1.36 | 0.62 | 0.66 | 0.07 | 61 | 17 | 22 | 47 | 22 | 27 | 2.9 | 617 |
| Sellaphora seminulum (Grun.) Mann | 305 | 131 | 714 | 1.42 | 0.43 | 0.31 | 1.22 | 0.57 | 0.55 | 0.06 | 60 | 23 | 17 | 48 | 23 | 26 | 3.2 | 706 | |
| Placoneis placentula (Ehr.) Hienzerling | 308 | 157 | 607 | 1.55 | 0.52 | 0.42 | 1.58 | 0.47 | 0.69 | 0.07 | 57 | 23 | 20 | 53 | 17* | 26 | 3.3 | 47 | |
| Melosira varians Agardh | 309 | 138 | 690 | 1.66 | 0.36 | 0.36 | 1.40 | 0.70 | 0.49 | 0.06 | 64 | 18 | 18 | 50 | 26 | 22 | 2.7 | 1203 | |
| Gomphonema lingulatiforme L.-B. & Reich. | 313 | 117 | 834 | 1.80 | 0.48 | 0.30 | 1.43 | 0.49 | 0.66 | 0.07 | 64 | 22 | 13.7 | 50 | 18* | 28 | 3.3 | 130 | |
| Psammothidium lauenburgianum (Hust.) Round & Bukht. | 317 | 159 | 631 | 2.88 | 0.25 | 0.30 | 1.94 | 1.33 | 0.34 | 0.04 | 81** | 9 | 10* | 52 | 36** | 11* | 1.3* | 30 | |
| Navicula minima Grun. | NAmin | 319 | 140 | 729 | 1.71 | 0.35 | 0.31 | 1.44 | 0.64 | 0.44 | 0.06 | 66 | 18 | 15 | 52 | 25 | 21 | 2.9 | 1672 |
| Gomphonema mehleri Camburn | 318 | 215 | 472 | 2.51 | 0.10 | 0.15 | 1.92 | 0.67 | 0.12* | 0.04 | 85** | 4* | 11* | 66** | 29** | 5* | 1.4* | 52 | |
| Gomphonema minutum (Ag.) Ag. | 324 | 131 | 802 | 1.90 | 0.27 | 0.38 | 1.64 | 0.74 | 0.42 | 0.04 | 67 | 14 | 18 | 55 | 26 | 18 | 1.9 | 767 | |
| Cocconeis placentula var. euglypta Ehr. | 326 | 146 | 726 | 2.00 | 0.30 | 0.34 | 1.57 | 0.71 | 0.47 | 0.06 | 70 | 14 | 16 | 52 | 25 | 20 | 2.4 | 1262 | |
| Nitzschia sinuata var. delognei (Grun.) L.-B. | 335 | 231 | 485 | 2.48 | 0.19 | 0.30 | 1.76 | 0.75 | 0.33 | 0.04 | 80** | 8* | 12 | 57 | 26 | 16 | 1.6 | 25 | |
| Gomphonema mexicanum Grun. | GOmex | 338 | 147 | 778 | 2.07 | 0.43 | 0.21 | 1.24 | 0.65 | 0.72 | 0.09 | 72 | 19 | 9* | 44 | 23 | 29 | 3.5 | 35 |
| Rhopalodia gibba (Ehr.) Müller | RPgibba | 339 | 122 | 942 | 2.39 | 0.32 | 0.58 | 1.78 | 0.80 | 0.92 | 0.07 | 66 | 14 | 20 | 47 | 22 | 29 | 2.1 | 123 |
| Navicula germanii Wallace | 339 | 149 | 769 | 1.80 | 0.50 | 0.42 | 1.50 | 0.71 | 0.67 | 0.07 | 62 | 20 | 18 | 48 | 24 | 25 | 3.0 | 975 | |
| Sellaphora pupula (Kütz.) Mereschkowsky | 342 | 143 | 820 | 1.74 | 0.42 | 0.42 | 1.52 | 0.65 | 0.64 | 0.07 | 61 | 20 | 19 | 49 | 22 | 25 | 3.1 | 1064 | |
| Ctenophora pulchella (Ralfs ex Kütz.) Will. & Round | Cpulch | 342 | 163 | 716 | 0.86 | 0.67 | 0.53 | 1.18 | 0.57 | 0.70 | 0.06 | 41 | 32 | 27 | 45 | 22 | 30 | 2.7 | 66 |
| Navicula stroemii Hust. | NAstroem | 343 | 115 | 1021 | 1.98 | 0.20 | 0.65 | 1.79 | 0.98 | 0.30 | 0.03 | 65 | 8* | 27 | 56 | 30** | 12* | 1.4* | 26 |
| Cymbella affinis Kütz. | 347 | 170 | 708 | 2.28 | 0.21 | 0.41 | 1.95 | 0.76 | 0.37 | 0.05 | 70 | 10 | 20 | 58 | 25 | 16 | 1.8 | 870 | |
| Diatoma vulgaris Bory | 355 | 188 | 670 | 2.10 | 0.35 | 0.48 | 1.75 | 0.80 | 0.56 | 0.05 | 66 | 15 | 19 | 52 | 25 | 21 | 2.1 | 693 | |
| Achnanthes exigua var. elliptica Hust. | 359 | 207 | 622 | 1.67 | 0.78 | 0.54 | 1.77 | 0.59 | 0.82 | 0.11** | 53 | 26 | 21.6 | 53 | 19 | 25 | 3.3 | 26 | |
| Diatoma moniliformis Kütz. | DAmonil | 361 | 168 | 774 | 0.84 | 0.14 | 0.85 | 1.20 | 0.70 | 0.33 | 0.04 | 45 | 10 | 45** | 52 | 30** | 16 | 1.9 | 91 |
| Nitzschia dissipata (Kütz.) Grun. | 361 | 152 | 855 | 2.12 | 0.35 | 0.50 | 1.80 | 0.85 | 0.56 | 0.06 | 65 | 15 | 20 | 52 | 25 | 21 | 2.2 | 1324 | |
| Navicula menisculus Schumann | 361 | 165 | 791 | 2.39 | 0.33 | 0.41 | 1.94 | 0.83 | 0.46 | 0.06 | 70 | 14 | 16 | 55 | 25 | 18 | 2.1 | 655 | |
| Navicula‘aff. subminuscula NAWQA EAM’ | 364 | 222 | 597 | 2.94 | 0.24 | 0.27 | 1.98 | 0.92 | 0.29 | 0.05 | 80** | 9 | 11* | 57 | 28 | 14* | 1.6 | 33 | |
| Navicula capitata Ehr. | NAcapita | 366 | 147 | 908 | 1.77 | 0.51 | 0.42 | 1.53 | 0.77 | 0.65 | 0.07 | 60 | 22 | 18 | 48 | 25 | 24 | 2.9 | 709 |
| Nitzschia palea var. tenuirostris Grun. | 368 | 159 | 853 | 1.93 | 0.47 | 0.41 | 1.64 | 0.97 | 0.55 | 0.06 | 64 | 20 | 16 | 49 | 29** | 19 | 2.4 | 192 | |
| Caloneis bacillum (Grun.) Cl. | 369 | 165 | 824 | 2.02 | 0.40 | 0.46 | 1.79 | 0.75 | 0.60 | 0.06 | 63 | 18 | 19 | 52 | 23 | 22 | 2.3 | 824 | |
| Navicula cryptotenella L.-B. | 371 | 168 | 817 | 2.21 | 0.35 | 0.43 | 1.87 | 0.86 | 0.52 | 0.05 | 67 | 15 | 18 | 53 | 26 | 19 | 2.1 | 1620 | |
| Encyonopsis microcephala (Grun.) Kram. | 380 | 169 | 857 | 2.20 | 0.23 | 0.40 | 2.20 | 0.76 | 0.35 | 0.04 | 67 | 10 | 23 | 62** | 23 | 13* | 1.5* | 295 | |
| Rhoicosphenia curvata (Kütz.) Grun. | 384 | 173 | 851 | 2.08 | 0.48 | 0.51 | 1.78 | 0.87 | 0.68 | 0.06 | 62 | 19 | 19 | 50 | 25 | 23 | 2.2 | 1548 | |
| Synedra delicatissima W. Smith | 386 | 119 | 1253 | 1.95 | 0.33 | 0.10 | 1.96 | 0.50 | 0.56 | 0.03 | 68 | 12 | 20 | 60** | 18 | 20 | 1.5* | 33 | |
| Navicula symmetrica Patrick | 388 | 172 | 877 | 2.18 | 0.50 | 0.51 | 1.74 | 0.86 | 0.79 | 0.07 | 63 | 18 | 19 | 48 | 25 | 24 | 2.7 | 608 | |
| Navicula capitatoradiata Germ. | 390 | 195 | 782 | 2.33 | 0.36 | 0.49 | 1.96 | 0.90 | 0.52 | 0.06 | 67 | 14 | 19 | 54 | 26 | 19 | 2.1 | 1194 | |
| Navicula gregaria Donkin | 392 | 169 | 910 | 1.95 | 0.58 | 0.53 | 1.70 | 0.86 | 0.76 | 0.07 | 59 | 21 | 20 | 48 | 25 | 24 | 2.4 | 1344 | |
| Nitzschia palea (Kütz.) W. Smith | 398 | 170 | 933 | 2.08 | 0.53 | 0.55 | 1.82 | 0.87 | 0.77 | 0.08 | 60 | 20 | 20 | 49 | 24 | 24 | 2.7 | 1522 | |
| Diploneis parma Cl. | 398 | 162 | 979 | 1.12 | 0.59 | 0.26 | 1.04 | 0.53 | 0.81 | 0.06 | 54 | 36 | 10* | 40 | 19 | 38** | 2.9 | 35 | |
| Nitzschia amphibia Grunow | 400 | 201 | 794 | 2.26 | 0.51 | 0.45 | 1.87 | 0.81 | 0.69 | 0.07 | 65 | 19 | 16 | 51 | 24 | 23 | 2.5 | 1456 | |
| Navicula lanceolata (Ag.) Ehr. | 406 | 196 | 843 | 1.94 | 0.59 | 0.63 | 1.83 | 0.92 | 0.81 | 0.06 | 56 | 21 | 23 | 49 | 25 | 24 | 2.0 | 679 | |
| Nitzschia inconspicua Grun. | 407 | 167 | 995 | 2.07 | 0.55 | 0.65 | 1.77 | 0.88 | 0.92 | 0.08 | 58 | 20 | 22 | 47 | 24 | 27 | 2.5 | 1374 | |
| Nitzschia frustulum (Kütz.) Grun. | 413 | 177 | 962 | 2.08 | 0.45 | 0.55 | 1.72 | 0.84 | 0.79 | 0.07 | 62 | 18 | 20 | 48 | 24 | 26 | 2.7 | 1153 | |
| Nitzschia heufleriana Grun. | 416 | 215 | 805 | 2.56 | 0.35 | 0.71 | 2.11 | 1.08 | 0.72 | 0.05 | 65 | 12 | 23 | 50 | 26 | 22 | 1.5* | 45 | |
| Amphora libyca Ehr. | 416 | 188 | 918 | 2.38 | 0.47 | 0.53 | 2.05 | 0.92 | 0.67 | 0.07 | 64 | 17 | 19 | 52 | 25 | 21 | 2.3 | 582 | |
| Cocconeis pediculus Ehr. | 422 | 223 | 798 | 2.59 | 0.41 | 0.62 | 2.26 | 1.03 | 0.61 | 0.06 | 65 | 15 | 20 | 54 | 25 | 19 | 1.8 | 969 | |
| Achnanthes pinnata Hust. | ACpin | 424 | 200 | 895 | 3.18 | 0.79 | 0.59 | 2.52 | 1.39 | 0.68 | 0.06 | 67 | 20 | 13 | 51 | 29** | 18 | 1.6 | 44 |
| Diploneis pseudovalis Hust. | 434 | 183 | 1026 | 2.70 | 0.70 | 0.48 | 2.39 | 0.63 | 0.99 | 0.06 | 65 | 20 | 16 | 56 | 17* | 25 | 1.8 | 52 | |
| Denticula elegans Kütz. | 436 | 226 | 838 | 2.48 | 0.30 | 0.87 | 2.59 | 0.86 | 0.55 | 0.07 | 62 | 10 | 28** | 59 | 21 | 18 | 2.1 | 81 | |
| Nitzschia filiformis (W. Smith) V. H. | 436 | 120 | 1581 | 1.20 | 0.80 | 0.57 | 1.26 | 0.69 | 1.19 | 0.09 | 47 | 30 | 23 | 41 | 20 | 36** | 3.1 | 163 | |
| Navicula trivialis L.-B. | NAtriv | 440 | 234 | 826 | 2.74 | 0.45 | 0.45 | 2.19 | 1.07 | 0.51 | 0.07 | 70 | 15 | 14 | 54 | 28 | 16 | 2.2 | 670 |
| Surirella suecica Grun. | 442 | 199 | 982 | 2.16 | 0.46 | 0.54 | 1.96 | 0.58 | 0.83 | 0.07 | 62 | 17 | 21 | 53 | 18* | 27 | 2.9 | 32 | |
| Navicula reichardtiana L.-B. | 442 | 225 | 867 | 2.68 | 0.39 | 0.59 | 2.31 | 1.08 | 0.56 | 0.06 | 66 | 14 | 19 | 54 | 26 | 17 | 1.7 | 764 | |
| Navicula lenzii Hust. | 444 | 233 | 843 | 2.94 | 0.29 | 0.33 | 2.45 | 0.98 | 0.29 | 0.05 | 75 | 11 | 14 | 61** | 26 | 11* | 1.8 | 48 | |
| Achnanthes daui Foged | ACdaui | 448 | 194 | 1033 | 2.56 | 0.37 | 1.09** | 2.03 | 0.91 | 1.39 | 0.18** | 58 | 11 | 32** | 44 | 19 | 33 | 4.1 | 34 |
| Navicula tripunctata (Müller) Bory | 453 | 249 | 822 | 2.81 | 0.44 | 0.61 | 2.41 | 1.10 | 0.61 | 0.06 | 67 | 14 | 19 | 55 | 26 | 18 | 1.7 | 1039 | |
| Nitzschia acicularis (Kütz.) W. Smith | 455 | 211 | 982 | 2.61 | 0.48 | 0.56 | 2.13 | 1.13 | 0.72 | 0.07 | 65 | 16 | 18 | 50 | 27 | 21 | 2.2 | 518 | |
| Nitzschia palea var. debilis (Kütz.) Grun. | 460 | 214 | 989 | 2.56 | 0.52 | 0.61 | 2.06 | 1.12 | 0.79 | 0.08 | 64 | 17 | 19 | 48 | 27 | 22 | 2.6 | 595 | |
| Surirella minuta Bréb. | 462 | 209 | 1023 | 2.49 | 0.50 | 0.61 | 2.13 | 1.11 | 0.65 | 0.07 | 63 | 17 | 20 | 51 | 27 | 20 | 2.4 | 661 | |
| Gomphonema olivaceum (Horn.) Bréb. | 468 | 234 | 935 | 2.79 | 0.47 | 0.74 | 2.43 | 1.22 | 0.71 | 0.06 | 63 | 15 | 22 | 52 | 27 | 19 | 1.7 | 733 | |
| Fallacia pygmaea (Kütz.) Stickle & Mann | 469 | 228 | 964 | 2.54 | 0.54 | 0.64 | 2.13 | 1.04 | 0.78 | 0.08 | 63 | 17 | 20 | 50 | 25 | 22 | 2.6 | 533 | |
| Amphora pediculus (Kütz.) Grun. | AMped | 470 | 242 | 912 | 2.75 | 0.51 | 0.60 | 2.35 | 1.14 | 0.67 | 0.06 | 65 | 17 | 18 | 53 | 26 | 19 | 1.7 | 1626 |
| Gomphonema affine Kütz. | 481 | 275 | 839 | 2.96 | 0.50 | 0.48 | 2.32 | 1.29 | 0.51 | 0.05 | 73 | 15 | 13 | 53 | 30** | 14 | 1.8 | 67 | |
| Navicula subminuscula Manguin | 495 | 253 | 971 | 2.68 | 0.58 | 0.68 | 2.12 | 1.03 | 0.89 | 0.09 | 63 | 18 | 19 | 48 | 24 | 25 | 2.6 | 678 | |
| Craticula citrus (Krass.) Reichardt | CRcitr | 499 | 356 | 700 | 3.62** | 0.58 | 0.48 | 2.67 | 1.56** | 0.79 | 0.09 | 74 | 13 | 13 | 51 | 30** | 17 | 2.1 | 54 |
| Surirella brebissonii Kram. & L.-B. | 504 | 233 | 1090 | 2.02 | 0.71 | 0.86 | 2.06 | 1.72** | 1.04 | 0.09 | 52 | 24 | 25 | 45 | 24 | 28 | 3 | 156 | |
| Nitzschia pusilla Grun. | 505 | 165 | 1545 | 1.81 | 0.40 | 0.73 | 1.57 | 0.79 | 0.93 | 0.08 | 54 | 17 | 28** | 45 | 23 | 30 | 2.9 | 88 | |
| Navicula ingenua Hust. | 508 | 218 | 1183 | 1.71 | 1.00** | 0.43 | 1.52 | 0.70 | 1.14 | 0.07 | 52 | 33 | 15 | 43 | 21 | 34 | 2.4 | 61 | |
| Amphora veneta Kütz. | 515 | 246 | 1079 | 2.90 | 0.89 | 0.79 | 2.39 | 0.98 | 1.47** | 0.11** | 59 | 22 | 19 | 46 | 20 | 31 | 2.5 | 180 | |
| Navicula viridula (Kütz.) Kütz. | 515 | 229 | 1159 | 2.74 | 0.65 | 0.86 | 3.08** | 1.24 | 0.64 | 0.06 | 57 | 18 | 25 | 58 | 24 | 17 | 1.6 | 121 | |
| Mastogloia smithii Thwaites | MSsmith | 519 | 249 | 1079 | 3.52** | 0.48 | 0.53 | 2.88** | 1.36 | 0.61 | 0.04 | 72 | 12 | 16 | 57 | 27 | 16 | 0.8* | 38 |
| Surirella brebissonii var. kuetzingii Kram. & L.-B. | 520 | 254 | 1067 | 3.16 | 0.65 | 0.63 | 2.48 | 1.41 | 0.71 | 0.06 | 68 | 17 | 15 | 51 | 29** | 18 | 1.4* | 31 | |
| Nitzschia filiformis var. conferta (Reich.) L.-B. | NIfilcon | 521 | 130 | 2089 | 1.29 | 1.29** | 0.57 | 1.14 | 1.04 | 1.69** | 0.11** | 48 | 37 | 15 | 32* | 23 | 42** | 2.8 | 27 |
| Gyrosigma nodiferum (Grun.) Reimer | 522 | 250 | 1091 | 3.03 | 0.75 | 0.80 | 2.52 | 0.80 | 1.32 | 0.07 | 63 | 19 | 18 | 51 | 17* | 30 | 1.9 | 132 | |
| Simonsenia delognei (Grun.) L.-B. | 524 | 304 | 902 | 3.27 | 0.70 | 0.53 | 2.45 | 1.55** | 0.73 | 0.06 | 68 | 18 | 14 | 49 | 32** | 18 | 1.5 | 181 | |
| Navicula caterva Hohn & Hellerman | 525 | 292 | 942 | 3.52** | 0.56 | 0.64 | 2.62 | 1.43** | 0.72 | 0.06 | 69 | 15 | 16 | 52 | 28 | 19 | 1.4* | 110 | |
| Navicula salinarum Grun. | NAsalin | 527 | 243 | 1146 | 2.25 | 1.32** | 0.68 | 1.90 | 1.16 | 1.24 | 0.08 | 51 | 32 | 17 | 42 | 26 | 29 | 2.6 | 51 |
| Trybionella levidensis W. Smith | 541 | 268 | 1091 | 2.89 | 0.92 | 1.03 | 2.44 | 0.95 | 1.47** | 0.10** | 56 | 22 | 22 | 46 | 20 | 32 | 2.4 | 125 | |
| Nitzschia elegantula Grun. | 541 | 207 | 1416 | 2.79 | 0.39 | 1.07** | 2.32 | 1.19 | 1.16 | 0.11** | 57 | 14 | 29** | 47 | 23 | 27 | 2.8 | 37 | |
| Navicula exilis Kütz. | 547 | 308 | 973 | 3.28 | 0.81 | 0.63 | 2.54 | 1.58** | 0.90 | 0.07 | 65 | 19 | 16 | 48 | 30** | 20 | 1.8 | 261 | |
| Sellaphora pupula var. elliptica (Hust.) Bukht. | SEpupell | 551 | 332 | 914 | 3.44** | 0.63 | 0.64 | 2.85** | 1.78** | 0.64 | 0.07 | 68 | 16 | 16 | 52 | 32** | 15 | 1.4* | 28 |
| Nitschia silicula Archibald | 553 | 299 | 1026 | 3.74** | 0.88 | 0.81 | 2.92** | 1.58** | 1.29 | 0.09 | 63 | 19 | 18 | 47 | 27 | 25 | 1.7 | 71 | |
| Nitzschia dubia W. Smith | 553 | 225 | 1361 | 2.56 | 1.27** | 0.57 | 1.81 | 1.28 | 1.37 | 0.07 | 56 | 29 | 15 | 40 | 26 | 32 | 1.6 | 30 | |
| Diploneis puella (Schumann) Cl. | 569 | 290 | 1117 | 2.54 | 0.81 | 1.06** | 2.53 | 0.9 | 1.3 | 0.1 | 54 | 21 | 26 | 49 | 20 | 29 | 2.6 | 158 | |
| Cymatopleura apiculata W. Smith | CTap | 573 | 406 | 807 | 3.78** | 0.77 | 0.67 | 2.99** | 1.82** | 0.68 | 0.07 | 70 | 16 | 14 | 52 | 32** | 15 | 1.2* | 54 |
| Pleurosira laevis (Ehr.) Compère | 573 | 292 | 1122 | 2.70 | 1.08** | 0.80 | 2.28 | 1.50** | 1.40 | 0.11** | 53 | 27 | 21 | 41.2 | 27 | 30 | 2.4 | 44 | |
| Plagiotropis lepidoptera var. proboscidea (Cl.) Reimer | 582 | 277 | 1225 | 3.01 | 1.47** | 1.01 | 2.56 | 0.92 | 1.87** | 0.11** | 54 | 27 | 19 | 46 | 18* | 34** | 2.2 | 34 | |
| Navicula erifuga L.-B. | 613 | 298 | 1262 | 2.92 | 0.66 | 0.96 | 2.55 | 1.38 | 1.15 | 0.10 | 58 | 17 | 24 | 47 | 26 | 25 | 2.2 | 625 | |
| Navicula recens L.-B. | 614 | 345 | 1091 | 3.05 | 1.06** | 1.21** | 2.80 | 1.19 | 1.53** | 0.09 | 55 | 22 | 24 | 47 | 22 | 29 | 1.9 | 319 | |
| Terpsinoe musica Ehr. | 615 | 397 | 953 | 3.45** | 1.47** | 0.87 | 3.25** | 0.71 | 1.88** | 0.09 | 58 | 25 | 17 | 53 | 13* | 32 | 1.9 | 35 | |
| Navicula sanctaecrucisØstrup | 619 | 385 | 995 | 3.20 | 1.30** | 1.16** | 3.13** | 0.93 | 1.83** | 0.10** | 55 | 24 | 22 | 50 | 17* | 31 | 2.1 | 81 | |
| Denticula kuetzingii Grun. | DNkuetz | 622 | 290 | 1334 | 3.66** | 0.35 | 1.04** | 2.80 | 1.52** | 1.31 | 0.06 | 62 | 9* | 29** | 46 | 26 | 27 | 1.3* | 34 |
| Navicula veneta Kütz. | NAveneta | 625 | 304 | 1285 | 2.95 | 0.48 | 1.08** | 2.70 | 1.24 | 1.04 | 0.10 | 58 | 14 | 28** | 50 | 24 | 24 | 2.5 | 442 |
| Surirella brightwellii W. Smith | 630 | 366 | 1081 | 3.22 | 1.11** | 0.93 | 3.05** | 1.22 | 1.69** | 0.10 | 55 | 27 | 18 | 48 | 20 | 30 | 1.8 | 26 | |
| Amphora‘sp. 1 ANS WRC’ | 634 | 429 | 938 | 3.44** | 1.65** | 1.65** | 3.69** | 1.01 | 2.30** | 0.11** | 49 | 24 | 27 | 50 | 15* | 33 | 1.9 | 37 | |
| Nitzschia liebetruthii Rab. | 653 | 282 | 1510 | 2.13 | 0.73 | 1.01 | 2.28 | 0.81 | 1.21 | 0.11** | 50 | 19 | 31** | 50 | 19 | 29 | 2.7 | 66 | |
| Nitzschia supralitorea L.-B. | 656 | 242 | 1778 | 2.70 | 0.69 | 0.84 | 2.20 | 1.20 | 1.54** | 0.08 | 59 | 22 | 19 | 43 | 22 | 33 | 2 | 68 | |
| Tryblionella hungarica (Grun.) Mann | 667 | 366 | 1213 | 3.38** | 0.82 | 1.09** | 3.07** | 1.42** | 1.29 | 0.10 | 58 | 18 | 24 | 49 | 24 | 25 | 1.9 | 265 | |
| Pleurosigma salinarum Grun. | 673 | 454 | 998 | 3.62** | 1.46** | 1.21** | 3.42** | 1.22 | 1.97** | 0.10** | 56 | 24 | 20 | 49 | 18 | 31 | 1.7 | 38 | |
| Nitzschia solita Hust. | 676 | 341 | 1340 | 3.05 | 0.57 | 0.93 | 2.63 | 1.37 | 1.09 | 0.10 | 60 | 15 | 25 | 48 | 26 | 24 | 2.3 | 212 | |
| Nitzschia bita Hohn & Hellerman | NBita | 695 | 433 | 1117 | 3.86** | 1.24** | 1.27** | 3.32** | 1.05 | 2.22** | 0.08 | 59 | 21 | 20 | 48 | 17* | 33 | 1.4* | 35 |
| Tryblionella apiculata Greg. | TYapi | 695 | 384 | 1259 | 3.55** | 0.81 | 1.15** | 3.05** | 1.60** | 1.30 | 0.08 | 59 | 17 | 23 | 48 | 26 | 25 | 1.6 | 325 |
| Navicula salinicola Hustedt | NAsalc | 697 | 150 | 3228 | 1.16 | 1.48** | 0.80 | 1.47 | 1.14 | 2.31** | 0.13** | 38* | 40** | 22 | 34* | 20 | 43** | 2.8 | 29 |
| Nitzschia reversa W. Smith | 703 | 306 | 1614 | 2.62 | 0.91 | 1.34** | 2.49 | 1.55** | 1.77** | 0.12** | 49 | 21 | 30** | 41 | 25 | 32 | 2.3 | 88 | |
| Tabularia fasciculata (Ag.) Snoeijs | TAfasc | 719 | 181 | 2858 | 1.80 | 1.29** | 0.60 | 1.69 | 1.17 | 1.47** | 0.09 | 50 | 33 | 17 | 40 | 25 | 34 | 2.1 | 109 |
| Nitzschia umbonata (Ehr.) L.-B. | Numb | 759 | 476 | 1208 | 4.14** | 0.96 | 1.14** | 3.42** | 1.98** | 1.22 | 0.08 | 63 | 18 | 19 | 49 | 29** | 21 | 1.2* | 28 |
| Biremis circumtexta (Meist. ex Hust.) L.-B. & Witkowski | BIcircum | 902 | 461 | 1762 | 3.52** | 0.62 | 2.07** | 3.03** | 2.20** | 1.21 | 0.19** | 53 | 12 | 35** | 42 | 30** | 24 | 3.4 | 36 |
- * - extremely low, ** - extremely high optimum.
Discussion
Effect of conductivity
The relative position of species along the conductivity gradient in this study generally corresponds to the affinities reported by others. Many species with low conductivity optima were classified as halophobous by Kolbe (1927, 1932), Hustedt (1957) and other authors. Species commonly classified as halophilous or mesohalobous had relatively high, but probably underestimated, conductivity optima in our study. Species that are known to be abundant in brackish waters, such as Diatoma moniliformis, Ctenophora pulchella and Tabularia fasciculata, had apparent optima below 1000 μS cm−1, which could be considered as a boundary between brackish and freshwaters. This underestimation of optima may be caused by the relatively low occurrence of brackish waters in our dataset and, hence, the truncated distribution of T. fasciculata and other species with relatively high position along the gradient of conductivity. The placement of optima of other brackish water species far from the high end of the conductivity gradient (i.e. D. moniliformis, C. pulchella) is more difficult to explain. Possibly, some populations in the NAWQA dataset could be freshwater ecotypes of those species. The apparent conductivity optima reported from some regional studies on U.S. rivers differ considerably from our results, but the rank of the diatom taxa on the conductivity scale is usually the same or nearly so. Optima reported by Bahls, Weber & Jarvie (1984) were generally much higher than those reported in the present study because conductivity was higher (median value 1752 μS cm−1) in their Montana dataset. Conductivity optima reported by Leland, Brown & Mueller (2001) for California rivers were somewhat lower for the taxa with relatively low optima, and higher for diatoms with relatively high optima.
Effect of major ions
In most earlier studies of diatom species distribution in relation to salinity, the salinity gradient was primarily the result of a variation in concentration of a single salt, NaCl (Kolbe, 1927, 1932; Hustedt, 1957). As a result, it was difficult to distinguish the effects of specific ions from the overall effect of osmotic pressure. Hustedt (1957) noted that diatoms of continental waters respond mostly to osmotic pressure, and not the concentration of a particular salt. Experiments also showed that osmotic pressure in the medium is an important factor limiting growth of freshwater diatoms (Cleave, Porcella & Adams, 1981), or influencing their nutrient uptake (Tuchman, Theriot & Stoermer, 1984). As a result, conductivity or other measures of total ionic strength often explain much of the variation among diatom assemblages.
The importance of ionic composition to diatom distributions became obvious when datasets including various water types were studied. Investigations by Blinn (1993), Fritz, Juggins & Battarbee (1993), Gasse, Juggins & Ben Khelifa (1995), and Cumming et al. (1995) elucidated the importance of ionic composition in accounting for differences in diatom assemblages in saline lakes. Inclusion of different water types in river datasets revealed the importance of water chemistry for diatom community structure in lotic environments (e.g. Cholnoky, 1968; Sabater & Roca, 1992; Ziemann, 1997). Laboratory data provided additional evidence that concentration of specific ions influences growth of diatoms (e.g. Kopczyńska, 1979; Rao, Duraisamy & Kannan, 1983; Saros & Fritz, 2000, 2002). Patrick & Reimer (1966), Ziemann (1971, 1997), Sabater & Roca (1992), Round & Bukhtiyarova (1996), and Pipp (1997) pointed out the great difference between diatom communities in calcareous and calcium-poor rivers. In our study, the gradient of (Ca2+) and (HCO + CO
+ CO ) was the strongest among all variables related to major ions. We were able to distinguish species at the lower end of the conductivity gradient that had either high or low affinity towards calcium bicarbonate type of water. Not surprisingly, species with known low pH optima (Eunotia and Frustulia spp.) had lower optima for [Ca2+] and [HCO
) was the strongest among all variables related to major ions. We were able to distinguish species at the lower end of the conductivity gradient that had either high or low affinity towards calcium bicarbonate type of water. Not surprisingly, species with known low pH optima (Eunotia and Frustulia spp.) had lower optima for [Ca2+] and [HCO + CO
+ CO ] than alkaliphilous species of the genera Gomphonema, Gomphoneis, Cymbella, and diatoms Hannaea arcus and Diatoma mesodon. Sabater & Roca (1992) noted that calcareous springs in the Pyrenees were dominated by various species of Cymbella, along with Denticula tenuis and Achnanthes minutissima. In our dataset, the species with highest affinity towards calcium also belonged mainly to the genus Cymbella (Table 3, Fig. 3a). Calciphilous Cymbella and Gomphonema also have relatively high optima for [HCO
] than alkaliphilous species of the genera Gomphonema, Gomphoneis, Cymbella, and diatoms Hannaea arcus and Diatoma mesodon. Sabater & Roca (1992) noted that calcareous springs in the Pyrenees were dominated by various species of Cymbella, along with Denticula tenuis and Achnanthes minutissima. In our dataset, the species with highest affinity towards calcium also belonged mainly to the genus Cymbella (Table 3, Fig. 3a). Calciphilous Cymbella and Gomphonema also have relatively high optima for [HCO + CO
+ CO ], and it is difficult to distinguish the effect of that factor from the effect of [Ca2+]. Some studies have shown that calcium affects diatom motility (Cohn & Disparti, 1994) and adhesion to surfaces (Cooksey & Cooksey, 1988), but exact physiological mechanisms responsible for the higher or lower affinity of diatoms to calcium (or the other alkaline cations) are still not known. Furthermore, concentration of divalent cations (Ca2+ and Mg2+) is highly correlated with the amount of dissolved HCO
], and it is difficult to distinguish the effect of that factor from the effect of [Ca2+]. Some studies have shown that calcium affects diatom motility (Cohn & Disparti, 1994) and adhesion to surfaces (Cooksey & Cooksey, 1988), but exact physiological mechanisms responsible for the higher or lower affinity of diatoms to calcium (or the other alkaline cations) are still not known. Furthermore, concentration of divalent cations (Ca2+ and Mg2+) is highly correlated with the amount of dissolved HCO and pH. It is not clear which of these factors has the greatest effect on the growth of diatoms.
and pH. It is not clear which of these factors has the greatest effect on the growth of diatoms.
Species with relatively high per cent equivalent optima for Mg2+ (Bizemis circumtexta, Nitzschia umbonata, Cymatopleura apiculata, Sellaphora pupula var. elliptica, Navicula exilis, Simonsenia delognei) were found mostly at the high end of the conductivity spectrum. Many diatoms with relatively high optima for per cent of base cations had low optima for %Na+ or %K+ and vice versa, once again confirming the observation that M : D ratio is an important factor affecting diatoms.
The position of diatom species along the [Cl−] gradient in our study generally corresponds to the relative ranking of those species along this gradient given by Kolbe (1927, 1932), Hustedt (1957), and van Dam et al. (1994). Apparent chloride optima for diatoms in the dataset of 257 dilute lakes of the north-eastern U.S.A. (Dixit et al., 1998) are, in general, lower than [Cl−] optima in our study because of the lower [Cl−] range of the former dataset. The highest optima for [Cl−] and [Na+] in the NAWQA dataset were observed in species with high conductivity optima (Table 4). When, however, the proportion of these ions was considered, the highest %Na+ and %Cl− optima were observed among species with either highest or lowest conductivity optima. Many of the species of Eunotia, Stauroneis and Frustulia had relatively high optima for the proportion of Na+ and Cl− in accordance with dominance of these ions in some dilute rivers of eastern coastal areas. Unlike species with high conductivity and high NaCl proportion optima, these diatoms also had relatively high %K+ optima. Dionisio-Sese & Miyachi (1992) showed that chloride ions could be toxic to some freshwater algae because they inhibit carbonic anhydrase, an enzyme responsible for the hydration of carbon dioxide during photosynthesis. Our results confirm that the effect of Cl− on diatom community composition is certainly different from the effect of total ionic strength.
The highest [SO ] optima were found in species with high conductivity optima (Bizemis circumtexta, Nitzschia reversa), but high per cent equivalent of SO
] optima were found in species with high conductivity optima (Bizemis circumtexta, Nitzschia reversa), but high per cent equivalent of SO was favoured also by other diatoms such as Diatoma moniliformis, Brachysira microcephala and Eunotia exigua. In the coal-mining region of Montana, according to Bahls et al. (1984), diatoms with highest [SO
was favoured also by other diatoms such as Diatoma moniliformis, Brachysira microcephala and Eunotia exigua. In the coal-mining region of Montana, according to Bahls et al. (1984), diatoms with highest [SO ] optima were Amphora coffeaformis, Diatoma tenue (D. moniliformis accordingly to the drawing on p. 44), Cymbella pusilla, Diploneis pumila var. smithii, Epithemia adnata, Navicula cincta var. rostrata, N. cryptocephala var. veneta, N. pavillardii, Nitzschia amphibia, N. closterium, N. obtusa, Rhopalodia gibba, Synedra famelica, S. fasciculata. It is significant that, in the Montana dataset, increased conductivity was most often associated with Na2SO4 pollution, and that most of the mentioned species inevitably had high optima for all three parameters: Na+, SO
] optima were Amphora coffeaformis, Diatoma tenue (D. moniliformis accordingly to the drawing on p. 44), Cymbella pusilla, Diploneis pumila var. smithii, Epithemia adnata, Navicula cincta var. rostrata, N. cryptocephala var. veneta, N. pavillardii, Nitzschia amphibia, N. closterium, N. obtusa, Rhopalodia gibba, Synedra famelica, S. fasciculata. It is significant that, in the Montana dataset, increased conductivity was most often associated with Na2SO4 pollution, and that most of the mentioned species inevitably had high optima for all three parameters: Na+, SO and conductivity. There is little certainty which factor in particular was responsible for their competitive advantage in polluted rivers. We did not encounter many diatoms characteristic of sulphate-rich North American lakes (Fritz et al., 1993; Cumming et al., 1995), presumably because of the low representation of naturally highly mineralised sulphate-rich rivers in the NAWQA study. On the contrary, most of the rivers with high %SO
and conductivity. There is little certainty which factor in particular was responsible for their competitive advantage in polluted rivers. We did not encounter many diatoms characteristic of sulphate-rich North American lakes (Fritz et al., 1993; Cumming et al., 1995), presumably because of the low representation of naturally highly mineralised sulphate-rich rivers in the NAWQA study. On the contrary, most of the rivers with high %SO in our dataset had an increased conductivity and [SO
in our dataset had an increased conductivity and [SO ] because of mine drainage pollution. Sulphates in mine drainage often cause a significant decrease of water pH. In those cases, acidophilic diatom flora consisting mostly of Eunotia, Frustulia and Pinnularia develop despite relatively high total ionic content of the water (Hancock, 1973; Verb & Vis, 2000). High variation in diatom assemblages associated with elevated sulphate concentration is certainly because of a combined response of diatoms to the concentration of SO
] because of mine drainage pollution. Sulphates in mine drainage often cause a significant decrease of water pH. In those cases, acidophilic diatom flora consisting mostly of Eunotia, Frustulia and Pinnularia develop despite relatively high total ionic content of the water (Hancock, 1973; Verb & Vis, 2000). High variation in diatom assemblages associated with elevated sulphate concentration is certainly because of a combined response of diatoms to the concentration of SO , water pH and total mineral content.
, water pH and total mineral content.
Use of the autecological data
Optima presented in Table 4 are based on samples collected from a variety of habitats, from rivers ranging widely in size, slope and geographical location. All these factors undoubtedly introduce noise in the species response to ions. Nevertheless, the autecological characteristics calculated from the NAWQA dataset are more representative for most U.S. rivers than optima derived from datasets with limited number of observations. These autecological data are useful for the purposes of water quality assessment and further understanding of the ecology of diatoms.
Our results demonstrate that diatom assemblages are distributed continuously along gradients of conductivity and major ions. For practical application of the weighted average values to ecological assessments, the taxa could be assigned to categories according to their affinities. For example, conductivity range could be divided into low, medium and high-conductivity waters or into more finely defined categories. Sets of categories could be established to best meet the needs of individual studies. Differences in the proportion of individual diatoms in the categories could be used to assess differences among samples from different sites or between time periods. In the present paper, we preferred not to simplify autecological data by converting weighted average values to an arbitrarily chosen ordinal scale. The combination of optima presented in Table 4 could be considered as the optimal ionic composition of river water for each taxon. Monitoring the changes in the ionic composition could be carried out by simple observation of shifts in the dominant taxa or by inferring ion concentrations or conductivity using reported optima and some numerical procedure, for instance weighted averaging. Community analysis presented here shows that concentrations of the specific ions explain a higher proportion of variation in the diatom data than ionic proportions. This is mainly because the proportion of individual ions is usually important over a limited range of salinity or osmotic pressure. Therefore, ionic proportion optima are most meaningful when applied in conjunction with conductivity or other measure of the total salt content.
Future work on ecology and taxonomy of diatoms in North America will undoubtedly refine the data presented here. Creation of regional calibration datasets will make it possible to develop finely tuned models to quantitatively infer conductivity and ion concentrations, as is now often performed for lakes (e.g. Fritz et al., 1993; Cumming et al., 1995). The results obtained in this study also show the significant value of large-scale monitoring programmes, such as NAWQA, for obtaining autecological data for organisms important in biological monitoring.
Acknowledgments
This research was supported by the U.S. Geological Survey NAWQA Program through a cooperative agreement with The Academy of Natural Sciences. We thank C. Couch for her guidance. We are grateful to L. Bahls, T. Clason, W. Cody, K. Manoylov, L. Marr, E. Morales, C. Reimer, N.-A. Roberts, and D. Winter who analysed diatom samples, and to F. Acker, P. Cotter, and K. Sprouffske, who managed the Phycology Section database and assisted with technical aspects of data analysis.




