Allozyme and microsatellite genetic variation in natural samples of zebrafish, Danio rerioGenetische Variation von Allozymen und Mikrosatelliten bei Wildfängen des Zebrafisches
Abstract
enIn this paper, we report the results from allozyme and microsatellite markers in natural populations of the zebrafish, a species of great significance in biological studies. Four zebrafish wild samples from West Bengal, India, were analysed in a preliminary survey of levels and patterns of genetic variation. Results indicate high levels of genetic variability and weak genetic structure, although the latter is consistent with the geographical features of the area under study, sampling sites being located in the Ganges and Brahmaputra delta region, which is characterized by high waterways connectivity.
Zusammenfassung
deDanio rerio In diesem Artikel werden die Ergebnisse einer Studie über Allozyme und Mikrosatelliten in natürlichen Populationen des für die biologische Forschung bedeutsamen Zebrafisches dargestellt.
Vier Sammlungen von Wildfängen aus Westbengalen, Indien, wurden in einer vorläufigen Untersuchung in Hinblick auf das Ausmaß und Muster ihrer genetischen Variation analysiert. Die Ergebnisse weisen auf einen hohen Grad genetischer Variabilität bei geringer genetischer Strukturierung hin. Letzteres ist jedoch mit den geographischen Gegebenheiten des untersuchten Gebiets übereinstimmend. Die Fundorte liegen im Deltagebiet von Ganges und Brahmaputra, das sich durch eine hohe Vernetzung der Wasserwege auszeichnet.
Introduction
The zebrafish [Danio rerioHamilton-Buchanan (1822)] stands, through the last decades, as the most appreciated model organism in vertebrates biology, its use ranging from genetics and developmental biology to ecotoxicology. Due to its well-known features of easy rearing and fast reproduction and the large amount of data on its biology, this species could also become a model for the development of aquaculture strategies aimed at preserving the genetic resources of the commercial stocks. Knowledge about developmental patterns and their genetic basis offers an excellent background for the monitoring of genetic and morphological modifications related to rearing conditions. This possibility highlights the need to acquire a thorough understanding of the genetic variation in natural populations of this species. However, despite its wide laboratory use, very little information is available about levels and patterns of genetic variation in natural populations (McCune et al. 2002) or in the commercially available stocks commonly used in molecular and developmental studies.
The natural range of zebrafish includes the Ganges and Brahmaputra basins in India, Bangladesh, Nepal, Bhutan and northern Myanmar (Laale 1977), where it inhabits still and slow-moving water bodies with abundant submerged vegetation (Talwar and Jhingran 1992). The species is also known to haunt rice fields and temporarily flooded lands. No obvious geographical barriers exist in the area involved in our study (West Bengal, India). The intricate network of canals and highly connected waterways could indeed represent a suitable condition for extensive gene flow across zebrafish stocks. However, as active dispersal capacity of the individuals is presumably limited because of their small size, the effectiveness of gene exchange would probably imply quite continuous habitat occupancy.
Nonetheless, habitat degradation could be a major threat for this species, because of very dense human presence over most of its distribution range. In fact, D. rerio is currently listed in IUCN (International Union for Conservation of Nature and Natural Resources) category Low Risk nearly threatened (LR-nt) according to the National Bureau of Fish Genetic Resources of India.
In the present study, microsatellite and allozyme markers were used to investigate the genetic variation and structure of D. rerio wild samples from West Bengal, India and to provide a first survey of the genetic diversity in D. rerio's natural populations. In this way, a complementary picture of the different levels of variation and evolutionary information provided by the two markers are expected.
Microsatellites are, nowadays, the marker of choice in fine genetic structure determination. Due to its high variability and likely neutrality, they seem to be more valuable markers than allozymes to reveal, even from small samples, weak genetic structuring related to historical and geographical factors on genetic variation. In fact, several studies showed that microsatellites are more effective than allozymes at revealing population heterogeneity (Bentzen et al. 1996; O'Connel et al. 1997; Estoup et al. 1998; Ross et al. 1999), although other comparative studies indicate that this is not always the case (Lehmann et al. 1996; Barker et al. 1997). Furthermore, the study of allozyme variability allows comparisons of genetic variability data within a wide range of different organisms, because of the availability of a set of comparable markers. Monitoring of allozyme variation could also allow the direct observation of changes in loci of known function, which can be a valuable tool in aquaculture-oriented research because of its potential ability to reveal selection-driven changes in the genetic variation of stocks.
Materials and Methods
We analysed 141 individuals from four locations of West Bengal, India. Samples from Nadia (NDA, 50 individuals), Hugli (HBL, 38 individuals), and 24 Parganas N (PRN, 18 individuals) were collected about 50 km from each other, while the sample (CCB, 38 individuals) from Koch-Bihar was collected approximately 400 km North from the other locations. Sampling is representative of a small portion of the species’ range and, in addition, it has been carried out by local operators so that any information about the ecological features of the sampling sites are lacked, as well as their exact location (approximate points are given in the map, Fig. 1). On the contrary, the relative position of the sampling sites, allowed to peer at the distribution of genetic variation by comparing differentiation within a little cluster of closely situated spots (samples NDA, HBL, PRN) with levels of differentiation showed by populations sampled much more apart (CCB). Animals were transferred alive to our laboratory and kept in 100 l tanks. The field samples analysed in this study experienced harsh conditions during transport, which caused an overall mortality rate of about 10%. Moreover, they had been kept in tanks for almost 2 years prior to this study, suffering further mortality, which can be estimated at 5–20%.
Map showing approximate position of wild zebrafish sampling sites in West Bengal (India). The area of occurrence of Danio rerio is shown in the box at upper left (shaded area)
Microsatellite and allozyme assays
The DNA extraction was performed from eye fresh tissue using the Easy DNA kit by Invitrogen (Groningen, The Netherlands) and applying number 3 Easy Kit protocol with minor modifications. Extracted DNA was suspended to a final volume of 100 μl and stored at −70°C.
Sample populations were screened across six polymorphic microsatellite loci (namely Z562, Z669, Z851, Z953, Z1213 and Z1233) belonging to six different linkage groups. Primers’ sequences are available from the zebrafish web site (http://zebrafish.mgh.harvard.edu/papers/zf_map/primers.html; Knapik et al. 1996, 1998). Locus Z1213 and locus Z669 included only dinucleotide repeats. The remaining four loci (i.e. Z562, Z851, Z953 and Z1233) included both dinucleotide repeats and short trinucleotide repeat inserts. Therefore, a strict stepwise mutation model (SMM) based on dinucleotide units could not be generally assumed.
Amplification reactions of genomic DNA were carried out in a total volume of 25 μl on an Applied Biosystems (Foster City, CA, USA) Gene Amp 9600 PCR System. The reaction mixture contained: 50–100 ng genomic DNA; 2 mM MgCl2; 800 μM dNTP; 32.15 ng of each primer (150–170 nM); 0.625 U ABI AmpliTaqTM DNA polymerase (Applied Biosystems); 2.5 μl ABI AmpliTaqTM 10x PCR buffer. Cycling conditions varied among loci and are available from the authors upon request. Fragment length was determined on automatic sequencer ABI PrismTM 310 Genetic Analyzer using ABI PrismTM software GeneScanTM 2.0.2 (Applied Biosystems). Genotypes were scored by assessment of distribution gaps in amplified fragments size.
Allozyme electrophoretic analysis was performed on water solutions of liver homogenate. Seventeen enzymatic systems were analysed for a total of 18 loci: Acp, Ak, Ca, Ck, Gapd, Got, Gpi, G6pd, Idh, Ldh, Mdh, Me, Pep-1, Pep-2, Pgm, 6Pgd, Tpi, Xdh. The genetic nomenclature of the protein-coding loci follows the guidelines of Shaklee et al. (1990). Runs were carried out on cellulose acetate gel (CellogelTM, MALTA Chemetron, Milano, Italy) and stained following Brewer and Sing (1970), Ayala (1972) and Richardson (1986). Details on conditions are available from the authors.
Statistical analyses
Genetic variation at both allozyme and microsatellite loci was evaluated in terms of percentage of polymorphic loci (95% polymorphism criterion), allelic richness (Rs) and expected heterozygosity (HE). Allelic richness was calculated using fstat 1.2 package (Goudet 1995), according to El Mousadik and Petit (1996); expected heterozygosity was computed following Nei (1978) as implemented in genetix (Montpellier, France, Belkhir et al. 1996–2001) package. The level of inbreeding was assessed using FIS (Weir and Cockerham 1984) as implemented in the fstat 1.2 package (Goudet 1995), which also provides an estimate of significance by randomization of alleles between individuals within populations. Hardy–Weinberg equilibrium deviations were analysed by Fisher exact test as implemented in genepop (Raymond and Rousset 1995).
The genetic structure analysis was performed in anova framework using the program arlequin 2.0 (Geneva, Switzerland, Schneider et al. 2000). As no group was defined, FST estimate can be considered equivalent to the Weir and Cockerham's (1984)θ. Fixation indices significance was tested by permutation of genotypes among samples. Standard errors on FST were calculated using the fstat package with a jack-knifing procedure over all loci.
Genotypic differentiation in the whole set of wild samples was tested by a G-test implemented in package genepop (Raymond and Rousset 1995), employing a Markov Chain with 1000 dememorizations, 100 batches and 1000 iterations per batch.
For the microsatellite genetic structure analysis, the index RST which is based on the variance in allele sizes, has also been computed using arlequin 2.0. F-statistics are expected to underestimate population differentiation when mutation rate is high compared with migration under a non-infinite allele mutation model (Hedrick 1999; Balloux et al. 2000; Balloux and Goudet 2002; Balloux and Lugon-Moulin 2002). However, when migration rate is high (Nm ≥ 10), FST is a better estimator of genetic differentiation than RST even under a strict SMM, because of its lower associated variance (Balloux and Goudet 2002; Balloux and Lugon-Moulin 2002).
Pairwise multilocus FST (θ) matrices based on both allozyme and microsatellite data were computed according to Weir and Cockerham (1984) using fstat. Significance of differentiation values was assessed by randomization of genotypes among samples. p-Values were adjusted using the Bonferroni correction to a nominal level of 0.05 (Rice 1989).
Finally, we used an individual assignment method based on that described by Paetkau et al. (1995, 1997) and implemented by arlequin, to evaluate genetic affinities among individuals. This method assigns an individual to the population in which its multilocus genotype has the highest likelihood of occurring, assuming Hardy–Weinberg equilibrium and linkage equilibrium in all locus–population combinations. Significance of assignments was computed as the ratio of the likelihood of ‘critical populations’ (i.e. the most likely and the second most likely population) according to Banks and Eichert (2000).
Results and Discussion
Genetic variability
Table 1 shows number of alleles, allelic richness, and observed and expected heterozygosity for each population at each microsatellite and enzymatic loci.
| Locus | CCB | NDA | PRN | HBL | |
|---|---|---|---|---|---|
| Allozyme loci | |||||
| ACP | A(N) | 1(37) | 1(49) | 1(18) | 2(38) |
| R s | 1.000 | 1.000 | 1.000 | 1.342 | |
| H E | 0.000 | 0.000 | 0.000 | 0.026 | |
| H O | 0.000 | 0.000 | 0.000 | 0.026 | |
| CA | A(N) | 5(37) | 4(48) | 4(18) | 3(37) |
| R s | 3.918 | 3.462 | 3.993 | 2.998 | |
| H E | 0.579 | 0.582 | 0.667 | 0.589 | |
| H O | 0.351 | 0.417 | 0.500 | 0.460 | |
| GAPD | A(N) | 3(34) | 2(47) | 2(17) | 3(36) |
| R s | 2.771 | 2.000 | 2.000 | 2.359 | |
| H E | 0.399 | 0.483 | 0.371 | 0.305 | |
| H O | 0.382 | 0.362 | 0.353 | 0.250 | |
| GOT | A(N) | 4(35) | 3(47) | 1(17) | 1(35) |
| R s | 2.595 | 1.553 | 1.000 | 1.000 | |
| H E | 0.163 | 0.042 | 0.000 | 0.000 | |
| H O | 0.114 | 0.043 | 0.000 | 0.000 | |
| GPI | A(N) | 6(38) | 7(48) | 4(18) | 7(38) |
| R s | 3.318 | 4.410 | 3.428 | 4.349 | |
| H E | 0.199 | 0.381 | 0.257 | 0.350 | |
| H O | 0.211 | 0.333 | 0.278 | 0.342 | |
| G6PD | A(N) | 4(34) | 4(45) | 4(15) | 5(32) |
| R s | 3.87 | 3.288 | 3.866 | 4.054 | |
| H E | 0.644 | 0.642 | 0.632 | 0.667 | |
| H O | 0.352 | 0.444 | 0.267 | 0.344 | |
| MDH | A(N) | 2(35) | 1(48) | 2(18) | 1(37) |
| R s | 1.608 | 1.000 | 1.722 | 1.000 | |
| H E | 0.056 | 0.000 | 0.056 | 0.000 | |
| H O | 0.057 | 0.000 | 0.056 | 0.000 | |
| ME | A(N) | 1(36) | 1(48) | 2(18) | 1(36) |
| R s | 1.000 | 1.000 | 1.722 | 1.000 | |
| H E | 0.000 | 0.000 | 0.056 | 0.000 | |
| H O | 0.000 | 0.000 | 0.056 | 0.000 | |
| PEP1 | A(N) | 3(19) | 1(43) | 2(13) | 2(33) |
| R s | 2.368 | 1.000 | 2.000 | 1.394 | |
| H E | 0.104 | 0.000 | 0.148 | 0.030 | |
| H O | 0.105 | 0.000 | 0.154 | 0.030 | |
| PEP2 | A(N) | 3(23) | 3(37) | 2(15) | 3(33) |
| R s | 2.925 | 2.931 | 2.000 | 2.944 | |
| H E | 0.444 | 0.400 | 0.287 | 0.362 | |
| H O | 0.391 | 0.378 | 0.200 | 0.364 | |
| PGM | A(N) | 2(37) | 2(47) | 1(16) | 3(36) |
| R s | 1.351 | 1.733 | 1.000 | 2.341 | |
| H E | 0.027 | 0.082 | 0.000 | 0.133 | |
| H O | 0.027 | 0.085 | 0.000 | 0.083 | |
| 6PGD | A(N) | 2(34) | 4(40) | 2(16) | 3(32) |
| R s | 1.622 | 3.735 | 1.970 | 2.777 | |
| H E | 0.058 | 0.451 | 0.121 | 0.278 | |
| H O | 0.059 | 0.425 | 0.125 | 0.313 | |
| TPI | A(N) | 2(23) | 1(48) | 1(16) | 1(38) |
| R s | 1.565 | 1.000 | 1.000 | 1.000 | |
| H E | 0.044 | 0.000 | 0.000 | 0.000 | |
| H O | 0.044 | 0.000 | 0.000 | 0.000 | |
| XDH | A(N) | 4(36) | 2(44) | 2(18) | 2(38) |
| R s | 2.317 | 1.295 | 1.722 | 1.57 | |
| H E | 0.108 | 0.023 | 0.056 | 0.052 | |
| H O | 0.111 | 0.023 | 0.056 | 0.053 | |
| Mean1 | A | 2.556 | 2.222 | 1.889 | 2.278 |
| SD1 | 1.542 | 1.665 | 1.079 | 1.638 | |
| Mean1 | R s | 2.013 | 1.856 | 1.801 | 1.896 |
| SD1 | 1.025 | 1.160 | 1.000 | 1.118 | |
| Mean1 | H E | 0.157 | 0.171 | 0.147 | 0.155 |
| SD1 | 0.212 | 0.239 | 0.215 | 0.218 | |
| Mean1 | H O | 0.123 | 0.139 | 0.114 | 0.126 |
| SD1 | 0.147 | 0.187 | 0.149 | 0.165 | |
| Microsatellite loci | |||||
| Z562 | A(N) | 7(36) | 4(50) | 4(17) | 5(35) |
| R s | 5.464 | 3.230 | 4.000 | 4.873 | |
| H E | 0.501 | 0.535 | 0.690 | 0.679 | |
| H O | 0.417 | 0.420 | 0.647 | 0.600 | |
| Z669 | A(N) | 14(38) | 11(50) | 9(18) | 11(35) |
| R s | 11.116 | 9.478 | 8.878 | 9.085 | |
| H E | 0.893 | 0.869 | 0.884 | 0.875 | |
| H O | 0.921 | 0.880 | 0.833 | 0.944 | |
| Z851 | A(N) | 22(38) | 17(50) | 16(18) | 20(35) |
| R s | 16.142 | 12.580 | 15.386 | 14.615 | |
| H E | 0.946 | 0.908 | 0.946 | 0.925 | |
| H O | 0.974 | 0.900 | 1.000 | 0.971 | |
| Z953 | A(N) | 3(38) | 4(50) | 3(18) | 3(34) |
| R s | 2.418 | 3.007 | 2.889 | 2.964 | |
| H E | 0.254 | 0.310 | 0.452 | 0.494 | |
| H O | 0.237 | 0.300 | 0.611 | 0.588 | |
| Z1213 | A(N) | 35(38) | 28(50) | 19(16) | 27(34) |
| R s | 21.179 | 16.235 | 19.000 | 19.823 | |
| H E | 0.965 | 0.919 | 0.968 | 0.966 | |
| H O | 0.974 | 0.900 | 0.938 | 0.912 | |
| Z1233 | A(N) | 16(37) | 16(50) | 8(16) | 12(33) |
| R s | 12.456 | 11.310 | 8.000 | 10.900 | |
| H E | 0.895 | 0.881 | 0.869 | 0.901 | |
| H O | 0.784 | 0.860 | 0.625 | 0.818 | |
| Mean | R s | 11.463 | 9307 | 9.692 | 10.377 |
| SD | 6.859 | 5.280 | 6.345 | 6.235 | |
| Mean | A | 16.167 | 13.333 | 9.833 | 13.000 |
| SD | 11.409 | 9.114 | 6.431 | 9.099 | |
| Mean | H E | 0.743 | 0.737 | 0.802 | 0.803 |
| SD | 0.295 | 0.254 | 0.197 | 0.184 | |
| Mean | H O | 0.718 | 0.710 | 0.776 | 0.801 |
| SD | 0.316 | 0.274 | 0.171 | 0.171 | |
- 1 Includes four monomorphic loci.
- CCB, Koch-Bihar; NDA, Nadia; PRN, 24 Parganas N; HBL, Hugli.
All samples showed high genetic variability for both allozyme (proportion of polymorphic loci, P = 38.9 ± 4.5%) and microsatellite (P = 100%) loci, with mean expected heterozygosity (HE: Nei 1978) of 0.158 ± 0.01 and 0.771 ± 0.036 for allozyme and microsatellite loci, respectively. The amount of genetic variability was not substantially different among samples, although CCB sample shows the highest allelic richness at both allozyme and microsatellite loci. Allele frequencies for microsatellite and allozyme loci are shown in Appendix I and Appendix II, respectively. Two microsatellite loci (Z562 and Z953) show low or moderate variability (less than 7 alleles per sample), three (Z669, Z851 and Z1233) have an allele number per population between 8 and 22, while locus Z1213 is extremely variable with allele numbers up to 35 (Appendix I).
| Locus | Allele | CCB | NDA | PRN | HBL | |
|---|---|---|---|---|---|---|
| Z562 | N | 36 | 50 | 17 | 35 | |
| 159 | 0.0139 | 0.0000 | 0.0000 | 0.0000 | ||
| 189 | 0.0139 | 0.0000 | 0.0000 | 0.0000 | ||
| 191 | 0.6944 | 0.5700 | 0.4706 | 0.4857 | ||
| 193 | 0.0833 | 0.3800 | 0.2647 | 0.2714 | ||
| 195 | 0.0278 | 0.0300 | 0.1765 | 0.0571 | ||
| 197 | 0.1111 | 0.0200 | 0.0000 | 0.1143 | ||
| 199 | 0.0556 | 0.0000 | 0.0882 | 0.0714 | ||
| Z669 | N | 38 | 50 | 18 | 35 | |
| 118 | 0.0132 | 0.0500 | 0.1667 | 0.1714 | ||
| 120 | 0.0000 | 0.0000 | 0.0000 | 0.0143 | ||
| 122 | 0.0132 | 0.0000 | 0.0000 | 0.0286 | ||
| 124 | 0.0789 | 0.1200 | 0.1944 | 0.1429 | ||
| 126 | 0.0395 | 0.0700 | 0.0556 | 0.0000 | ||
| 128 | 0.0526 | 0.0900 | 0.1944 | 0.1000 | ||
| 130 | 0.1579 | 0.0200 | 0.1111 | 0.0571 | ||
| 132 | 0.1579 | 0.1600 | 0.0833 | 0.2286 | ||
| 134 | 0.1974 | 0.2400 | 0.0833 | 0.1714 | ||
| 136 | 0.0921 | 0.0000 | 0.0000 | 0.0429 | ||
| 138 | 0.0789 | 0.0000 | 0.0000 | 0.0286 | ||
| 140 | 0.0263 | 0.1500 | 0.0833 | 0.0143 | ||
| 144 | 0.0526 | 0.0300 | 0.0278 | 0.0000 | ||
| 146 | 0.0000 | 0.0400 | 0.0000 | 0.0000 | ||
| 154 | 0.0132 | 0.0000 | 0.0000 | 0.0000 | ||
| 186 | 0.0000 | 0.0300 | 0.0000 | 0.0000 | ||
| 188 | 0.0263 | 0.0000 | 0.0000 | 0.0000 | ||
| Z851 | N | 38 | 50 | 18 | 35 | |
| 108 | 0.0263 | 0.0700 | 0.1389 | 0.1286 | ||
| 112 | 0.0000 | 0.0100 | 0.0000 | 0.0000 | ||
| 114 | 0.0526 | 0.0000 | 0.0000 | 0.0143 | ||
| 117 | 0.0132 | 0.0000 | 0.0000 | 0.0000 | ||
| 118 | 0.0132 | 0.0500 | 0.0556 | 0.0286 | ||
| 120 | 0.0263 | 0.0400 | 0.0278 | 0.0286 | ||
| 122 | 0.0789 | 0.0300 | 0.0556 | 0.0714 | ||
| 124 | 0.0395 | 0.1700 | 0.0278 | 0.1714 | ||
| 126 | 0.0921 | 0.1800 | 0.1111 | 0.1286 | ||
| 128 | 0.1053 | 0.1100 | 0.0833 | 0.0429 | ||
| 130 | 0.0789 | 0.0500 | 0.0000 | 0.0571 | ||
| 132 | 0.0658 | 0.0700 | 0.0556 | 0.0429 | ||
| 134 | 0.0263 | 0.0700 | 0.1111 | 0.0143 | ||
| 136 | 0.0263 | 0.0000 | 0.0556 | 0.0143 | ||
| 138 | 0.0526 | 0.0100 | 0.0556 | 0.0714 | ||
| 140 | 0.1053 | 0.0100 | 0.0278 | 0.0571 | ||
| 142 | 0.0658 | 0.0300 | 0.0556 | 0.0429 | ||
| 144 | 0.0526 | 0.0000 | 0.0000 | 0.0000 | ||
| 146 | 0.0263 | 0.0000 | 0.0000 | 0.0143 | ||
| 148 | 0.0132 | 0.0300 | 0.0000 | 0.0143 | ||
| 150 | 0.0132 | 0.0100 | 0.0000 | 0.0286 | ||
| 152 | 0.0132 | 0.0000 | 0.0833 | 0.0143 | ||
| 154 | 0.0000 | 0.0000 | 0.0278 | 0.0143 | ||
| 160 | 0.0132 | 0.0600 | 0.0278 | 0.0000 | ||
| Z953 | N | 38 | 50 | 18 | 34 | |
| 96 | 0.0132 | 0.1400 | 0.2778 | 0.2647 | ||
| 98 | 0.8553 | 0.8200 | 0.6944 | 0.6618 | ||
| 99 | 0.0000 | 0.0300 | 0.0278 | 0.0000 | ||
| 100 | 0.1316 | 0.0100 | 0.0000 | 0.0735 | ||
| Z1213 | N | 38 | 50 | 16 | 34 | |
| 88 | 0.0000 | 0.0100 | 0.0000 | 0.0000 | ||
| 90 | 0.0000 | 0.0100 | 0.0313 | 0.0000 | ||
| 92 | 0.0000 | 0.0100 | 0.0000 | 0.0000 | ||
| 94 | 0.0132 | 0.0400 | 0.0000 | 0.0441 | ||
| 96 | 0.0132 | 0.0000 | 0.0313 | 0.0000 | ||
| 98 | 0.0132 | 0.0600 | 0.0000 | 0.0441 | ||
| 100 | 0.0132 | 0.0100 | 0.0313 | 0.0000 | ||
| 102 | 0.0132 | 0.0700 | 0.0938 | 0.1029 | ||
| 104 | 0.0395 | 0.0100 | 0.0000 | 0.0294 | ||
| 106 | 0.0658 | 0.0300 | 0.0625 | 0.0588 | ||
| 108 | 0.0526 | 0.0000 | 0.0000 | 0.0294 | ||
| 110 | 0.0132 | 0.0200 | 0.0625 | 0.0000 | ||
| 112 | 0.0395 | 0.0200 | 0.0313 | 0.0147 | ||
| 114 | 0.0526 | 0.0000 | 0.0938 | 0.0000 | ||
| 116 | 0.0395 | 0.0100 | 0.0625 | 0.0000 | ||
| 118 | 0.1316 | 0.0900 | 0.0313 | 0.0000 | ||
| 120 | 0.0395 | 0.0100 | 0.0000 | 0.0294 | ||
| 122 | 0.0263 | 0.0000 | 0.0938 | 0.0147 | ||
| 124 | 0.0395 | 0.0000 | 0.0000 | 0.0588 | ||
| 126 | 0.0132 | 0.0000 | 0.0625 | 0.0294 | ||
| 128 | 0.0395 | 0.0300 | 0.0625 | 0.0735 | ||
| 130 | 0.0132 | 0.0900 | 0.0000 | 0.0441 | ||
| 132 | 0.0395 | 0.0600 | 0.0313 | 0.0294 | ||
| 134 | 0.0395 | 0.0100 | 0.0313 | 0.0441 | ||
| 136 | 0.0132 | 0.0100 | 0.0000 | 0.0000 | ||
| 138 | 0.0132 | 0.0300 | 0.0625 | 0.0147 | ||
| 140 | 0.0395 | 0.0200 | 0.0313 | 0.0588 | ||
| 142 | 0.0132 | 0.0100 | 0.0000 | 0.0147 | ||
| 144 | 0.0000 | 0.0200 | 0.0000 | 0.0147 | ||
| 146 | 0.0395 | 0.0200 | 0.0000 | 0.0294 | ||
| 148 | 0.0132 | 0.0200 | 0.0000 | 0.0000 | ||
| 150 | 0.0132 | 0.0200 | 0.0000 | 0.0147 | ||
| 152 | 0.0132 | 0.0000 | 0.0000 | 0.0294 | ||
| 154 | 0.0132 | 0.0000 | 0.0000 | 0.0000 | ||
| 156 | 0.0132 | 0.2300 | 0.0625 | 0.0147 | ||
| 158 | 0.0132 | 0.0000 | 0.0000 | 0.0441 | ||
| 160 | 0.0263 | 0.0000 | 0.0000 | 0.0441 | ||
| 162 | 0.0000 | 0.0000 | 0.0313 | 0.0441 | ||
| 164 | 0.0132 | 0.0000 | 0.0000 | 0.0000 | ||
| 166 | 0.0132 | 0.0300 | 0.0000 | 0.0294 | ||
| Z1233 | N | 37 | 50 | 16 | 33 | |
| 124 | 0.0405 | 0.0100 | 0.0000 | 0.0303 | ||
| 126 | 0.0000 | 0.0900 | 0.0625 | 0.0455 | ||
| 127 | 0.0000 | 0.0500 | 0.0000 | 0.0000 | ||
| 128 | 0.0135 | 0.0300 | 0.0938 | 0.0606 | ||
| 130 | 0.0811 | 0.0300 | 0.2188 | 0.1212 | ||
| 132 | 0.0811 | 0.1000 | 0.0938 | 0.0758 | ||
| 134 | 0.2568 | 0.0500 | 0.1563 | 0.1818 | ||
| 136 | 0.0676 | 0.1600 | 0.2188 | 0.1061 | ||
| 137 | 0.0000 | 0.0100 | 0.0000 | 0.0000 | ||
| 138 | 0.0135 | 0.2500 | 0.1250 | 0.1667 | ||
| 140 | 0.1081 | 0.1000 | 0.0000 | 0.0303 | ||
| 142 | 0.0270 | 0.0600 | 0.0000 | 0.0909 | ||
| 144 | 0.0135 | 0.0000 | 0.0000 | 0.0000 | ||
| 146 | 0.0676 | 0.0200 | 0.0313 | 0.0303 | ||
| 148 | 0.0946 | 0.0000 | 0.0000 | 0.0000 | ||
| 150 | 0.0405 | 0.0200 | 0.0000 | 0.0000 | ||
| 152 | 0.0541 | 0.0000 | 0.0000 | 0.0606 | ||
| 154 | 0.0000 | 0.0100 | 0.0000 | 0.0000 | ||
| 158 | 0.0270 | 0.0000 | 0.0000 | 0.0000 | ||
| 160 | 0.0000 | 0.0100 | 0.0000 | 0.0000 | ||
| 178 | 0.0135 | 0.0000 | 0.0000 | 0.0000 |
- CCB, Koch-Bihar; NDA, Nadia; PRN, 24.
- Parganas N; HBL, Hugli.
| Locus | Allele | CCB | NDA | PRN | HBL | |
|---|---|---|---|---|---|---|
| ACP | N | 37 | 49 | 18 | 38 | |
| 98 | 0.0000 | 0.0000 | 0.0000 | 0.0132 | ||
| 100 | 1.0000 | 1.0000 | 1.0000 | 0.9868 | ||
| Ak | N | 38 | 49 | 18 | 28 | |
| 100 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | ||
| Ca | N | 37 | 48 | 18 | 37 | |
| 98 | 0.0270 | 0.0208 | 0.1111 | 0.0000 | ||
| 99 | 0.2432 | 0.2500 | 0.2778 | 0.2568 | ||
| 100 | 0.5946 | 0.5833 | 0.5000 | 0.5676 | ||
| 101 | 0.1216 | 0.1458 | 0.1111 | 0.1757 | ||
| 102 | 0.0135 | 0.0000 | 0.0000 | 0.0000 | ||
| Ck | N | 38 | 49 | 18 | 38 | |
| 100 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | ||
| Gapd | N | 34 | 47 | 17 | 36 | |
| 98 | 0.0000 | 0.0000 | 0.0000 | 0.0139 | ||
| 100 | 0.2059 | 0.3936 | 0.7647 | 0.8194 | ||
| 102 | 0.7500 | 0.6064 | 0.2353 | 0.1667 | ||
| 104 | 0.0441 | 0.0000 | 0.0000 | 0.0000 | ||
| Got | N | 35 | 47 | 17 | 35 | |
| 98 | 0.0571 | 0.0106 | 0.0000 | 0.0000 | ||
| 100 | 0.9143 | 0.9787 | 1.0000 | 1.0000 | ||
| 102 | 0.0143 | 0.0000 | 0.0000 | 0.0000 | ||
| 104 | 0.0000 | 0.0106 | 0.0000 | 0.0000 | ||
| 106 | 0.0143 | 0.0000 | 0.0000 | 0.0000 | ||
| Gpi | N | 38 | 48 | 18 | 38 | |
| 92 | 0.0132 | 0.0938 | 0.0000 | 0.0000 | ||
| 96 | 0.0132 | 0.0417 | 0.0278 | 0.0263 | ||
| 97 | 0.0132 | 0.0208 | 0.0000 | 0.0132 | ||
| 98 | 0.0000 | 0.0417 | 0.0278 | 0.0263 | ||
| 100 | 0.8947 | 0.7813 | 0.8611 | 0.8026 | ||
| 102 | 0.0263 | 0.0104 | 0.0833 | 0.0263 | ||
| 104 | 0.0395 | 0.0104 | 0.0000 | 0.0921 | ||
| 106 | 0.0000 | 0.0000 | 0.0000 | 0.0132 | ||
| G6pd | N | 34 | 45 | 15 | 32 | |
| 96 | 0.4265 | 0.4778 | 0.4667 | 0.4063 | ||
| 98 | 0.0735 | 0.2000 | 0.1000 | 0.1563 | ||
| 99 | 0.0000 | 0.0000 | 0.0000 | 0.0156 | ||
| 100 | 0.4118 | 0.3111 | 0.4000 | 0.3906 | ||
| 102 | 0.0882 | 0.0111 | 0.0333 | 0.0313 | ||
| Idh | N | 38 | 49 | 18 | 38 | |
| 100 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | ||
| Ldh1 | N | 38 | 49 | 18 | 38 | |
| 100 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | ||
| Mdh | N | 35 | 48 | 18 | 37 | |
| 98 | 0.0000 | 0.0000 | 0.0278 | 0.0000 | ||
| 100 | 0.9714 | 1.0000 | 0.9722 | 1.0000 | ||
| 102 | 0.0286 | 0.0000 | 0.0000 | 0.0000 | ||
| Me | N | 36 | 48 | 18 | 36 | |
| 98 | 0.0000 | 0.0000 | 0.0278 | 0.0000 | ||
| 100 | 1.0000 | 1.0000 | 0.9722 | 1.0000 | ||
| Pep-1 | N | 19 | 43 | 13 | 33 | |
| 98 | 0.0263 | 0.0000 | 0.0000 | 0.0000 | ||
| 100 | 0.9474 | 1.0000 | 0.9231 | 0.9848 | ||
| 102 | 0.0263 | 0.0000 | 0.0769 | 0.0152 | ||
| Pep-2 | N | 23 | 37 | 15 | 33 | |
| 98 | 0.0652 | 0.0811 | 0.0000 | 0.0909 | ||
| 100 | 0.7174 | 0.7568 | 0.8333 | 0.7879 | ||
| 102 | 0.2174 | 0.1622 | 0.1667 | 0.1212 | ||
| Pgm | N | 37 | 47 | 16 | 36 | |
| 98 | 0.0000 | 0.0426 | 0.0000 | 0.0278 | ||
| 100 | 0.9865 | 0.9574 | 1.0000 | 0.9306 | ||
| 102 | 0.0000 | 0.0000 | 0.0000 | 0.0417 | ||
| 104 | 0.0135 | 0.0000 | 0.0000 | 0.0000 | ||
| 6Pgd | N | 34 | 40 | 16 | 32 | |
| 96 | 0.0000 | 0.0875 | 0.0000 | 0.0469 | ||
| 97 | 0.0000 | 0.0500 | 0.0000 | 0.0000 | ||
| 100 | 0.9706 | 0.7250 | 0.9375 | 0.8438 | ||
| 102 | 0.0294 | 0.1375 | 0.0625 | 0.1094 | ||
| Tpi | N | 23 | 48 | 16 | 38 | |
| 98 | 0.0217 | 0.0000 | 0.0000 | 0.0000 | ||
| 100 | 0.9783 | 1.0000 | 1.0000 | 1.0000 | ||
| Xdh | N | 36 | 44 | 18 | 38 | |
| 100 | 0.9444 | 0.9886 | 0.9722 | 0.9737 | ||
| 101 | 0.0139 | 0.0000 | 0.0278 | 0.0000 | ||
| 102 | 0.0278 | 0.0114 | 0.0000 | 0.0263 | ||
| 103 | 0.0139 | 0.0000 | 0.0000 | 0.0000 |
Knapik et al. (1996) reported the allelic variation in a few individuals from four laboratory strains at 102 microsatellite loci, including Z562, Z953 and Z1213. As far as a comparison is possible, given the different size-calling techniques employed, the range of variation revealed was higher than the range scored by those authors, yet encompassing it at loci Z953 and Z1213, but not at locus Z562. This discrepancy could result from differences in size-calling, given that laboratory strains display an allele-size range just narrower than natural samples, although displaced some 10 bp above. Nevertheless, the strain the authors (Knapik et al. 1996) refer to as IN, deriving from wild individuals from ‘northeast of India’, only harboured allele 199, which also occurs in three of the natural samples examined from West Bengal. It is, therefore, indeed possible that alleles displayed by laboratory strains point to their origin from different regions of the species range.
Loci Z562, Z1233 and Z669 exhibited a clear gap in the distribution of allele sizes (Appendix I). Considering the homogeneity of the samples as to allele size distribution, and the occurrence of outlying alleles in heterozygous state, it is quite unlikely that these gaps result from migration from genetically different populations. At locus Z1233 the gap is only 18 bp long, so that we can hypothesize that, even under a SMM, intermediate alleles were lost either in the sample, due to sampling error, or in the population, due to genetic drift. In the case of alleles 186 and 188 at locus Z669, given their occurrence in three individuals in two populations, ancestral large-size mutation events (or, possibly, a single event) (Estoup et al. 1995; Estoup and Cornuet 1999; Sunnucks et al. 1996) could be the most likely origin of the gap. The core sequence of locus Z562 (available at http://www.zebrafish.mgh.harvard.edu) is slightly more than 30 bp long, although it was determined by the authors on alleles nominally longer than those occurring in our study sample. The gap separating allele 159 to the closest allele of locus Z562 is 30 bp. Therefore, in the present study, we argued that this gap probably derives from a large deletion involving some of the flanking region (Grimaldi and Crouau-Roy 1997).
Two of the scored alleles (allele 117 at locus Z851 and allele 99 at locus Z953) do not fit a mutation model based on dinucleotide repeats insertion–deletion. Cloning and sequencing of individual alleles were not carried out, but reference sequences of both loci (http://www.zebrafish.mgh.harvard.edu) contain short trinucleotide repeats which could be involved in these alleles’ emergence.
The small number of microsatellite loci analysed and their marked differences in molecular structure and variation levels, suggest some caution in interpreting mean values of these metrics in terms of genomic variability.
Heterozygosity values were slightly lower than the ones typically reported in marine pelagic species (Bentzen et al. 1996; Shaw et al. 1999; Buonaccorsi et al. 2001). They were, indeed, of the same order of those met in anadromous and freshwater species by Bernatchez et al. (1998) and Rüber et al. (2001), and higher than those shown by small and fragmented salmonid populations (Estoup et al. 1998; Neraas and Spruell 2001). Furthermore, comparison of variability observed in enzymatic loci with data relating to most fish species (Kirpichnikov 1992), offered further indication of a substantial amount of variation in the populations under study. This constitutes a good premise for the use of the species as an aquaculture model, as the occurrence of a considerable amount of genetic variation is a necessary prerequisite to study changes in patterns and levels of variation under rearing conditions.
For the microsatellite loci the FIS values over all loci in the assayed samples were not significantly different from zero. Hardy–Weinberg equilibrium at microsatellite loci was confirmed by Fisher exact test, allowing ruling out the occurrence of null alleles. For allozymes, FIS values were significantly higher than zero in three of four samples. One locus (G6pd) showed heterozygotes deficiency in all samples (Fisher exact test: 0.0001 < p < 0.001), while no other loci showed strictly significant disequilibrium. Wahlund effect can be excluded considering that no significant disequilibrium could be recovered both in microsatellite loci and most of the allozyme loci. An explanation might reside in the occurrence of some type of selection on particular enzymatic genotypes. It is indeed possible that differential mortality of genotypes will have occurred during captivity (see Materials and Methods) (Allegrucci et al. 1994, for a similar example on the Mediterranean sea bass).
Genetic structure
Analysis of microsatellite data revealed a weak, although highly significant genetic structure, FST (θ) and RST values being 0.026 ± 0.005 (p < 0.0001) and 0.025 (p < 0.015), respectively, showing low levels of differentiation. As expected in the case of high levels of gene flow (Balloux and Goudet 2002; Balloux and Lugon-Moulin 2002), these values were very similar to each other. Lower significance of RST value was also expected because of its larger associated variance compared with FST. Considering that some of the microsatellite loci used in this study have complex sequences and irregular patterns of variation (see above), the FST estimates, which does not assume a SMM, appear, in these circumstances, a more reliable indicator of genetic differentiation than RST (see Materials and Methods for details).
The allozyme overall FST value was higher than the one for the microsatellite loci although it has a large standard error (θ = 0.057 ± 0.056; p < 0.00001). Such larger variance is apparently due to divergent indications provided by individual polymorphic loci, as the FST values per locus range from −0.009 (Ca, p = 0.92571) to 0.297 (Gapd, p < 0.00001).
For both allozyme and microsatellite data, G-test allowed to compellingly reject the hypothesis of no genetic differentiation among the whole set of wild populations (p < 0.0001).
Some geographical signal could be detected in both allozyme and microsatellite pairwise FST matrices (Table 2): the Koch-Bihar (CCB) sample, collected 400 km apart from the others, exhibited the highest differentiation values, followed by the sample from Nadia (NDA). The two populations from Parganas 24 (PRN) and Hugli (HBL) showed very low FST that was not significant in allozyme data matrices. As mentioned in the Materials and Methods section, we do not have exact information on the geographical position of sampling sites. Consequently, cannot tell whether the more marked genetic differentiation of NDA sample, relative to HBL and PRN, is associated or not with greater geographical distance, nor were able to conduct a more accurate geographical analysis to test for the presence of isolation by distance. The picture that can be drawn out from our results, however, looks quite consistent with the hypothesis that the distribution of D. rerio in the area under study is fairly continuous and no significant barriers to gene flow occur along the waterways.
| CCB | NDA | PRN | HBL | |
|---|---|---|---|---|
| Koch-Bihar (CCB) | 0.040* | 0.035* | 0.027* | |
| Nadia (NDA) | 0.021* | 0.022* | 0.019* | |
| 24 Parganas N (PRN) | 0.082* | 0.045* | 0.002* | |
| Hugli (HBL) | 0.113* | 0.055* | -0.010 |
- Above diagonal: values from microsatellite data (six loci). Below diagonal: values from allozyme data (18 loci). *Nominal adjusted p-value <0.05 (Bonferroni correction).
Genetic differentiation among populations was also investigated using the genotype assignment method. The results suggest some discrimination between all pairs of samples with both classes of markers. Fig. 2 shows the log-log plots relating to samples HBL and PRN, the samples that exhibited the lowest level of genetic differentiation and non-significant FST value from allozyme data.
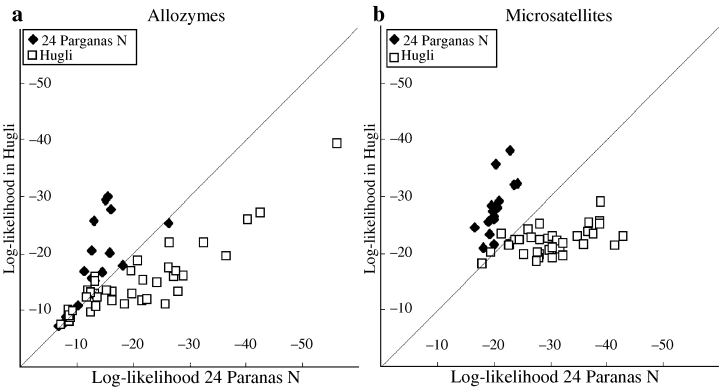
Genotypes assignment. Log-likelihood in samples 24 Parganas N versus Hugli of individual multigenotypes from both populations. Genotypes lying below diagonal have lower likelihood in 24 Parganas than in Hugli and are assigned to Hugli and vice versa
The allozyme plot (Fig. 2a) shows a considerable overlap of individuals belonging to the two samples. Correct assignment was, in fact, obtained for 48.2% of genotypes at a significance level of 0.001 (57.1% at 0.01 level). On the contrary, the overlap in the microsatellites plot (Fig. 2b) is lower than for the allozyme plot, as correct assignments were obtained for 84.9% (p < 0.001; when considering a threshold of p < 0.01 this value raises to 88.8%) of the individuals. These values are quite lower than the mean values for all pairwise comparisons of samples, which are 89.7% (p < 0.001) and 92.9% (p < 0.01). Nevertheless, the high proportion of significant correct assignments again indicates that microsatellite set allows resolving between poorly differentiated samples better than allozymes do.
When all the 141 individuals from our samples were considered, the allozyme data allowed correct assignment of 40.6% of individual multilocus genotypes to their sample of origin (p < 0.001; 46.8% at 0.01 level). Higher efficiency was again shown by microsatellite markers, with 67.7% of individuals correctly assigned at 0.001 significance level and 73.6% with p < 0.01. It could be worth noting that when testing correct assignment among the whole set of population, one has to consider the likelihood of assignment to any of them, so that proportion of correct assignments can be lower than when testing between only two samples (see the Materials and methods section for details).
In the analysis of genetic structure, microsatellite markers provided a more accurate picture than allozymes. In fact, they displayed a far lower standard error in FST values and better resolution in the genotype assignment test. The higher polymorphism revealed by microsatellites is usually considered as the most likely explanation for the better performance of this marker compared with allozymes. Nonetheless, a different sensitivity of these two markers to environmental factors could also account for a different performance in the estimation of gene flow. Selection acting on allozyme genotypes has been demonstrated in both artificial and natural conditions (Koehn et al. 1976; Oakeshott et al. 1982; Allegrucci et al. 1994; Pogson et al. 1995). Indeed, selection is a possible explanation of the divergent patterns of differentiation between single enzymatic loci that we observed in zebrafish samples. Conflicting patterns of differentiation displayed by allozyme and microsatellite markers have been attributed to selective factors by Lemaire et al. (2000) in Mediterranean sea bass populations on the basis of previous studies by Allegrucci et al. (1994, 1997). These results support the value of comparisons between data sets from different classes of markers such as microsatellites and allozymes, on account of the different evolutionary information they provide.
Acknowledgements
We are very grateful to Gabriele Gentile, Adalgisa Caccone, Claudio Ciofi and two anonymous reviewers for providing useful criticism in a first draft of the manuscript. Axel Weber provided The German Summary. Financial support was granted from the Italian National Council of Researches (CNR) to Stefano Cataudella.




