Genetic Influences on Growth Traits of BMI: A Longitudinal Study of Adult Twins
Abstract
Objective: To investigate the interplay between genetic factors influencing baseline level and changes in BMI in adulthood.
Methods and Procedures: A longitudinal twin study of the cohort of Finnish twins (N = 10,556 twin individuals) aged 20–46 years at baseline was conducted and followed up 15 years. Data on weight and height were obtained from mailed surveys in 1975, 1981, and 1990.
Results: Latent growth models revealed a substantial genetic influence on BMI level at baseline in males and females (heritability (h2) 80% (95% confidence interval 0.79–0.80) for males and h2 = 82% (0.81, 0.84) for females) and a moderate-to-high influence on rate of change in BMI (h2 = 58% (0.50, 0.69) for males and h2 = 64% (0.58, 0.69) for females). Only very weak evidence for genetic pleiotropy was observed; the genetic correlation between baseline and rate of change in BMI was very modest (−0.070 (–0.13, −0.068) for males and 0.04 (0.00, 0.08) for females.
Discussion: Our population-based results provide a basis for identifying genetic variants for change in BMI, in particular weight gain. Furthermore, they demonstrate for the first time that such genetic variants for change in BMI are likely to be different from those affecting level of BMI.
Introduction
Genetic influences on BMI (kg/m2) and obesity are well-established (1,2,3), and genes and genomic regions have been associated with BMI, other measures of obesity, and obesity-related phenotypes (4). Family, twin, and adoption studies indicate that in most populations and age groups interindividual genetic differences account for a large portion of interindividual differences in weight and obesity.
While genetic effects on weight and obesity are well established, the genetics of changes in weight in adults is less well known and characterized. Fabsitz and coauthors (5) showed substantial heritability (∼70%) of maximum BMI and trends in adult weight gain in 514 male twin pairs examined for the first time during military induction at the mean age of 20 years and examined four times during a 43-year follow-up. A similar substantial heritability (from 57 to 86%) of change in BMI over a decade was reported by Austin and coauthors (6) from two examinations of 315 middle-aged, female twin pairs. Within-pair correlations for 6-year change in weight were modest (0.29 and 0.07 for monozygotic (MZ) and dizygotic (DZ) men, and 0.25 and 0.05 for MZ and DZ women, respectively) when adjusting for age and initial BMI in 5,967 same-sex nonpregnant Finnish twin pairs measured in 1975 and 1981 (7). A family resemblance of 7-year changes in BMI in 521 Canadian families was reported by Hunt and coauthors (8) (heritability = 14%). In the Framingham family data, substantial heritability (24%) for rate of weight change in adulthood was also observed over a 24-year follow-up period (9). This is in contrast to the absence of (additive) genetic contribution to the average change in BMI in Framingham families observed over a 20-year follow-up period reported by Coady and coauthors (10).
Despite substantial genetic effects on both BMI and rate of weight change, it is not clearly known whether genetic effects on (level of) BMI are the same as those influencing rate of change in BMI. In none of the studies referred above, the growth traits of BMI or weight were analyzed simultaneously allowing for mutual dependence between the traits. Therefore, we sought to characterize in more detail the genetic architecture of rate of BMI change in relation to BMI level based on data from three surveys of the Finnish Twin Cohort over a 15-year period. We use latent growth models to investigate sources of influence on individual differences in BMI in latent variables of intercept (expected level of BMI at first measurement) and slope (rate of change in BMI) and their mutual dependency. This class of models allows for biometric analysis of sources of influence on individual differences in growth.
Methods and procedures
Subjects
The data were derived from the older cohort of the Finnish Twin Cohort Study (11). The baseline questionnaire was mailed in 1975 to all same-sex Finnish twin pairs born before 1958 and both co-twins alive in 1974. The response rate to this questionnaire was 89%. A follow-up questionnaire was sent in 1981 to all twin pairs to whom the baseline questionnaire had been sent regardless of whether they had participated in the 1975 survey. The response rate in the first follow-up survey was 84%. In 1990, a questionnaire was mailed to twins who had participated in at least one of the previous surveys. In the 1990 survey, twins born before 1930 were excluded, and both twins needed also to be alive. The response rate in the second follow-up survey was 77%.
Zygosity was assessed in the 1975 and 1981 surveys with questions about the similarity of appearance of a twin pair at an early school age. The reliability of this questionnaire method for classifying zygosity was assessed in a Finnish study by using 11 blood markers in a sample of 104 twin pairs classified as MZ or DZ (12). The observed agreement between the results of the blood tests and the questionnaire subsample was 100%. The probability of misclassification of a twin pair was estimated to be <2%.
Height and weight were self-reported, and they were asked for in an identical fashion in each survey. Height was given in centimeters and weight in kilograms, and, when necessary, the values were rounded to the nearest integral number. The validity of self-reports of height and weight was examined in a subsample of 100 male and 127 female twin individuals who had replied to the 1990 questionnaire. A clinical examination several years after the participants had returned the questionnaire showed that the correlation between self-reported and measured BMI was 0.89 in men and 0.90 in women (13). This suggests good reliability of self-reports of BMI.
BMI data were available on 10,556 out of 11,561 twins who were alive in 1990 and aged 20–46 years and who had returned questionnaires in all 3 years (1975, 1981, and 1990). These make up 735 female MZ, 499 male MZ, 1,265 female same-sex DZ and 1,013 male same-sex DZ intact pairs, which is a total of 3,512 intact pairs completing all three measurements. A further 3,532 twin individuals without a co-twin also have complete data. The low MZ/DZ ratio reflects the high rate of DZ twinning in Finland in the middle of the last century.
Before analyses, we transformed BMI by natural logarithm (lnBMI) to approximate normality in distribution given the skewness of BMI. Hence by BMI we refer to the scale of natural logarithm of BMI unless otherwise stated. Because sex differences in BMI probably reflect sex differences in body composition, all analyses were done separately in the male and female samples.
The analysis had two parts. First we undertook a descriptive analysis of marginal change in level of BMI by age and then did the biometric analysis described below.
The marginal change in level of BMI (mean of BMI) vs. mean age was estimated for both males and females for the three age groups 20–28, 28–37, and 37–46, defined by age at baseline (1975).
Longitudinal biometric analyses
Linear latent growth curve models were fitted to the Finnish longitudinal sample. We used all those twins that completed all three measurements. Furthermore, to check robustness of results toward missing observations, we used the whole sample assuming missing at random for those that did not complete all three measurements.
The latent growth curve models allow for biometric analysis of sources of influence on individual differences in growth. Briefly, if lnBMIij denotes level of the logarithm of BMI for the ith individual at timepoint j (years) then our linear model is given by
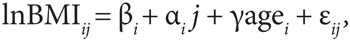
where βi and αi are the individual growth variables, intercept, and slope, respectively. The residuals are denoted by ɛij, and agei is individual age at baseline, which has a fixed effect denoted by γ (14). This model allows for simultaneous analysis of growth variables and their mutual interplay. The variance–covariance structure of the individual growth variables may be decomposed into a sum of genetic and environmental components (15) (see 1). From these components, we obtain estimates of heritability of the growth curve variables. Furthermore, we obtain genetic and environmental correlations between latent variables revealing possible pleiotropy.
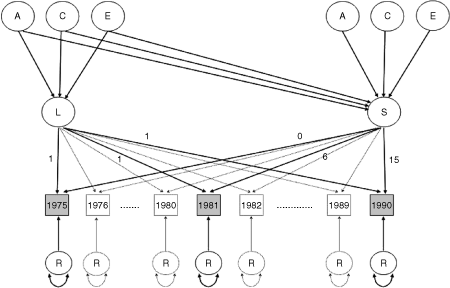
: Path-diagram of linear ACE growth curve model (for one individual) centered on calendar-time and applied to Finnish longitudinal data. Letters A, C, and E denote additive genetic, common environmental, and nonshared environmental effect, respectively. L and S denote level at baseline (intercept) and rate of change (slope), respectively, and R denotes the residual effect.
The bivariate linear growth curve models are centered on (calendar) time. Hence the time-evolution is implemented so that time equals 0 at the first measurement in 1975, 1 in 1976, and so on up to time-weight 15 on the slope at the third and last measurement in 1990. This representation allows for difference in years between measurements and gives the interpretation of intercept as the level at the first measurement. We adjusted for differences in age at baseline by including this information as a fixed effect for each individual in the model. Hence the latent variables of individual growth, intercept, and slope have the interpretation of age at baseline specific level in BMI at first measurement and change in BMI per year, respectively.
Models were fitted to the raw data, considering four zygosity groups: MZ males, MZ females, DZ males, and DZ females. Estimation proceeded by standard maximum likelihood estimation assuming a bivariate normal distribution of latent variables and that these are independent of the residuals. We first considered a saturated model specified by constraining, for males and females separately, mean, variance, and within-twin cross-trait covariance of intercept and slope to be the same for twin and co-twin, MZ and DZ pairs, and also by constraining cross-twin cross-trait covariances (of twin's level with co-twin's slope and vice versa) to be equal within each zygosity-by-sex group. This implements the rather natural assumption of symmetry between twin and co-twin and that twins are (as individuals) from the same base population. From this model, we obtained measures of similarity to compare for MZ and DZ pairs: within-pair (intraclass) correlation and cross-twin cross-trait correlation (i.e., correlation of twin intercept with co-twin slope and vice versa). Furthermore, we obtained individual correlation of intercept with slope.
Finally, we fitted biometric growth curve models allowing for differential genetic and environmental sources of variation both between latent factors (i.e., intercept and slope) of the growth curve and between sexes, and we estimated the genetic and environmental influences on intercept and slope under the best fitting model. The best fitting model was selected on the basis of the lowest Akaike information criterion (16) relative to the saturated model.
All analyses were carried out using the Stata (StataCorp, College Station, TX) (17) and Mx (Virginia Commonwealth University, Richmond, VA) (18) statistical packages. Mx-scripts implementing bivariate growth curve models can be downloaded from the Mx-script library (www.psy.vu.nlmxbib) and (19).
Results
BMI level by age
The marginal change in level of BMI versus mean age was estimated from the longitudinal measurements and presented in 2. For females, a linear increase in mean of (logarithm of) BMI with increasing age in all three age groups can be observed. For males, an almost proportional increase in mean BMI with age was observed. However, a slight leveling off in increasing mean BMI with increasing mean age was indicated.
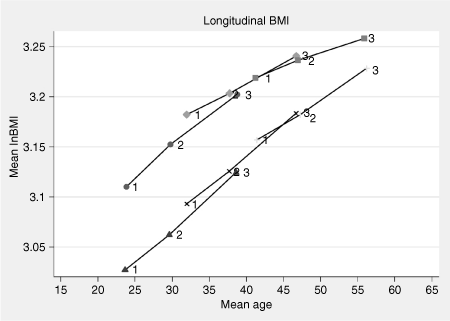
: Mean lnBMI by mean age for males (upper) and females for each cohort is determined by age of first measurement (i.e., age in 1975). The cohort of males aged 20–28 in 1975 are denoted by circles, cohort 28–37 by diamonds, and cohort 37–46 by squares. The corresponding female cohorts are denoted by triangle, cross, and plus, respectively. lnBMI, BMI by natural logarithm.
Longitudinal biometric analyses
Estimates of correlations for both sexes by zygosity are presented in Table 1. These are based on the full bivariate longitudinal growth curve model assuming equal means and variances within pairs (with likelihood, i.e., two times log of likelihood, equal to 62,987.079 with 28,342 degrees of freedom). The assumption of equal means and variances within pairs, regardless of twin type, was assessed by comparison with the saturated (unrestricted) model, and no sign of violation was observed.
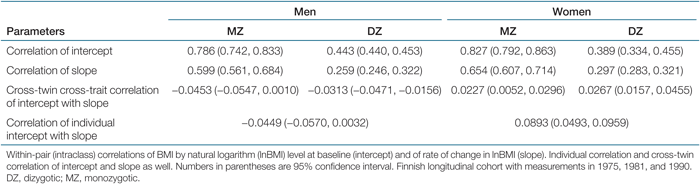 |
The estimates of within-pair (intraclass) correlation of BMI level at baseline (intercept) and correlation of rate of change in BMI (slope) showed that MZ pairs were more correlated than DZ pairs, which suggests the presence of a genetic influence for both traits. The cross-twin cross-trait correlations showed that the baseline BMI of one twin seem to be little correlated with the rate of change of the BMI of the co-twin and vice versa for both MZ and DZ pairs, males and females. The correlation of individual baseline BMI with rate of change of the BMI was small. This suggests that initial level of BMI (from the first measurement adjusted for age at baseline) will have little or no influence on predicting the rate of change in BMI. This result examined in more detail below using biometric modeling to see if a similar result will hold at the level of genetic influence.
The most parsimonious and best fitting submodel of the full growth model described above was the AE model for both males and females (Δχ26 = 4.296, P value = 0.64). Hence variance of individual intercept and of slope is a sum of additive genetic variance and unique environmental variance. Using the expression of individual growth of the previous section and estimates of mean intercept, mean slope, and coefficient of age at baseline from Table 2, expected BMI may be estimated. For instance, females aged 30 years in 1975 would on average have a BMI of 22.4 kg/m2 in 1981. While the mean intercept was higher for males than for females, the mean slope was slightly higher for females than for males. Furthermore, the effect of differences in age at baseline was slightly higher for females than for males. The variance of the latent traits was similar for the two sexes and was approximately constant over the age groups indicating no serious deviances from the model.
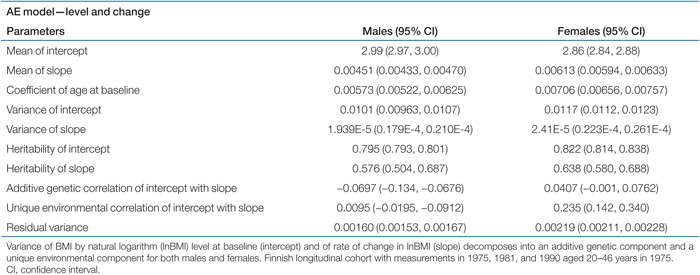 |
The estimates of heritability in Table 2 provide evidence for substantial genetic influence on BMI level at baseline, as expected, and a moderate-to-high influence on rate of change in BMI for both males and females. The proportion of variance in level of BMI due to additive genetic effects was ∼80% (80% in men and 82% in women) and for rate of change ∼60% (58% in men and 64% in women). The additive genetic correlation of intercept with slope was very low (−0.07 in men and 0.04 in women), indicating that level and change appear to be governed by different genetic factors. While the unique environmental correlation of intercept with slope was low (0.01) for males, it was moderate (0.24) for females. The above results obtained for the 3,512 intact twin pairs and 10,556 twins (out of 11,561) completing all three measurements were almost unchanged when using the full sample (N = 11,561) for the estimation, which indicates certain robustness against the relatively few missing values in the sample.
Discussion
While growth in children is certainly under genetic influence (20) as is the level of the BMI in adulthood (1,2), less is known about what extent genes influence change in BMI in adult life. In particular, it is poorly understood how genetic influence on level relates to genetic influence on change. A better understanding of the complex underlying genetics for BMI and weight change is highly desirable and may provide information for specific prevention programs accounting for interindividual genetic differences.
Our study is the first to simultaneously analyze level and change in BMI using a population-based longitudinal cohort of adult twins. We found a moderate-to-high genetic influence on change in BMI, and moreover, the correlation of genetic effects on change with genetic effects on level at baseline was very low.
The validity of these findings assumes that environmental factors of importance for the trait act in the same way for MZ and DZ twins (the “equal environments assumption”). Many such factors may be suspected (such as social support, closeness in residence, etc.) that would inflate our estimates of genetic influence; however, earlier studies of BMI in twins have tested this assumption and have found it to hold (1).
Our modeling approach assumes that long-term (15 year) individual BMI trajectories in the cohort of young adults aged 20–46 years at baseline is adequately described by individual initial level and rate of change. The variances of these latent variables are nearly constant over the age groups, indicating a certain robustness toward deviation from proportionality in individual change in BMI with age in the given age range. We observed that the average rate of weight gain is similar for all age groups (birth cohorts) for women, while for men a certain leveling off from linearity in increasing lnBMI with age was found. This in accordance with results obtained by Lahti-Koski et al. (21), based on surveys in Finland from 1972 to 1997, showing that males born in more recent years gain weight faster than males born earlier.
The relationship of baseline weight with future weight gain patterns differs by age and sex. In adults, who have attained their full height, weight gain is generally not strongly associated with initial BMI as apparent from the results of several recent studies (22,23,24,25,26).
It should be noted that heritability estimates often differ between twin studies and traditional family-based studies due to differences in the study designs and in the underlying assumptions (1). Heritability estimates, as a ratio of genetic to overall variance, are specific to the population studied. Hence heritability estimates may differ because of differences in the genetic makeup of a population, as well as cultural, temporal, and environmental reasons. Many twin studies, which allow for better disentanglement of environmental and genetic origin of effects than traditional family studies, have shown that ∼70–80% of the overall variation in (level of) BMI can be attributed to genetic differences between individuals. This seems to be a rather consistent finding in various countries in different time periods (2). Based on this knowledge, there are several studies and projects aimed at identifying genetic variants for level of BMI (27,28,29) and also for obesity (4,30). It is argued (29) that there is a lack of consistency in detecting chromosomal loci that are linked to obesity-related traits and that this may partly be due to variability and inaccuracy in the phenotype definition. Several other factors may play a role for inconsistency in linkage results such as lack of power and genetic heterogeneity in the population.
Change in BMI, in particular during the age period of average weight gain among young and middle-aged adults (from ∼20 to 55 years), may be a particularly important phenotype from the public health point of view. Both animal and human studies indicate that there are powerful physiological reactions in association with change in BMI. For instance, weight loss seems to induce a pronounced stimulation of the appetite and a long-lasting fall in metabolic rates (31,32,33). Similarly, the response to long-term overfeeding in humans is genetically influenced, and candidate genes have been observed (34,35). In the short term, previous weight loss predicts weight gain and vice versa, based on data from multiple repeated measures in the Nurses' Health study (36), consistent with a strong homeostatic influence on individual weight change pattern. Evidence for a long-term genetic influence on change in BMI is given in the present study as observed in American twin (5) and family (9) studies. This influence on change persists when taking level of BMI into account as the present study demonstrates. In the Framingham family data, some evidence for long-term weight change by linkage on chromosomes 1 and 20, and potential candidate genes was also found (9).
The moderate-to-high heritability of change in BMI demonstrated in these studies is based upon the assumption of no gene–environment interaction. As shown in Bouchard et al. (34), gene–environment interactions affect energy balance, and implications thereof may play an important role in early diagnosis of individuals at risk for developing long-term metabolic problems and obesity. The low correlation of genetic effects on change with genetic effects on level at baseline shown in the present study may have implications for the identification of relevant factors for gene–environment interactions of body mass change.
The genetic influence on change in BMI may be of a polygenic origin, that is, many rather common variants may be present in the population, each with a modest effect, in accordance with the common disease/common variant hypothesis. A recent genome-wide association study (37) identified a novel obesity gene, FTO, which nonetheless accounted for only 1% of the variance of BMI; further reports have confirmed that the association has been observed in multiple populations so far (38). The FTO gene affected BMI in both childhood and adult samples but did not affect birthweight (37). An evolutionary viewpoint is that these common variants may be genes that act beneficially for energy-conserving mechanisms in the human body, which is of high importance in periods of low food supply (“thrifty genes” (39)). The same genes may induce weight gain in periods of good food supply; some gene variants would be more efficient in this than others. It is also possible that the genetic mechanisms regulating weight gain are different during growth and adulthood. Thus our findings do not readily extend to children and adolescents. Likewise, they may not extend to old age, where weight change due to loss of lean body mass (mainly muscle) becomes an important component compared to changes in body fat.
Our findings provide basis for searching for genes affecting change in BMI. However, attempts at identifying genetic variants for change, in particularly weight gain, may include variants different from those affecting level of BMI since the initial level, i.e., BMI as a young adult, does not seem to have been genetically correlated with rate of change in BMI over the subsequent 15 years. The pathogenesis of obesity may have developmental phases distinguished by the action of distinct sets of genes.
Disclosure
The authors declared no conflict of interest.
Acknowledgments
This paper originates from the GENOMEUTWIN project which is supported by the European Union Contract No. QLG2-CT-2002-01254. KS was supported by the Academy of Finland (grant no. 108297). The Finnish Twin Cohort study is part of the Academy of Finland Centre of Excellence in Complex Disease Genetics.





