Original Paper
A pseudoelastic model for mechanical twinning on the microscale
R. Glüge, A. Bertram,
T. Böhlke,
E. Specht,
A. Bertram
Otto-von-Guericke-Universität, Institut für Mechanik, Universitätsplatz 2, 39106 Magdeburg, Germany
Search for more papers by this authorT. Böhlke
Karlsruhe Institut für Technologie (KIT), Institut für Technische Mechanik, Postfach 6980, 76128 Karlsruhe, Germany
Search for more papers by this authorE. Specht
Otto-von-Guericke-Universität, Institut für Mechanik, Universitätsplatz 2, 39106 Magdeburg, Germany
Search for more papers by this authorR. Glüge, A. Bertram,
T. Böhlke,
E. Specht,
A. Bertram
Otto-von-Guericke-Universität, Institut für Mechanik, Universitätsplatz 2, 39106 Magdeburg, Germany
Search for more papers by this authorT. Böhlke
Karlsruhe Institut für Technologie (KIT), Institut für Technische Mechanik, Postfach 6980, 76128 Karlsruhe, Germany
Search for more papers by this authorE. Specht
Otto-von-Guericke-Universität, Institut für Mechanik, Universitätsplatz 2, 39106 Magdeburg, Germany
Search for more papers by this authorAbstract
A pseudoelastic model for the simulation of deformation twinning on the microscale is develope and coupled with a crystal plasticity model for crystallographic slip. The material parameters are adopted to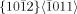 
twinning and basal glide in a magnesium alloy. Special attention is drawn to the energy invariance of conjugate twin systems that emerges when twinning is treated elastically. The model is tested in three characteristic FE simulations, namely a simple shear test parallel and inclined to a twin system and an elongation test of a notched band. The slip-twin interaction is studied, as well as the practical implications of the strain energy invariance. Some characteristics of twinning could be reproduced. The most important observations are that the load drop at the twin nucleation, the cusp shape of the twin tip in the absence of slip and the kink patterns that evolve in slip-twin interaction could be simulated.
References
- [1]R. Abeyaratne and J. Knowles, Evolution of Phase Transitions – A Continuum Theory (Cambridge University Press, Cambridge, 2006).
- [2]E. Acerbi, G. Bouchitté, and I. Fonseca, Relaxation of convex functionals: The gap problem, Annales de l' Institut Henri Poincaré (C) Analyse non linéaire 20, 359–390 (2003).
- [3]G. Andrews, On the existence of solutions of the equation utt = uxxt + σ (ux)x, J. Differ. Equ. 35, 200–231 (1980).
- [4]G. Andrews and J. Ball, Asymptotic behaviour and changes of phase in one-dimensional nonlinear viscoelasticity, J Differ. Equ. 44, 306–341 (1982).
- [5]R. Asaro and A. Needleman, Overview 42: Texture development and strain-hardening in rate dependent polycrystals, Acta Metall. 33, 923–953 (1985).
- [6]A. Atai and D. Steigmann, Coupled deformations of elastic curves and surfaces, Int. J. Solids Struct. 35, 1915–1952 (1998).
- [7]J. Ball and R. James, Fine phase mixtures as minimizers of energy, Arch. Ration. Mech. Anal. 100, 13–52 (1987).
- [8]J. Ball and R. James, Proposed experimental tests of a theory of fine microstructure, and the two-well problem, Philos. Trans. R. Soc. Lond. A 338, 389–450 (1992).
- [9]J. Ball, Convexity conditions and existence theorems in nonlinear elasticity, Arch. Ration. Mech. Anal. 63, 337–403 (1977).
- [10]J. Ball, P. Holmes, R. James, R. Pego, and P. Swart, On the dynamics of fine structure, J. Nonlinear Sci. 1, 17–90 (1991).
10.1007/BF01209147 Google Scholar
- [11]A. Bertram, Elasticity and Plasticity of Large Deformations (Springer Verlag, Berlin, 2005).
- [12]T. Böhlke, The Voigt bound of the stress potential of isotropic viscoplastic FCC polycrystals, Arch. Mech. 56, 423–443 (2004).
- [13]T. Böhlke and A. Bertram, The evolution of Hooke's law due to texture development in polycrystals, Int. J. Solids Struct. 38, 9437–9459 (2001).
10.1016/S0020-7683(01)00130-5 Google Scholar
- [14]G. Bolling and R. Richman, Continual mechanical twinning, Parts I, II, III Acta Metall. 13, 709–757 (1965); Continual mechanical twinning, Parts IV, V, Acta Metall. 14, 637–647 (1965).
- [15]V. Boyko, R. Garber, and A. Kossevich, Reversible Crystal Plasticity (AIP Press, New York, 1994).
- [16]R. Cahn, Plastic deformation of alpha-uranium: twinning and slip, Acta Metall. 53, 49–70 (1953).
- [17]J. Christian and S. Mahajan, Deformation twinning, Prog. Mater. Sci. 39, 1–157 (1995).
- [18]C. Collins, Computation of twinning, The IMA Volumes in Mathematics and its Applications Vol. 54, (Springer, Berlin, Heidelberg, New York, 1993), pp. 39–50.
- [19]C. Dafermos, The mixed initial-boundary value problem for the equations of nonlinear one-dimensional viscoelasticity, J. Differ. Equ. 6, 71–86 (1969).
- [20]E. Emles, Principles of Magnesium Technology (Pergamon, Oxford, 1966).
- [21]J. Ericksen, Equilibrium of bars, J. Elast. 5, 191–202 (1975).
- [22]J. Ericksen, The Cauchy-Born hypothesis for crystals, in: Phase Transformations and Material Instabilities in Solids, edited by M. Gurtin (Academic Press, New York, 1984), pp. 61–77.
- [23]J. Ericksen, Twinning of Crystals, IMA Preprint Series Univ. Minnesota 95, 1–18 (1984).
- [24]R. Glüge and J. Kalisch, A Lower Bound Estimation of a Twinning Stress for Mg by a Stress Jump Analysis at the Twin-parent Interface, in: Micro-Macro-Interactions in Structured Media and Particle Systems, edited by A. Bertram and J. Tomas (Springer-Verlag, Berlin, Heidelberg, New York, 2008).
- [25]S. Govindjee, A. Mielke, and G. Hall, The free energy of mixing for n-variant martensitic phase transformations using quasi-convex analysis, J. Mech. Phys. Solids 51, 1–26 (2003).
- [26]M. Greenberg, On the existence, uniqueness, and stability of the equation ρ0 xtt = e(xx)xxx + λ xxxt, J. Math. Anal. Appl. 25, 575–591 (1969).
- [27]M. Greenberg and R. MacCamy, On the exponential stability of solutions of e(ux)uxx + λ uxtx = ρ utt, J. Math. Anal. Appl. 31, 406–417 (1970).
- [28]M. Greenberg, R. MacCamy, and V. Mizel, On the existence, uniqueness, and stability of solutions of the equation σ′(ux)uxx + λ uxtx= ρ0 utt, J. Appl. Math. Mech. 17, 707–728 (1968).
- [29]P. Haasen, Physical Metallurgy, 3rd edition (Cambridge University Press, Cambridge, 1996).
- [30]R. Hill, On constitutive inequalities for simple materials-I, J. Mech. Phys. Solids 16, 229–242 (1968).
- [31]Q. Hu, L. Li, and N. Ghoneim, Stick-slip dynamics of coherent twin boundaries in copper, Acta Mater. 57, 4866–4873 (2009).
- [32]J. Hutchinson, Bounds and self-consistent estimates for creep of polycrystalline materials, Proc. R. Soc. Lond. A 348, 101–127 (1976).
- [33]K. Kawabata, Y. Hosokawa, T. Saga, and T. Sambongi, Real-time observation of twin boundary motion in crystals: an ideal dry friction system, Tribology Letters 9, 41–44 (2000).
- [34]P. Klouček and M. Luskin, The computation of the dynmaics of the martensitic transformation, Contin. Mech. Thermodyn. 6, 209–240 (1994).
- [35]D. Kochmann and K. Le, A continuum model for initiation and evolution of deformation twinning, J. Mech. Phys. Solids 57, 987–1002 (2009).
- [36]M. Lambrecht, C. Miehe, and J. Dettmar, Energy relaxation of non-convex incremental stress potentials in a strain-softening elastic-plastic bar, Int. J. Solids Struct. 40, 1369–1391 (2003).
- [37]B. Li and E. Ma, Atomic shuffling dominated mechanism for deformation twinning in magnesium, Phys. Rev. Lett. 103, 35503-1-4 (2009).
- [38]B. Li and E. Ma, Zonal dislocations mediating {1011}〈1012〉 twinning in magnesium, Acta Mater. 57, 1734–1743 (2009).
- [39]S. Lubenets, V. Startsev, and L. Fomenko, Elastic Twinning in In-10 Wt% Pb Alloy, Krist. Tech. 15, K78–K80 (1980).
- [40]I. Müller and P. Villaggio, A model for an elastic-plastic body, Arch. Ration. Mech. Anal. 65, 25–46 (1977).
- [41]P. Neumann, Vereinfachung kristallographischer Rechnungen in hexagonalen Gittern durch konsequente Benutzung des vierachsigen hexagonalen Koordinatensystems, phys. stat. sol. 17, K71–K74 (1966).
- [42]M. Ortiz and E. Repetto, Nonconvex energy minimization and dislocation structures in ductile single crystals, J. Mech. Phys. Solids 47, 397–462 (1999).
- [43]S. Pagano and P. Alart, Solid-solid phase transition modelling: relaxation procedures, configurational energies and thermomechanical behaviours, Int. J. Eng. Sci. 37, 1821–1840 (1999).
- [44]R. Pego, Phase transitions in one-dimensional nonlinear viscoelasticity: Admissibility and stability, Arch. Ration. Mech. Anal. 97, 353–394 (1987).
- [45]M. Peigney, A non-convex lower bound on the effective energy of polycrystalline shape memory alloys, J. Mech. Phys. Solids 57, 970–986 (2009).
- [46]M. Pitteri and G. Zanzotto, Continuum Models for Phase Transitions and Twinning in Crystals (Chapman and Hall/CRC, London, 2002).
- [47]E. Roberts and P. Partridge, The accommodation around {10 bar 1 2}〈 bar 1 011 〉 twins in magnesium, Acta Metall. 14, 513–527 (1966).
- [48]B. Schmidt, Linear Γ-limits of multiwell energies in nonlinear elasticity theory, Contin. Mech. Thermodyn. 20, 375–396 (2008).
- [49]M. Shiekhelsouk, V. Favier, K. Inal, and M. Cherkaoui, Modelling the behaviour of polycrystalline austenitic steel with twinning-induced plasticity effect, Int. J. Plast. 25, 105–133 (2009).
- [50]M. Sidi Ammi and D. Torres, Regularity of Solutins of the Autonomous Integrals of the Calculus of Variations, in: Differential Equations, Chaos and Variational Problems, (Springer, Berlin, Heidelberg, New York, 2008).
- [51]S. Silling, Phase changes induced by deformation in isothermal elastic crystals, J. Mech. Phys. Solids 37, 293–316 (1989).
- [52]G. Simmons and H. Wang, Single Crystal Elastic Constants and Calculated Aggregate Properties: A Handbook (The MIT Press, Cambridge, MA, 1971).
- [53]J. Simo and T. Hughes, Computational Inelasticity (Springer-Verlag, New York, 1998).
- [54]J. Stark, Mechanical twinning in crystals, Phys. Rev, B 38, 1139–1142 (1988).
- [55]P. Swart and P. Homes, Energy minimization and the formation of microstructure in dynamic antiplane shear, Arch. Ration. Mech. Anal. 121, 37–85 (1992).
- [56]C.A. Truesdell and W. Noll, The Non-linear Field Theories of Mechanics, in: Encyclopedia of Physics, Vol. III/3 (Springer, Berlin, 1965).
- [57]Y. Wang, Y. Jin, and A. Khachaturyan, The Effects of Free Surfaces on Martensite Microstructures: 3D Phase Field Microelasticity Simulation Study, Acta Mater. 52(4), 1039–1050 (2004).
- [58]G. Zanzotto, On the material symmetry group of elastic crystals and the Born rule, Arch. Ration. Mech. Anal. 121, 1–36 (1992).
- [59]G. Zanzotto, The Cauchy-Born hypothesis, Nonlinear elasticity and mechanical twinning in crystals, Acta Crystallogr. A 52, 839–849 (1996).
