Simulation of Ladle Refining Reactions in Si–Mn-Killed Steel
Abstract
Steel quality, to a large extent, is controlled by ladle refining reactions. The understanding of such reactions can help to prevent the formation of unwanted phases and improve the overall high-temperature process control. A new approach, namely, the multioxide inclusion kinetic model has been recently developed to simulate steel–inclusion reactions in liquid steel. The coupling of this kinetic model with a multicomponent, multiphase steel–slag reaction interface model leads to an overall model framework to predict the evolution of steel, slag, and inclusion composition. The current work shows the application of the model to simultaneous deoxidation and desulphurization during ladle refining of Si–Mn-killed steel. The model shows good performance with industrial data. It is demonstrated that for ladle refining practices, silica-rich slags should be strictly used with basicity (CaO/SiO2) between 1 and 1.2 and with Al2O3 content less than 5 wt%. Additional simulations are also carried out to reveal the capability of the model to aid in online process control. Finally, certain limitations of the current model are discussed.
1 Introduction
Ladle refining is commonly used industrially to make steel more amenable to processes like deoxidation, desulphurization, temperature management, and composition control.[1] Complex deoxidation by Si and Mn is beneficial for certain steel products including tire cords, springs, saw wire, and other thin strip cast steels.[2] This is because the use of such deoxidants leads to the formation of low-melting inclusions in place of high-melting aluminates. The latter is encountered predominantly when Al is used for deoxidation and has been seen to cause nozzle clogging,[3] in addition to impairing steel deformability.[4]
In Si–Mn-killed steels, oxide inclusions resulting from deoxidation typically belong to the MnO-SiO2–Al2O3 system.[5] In order to control the Al2O3 content in the inclusions without calcium treatment, slags with low basicity and low Al2O3 content[5, 6] are used to help generate favorable inclusions. However, such low-basicity slags have been reported to have poor desulphurization characteristics[7] due to their poor sulfide capacity. In principle, to realize low sulfur limits, a slag with high basicity and low oxygen activity in the bulk steel is desired.[1] Bhansali et al.[8] recently showed that although the amount of dissolved oxygen in the steel is controlled by the amount of deoxidizers added to the steel, slag compositions can also exert control on the [O] content.[9] To track such multifaceted physicochemical reactions together with the effect of dynamic changes taking place in the ladle, the development of an integrated model, linked to processing variables, can be helpful. This will allow steelmakers to not only anticipate process uncertainties but help them optimize process parameters to have better casting schedules.
Over the years, a number of kinetic models have been proposed for refining Al-killed steel, principally utilizing either the reaction zone model[10-16] or the reaction interface model.[17-23] Reaction zone models assume equilibrium between the metal and the inclusions, and as a result, predict only the types of equilibrium inclusions. To date, only a few reaction zone models have so far been developed for industrial refining of Si–Mn-killed steels, for example, see refs. [14, 15, 24]. These do not incorporate steel–inclusion reactions nor have they been compared to industrial inclusion analysis data. Reaction interface models are not limited to single-equilibrium inclusion composition; however, if competition between different oxide inclusions is not included, they will predict a single, average, inclusion composition.[9, 17, 20] Such a prediction is not supported by the large range of inclusion compositions found in steel plant samples. To fully simulate all possible conditions requires that the model allows inclusions to exist at any composition in the available range and that the thermodynamic stability be represented as a function of composition. In a previous work by one of the authors,[9] this approach was found to be not feasible computationally. Therefore, capturing the diversity of the oxide inclusion population needs a different approach.
Recently, the authors developed a model, namely, multioxide inclusion (MOI) kinetic model,[25] which has the ability to track with time, the competition between inclusions of different compositions, and thereby appropriately representing the evolution of the inclusion population. Essentially, this model considers a large number of “seeds” of different compositions with negligible volume. Note that the negligible volume is important so that a large number of seeds can exist indefinitely without perturbing the mass balance. The thermodynamics and kinetics of inclusion formation then “decide” which seeds grow and become significant or shrink and disappear over time. Building on our previous study which validated the MOI approach, the current work extends the datasets to probe the effects of different industrial refining practices on the temporal variation of [Al], [S], and [O] in steel and the inclusion composition. Specifically, the objective is to further validate this approach using additional plant data and demonstrate that a steel–slag–inclusion reaction interface model (incorporating the MOI model and Graham and Irons’ steel–slag model[21]) offers the ability to simulate the evolution of actual inclusion populations as well as the deoxidation and desulphurization trajectory. Following this, the effect of different steel, slag, process, and inclusion variables is demonstrated through extensive parametric studies. Finally, the extension of the model to other industrial scenarios and limitations is presented.
2 Mathematical Model
2.1 Overview
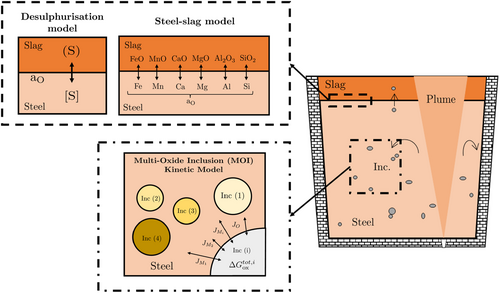
The model adopted in this work consists of two parts (refer to Figure 1) that take into consideration 1) steel–slag reactions (i.e., the steel–slag model + desulphurization model) and 2) steel–inclusion reactions (i.e., the MOI kinetic model). The major equations used in the overall model are summarized in Table 1. Specifically, the thermodynamic and kinetic equations for the steel–slag and steel–inclusion reactions that have been used to solve for the temporal evolution of the composition of the steel, slag, and inclusion phases have been listed. The model assumptions, parameters, numerical methodology, and calculation flowsheet details have been described in detail elsewhere.[21, 25]
| Phase interactiona) | Description | Equations | |
|---|---|---|---|
| Steel–slag | Reaction at steel–slag interface | (1) | |
| Equilibrium condition | (2) | ||
| Activity of steel species | (3) | ||
| Composition change of bulk steel species | (4) | ||
| Composition change of bulk slag species | (5) | ||
| Steel–inclusion | Reaction at steel–inclusion interface | (6) | |
| Equilibrium condition | (7) | ||
| Equilibrium constant | (8) | ||
| Gibbs free energy change during inclusion formation | (9) | ||
| Mass transfer rate across steel/inclusion interface | (10) | ||
| Mass flux balance | (11) | ||
| Inclusion of chemical size growth | (12) |
- a) f i : Henrian activity coefficient of i; MWi: Molar weight of i (kg mol−1); : Mole fraction of i in bulk; : Mole fraction of i at interface; Vst/sl: Volume of steel/slag (m3); xi: Stoichiometric coefficient of ith deoxidizer element; Keq,i: Equilibrium constant of oxide i; : Gibbs energy change during formation of inclusion i (J mol−1); : Gibbs energy change of mixing during formation of inclusion i (J mol−1); : Gibbs energy change of solid inclusion formation (J mol−1); R: Gas constant (J mol−1 K−1); r: inclusion radius (m); α: Ratio of steel (Fe) to inclusion molar volumes (mean volume per atom); : Mole fraction of oxygen in the oxide inclusion.
For the first part, the multicomponent steel–slag kinetic model developed by Graham and Irons[21] was used, based on the mixed coupled reaction interface model proposed by Robertson et al.[26] This model assumes that the rates of reaction are controlled by multicomponent transport in both metal and slag. Additionally, the chemical reactions are considered to be fast at the slag–metal interface, thus maintaining local equilibrium. This steel–slag kinetic model is linked with a desulphurization model to simulate the [S] behavior in steel, utilizing the interfacial oxygen concentration. The desulphurization model is further described in Section 2.2.
For the second part, the steel–inclusion reactions are described by a thermokinetic model recently published by the authors,[25] which predicts the amount and size changes of multiple oxide inclusions based on the composition of the steel. This model is based on equilibrium thermodynamics ()[27] and mass fluxes (Ji). The equilibrium constants for the different reactions ([M]–[O]) have been sourced from ref. 21 while details of the inclusion parameters can be found in ref. 25. For the system under consideration (MnO–SiO2–Al2O3), the oxide inclusions considered are 1) SiO2 (s), 2) MnO · SiO2 (l), 3) 2MnO · SiO2 (l), 4) Al2O3 (s), 5) MnO.Al2O3 (s), and 6) 3MnO.3SiO2.Al2O3 (l). The choice of compositions selected to model the liquid inclusions has been made based on the stoichiometries that are known to exist in the solid state in the MnO–SiO2–Al2O3 system. This was made entirely for convenience and as stated above, each of the liquid inclusion types has been assigned the thermodynamic properties of a liquid inclusion of that specific composition. Furthermore, this choice was 1) based on experimental observations[5, 6, 8] and 2) made to have less computational expense while allowing one to model predominant inclusion phases in liquid steel. It would have been equally possible to have chosen compositions that were not known to exist in the solid state, but a choice had to be made to maintain the simplicity of the model. The authors’ previous work has shown that this simplification offers a reasonable prediction of experimental behavior,[25] including a realistic inclusion population.
2.2 Desulphurization Model
| CaO | SiO2 | FeO | MgO | MnO | Al2O3 | |
|---|---|---|---|---|---|---|
| Λi | 1.0 | 0.48 | 0.51 | 0.78 | 0.59 | 0.61 |
2.3 Determination of Activities of Species
For the thermodynamics of the chemical reactions, the activities of each species within different phases are required. The activities in the liquid steel were calculated using a subroutine utilizing the unified interaction parameter formalism by Bale and Pelton.[31] The activities of the slag components were calculated using a subroutine involving the Gaye and co-workers’ cell model[32, 33] for slags. Please note that the contribution of S2− and F− toward oxide activity calculation was not considered in the cell model since oxides constituted more than 90 wt% of the slag. Finally, the inclusion oxide activities were calculated using the subregular solution model developed by Xiaobing et al.[34] instead of the cell model, due to its better accuracy for the CaO–MnO–SiO2–Al2O3 system.
2.4 Determination of Mass Transfer Coefficients
where T is the temperature of the steel (K), N refers to the number of plugs, and Pt is the pressure of molten steel at a depth of h (Pa).
3 Description of Simulation Studies
In order to validate the model, data from two industrial trials pertaining to the ladle refining process of Si–Mn-killed steel have been used. A brief description of each process, denoted as C1 and C2, is provided in Table 4. The details of the sampling and analysis procedures can be found in refs. [8, 15]. After validating the model against literature data, parametric studies were carried out to understand the role of different steel, slag, process, and inclusion variables on the model results, specifically, inclusion composition, [Al], [S], and [O] variations with time. The base steel and slag compositions for these simulations are denoted as P1. Table 5 and 6 show the chemical compositions of the steel and slag for C1, C2, and P1, while the corresponding model initialization parameters are provided in Table 7 and 8. Finally, the composition and recovery rates of the additions are listed in Table 9. The temperature of the steel was chosen to be 1873 K which decreases with stirring at a rate of 1.33 K min−1.[21]
| Case | Authors | References | Route | Steel grade | Comments |
|---|---|---|---|---|---|
| C1 | Peter et al. | [15] | EAF-LF-CC | Low-C steel | Deoxidation in LF; FeSi (120 kg) and SiMn (2126 kg) were used for deoxidation. Other additions include spar (340 kg), lime (1281 kg), MgO (54 kg), FeV (45 kg); CaSi (9 kg), oxidized skull/Fe2O3 (104 kg); steel and slag composition data were reported; METSIM model was used for dynamic simulation. |
| C2 | Bhansali et al. | [8] | EAF-LF-CC | Low-C steel | Deoxidation in LF; Preweighed mixture of SiMn, dolomite, silica sand, and lime was added in the ladle after tap; steel compositions, initial slag composition, and inclusion analysis were reported; FactSage thermodynamic calculations were performed. |
| Case | C | Mn | Si | Al | Ca | S | O | Fe |
|---|---|---|---|---|---|---|---|---|
| C1 | 0.06 | 0.11 | 0.005 | 0.003 | 0.00 | 0.047 | 0.050a) | Bal. |
| C2 | 0.06 | 1.05 | 0.27 | 0.001 | 0.0005 | 0.021 | 0.052 | Bal. |
| P1 | 0.06 | 1.00 | 0.25 | 0.001 | 0.0005 | 0.020 | 0.030 | Bal. |
- a) indicates that the parameter is assumed.
| Case | CaO | SiO2 | Al2O3 | MgO | FeO | MnO | CaS | CaF2 | Basicity |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 40 | 25 | 3.5 | 14 | 8 | 4 | 0.1 | 1 | 1.60 |
| C2 | 44 | 28 | 7 | 10 | 0.7 | 0.4 | 0.001 | – | 1.57 |
| P1 | 44 | 28 | 8 | 10 | 0.7 | 0.4 | 0.001 | – | 1.57 |
| Parameter | Symbol | Units | C1 | C2 |
|---|---|---|---|---|
| Steel mass | W st | ton | 120 | 170 |
| Slag mass | W sl | ton | 2.5 | 3 |
| Ladle diameter | D L | m | 2.612 | 2.612a) |
| Effective steel/slag reaction area | A | m2 | 7.11 | 7.11a) |
| Mass transfer capacity | K | s−1 | ||
| Inclusion number density | N t | m−3 | 1 × 1013 | 1 × 1013 |
| Initial inclusion diameter | d | μm | 1 | 1 |
| Gas flow rate | Q | Nm3 h−1 | 11.24 | 11.24a) |
| Plugs | N | − | 1 | 2 |
| Time step (steel–inclusion model) | s | 0.05 | 0.05 | |
| Time step (steel–slag model) | s | 1 | 1 |
- a) indicates that the parameter is assumed.
| CaO | SiO2 | Al2O3 | MgO | FeO | MnO | CaS | |
|---|---|---|---|---|---|---|---|
| C1 | 0.1 | 0.2 | 0.3 | 0.1 | 0.1 | 0.25 | 0.1 |
| C2 | 0.1 | 0.2 | 0.3 | 0.1 | 0.1 | 0.1 | 0.1 |
| C | Mn | Si | Al | Ca | S | Fe | Recovery [%] | |
|---|---|---|---|---|---|---|---|---|
| FeSi | 0.05 | 0.212 | 79.96 | 1.12 | 0.08 | – | Bal. | 75 |
| SiMn | 1.00 | 71.80 | 16.3 | – | 0.001 | 0.007 | Bal. | 85 |
| CaSi | 1.00 | – | 65.00 | – | 33.00 | 0.040 | Bal. | 30 |
Please note that some model inputs were not available in the original research articles and thus, had to be assumed based on existing process knowledge. These parameter estimates are denoted with “*” in the tables. For C1, the initial concentration of dissolved oxygen was assumed based on the oxygen content of steel arriving from a typical electric arc furnace (EAF) (≈500 ppm).[8] For C2, the model parameters, ladle dimensions, and gas flow rate were not available and were assumed to be the same as those in C1. This is justified because of the similar tonnages of steel in C1 and C2. The flow rate chosen for C2 (11.24 Nm3 hr−1) is consistent with typical gas flow rates (7–12 Nm3 hr−1) reported for refining other Si–Mn-killed steels.[8, 36, 37]
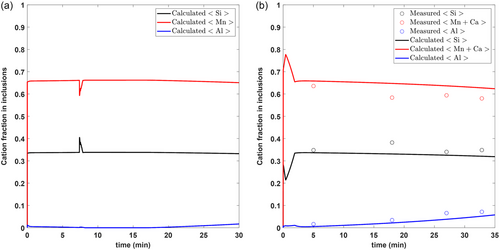
To complete the model, a few additional assumptions and considerations are required. First, the alloy addition rate is tuned to match the dissolution and mixing rate determined from the measured steel composition data (for C1). Second, the alloy and slag additions (shown in Table 4) are input to the model as an auxiliary file (for C1). Third, although the current case studies reported the use of Ca injection, the model was not constructed to account for Ca injection because of its relatively infrequent use for Si–Mn-killed steels. However, this approach has not significantly diminished the usefulness of these datasets in validating the current model because ref. 8 demonstrated that the amount of Ca additions caused very less Ca pickup within inclusions. In order to compare the model and experimental results, the <Mn> in inclusions (model) is compared with the <Ca + Mn> in inclusions (trials). Fourth, the refractory–steel reactions have not been included in our simulations since Mg pickup is typically negligible under these conditions,[16] thus, not affecting the inclusion composition significantly. The temperature loss during stirring has been fixed at 1.33 °C min−1 (starting temperature 1600 °C).[21]
4 Comparison of Model Predictions to Industrial Data
In this section, the model results have been compared with steel, slag, and inclusion data that were available from the reported literature. Figure 2 shows the comparison of steel composition measurements ([Si], [Mn], [C], [Al], [S]) with that obtained from the model. As shown, excellent agreement is achieved for both C1 and C2. From the model predictions, it was found that the variation of species with high concentrations ([Si], [Mn], [C]) is dictated essentially by the amount of additions and the rate at which they dissolve and mix, whereas the variation of species with lower concentrations ([Al], [S]) is dictated by the steel–slag reactions and the mutual interaction with the inclusions.
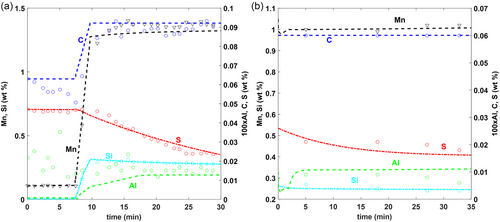
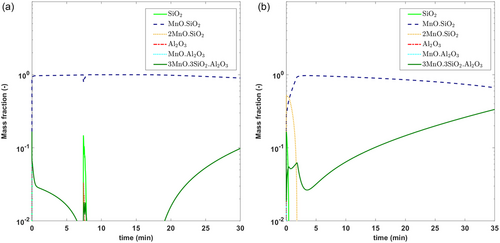
Figure 3 shows the comparison of reported average inclusion composition data with model predictions, while Figure 4 shows the formation of different inclusion phases with time. It can be seen the model predictions show great agreement with that obtained from industrial trial C2. Figure 4 also shows that the types of inclusions in these steel and slag conditions lie primarily between Mn silicates and Mn aluminosilicates. This coincides with what is observed in actual inclusion analysis data reported for C2. Unfortunately, since no inclusion information was reported for C1, it is difficult to validate the model predictions. However, the authors strongly believe that similar observations are likely to be found.
5 Results and Discussion
5.1 Parametric Study
Following the validation of the model in Section 4, the remaining sections use the model to explore the effects of various composition and process parameters. The base steel and slag composition are shown as P1 in Table 5 and 6. Wherever not mentioned, the model parameters for P1 are the same as C2. Figure 5-11 show the results of a series of simulations carried out with different steel and slag composition variables. For one set of simulations, the [Al] and [O] contents within the steel were varied. For a second set of simulations, the basicities (R = CaO/SiO2), (C/A = CaO/Al2O3), and (FeO + MnO) were changed. For a third set of simulations, the process variables, specifically, the effect of stirring rate and local reoxidation have been studied. Finally, the effect of different inclusion number densities was studied.
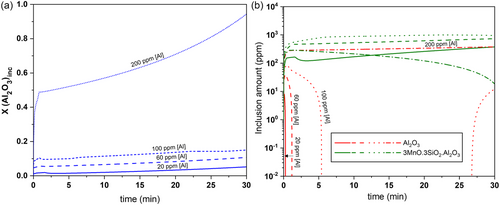
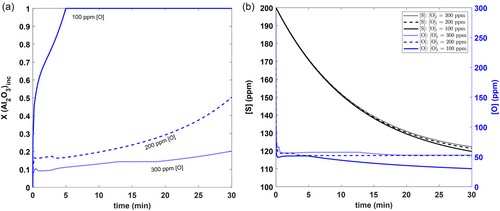
5.1.1 Effect of Steel Composition
Figure 5 shows the effect of initial [Al] content on the average Al2O3 inclusion content along with the types of inclusions forming within the steel with time. In Figure 5a, at low levels of [Al], it can be noticed that the fraction of pure Al2O3 remains low with complex Mn aluminosilicate mostly precipitating (Refer Figure 5a). However, above a certain limit (here, around 200 ppm), a significant fraction of the precipitates are pure Al2O3, with only a small amount of the Al forming complex inclusions. This point is further indicated in Figure 5b, whereby for low [Al], the fraction of pure Al2O3 decreases with time, but for high [Al] (i.e., 200 ppm), the fraction of pure Al2O3 increases with time, along with Mn silicates (not shown in the figure). Please note that the identified 200 ppm limit is a strong function of the oxygen content in the steel. Also, it can be expected that in such a case, Mn aluminosilicates will be rich in Al. As shown in Figure 5, the inclusion composition is affected by a change in the [Al] levels, which is due to the fast steel–inclusion kinetics at the given inclusion population density.[38] In reality, [Al] reduced at the steel–slag interface may not be readily available for reaction for all the inclusions in the ladle, especially at lower concentration of [Al], which constitutes a potential rate-determining step. Such effects, however, are not present in this model, which currently considers a homogenized melt at all times.
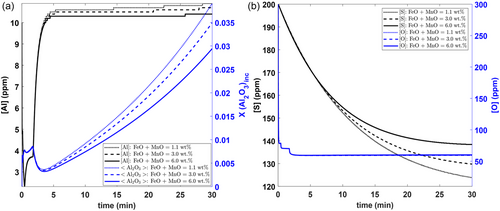
Figure 6 shows the effect of initial [O] content on the average Al2O3 content of inclusions, the [O] variation with time, and the [S] variation with time. From Figure 6a, it can be seen that lowering the initial oxygen levels leads to more Al-rich inclusions along with pure alumina. This is because the driving force for forming other inclusion phases is not high in these conditions. Figure 6b shows that [O] is predicted to drop suddenly in the beginning of refining due to the high driving force for oxide formation. Additionally, a decrease in initial [O] content is also shown to lead to lower final [O] contents, as dictated by the Al–O deoxidation equilibrium. It can also be seen that the [S] level drops with time, albeit at a much slower rate than [O]. However, desulphurization is minimally affected by a change in initial oxygen levels.
5.1.2 Effect of Slag Composition
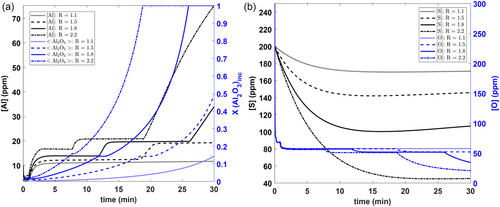
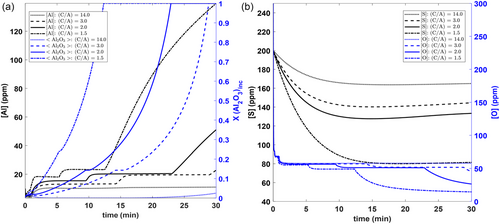
Figure 7-9 show the effect of basicity (R = CaO/SiO2), (C/A = CaO/Al2O3), and (FeO + MnO) on the evolution of 1) the [Al] content and the average Al2O3 content within all inclusions and 2) deoxidation and desulphurization of the steel.
It can be seen in Figure 7a that a slag with higher basicity ((R = CaO/SiO2) will promote more Al pickup due to the lower silica in the slag (higher Al2O3 in slag). This, in turn, promotes more Mn aluminosilicates and alumina inclusions within the steel. The Al pickup from slags is further discussed in our previous article.[9] Figure 7b again shows that lower final [O] levels are reached due to precipitation deoxidation with an increase in basicity. On the other hand, lower [S] levels can be realized with higher-basicity slags especially with R ≈ 2–2.5 since such slags exhibit higher sulfide capacities.[39]
Figure 8a shows that a decrease in the (C/A = CaO/Al2O3) ratio (obtained by changing the Al2O3/SiO2 ratio in the slag) leads to more Al pickup in steel and greater Al2O3 within all inclusions. This again suggests that alumina-rich slags cannot be utilized for such steels. However, with lower C/A ratios, lower final [O] levels are obtained since more [Al] is available to react with [O]. Furthermore, it is seen that a greater extent of desulphurization is obtained with lower (C/A) ratios. This is because of higher Al2O3 and lower SiO2 within the slag (i.e., higher basicity).
5.1.3 Effect of Process Variables
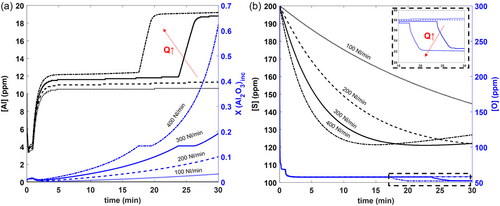
Figure 10 shows the effect of different gas stirring rates on the evolution of the [Al] content and the average Al2O3 content within all inclusions and the deoxidation and the desulphurization of the steel. As shown in Figure 10a, more mass transfer (Al pickup) is promoted at the steel/slag interface at higher gas flow rates, thus increasing the average Al2O3 content within all inclusions. Figure 10b shows that deoxidation is minimally affected by higher gas stirring rates (until longer times), while desulphurization is significantly affected. However, after about 15 min, Figure 10a shows a significant increase in [Al] within the steel at both 300 and 400 NL min−1. This is a result of more inclusion precipitation reactions within the steel, leading to further deoxidation of the steel. It can be seen that at higher gas flow rates (300 and 400 NL min−1), [S] reaches a minimum value, at which point it begins to revert into the steel. This is attributed to numerical artifact caused by a coarse time step at high gas flow rates. This happens when high stirring rates increase the mass transfer rates at the steel/slag interface. Choosing a smaller time step would have prevented this artifact but for the sake of simulating actual steelmaking practices in reasonable times, was kept at 1 s. Please note that the contribution of air reoxidation (through an open “slag eye”) can be significant with higher stirring rates, affecting the [O] and [S] and inclusion population dynamics.[40] However, this phenomenon is not currently considered in the model.
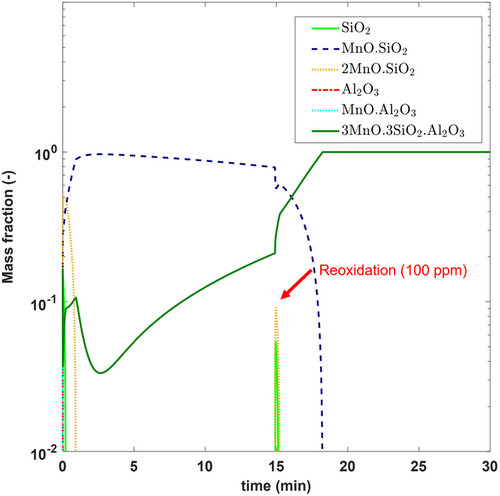
Figure 11 shows the effect of local reoxidation on the precipitation sequence of all inclusions included within the model. As shown, a sudden increase in oxygen (≈100 ppm [O]) at 15 min leads to the destabilization of Mn silicates. This results in the formation of additional Mn aluminosilicates due to the reaction between the excess [O] with [Al] and existing inclusions.
5.1.4 Effect of Inclusion Number Density Within Steel
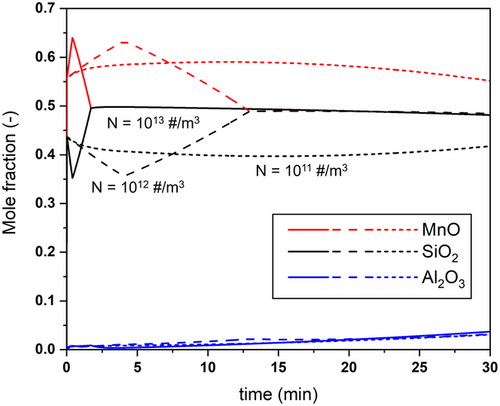
The simulations conducted above assumed a constant number density for the inclusion population,[17] with all inclusions having the same size. Figure 12 shows how the average composition of inclusions evolves for three different average number densities, , and 1013 m−3. As shown, a lower value for Nt leads to an increase in the time that it takes for the compositional equilibrium between inclusion and melt to be reached. This indicates that an instantaneous, local equilibrium assumption between steel and inclusions might not always hold throughout the entire refining time. Furthermore, the inclusion concentration is known to decrease with time as inclusions get removed from the steel by the slag and/or by the refractory walls.[1] This combined with the results shown in Figure 12 demonstrates the importance of considering an evolving inclusion number density. Such phenomena will be included in a future model.
The current study provides a comprehensive basis for many aspects of ladle metallurgy in Si–Mn-killed steels by conducting a wide range of simulations with the proposed steel–slag–inclusion model. From the simulations conducted with different slag compositions, a top slag with a basicity of 1.0–1.2 with an Al2O3 content of less than 5 wt% is suggested to be used for optimum inclusion composition control. However, higher initial [S] in steel cannot be reduced to a considerable extent in the ladle furnace with such slags at moderate stirring. Resorting to slag adjusting or longer refining times in vacuum degassing stations can be useful in such cases. Furthermore, the (FeO + MnO) should be minimized to avoid affecting [S] removal rates although it helps in decreasing [Al] pickup rates in the steel.
5.2 Industrial Applications
Having conducted a wide number of parametric analyses, the model is now applied to three other industrial situations: a slag-changing operation and two additional steel grades, to further demonstrate its capabilities.
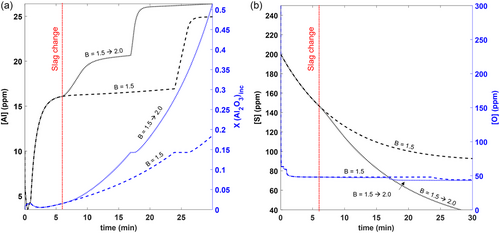
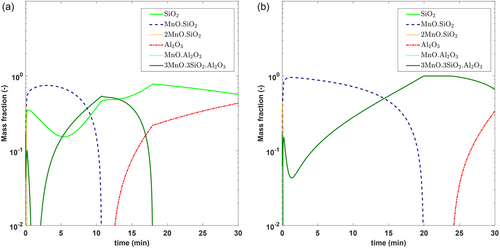
In an effort to improve desulphurization, certain steel producers[36, 41-43] have opted to change the slag basicity during refining. Similar to a previous study,[44] in this study, the slag basicity was increased from 1.5 to 2.0 by adding 250 kg CaO to the slag (denoted as P1) after about 6 min of refining. The modeling results are presented in Figure 13. As shown, the effect of the slag change is to increase the [Al] in the melt (and correspondingly increase the alumina and Al-rich inclusions), but concurrently decrease the [S]. Thus, one of the uses of this model is in process optimization, in order to determine the ideal window for minimizing both [Al] and [S].
As was seen in the parametric analysis, the steel compositional variables play an important role in controlling the inclusion composition. Figure 14 shows how the current model can be used to predict inclusion composition for two different steel chemistries, a typical Si-killed spring steel and a tire cord (high-carbon grade) steel (S1 and S2 in Table 10).
| Case | C | Mn | Si | Cr | Al | Ca | S | O | Fe |
|---|---|---|---|---|---|---|---|---|---|
| S1 | 0.55 | 1.00 | 0.70 | 0.67 | 0.001 | 0.0005 | 0.020 | 0.030 | Bal. |
| S2 | 0.81 | 0.76 | 0.25 | – | 0.001 | 0.0005 | 0.020 | 0.030 | Bal. |
Figure 14a shows the inclusion precipitation sequence for S1 and also identifies that silica inclusions constitute the major fraction. This prediction is consistent with experimental observations,[45] where the majority of inclusions are encountered in grades, where [Mn]/[Si]<1 are mostly silica or silicates (e.g., mullite). In contrast, Figure 14b shows that the inclusion precipitation sequence for S2 includes not only Mn silicates but also Mn aluminosilicates. This prediction is consistent with the fact that in such steels, the inclusions are reported to belong to mostly Al-rich Mn aluminosilicates.[44]
5.3 Comparison with Al-Killed Steel
In the context of this study, it is worthwhile pointing out certain differences between killing practices that are typically used for other high-Mn, high-Al steel grades. First, higher [Al] contents in Al-killed steel lead to lower [O] and [S] levels in steel than Si–Mn-killed steels.[1] However, this comes at the cost of producing alumina inclusions. These often turn into Mg spinels and calcium aluminates[17] (post-Ca treatment), most of which are responsible for nozzle clogging. In Si–Mn-killed steel, as seen earlier, Mn silicates and Mn aluminosilicates are the inclusions most likely to be encountered, with the former being preferred for smooth casting operations. Moreover, as shown in Section 5.1.1, high initial [Al] in steel can be detrimental to Si–Mn-killed steel production. The current findings indicate that FeSi ferroalloy with a high Al fraction can seldom be used for deoxidation and that the permissible level of Al impurity within the ferroalloy should be fairly small. Second, the types of slags used in Si–Mn-killed steels should be silica rich, in contrast to alumina-rich slags in Al-killed steels. The result of this is that very low [S] levels cannot be reached due to Si-rich slag's lower sulfide capacities. Additionally, the contribution of slag toward additional deoxidation in Si–Mn-killed steel seems to be more pronounced since [O] levels in Al-killed steels are already very low (≈ 2-5 ppm) postdeoxidation.
5.4 Inclusion Formation at Low Oxygen Concentrations
This study also showed that a high initial [O] in steel could lead to lowering of alumina content within the inclusions. This was also recently observed in practice.[46] It is interesting to note that high-carbon steels have lower initial oxygen levels based on [C]–[O] equilibrium.[46] As a result, the total mass of inclusions produced from the deoxidation process should be small due to low supersaturation for inclusion nucleation and growth. However, in practice, inclusions are seen to be present in abundance in such steels, which suggests the participation of impurity elements in ferroalloys like Al during the deoxidation process. The conditions in which certain unstable oxide inclusions form and prevail at low oxygen potentials need further investigation.
5.5 CaO-Based Inclusions in Si–Mn-Killed Steel
Studies[45, 47-49] have found CaO in the inclusions, whose source was believed to be from slag droplets rather than from Ca pickup, resulting from the chemical reactions between the steel and slag. This mechanism was proposed because the concentration of [Al] in steel was deemed insufficient to reduce CaO from the slag and the initial solubility of Ca in steel was low.[50] Although not shown in this article, this was also seen in our simulations where Ca pickup in steel from slag was negligible. These observations have led researchers to seek another mechanism for the formation of CaO-containing inclusions. The most viable appears to be emulsification during high stirring periods in producing exogenous inclusions, as shown by Valentin et al.[51] Furthermore, these inclusions generated from slag droplets can further interact with existing endogenous deoxidation inclusions, resulting in Ca-containing complex oxide inclusions. The incorporation of CaO–SiO2–Al2O3-based inclusions and their interactions in the model will certainly be interesting in the future but are not in the scope of the current work.
5.6 Ca Treatment in Si–Mn-Killed Steel
A few steelmakers have resorted to Ca treatment[8, 15, 44, 52, 53] to reduce the melting point of the primary oxide inclusions in Si–Mn-killed steels. However, the conditions when it is needed have not been entirely well rationalized since liquid inclusions seem to form in ideal conditions, and Ca recovery is considered to be small.[49] Furthermore, the presence of high [S] can interfere with the Ca treatment process. Tienkink et al.[52] indicated that Ca helps reduce incidents of irregular flow through metering nozzles and suggested that Ca helps control the inclusion composition when the Al2O3 content within the inclusions is higher than 20%. In this regard, the current model is capable of providing a prognosis for such unwanted casting problems. Specifically, it is able to predict the Al2O3 content in the inclusions along with the conditions in which alumina inclusions precipitate. However, to capture the efficiency and frequency of the Ca treatment process, including Ca–inclusion interactions can be an important addition to the model. This will be left as a topic of future study.
5.7 Evaluation of Steel/slag Mass Transfer
From the simulation results presented in Section 5.1.3, it was clearly noticed that mass transfer between steel and slag plays an important role in refining kinetics of [S], [O], and [Al], among others, which essentially is described by the mass transfer coefficients of different species. Since the ladle is dominated by inertial forces, different correlations have been proposed based on the effective stirring power or gas flow rate in some instances.[54] However, it has been seen that there is a clear lack of unification among the expressions, as shown in Figure 15, which displays the relationship between mass transfer capacity (mtc) and stirring power. The exact source of these differences has been somewhat puzzling and warrants further attention from a fundamental standpoint. As can be observed, many authors have not used two-regime mtc relationships as Asai et al.[55] suggested and what is found to exist in many other cold experiment studies.[54] This has been primarily attributed to mass transfer acceleration caused by emulsification. The possible reasons for this noticeable disagreement could be differences in reactor configurations, plug geometries, operation parameters, and slag liquidus temperatures, in addition to temperature fluctuations and gas flow inconsistencies. In most situations, the mass transfer coefficients are tuned to match the composition trajectories of species in the bulk steel and are often well justified. The current study used the relationship chosen in Graham and Irons’ work, which seems to work below the onset of emulsification ( 60 W ton−1[55]). It is worth pointing out that most authors in the past have reported an incorrect value of B in Equation (21) (0.006 instead of 6 × 10−6) to estimate the mass transfer capacity derived by Graham and Irons’ work, which can often be misleading.

6 Conclusion
In this work, a fundamentals-based kinetic model was developed and applied to predict ladle-refining reactions for Si–Mn-killed steels. Particularly, the model was able to simulate the evolution of actual inclusion populations along with the deoxidation and desulphurization trajectory in the steel, subject to various simultaneous chemical reactions. The industrial measurements taken from previous literature were well reproduced through the calculated results from the model, which shows the adequacy of the model features to simulate situations of practical interest to steelmakers. Different parametric analyses revealed the effect of important steel, slag, inclusion, and process variables on the refining reactions quantitatively.
The model showed that the amount of alloy additions and the rate at which they dissolve and mix decide the variation of species with higher concentrations ([Si], [Mn], [C]). On the other hand, the reactions at the steel–slag interface along with the mutual interaction of the solutes with the existing inclusions decide the variation of species with lower concentrations ([Al], [S], [O]). The model is able to identify limiting concentrations of initial [Al] and [O] in the steel that lead to a low alumina content within the oxide inclusions, which vary with different steel grades. Based on multiple model calculations, slag basicity of around 1 with an Al2O3 content of less than 5 wt% can be suggested to realize optimum control of inclusion composition. Furthermore, the duration of the refining time and the timing of slag basicity change could be informed from the model so as to obtain a better extent of desulphurization. The model showed that reoxidation of steel can lead to a new population of inclusions while destabilizing existing inclusions, through the reaction of excess oxygen with the existing solutes and inclusions in the steel. It was also seen that the inclusion number concentration in steel exerts a role in the time needed for steel–inclusion reactions to reach equilibrium, affecting the compositional trajectory of inclusions. Overall, the model has been able to demonstrate that it can be used in a wide range of operating conditions. This should be able to assist practitioners in improving the refining process for that particular steel grade, although the nature of refining practices differs across steel plants. This work has also pointed out the need for more fundamental studies to clarify certain aspects of the refining process such as the accurate determination of steel/slag mass transfer coefficients.
Acknowledgements
The authors are grateful to the members of McMaster Steel Research Centre, Natural Sciences and Engineering Research Council of Canada (NSERC), and Nucor Steel.
Conflict of Interest
The authors declare no conflict of interest.
Open Research
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.




