Combined assessment of early and late-phase outcomes in orphan drug development
Abstract
In drug development programs, proof-of-concept Phase II clinical trials typically have a biomarker as a primary outcome, or an outcome that can be observed with relatively short follow-up. Subsequently, the Phase III clinical trials aim to demonstrate the treatment effect based on a clinical outcome that often needs a longer follow-up to be assessed. Early-phase outcomes or biomarkers are typically associated with late-phase outcomes and they are often included in Phase III trials. The decision to proceed to Phase III development is based on analysis of the early-Phase II outcome data. In rare diseases, it is likely that only one Phase II trial and one Phase III trial are available. In such cases and before drug marketing authorization requests, positive results of the early-phase outcome of Phase II trials are then likely seen as supporting (or even replicating) positive Phase III results on the late-phase outcome, without a formal retrospective combined assessment and without accounting for between-study differences. We used double-regression modeling applied to the Phase II and Phase III results to numerically mimic this informal retrospective assessment. We provide an analytical solution for the bias and mean square error of the overall effect that leads to a corrected double-regression. We further propose a flexible Bayesian double-regression approach that minimizes the bias by accounting for between-study differences via discounting the Phase II early-phase outcome when they are not in line with the Phase III biomarker outcome results. We illustrate all methods with an orphan drug example for Fabry disease.
1 INTRODUCTION
Drug development programs typically include exploratory (Phase II) and confirmatory (Phase III) randomized controlled trials (RCTs) to assess the efficacy, safety and appropriate dosages of an experimental (new) treatment. For regular “large disease” drug development programs decisions to conduct a Phase III trial are based on positive Phase II trials. If these trials are only retrospectively evaluated in combination, that is, during the drug marketing authorization request, the ad hoc synthesis may induce a form of decision-induced bias (the succeeding trials are only conducted when the first trials were positive). Such a bias is not an issue if the early and late Phase trials are prospectively considered in the design phase (eg, a seamless approach).
However, it is not uncommon that in rare diseases, no more than two independent RCTs are conducted and available, one exploratory and one confirmatory.1 Phase II primary endpoints are typically biomarkers or surrogate outcomes.2 Phase III primary clinical outcomes are likely established endpoints and they may either require (1) larger sample sizes, (2) more costly collection, (3) to be observed after a considerable time, or (4) be more variable outcomes than early-phase outcomes, therefore, even if N = N2 + N3 number of patients participate in both trials, only N3 patients will be available to provide responses for the primary clinical outcome of interest. Biomarkers (early-phase) and secondary clinical outcomes are often observed earlier and, therefore, easily included in both trials and, hence, available for all N patients. After both trials have been conducted, inference on the treatment efficacy is typically performed by evaluating the late-phase outcome responses of N3 patients. In a rare disease setting, N3 may not be large enough to solidly confirm treatment efficacy. In assessing the totality of evidence, the positive results from the Phase II trial could retrospectively be seen as supportive, even if the two clinical trials were designed/conducted independently, as typically the early-phase outcome would be assumed to be associated with the late phase primary clinical outcome. Throughout the article the terms “retrospective (ly)” denote the retrospective combination of the available Phase II and Phase III trial after both trials are completed and their final results are available.
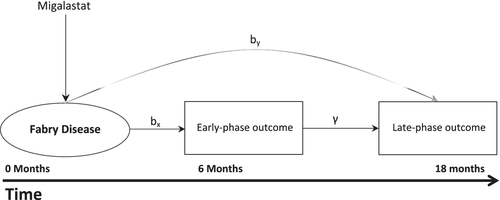
For example, Galafold (migalastat) acquired marketing authorization as an orphan drug for the treatment of Fabry disease in 2016 within Europe. Fabry disease is a rare, progressive disorder with an estimated prevalence of 1:117 000 to 1:40 000.3 The condition affects major organs and may result in life-threatening events. Until then, standard treatment for Fabry disease consisted of Enzyme Replacement Therapy.3 Two main studies were submitted during the marketing authorization of migalastat; one randomized, placebo-controlled (AT1001-011, migalastat vs Placebo) superiority study and one active comparison randomized trial (AT1001-012, migalastat vs Enzyme Replacement Therapy), with a noninferiority design.
In trial 011 patients switched to migalastat 6 months postrandomization, while in trial 012 primary follow-up was considerably longer, with switching taking place 18 months postrandomization. In the first trial, the change in average globotriaosylceramide (GL-3) inclusions from baseline to 6 months was the primary outcome which produced nonconclusive evidence. The second trial utilized the annualized change in glomerular filtration rate (eGFR) at month 18 as primary clinical outcome (Table 1). Both GL-3 and the annualized change in eGFR at month 6 were collected in both trials (011 and 012). No strong correlation has been established in the literature between the GL-3 outcome and the change in glomerular filtration rate (eGFR).4
| Study number | Duration | Annualized rates of change in eGFR from baseline to month 6 | Annualized rates of change in eGFR from baseline to month 18 | Sample size | Start date |
|---|---|---|---|---|---|
| AT1001-011 | 6 months | Collected | Not collected | 67 | August 2009 |
| AT1001-012 | 18 months | Collected | Collected | 52 | December 2010 |
In study 011 after 6 months of treatment with migalastat 150 mg, eGFR values increased, whereas in the placebo treated group eGFR values declined.3 This outcome among other secondary results led to the conduct of study 012. In trial 011, all patients treatment switched to migalastat at 6 months, an action that restricts the observation of a treatment effect on the primary late-phase outcome. Given the limited available data, evidence from both trials were retrospectively (ad hoc) assessed for the final approval decision.
Analysis methods that use the relation between early and late-phase outcomes may be applied to retrospectively, but formally, synthesize the evidence on treatment efficacy across the two trials. Engel and Walstra5 formulated a double-regression (DR) approach, which can aid in more precise treatment effect estimation, by accounting for unobserved late-phase outcome responses via observed early-phase outcome responses. Their method utilizes the correlation to ultimately inform the mean and variance estimates of the treatment effect on the late-phase outcomes. For large samples their method has the potential to increase precision. However, for small sample sizes this is not necessarily true.6 Previously, in RCTs the DR approaches have been suggested mainly to inform treatment selection during interim analysis in seamless Phase II/III designs.7-9 Double-regression methods can be even generally applied wherever there is possibility to include early outcome information in decision making during the course of a trial.10
A Bayesian double-regression (BDR) analogue can be readily constructed11 which maintains similar limitations to the frequentist alternative but could flexibly model the two Phase III outcomes' data. Such a model can include historical trial data (ie, Phase II early-phase outcome data or external information on the early and late-phase outcome correlation) as a elicited prior distributions.12 Furthermore, this Bayesian model accounts for the uncertainty around each parameter during the borrowing of information.
In this article, we investigate how to model and estimate the efficacy of a new treatment on the late-phase clinical outcome, using data on early-phase outcomes from both trials. Most literature on double-regression focuses on design aspects such as interim analysis or seamless design of phase II/III trials, though, in the present article we propose methods that would be applied retrospectively (ad hoc) only after the Phase III trial. We propose and investigate methods that either account or do not account for the potential decision-induced bias when combining retrospectively the Phase II and Phase III trials. We investigate the two proposed models, the bias corrected DR approach and the flexible Bayesian approach regarding their performance to estimate the treatment effect on the late-phase outcome. We focus on two related key problems: (1) the magnitude of the type 1 error inflation when retrospectively combining data from Phase II and III and (2) how to estimate the treatment effect on the late-phase outcome, using results from both studies and we assess this estimate in terms of bias and variance.
The article is organized as follows. First, we describe a bivariate linear model, we introduce its conditional form and we formalize the (often visual) retrospective pooling by utilizing DR with nonavailable Phase II late-phase outcome data, then briefly discuss specific model variations, for example, the single-regression (SR) approach. We introduce the problem of decision-induced bias moving from Phase II to Phase III based on the Phase II early-phase outcome in Section 3 and then provide an approximate analytical solution. In Section 4, we propose and formulate a Bayesian two-step solution to the estimation problem, a model that down-weights the impact of the biomarker data via a historical power prior. This prior dynamically accounts for the bias in estimating the same treatment effect across the two trials, by accounting for additional between-trial differences (variability) around the biomarker outcome effect. The article ends with a discussion and steps for further research.
2 MODELS FOR THE JOINT PHASE II AND III DATA
Consider a Phase II trial of total sample size N2 and a Phase III trial of total sample size N3. For both trials it is assumed that a number of patients (Nk = nck + nek, nk = Nk/2, k = 2, 3) are randomized to the control and experimental treatment. Let us denote Yik the late-phase treatment response for patient i in trial k and Xik the early-phase treatment response for patient i in trial k, k = 2, 3, i = 1, 2, … Nk.
2.1 Bivariate modeling for early-phase and late-phase outcomes between studies
2.2 Double regression to estimate the effect of primary late-phase outcome
At the end of both trials early-phase outcome data X for N = N2 + N3 patients and late-phase outcome data Y3 for only N3 patients are observed. As Y2 is not observed, Y = Y3 and X = (X2, X3) now denote the observed late-phase and early-phase outcome data which correspond to patients of Phase II and Phase III trials. Y corresponds to the outcome of interest related to which estimation and hypothesis testing will be performed in N3 patients. The DR utilizes the relation between early-phase and late-phase outcomes and allows estimation of the main parameter of interest, the treatment effect on the late-phase clinical outcome, by (Figure 1).
2.3 Bayesian (double-) regression
We can model the Phase II biomarker data (X2) via a Bayesian SR, of N2 patients and we can utilize the posterior distribution Markov Chain Monte Carlo sample draws to construct a prior on a BDR model on the Phase III early-phase outcome data as follows.
The prior on uniformly weights our prior considerations around the correlation parameter. In order to mimic model (m2) we have set normal distribution priors based on Phase II posterior effect and variance mean estimates of the early-phase outcome parameters (). To further mimic model (m2) we inform the prior based on the posterior model variance samples from Phase II early-phase outcome data, that is, fitting them over an optimized gamma prior distribution, . The above two-step procedure will allow for possible discounting of the Phase II trial by down-weighing the early-phase historical outcome data, which is further discussed in section 4.
In comparison to the direct Bayesian analogue of model (m2), where the strength of the relationship between early and late-phase endpoints becomes clear only after combining the posterior mean estimates via the parameter, model (m3) is more intuitive, as it directly models the correlation () between the two outcomes, and it directly produces posterior Markov Chain Monte Carlo draws from by. Therefore, under such a fully Bayesian approach there is no need for numerical addition of treatment effect mean estimates.11 Posterior inference can be obtained via traditional Markov Chain Monte Carlo application software (ie, JAGS13) or even analytically under convenient prior distributions.12 In this Bayesian model we assume that hypothesis testing for H0 vs H1 will be performed by utilizing posterior probabilities as where .
If we set the correlation very close to zero; that is, , then, the Phase III trial late-phase outcome data are evaluated individually under a standard (Bayesian) linear SR model. In comparison to the SR models, the advantage of models (m2), Bayesian (m2) and (m3) rest in their ability to numerically calculate/imitate the impact of accounting for the Phase II early-phase outcome data in analyzing the late-phase outcome. Additional details of the (Bayesian) SR models can be found in Appendix A.
3 TYPE 1 ERROR INFLATION AND BIAS DUE TO SELECTION BASED ON EARLY-PHASE OUTCOME RESULTS
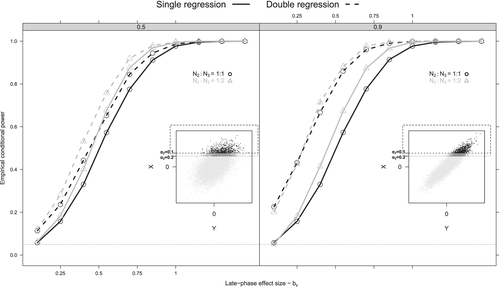
As we observe in (eq3), the inflation in MSE depends on (i) the decision threshold to initiate the Phase III trial through parameter, (ii) the Phase II early-phase outcome mean () and variance ), (iii) the number of patients in the Phase II trial (n2) and (iv) and the magnitude of the correlation (). An increase in results in an increase of MSE, while as n2 decreases, the MSE increases as well. A similar behavior is observed in terms of Type I error (Figure 2). More specifically, Type I error rates increase considerably with higher , while the power curves, in general, increase with more patients being allocated to the Phase III trial (n3) (Figure 2).
The above expressions hold when treatment arms within studies are equal. Nonetheless, similar analytical expressions for unequal within study allocation ratios, can be acquired by appropriately changing the variances of in Appendix B.1 based on the treatment arms sample sizes. For example, if the allocation ratio between arms in the Phase II trial equals to 1:2, then the Phase II early-phase endpoint variance increases, and the introduced bias could be reduced by half.
4 BIAS REDUCTION BY ACCOUNTING FOR BETWEEN-TRIAL EARLY-PHASE OUTCOME VARIABILITY
All models above, including the bias corrected model, assume that the true overall treatment effect remains common between trials, no between-study variability on the early and late-phase outcomes exist and therefore, all N observations are derived from the same population. Phase II vs Phase III trials typically do not have similar protocols, as the Phase II trials are usually more restrictive in patient inclusions, therefore, exploring between-study variability becomes relevant.
The decision-induced bias discussed in Section 3, would materialize as difference in treatment effects between the two available trials as well. Therefore, accounting for between-study variability may act as a less rough approach to minimize this decision-induced bias. A proper estimation of the between-trial early-phase outcome variance is not feasible with just two available studies,14-17 therefore, in this article we choose not estimate but only account for this variance to aid towards the reduction of the bias.
To achieve this, we utilize a mechanism based on power priors to account for the between-study differences within a Bayesian framework.18 By estimating a power parameter that represents conflict between the early-phase outcome data of the two available trials, model (m3) can be further extended to account for the early-phase outcome effect excess between-trial variability, along with any other biases.18-20
4.1 Bayesian flexible double-regression
The conditional set-up of model (m5) remains similar to (m3). Now dynamic informative power priors parametrized through are placed on the early-phase endpoint's parameters ax and bx. Such priors control the borrowing of the historical data and discount the early-phase prior in case of treatment effect's disagreement. We chose to model the parameters univariately to aid any formulation of elicited informative priors on ay, by, and , though, a wishart prior on the covariance matrix (m1) could have jointly accounted for the association between the model parameters.
4.1.1 Estimation of
In model (m5), similarly to model (m3), we are interested in the late-phase overall primary outcome effect by and we assume that hypothesis testing for H0 vs H1 will be performed by utilizing posterior probabilities as where .
5 SIMULATION STUDY
The main four approaches discussed are summarized in Table 2. The corrected double-regression approach as shown in Section 3 can be considered a rough (approximate) approach to minimize the decision-induced bias. The Bayesian flexible double-regression approach minimizes this bias by accounting for between-trial differences without ad hoc corrections. Their relative performance in the analysis of the Phase III late-phase outcome data, also in comparison to the two more trivial approaches (single and double-regression) is the main focus of the simulation study.
| Abbreviation | Model | (F)requentist/ (B)ayesian | Early/late-phase | Phase (II/III) |
|---|---|---|---|---|
| (B)SR | (Bayesian) single-regression | F/B | Late phase | III |
| (B)DR | (Bayesian) double-regression | F/B | Early and late phase | II+III |
| DRC | Double-regression corrected | F | Early and late phase | II+III |
| BFDR | Bayesian flexible double-regression | B | Early and late phase | II+III |
For illustrative purposes, we assume that the two available Phase II and Phase III trials had a similar control treatment, therefore, the Phase III trial would have been designed as a placebo-controlled trial. In this section, we assume that the decision to conduct the Phase III trial was taken on the basis of available evidence in the first Phase II trial on a single early-phase outcome. At the end of the Phase II trial, individual data of N patients are available on the early-phase and data of N3 are available on the late-phase outcomes. The simulation study results were derived from a bivariate normal model simulation strategy as described in Appendix C.
The SR, DR, DRC methods ignore any between-study variability and therefore assume a different underlying data generating model in comparison to the Bayesian flexible double-regression (BFDR) approach. Even though, they are not directly comparable (Table 2), we empirically compared the four aforementioned statistical methods by generating at least 10 000 simulated combinations of the two available trials data. To do so, we simulated scenarios of the final trial analysis on the late-phase primary endpoint assuming a variety of combinations between the early-phase (bx) and late-phase (by) outcome treatment effects. The latter were varied as (Scenario I) by = bx = 0, (Scenario II) by = bx = 0.6, (Scenario III) bx2, by2 = 0, bx3, by3 = 0.2, and (Scenario IV) by = 0.6, bx = 0, we assumed that , the alpha level of the early-phase primary outcome of Phase II trial, while all within-study variances were set equal to 1. In the simulation setup we introduce a simulative parameter that place additional between-trial variance on the early-phase () and late-phase () outcomes (see Appendix C for details). Specific alternative versions of scenarios I and II were produced by varying and .
The first (I) scenario describes variations of the strict null () and null hypothesis with additional between-trial variance (), while the second (II) scenario describes a common alternative hypothesis on both outcomes and trials. Scenario III can occur when heterogeneous populations are selected for the Phase II and Phase III trial, while the fourth (IV) scenario describes a situation where the late-phase outcome true effect exists but the early-phase outcome equals to 0. All remaining settings (ie. number of trials (k), total sample sizes N, sample size ratio between trials N2 : N3, within-study allocation ratios nck : nek) were reflective of a typical rare disease setting and based on the Galafold example (Table 1). All simulations were performed via R23 and JAGS.13
5.1 (Strict) null hypothesis scenario (I: by = bx = 0)
The BFDR results in treatment effects closer to the SR estimates than the DR approach under the null hypothesis simulation (Scenario I—Table 3). The DRC approach presents a similar behavior producing late-phase effect estimates even closer to the SR than the BFDR approach. In the three null hypothesis scenarios I(b-d) (by = bx = 0), DR results in the largest estimated treatment effect and produces the largest type I error inflation while DRC generally inflates the Type I error the least among the three investigated methods. An interesting exception that we further discuss in Section 7, is observed in scenario Ia, where the BFDR approach produces stricter error rates than the DRC approach. In general, the SR method controls type I error the most, while the DR method controls type I error the least. The DR and DRC methods consistently produce the smallest C(r)Is, while the BFDR method produces the largest C(r)Is among the investigated methods.
| Scenario | Model | Mean/Posterior mean by | Type I error | C(r)I widths | |
|---|---|---|---|---|---|
| : (0.05 · 0.1 · 0.2) | : (0.05 · 0.1 · 0.2) | : (0.05 · 0.1 · 0.2) | |||
| Ia. by = bx = 0 | SR | 0.001 · 0.003 · 0.002 | 0.057 · 0.054 · 0.053 | 1.138 · 1.138 · 1.136 | |
| DR | 0.256 · 0.220 · 0.178 | 0.318 · 0.247 · 0.183 | 0.808 · 0.810 · 0.811 | ||
| DRC | 0.087 · 0.075 · 0.063 | 0.079 · 0.066 · 0.060 | 0.810 · 0.812 · 0.813 | ||
| BFDR | 0.170 · 0.156 · 0.133 | 0.054 · 0.037 · 0.022 | 1.343 · 1.330 · 1.319 | ||
| b. by = bx = 0 | SR | 0.000 · 0.003 · 0.002 | 0.055 · 0.053 · 0.054 | 1.138 · 1.138 · 1.138 | |
| DR | 0.141 · 0.123 · 0.100 | 0.148 · 0.130 · 0.114 | 1.010 · 1.010 · 1.011 | ||
| DRC | −0.028 · −0.022 · −0.015 | 0.045 · 0.047 · 0.048 | 1.012 · 1.012 · 1.012 | ||
| BFDR | 0.089 · 0.083 · 0.071 | 0.070 · 0.066 · 0.056 | 1.211 · 1.206 · 1.203 | ||
| c. by = bx = 0 | SR | 0.002 · 0.004 · 0.002 | 0.058 · 0.054 · 0.054 | 1.188 · 1.187 · 1.187 | |
| DR | 0.246 · 0.211 · 0.171 | 0.267 · 0.211 · 0.164 | 0.896 · 0.898 · 0.899 | ||
| DRC | 0.006 · 0.007 · 0.009 | 0.041 · 0.042 · 0.042 | 0.883 · 0.885 · 0.887 | ||
| BFDR | 0.136 · 0.126 · 0.109 | 0.069 · 0.052 · 0.037 | 1.330 · 1.318 · 1.309 | ||
| d. by = bx = 0 | SR | 0.000 · 0.002 · 0.003 | 0.055 · 0.053 · 0.054 | 1.188 · 1.188 · 1.187 | |
| DR | 0.135 · 0.117 · 0.097 | 0.139 · 0.122 · 0.110 | 1.067 · 1.068 · 1.068 | ||
| DRC | 0.002 · 0.004 · 0.006 | 0.059 · 0.058 · 0.059 | 1.064 · 1.065 · 1.065 | ||
| BFDR | 0.073 · 0.069 · 0.060 | 0.076 · 0.072 · 0.065 | 1.209 · 1.205 · 1.201 |
- Note: The first line SR of each scenario (I) presents a frequentist single-regression on the Phase III late-phase outcome data. DR correspond to the frequentist double-regression. Last, the DRC lines present the result for the bias corrected double-regression approach and the BFDR lines present the results for the Bayesian flexible double-regression approach. and denotes the alpha level of the early-phase primary outcome of the phase II trial.
5.2 Alternative hypothesis scenario (II: by = bx = 0.6)
In scenario II (by = bx = 0.6), all methods identified a treatment effect close to the true value (Table 4). The empirical power to identify a treatment effect is usually large for the BFDR, and considerably larger for the DRC than SR approach. Among the DRC and BFDR methods, BFDR produces treatment effect means closest to the true value. In scenario IIa (), DRC performs better in terms of 95% coverage whereas in scenario IIb where 0.3, BFDR results in coverage closest to 95%. The C(r)Is widths retained a similar behavior to the null hypothesis scenarios.
| Scenario | Model | Mean/Posterior mean by | Power | 95% coverage | C(r)I widths | |
|---|---|---|---|---|---|---|
| : (0.05 · 0.1 · 0.2) | : (0.05 · 0.1 · 0.2) | : (0.05 · 0.1 · 0.2) | : (0.05 · 0.1 · 0.2) | |||
| IIa. by = bx = 0.6 | SR | 0.598 · 0.596 · 0.598 | 0.659 · 0.655 · 0.658 | 0.940 · 0.940 · 0.942 | 1.138 · 1.137 · 1.138 | |
| DR | 0.643 · 0.625 · 0.612 | 0.942 · 0.924 · 0.909 | 0.954 · 0.952 · 0.951 | 0.811 · 0.812 · 0.812 | ||
| DRC | 0.634 · 0.621 · 0.611 | 0.935 · 0.920 · 0.907 | 0.956 · 0.954 · 0.952 | 0.812 · 0.812 · 0.813 | ||
| BFDR | 0.632 · 0.617 · 0.607 | 0.663 · 0.634 · 0.612 | 0.997 · 0.997 · 0.997 | 1.304 · 1.304 · 1.305 | ||
| b. by = bx = 0.6 | SR | 0.598 · 0.596 · 0.598 | 0.626 · 0.624 · 0.625 | 0.940 · 0.941 · 0.942 | 1.188 · 1.187 · 1.188 | |
| DR | 0.647 · 0.628 · 0.614 | 0.888 · 0.866 · 0.848 | 0.948 · 0.949 · 0.940 | 0.898 · 0.899 · 0.900 | ||
| DRC | 0.634 · 0.621 · 0.612 | 0.876 · 0.859 · 0.845 | 0.950 · 0.949 · 0.946 | 0.896 · 0.898 · 0.899 | ||
| BFDR | 0.629 · 0.615 · 0.607 | 0.648 · 0.622 · 0.610 | 0.989 · 0.989 · 0.990 | 1.292 · 1.293 · 1.293 | ||
| III. bx3, by3 = 0.2, | SR | 0.202 · 0.204 · 0.202 | 0.173 · 0.169 · 0.168 | 0.941 · 0.941 · 0.945 | 1.188 · 1.187 · 1.187 | |
| bx2, by2 = 0 | DR | 0.363 · 0.328 · 0.289 | 0.470 · 0.399 · 0.337 | 0.906 · 0.931 · 0.950 | 0.894 · 0.896 · 0.898 | |
| DRC | 0.226 · 0.221 · 0.214 | 0.244 · 0.232 · 0.223 | 0.961 · 0.963 · 0.968 | 0.883 · 0.886 · 0.889 | ||
| BFDR | 0.315 · 0.296 · 0.271 | 0.194 · 0.158 · 0.125 | 0.985 · 0.987 · 0.991 | 1.307 · 1.299 · 1.296 | ||
| IV. by = 0.6, bx = 0 | SR | 0.602 · 0.602 · 0.602 | 0.626 · 0.626 · 0.630 | 0.941 · 0.941 · 0.945 | 1.188 · 1.188 · 1.187 | |
| DR | 0.846 · 0.846 · 0.771 | 0.988 · 0.988 · 0.971 | 0.828 · 0.828 · 0.906 | 0.896 · 0.896 · 0.899 | ||
| DRC | 0.606 · 0.606 · 0.609 | 0.870 · 0.870 · 0.869 | 0.960 · 0.960 · 0.967 | 0.883 · 0.883 · 0.887 | ||
| BFDR | 0.735 · 0.735 · 0.708 | 0.736 · 0.736 · 0.743 | 0.970 · 0.971 · 0.985 | 1.329 · 1.330 · 1.309 |
- Note: The first line SR of each scenario (II,III,IV) presents a frequentist single-regression on the Phase III late-phase outcome data. DR correspond to the frequentist double-regression. Last, the DRC lines present the result for the bias corrected double-regression approach and the BFDR lines present the results for the Bayesian flexible double-regression approach. denotes the alpha level of the early-phase primary outcome of the phase II trial. In Scenario III the correction for the DRC method is calculated based on that the true late-phase outcome effect is equal to 0.2.
5.3 Scenarios III and IV
In scenario III (by2 = 0, by3 = 0.2, bx2 = 0, bx3 = 0.2), the BFDR produces similar findings to the DR approach, while the DRC method discards most Phase II information and its results are close to the SR approach (Table 4). DRC retains a comparable behavior in scenario IV (by = 0.6, bx = 0), where it discards most of the decision-induced bias and it produces results closer to the analysis of the Phase III study alone. In scenarios III, IV, as well as I, the naive pooling represented via the formal DR method, systematically and largely overstates our confidence in treatment efficacy.
5.4 Summary of simulation results
Among the four methods, the single regression performed best in terms of type I error followed closely by the DRC. Similarly, the approach that led to the least bias was the SR, again followed closely by the DRC. The DRC and DR methods resulted in the narrowest intervals. The intervals of the BFDR were comparable or larger than these of the SR. In terms of power, the DR method showed the highest gain, closely followed by the DRC. Finally, the SR and DRC both attained coverage close to nominal levels.
Overall, the DRC resulted in similar operational characteristics to the SR but it demonstrated a large gain in empirical power under the alternative hypothesis scenarios in comparison to the SR (Tables 3 and 4).
6 DISCUSSION
In a drug development procedure, it is not uncommon that positive Phase II results on early-phase (biomarker) outcomes are not predictive of a Phase III success on late-phase clinical outcomes. If Phase II and Phase III results are then assessed (perhaps informally) jointly to support efficacy, this retrospective (ad hoc)) assessment may be subject to decision-induced bias and may increase uncertainty of the true primary late-phase treatment effect. Such an informal combination of results may increase to a great extent (more than three times) the Type I error rate of null hypothesis, rendering the retrospectively combined late-phase true treatment effect misleading. Especially in rare diseases, where the validation of early-phase surrogate endpoints can become problematic, due to the small and often heterogeneous populations, the small sample sizes and the insufficient number of available trials, only late-phase hard endpoints are usually appropriate to prove treatment efficacy.
In this article, in addition to identifying and investigating the above issue, we explored methods that can be utilized in order for early and late Phase trial data to be combined retrospectively (ie, right before drug marketing authorization request), while accounting for the underlying decision-induced bias. The flexible BDR includes the borrowing of historical information, while this model downgrades the historical prior upon early-phase outcome data conflict. The DRC method approximately corrects the biased late-phase mean effect and variance estimate.
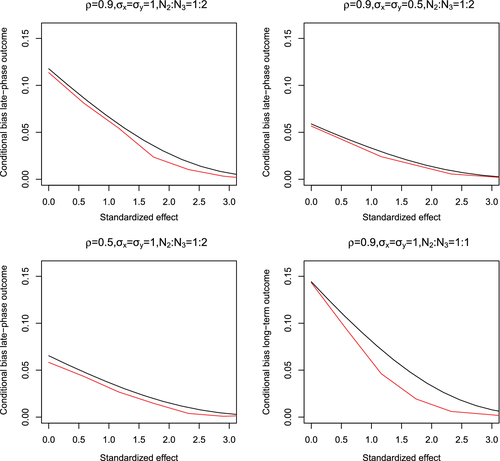
In most scenarios, the DRC method better controls the Type I error and bias than the DR and BFDR methods. This is not observed in scenario Ia, where the BFDR controls better the Type I error than the DRC. This possibly happens because the BFDR approach completely downgrades the impact of Phase II trial when its early-phase treatment effect is different than the Phase III trial early-phase treatment effect. Therefore, on average the Bayesian approach becomes less prone to false-positive results based on possible very positive Phase II early-phase outcome trial effects when is low and/or is high (see, black dots of inner right panel of Figure 2). On the contrary, the DRC corrects the Phase II effect and then utilizes both Phase II and Phase III effects without heavily downgrading the Phase II results data upon data conflict. The DRC requires a known but despite being approximate, it applies a more direct (decision-based) penalty to the Phase II effect than the Bayesian approach; which could explain its overall better performance in the simulation.
Both the BFDR and the DRC methods would be an attractive solution to the increased Type I error of the informal retrospective combination of two small available trials. The consideration of these methods was shown to be rather important when, (i) the preceding Phase II trial conservatively (ie, alpha level was small) resulted to the Phase III trial and/or (ii) the association of utilized early and late-phase outcomes is high. An informal combination of results across Phases often happens when both of the above hold, though, when neither holds then the complexity of suggested methods may outweigh the gains of their application.
Alternative versions of the BFDR model could be developed and they may perform more optimally in comparison to the current (ie, in terms of controlling the overall type I error) when applied on the flexible BDR via the use of an alternative guided value.18-20 The power parameter is imposed on the early-phase endpoint and only indirectly affects the primary late-phase endpoint, therefore, inference on the late-phase endpoint via alternative guided values on the early-phase endpoints could be expected to be more comparable to some extent.
An alternative approach that controls type I error on the late-phase outcome, while borrowing historical information, may also provide a more formal solution.19 Future research could compare these alternatives vis-á-vis each other or with other methods. More covariates could be included, and then their performance could be tested with ease as all presented models are readily generalizable to full regressions. In this article, we set independent informative priors on the model parameters, however, accounting for the correlation between these parameters could also be considered through a well-defined informative Wishart prior on the whole covariance matrix. Finally, in this work, we accounted for but did not estimate between-study variance. Due to the only two available studies, a proper estimation of the between-study outcome variability is currently known to be almost nonfeasible.14-17
In the motivating example we assumed that both trials were superiority trials, while if we had kept the initial designs, different strategies may have been more appropriate. Nonetheless, examples of two superiority trials, one Phase II and one Phase III, exist in the literature. For example, the drug development program of thalidomide for the treatment of multiple myeloma contained two randomized superiority clinical studies of similar design, a supportive (GISMM2001) and a main study (IFM 99-06), that compared melphalan-prednisone (control treatment) to thalidomide (experimental treatment).2 The supportive study was shorter and it reported clinical response rates and event free survival as primary endpoints. The main study was longer in duration and it reported overall survival, as main endpoint and clinical response rates and event free survival, as secondary endpoints. The suggested methodology could be tailored to account for the possibility of decision-induced bias under survival and other types of outcomes and even to combine different study designs.
Throughout the article normality was assumed, an assumption that could be challenged with rare diseases sample sizes.1-3 We approximated a truncated normal with a normal distribution with mean and variance equal to that of the former. This decision was made to aid calculations on the distribution mixture (Appendix B). Better approximations for the truncated normal distribution may exist, such as the chi-square distribution and their performance could be explored as well.24 We should note that for moderately sized N2 in comparison to N and small correlation between the two outcomes, a SR might be more efficient than a DR, due to the noise introduced by the early-phase outcome.5 In the simulation study we assumed that the Phase II trial had equal allocation between trial arms, while the Phase III trial had allocation equal to 1:2 between the control vs treatment arm. We expect that our findings would be comparable under different allocations between arm sample sizes, though further investigation could provide more insights between the relative performance of BDR and DRC methods.
In this article, we performed a post hoc (retrospective) combination of available information after the conduct of the Phase II and Phase III trial. However, it may be very relevant to (prospectively) plan to pool the data from both studies and to use the early-phase outcomes of the Phase II study to increase the precision, with which the efficacy on late-phase outcome is estimated overall.7-9 An alternative strategy could be to conduct one single trial with interim analysis, then, based on the observed treatment effects on the early-phase endpoints decide whether to follow-up the patients.8
To conclude, especially in a small population context, the often informal retrospective pooling of a single Phase II early-phase outcome data to support the true late-phase outcome data inference at the end of a single confirmatory Phase III trials could induce bias and it should be performed via formal numerical approaches. Such approaches should control this decision-induced bias, in order to avoid inflating the Type I error under the null hypothesis and prevent overestimating our beliefs on the primary treatment effect. We hope that this article, except for introducing possible solutions, raises awareness of potential mishaps with post hoc combinations of trial outcome results.
ACKNOWLEDGEMENTS
This work has been funded by the FP7-HEALTH-2013-INNOVATION-1 project Advances in Small Trials Design for Regulatory Innovation and Excellence (ASTERIX) Grant Agreement No. 603160.
APPENDIX A: DETAILS OF (BAYESIAN) UNIVARIATE MODEL
The standard linear SR reference model to demonstrate late-phase treatment efficacy assumes , where denotes the true outcome variance, t denotes a vector of length n3 indicating whether a patient receives control or experimental treatment.
A conjugate Bayesian analogue (BSR) of the model above can be expressed also as above where ay, by, and are random variables and need a prior distribution. This model offers the flexibility to directly impact inference via placing informative priors on parameters ay, by, and . Model B(SR) corresponds exactly to the aforementioned model SR under convenient noninformative priors on ay, by, and .12
In the above SR model, we are interested in and we assume that hypothesis testing for H0 : by = 0 vs H1 : by > 0 will be evaluated as , where is the standard normal quantile. In the Bayesian SR analogue, we are interested in by and we assume that hypothesis testing for H0 vs H1 will be performed by utilizing posterior probabilities as where .
APPENDIX B: DERIVATION OF
B.1 Derivation of Bias(by)
We assume that we can approximate a truncated normal with a normal distribution with updated mean and variance as follows .25 The overall would be a mixture of the above density functions.
B.2 Derivation of
From (eqA2), , an estimate of which can be derived as , where follows from the regression of X|t on N patients.
B.3 Derivation of
APPENDIX C: BIVARIATE NORMAL SIMULATION
parameter indicates how the early-phase and late-phase outcome are related across all available studies. In our framework we only have available summary value on both early and late-phase outcomes from only a single Phase III trial. Therefore, for simplicity in the simulation study we assume that the between-study correlation equals to zero .
We applied an alternative model that generates data in two stages to check for results' robustness with no observed noticeable variations in relative performances.
APPENDIX D: FIGURES AND TABLES
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are openly available in GitHub at https://github.com/kpatera/data-earlylate.




