System dynamics at sixty: the path forward

The challenge

The field of system dynamics just marked the 60th anniversary of its founding by the late Jay Forrester, who passed away at the age of 98 in November 2016. The 50th anniversary provided an occasion to look back and celebrate the many accomplishments in the field (Sterman, 2007). There have been many important contributions since then, some presented in this special issue marking the 60th anniversary. These include methodological advances expanding the system dynamics toolkit to more robust methods to capture network dynamics (Lamberson, 2018), the interaction of dynamics at multiple timescales (Ford, 2018), experimental studies of group modeling (McCardle-Keurentjes et al., 2018) and insights arising from integration of system dynamics and operations research (Ghaffardzadegan and Larson, 2018), along with applications in medicine (Rogers et al., 2018), epidemiology (Tebbens and Thompson, 2018), health care (Minyard et al., 2018), climate change (BenDor et al., 2018), environmental policy (Kapmeier and Gonçalves, 2018), and organizational transformation (Rydzak and Monus, 2018).

Despite these advances, we live in a time of growing threats to society and human welfare. On this anniversary we must therefore also look forward. What must be done now to improve theory and practice, education and training, so that the next decades see even more progress and impact than the last? Jay himself recognized the need for significant changes in system dynamics to realize its full promise (Forrester, 2007a).

I begin with a brief review of Jay's career and contributions in servomechanisms, digital computation, the management of large-scale projects, and system dynamics. I argue that his contributions are widely misunderstood. The main lesson of Jay's several careers does not lie in the particular tools or methods he developed, but in the need for continual innovation to solve important and difficult problems. Close examination of Jay's life reveals a relentless effort to make a difference on real and pressing problems. To do so, in each of his careers, Jay studied the then-new advances in tools and methods developed in any discipline relevant to the problem he sought to address, mastering the state of the art—and then built on those advances. The failure to appreciate Jay's real contribution is a significant problem today in the field of system dynamics. Despite many successes, too many in the field continue to develop models the way Jay did in the 1950s, 60s and 70s, adhering to outdated methods for model development, testing and communication, and closing themselves off from important developments in other fields. The result is a gap between best practice and what is often done.

Sixty years after Jay brilliantly synthesized feedback control theory, numerical methods, and digital computation to create the field of system dynamics, we must close the “knowing–doing gap” (Pfeffer and Sutton, 2000) that has emerged, then innovate again. I outline developments in other disciplines we must embrace to close the gap and improve the rigor, reliability and impact of system dynamics research and practice.

A bold innovator

After college, Jay joined MIT and the servomechanisms lab, then newly founded by Gordon Brown. The war was underway; Jay's master's thesis was to design and test a servomechanism to stabilize the radar antennae on naval ships (Figure 1). To do so, Jay mastered the state of the art in feedback control systems, both theory and practice. Then he innovated: the servo would have to generate large forces to keep the heavy antenna vertical despite high winds and the pitch, roll and yaw of the ship beneath. Doing so required very high gain in the control loop while maintaining stability. “Departing from my training in electrical engineering, the work focused on designing mechanical hydraulic variable speed pumps, motors, and high-gain hydraulic amplifiers because at that time the military mistrusted vacuum tubes in anything except radios.” Jay built a positive feedback loop into the hydraulic amplifier of the servo, finding that with sufficient phase lag the positive feedback would actually stabilize the system while generating the needed gain: 20,000 to 1. However, the patent office initially rejected Jay's patent application. As Jay told it, the patent examiner declared that everyone knew a positive feedback loop was destabilizing so the thing would never work.

Meanwhile, Jay had built a prototype and had it running in the servo lab at MIT. Clearly, as the old joke goes, it worked in practice, even if it didn't work in theory. But Jay was not satisfied. He knew that having it work in the lab would not be enough: to survive wartime conditions, the servo had to be robust in operation and survive what was likely to be inadequate maintenance. As he related the story to me, “I knew the Navy boys would not always be able to maintain it properly.” Jay went down to Revere beach, just north of Boston, collected a large bucket of seawater, including sand and other debris, then, back at the lab, replaced most of the hydraulic fluid with the brine and “ran it for months that way” (Forrester, personal communication).

Film of the Lexington on fire after the attack is available at https://youtu.be/ePdR6CF1SD0.

Jay's relentless focus on robustness, reliability, and designing the system so that ordinary people could use and maintain it under realistic operating conditions carried over into all his later work in computing, intercontinental air defense, and system dynamics.

After the war Jay embarked on a project to develop a flight simulator intended to test designs for aircraft before they were built. Initially envisioned as an analog simulator, he concluded that analog computing could never work in such a demanding real-time task. Instead, Jay decided to develop the simulator “around the untested concept of a digital computer.” The result was Whirlwind, the first reliable, high-speed digital computer capable of real-time control (Green, 2010).2

The Whirlwind project began in 1947. Already by March 1949 Jay had formulated a vision of the innovations needed to turn computers from mere tabulation tools into devices that could control complex systems in real time and carry out simulations (Figure 6). To do so Whirlwind required speed and storage capabilities far beyond those of any existing machine. As he had done in the servo lab, Jay built on state-of-the-art theory and applications. Jay cast his net widely, attending important conferences where leaders in computing such as John von Neumann and Alan Turing debated fundamental issues in the design of computing hardware and software, from how numbers should be represented, to basic architecture, programming, memory, input/output devices and more. Jay spent considerable effort mastering prior work, taking careful notes on books, papers and reports from many disciplines and sources, from a monograph on “Primitive Number Systems” to the design of the proposed Harvard Mark IV (Figure 7).

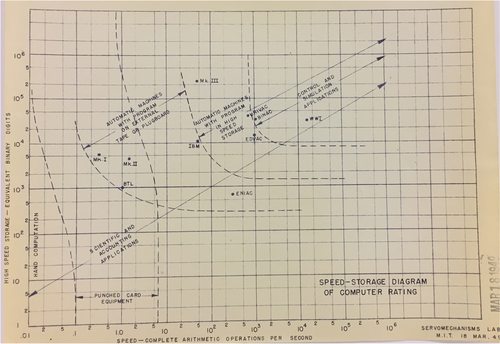
Jay and the Whirlwind team, including Bob Everett, Jay's right-hand man from Whirlwind on, who later became the head of the MITRE Corporation (MIT Research and Engineering), created dozens of innovations that proved critical in the development of computing. Jay famously invented core memory, the first inexpensive, durable memory device for digital computers. Core memory became the standard memory system for computers for decades, remaining in use long after transistors and solid-state devices were developed—for example, landing on the moon with the Apollo missions.

Whirlwind became the basis for the SAGE air defense system, the first transcontinental command, control and communication system. Deployed during the Cold War, SAGE integrated radar and other data to provide real-time early warning against possible Soviet attack. SAGE's Whirlwind-based computers integrated these data, then computed flight plans and targeting information for interceptor aircraft and missiles and sending those data out to the field. Once again, Jay and his team built on the rapidly evolving state of the art in communication theory, computing, radar, manufacturing and other fields to develop a system to meet the mission. The innovations Jay and the SAGE team pioneered include “the modem, the mouse [light gun], multi-tasking, array processing, computer learning, fault detection, magnetic memory, and interactive computer graphics” (http://history.sandiego.edu/GEN/20th/sage.html).

Industrial Dynamics presented the results: a novel, innovative method to develop realistic and useful models of complex organizations. He articulated principles for model conceptualization, formulation, testing and policy analysis, and presented tools and models demonstrating how to do it. These innovations included the DYNAMO simulation language developed by Jack Pugh and diagramming conventions to represent stocks, flows, feedback processes, time delays and other key concepts. They included standards for model documentation and replicability so others could use and build on the work. They included subtle and nuanced principles for model formulation including the importance of “detecting the guiding policy” to capture the behavioral decision processes actually used (ID, Ch. 10). They included guidelines for model evaluation and testing. And, as he had done with servos, Whirlwind and SAGE, he designed system dynamics to be implementable and useful given the state of the computing technology of the day. He did not try to build comprehensive models of a firm or economy. Instead, he built models that could be simulated and analyzed fast enough to be useful in solving specific problems. Nearly six decades after publication, Industrial Dynamics remains a classic and essential text in the education of every modeler.

To summarize: in each of his careers, “from the ranch to system dynamics”, Jay focused on important problems. To do so he mastered the theory and methods relevant to the problem at hand, then built upon them to create new innovations needed to solve the problem. His greatest contribution was that process, not the particular artifacts resulting from it. We do not celebrate his servo, Whirlwind, core memory, and SAGE because they are the state of the art today. We celebrate them because they were the result of a process for problem solving and innovation that was extraordinarily fruitful, time and time again. The same holds for system dynamics. Just as we would not go back to the days of core memory and vacuum tubes, of punch cards and DYNAMO, we should not hold fast to methods for the development and analysis of system dynamics models that have outlived their useful life and for which better methods now exist. If Jay were a young man entering the field of system dynamics today, he would not defend as sufficient nor rely on methods and tools that were once the state of the art but are no longer. He would not isolate himself from what other disciplines and communities offer. Rather, ever focused on solving important problems, he would master the theories and methods now available, using them where appropriate and building on them to create new tools where needed to propel the field of system dynamics to new frontiers. Fortunately, many in the field are following Jay's process, connecting with other disciplines, forging links to other communities, using the tools others have developed and then building upon them.

Model architecture: compartments, agents and networks

Jay's innovations in the Whirlwind project made it possible for computers to carry out tasks in real time, including process control and engineering simulations. These innovations also made simulation models of organizations possible, freeing us from the narrow boundaries and unrealistic simplifying assumptions needed to yield analytically tractable models. For the first time, scholars and practitioners could build realistic models of markets, organizations and other complex systems—models far surpassing the complexity of prior work.

However, the approach Jay developed must be understood as a product of the context in which it emerged (Richardson, 1991, provides thoughtful discussion and contrasts Jay's approach to other systems approaches). When Jay created system dynamics, computers were scarce, expensive, hard to use and snail-slow. Jay, Jack Pugh and others developed tools and guidelines for model development consistent with the capabilities of computers of the day. Principal among these was the use of compartment models, in which the entities and actors relevant to the problem at hand are aggregated into a relatively small number of stocks. Compartment (or box) models are widely used in fields from atmospheric chemistry to zoology and remain highly useful today. However, compartment models cannot represent heterogeneity in members of a compartment, nor is it possible to track the entry and exit of individual items; the contents of every compartment are perfectly mixed, so the probability that an item will exit the stock in the next instant is independent of how long the item has been in the stock. Jay recognized the limitations of these simplifying assumptions, and provided guidelines to help modelers know when it is appropriate to disaggregate a stock into more categories (stocks) to capture heterogeneity, and how to model situations in which an item's exit from a stock is not independent of its entry date (see, e.g., ID, Ch. 11, and Jay's formulations for material and information delays, including the Erlang family and the pipeline delay, and his analysis of their significance and frequency response in ID, Ch. 9 and Appendices E, G, H and N). Heterogeneity is commonly introduced into compartment models by disaggregating single stocks into multiple compartments, as, for example, in aging chains or to represent subsets of the total stock that differ along important dimensions. For example, capital stock can be disaggregated into plant and equipment, customers can be disaggregated by attributes including preferences, location, etc., with as many categories as needed for the purpose (Sterman, 2000, ch. 6).

The exponential growth of computing power has led to the development of new model architectures in which the aggregation assumptions of compartment models are relaxed, including agent-based (individual-based) models (e.g., Epstein, 2007), patch models (e.g., Pickett and White, 1985; see Struben and Sterman, 2008, for an application in system dynamics) and network models (e.g., Strogatz, 2001). However, many introductory system dynamics courses continue to teach compartment models only, defending the high level of aggregation even when inappropriate for the problem at hand. This is a residue of the time when computers were so slow that highly disaggregated models of important problems could not be simulated. That constraint is largely relaxed today, yet too many in the field continue to set up a false opposition between “system dynamics” and “agent-based” models. Worse, too many people, inside and outside the field, erroneously equate “system dynamics” with deterministic compartment models with continuous values for the state variables and formulated in continuous time, in contrast to models that represent individual agents, use discrete time, or include stochastic elements. This is a serious error and a false choice rooted in a confusion about what system dynamics is.3

The persistence of the myth that system dynamics models are deterministic is particularly puzzling since Forrester's first system dynamics model was stochastic, and Jay devoted considerable attention to the proper representation of noise in dynamic models, including methods to specify the power spectrum of random disturbances (ID, ch. 10.7; Appendix F). His discussion of this modeling choice is subtle and nuanced.

Jay clearly counsels against assuming that the order and specification of delays does not matter; the third-order delay he used was instead a “compromise” that provided the lowest-order (and thus least computationally demanding) member of the Erlang family with reasonable impulse- and frequency-response characteristics (specifically, the impulse response of the third-order delay, like many real-life processes, shows no immediate response to a change in its input). This compromise was a pragmatic decision dictated by limitations on computer memory and speed, and on the availability of the data required to identify and estimate the impulse response distribution. Today, both these constraints have been significantly relaxed, and it is often possible to specify the order, mean delay time and other characteristics of delays that best represent the process and fit the data (see Sterman, 2000, ch. 11, for examples).

System dynamics models can be implemented using a variety of different simulation architectures. These vary in their representation of time (continuous or discrete), state variables (continuous or discrete), and uncertainty (stochastic or deterministic). Ordinary differential equations, stochastic differential equations, discrete event simulations, agent-based models and dynamic network models are common computational architectures offering different choices on these dimensions. Today, many software programs are available to implement these architectures, and some allow hybrid models—for example, models that have compartments (aggregated stocks) for some state variables and individual agents for others. Both compartment and individual-level models can be formulated in continuous or discrete time, with continuous or discrete quantities, and either can be deterministic or stochastic.

Any mechanism can be specified at various levels of aggregation. For example, to model the spread of infectious diseases one could use an aggregated compartment model such as the classic SIR model and its variants (Sterman, 2000, ch. 9), in which all individuals in a community are aggregated into compartments representing the susceptible, infectious and removed (recovered or deceased) populations. If needed, the model could be disaggregated into multiple compartments to represent any relevant dimensions of heterogeneity, such as age, gender, immune system status, location (at multiple scales, from nation or province to postal code or even finer), or by patterns of activity that determine contacts with others. High-impact examples include the disaggregated compartment models developed by Thompson, Tebbens and colleagues and used by WHO and CDC to design policy to support the Global Polio Eradication Initiative (Thompson and Tebbens, 2007, 2008; Thompson et al., 2015; Tebbens and Thompson, 2018, this issue). Alternatively, one could capture aspects of the contact networks among individuals by considering their pair-wise interactions (as demonstrated for system dynamics applications by Lamberson, 2018, this issue, building on Keeling et al., 1997; see also Lamberson, 2016). Or one could move to an individual-based model in which each individual is represented separately. Where the SIR compartment model has three states, the individual-level SIR model portrays each individual as being either susceptible, infectious, or removed, and could potentially include heterogeneous individual-level attributes including location, travel patterns, social networks, and others that determine the hazard rates of state transitions (see, e.g., Waldrop, 2018, and the work of the MIDAS Group (Models of Infectious Disease Agent Study), https://www.epimodels.org/). Obviously, individual-level (agent) models include stocks, flows and feedback loops, just as compartment models do. Where the stock of susceptible individuals in the compartmental SIR model is a single state variable and is reduced by the aggregate flow of new cases (infection), the stock of susceptible individuals in the agent-based model is the sum of all those currently susceptible, and the aggregate flow of new cases is the sum of those becoming infected. In the agent-based model the hazard rate that each susceptible individual becomes infected is determined by the rate at which each comes into contact with any infectious individuals and the probability of infection given contact, closing the reinforcing feedback by which the contagion spreads. In the compartment model the hazard rate of infection is the same for all individuals, while it can differ across individuals in the agent-based model. The feedback structure, however, is the same (see Rahmandad and Sterman, 2008, for an explicit comparison of individual and compartment models in epidemiology).

Similarly, recent developments now allow models to capture dynamics at multiple timescales, something Forrester generally avoided. Forrester argued that the purpose of a model would determine the timescale of interest, writing, “For a simple model to be used over a short time span, certain quantities can be considered constants that for a model dealing with a longer time horizon should be converted into variables. Those new variables would in turn depend on more enduring parameters” (Forrester, 1980, p. 559). Likewise, variables that change very quickly relative to the time horizon of the model can be assumed to take their equilibrium values. For example, a model of resource dynamics with a time horizon of a century or more need not consider the rapid fluctuations in inventories of processed natural resources that give rise to commodity price cycles. For many purposes the assumption of weak couplings across timescales is acceptable, but for a number of important problems fast and slow dynamics are inextricably coupled. Computational constraints when Forrester first formulated guidelines for system dynamics made it difficult, if not impossible, to capture both fast and slow dynamics in a single model: doing so increased simulation times unacceptably and potentially leads to instability from errors in numerical integration; the “stiff system problem” (e.g., Press et al., 2007, ch. 17.5). Today methods for multiscale modeling, where submodels operating at different temporal (and spatial) scales are integrated, are advancing rapidly and used in problems from quantum chemistry to climate change (e.g., Hoekstra et al., 2014). Ford (2018, this issue), illustrates methods to couple fast and slow dynamics in system dynamics models, with practical examples in the electric power industry where hourly, daily and seasonal variations in load and generation (particularly with the rise of variable distributed renewables such as wind and solar) interact importantly with slow dynamics around the evolution of generation capacity and end-user capital stocks.

There is no “correct” level of aggregation independent of model purpose. In the epidemiology example, it may seem obvious that the individual level is more correct than the aggregated level. But there is nothing uniquely privileged about the individual level: one could, in principle, further disaggregate such a model to capture the different organs and systems within each individual, or even further, to the cellular level. But why stop there? Cells and the viruses that attack them consist of still smaller structures (organelles, lipids, proteins and other molecules). Molecules consist of atoms; atoms of protons, neutrons and electrons; protons and neutrons of quarks.... At the other end of the spectrum, the purpose of the model may require a more aggregated approach because the data needed to identify structure and estimate parameters for a highly disaggregated model may not be available. Pragmatic considerations also sometimes favor aggregated models. The computational burden and long simulation times of highly disaggregated models can limit the ability to carry out sensitivity analysis (both parametric and structural), quickly change model structure and parameters when the situation is evolving rapidly, or enable key stakeholders to design and test assumptions and policies for themselves to build their confidence in the model and motivate the implementation of model-based recommendations.

Climate models provide a good illustration. To advance basic scientific understanding of climate dynamics and the effects of greenhouse gases on global warming, scientists develop models of immense complexity. These General Circulation Models (GCMs) divide the atmosphere into a three-dimensional lattice and then simulate, for each cell in the lattice, the equations of motion governing flows of energy, moisture and other physical quantities across cells, including momentum, mass, heat and radiative energy transfer, similar to the models used so successfully in short- and medium-range weather forecasting. Modern climate models couple atmospheric dynamics to the ocean, land, and biosphere and are known as coupled AOGCMs (Atmosphere–Ocean GCMs). As computing power has grown, the distance between lattice points and the time step for simulation have shrunk, increasing model accuracy; current models use a grid size of the order of 1° of latitude and longitude and have 20 or more layers for the atmosphere; the resulting number of cells is on the order of millions, each computed every time step. Although these models run on some of the largest supercomputers in the world it can take days, weeks or more to run a single simulation.4 Thus, while AOGCMs are essential for progress in basic scientific understanding, they are not useful for the rapid policy design, sensitivity analysis and interactive learning that can support policymakers, negotiators, and educators. Therefore, Climate Interactive and MIT developed the C-ROADS climate policy model (Fiddaman, 2002, 2007; Sterman et al., 2012, 2013; Sterman, 2015; Holz et al., 2018; http://climateinteractive.org). C-ROADS is a member of the family of Simple Climate Models (SCMs), consisting of low-dimensional compartment models of the carbon cycle and climate (see also the ESCIMO model; Randers et al., 2016). C-ROADS captures the emissions, other fluxes and atmospheric stocks of CO₂, methane, nitrous oxide, many species of fluorinated hydrocarbons and other greenhouse gases, along with the fluxes of carbon and heat among the atmosphere, biosphere and a four-layer ocean. C-ROADS also models climate change impacts including ocean acidification and sea level rise. Without the fine detail of the AOGCMs, SCMs must be parameterized to match both the historical data and output of ensembles of simulations of multiple AOGCMs across a wide range of scenarios for future greenhouse gas emissions; Sterman et al. (2013) provides a quantitative assessment of model fit for CO₂ and CH₄ concentrations, global mean surface temperature anomaly, and sea level rise, with low measures of error (e.g., root mean square error, Theil inequality statistics). C-ROADS thus matches the aggregate behavior of the AOGCMs but runs in less than 1 second on ordinary laptops. Users can design policies, vary parameters, and try any experiments they like and receive feedback immediately, thus enabling them to learn for themselves and assess new proposals at the cadence required in negotiations and educational experiences (Rooney Varga et al., 2018).

The capabilities and speed of computers today have greatly relaxed the constraints on model size and level of aggregation compared to the 1950s, when Forrester created system dynamics. But constraints still exist, and always will. No matter how fast computers become, comprehensive models of a system are impossible. As Mihailo Mesarovic, a developer of early global simulations, noted: “No matter how many resources one has, one can envision a complex enough model to render resources insufficient to the task” (Meadows et al., 1982, p. 197). Modelers should choose the simulation architecture and level of aggregation most appropriate for the purpose of the model—that is, best suited to solve the problem. Typically, aggregate models are easier to represent in differential equation frameworks (compartment models, whether continuous or discrete, deterministic or stochastic), while disaggregation to capture important degrees of heterogeneity across members of the population may call for an individual-based architecture (again, deterministic or stochastic). And just as one should carry out sensitivity analysis to assess the impact of parameter uncertainty, structural sensitivity tests assessing the similarities and differences across levels of aggregation and model architectures are needed. For example, Rahmandad and Sterman (2008) compared continuous, aggregated compartment models to individual-based models in the context of epidemiology and the diffusion of infectious diseases (see also Lamberson, 2018, this issue).

In sum, the goal of dynamic modeling is sometimes to build theoretical understanding of complex dynamic systems, sometimes to implement policies for improvement, and often both. To do so, system dynamics modelers seek to include a broad model boundary that captures important feedbacks relevant to the problem to be addressed; represent important structures in the system including accumulations and state variables, delays and nonlinearities; use behavioral decision rules for the actors and agents, grounded in first-hand study of the relevant organizations and actors; and use the widest range of empirical data to specify the model, estimate parameters, and build confidence in the results. System dynamics models can be implemented using a wide range of methods, including differential equations, difference equations or discrete event simulation; aggregated or disaggregated compartment models or individual-based models; deterministic or stochastic models; and so on.

Asking “Should I build a system dynamics or agent-based model?” is like going to the hospital after an accident and having the doctor say “Would you like to be treated or do you want surgery? The choice is not between treatment in general and any particular treatment, but among the different treatments available. You seek the best treatment for your condition, and you expect doctors to learn and use the best options as new ones become available. In the same way, computational capabilities today have expanded the options for dynamic modeling. Good modelers choose the model architecture, level of aggregation and simulation method that best meet the purpose of the study, taking account of computational requirements, data availability, the time and resources available, the audience for the work, and the ability to carry out sensitivity analysis, understand the behavior of the model, and communicate the results and the reasons for them to the people they seek to influence.

Evidence-based modeling: qualitative and quantitative data sources

Forrester argued early and correctly that data are not only numerical data and that “soft” (unquantified) variables should be included in our models if they are important to the purpose. Jay noted that the quantified data are a tiny fraction of the relevant data needed to develop a model and stressed the importance of written material and especially the “mental data base” consisting of the mental models, beliefs, perceptions and attitudes of the actors in the system. His emphasis on the use of unquantified data was, at the time, unusual, if not unique, among modelers in the management sciences and economics, some of whom attacked his position as unscientific. Jay's response: “To omit such variables is equivalent to saying they have zero effect—probably the only value that is known to be wrong!” (ID, p. 57). Omitting structures or variables known to be important because numerical data are unavailable to specify and estimate them is less scientific and less accurate than using expert judgment and other qualitative data elicitation techniques to estimate their values. Omitting important processes because we lack numerical data to quantify them leads to narrow model boundaries and biased results—and may lead to erroneous or harmful policy recommendations.

Jay's approach is often oversimplified by newcomers to the field as just “talking to people”. In fact, he recommended that modelers embed themselves in the system, similar to the methods of the ethnographer or cultural anthropologist: “first-hand knowledge can be obtained only by living and working where the decisions are made and by watching and talking with those who run the economic [or any] system” (Forrester, 1980, p. 557).

Still, Jay was confident that he could “detect the guiding policy” through observation and interviews, writing, “We usually start already equipped with enough descriptive information to begin the construction of a highly useful model” (ID, p. 57). However, Jay's years of experience managing complex programs such as Whirlwind and SAGE gave him extensive first-hand knowledge and deep insight into organizations, enabling him to be an effective interviewer. Few of us have such knowledge. Far more important, today we know that there are many pitfalls and biases in the elicitation of mental models from subject matter experts or the actors in a system.

Jay recognized one important bias in information gained from interviews and observation. He noted that the mental data base includes three types of data: (i) observations about the structure of the system and the policies governing system flows; (ii) actual observed system behavior; and (iii) expectations about the behavior of the whole system. He recognized that people's expectations about system behavior were not reliable: they “represent intuitive solutions to the nonlinear, high-order systems of integral equations that reflect the structure and policies of real systems. Such intuitive solutions to complicated dynamic systems are usually wrong” (Forrester, 1980, p. 556). Subsequent research revealed that Jay was correct, but wildly overoptimistic: a large body of work shows not only that people do poorly anticipating the behavior of complex systems, but that even highly educated people with significant training in STEM fields (science, technology, engineering or mathematics) cannot correctly identify the behavior of even a single stock from knowledge of its flows, without any feedbacks, time delays, nonlinearities or other attributes of complex systems (Booth Sweeney and Sterman, 2000; Cronin et al., 2009).

Research since Jay's pioneering studies shows that mental models are often unreliable and biased even regarding policy, structure and actual behavior, and that verbal accounts, even carefully elicited and cross-checked, often do not reveal the causal structure of a system, the decision processes of the informant or other actors, or even accurate accounts of events and behavior. Today we know that many judgments and decisions arise rapidly, automatically, and unconsciously from so-called “system 1” neural structures, in contrast to the slow, “system 2” structures underlying effortful, conscious deliberation (e.g., Sloman, 1996; Kahneman, 2011. Lakeh and Ghaffarzadegan, 2016, explore implications for system dynamics). Perceptions, judgments and decisions arising from system 1 are often systematically wrong, with examples ranging from optical illusions to violations of basic rules of logic to stereotyping and the fundamental attribution error to the dozens of “heuristics and biases” documented in the behavioral decision-making and behavioral economics literature (e.g., Gilovich et al., 2002).

Worse, we are all subject to implicit (unconscious) racial, gender and other biases (Greenwald and Banaji, 1995). These and other errors and biases afflict lay people and experts alike. Indeed, experts are often more vulnerable to them. Overconfidence bias provides a telling example: people tend to be overconfident in their judgments, significantly underestimating uncertainty. In many settings, training and expertise do not improve accuracy (e.g., Sanchez and Dunning, 2018). Further, “Some epistemic vices or cognitive biases, including overconfidence, are ‘stealthy’ in the sense that they obstruct their own detection. Even if the barriers to self-knowledge can be overcome, some problematic traits are so deeply entrenched that even well-informed and motivated individuals might be unable to correct them. One such trait is overconfidence” (Cassam, 2017, p. 1).

Interviewers are subject to the same errors and biases as their subjects. Bias can arise because the sample of informants selected is not representative; social pressures often lead people to tell interviewers what they believe the interviewer wants to hear or what they believe will enhance their status in the eyes of the interviewer; talking to people in groups can lead to groupthink and silencing of individuals with minority views or views diverging from those of superiors and authority figures (e.g., Janis, 1982; Perlow and Repenning, 2009, develop a system dynamics model showing how silencing can be self-reinforcing).

Psychologists, sociologists, ethnographers and other social scientists have developed methods to identify and mitigate these biases, both in sample selection and protocols for data elicitation. Sample selection techniques include both probability and non-probability (purposive) methods, including random, stratified and cluster sampling, maximum variation, typical case, critical case, and snowball (respondent-based) sampling methods, among others. Each has strengths and weaknesses. For example, stratified methods are useful when a representative sample of the underlying population is needed, and snowball sampling is particularly useful to identify social networks and “hidden” populations such as individuals who fear authority (e.g., drug users). With any method one must work carefully to capture important subpopulations whose omission would bias the results—for example, interviewing current employees but not those who quit, or current customers and not those who switched to competitors.

Protocols for eliciting people's knowledge, beliefs and preferences include interviews, ethnographic study, survey methods, focus groups, conjoint analysis, nominal group technique, concurrent verbal protocols, and many others (the literature is vast; see, e.g., Ericsson and Simon, 1993; Miles et al., 2014; Agarwal et al., 2015; Turco, 2016; Glaser and Strauss, 2017). Such methods have been used in system dynamics to, among others, elicit customer preferences (e.g., Sterman, 2000, ch. 2; Barabba et al., 2002), complement statistical analysis of decision making in experimental studies (Kampmann and Sterman, 2014), understand medical decision making (Rudolph et al., 2009) and to elicit reliable estimates of nonlinear relationships from managers (Ford and Sterman, 1998); Minyard et al. (2018, this issue) illustrate by evaluating the effectiveness of the ReThink Health simulation model (https://www.rethinkhealth.org) in catalyzing health system innovation at the community level.

Formal methods to extract meaning and underlying themes and constructs from data include factor analysis, sentiment analysis and other statistical techniques. Formal coding of data is often important and should be done by multiple coders who are blind to the hypotheses of the researcher, with inter-rater reliability assessed and reported. Keith et al. (2017) provide a good example in the context of gathering data for a system dynamics model, using multiple coders to estimate the existence and length of wait lists for the Toyota Prius from press reports, then using the resulting data to test hypotheses about how wait lists affect product adoption. (Do wait lists frustrate potential buyers and slow diffusion, or create buzz and excitement that increases demand?)

Triangulation—using multiple data sources and research methods, both quantitative and qualitative—provides important checks on reliability and helps identify gaps and biases that any one method cannot. System dynamics is particularly well suited to the use of multiple methods; see, for example, Barabba et al. (2002) for an application in business strategy, and Sterman et al. (1997), who integrated quantitative time series and cross-sectional data at several levels of aggregation with interviews, documents and other qualitative data in a formal model exploring the unintended consequences of a successful quality improvement program at semiconductor firm Analog Devices.

Many of the techniques discussed above did not exist when Forrester wrote about the importance of qualitative data. Progress since then in psychology, ethnography, sociology, marketing and other fields has built methods to elicit and analyze qualitative data that modelers in all fields can use to generate reliable, useful knowledge. Convenience samples and just “talking to people” are no longer acceptable.

As important as qualitative methods and data remain, it is important to use proper statistical methods to estimate parameters and assess the ability of a model to replicate historical data when numerical data are available— and to find ways to measure when they aren't. Unfortunately, some modelers discount the role of numerical data and formal methods to estimate model parameters and assess the ability of a model to replicate historical data. They argue that qualitative insights are more important than numerical precision. This practice is often justified as being consistent with Forrester's emphasis on the importance of qualitative data. It is, however, a serious error. Ignoring numerical data and failing to use statistical tools when appropriate increases the chance that the insights derived from a model will be wrong or harmful.

To develop reliable knowledge, we must bring the best available data to bear for the problem we seek to address. Following Jay's advice, we must find a way to measure what we need to know. We should not accept the availability of numerical data as given, outside the boundaries of our project or research. Once we recognize the importance of a concept, we can almost always find ways to measure it. Within living memory there were no national income accounts, no survey methodologies to assess political sentiment, no psychological inventories for depression or subjective well-being, no protocols for semi-structured interviews or coding criteria for ethnographic data. Today many apparently soft variables such as customer perceptions of quality, employee morale, investor optimism, and political values are routinely quantified with tools such as surveys, conjoint analysis and content and sentiment analysis. Of course, all measurements are imperfect. Metrics for so-called soft variables continue to be refined, just as metrics for so-called hard variables are. Often the greatest benefit of a modeling project is to identify the importance of and then measure important concepts previously ignored or unquantified.

To illustrate, consider Homer's (1987, 2012) model of the diffusion of new medical technologies. The model has a broad boundary and significant structure far beyond the classic Bass diffusion model (Bass, 1969; Sterman, 2000, ch. 9), including endogenous adoption and disadoption by doctors, marketing, use (including initial and repeat purchases), patient eligibility criteria, technological improvement, patient outcomes both beneficial and harmful, and evaluation of safety and efficacy. Homer tested the model with two case studies exhibiting very different adoption/diffusion patterns, the cardiac pacemaker and the broad-spectrum antibiotic clindamycin (a good example of the contrasting case method). In each case Homer sought the widest range of data, using triangulation to help specify the model and estimate parameters and relationships. For the pacemaker, this meant extensive interviews with clinicians, researchers, and representatives of pacing companies, including many pacing pioneers. Homer even attended two pacemaker implantation procedures, donning the required lead vest to avoid fluoroscope radiation exposure.

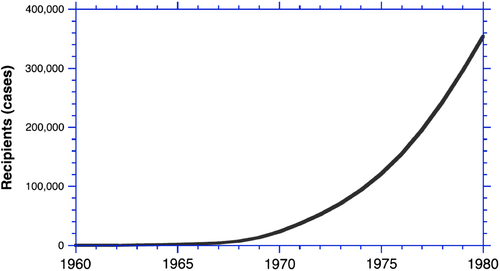
The pacemaker was and remains one of the most successful medical innovations, expanding from the first implantation in 1960 to more than 350,000 per year by 1980 in the U.S.A. alone. Growth was steady and smooth (Figure 8). As the patient base for pacemakers expanded to include milder arrhythmias, the need for follow-up studies assessing benefits and risks grew. However, at the time, no data were available reporting the number of follow-up cases published over time. Given the smooth growth in patients receiving pacemakers it seemed reasonable to assume that follow-up studies grew smoothly as well and build that assumption into the model. None of the experts Homer interviewed suggested anything else. Homer, however, believed it was necessary to find out. At that time (the early 1980s) there was no Internet or electronic databases to automate the search of medical journals. To gather the data, Homer spent days in the Harvard Medical School library stacks, examining, by hand, every issue of the relevant cardiology journals from 1960 through 1980. He coded every follow-up study reported, tabulating the number of patients reported in each, the medical conditions making them eligible for pacing, and the outcomes. The work was painstaking and slow. But it yielded data no one had previously compiled, including time series showing the number of follow-up cases published per year and how eligibility criteria for pacing had expanded over time.

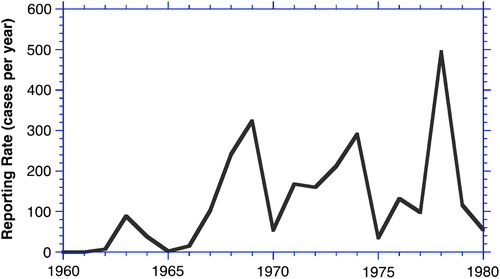
Contrary to intuition and what might be expected from the fact that none of the experts Homer interviewed suggested anything else, evaluations did not exhibit smooth growth. Instead, there was a pronounced cycle in follow-up reporting, with a period of about 5 years (Figure 9). This surprising outcome required Homer to expand the model structure to include a delay in the execution and publication of follow-up studies and to model the behavioral decision rule governing the initiation of studies (Figure 10). Researchers and clinicians initiate follow-up studies when they perceive that the published evaluative data fall short of the amount needed to properly assess the safety and efficacy of pacing for particular subsets of patients. But it takes time to propose, gain approval and funding, initiate, complete and publish these follow-up studies. Researchers and journal editors generally do not know how many evaluations are in the “supply chain” of research being done by all relevant investigators and journals when they decide whether to initiate or publish a new study. The result, as in classic supply-chain models (Forrester, 1961; Sterman, 1989), is overshoot and oscillation, as the initiation of new studies continues even after sufficient studies are in the pipeline to provide the needed data.

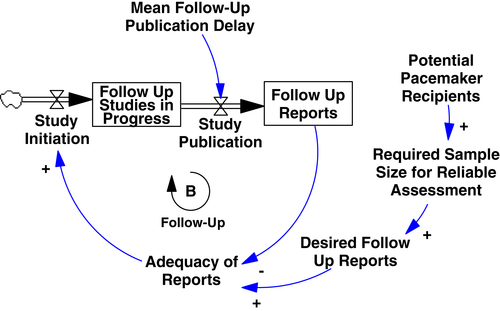
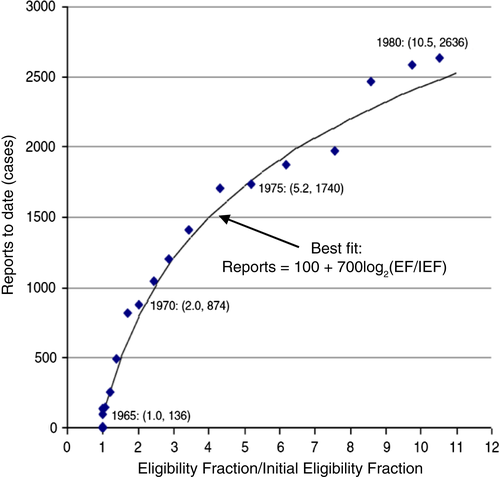
Armed with the quantitative data, Homer could estimate the relationship between the size of the pacing-eligible population and the number of follow-up cases required for reliable inferences about safety and efficacy. Basic sampling theory suggests that the required sample size for follow-up studies would scale with the square root of the pacing-eligible population. Homer found an excellent fit to the data (Figure 11). To estimate the nature and length of the publication delay, note that the multi-stage nature of the follow-up supply chain (initiation, approval, funding, execution, and so on) suggests a high-order delay, but Homer did not merely assume this to be the case; instead, he experimented with different delay types, finding that a third-order delay with a mean delay time of 1.25 years fit the data best (Figure 12).

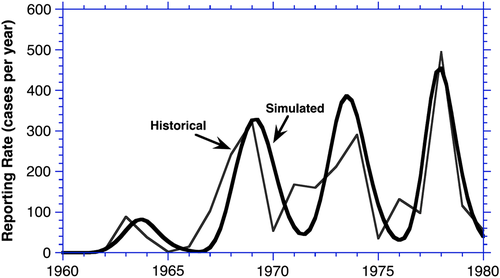
The oscillations in evaluations Homer found are not merely a curiosity but have significant policy implications. During troughs in publications, follow-up data became increasingly dated, providing a poor guide to the benefits and risks as pacemakers improve and new patient populations become eligible for pacing. During such times, clinicians would be flying blind, perhaps being too aggressive and placing at risk certain new patients who would benefit little; or perhaps being too conservative and failing use pacing for others who could benefit substantially.

Policy analysis with the model led Homer to endorse the use of large clinical registries for new medical technologies as a supplement to randomized clinical trials and evaluative studies. Registries, typically overseen by federal agencies such as the National Institutes of Health, require clinicians to continuously report outcomes for their patients. Registries generate a steady flow of information and shorten the delay in the evaluation process, thus keeping up with changes in the technology and its application. They are widely used today, having proven helpful in the early identification of harmful side effects and unexpected benefits for certain patient subsets.

The lesson is clear: it would have been easy for Homer to rely on “common sense” and assume that the publication of follow up studies followed the smooth growth of pacing. Instead, his careful empirical work revealed a surprising phenomenon with important implications (see also Homer, 1996).

Parameter estimation and model analysis

When Forrester first formulated principles for system dynamics practice, numerical data were scarce and many of the tools described above for qualitative data elicitation and quantified measurement did not exist. Furthermore, the tools for statistical estimation of parameters were not well developed compared to today and often inappropriate for use in complex dynamic systems. Given the limitations of computing at the time, multiple linear regression was the most widely used econometric tool. However, linear regression and related methods (e.g., ANOVA) impose assumptions that are routinely violated in complex dynamic systems. These include perfect specification of the model, no feedback between the dependent and independent variables, no correlations among the independent variables, no measurement error, and error terms that are i.i.d. normally distributed. And, of course, classical multiple regression and similar statistical methods only revealed correlations among variables and could not identify the genuine causal relationships modelers sought to capture.

Given these limitations, Jay and other early modelers, including economists, sociologists and others, faced a dilemma: they could estimate parameters and relationships in their models using econometric methods and provide quantitative measures of model fit to the data, but at the cost of constraining the structure of their models to the few constructs for which numerical data existed and using estimation methods that imposed dubious assumptions; or they could use qualitative and quantitative data to build models with broad boundaries, important feedbacks, and nonlinearities, at the cost of estimating parameters by judgment and expert opinion when statistical methods were impossible or inappropriate. Forrester and early system dynamics practitioners opted for the latter. Much controversy in the early years surrounded the different paths modelers trained in different traditions chose when faced with these strong tradeoffs.

Today, data have never been more abundant. Methods to reliably measure previously unquantified concepts, unavailable to Jay, are now essential. Rigorous data collection, both qualitative and quantitative, opens up new opportunities for formal estimation of model parameters, relationships and structure, to assess the ability of models to replicate the historical data, and to characterize the sensitivity of results to uncertainty, providing more reliable and useful insights and policy recommendations. Rahmandad et al. (2015) provide an excellent survey of these methods, with examples and tutorials.

System dynamics modelers have long sought methods to test models and assess their ability to replicate historical data (e.g., Barlas, 1989, 1996; Sterman, 2000, ch. 21; Saysel and Barlas, 2006; Yücel and Barlas, 2015, provide an overview of many tests to build confidence in dynamic models, including their ability to fit historical data, robustness under extreme conditions, and generalizability). But system dynamics modelers were not the only ones concerned with the limitations of early statistical methods. Engineers, statisticians and econometricians worked to develop new methods to overcome the limitations of traditional methods. By the late 1970s, control theory methods designed to handle feedback-rich models with measurement error and multicollinearity, such as the Kalman filter, were introduced into system dynamics (Peterson, 1980). Faster and more capable computing spurred the development of methods to estimate parameters in nonlinear systems, avoid getting stuck on local optima in parameter space, deal with autocorrelation and heteroscedasticity, and especially model misspecification and causal identification (see below). These methods include indirect inference (Gourieroux et al., 1993; Hosseinichimeh et al., 2016), the simulated method of moments (McFadden, 1989; Jalali et al., 2015), Generalized Model Aggregation (Rahmandad et al., 2017) and extended Kalman and particle filters (Fernández-Villaverde and Rubio-Ramírez, 2005). Bootstrapping and subsampling (see, e.g., Politis and Romano, 1994; Dogan, 2008; Struben et al., 2015) and Markov chain Monte Carlo and related Bayesian methods (Ter Braak, 2006; Vrugt et al., 2009; Osgood and Liu, 2015) became feasible for models of realistic size and complexity, enabling modelers to estimate parameters and the confidence intervals around them without making unrealistic assumptions about the properties of the models and error terms. Methods for sensitivity analysis that were difficult or impossible to use when Forrester first formulated system dynamics can now be run quickly even on large models. These methods include standard multivariate Monte Carlo, Latin hypercube, and others. Methods for formal analysis of model behavior have also been developed so that understanding the origin of the behavior in a complex model is no longer a matter of intuition or trial and error (Mojtahedzadeh et al., 2004; Kampmann and Oliva, 2009; Saleh et al., 2010; Kampmann, 2012; Oliva, 2015, 2016; Rahmandad et al., 2015, Part II). New methods for policy optimization have also been developed (see Rahmandad et al., 2015; Vierhaus et al., 2017, Part III).

System dynamics models seek to capture the causal structure of a system because they are used to explore counterfactuals such as the response of a system to new policies. Distinguishing genuine causal relationships from mere correlations remains a critical issue. The gold standard for causal attribution is experiment, particularly the RCT (Randomized Controlled Trial). However, in many settings, particularly in the human and social systems where system dynamics is often used, RCTs and experiments are often prohibitively expensive, time consuming, unethical or simply impossible. We have only one Earth and cannot compare our warming world to a control world in which fossil fuels were never used; we cannot randomly assign half the citizens of the U.S.A. to a world where those convicted of first-degree murder are executed and half to a world without executions to determine whether capital punishment deters murder. Nevertheless, there has been dramatic progress in tools and methods to carry out rigorous RCTs in social systems. These include methods to enhance replicability and avoid “p-hacking” (cherry picking samples and models to get statistically significant results; see Simmons et al., 2011) and the “replication project” (Open Science Collaboration, 2015). RCTs are also no longer restricted to the laboratory but include many large-scale field experiments (Duflo and Banerjee, 2017). Many RCTs in social systems today are carried out in difficult circumstances and provide important insights into policies to reduce poverty and improve human welfare (see, e.g., the work of MIT's Poverty Action Lab, https://www.povertyactionlab.org).

System dynamics has long used experimental methods (Sterman, 1987, 1989), and experimental research in dynamic systems is robust (e.g., Booth Sweeney and Sterman, 2000; Moxnes, 2001, 2004; Croson and Donohue, 2005; Kopainsky and Sawicka, 2011; Arango et al., 2012; Gonzalez and Wong, 2012; Kampmann and Sterman, 2014; Lakeh and Ghaffarzadegan, 2015; Özgün and Barlas, 2015; Sterman and Dogan, 2015; Villa et al., 2015; Gary and Wood, 2016). Many of these studies involve individuals or small groups and have provided important insights into how people understand, perform in and learn from experience in dynamic systems. Still, many settings involve group decision-making. Experimental work involving groups offers important opportunities; for example, McCardle-Keurentjes et al. (2018, this issue), who report an experiment evaluating whether system dynamics tools such as causal diagrams improved performance of individuals in a group model building workshop. Extending experimental methods to group behavior and large-scale field settings is a major opportunity to conduct real-world tests of the theories and policies emerging in the broad boundary, feedback-rich models typical in system dynamics.

Despite progress in methods for and the scope of experimental methods, experimentation remains impossible in many important contexts. Absent rigorous RCTs, researchers often seek to estimate causal structure and relationships via econometric methods. Although we cannot randomly assign murderers to execution versus prison to assess the deterrent effect of capital punishment, we might estimate the effect by comparing states or countries where the death penalty is legal to those where it is not. Of course, states differ from one another on multiple dimensions, including socio-demographic characteristics of the population (age, race, education, religion, urban vs. rural, family structure, etc.), economic conditions (income, unemployment, etc.), climate, cultural attitudes, political orientation, and a host of others. Such studies are extremely common, typically using panel data and specifying regression models using fixed effects to control for those differences deemed to be important. The hope is that controlling for these differences allows the true impact of capital punishment on the murder rate (or any other effect of interest) to be estimated. The problem is that one cannot measure or even enumerate all the possible differences among the states that could potentially influence the murder rate. If any factors that affect the murder rate are omitted, the results will be biased, particularly if, as is common, the omitted factors are correlated with those factors that are included (omitted variable bias), and especially if a state's decision to use the death penalty was affected by any of these conditions, including the murder rate itself (endogeneity bias).

These are more than theoretical concerns. Leamer (1983), in a provocatively titled article, “Let's take the ‘con’ out of econometrics”, showed that choosing different control variables in panel data regressions led to statistically significant results indicating that a single execution either prevented many murders or actually increased them. He concluded “that any inference from these data about the deterrent effect of capital punishment is too fragile to be believed” (Leamer, 1983, p. 42). The results challenged the econometric community to take identification seriously: if econometric methods cannot identify causal relationships then the results of such models cannot provide reliable advice to policymakers.

The result was the “identification revolution”, an explosion in methods for causal inference using formal estimation (see Angrist and Pischke, 2010, whose paper is titled “The Credibility Revolution in Empirical Economics: How Better Research Design Is Taking the Con out of Econometrics”). These methods include natural experiments (e.g., Taubman et al., 2014) and, when true random assignment is not possible, quasi-experimental methods, including regression discontinuity, difference-in-difference and instrumental variables (see Angrist and Pischke, 2009).5

Robust methods for parameter estimation, identification, assessment of goodness of fit, and parametric and structural sensitivity analysis are now available, not only in econometrics but also in engineering, artificial intelligence and machine learning (e.g. Pearl, 2009; Pearl and Mackenzie, 2018. Abdelbari and Shafi, 2017, offer an application in system dynamics). Following Jay's example, system dynamics modelers should master the state of the art and use these tools, follow new developments as the tools continue to evolve, and innovate to develop new methods appropriate for the models we build.

The advent of “big data” and analytics including machine learning, various artificial intelligence methods and the ability to process data sets of previously unimaginable size also create unprecedented opportunities for dynamic modelers. These detailed data sources provide far greater temporal and spatial resolution, generating insight into empirical issues relevant to important questions. For example, Rydzak and Monus (2018, this issue) provide detailed empirical evidence on networks of collaboration among workers from different departments in industrial facilities and model how these evolved over time to explain why one facility was successful in improving maintenance and reliability while another struggled. In the social realm, the integration of big data sets describing population density, the location of homes, schools, businesses and other buildings, road networks, social media and cell phone activity provide the granular data needed to specify patterns of commuting, communication, travel and social interactions. These are essential in developing individual-level models to build understanding of and design policies to respond to, for example, natural disasters, terrorist attacks, and outbreaks of infectious diseases (Eubank et al., 2004; Venkatramanan et al., 2018; Waldrop, 2018).

Big data also enable important theoretical developments in dynamics. For example, most work in networks has focused on static networks, while many important real-world networks are dynamic, with new nodes created and lost, and links among them forged and broken, over time, both exogenously and endogenously. Consider two examples. First, the famous “preferential attachment” algorithm (Barabási and Albert, 1999) generates so-called “scale-free” networks that closely resemble many real networks because it embodies a powerful positive feedback loop in which new nodes arising in the network are more likely to link to existing nodes with more links than to nodes with few links, further increasing the probability that other nodes will link to the popular ones. Second, conventional wisdom has held that the presence of transient (“temporal”) links compromises information diffusion, exploration, synchronization and other aspects of network performance, including controllability. In contrast, Li et al. (2017) develop formal models and simulations based on a range of real dynamic networks, from the yeast proteome to cell phones, showing that “temporal networks can, compared to their static counterparts, reach controllability faster, demand orders of magnitude less control energy, and have control trajectories that are considerably more compact than those characterizing static networks.” System dynamics modelers who embrace big data, analytics and modern dynamical systems theory will find tremendous opportunities for rigorous work that can address critical challenges facing humanity.

Rigor or rigor mortis?

The description violates fundamental principles for good modeling, including that one must always model a problem, never the system; that one should involve the people one hopes to influence in the modeling process from the beginning; and that modeling is iterative, with the need to revise and improve the model arising from testing (see Forrester, 1961, Appendix O and many other passages; also Sterman, 2000, ch. 3; Repenning et al., 2017). The procedure recommended in the quoted passage jumps directly from model formulation to “deriving understanding and … policy insights” and then “implementing changes resulting from these understandings and insights”. Nowhere is there any call for the use of evidence of any kind, qualitative or quantitative, nor the importance of multiple methods, estimating and justifying parameters, assessing and testing the model and the sensitivity of results to uncertainty in assumptions, or any other core elements of the scientific method. At best, such descriptions, which are not limited to this passage, will result in poor-quality work that will have no impact. At worst, policies based on such weakly grounded and poorly tested “insights” put people at risk of harm.

Despite the rapid progress in methods for parameter estimation, statistical inference, and causal attribution in complex dynamic systems, some continue to argue, wrongly, that formal estimation of model parameters is not possible or not necessary. Today, best practice leverages the rapid progress in data availability and methods for parameter estimation and causal inference in complex dynamic systems. Discussing policy based on model simulations without presenting any formal measures of goodness of fit or evidence to justify the parameters and assess the uncertainty around them and in results is simply not acceptable.

Some go farther and argue that “quick and dirty” models are good enough, that expert judgment—often their own—is a sufficient basis for the choice of model boundary, formulations, and parameter values, that subjective judgment—again, often their own—of model fit to historical data is sufficient. After all, the alternative is that managers and policymakers will continue to use their mental models to make consequential decisions. Surely, it is argued, even a simple model, or even a causal diagram or system archetype is a better basis for decision making. Such claims must be tested rigorously. So far, the evidence does not support them (e.g. McCardle-Keurentjes et al., 2018, this issue). Learning in and about complex systems requires constant iteration between experiments in the virtual world of models, where costs and risks are low, and interventions in the real world, where experiments are often costly and risky (Sterman, 1994). Failing to test models against evidence and through experiments in the real world cuts these critical feedbacks. Replacing a poor mental model with a diagram, archetype, or simulation that is not grounded in evidence and is poorly tested may create more harm by providing false confidence and more deeply embedding flawed mental models.

Even more pernicious is the claim that the methods outlined here are only relevant for academic work, or that those who advocate for greater scientific rigor are motivated only to have their work published in academic journals, instead of working on the grand challenges, as Jay called upon us to do. Publishing for the sake of publishing is indeed a waste of resources and talent. Publishing is a means, not an end. We should strive to publish our work in the best academic journals because peer review provides valuable feedback, helping us uncover errors and improve our work (Repenning, 2004). We should strive to publish our work because publication enables others to learn about, use and build on it. We should strive to publish because, yes, publication in respected journals is how academics gain tenure. Promotion and tenure are, like publishing, not an end in themselves. They are the means that provide the academic freedom that enables scholars to work on the important issues, whether they are in vogue or not. Promotion and tenure are the means through which the next generation of researchers and practitioners are trained. The growth of any technical, research-based field including system dynamics depends on the gain of the fundamental reinforcing feedback in which scholars train the next generation of doctoral students, who then go on to their own academic posts, advance the state of the art and train still more students (see Ghaffardzadegan and Larson, 2018, this issue).7 Those who continue to use outdated, inferior and unacceptable methods will not—and should not—succeed in academia. The reinforcing feedback will falter, severely constraining the growth and impact of the field.

Far more important, whether we are academics or practitioners, consultants or K-12 educators, whether we are qualitative or quantitative, whether our goal is understanding or impact, we must use the scientific method because it is the most effective method yet devised to avoid fooling ourselves, to overcome superstitious learning and the cognitive traps, errors and biases afflicting us all. We must use the best available methods and evidence because that is how we find error, improve our understanding, and discover robust and reliable insights that can make lasting contributions to the critical challenges we face.

The path ahead

Throughout his remarkable life, Jay Forrester always worked on problems that matter, time and again risking his reputation, career, and, as his work on the USS Lexington showed, even his life. To do so he mastered the theory and methods relevant to each new problem he tackled and created new innovations when needed to solve them. He always held himself and others to uncompromising standards of excellence. His enduring legacy is that process, not the particular artifacts resulting from it, whether core memory, Whirlwind, SAGE—or the particular system dynamics models he built. Jay always dared us to have courage, be bold, and work on the most important challenges facing humanity. We must follow his example. We must master the state of the art and modern methods to develop, test, communicate, and implement rigorous, reliable and effective insights into the dynamics of complex systems, wherever they originated. Where needed, we must innovate to develop new methods to address the pressing challenges we face. We must hold ourselves to the highest standards for rigorous inquiry. The need is great. The path may be difficult. Will we take it?

Biography

John Sterman is the Jay W. Forrester Professor of Management at the MIT Sloan School of Management, and Director of the MIT System Dynamics Group.