Differential graphical games for H∞ control of linear heterogeneous multiagent systems
Corresponding Author
Farnaz Adib Yaghmaie
Department of Electrical Engineering, Linköping University, Linköpin, Sweden
School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore
Farnaz Adib Yaghmaie, Department of Electrical Engineering, Linköping University, 58 183 Linköping, Sweden.
Email: [email protected]
Search for more papers by this authorKristian Hengster Movric
Department of Control Engineering, Faculty of Electrical Engineering, Czech Technical University in Prague, Prague, Czech
Search for more papers by this authorFrank L. Lewis
University of Texas at Arlington Research Institute, The University of Texas at Arlington, Arlington, Texas
Qian Ren Consulting Professor, Northeastern University, Shenyang, China
Search for more papers by this authorRong Su
School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore
Search for more papers by this authorCorresponding Author
Farnaz Adib Yaghmaie
Department of Electrical Engineering, Linköping University, Linköpin, Sweden
School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore
Farnaz Adib Yaghmaie, Department of Electrical Engineering, Linköping University, 58 183 Linköping, Sweden.
Email: [email protected]
Search for more papers by this authorKristian Hengster Movric
Department of Control Engineering, Faculty of Electrical Engineering, Czech Technical University in Prague, Prague, Czech
Search for more papers by this authorFrank L. Lewis
University of Texas at Arlington Research Institute, The University of Texas at Arlington, Arlington, Texas
Qian Ren Consulting Professor, Northeastern University, Shenyang, China
Search for more papers by this authorRong Su
School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore
Search for more papers by this authorSummary
Differential graphical games have been introduced in the literature to solve state synchronization problem for linear homogeneous agents. When the agents are heterogeneous, the previous notion of graphical games cannot be used anymore and a new definition is required. In this paper, we define a novel concept of differential graphical games for linear heterogeneous agents subject to external unmodeled disturbances, which contain the previously introduced graphical game for homogeneous agents as a special case. Using our new formulation, we can solve both the output regulation and H∞ output regulation problems. Our graphical game framework yields coupled Hamilton-Jacobi-Bellman equations, which are, in general, impossible to solve analytically. Therefore, we propose a new actor-critic algorithm to solve these coupled equations numerically in real time. Moreover, we find an explicit upper bound for the overall
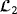 -gain of the output synchronization error with respect to disturbance. We demonstrate our developments by a simulation example.
-gain of the output synchronization error with respect to disturbance. We demonstrate our developments by a simulation example.
REFERENCES
- 1Hengster-Movric K, Lewis FL, Sebek M. Distributed static output-feedback control for state synchronization in networks of identical LTI systems. Automatica. 2015; 53: 282-290.
- 2Ma C-Q, Zhang J-F. Necessary and sufficient conditions for consensusability of linear multi-agent systems. IEEE Trans Autom Control. 2010; 55(5): 1263-1268.
- 3Scardovi L, Sepulchre R. Synchronization in networks of identical linear systems. Automatica. 2009; 45(11): 2557-2562.
- 4Adib Yaghmaie F, Lewis FL, Su R. Output regulation of linear heterogeneous multi-agent systems via output and state feedback. Automatica. 2016; 67: 157-164.
- 5Wieland P, Sepulchre R, Allgöwer F. An internal model principle is necessary and sufficient for linear output synchronization. Automatica. 2011; 47(5): 1068-1074.
- 6Huang C, Ye X. Cooperative output regulation of heterogeneous multi-agent systems: an H∞ criterion. IEEE Trans Autom Control. 2014; 59: 267-273.
- 7Yang N, Xiao J-W, Xiao L, Wang Y-W. Non-zero sum differential graphical game: cluster synchronisation for multi-agents with partially unknown dynamics. Int J Control. 2018: 1-12. https://doi.org/10.1080/00207179.2018.1441550
- 8Adib Yaghmaie F, Su R, Lewis FL, Xie L. Multi-party consensus of linear heterogeneous multi-agent systems. IEEE Trans Autom Control. 2017; 62(11): 5578-5589.
- 9Wang Y-W, Liu X-K, Xiao J-W, Shen Y. Output formation-containment of interacted heterogeneous linear systems by distributed hybrid active control. Automatica. 2018; 93: 26-32.
- 10Wang X, Hong Y, Huang J, Jiang Z-P. A distributed control approach to a robust output regulation problem for multi-agent linear systems. IEEE Trans Autom Control. 2010; 55(12): 2891-2895.
- 11Lunze J. Synchronization of heterogeneous agents. IEEE Trans Autom Control. 2012; 57(11): 2885-2890.
- 12Adib Yaghmaie F, Lewis FL, Su R. Output regulation of heterogeneous linear multi-agent systems with differential graphical game. Int J Robust Nonlinear Control. 2016; 26: 2256-2278.
- 13Liu Y, Jia Y. Robust H∞ consensus control of uncertain multi-agent systems with time delays. Int J Control Autom Syst. 2011; 9(6): 1086-1094.
- 14Yang X, Wang J. Finite-gain
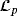 consensus of multi-agent systems. Int J Control Autom Syst. 2013; 11(4): 666-674.
consensus of multi-agent systems. Int J Control Autom Syst. 2013; 11(4): 666-674.
- 15Adib Yaghmaie F, Hengster Movric K, Lewis FL, Su R, Sebek M. H∞-output regulation of linear heterogeneous multiagent systems over switching graphs. Int J Robust Nonlinear Control. 2018; 28(13): 3852-3870.
- 16Jiao Q, Modares H, Lewis FL, Xu S, Xie L. Distributed l2-gain output-feedback control of homogeneous and heterogeneous systems. Automatica. 2016; 71: 361-368.
- 17Zhang M, Saberi A, Grip HF, Stoorvogel AA. H∞ almost output synchronization for heterogeneous networks without exchange of controller states. IEEE Trans Control Netw Syst. 2015; 2(4): 348-357.
- 18Liu D, Li H, Wang D. Online synchronous approximate optimal learning algorithm for multi-player non-zero-sum games with unknown dynamics. IEEE Trans Syst Man Cybern Syst. 2014; 44(8): 1015-1027.
- 19Vamvoudakis KG, Lewis FL. Multi-player non-zero-sum games: online adaptive learning solution of coupled Hamilton-Jacobi equations. Automatica. 2011; 47(8): 1556-1569.
- 20Vamvoudakis KG, Lewis FL, Hudas GR. Multi-agent differential graphical games: online adaptive learning solution for synchronization with optimality. Automatica. 2012; 48(8): 1598-1611.
- 21Jiao Q, Modares H, Xu S, Lewis FL, Vamvoudakis KG. Multi-agent zero-sum differential graphical games for disturbance rejection in distributed control. Automatica. 2016; 69: 24-34.
- 22Bian T, Jiang Z-P. Value iteration and adaptive dynamic programming for data-driven adaptive optimal control design. Automatica. 2016; 71: 348-360.
- 23Vrabie D, Pastravanu O, Abu-Khalaf M, Lewis FL. Adaptive optimal control for continuous-time linear systems based on policy iteration. Automatica. 2009; 45(2): 477-484.
- 24Liu D, Li H, Wang D. Neural-network-based zero-sum game for discrete-time nonlinear systems via iterative adaptive dynamic programming algorithm. Neurocomputing. 2013; 110: 92-100.
- 25Vrabie D, Lewis F. Adaptive dynamic programming for online solution of a zero-sum differential game. J Control Theory Appl. 2011; 9(3): 353-360.
10.1007/s11768-011-0166-4 Google Scholar
- 26Lewis FL, Vrabie D. Reinforcement learning and adaptive dynamic programming for feedback control. IEEE Circuits Syst Mag. 2009; 9(3): 32-50.
- 27Sutton RS, Barto AG. Reinforcement Learning: An Introduction. Vol. 1: Cambridge, MA: MIT Press; 1998.
- 28Yaghmaie FA, Braun DJ. Reinforcement learning for a class of continuous-time input constrained optimal control problems. Automatica. 2019; 99: 221-227.
- 29Isidori A. Nonlinear Control Systems. London, UK: Springer Science & Business Media; 2013.
- 30Huang J. Nonlinear Output Regulation: Theory and Applications. Vol. 8. Philadelphia, PA: SIAM; 2004.
10.1137/1.9780898718683 Google Scholar
- 31Lewis FL, Vrabie D, Syrmos VL. Optimal Control. Hoboken, NJ: John Wiley & Sons; 2012.
- 32Horn RA, Johnson CR. Topics in Matrix Analysis. Cambridge, UK: Cambridge University Press; 1991.
10.1017/CBO9780511840371 Google Scholar
- 33Khalil HK. Nonlinear Systems. Vol. 2. Upper Saddle River, NJ: Prentice-Hall; 1996.
- 34Adib Yaghmaie F, Lewis FL, Su R. Output regulation of heterogeneous multi-agent systems: a graphical game approach. Paper presented at: American Control Conference (ACC); 2015; Chicago, IL.




