Stability analysis and synthesis for linear impulsive stochastic systems
Shixian Luo
School of Automation Science and Engineering, South China University of Technology, Guangzhou 510640, China
Search for more papers by this authorCorresponding Author
Feiqi Deng
School of Automation Science and Engineering, South China University of Technology, Guangzhou 510640, China
Correspondence
Feiqi Deng, School of Automation Science and Engineering, South China University of Technology, Guangzhou 510640, China.
Email: [email protected]
Search for more papers by this authorWu-Hua Chen
College of Mathematics and Information Science, Guangxi University, Nanning, Guangxi 530004, China
Search for more papers by this authorShixian Luo
School of Automation Science and Engineering, South China University of Technology, Guangzhou 510640, China
Search for more papers by this authorCorresponding Author
Feiqi Deng
School of Automation Science and Engineering, South China University of Technology, Guangzhou 510640, China
Correspondence
Feiqi Deng, School of Automation Science and Engineering, South China University of Technology, Guangzhou 510640, China.
Email: [email protected]
Search for more papers by this authorWu-Hua Chen
College of Mathematics and Information Science, Guangxi University, Nanning, Guangxi 530004, China
Search for more papers by this authorSummary
This paper presents a general framework for analyzing stability of linear impulsive stochastic systems (LISSs). Some simple mean square stability criteria for the three types of LISSs are firstly derived by analyzing an equivalent system. By exploring the hybrid characteristics of impulsive systems, the novel quasi-periodic composite polynomial Lyapunov function and the time-varying discretized Lyapunov function are developed, which leads to unified dwell-time–based criteria for mean square stability and almost sure stability of LISSs without imposing the stability condition on continuous- and discrete-time dynamics. Next, based on the established stability criteria, the synthesis problem of state-feedback controller is solved. The computational complexity and the comparison with existing results on the deterministic systems are discussed. Finally, numerical examples are provided to illustrate the usefulness of the proposed results.
REFERENCES
- 1Haddad WM, Chellaboina V, Nersesov SG. Impulsive and Hybrid Dynamical Systems. Princeton, NJ: Princeton University Press; 2006.
10.1515/9781400865246 Google Scholar
- 2Michel AN, Hou L, Liu D. Stability of Dynamical Systems: Continuous, Discontinuous and Discrete Systems. Cambridge, MA: Birkhäuser Boston; 2008.
- 3Cai C, Teel AR, Goebel R. Smooth Lyapunov functions for hybrid systems part II: (pre) asymptotically stable compact sets. IEEE Trans Autom Control. 2008; 53(3): 734-748.
- 4Goebel R, Sanfelice RG, Teel AR. Hybrid dynamical systems. IEEE Control Syst Mag. 2009; 29(2): 28-93.
- 5Antunes DJ, Hespanha JP, Silvestre CJ. Volterra integral approach to impulsive renewal systems: application to networked control. IEEE Trans Autom Control. 2012; 57(3): 607-619.
- 6Teel AR, Subbaraman A, Sferlazza A. Stability analysis for stochastic hybrid systems: a survey. Automatica. 2014; 50(10): 2435-2456.
- 7Liu X. Stability of impulsive control systems with time delay. Math Comput Model. 2004; 39(4-5): 511-519.
10.1016/S0895-7177(04)90522-5 Google Scholar
- 8Yang Z, Xu D. Stability analysis and design of impulsive control systems with time delay. IEEE Trans Autom Control. 2007; 52(8): 1448-1454.
- 9Chen W-H, Zheng WX. Robust stability and H∞-control of uncertain impulsive systems with time-delay. Automatica. 2009; 45(1): 109-117.
- 10Lu J, Ho DWC, Cao J. A unified synchronization criterion for impulsive dynamical networks. Automatica. 2010; 46(7): 1215-1221.
- 11Li X, Bohner M, Wang C-K. Impulsive differential equations: periodic solutions and applications. Automatica. 2015; 52: 173-178.
- 12Wu X, Tang Y, Zhang W. Input-to-state stability of impulsive stochastic delayed systems under linear assumptions. Automatica. 2016; 66: 195-204.
- 13Zhang Y. Global exponential stability of delay difference equations with delayed impulses. Math Comput Simul. 2017; 132: 183-194.
- 14Zhang Y. Robust stability H∞, control of discrete-time uncertain impulsive systems with time-varying delay. Circuits Syst Signal Process. 2016; 35(11): 3882-3912.
- 15Li C, Shi J, Sun J. Stability of impulsive stochastic differential delay systems and its application to impulsive stochastic neural networks. Nonlinear Anal Theory Methods Appl. 2011; 74(10): 3099-3111.
- 16Chen W-H, Wang J-G, Tang Y-J, Lu X. Robust H∞ control of uncertain linear impulsive stochastic systems. Int J Robust Nonlinear Control. 2008; 18(13): 1348-1371.
- 17Liu B. Stability of solutions for stochastic impulsive systems via comparison approach. IEEE Trans Autom Control. 2008; 53(9): 2128-2133.
- 18Xu L, Xu D. Mean square exponential stability of impulsive control stochastic systems with time-varying delay. Phys Lett A. 2009; 373(3): 328-333.
- 19Lu J, Kurths J, Cao J, Mahdavi N, Huang C. Synchronization control for nonlinear stochastic dynamical networks: pinning impulsive strategy. IEEE Trans Neural Netw Learn Syst. 2012; 23(2): 285-292.
- 20Zhang W, Tang Y, Miao Q, Fang J-A. Synchronization of stochastic dynamical networks under impulsive control with time delays. IEEE Trans Neural Netw Learn Syst. 2014; 25(10): 1758-1768.
- 21Cheng P, Deng F, Yao F. Exponential stability analysis of impulsive stochastic functional differential systems with delayed impulses. Commun Nonlinear Sci Numer Simul. 2014; 19(6): 2104-2114.
- 22Amato F, Ambrosino R, Ariola M, De Tommasi G. Robust finite-time stability of impulsive dynamical linear systems subject to norm-bounded uncertainties. Int J Robust Nonlinear Control. 2011; 21(10): 1080-1092.
- 23Amato F, Carannante G, De Tommasi G. Input-output finite-time stabilisation of a class of hybrid systems via static output feedback. Int J Control. 2011; 84(6): 1055-1066.
- 24Briat C. Convex conditions for rubust stability analysis and stabilization of linear aperiodic impulsive and sampled-data systems under dwell-time constraints. Automatica. 2013; 49(11): 3449-3457.
- 25Briat C. Theoretical and numerical comparisons of looped functionals and clock-dependent Lyapunov functions—The case of periodic and pseudo-periodic systems with impulses. Int J Robust Nonlinear Control. 2015; 26(10): 2232-2255.
- 26Briat C, Seuret A. Convex dwell-time characterizations for uncertain linear impulsive systems. IEEE Trans Autom Control. 2012; 57(12): 3241-3246.
- 27Sakthivel R, Rathika M, Malik M. Robust reliable control of uncertain nonlinear stochastic systems subject to actuator fault. Int J Gen Syst. 2017; 46(1): 1-26.
- 28Kozin F. A survey of stability of stochastic systems. Automatica. 1969; 5(1): 95-112.
- 29Mao X. Stochastic Differential Equations and Applications. Second ed. Chichester, UK: Howrwood Publishing Limited; 2007.
- 30Lee SH, Park MJ, Kwon OM, Sakthivel R. Master-slave synchronization for nonlinear systems via reliable control with Gaussian stochastic process. Appl Math Comput. 2016; 290: 439-459.
- 31Hu L, Mao X. Almost sure exponential stabilization of stochastic systems by state-feedback control. Automatica. 2008; 44(2): 465-471.
- 32Sakthivel R, Selvi S, Mathiyalagan K, Arunkumar A. Robust reliable sampled-data H∞ control for uncertain stochastic systems with random delay. Complexity. 2015; 21(1): 42-58.
- 33Briat C, Seuret A. A looped-functional approach for robust stability analysis of linear impulsive systems. Syst Control Lett. 2012; 61(10): 980-988.
- 34Zhang W, Chen B-S.
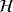-representation and applications to generalized Lyapunov equations and linear stochastic systems. IEEE Trans Autom Control. 2012; 57(12): 3009-3022.
- 35Chesi G. On the complexity of sos programming: formulas for general cases and exact reductions. Paper presented at: SICE International Symposium on Control Systems (ISCS); 2017; Okayama, Japan.
- 36Chen W-H, Zheng WX. Robust Stabilization of delayed Markovian jump systems subject to parametric uncertainties. Paper presented at: 46th IEEE Conference Decision Control; 2007; New Orleans, LA.
- 37Papachristodoulou A, Anderson J, Valmorbida G, Prajna S, Seiler P, Parrilo PA. SOSTOOLS: sum of squares optimization toolbox for MATLAB v3.00; 2013.
- 38Sturm JF. Using, SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optim Methods Softw. 2001; 11(1-2): 625-653.
