Robustness analysis of uncertain discrete-time systems with dissipation inequalities and integral quadratic constraints
Corresponding Author
Bin Hu
Aerospace Engineering and Mechanics Department, University of Minnesota, Minneapolis, MN, USA
Correspondence to: Bin Hu, University of Minnesota, 107 Akerman Hall, 110 Union St SE, Minneapolis, MN, USA.
E-mail: [email protected]
Search for more papers by this authorMárcio J. Lacerda
Aerospace Engineering and Mechanics Department, University of Minnesota, Minneapolis, MN, USA
Search for more papers by this authorPeter Seiler
Aerospace Engineering and Mechanics Department, University of Minnesota, Minneapolis, MN, USA
Search for more papers by this authorCorresponding Author
Bin Hu
Aerospace Engineering and Mechanics Department, University of Minnesota, Minneapolis, MN, USA
Correspondence to: Bin Hu, University of Minnesota, 107 Akerman Hall, 110 Union St SE, Minneapolis, MN, USA.
E-mail: [email protected]
Search for more papers by this authorMárcio J. Lacerda
Aerospace Engineering and Mechanics Department, University of Minnesota, Minneapolis, MN, USA
Search for more papers by this authorPeter Seiler
Aerospace Engineering and Mechanics Department, University of Minnesota, Minneapolis, MN, USA
Search for more papers by this authorSummary
This paper presents a connection between dissipation inequalities and integral quadratic constraints (IQCs) for robustness analysis of uncertain discrete-time systems. Traditional IQC results derived from homotopy methods emphasize an operator-theoretic input–output viewpoint. In contrast, the dissipativity-based IQC approach explicitly incorporates the internal states of the uncertain system, thus providing a more direct procedure to analyze uniform stability with non-zero initial states. The standard dissipation inequality requires a non-negative definite storage function and ‘hard’ IQCs. The term ‘hard’ means that the IQCs must hold over all finite time horizons. This paper presents a modified dissipation inequality that requires neither non-negative definite storage functions nor hard IQCs. This approach leads to linear matrix inequality conditions that can provide less conservative results in terms of robustness analysis. The proof relies on a key J-spectral factorization lemma for IQC multipliers. A simple numerical example is provided to demonstrate the utility of the modified dissipation inequality. Copyright © 2016 John Wiley & Sons, Ltd.
References
- 1Megretski A, Rantzer A. System analysis via integral quadratic constraints. IEEE Transactions on Automatic Control 1997; 42: 819–830.
- 2Zhou K, Doyle J, Glover K. Robust and Optimal Control. Prentice-Hall: Englewood Cliffs, NJ, 1996.
- 3Skogestad S, Postlethwaite I. Multivariable Feedback Control. John Wiley and Sons: Chichester, 2005.
- 4Lessard L, Recht B, Packard A. Analysis and design of optimization algorithms via integral quadratic constraints. SIAM Journal on Optimization 2016; 26(1): 57–95.
- 5Zames G, Falb PL. Stability conditions for systems with monotone and slope-restricted nonlinearities. SIAM Journal of Control 1968; 6(1): 89–108.
- 6Carrasco J, Turner MC, Heath WP. Zames–Falb multipliers for absolute stability: from O'Sheas contribution to convex searches. European Control Conference, Linz, Austria, 2015; 1261–178.
- 7Jönsson U. Lectures on input-output stability and integral quadratic constraints, Royal Institute of Technology (KTH), 2001.
- 8Willems JC. Dissipative dynamical systems part I: general theory. Archive for Rational Mech. and Analysis 1972; 45(5): 321–351.
- 9Willems JC. Dissipative dynamical systems part II: linear systems with quadratic supply rates. Archive for Rational Mech. and Analysis 1972; 45(5): 352–393.
- 10Bart H, Gohberg I, Kaashoek MA. Minimal Factorization of Matrix and Operator Functions. Birkhäuser: Boston, 1979.
10.1007/978-3-0348-6293-6 Google Scholar
- 11Ionescu V, Oară C, Weiss M. Generalized Riccati Theory and Robust Control: A Popov Function Approach. Wiley: Chichester, England, 1999.
- 12Carrasco J, Seiler P. Integral quadratic constraint theorem: a topological separation approach. IEEE Conf. on Decision and Control, Osaka, 2015; 5701–5706.
- 13Pfifer H, Seiler P. Robustness analysis of linear parameter varying systems using integral quadratic constraints. International Journal of Robust and Nonlinear Control 2015; 25(15): 2843–2864.
- 14Veenman J, Scherer C. Stability analysis with integral quadratic constraints: a dissipativity based proof. IEEE Conf. on Decision and Control, Florence, 2013; 3770–3775.
- 15Seiler P. Stability analysis with dissipation inequalities and integral quadratic constraints. IEEE Transactions on Automatic Control 2015; 60(6): 1704–1709.
- 16Pfifer H, Seiler P. Less conservative robustness analysis of linear parameter varying systems using integral quadratic constraints. To appear in International Journal of Robust and Nonlinear Control 2016.
- 17Meinsma G. J-spectral factorization and equalizing vectors. Systems and Control Letters 1995; 25: 243–249.
- 18Engwerda J. LQ Dynamic Optimization and Differential Games (1st edn). Wiley: Chichester, England, 2005.
- 19Engwerda J. Uniqueness conditions for the affine open-loop linear quadratic differential game. Automatica 2008; 44: 504–511.
- 20Megretski A. KYP lemma for non-strict inequalities and the associated minimax theorem, 2010. Arxiv.
- 21Pfifer H, Seiler P. Integral quadratic constraints for delayed nonlinear and parameter-varying systems. Automatica 2015; 56: 36–43.
- 22Turner MC, Kerr ML. L2 gain bounds for systems with sector bounded and slope-restricted nonlinearities. International Journal of Robust and Nonlinear Control 2012; 22(13): 1505–1521.
- 23Kao C. On stability of discrete-time LTI systems with varying time delays. IEEE Transactions on Automatic Control 2012; 57: 1243–1248.
- 24Kao C, Chen M. Robust estimation with dynamic integral quadratic constraints: the discrete-time case. IET Control Theory and Applications 2013; 7: 1599–1608.
- 25Wang S, Heath W, Carrasco J. A complete and convex search for discrete-time noncausal FIR Zames–Falb multipliers. IEEE Conf. on Decision and Control, Los Angeles, 2014; 3918–3923.
- 26Cantoni M, Jönsson U, Khong SZ. Robust stability analysis for feedback interconnections of time-varying linear systems. SIAM J. of Control Optim. 2013; 51(1): 353–379.
- 27Khong SZ, Lovisari E, Rantzer A. A unifying framework for robust synchronisation of heterogeneous networks via integral quadratic constraints. IEEE Transactions on Automatic Control 2016; 61(5): 1297–1309.
- 28Dai L. Singular control systems, Lecture Notes in Control and Information Sciences, vol. 118. Springer: Heidelberg, 1989.
- 29Hu B, Seiler P. Exponential decay rate conditions for uncertain linear systems using integral quadratic constraints. To appear in IEEE Transactions on Automatic Control 2017.
- 30Vinnicombe G. Uncertainty and Feedback -
 Loop-Shaping and the ν-Gap Metric. Imperial College Press: London, 2001.
Loop-Shaping and the ν-Gap Metric. Imperial College Press: London, 2001.
- 31Khalil HK. Nonlinear Systems (3rd edn). Prentice Hall: Upper Saddle River, NJ, 2001.
- 32Heath W, Wills A. Zames–Falb multipliers for quadratic programming. IEEE Conf. on Decision and Control, Seville, 2005; 963–968.
- 33Kao C, Lincoln B. Simple stability criteria for systems with time-varying delays. Automatica 2004; 40: 1429–1434.
- 34Francis B. A Course in H∞ Control Theory. Springer-Verlag: Heidelberg, 1987.
10.1007/BFb0007371 Google Scholar
- 35Jones BL, Kerrigan EC, Morrison JF. A modeling and filtering framework for the semi-discretised Navier–Stokes equations. European Control Conference, Budapest, 2009; 1215–1220.
- 36Varga A. Task I.A.1 - Selection of basic software tools for standard and generalized state-space systems and transfer matrix factorizations. Technical Report, Subroutine Library in Systems and Control Theory (SLICOT), 1998.
- 37Kågström B, Poromaa P. Computing eigenspaces with specified eigenvalues of a regular matrix pair (A, B) and condition estimation: theory, algorithms and software. Numerical Algorithms 1996; 12(2): 369–407.
- 38Schaft A. l2-Gain and Passivity in Nonlinear Control. Springer-Verlag New York, Inc.: New York, 1999.
- 39Jönsson U. Stability analysis with Popov multipliers and integral quadratic constraints. Systems & Control Letters 1997; 31(2): 85–92.
- 40Helmersson A. An IQC-based stability criterion for systems with slowly varying parameters. Technical Report LiTH-ISY-R-1979, Linköping University, 1997.
- 41Fu M, Dasgupta S, Soh YC. Integral quadratic constraint approach vs. multiplier approach. Automatica 2005; 41: 281–287.
- 42Başar T, Olsder GJ. Dynamic Noncooperative Game Theory (2nd edn). SIAM: Philadelphia, 1999.
- 43Başar T, Bernhard P. H∞-Optimal Control and Related Minimax Design Problems (2nd edn). Birkhäuser: Boston, 1995.
10.1007/978-0-8176-4757-5 Google Scholar
- 44Molinari B. The stabilizing solution of the discrete algebraic Riccati equation. IEEE Transactions on Automatic Control 1975; 20(3): 396–399.
- 45Horn RA, Johnson CR. Matrix Analysis. Cambridge University Press: New York, 1990.
- 46Farhood M, Dullerud G. Control of nonstationary LPV systems. Automatica 2008; 44(8): 2108–2119.
- 47Farhood M. LPV control of nonstationary systems: A parameter-dependent Lyapunov approach. IEEE Transactions on Automatic Control 2012; 57(1): 209–215.
- 48Wu F. Control of linear parameter varying systems. Ph.D. Thesis, University of California, Berkeley, 1995.
- 49Wu F, Yang X, Packard A, Becker G. Induced
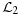 norm control for LPV systems with bounded parameter variation rates. International Journal of Robust and Nonlinear Control 1996; 6: 983–998.
norm control for LPV systems with bounded parameter variation rates. International Journal of Robust and Nonlinear Control 1996; 6: 983–998.
- 50Rantzer A. On the Kalman–Yakubovich–Popov lemma. Systems and Control Letters 1996; 28(1): 7–10.
- 51 CVX Research Inc.. CVX: Matlab software for disciplined convex programming, version 2.0, 2012. Available from: http://cvxr.com/cvx (Accessed on February 2016) .
- 52Grant M, Boyd S. Graph implementations for nonsmooth convex programs. In Recent advances in learning and control, V Blondel, S Boyd, H Kimura (eds)., Lecture Notes in Control and Information Sciences. Springer-Verlag Limited: Heidelberg 2008; 95–110.
- 53Tutuncu RH, Toh KC, Todd MJ. Solving semidefinite-quadratic-linear programs using SDPT3. Mathematical Programming Ser. B 2003; 95: 189–217.
- 54Toh KC, Todd MJ, Tutuncu RH. SDPT3 – a Matlab software package for semidefinite programming. Optimization Methods and Software 1999; 11: 545–581.
- 55Katayama T. (J, J')-Spectral factorization and conjugation for discrete-time descriptor system. Circuits, Systems and Signal Processing 1996; 15(5): 649–669.
- 56Ionescu V, Oara C, Weiss M. General matrix pencil techniques for the solution of algebraic Riccati equations: a unified approach. IEEE Transactions on Automatic Control 1997; 42(8): 1085–1097.
- 57Ionescu Vlad, Weiss Martin. On computing the stabilizing solution of the discrete-time Riccati equation. Linear Algebra and its Applications 1992; 174: 229–238.




