Quantum computation for pricing the collateralized debt obligations
Funding information: National Key R&D Program of China, 2019YFA0308700; 2017YFA0303700; National Natural Science Foundation of China, 61734005; 11761141014; 11690033; 11904229; Science and Technology Commission of Shanghai Municipality (STCSM), 21ZR1432800; 17JC1400403; Shanghai Municipal Education Commission (SMEC), 2017-01-07-00-02-E00049
Abstract
Collateralized debt obligation (CDO) has been one of the most commonly used structured financial products and is intensively studied in quantitative finance. By setting the asset pool into different tranches, it effectively works out and redistributes credit risks and returns to meet the risk preferences for different tranche investors. The copula models of various kinds are normally used for pricing CDOs, and the Monte Carlo simulations are required to get their numerical solution. Here we implement two typical CDO models, the single-factor Gaussian copula model and normal inverse Gaussian copula model, and by applying the conditional independence approach, we manage to load each model of distribution in quantum circuits. We then apply quantum amplitude estimation as an alternative to Monte Carlo simulation for CDO pricing. We demonstrate the quantum computation results using IBM Qiskit. Our work addresses a useful task in finance instrument pricing, significantly broadening the application scope for quantum computing in finance.
1 INTRODUCTION
Quantum computing for finance applications is an emerging field with quickly growing popularity. The finance industry involves various numerical and analytical tasks, for example, derivative pricing, credit rating, Forex algorithm trading, portfolio optimization, and so forth. They all demand heavy quantitative work, and the improved calculation speed and precision would bring significant social value. Quantum computing aims at these very targets.1 Early studies focused on improving finance models with basic quantum mechanics.2-4 Schrodinger equations and Feynman's path integral were suggested to solve stochastic differential equations for pricing interest rate derivatives,2 and Heisenberg uncertainty principle was used to interpret the leptokurtic and fat-tailed distribution of stock price volatilities.4 Recent studies tend to utilize quantum advantages as a faster computing machine. Algorithms that can be implemented in quantum circuits, such as amplitude estimation,5 quantum principle component analysis (PCA),6 quantum generative adversarial network (QGAN),7 the quantum-classical hybrid variational quantum eigensolver (VQE),8 and quantum-approximate-optimization-algorithm (QAOA),9 spring up and begin to be applied to various financial quantitative tasks.10-15
Within all sectors of quantitative finance, the Monte Carlo simulation always plays a significant role,16-18 as only a few stochastic equations for derivative pricing have found analytical solutions,19, 20 while most can only be solved numerically by repeating random settings a great many times in an uncertainty distribution (e.g., normal or log-normal distribution), which therefore consumes much time. The quantum amplitude estimation (QAE) algorithm was raised5 in 2002. It is newly suggested as a promising alternative to the Monte Carlo method, as it shows a quadratic speedup comparing to the latter.10 So far, applications of QAE for option pricing11 and credit risk analysis12 have been demonstrated.
Considering the wide use of Monte Carlo simulation and the large variety of pricing models, the involvement of quantum techniques in finance is still at its infancy. Credit derivatives are frequently mentioned financial instruments because of the strong demand for tackling default risks in finance industry. Collateralized debt obligation (CDO) is a multi-name credit derivative backed on a pool of portfolios of defaultable assets (loans, bonds, credits, etc.). CDO then packages the portfolio into several tranches with different returns and priorities to suffer the default loss.18 CDO can effectively protect the senior tranche from the loss, but too many default events in the pool would still make the CDO collapsed, which was the case during the subprime financial crisis in 2008. Many voices were then made for improving the CDO pricing model and strengthening regulations in various aspects. Nonetheless, the CDO itself is a useful credit instrument that can work out and redistribute credit risks in a very quantitative way. So far, however, the implementation of complex credit instruments like CDO in quantum algorithms has never been reported.
In this work, we present the first quantum circuit implementation for CDO pricing using IBM Qiskit.21 To address the correlations among a large number of assets in the CDO pool, we use both the common Gaussian copula model22 and an improved model, the normal inverse Gaussian (NIG) copula model23, 24 that can interpret the skewness and kurtosis of the real markets which the Gaussian distribution cannot portray.25-27 We follow a conditional independence approach to load the correlated distributions in the quantum circuits, and then use quantum comparators and QAE algorithm to calculate the losses in different tranches. We demonstrate the quantum computation results for a CDO that matches the classical Monte Carlo method, suggesting a promising approach for pricing various derivatives.
2 THE CDO STRUCTURE AND PRICING MODELS
2.1 The CDO tranche structures
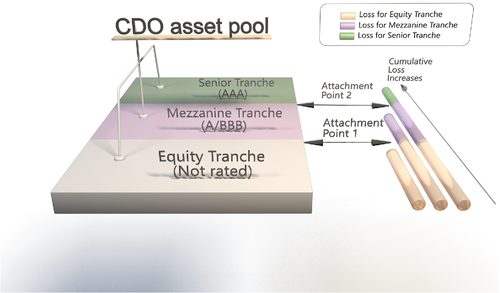
The CDO pool is normally divided into three tranches: the equity, mezzanine, and senior tranche. As shown in Figure 1, when defaults occur, the equity tranche investors bear the loss first, then the mezzanine tranche investors if the loss is greater than the first attachment point. Only when the loss is greater than the second attachment point, will the senior tranche investors lose money. Therefore, senior tranche has the priority of receiving principle and interest payment, and the best protection from risk while having the lowest return.
Let  and
and 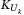 denote the lower and upper attachment point for tranche k, respectively. When defaults occur, the buyer of the tranche k will bear the loss in excess of
denote the lower and upper attachment point for tranche k, respectively. When defaults occur, the buyer of the tranche k will bear the loss in excess of 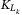 , and up to
, and up to 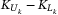 .
.
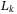 denotes the loss suffered by the holders of tranche k. There is:
denotes the loss suffered by the holders of tranche k. There is: 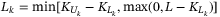 . As there are various default scenarios under some uncertainty distribution, we evaluate the expectation value of the tranche loss
. As there are various default scenarios under some uncertainty distribution, we evaluate the expectation value of the tranche loss 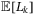 for each tranche k:
for each tranche k: 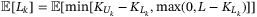 . Then we can get the fair spread for this tranche denoted as
. Then we can get the fair spread for this tranche denoted as 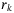 :
:
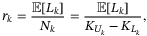 (1)
(1)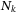 is the notional value of tranche k of the portfolio, which can be calculated by
is the notional value of tranche k of the portfolio, which can be calculated by 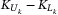 . To arrive at a fair price of a CDO, the return for investors of each tranche should be consistent with the expected loss the investors would bear. Therefore, such a fair spread is considered as the return for this tranche.
. To arrive at a fair price of a CDO, the return for investors of each tranche should be consistent with the expected loss the investors would bear. Therefore, such a fair spread is considered as the return for this tranche.2.2 The conditional independence approach
Usually the pool in CDO is a portfolio of correlated assets. Their default events are not independent, which can be modeled using the single-factor Gaussian copula.
Meanwhile, through years' practice on the Gaussian model, it is found not to well portray the phenomena in real CDO markets, for example, the “correlation smile.”25 In 2005, the NIG model was introduced to CDO pricing. In fact, price volatilities in derivative markets seldom show perfect Gaussian distribution. NIG can flexibly introduce a target skewness and kurtosis which the Gaussian model cannot achieve.25-27 Explanation for NIG distribution and its probability density function (pdf) can be seen in Supplementary Appendix I.
For either the Gaussian copula or NIG copula model, both of them can use the conditional independence approach28 originally developed by Vašíček29, 30 for the multivariate distribution problems. Consider a portfolio that comprises n assets, each with an independent default risk  , and a correlation
, and a correlation 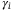 with the systematic risk Z. The latent variables
with the systematic risk Z. The latent variables 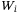 can be used:
can be used: 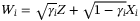 , where
, where 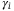 s are correlation parameters that can be obtained by calibrating the market data.
s are correlation parameters that can be obtained by calibrating the market data. 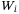 ,
, 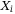 , and Z generally follow the same type of uncertainty distribution, that is, the three all follow a Gaussian-type distribution in the Gaussian copula model.
, and Z generally follow the same type of uncertainty distribution, that is, the three all follow a Gaussian-type distribution in the Gaussian copula model.
 be the original default probability for asset i that is uncorrelated to Z. Via detailed derivation,28 the default probability under z, a detailed certain level of the systematic risk Z, follows:
be the original default probability for asset i that is uncorrelated to Z. Via detailed derivation,28 the default probability under z, a detailed certain level of the systematic risk Z, follows:
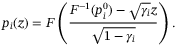 (2)
(2)Equation (2) is derived for very general scenarios.28 F stands for the cumulative distribution function that Z follows, which can be any continuous and strictly increasing distribution function, and in this content, they are Gaussian for the Gaussian copula model or NIG for the NIG copula model. 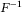 stands for the inverse of distribution F.
stands for the inverse of distribution F.
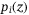 . The default event
. The default event 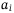 has a Bernoulli distribution, that is,
has a Bernoulli distribution, that is, 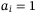 means to default and
means to default and 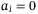 for no default. Given
for no default. Given 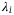 , the loss that would incur for asset i when default happens, the total loss is certainly
, the loss that would incur for asset i when default happens, the total loss is certainly 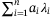 . Consider the probability for
. Consider the probability for 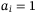 is
is 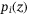 , the expectation for the total loss would be:
, the expectation for the total loss would be:
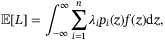 (3)
(3)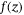 is the probability density function (PDF) of a systematic risk level z. For Gaussian distribution with a variance
is the probability density function (PDF) of a systematic risk level z. For Gaussian distribution with a variance 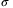 , integrating z from
, integrating z from 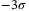 to
to 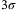 would cover 99.73% of the distribution. After obtained the expected total loss from Equation (3), we can refer to Equation (1) to get the tranche loss and hence fulfill CDO pricing for each tranche. More derivations for the conditional independence approach and the Monte Carlo method for calculating the tranche loss are given in Supplementary Appendix II.
would cover 99.73% of the distribution. After obtained the expected total loss from Equation (3), we can refer to Equation (1) to get the tranche loss and hence fulfill CDO pricing for each tranche. More derivations for the conditional independence approach and the Monte Carlo method for calculating the tranche loss are given in Supplementary Appendix II.3 QUANTUM CIRCUIT CONSTRUCTION
The quantum circuit framework is demonstrated in Figure 2. To apply quantum computation for CDO pricing, the primary task is to load the correlated default risk for each asset of the portfolio into the quantum circuit. Either the Gaussian or NIG model can be loaded following a previous circuit approach12 for the conditional independence model. This involves the operator 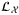 ,
, 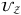 , and
, and 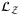 , and then sum up the total loss using operator
, and then sum up the total loss using operator  .
.
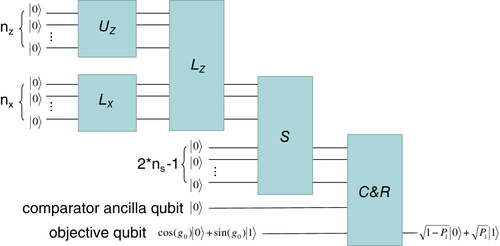
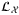 to load the assets with non-correlated independent default risks, uses operator
to load the assets with non-correlated independent default risks, uses operator  to load Z distribution, and uses operator
to load Z distribution, and uses operator 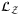 to address the correlation among asset default risks. The total portfolio loss is summed up using operator
to address the correlation among asset default risks. The total portfolio loss is summed up using operator 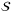 . Then it comes to the comparator operator
. Then it comes to the comparator operator 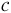 and the piecewise linear rotation operator
and the piecewise linear rotation operator 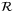 to calculate the tranche loss, which is related to
to calculate the tranche loss, which is related to 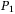 , the probability of the objective qubit at the state
, the probability of the objective qubit at the state 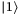 after rotation. Detailed circuit for each operator is provided in the Supplementary Appendix
after rotation. Detailed circuit for each operator is provided in the Supplementary Appendix3.1 Load uncorrelated default using operator 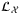
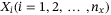 using linear Y-rotation gate. The default probability
using linear Y-rotation gate. The default probability 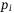 for each asset i can be obtained from its historical performance. The operator
for each asset i can be obtained from its historical performance. The operator 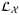 involves
involves 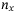 qubits to load the
qubits to load the 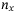 independent assets. For each of the
independent assets. For each of the 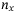 qubits, operator
qubits, operator 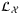 inputs the initial state
inputs the initial state 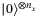 and outputs the state:
and outputs the state:
 (4)
(4)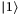 encodes the default probability
encodes the default probability 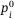 . See Supplementary Appendix III for the circuit for operator
. See Supplementary Appendix III for the circuit for operator 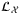 .
.3.2 Load Z distribution using operator 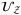
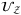 before operator
before operator 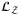 . We use
. We use 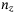 qubits to discretize the distribution to
qubits to discretize the distribution to  slots. The y axis for these slots is the probability of Z, that is, the PDF function
slots. The y axis for these slots is the probability of Z, that is, the PDF function 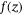 . For Gaussian distribution function, the
. For Gaussian distribution function, the 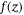 values can be loaded using the built-in codes of uncertainty model in Qiskit, and we contribute the similar codes for NIG distribution. Essentially, operator
values can be loaded using the built-in codes of uncertainty model in Qiskit, and we contribute the similar codes for NIG distribution. Essentially, operator 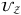 inputs the state
inputs the state  for these
for these 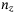 qubits, and outputs
qubits, and outputs 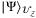 , a superposition of
, a superposition of 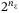 entangled states:
entangled states:
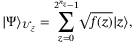 (5)
(5)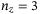 ,
, 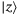 ranges from
ranges from 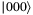 to
to 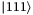 , corresponding to
, corresponding to  3
3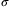 to 3
to 3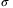 of the Gaussian distribution. Operator
of the Gaussian distribution. Operator 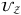 is constructed via a series of controlled-not gates and unitary rotations. See Supplementary Appendix IV for the circuit of operator
is constructed via a series of controlled-not gates and unitary rotations. See Supplementary Appendix IV for the circuit of operator 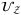 and a brief derivation via matrix calculations.
and a brief derivation via matrix calculations.3.3 Load correlated default using operator 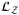
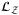 . In short, operator
. In short, operator 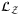 inputs
inputs 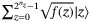 and
and 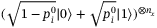 from
from 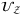 and
and 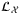 , respectively, and outputs the further entangled state:
, respectively, and outputs the further entangled state:
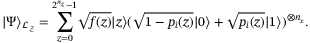 (6)
(6)We use affine mapping12 to encode the influence of a z value for the lower 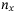 qubits. For instance, with
qubits. For instance, with 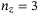 qubits, for
qubits, for 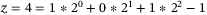 , Qubit 1 and Qubit 3 turn on their controlled gates, while Qubit 2 does not switch on its controlled gate, so that the value
, Qubit 1 and Qubit 3 turn on their controlled gates, while Qubit 2 does not switch on its controlled gate, so that the value 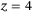 is considered for the
is considered for the 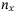 qubits, and there is a probability of
qubits, and there is a probability of 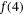 for z being 4. Meanwhile, there are also many linear Y-rotation gates
for z being 4. Meanwhile, there are also many linear Y-rotation gates 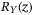 working on the
working on the 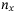 qubits, which change the probability for state
qubits, which change the probability for state 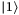 from
from 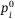 to
to 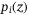 . The expression for
. The expression for 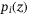 as a function of z and the correlation-free
as a function of z and the correlation-free 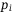 just follows Equation (2), which derives the slope and offset for the rotation gate for operator
just follows Equation (2), which derives the slope and offset for the rotation gate for operator 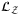 , that is,
, that is, 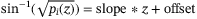 . See derivation of slope and offset in Supplementary Appendix V. The quantum circuit for operator
. See derivation of slope and offset in Supplementary Appendix V. The quantum circuit for operator 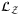 is provided in Supplementary Appendix VI.
is provided in Supplementary Appendix VI.
3.4 Load total loss using operator 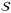
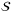 to sum up the loss due to all default events in this asset pool. The sum of loss equals to
to sum up the loss due to all default events in this asset pool. The sum of loss equals to 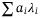 , where
, where 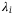 is the loss given default for asset i, and
is the loss given default for asset i, and 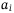 is 1 if asset i default and is 0 vice versa. The amplitude for
is 1 if asset i default and is 0 vice versa. The amplitude for 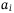 at the quantum state
at the quantum state 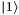 is
is 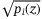 . That is, the probability for
. That is, the probability for 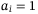 is
is 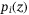 , where
, where 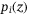 is given by operator
is given by operator 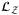 . The maximum loss would be
. The maximum loss would be 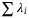 when all assets default, so ensuring the maximum loss to be encoded needs
when all assets default, so ensuring the maximum loss to be encoded needs 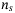 qubits that
qubits that 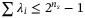 . The operator
. The operator 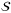 uses
uses 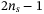 qubits following the previous design of sum operator.12 It inputs the state:
qubits following the previous design of sum operator.12 It inputs the state:  , and outputs the state:
, and outputs the state:
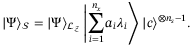 (7)
(7)The first 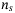 qubits are used to load the sum of loss
qubits are used to load the sum of loss  . Given the probability for
. Given the probability for 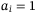 is
is 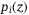 , the expectation of total loss is
, the expectation of total loss is 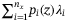 . The next
. The next 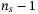 qubits are used as the carry qubits
qubits are used as the carry qubits 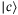 . See details on the circuit and a simple proof that the sum operator indeed loads the expectation value of the total loss
. See details on the circuit and a simple proof that the sum operator indeed loads the expectation value of the total loss 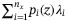 in Supplementary Appendix VII.
in Supplementary Appendix VII.
In short, the output after operator S is consistent with the expression for total loss given in Equation (3). The next step is to compare the total loss with the attachment points for each tranche and work out the tranche loss.
3.5 Load tranche loss using operator 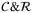
We use the comparator operator 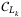 (
(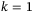 , 2, and 3) to compare the sum of loss with the fixed lower attachment point
, 2, and 3) to compare the sum of loss with the fixed lower attachment point 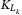 for each tranche k. The comparator has been used to compare the underlying asset value with the striking price for option pricing in a recent work.11 The operator
for each tranche k. The comparator has been used to compare the underlying asset value with the striking price for option pricing in a recent work.11 The operator 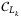 would flip the comparator ancilla qubit from
would flip the comparator ancilla qubit from 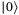 to
to 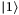 if
if 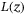 , the sum of loss under a systematic risk level z, is higher than
, the sum of loss under a systematic risk level z, is higher than 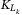 , and would keep
, and would keep 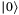 otherwise.
otherwise.
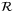 will also rotate the state of an objective qubit under the control of the comparator ancilla qubit. The operator
will also rotate the state of an objective qubit under the control of the comparator ancilla qubit. The operator 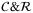 inputs the state
inputs the state 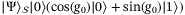 and outputs the state
and outputs the state 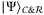 :
:
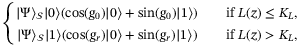 (8)
(8)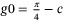 , and c is a scaling factor.
, and c is a scaling factor. 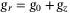 , where
, where  can be implemented using controlled Y-rotations, and it is mapped to integer value
can be implemented using controlled Y-rotations, and it is mapped to integer value 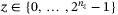 . Note that there is an upperbound breakpoint
. Note that there is an upperbound breakpoint 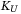 as well, so we set another comparator operator
as well, so we set another comparator operator 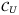 that encodes
that encodes 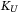 , and
, and 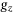 finally reads as:
finally reads as:
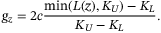 (9)
(9)With such settings 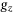 would be in the range
would be in the range 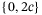 , and by choosing a small scaling parameter c, which is generally set as 0.1 in this work, we can ensure
, and by choosing a small scaling parameter c, which is generally set as 0.1 in this work, we can ensure 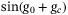 in a monotonously increasing regime. See Supplementary Appendix VIII for the quantum circuit of operator
in a monotonously increasing regime. See Supplementary Appendix VIII for the quantum circuit of operator  .
.
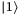 is expressed as
is expressed as 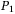 , and it is found to have a relationship with the tranche loss:
, and it is found to have a relationship with the tranche loss:
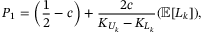 (10)
(10)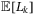 is the expectation of loss for a certain tranche k, for instance, the loss for equity tranche when setting
is the expectation of loss for a certain tranche k, for instance, the loss for equity tranche when setting 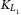 and
and 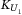 . See detailed derivation for Equation (10) in Supplementary Appendix IX.
. See detailed derivation for Equation (10) in Supplementary Appendix IX.3.6 Calculate tranche loss using QAE
Then it comes to the issue how to read the value of 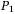 . QAE has been demonstrated as a good alternative to Monte Carlo simulation31 for finance pricing.10-13 In this work, QAE that estimates
. QAE has been demonstrated as a good alternative to Monte Carlo simulation31 for finance pricing.10-13 In this work, QAE that estimates 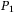 allows us to obtain the CDO tranche loss and return. The canonical QAE algorithm was raised in 2002,5 which is to map the amplitude to be estimated (
allows us to obtain the CDO tranche loss and return. The canonical QAE algorithm was raised in 2002,5 which is to map the amplitude to be estimated (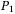 in this case) to the discretized value using m additional qubits via controlled rotations and inverse quantum Fourier transform (QFT). QAE can achieve quadratic speedup, but involvement of inverse QFT requires exponentially increasing circuit depths. Therefore, there arising a series of adapted QAE methods to reduce the complexities of quantum circuits.32-34 Here we implement an iterative QAE32 (IQAE) for our tranche pricing task. IQAE was raised in late 2019 and it has now become widely used, for example, the Qiskit module has replaced the canonical QAE with QAE for many tutorial modules. The methods for both canonical QAE and iterative QAE are provided in Supplementary Appendix X.
in this case) to the discretized value using m additional qubits via controlled rotations and inverse quantum Fourier transform (QFT). QAE can achieve quadratic speedup, but involvement of inverse QFT requires exponentially increasing circuit depths. Therefore, there arising a series of adapted QAE methods to reduce the complexities of quantum circuits.32-34 Here we implement an iterative QAE32 (IQAE) for our tranche pricing task. IQAE was raised in late 2019 and it has now become widely used, for example, the Qiskit module has replaced the canonical QAE with QAE for many tutorial modules. The methods for both canonical QAE and iterative QAE are provided in Supplementary Appendix X.
4 RESULT ANALYSIS
We consider an example to show the pricing for CDO tranches. As listed in Table 1, the CDO pool has four assets, each showing a default probability 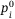 , a sensitivity to the systematic risk
, a sensitivity to the systematic risk 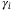 and a loss given default
and a loss given default 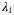 .
.
| Asset i | 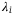 |
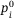 |
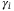 |
|---|---|---|---|
| 1 | 2 | 0.3 | 0.05 |
| 2 | 2 | 0.1 | 0.15 |
| 3 | 1 | 0.2 | 0.1 |
| 4 | 2 | 0.1 | 0.05 |
The CDO is divided into three tranches: the equity, mezzanine, and senior tranches. Values for the lower attachment point 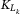 and upper attachment point
and upper attachment point 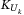 for three tranches are provided in Table 2.
for three tranches are provided in Table 2.
| Tranche name | Lower 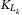 |
Upper 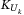 |
|---|---|---|
| Equity | 0 | 1 |
| Mezzanine | 1 | 2 |
| Senior | 2 | 7 |
For this task, we need 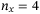 qubits to represent the four assets in operator
qubits to represent the four assets in operator 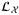 , and
, and 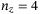 qubits in operator
qubits in operator 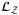 to make
to make 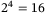 slots for the uncertainty distribution of systematic risk Z. We implement Gaussian (Figure 3A) and NIG (Figure 3B) distribution for Z.
slots for the uncertainty distribution of systematic risk Z. We implement Gaussian (Figure 3A) and NIG (Figure 3B) distribution for Z.
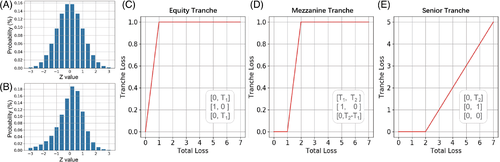
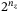 different z values using
different z values using 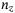 qubits follow the Gaussian distribution (mean = 0, variance = 1) in (A) and the NIG distribution (skewness = 1, kurtosis = 6, mean = 0, variance = 1) in (B). For both distributions, the range is from
qubits follow the Gaussian distribution (mean = 0, variance = 1) in (A) and the NIG distribution (skewness = 1, kurtosis = 6, mean = 0, variance = 1) in (B). For both distributions, the range is from 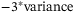 to
to 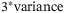 . (C–E) The tranche loss as a function of cumulative loss for (C) equity tranche, (D) mezzanine tranche, and (E) senior tranche. In the white box in (C–E), the first, second, and third array, respectively, show the breakpoints, slopes, and offsets for this tranche.
. (C–E) The tranche loss as a function of cumulative loss for (C) equity tranche, (D) mezzanine tranche, and (E) senior tranche. In the white box in (C–E), the first, second, and third array, respectively, show the breakpoints, slopes, and offsets for this tranche. 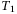 is the attachment point between equity and mezzanine tranche, while
is the attachment point between equity and mezzanine tranche, while 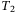 is that between mezzanine and senior tranche
is that between mezzanine and senior trancheFor NIG distribution, by setting the parameters given in Supplementary Appendix I, it shows a skewness of 1 and kurtosis of 6, which are consistent with a real CDO market.25 Comparing with Gaussian distribution, this is narrower and centered to the left.
The step after loading distribution is to calculate the cumulative loss. The maximal loss is 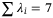 for this portfolio. Therefore, we can use
for this portfolio. Therefore, we can use 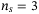 qubits to encode the total loss in the weighted sum operator
qubits to encode the total loss in the weighted sum operator 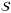 .
.
The pricing of the tranche loss is similar to the call option pricing, where there is a linear “payoff function” that goes up from zero after the option striking price or, for the CDO tranche, the attachment point. The tranche loss as a function of the total cumulative loss is given in Figure 3C–E for this specific example. We can use the built-in code named “PwlObjective” for the piecewise linear rotation function in operator 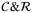 . The built-in function uses the “breakpoints” array to record the attachment points, and uses the “slopes” and “offsets” arrays in which slope k and offset k correspond to these for the line segment between breakpoint
. The built-in function uses the “breakpoints” array to record the attachment points, and uses the “slopes” and “offsets” arrays in which slope k and offset k correspond to these for the line segment between breakpoint 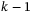 and breakpoint k. Note the offset is the y-axis value for the starting point of the line segment, instead of the intercept by extending the line segment to the y axis. The breakpoints, slopes and offsets for the tranche loss function in this specific case study are shown in each figure in Figure 3C–E, which can be very straightforwardly calculated. These are used as the input parameters for the built-in piecewise linear rotation function.
and breakpoint k. Note the offset is the y-axis value for the starting point of the line segment, instead of the intercept by extending the line segment to the y axis. The breakpoints, slopes and offsets for the tranche loss function in this specific case study are shown in each figure in Figure 3C–E, which can be very straightforwardly calculated. These are used as the input parameters for the built-in piecewise linear rotation function.
We then use IQAE to estimate 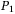 and convert it to the tranche loss according to Equation (4). We use the QASM cloud backend that is in the noisy intermediate-scale quantum (NISQ) environment. Figure 4 demonstrates the calculated tranche loss for an NIG distribution (Figure 3B) using IQAE (with a precision parameter
and convert it to the tranche loss according to Equation (4). We use the QASM cloud backend that is in the noisy intermediate-scale quantum (NISQ) environment. Figure 4 demonstrates the calculated tranche loss for an NIG distribution (Figure 3B) using IQAE (with a precision parameter  and a confidence interval parameter
and a confidence interval parameter 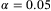 ), the expected wavefunction results from the quantum circuit and the classical Monte Carlo method. The results for different approaches match well. The IQAE results, as indicated by a blue bar with different widths, give a confidence level of
), the expected wavefunction results from the quantum circuit and the classical Monte Carlo method. The results for different approaches match well. The IQAE results, as indicated by a blue bar with different widths, give a confidence level of 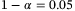 , while QAE estimates a few different values, each with a certain probability (see Figure A10 in the Supplementary Appendix).
, while QAE estimates a few different values, each with a certain probability (see Figure A10 in the Supplementary Appendix).
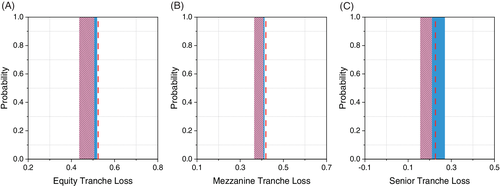
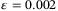 and
and 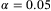 for IQAE using QASM simulator. Red dashed lines indicate definite matrix calculation result of the quantum circuit. The pink shading areas indicate the Monte Carlo results, which are obtained by finding the range of 20 sets of Monte Carlo simulations, each set having 1000 random repetitions
for IQAE using QASM simulator. Red dashed lines indicate definite matrix calculation result of the quantum circuit. The pink shading areas indicate the Monte Carlo results, which are obtained by finding the range of 20 sets of Monte Carlo simulations, each set having 1000 random repetitionsWhen Z follows Gaussian distribution (Figure 3A), consistent results have also been obtained, as shown in Figure A11 in the Supplementary Appendix. Still, the NIG results slight differs from the Gaussian results with a relatively lower tranche loss, especially for the senior tranche loss, which is 0.2233 for NIG and 0.2301 for Gaussian distribution, both obtained via the matrix calculation result for related quantum circuits. This can be due to the skewed distribution for NIG, which makes more positive z values than the Gaussian one, so that expected total loss will be relatively lower considering a negative 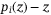 relationship given in Equation (2) and a positive
relationship given in Equation (2) and a positive 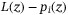 relationship given in Equation (4). Therefore, if the real market follows an NIG distribution while we use Gaussian distribution to model it, we would overestimate the expected tranche loss.
relationship given in Equation (4). Therefore, if the real market follows an NIG distribution while we use Gaussian distribution to model it, we would overestimate the expected tranche loss.
With the calculated tranche loss, we can price the CDO tranche return according to Equation (1). The notional value N for the equity tranche, mezzanine tranche, and senior tranche is 1, 1, and 5, respectively, by calculating 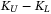 for each tranche. For equity, mezzanine, and senior tranche, the expected tranche loss via IQAE gives 52.0%, 41.7% and 23.8%. Then the tranche return for these tranches are 52.0%, 41.7% and 4.76%, respectively. The low return for the senior tranche is consistent with the practice in reality. Such a low value is first due to the last sequence to bear the loss, and second owing to its large notional value, which is normally above 80% of the sum for the three tranches.
for each tranche. For equity, mezzanine, and senior tranche, the expected tranche loss via IQAE gives 52.0%, 41.7% and 23.8%. Then the tranche return for these tranches are 52.0%, 41.7% and 4.76%, respectively. The low return for the senior tranche is consistent with the practice in reality. Such a low value is first due to the last sequence to bear the loss, and second owing to its large notional value, which is normally above 80% of the sum for the three tranches.
It is worth noting that the returns for equity and mezzanine tranche in the case study of the main text are a bit too high, comparing to the custom returns that would be around 15%–25% and 5%–15% for the equity and mezzanine tranche, respectively.18 It is partially because that default probabilities 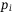 s are a bit high. One more reason is that we ignore the recovery rate of the asset in order to focus on the essential structure. The recovery rate
s are a bit high. One more reason is that we ignore the recovery rate of the asset in order to focus on the essential structure. The recovery rate 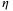 , which is generally set as 40%, means that when asset defaults, some values can be recovered by ways like selling real estates to get funds to compensate investors. Then the maximum loss would equal to the total notional value multiplies (
, which is generally set as 40%, means that when asset defaults, some values can be recovered by ways like selling real estates to get funds to compensate investors. Then the maximum loss would equal to the total notional value multiplies (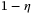 ). In this example, the loss given default
). In this example, the loss given default 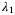 to
to 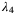 would become 1.2, 1.2, 0.6, and 1.2, while the tranche attachment points keep unchanged. This would bring down the tranche loss.
would become 1.2, 1.2, 0.6, and 1.2, while the tranche attachment points keep unchanged. This would bring down the tranche loss.
We further conduct a robustness analysis on the quantum computation method for CDO tranche pricing, with details given in Supplementary Appendix XI. We have noticed that the scaling factor c is introduced in the operator 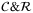 , and it has to be small enough to make the approximation
, and it has to be small enough to make the approximation 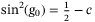 satisfied. Therefore, a smaller value of c tends to be more accurate. The IQAE parameters, including the confidence interval parameter
satisfied. Therefore, a smaller value of c tends to be more accurate. The IQAE parameters, including the confidence interval parameter  and the precision parameter
and the precision parameter 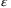 , are investigated as well. We find that
, are investigated as well. We find that 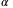 does not have a prominent influence on the range of the result, that is, the bar width, while
does not have a prominent influence on the range of the result, that is, the bar width, while 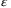 has a severe impact, and the result is satisfactory only when
has a severe impact, and the result is satisfactory only when 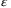 goes down to 0.002 or below. For all these quantum computing parameters, the senior tranche is most sensitive to the changes. This can be due to its last sequence to bear loss. While little fluctuation would not change the result for other tranches, a slight decrease of total loss can possibly exempt the loss due for the senior tranche. We also introduce up to
goes down to 0.002 or below. For all these quantum computing parameters, the senior tranche is most sensitive to the changes. This can be due to its last sequence to bear loss. While little fluctuation would not change the result for other tranches, a slight decrease of total loss can possibly exempt the loss due for the senior tranche. We also introduce up to 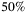 fluctuations of either the independent probability of default
fluctuations of either the independent probability of default 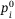 or the correlation to systematic risk,
or the correlation to systematic risk, 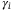 , and find that the fluctuation of
, and find that the fluctuation of 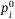 has a stronger influence on the tranche loss comparing to
has a stronger influence on the tranche loss comparing to 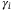 . We show that each tranche loss shows an increasing and decreasing trend with
. We show that each tranche loss shows an increasing and decreasing trend with 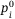 and
and 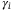 , respectively, which is consistent with the theoretical conditional independence approach in Eq.(2). In addition, an analysis is given in Supplementary Appendix XII to show how different operators scale with
, respectively, which is consistent with the theoretical conditional independence approach in Eq.(2). In addition, an analysis is given in Supplementary Appendix XII to show how different operators scale with 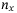 ,
, 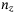 , and
, and 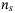 . It suggests that
. It suggests that 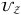 and
and 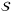 consume heavy circuit depth and it is worth investigation for further optimization for those operators.
consume heavy circuit depth and it is worth investigation for further optimization for those operators.
5 DISCUSSION AND CONCLUSION
The CDO is a relatively advanced and complex structured finance product, and the credit market plays a significant role in the finance industry. Therefore, despite there were some disputes on CDOs during the 2008 financial crisis, CDOs are still widely studied in quantitative finance, and inspire the work of pricing more credit derivatives, which now include a wide range of products like credit default swaps (CDS) and credit valuation adjustment (CVA).
The CDOs are being improved with various financial models considering the inadequacy of early single-factor Gaussian copulas. In this work, we implement the NIG model as an alternative to the Gaussian model. In general, the heavy-tailed distribution of factors in a one-factor copula model may always help to solve the correlation smile problem of the Gaussian copula model. For instance, there is also the variance gamma model that was first applied to option pricing35 and later found to be a good model for CDO pricing.36 Such improved models can also be calculated via quantum computation.
We have stated that the Monte Carlo is useful as only a few stochastic equations for derivative pricing have analytical solutions. It is also worth to note that there are many numerical methods which are being investigated and may work faster than Monte Carlo, for example, finite difference and Fourier transform methods. They would set up a higher classical benchmark that calls for further improvement of corresponding quantum algorithms.
Note that the quantum adaption of generative adversarial network7, 37 has now been considered as an effective way to load any distribution in quantum circuits15 and can be applied to more finance models. Besides, the parameter shift rule38, 39 has been raised to solve the issue of encoding gradients in quantum circuits, which facilitates the mapping of machine learning techniques in quantum algorithms. Furthermore, the trendy variational quantum algorithms that are suitable for NISQ environment, and the alternative approach using quantum annealing,40 may work on a large variety of optimization tasks in finance. In all, there's much room to explore for quantum computation in finance applications.
ACKNOWLEDGMENTS
Hao Tang thanks Prof. Stephen Schaefer's previous help for studies on fixed income and interest rate derivative at London Business School. The authors thank Jian-Wei Pan for helpful discussions. This research was supported by National Key R&D Program of China (2019YFA0308700, 2017YFA0303700), National Natural Science Foundation of China (61734005, 11761141014, 11690033, 11904229), Science and Technology Commission of Shanghai Municipality (STCSM) (21ZR1432800, 17JC1400403), and Shanghai Municipal Education Commission (SMEC) (2017-01-07-00-02-E00049). Xian-Min Jin acknowledges additional support from a Shanghai Talent Program.
CONFLICT OF INTEREST
The authors declare no competing interests.
AUTHOR CONTRIBUTIONS
Hao Tang and Xian-Min Jin conceived and supervised the project. Hao Tang and Anurag Pal designed the scheme. Anurag Pal wrote the Qiskit code. Hao Tang did Monte Carlo simulation. Hao Tang, Anurag Pal, Lu-Feng Qiao, Tian-Yu Wang, Jun Gao, and Xian-Min Jin analyzed the data and presented the figures. Hao Tang, Anurag Pal, and Tian-Yu Wang enriched the quantum circuit analysis in the Supplementary Appendix. Hao Tang wrote the article, including the Supplementary Appendix, with input from all the other authors.
Open Research
DATA AVAILABILITY STATEMENT
The data that support the plots within this article and other findings of this study are available from the corresponding author upon reasonable request.




