Security of quantum secure direct communication based on Wyner's wiretap channel theory
Summary
Quantum secure direct communication (QSDC) transmits secret messages directly over a quantum channel without the prior distribution of a key. Here, we apply Wyner's wiretap channel theory to analyze the security of QSDC protocols. The ideal protocol is treated as the main channel, and the effect of eavesdropping is treated as the wiretap channel. Entanglement-based QSDC protocols are analyzed in detail at first. We calculated the channel capacity of the wiretap channel, and hence, the secrecy channel capacity of the protocol. The security of single-photon–based QSDC protocols is studied through the equivalence between the entanglement-based protocols and single-photon–based protocols. We present a modified version of the single-photon-based DL04 protocol, which gives a higher secrecy capacity.
1 INTRODUCTION
In traditional cryptography, distributing a secret key is a vulnerable process. Quantum key distribution (QKD)1 can ensure the information-theoretic security of the distributed key based on the principle of quantum mechanics, thus ensuring the security of the message transmitted in the classic channel with one-time-pad encryption. An alternative way is to transmit the message in quantum channels directly. Such an idea has motivated a batch of protocols called quantum secure direct communication (QSDC), including the entanglement-based two-step protocols2, 3 and the single-photon–based DL04 protocol,4 and attracts widespread attention. Multistep QSDC with Greenberger-Horne-Zeilinger state and high-dimension QSDC with superdense coding have been proposed.5, 6 Lum et al explored the use of quantum data locking in QSDC.7 Massa et al proposed a QSDC protocol where the direction of transmission is anonymous.8 Shapiro et al investigated the use of quantum low probability of intercept to realize high rate QSDC.9 Furthermore, the measurement-device-independent protocols for QSDC, which could eliminate security loopholes with imperfect measurement devices, have been proposed.10-12 Device-independent QSDC protocol, which could eliminate all possible security loopholes associated with imperfect devices, has also been proposed quite recently.13
In recent years, there has been remarkable progress in practical realization of QSDC. In 2016, Hu et al completed the first experimental demonstration of DL04 protocol with faint laser, validating the feasibility of QSDC in a noisy environment.14 The two-step protocol was realized over 0.5-km optical fiber, showing the potential of its long-distance transmission.15 Zhang et al demonstrated the application of atomic quantum memory in the entanglement-based protocol.16 However, practical quantum memory is far from available. Sun et al solved the problem by proposing a practical scheme without quantum memory based on classical coding theory.17
In contrast to QKD, whose security has been proven over the last two decades,18-24 the security analysis of QSDC protocols has only recently debuted.25, 26 Qi et al26 analyzed the security of DL04 QSDC protocol using Wyner's wiretap channel theory,27 and set up a practical prototype, which can send secure messages directly at a distance of over 1.5 km with a transmission rate of 50 bps.
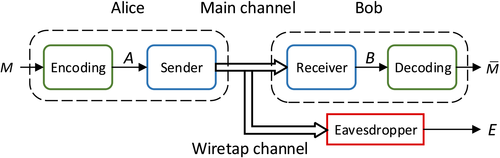
Since QSDC transmits secret messages directly over quantum channels, post-processing is not possible. Therefore, the security analysis of QSDC is completely different from that of QKD. Fortunately, there are many powerful tools in information theory that can help to complete this task. Wyner's wiretap channel theory proves that there exist coding schemes that can ensure the secure transmission of the messages if the secrecy capacity is greater than zero. The wiretap channel model includes a main channel from Alice to Bob and a wiretap channel from Alice to Eve, as shown in Figure 1. The model gives a secrecy capacity, which is the maximal secure transmission rate between Alice and Bob.
 after the receiver's output and decoding
after the receiver's output and decodingThe whole communication process of the two-step protocol3 includes the quantum part and the classical part. In the quantum part, Alice prepares N Einstein-Podolsky-Rosen (EPR) pairs and sends each half of them to Bob. On receiving the particles, Bob checks the error rates by sampling some of the qubits and measuring them in the σx or σz bases. Alice encodes her classical bit sequence A on the EPR pairs using dense coding and sends the remaining halves to Bob. Bob decodes the EPR pairs to get sequence B, which is the message received by Bob. The whole quantum part can be treated in a wiretap channel model, in which Alice sends some messages to Bob, while an eavesdropper tries to eavesdrop it. In the classical part, the information of eavesdropping checking is transmitted in a public channel where Eve can get all the information. The secrecy capacity, which is the maximal difference between the capacity of the main channel and the wiretap channel, can be calculated using the parameters from eavesdropping checking. This is in sharp contrast to classical communication where it is almost impossible for legitimate users to acquire the capacity of the wiretap channel. The quantum channel provides a powerful tool to probe eavesdropping, thus gives a tight estimation of the channel capacity.
In the following, we give a proof of the security of two-step QSDC based on the wiretap channel theory and calculate its secrecy capacity. We find that this capacity is slightly smaller than that obtained from the entanglement distillation scheme,18, 19 which is expected because of the complicated quantum processing involved. Wyner's theory is more appealing for practical applications as it does not use the complicated quantum operations as in the quantum distillation process. Moreover, the secrecy capacity of generic single-photon–based QSDC protocols is also obtained through the equivalence between entanglement-based protocols and single-photon–based protocols. Based on the result, we propose some modification on DL04 protocol to increase its secrecy capacity.
This paper is organized as follows. In Section 2, we describe the detailed process of two-step protocol. Then, we estimate the information leakage in the quantum part and give the secrecy capacity of the channel. In Section 3, the security of DL04 protocol is given. By modifying the DL04 protocol, we can get a larger secrecy capacity. In Section 4, we give a concise summary.
2 SECURITY ANALYSIS OF THE TWO-STEP QSDC PROTOCOL
- (1)
Prepare EPR pairs. Alice prepares 2n maximally entangled EPR pairs |ψ−⟩⊗2n, where
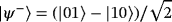 . Alice sends each half of the EPR pairs to Bob, which is called system B.
. Alice sends each half of the EPR pairs to Bob, which is called system B. - (2) Eavesdropping checking. Bob randomly chooses n qubits as check bits and measures them in the bases of σz or σx randomly. Then, Bob tells Alice the positions of the qubits and measurement bases he has chosen. Alice does the same measurement and shares her results with Bob. They can obtain quantum bit error rates (QBERs) in the two measured bases, εx and εz. If the QBERs exceed some threshold, which will be given later, the protocol aborts.
- (3)
Dense coding. Alice applies one of the following four unitary operations to her qubits to encode 00, 01, 10, 11, respectively,
Then, she sends them to Bob.
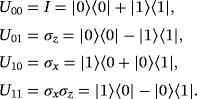 ()
() - (4) Decode message. On receiving the qubits from Alice, Bob combines the two halves of EPR pairs and measures them with Bell basis to obtain the message.
The degree of eavesdropping can be estimated through the QBER. It is worth noting that classical privacy amplification,28 which is used in QKD, is unsuitable for direct communication because part of intelligible information may be lost. In practical application, forward coding will be implemented.26 However, we will not go into the details here. In this section, we will estimate the lower bound of the secrecy capacity of two-step protocol.
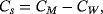 ()
()To estimate the wiretap channel capacity, we need to analyze the detailed process of eavesdropping. Our analysis follows the method of Renner et al.21 Firstly, we assume Eve performs a coherent attack. Specifically, Eve attaches her auxiliary system |E⟩ to system B and performs a unitary operation UBE, then she sends system B to Bob. The entire state of system B before the operation is the direct product of independent and identically distributed (i.i.d.) systems, ρB=[(|0⟩⟨0|+|1⟩⟨1|)/2]⊗2n. If a randomized permutation is applied to the qubits, the joint state of B and E, ρBE, can be seen as a direct product of i.i.d. subsystems ρBEsub asymptotically, according to quantum De Finetti theorem.31 In other words, we can construct a state ρBEsub to approximate ρBE:
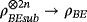 . It is sufficient to consider Eve's operation UBE on every subsystem separately, which is the case of collective attack. For convenience, subscript sub is neglected in the following discussion.
. It is sufficient to consider Eve's operation UBE on every subsystem separately, which is the case of collective attack. For convenience, subscript sub is neglected in the following discussion.
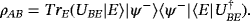 ()
()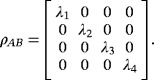 ()
()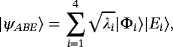 ()
()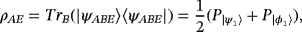 ()
()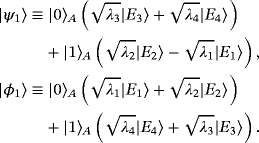
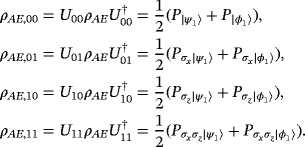
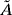 is encoded in some manner and assume
is encoded in some manner and assume
 , with a distribution
, with a distribution
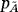 , where ai is a two-bit word. Applying Holevo bound,32 we get
, where ai is a two-bit word. Applying Holevo bound,32 we get
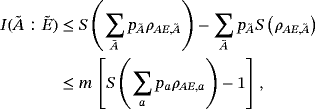 ()
()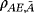 is system AE encoded with bit string {ai} and we have assumed each word ai has the same distribution pa. Therefore, it is sufficient to estimate the maximum of I(A:E) by analyzing one subsystem. The upper bound on I(A:E) gives the wiretap channel capacity (see Appendix A for details)
is system AE encoded with bit string {ai} and we have assumed each word ai has the same distribution pa. Therefore, it is sufficient to estimate the maximum of I(A:E) by analyzing one subsystem. The upper bound on I(A:E) gives the wiretap channel capacity (see Appendix A for details)
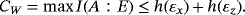 ()
()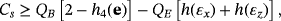 ()
()In addition, the random permutation to reduce coherent attack to collective attack and random local operation to eliminate nondiagonal elements of ρAB can be removed from the protocol. From the perspective of Alice and Bob, any random operation on system AB will introduce an external auxiliary system. Since the details of the operation are transmitted in the public channel, the auxiliary systems can be utilized by Eve and may increase her power. If the operations above are removed, the secrecy capacity above remains a lower bound.
Another method to ensure security is entanglement distillation originated from the works of Lo and Chau18 and Shor and Preskill.19 After the distribution of EPR pairs, they do an additional operation of entanglement distillation according to the result of eavesdropping checking. The achievable efficiency of entanglement distillation is 1−h(εx)−h(εz), then the secrecy capacity is Cs=[1−h(εx)−h(εz)][2−h4(e)], where the second item is the classical capacity between Alice and Bob after entanglement distillation. To make comparison, we can reasonably assume the qubits of each EPR pair go through the same quantum channel independently without loss. If the quantum channel is modeled as a lossless depolarizing channel
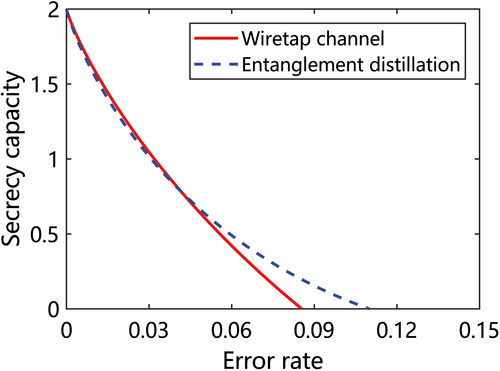
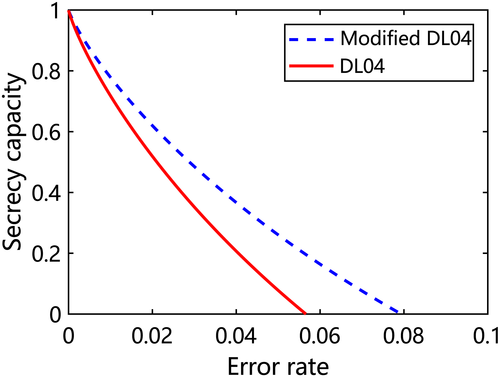
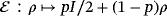 , the error rates of σx and σz measurement in eavesdropping checking are p/2. After both qubits of an EPR pair pass the channel, the depolarizing probability is 2p−p2.33 The secrecy capacities are plotted in Figure 2. The secrecy capacity of the wiretap channel method has less tolerance for error rate, but it can utilize practical classical coding, while the entanglement distillation method requires a quantum computer.
, the error rates of σx and σz measurement in eavesdropping checking are p/2. After both qubits of an EPR pair pass the channel, the depolarizing probability is 2p−p2.33 The secrecy capacities are plotted in Figure 2. The secrecy capacity of the wiretap channel method has less tolerance for error rate, but it can utilize practical classical coding, while the entanglement distillation method requires a quantum computer.
3 SECURITY OF THE SINGLE-PHOTON QSDC PROTOCOL
Generally speaking, single-photon–based protocols are more practical than entanglement-based protocols. Therefore, we construct a generic single-photon–based QSDC protocol and prove its security through the equivalence between the two kinds of protocols.
Firstly, we need to construct an equivalent two-way entanglement-based protocol. The protocol works as follows: (1) Bob prepares the EPR pairs in state
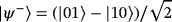 . (2) Bob sends each half of the pairs to Alice and does parameter estimation. (3) Alice applies encoding operation Uk on her halves and sends them to Bob. (4) Bob measures the pairs to decode. It is easy to find the equivalence between this two-way protocol and the original two-step protocol. Additionally, if Alice abandons dense coding and uses two operations, eg, I and σx, to encode the message, Bob simply needs to measure the two qubits separately to decode.
. (2) Bob sends each half of the pairs to Alice and does parameter estimation. (3) Alice applies encoding operation Uk on her halves and sends them to Bob. (4) Bob measures the pairs to decode. It is easy to find the equivalence between this two-way protocol and the original two-step protocol. Additionally, if Alice abandons dense coding and uses two operations, eg, I and σx, to encode the message, Bob simply needs to measure the two qubits separately to decode.
The generic two-way single-photon–based protocol is constructed as follows: (1) Bob prepares each qubit randomly in state
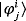 and sends them to Alice, where i∈{0,1} and
and sends them to Alice, where i∈{0,1} and
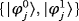 forms the basis of operator σj. (2) After Alice receives the qubits, they do parameter estimation by selecting some pairs randomly and measuring some observables such as σx or σz. (3) They sift out the qubits that cannot be effectively encoded by Alice. For example, if Alice is to apply Uk∈{I,σx} to encode, they sift out the qubits in σx basis since the states remain unchanged under σx operation. (4) Alice applies encoding operation Uk and sends them to Bob. (5) Bob measures the qubits in the basis in which they are prepared to decode.
forms the basis of operator σj. (2) After Alice receives the qubits, they do parameter estimation by selecting some pairs randomly and measuring some observables such as σx or σz. (3) They sift out the qubits that cannot be effectively encoded by Alice. For example, if Alice is to apply Uk∈{I,σx} to encode, they sift out the qubits in σx basis since the states remain unchanged under σx operation. (4) Alice applies encoding operation Uk and sends them to Bob. (5) Bob measures the qubits in the basis in which they are prepared to decode.
Next, we prove the equivalence between the two protocols above. For the generic two-way single-photon–based protocol, Eve interacts with the qubits sent by Bob and gets the state
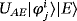 . After the encoding operation of Alice, Eve intercepts all the qubits and gets the state
. After the encoding operation of Alice, Eve intercepts all the qubits and gets the state
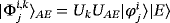 . For the two-way entanglement-based protocol without dense coding, the state of the whole system after the interaction of Eve and the encoding of Alice is |Φk⟩ABE=UkUAE|ψ−⟩|E⟩. Then, Bob measures his qubits in basis σj. If the measurement result is
. For the two-way entanglement-based protocol without dense coding, the state of the whole system after the interaction of Eve and the encoding of Alice is |Φk⟩ABE=UkUAE|ψ−⟩|E⟩. Then, Bob measures his qubits in basis σj. If the measurement result is
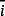 , we can verify
, we can verify
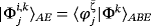 , neglecting the normalization factor.
, neglecting the normalization factor.
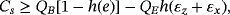 ()
()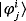 randomly in basis σx, σy, or σz and sends them to Alice. (2) Bob tells Alice which qubit is prepared in basis σy, then Alice measures those qubits in basis σy to get an error rate εy. (3) Alice applies encoding operation I,σy on the remaining qubits and sends them to Bob. (4) Bob measures the returned qubits in the basis in which he prepares them to decode. The lower bound of the secrecy capacity of this modified DL04 protocol is
randomly in basis σx, σy, or σz and sends them to Alice. (2) Bob tells Alice which qubit is prepared in basis σy, then Alice measures those qubits in basis σy to get an error rate εy. (3) Alice applies encoding operation I,σy on the remaining qubits and sends them to Bob. (4) Bob measures the returned qubits in the basis in which he prepares them to decode. The lower bound of the secrecy capacity of this modified DL04 protocol is
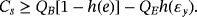 ()
()The performance of DL04 protocol and modified DL04 protocol under lossless depolarizing channel is shown in Figure 3.
In a general form, when they check the error rate in σu (u=x,y,z) basis and Alice uses {I,σu} as encoding operation, the secrecy capacity is Cs=QB[1−h(e)]−QEh(εu). Actually, the secrecy capacity is only constrained by the error rate of the corresponding basis of encoding operation.
4 CONCLUSION
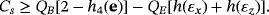 ()
()Our analysis is completed under the following assumptions. (1) There exist noise and loss in the quantum channel. (2) The entanglement source and measurement device are perfect. (3) The EPR pairs transmitted in a round are infinite. Compared with the method of entanglement distillation, the error rate threshold based on the wiretap channel theory is slightly smaller. This result implies the superiority of quantum coding to some extent since one-way entanglement distillation is equivalent to quantum error correction code.34
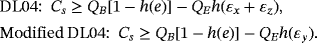 ()
()An in-depth analysis indicates that the eavesdropping capability of Eve can be fully described by the error rate in the basis of the encoding operator or, in other words, the phase error rate. The reason for the high performance of modified DL04 is that it can estimate Eve's eavesdropping capability more accurately.
The application of Wyner's wiretap channel theory to the security of QSDC provides a quantitative analysis of security for transmitting information deterministically. QSDC requires a forward coding scheme, which is different from QKD where only random numbers are transmitted. Forward coding has been studied in information theory, typical example was presented in the work of Tyagi and Vardy.30 As QSDC is the direct transmission of meaningful message rather than random strings, there exist potential wide applications in communication. The analysis presented here is a step toward the practical application of QSDC in realistic conditions.
ACKNOWLEDGEMENTS
This work was supported by China Aerospace Science and Technology Corporation; by the National Basic Research Program of China under grants 2017YFA0303700 and 2015CB921001; by the National Natural Science Foundation of China under grants 61727801, 61871257, and 11774197; and by the Key R&D Program of Guangdong Province under grant 2018B030325002. This work is supported in part by the Beijing Advanced Innovation Center for Future Chip (ICFC).
APPENDIX A:
THE DETAILED CALCULATION OF SECRECY CAPACITY OF TWO-STEP PROTOCOL
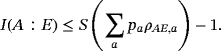 ()
()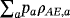 (refer to the work of Jozsa and Schlienz35 for Gram matrix method). The Gram matrix of
(refer to the work of Jozsa and Schlienz35 for Gram matrix method). The Gram matrix of
 is symmetric
is symmetric
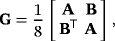
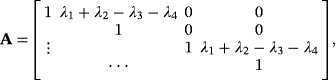
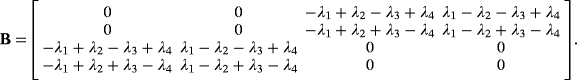
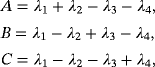
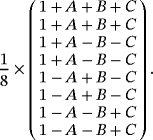
 ()
()
 ()
()
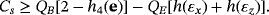 ()
()APPENDIX B:
THE DETAILED CALCULATION OF THE SECRECY CAPACITY OF DL04 PROTOCOL AND MODIFIED DL04 PROTOCOL
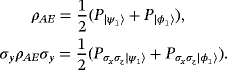
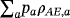 , where pa=1/2 for all a. The Gram matrix is
, where pa=1/2 for all a. The Gram matrix is
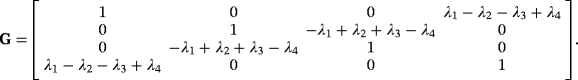
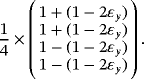
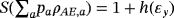 . Then, we have the mutual information
. Then, we have the mutual information
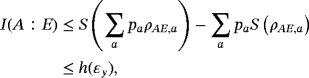
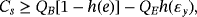 ()
()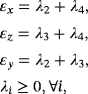 ()
()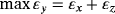 . The secrecy capacity of DL04 protocol is obtained by substituting this result into Equation B1
. The secrecy capacity of DL04 protocol is obtained by substituting this result into Equation B1
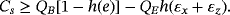 ()
()



