Numerical Simulations of Variable-Range Hopping
Abstract
Numerical simulations of variable-range hopping in 2D and 3D systems with states localized by the disorder are reviewed. Both interacting and noninteracting systems are considered. After reviewing the main theories for variable-range hopping, Mott's and Efros and Shkolvskii's, the numerical techniques are presented that are employed for this problem. Existing results are presented and some new ones obtained for this contribution, concentrating on the value of the proportionality constant on the characteristic temperatures of the different conduction laws and on the form of the pre-exponential factor.
1 Introduction
In systems with states localized by the disorder, transport at low temperatures is by hopping, i.e., jumps between localized states. At very low temperatures, it is often observed a regime with an activation energy that decreases as the temperature decreases, which is referred to as variable-range hopping (VRH). Mott[ 1 ] proposed that VRH is due to a trade off between the spatial and the energy penalties in the transition rates between states. If the temperature is very low, electrons prefer to jump further than they would do otherwise to find a site with low energy and minimize in this way the energy penalty. Mott obtained the expression for the conductivity in the noninteracting case, and Efros and Shklovskii[ 2 ] extended Mott's argument to interacting systems.
To obtain realistic values of the parameters involved in the VRH model a mapping of the dynamic of localized systems to a random resistor network (RRN) was developed[ 3 ] and percolation theory was applied to this model.[ 4 ]
Given the complexity of the problem and the fact that RRN and percolation theory do not take into account important correlations, numerical simulations were established as the main tool to study VRH. Early simulations were indirect,[ 5, 6 ] due to the computer capabilities at the time. Since the design of an efficient kinetic Monte Carlo algorithm due to Biham and first used in ref. 7 in 2002, extensive simulations have been performed. In next sections, we will review simulations that directly measure DC conductivity in different VRH regimes, but Monte Carlo has been also applied to other related problems: AC response,[ 7 ] nonlinear effects,[ 8 ] long-time relaxation,[ 9 ] and off-equilibrium ageing dynamics.[ 10, 11 ] All these works were restricted to 2D systems, trying to avoid finite-size effects due to computer limitations. Also, the analysis of 3D systems is harder because the formation of a percolation network introduces a non-negligible prefactor in the VRH law. Only recently, with the increase in computer capabilities, VRH conductivity in 3D systems has been obtained with kinetic Monte Carlo. We can expect to have more new studies in 3D systems in the near future. In this work, we review previous Monte Carlo simulations in 2D and 3D systems and also present some new results.
Both Mott's law and Efros and Shklovskii's law have been observed in many different types of materials and the list continues growing. Typical examples of Mott's law were reported in amorphous Si[ 12 ] and Ge,[ 13 ] and in indium oxide.[ 14 ] There is a huge number of experiments observing Efros and Shklovskii's law in many types of materials, including doped Si,[ 15 ] gallium arsenide,[ 16 ] and cadmium telluride.[ 17 ] In the most emblematic cases, the conductivity extended over more than eight orders of magnitude[ 12, 13 ] and the ratio of the characteristic temperature T 0 to the minimum temperature observed has reached a value of the order of 104.[ 14, 17-20 ] A critical review of experiments closed to the metal–insulator transition was done in ref. 21. VRH laws are useful to extract microscopic material parameters, such as the localization length, for which a proper knowledge of the numerical coefficients of the different characteristic temperatures is important.
In the next section, we describe the model used and the main elements needed to understand VRH behaviour. Then we present the numerical techniques employed to simulate the different VRH regimes. In Section 4, we review the main numerical results in the literature and compare the characteristic temperatures obtained for the VRH laws.
2 Hopping Conduction
The first ingredient to understand VRH transport are the transition rates, usually assumed to be due to the electron–phonon coupling, between the states. For interacting systems, these rates can connect states differing by the occupation of a single particle or by many particles. Another element needed to understand transport is how the hopping rates between states combine to give a finite conductance. Before discussing these elements, we specify the Hamiltonian often used in hopping conduction.
2.1 Model Hamiltonian
2.2 Hopping Transition Rates
2.3 Random Resistor Network
When the two sites are on opposite sides of the Fermi energy (we assume ) and otherwise .
Agam and Aleiner[ 26 ] studied memory effects in hopping percolation and concluded that the effective resistance of transitions between states at different sides of the Fermi level is diminished with respect to transitions between states on the same side of the Fermi level.
In the presence of interactions, correlations cannot be neglected, specially when simultaneous transitions are important. In this case, the previous RRN does not make sense, but one can still map the problem of the conductance onto an alternative RRN in which each node corresponds to a configuration and the resistor between to of them represents a transition between configurations.[ 27, 28 ]
2.4 Variable-Range Hopping
In the upper temperature range of hopping conduction, electrons follow the shortest possible path, since the energy penalty in the transition rates or in Equation (4) is smaller than the spatial penalty. In this case, conduction is activated. At low temperatures, carriers prefer to jump longer as T decreases to minimize the energy penalty and this regime is called VRH. The mechanism was proposed by Mott for noninteracting systems and extended by Efros and Shklovskii to interacting systems.
2.4.1 Mott's Law
The prefactor depends on the details of the problem, in particular on the electron–phonon coupling. For simplicity, it is usually assumed to be either constant, since many experimental observations are compatible with it, or a power–law dependence of temperature.
2.4.2 Coulomb Gap
To understand VRH in the presence of interactions, we must review first the concept of the Coulomb gap. Pollak[ 30 ] showed that interactions in strongly localized systems induce a depletion in the one-particle DOS, , which was termed the Coulomb gap. Efros and Shklovskii[ 2 ] found that the DOS must be zero at the Fermi level and the precise form of the gap by the following argument.
Extending Efros and Shklovskii's argument for the Coulomb gap to this interaction, one obtains a DOS growing exponentially with energy, starting from an exponentially small value at the Fermi level.[ 33, 34 ]
2.4.3 Efros and Shklovskii's Law
2.4.4 Activated Conductivity
The proportionality constant γ has to be obtained numerically.
3 Numerical Methods
The most important method in the calculation of VRH conduction has been the kinetic Monte Carlo approach, which can be applied equally well to both noninteracting and interacting systems. A second possibility, neglecting correlations, is to solve Kirchhoff's equations for the RRN. For interacting systems, one can obtain a set of low-energy many-particle states and from it calculate the conductivity by a percolation approach.
3.1 Monte Carlo Algorithms
This approach is quite efficient in the VRH regime, since there are no rejections due to the spatial part of the transition rates.
Besides one-electron transitions, one can consider a certain subset of two electron hops, which must cover a large range of hopping distances, since the critical hopping distance will increase with decreasing T.[ 44 ]
3.2 Random Resistor Networks
3.3 Percolation Approaches
Simultaneous transitions of many electrons should dominate the conductance process at very low temperatures, although there is debate of whether experimental results at low T are already in this regime. An approach based on percolation in configuration space has been developed to consider many-electron transitions. It starts from a set, as complete as possible, of low-energy configurations,[ 28, 45 ] and then calculates the effective resistances between them, given by the extension of (4) to many-electron transitions. To obtain the current carrying path, one considers a small resistance and constructs the clusters formed by configurations connected by resistances smaller than the one considered. The transitions crossing a given virtual boundary are labelled according to their net charge traversing the boundary. The resistance is increased until percolation is established in one of the clusters, which occurs when there is a closed path in configuration space with a net charge transfer across the boundary. The procedure is repeated for different temperatures.
3.4 Capacitance Network
To calculate the conductivity in the 2D-activated regime, we can use the Monte Carlo technique previously described, but one has to ensure that the interaction is consistent, meaning that the charging energy and the long-range part of the interaction are compatible. An efficient way to do so is through a capacitor network, where one assumes that the electric field lines mostly go from one of our sites to another site. One can think of the sites as grains close one to each other.[ 46 ]
Grains are randomly distributed and the corresponding junction network without crossings can be constructed using a Delaunay triangularization algorithm.[ 47 ] Each pair of grains is linked by a capacitance , extracted from a random distribution with average equal to C. The leakage of field lines to outside the system can be taken into account through capacitances to the ground, , and we assume .
4 Results
Both Mott's law and Efros and Shklovskii's law have been reproduced by numerical simulations in 2D and 3D systems. In Table 1 , we summarize the main results of these simulations. The type of VRH law studied is indicated in the first column. In the second column, we show the proportionality constant α, appearing in Mott's law, Equation (6), or β, appearing in Efros and Shklovskii's law, Equation (13), or γ, appearing in activated VRH, Equation (15), obtained by the simulations. In the third column, we present the value of the pre-exponential power law whenever this is (observed and) calculated. In the fourth and fifth columns, we report the numerical method and the size of the system employed, respectively. In the last column, we give the corresponding reference. We comment on the main results of the simulations separately for 2D and 3D systems.
| 2D | |||||
|---|---|---|---|---|---|
| Regime | α/β/γ | Prefactor | Method | Size | Reference |
| Mott | 13.0 | Monte Carlo | 200 × 200 | Tsigankov 2002[ 7 ] | |
| <6.04 | – | Master equation | 100 × 100 | Pasveer 2005[ 51 ] | |
| 2.0 ± 0.2 | Monte Carlo | 80 × 50 | Kinkhabwala 2006[ 53 ] | ||
| 7.52 ± 0.06 | RRN | 100 × 100 | This work | ||
| E-S | 5.8 | Monte Carlo | 200 × 200 | Tsigankov 2002[ 7 ] | |
| 7.2 | – | Percolation | 50 × 50 | Somoza 2006[29] | |
| 6.5±1.0 | – | Monte Carlo | 160 × 160 | Nguyen 2006[ 55 ] | |
| 1.4±0.3 | Monte Carlo | 80 × 50 | Kinkhabwala 2006[ 53 ] | ||
| Activated | 1.1 | – | Monte Carlo | 50 × 50 | Kaplan 2003[ 56 ] |
| 0.9 | – | Monte Carlo | 50 × 50 | This work | |
| 3D | |||||
| Regime | α/β | Prefactor | Method | Size | Reference |
| Mott | <10.24 | – | Master equation | 50 × 50 × 50 | Pasveer 2005[ 51 ] |
| 3.6±0.2 | Monte Carlo & RRN | 20 × 20 × 20 | Estelles 2021[ 57 ] | ||
| E-S | 3.40±0.02 | Monte Carlo | Roca-Gonzalez 2018[ 59 ] | ||
| 3.2±0.2 | Monte Carlo | 20 × 20 × 20 | This work | ||
4.1 2D systems
For computational reasons, simulations of VRH in 2D systems have been more frequent than for 3D systems and they have provided us with most of the knowledge we have about conduction mechanisms in hopping. There was a significant number of these studies between 2002 and 2006.
4.1.1 Mott's Law in 2D
Tsigankov and Efros did the first “modern” calculation of Mott's law (mainly to compare with Efros and Shklovskii's law) and found a proportionality constant , close to the percolation prediction, assuming a pre-exponential factor of the form . They employed for the first time the method of storing all the pairs with probabilities proportional to their corresponding spatial factor.
Pasveer et al.[ 49, 50 ] analyzed 2D systems with the master equation method, linearising the occupation probabilities with respect to the value at the equilibrium configuration and neglecting correlations. Their simulation showed a correct Mott's law, although they did not provide an value. They compared with a percolation analysis, which for their results produces . These authors presented a scaling theory for the current distribution of links as a function of the hopping distance and energy. They also argued that current fluctuations are intrinsic to VRH.[ 50 ]
Kinkhabwala et al.[ 51 ] in a large simulation studied both conductivity and shot noise in Mott's regime. They obtained and a prefactor proportional to . Kinetics in this work uses a in Equation (2) that depends on energy, as certainly should be expected in real phonon-activated systems.[ 4 ] This energy dependence should not affect the value of , at least at low temperature, but as this work is getting a rather low value, we believe that a direct comparison with other works is difficult.
In this contribution, we have calculated the conductivity using the RRN approximation for noninteracting 2D systems. The results are shown in Figure 1 , where we plot on a semilogarithmic scale as a function of . The statistical error bars are smaller than the size of the points on the graph. We note that a good Mott's law is obeyed with .
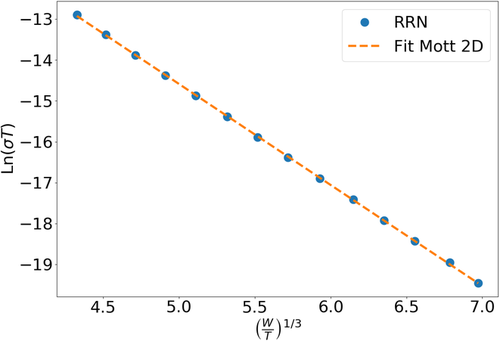
We consider that for noninteracting 2D systems, the most reliable simulation to determine is the one done by Tsigankov and Efros,[ 52 ] as RRN and master equation treatments neglect correlations. Nevertheless, taking a deeper look to their data, we appreciate that their fit to a Mott's law can be improved by removing some data points for the higher temperatures. By doing so, we obtain a fit with . This value is close to most of other calculations and we think is the best estimate up to date, although new simulations in a lower temperature range would be interesting.
4.1.2 Efros and Shklovskii's Law in 2D
Tsigankov and Efros did also the first large Monte Carlo calculation of VRH in interacting 2D systems and they confirmed Efros and Shklovskii's law with a proportionality constant , using a prefactor of the form , in good agreement with percolation predictions. They considered certain two-electron transitions and concluded that their contribution to the current was negligible.
Somoza et al.[ 28 ] studied the conductivity of 2D interacting systems by a percolation procedure in configuration space. They first obtained a large number of low electron configurations, calculate the transition rates between them and apply percolation in configuration space starting from the larger rates until a continuous path in real space is reached. They noted that the number of electrons involved increases with decreasing temperature. They got a proportionality constant for single-electron jumps. When many-electron hopping is allowed decreases leading to . There is a reduction of the order of 15%, which is relatively small, at least in 2D systems. A previous similar study[ 53 ] arrived to a much smaller value of , about an order of magnitude smaller than one-electron calculations. In contrast, Somoza et al.[ 28 ] concluded that many-electron transitions are crucial for energy relaxation.
Nguyen et al.[ 54 ] obtained a value of for the Efros and Shklovskii's law. They applied a gate to the system to screen the Coulomb interaction and showed signs of a crossover from this law to Mott's law at the high temperature range of VRH.
Kinkhabwala et al.[ 51 ] also extended their large numerical simulations, with slightly different dynamics, to 2D interacting systems and arrive at and at a large pre-exponential factor, . In their study, they focused mainly on nonlinear effects and shot noise.
Bergli et al.[ 44 ] studied the effects of the inclusion of some two- and three-electron transitions on conductivity and on relaxation by two complementary methods: a kinetic Monte Carlo algorithm and a master equation in configuration space. They concluded that these transitions are important in relaxation and do not change much conductivity in the range of temperatures accessible by Monte Carlo simulations.
We believe that the most reliable value of is still the one reported by Tsigankov and Efros,[ 52 ] using a kinetic Monte Carlo method, .
4.1.3 Activated Behavior in 2D
Kaplan et al.[ 55 ] did a Monte Carlo simulation of frustrated single-electron arrays, that can be mapped to 2D systems with very large dielectric constant. They found a roughly exponential gap in the DOS and an activated conductivity, in agreement with our previous arguments. They arrived to a proportionality constant .
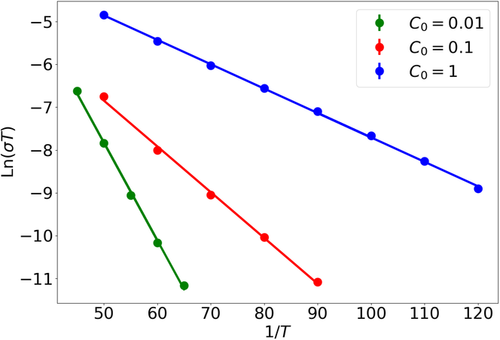
We have performed a simulation of 2D system of capacitors, which as we have mentioned can adequately represent systems with large dielectric constants. We obtained an activated behavior, as can be seen in Figure 2 , where we represent the conductivity versus for three values of the gate capacitance, . As before, the statistical error bars are smaller than the points on the graph. The activation energy increases as decreases and the screening length increases. From these results, we get . One can include disorder by considering nodes with fixed charges at random, not contributing to the current and creating a random on-site potential. Curiously enough, disorder screens out the long-range part of the interaction and produces a reduction of the activation energy.[ 46 ] A good estimate for the parameter γ could be a mean between the two values reported, i.e., .
4.2 3D Systems
4.2.1 Mott's Law in 3D
Numerical simulations of VRH in 3D systems have only been performed relatively recently. The first proper simulation of Mott's law in 3D systems was done by Pasveer et al.[ 49, 50 ] They used the master equation and linearized the occupation probabilities over the values at the equilibrium configuration. They obtained another lower boundary for the parameter . They span a small temperature range, so they could not appreciate any temperature dependence of the pre-exponential. These authors presented a scaling theory for the current distribution of links as a function of the hopping distance and energy. They also argued that current fluctuations are intrinsic to VRH.[ 50 ] Pasveer et al.[ 49, 50 ] analyzed 2D systems with the same method as 3D systems and obtained and no pre-exponential factor.
The slope of this law is clearly larger (in absolute value) than the slope of the hopping length as a function of temperature, equal to , and the two lengths basically coincide at the high temperature range, where conduction is by diffusion. In most of the regime suitable to simulations, and we believe that observed experimentally, the conduction mechanism is intermediate between diffusion and percolation. The percolation regime is only achieved at extremely low temperatures, hardly accessible both experimentally and numerically.
Agam and Aleiner[ 26 ] studied memory effects in VRH and concluded that they decrease the transition rates between normally occupied and unoccupied sites, with respect to those between sites with the same occupation. This effect produces a subleading contribution in the exponential dependence of the conductivity, which in practice can be identified with a change in the pre-exponential power law, and could explain the divergence mentioned above with percolation theory. Our simulation of 3D noninteracting systems is by far the largest,[ 56 ] so we think that the most reliable constant in the characteristic temperature is .
4.2.2 Efros and Shklovskii's Law in 3D
Chen and Skinner[ 58 ] calculated VRH conductivity of 3D interacting systems through the mapping of the standard model to a canonical model of a completely compensated semiconductor. They found that at low T and for long-ranged potentials, hopping proceeds along self-organized site subspaces having fractal dimension equal 2. They obtained for the proportionality constant in the characteristic temperature . Except stated explicitly, calculations on interacting systems only consider one-electron transitions.
Roca-Gonzalez et al.[ 59 ] did a small simulation of 3D interacting systems and they arrived at and a prefactor .
We perform here a large Monte Carlo simulation of 3D disordered systems with Coulomb interactions. The results are shown in Figure 3 , where one can appreciate that they span a large range of temperatures and almost four orders of magnitude in the conductivity. The value of the disorder energy is and the system size . The statistical error bars of the plotted values are smaller than the points on the graph. They fit well an Efros and Shklovskii's law with a power law pre-exponential. The fitting parameters are and an exponent of 0.65 in the pre-exponential. The dashed line in Figure 3 corresponds to the same law with a constant pre-exponential and in this case one would obtain , fairly different from the previous, more reliable value.
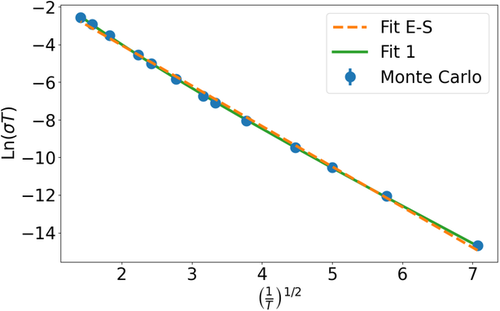
In the previous analysis, we have assumed that the conductivity exponent is equal to 1/2, but, given the importance of this assumption, it is interesting to check it explicitly. We do this by means of a variation of the so-called Zabrodskii's plot[ 60 ] introduced by Möbius,[ 61 ] which represents versus , where . If there is no temperature dependence of the pre-exponential factor, or if this is weak enough, the plot is a straight line with slope equal to the exponent in the exponential function.[ 61 ] In Figure 4 , we represent versus , where and are the coordinates of the ith point in Figure 2. We note that the data follow a relatively good straight line. The slope of the fitted straight line is , fully compatible with Efros and Shklovskii's exponent. A fit of the conductivity data to an exponential with a free exponent produces a value of the exponent equal to , compatible with the result of Zabrodskii's plot. We conclude that our results reproduce Efros and Shklovskii's law, although they are also compatible with a steeper DOS, as obtained in ref. 62. We would like to remark that the 1/2 exponent was obtained by Pollak through a powerful scaling argument that does not rely on conductivity being due to single-electron jumps.[ 63, 64 ]
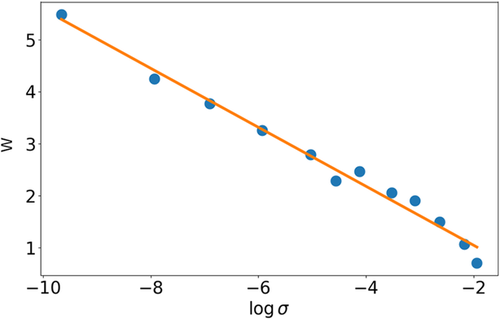
The relevance or not of many-electron jumps is probably the most important question still unsolved for VRH in interacting systems. The importance of these type of transitions is that it expected to increase with dimensionality, but it has not been analyzed in the context of 3D systems. As our simulation of Efros and Shklovskii's law in 3D systems is much larger than the previous one, we think that the most reliable constant characterising is the one obtained in it, .
5 Discussion
In interacting systems, nonlinear effects are very important. Conduction in the nonlinear regime has been simulated by several authors, but this subject is outside the scope of this review. This topic has drawn a lot of attention in recent years due to the bistability observed in systems close to the superconducting phase.[ 65-67 ] This instability is supposed to be driven by collective many-electron jumps. The role of these jumps must be reflected in the dependence of the dissipated power with the effective temperature of the electrons and a proper study is still lacking. A first calculation of this quantity was done by Caravaca et al.[ 8, 68 ] These authors also verified that, to a good extent, the hot electron model applies to VRH. According to this model, the conductivity of the system is entirely determined by an effective temperature for the electrons and does not depend on the bath temperature T. The existence of this effective temperature and its role in relaxation was studied numerically in ref. 69.
The role of many-electron jumps in VRH in interacting systems has not been settled until now, specially since numerical simulations taking them into account are still very difficult to perform. As they are influential in the bistability problem, the study of this important question may shine light on their role.
The Zabrodskii's plot, Figure 4, is also adequate to discriminate a possible transition from Efros and Shklovskii behavior to Mott's law at higher temperatures due to a thermal smearing of the Coulomb gap. Since we do not see any bending upward in the bottom right corner of this figure, we conclude that we do not observe any crossover. To detect such a crossover, it would be necessary to consider larger values of the disorder to make room, at relatively high temperatures, for a region following Mott's law before reaching hopping distances of the order of the lattice constant. For practical reasons, it would be convenient to study numerically this effect in 2D systems, what nobody has done to our knowledge, before considering 3D systems.
6 Conclusions
The kinetic Monte Carlo simulations performed up to date have clarified many aspects of conduction in the VRH regime for 2D systems as we have reviewed, but there are still some questions needing clarification. For example, it would be interesting to get from simulations the crossover from Efros and Shklovskii's law to Mott's law as temperature is increased.
The situation for 3D systems is more complicated, not only due to the computational resources needed but also because the temperature dependence of the prefactor of conductivity cannot be neglected. In this sense, it is surprising that there are experiments extending over four orders of magnitude in conductivity, showing no temperature dependence in the prefactor. Possibly this is due to a cancellation between the contributions coming from the establishment of a percolation network and from the phonons (usually neglected in simulations).
Despite these difficulties, the advance of computer capabilities has allowed some recent results in 3D systems. The simulation of 3D systems has just started, we believe that in a near future, we can expect more work dealing with different topics: nonlinear conductivity, AC response, slow relaxation phenomena, etc. Also, the recent work of Agam and Aleiner[ 26 ] needs confirmation from numerical simulations. The effect of correlations that they propose should be important at low temperatures.
To conclude, in the following table, we summarize the values that we have considered as the most reliable up to date for the proportionality constants of the different characteristic temperatures (Table 2 ).
| Law | 3D | 2D |
|---|---|---|
| Mott | ||
| Efros and Shklovskii | ||
| Activated | – |
Regarding the prefactor in all VRH laws, there are predictions in the percolation limit, but, at least in 3D systems present simulations do not seem to reproduce it, since they do not reach low enough temperatures and large enough system sizes. This is an open problem both in simulations and in real experiments.
Acknowledgements
We acknowledge support of Fundación Séneca (Spain) grant 19907/GERM/15 and of AEI (Spain)/FEDER(EU) grant PID2019-104272RB-C52/AEI/10.13039/501100011033. F.S. also acknowledges a grant from AEI (Spain), BES-2016-078542.
Conflict of Interest
The authors declare no conflict of interest.
Biographies

Miguel Ortuño works on disordered interacting systems, especially in the insulating regime. After a first degree in Universidad Autónoma de Madrid and a Ph.D. at the Cavendish Laboratory, University of Cambridge, he did a postdoc at University of California Riverside with Mike Pollak, who introduced him into this problem and with whom he has collaborated since then. Now, he is also interested in the superconductor–insulator transition and in the role of integrals of motion in quantum systems.

Francisco Estellés-Duart is a Ph.D. student at Applied Physics Department in Universidad de Murcia since 2017. His research is focused on the simulation of conductivity in disordered electron systems. He has previously worked in the simulation of the motion of vortices in Josephson junction arrays and crystal growth. He did his graduate and master's degree in Universitat de Valencia. His main research interests are semiconductor physics, superconductor physics, and computational physics.

Andrés M. Somoza graduated at Universidad Autonoma de Madrid where he also completed the Ph.D. working on theory of liquid crystals. He did a postdoctoral stay at University of Toronto working on kinetics of phase transitions as the main topic. Disorderd systems has been his main line of research during the last 20 years. Other area of research is quantum phase transitions.




