Protein Science
Volume 33, Issue 3 e4932
TOOLS FOR PROTEIN SCIENCE
Free Access

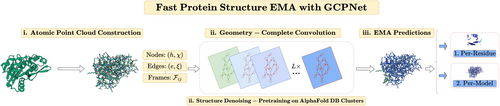
Protein structure accuracy estimation using geometry-complete perceptron networks

Alex Morehead, 

Corresponding Author

Alex Morehead

Department of Electrical Engineering and Computer Science, University of Missouri, Columbia, Missouri, USA

Correspondence

Alex Morehead, Jianlin Cheng, Department of Electrical Engineering and Computer Science, University of Missouri, Columbia, Missouri, 65211, USA.

Email: [email protected]; [email protected]

Search for more papers by this author
Jian Liu, 

Jian Liu

Department of Electrical Engineering and Computer Science, University of Missouri, Columbia, Missouri, USA

Search for more papers by this author
Jianlin Cheng, 

Corresponding Author

Jianlin Cheng

Department of Electrical Engineering and Computer Science, University of Missouri, Columbia, Missouri, USA

Correspondence

Alex Morehead, Jianlin Cheng, Department of Electrical Engineering and Computer Science, University of Missouri, Columbia, Missouri, 65211, USA.

Email: [email protected]; [email protected]

Search for more papers by this author
First published: 21 February 2024
https://doi.org/10.1002/pro.4932
Citations: 4

Review Editor: Nir Ben-Tal

Abstract

Estimating the accuracy of protein structural models is a critical task in protein bioinformatics. The need for robust methods in the estimation of protein model accuracy (EMA) is prevalent in the field of protein structure prediction, where computationally-predicted structures need to be screened rapidly for the reliability of the positions predicted for each of their amino acid residues and their overall quality. Current methods proposed for EMA are either coupled tightly to existing protein structure prediction methods or evaluate protein structures without sufficiently leveraging the rich, geometric information available in such structures to guide accuracy estimation. In this work, we propose a geometric message passing neural network referred to as the geometry-complete perceptron network for protein structure EMA (GCPNet-EMA), where we demonstrate through rigorous computational benchmarks that GCPNet-EMA's accuracy estimations are 47% faster and more than 10% (6%) more correlated with ground-truth measures of per-residue (per-target) structural accuracy compared to baseline state-of-the-art methods for tertiary (multimer) structure EMA including AlphaFold 2. The source code and data for GCPNet-EMA are available on GitHub, and a public web server implementation is freely available.

1 INTRODUCTION

Proteins are ubiquitous throughout the natural world, performing a plethora of crucial biological processes. Comprised of chains of amino acids, proteins carry out complex tasks throughout the bodies of living organisms, such as digestion, muscle growth, and hormone signaling. As a central notion in protein biology, the amino acid sequence of each protein uniquely determines its structure and, thereby, its function (Sadowski & Jones, 2009). However, the process of folding an amino acid sequence into a specific 3D protein structure has long been considered a fundamental challenge in protein biophysics (Dill & MacCallum, 2012).

Fortunately, in recent years, computational approaches to predicting the final state of protein folding (i.e., protein structure prediction) have advanced considerably (Jumper et al., 2021), to the degree that many have considered the problem of static protein tertiary structure prediction largely addressed (Al-Janabi, 2022). However, in relying on computational structure predictions for protein sequence inputs, a new problem in quality assessment arises (Kryshtafovych et al., 2019). In particular, how is one to estimate the accuracy of a predicted protein structure? Many computational approaches that aim to answer this question have previously been proposed (e.g., Siew et al., 2000; Wallner & Elofsson, 2003; Shehu & Olson, 2010; Uziela et al., 2016; Cao et al., 2016; Olechnovič & Venclovas, 2017; Cheng et al., 2019; Maghrabi & McGuffin, 2020; Yang et al., 2020; Alshammari & He, 2020; Hiranuma et al., 2021; Baldassarre et al., 2021; McGuffin et al., 2021; Lensink et al., 2021; Akdel et al., 2022; Edmunds et al., 2023; Maghrabi et al., 2023). Nonetheless, previous methods for estimation of protein structural model accuracy (EMA) do not sufficiently utilize the rich, geometric information provided by 3D protein structure inputs directly as a methodological component, which suggests that future methods for EMA that can learn expressive geometric representations of 3D protein structures may provide an enhanced means by which to quickly and effectively estimate the accuracy of a predicted protein tertiary structure.

In this work, we introduce a geometric neural network, the geometry-complete perceptron network (GCPNet) for estimating the accuracy of 3D protein structures (called GCPNet-EMA). As illustrated in Figure 1, GCPNet-EMA receives as its primary network input a 3D point cloud, a representation naturally applicable to 3D protein structures when modeling these structures as graphs with nodes (i.e., residues represented by Ca atoms) positioned in 3D Euclidean space (Morehead et al., 2023). GCPNet-EMA then featurizes such 3D graph inputs as a combination of scalar and vector-valued features such as the type of a residue and the unit vector pointing from residue i $$ i $$ to residue j $$ j $$ , respectively. Subsequently, following pretraining on Gaussian noised-cluster representatives from the AlphaFold Protein Structure Database (Jumper et al., 2021; Varadi et al., 2021), GCPNet-EMA applies several layers of geometry-complete graph convolution (i.e., GCPConv) using a collection of node-specific and edge-specific geometry-complete perceptron (GCP) modules to learn an expressive scalar and vector-geometric representation of each of its 3D graph inputs (Morehead & Cheng, 2023a). Lastly, using its learned finetuning representations, GCPNet-EMA predicts a scalar structural accuracy value indicating the method's predicted lDDT score (Mariani et al., 2013) for each node (i.e., residue). Estimates of a protein structure's global (i.e., per-model) accuracy can then be calculated as the average of its residues' individual lDDT scores, following previous conventions for EMA (Chen et al., 2023).

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
A high-level overview of GCPNet-EMA, our proposed method for protein structure EMA. Given an arbitrary 3D point cloud, GCPNet-EMA constructs a corresponding 3D graph representation of its input and learns latent scalar and vector features characterizing the input that can be used for downstream prediction tasks, following a structural denoising pretraining objective on AlphaFold Protein Structure Database cluster representatives corrupted with Gaussian noise. Accordingly, given a predicted 3D protein structure, GCPNet-EMA can provide both per-residue and per-model estimates of its structural accuracy. Zoom in for the best viewing experience.

2 RESULTS AND DISCUSSIONS

For the following experiments, we adopt the tertiary (multimer) test datasets of Chen et al. (2023) Liu et al. (2023b) as introduced in these corresponding works for general tertiary, CASP15 multimer, and general multimer EMA, respectively. Additional details regarding the construction and composition of these three datasets are given in Section 4.2. Following Chen et al. (2023), for tertiary structure EMA, we report the same set of computational metrics to reflect each method's performance for EMA, including the mean squared error (MSE), mean absolute error (MAE), and Pearson's correlation coefficient (Cor) at a per-residue and per-model (target) level. Similarly, for multimer structure EMA, we report the per-target Pearson's correlation (Cor) and Spearman's correlation (SpearCor) of each multimer structure EMA method. The definitions for each of these metrics are as follows:
MSE : 1 n ∑ i = 1 n y i − y ̂ i 2 , MAE : 1 n ∑ i = 1 n y i − y ̂ i , Cor : ∑ i = 1 n y ̂ i − y ̂ ¯ y i − y ¯ ∑ i = 1 n y ̂ i − y ̂ ¯ 2 ∑ i = 1 n y i − y ¯ 2 , SpearCor : 1 − 6 ∑ d i 2 n n 2 − 1 , $$ {\displaystyle \begin{array}{l}\mathrm{MSE}:\frac{1}{n}\sum \limits_{i=1}^n{\left({y}_i-{\hat{y}}_i\right)}^2,\kern1em \mathrm{MAE}:\frac{1}{n}\sum \limits_{i=1}^n\left|{y}_i-{\hat{y}}_i\right|,\\ {}\mathrm{Cor}:\frac{\sum_{i=1}^n\left({\hat{y}}_i-\overline{\hat{y}}\right)\left({y}_i-\overline{y}\right)}{\sqrt{\sum_{i=1}^n{\left({\hat{y}}_i-\overline{\hat{y}}\right)}^2}\sqrt{\sum_{i=1}^n{\left({y}_i-\overline{y}\right)}^2}},\\ {}\mathrm{SpearCor}:\kern0.5em 1-\frac{6\sum {d}_i^2}{n\left({n}^2-1\right)},\end{array}} $$
where n $$ n $$ is the number of samples across the test dataset; y i $$ {y}_i $$ is the ground-truth structural accuracy reported as a scalar value for the i $$ i $$ th protein structure; y ̂ i $$ {\hat{y}}_i $$ is a method's predicted structural accuracy as a scalar value for the i $$ i $$ th protein structure; v ¯ $$ \overline{v} $$ represents the mean of a variable v $$ v $$ across the test dataset; and d i = rank y i − y ̂ i $$ {d}_i=\operatorname{rank}\left({y}_i-{\hat{y}}_i\right) $$ denotes the difference between the ranks of y i $$ {y}_i $$ and y ̂ i $$ {\hat{y}}_i $$ (w.r.t. the sets of ground-truth and predicted structural accuracy values, respectively).

As shown in Table 1, for tertiary structure EMA, GCPNet-EMA without ESM embedding inputs (Lin et al., 2023) outperforms all baseline methods (Jumper et al., 2021; Olechnovič & Venclovas, 2017; Hiranuma et al., 2021; Chen et al., 2023) in terms of its MAE and Pearson's correlation in predicting per-residue lDDT scores. Similarly, GCPNet-EMA without ESM embeddings achieves competitive per-residue MSE and per-model MAE values in predicting lDDT scores compared to EnQA-MSA (Chen et al., 2023), the most recent state-of-the-art method for protein structure EMA. Analyzed jointly, GCPNet-EMA offers state-of-the-art lDDT predictions for each residue in a predicted protein structure and competitive per-model predictions overall, with more than 10% greater correlation to ground-truth lDDT scores for each residue compared to EnQA-MSA. Notably, in doing so, GCPNet-EMA also outperforms the lDDT score estimations produced by AlphaFold 2 (Jumper et al., 2021) in the form of its predicted lDDT (plDDT) scores. These results suggest that GCPNet-EMA should be broadly applicable for a variety of tasks in protein bioinformatics related to local and global tertiary structure EMA. In Figure 2, we show an example of a protein in the tertiary structure EMA test dataset for which AlphaFold overestimates the accuracy of its predicted structure but for which GCPNet-EMA's plDDT scores are quantitatively and qualitatively much closer to the ground-truth lDDT values, likely due to its large-scale structure-denoising-based pretraining on the afdb_rep_v4 dataset (Jamasb et al., 2024), a redundancy-reduced label-free subset of the AlphaFold Protein Structure Database (AFDB) (Jumper et al., 2021; Varadi et al., 2021).

TABLE 1. A comparison of GCPNet-EMA against baseline methods for protein tertiary structure EMA.
Method Per-residue Per-model
MSE ↓ $$ \downarrow $$ MAE ↓ $$ \downarrow $$ Cor ↑ $$ \uparrow $$ MSE ↓ $$ \downarrow $$ MAE ↓ $$ \downarrow $$ Cor ↑ $$ \uparrow $$
AF2-plDDT 0.0173 0.0888 0.6351 0.0105 0.0802 0.8376
DeepAccNet 0.0353 0.1359 0.3039 0.0249 0.1331 0.4966
VoroMQA 0.2031 0.4094 0.3566 0.1788 0.4071 0.3400
EnQA 0.0093 0.0723 0.6691 0.0031 0.0462 0.8984
EnQA-SE(3) 0.0102 0.0708 0.6224 0.0034 0.0434 0.8926
EnQA-MSA 0.0090 0.0653 0.6778 0.0027 0.0386 0.9001
GCPNet-EMA (pretraining, plDDT, and ESM) 0.0106 0.0724 0.7058 0.0031 0.0427 0.8687
GCPNet-EMA w/o pretraining 0.0107 0.0725 0.7048 0.0041 0.0482 0.8097
GCPNet-EMA w/ Null plDDT 0.6672 0.8022 0.2633 0.6305 0.7877 0.4131
GCPNet-EMA w/ null plDDT and w/o ESM 0.3342 0.5603 0.2139 0.3207 0.5548 0.2790
GCPNet-EMA w/o AF2 plDDT 0.0120 0.0759 0.6588 0.0051 0.0514 0.7633
GCPNet-EMA w/o pretraining or plDDT 0.0134 0.0803 0.6043 0.0066 0.0606 0.6744
GCPNet-EMA w/o ESM embeddings, 0.0092 0.0648 0.7482 0.0038 0.0420 0.8382
GCPNet-EMA w/o plDDT or ESM 0.0105 0.0707 0.7123 0.0042 0.0461 0.8076
  • Note: Results for methods performing best are listed in bold, and results for methods performing second-best are underlined. Pretraining indicates that a method was pretrained on the 2.3 million tertiary structural cluster representatives of the AFDB (i.e., the afdb_rep_v4 dataset (Jamasb et al., 2024)) via a 3D residue structural denoising objective, in which small Gaussian noise is added to residue positions and a method is tasked with predicting the added noise.
  • Abbreviations: Cor, Pearson's correlation coefficient; MAE, mean absolute error; MSE, mean squared error.
  • a A method that was selected for deployment via our publicly available protein model quality assessment server.
  • b A method that is specialized for estimating the quality of AlphaFold-predicted protein structures.
Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
An example of an AlphaFold-predicted test protein (PDB ID: 6W77, chain K) for which AlphaFold assigns overly-optimistic “very high” confidence values for its structural accuracy, whereas GCPNet correctly assigns “high” confidence values to the structure. Note in all the above subfigures that the coloring scheme for the per-residue plDDT values (i.e., structural confidence values) follows that used throughout the AlphaFold Protein Structure Database (Jumper et al., 2021; Varadi et al., 2021), where “very high” plDDT corresponds to blue; “high” plDDT corresponds to cyan; “low” plDDT corresponds to yellow; and “very low” plDDT corresponds to orange. As subcaptions for this figure, we also report the absolute error (AE) of each method's per-residue plDDT, averaged across all residues in the protein chain, to quantify each method's EMA performance. Zoom in for the best viewing experience.

Concerning CASP15 multimer structure EMA, Table 2 shows that GCPNet-EMA provides the most balanced performance compared to four single-model baseline methods (Jumper et al., 2021; Chen et al., 2023, 2023; Olechnovič & Venclovas, 2023) in terms of its per-target Pearson's and Spearman's correlation as well as its performance for ranking loss, for which it is better than AlphaFold 2 (i.e., AlphaFold-Multimer for multimeric benchmarking) plDDT yet marginally outperformed by VoroMQA-dark which is mostly uncorrelated with the quality of an individual decoy. Note that in contrast to tertiary structure EMA, for multimer structure EMA, we instead assess a method's ability to predict (a quantity correlated with) the TM-score of a given decoy corresponding to a protein target. Overall, these results demonstrate that, compared to state-of-the-art single-model multimer EMA methods, GCPNet-EMA offers robust, balanced multimer EMA performance in contemporary real-world EMA benchmarks such as CASP15.

TABLE 2. A comparison of GCPNet-EMA against baseline methods for CASP15 protein multimer structure EMA.
Method Cor SpearCor Loss
AF2-plDDT 0.3402 0.2641 0.1106
DProQA 0.0795 0.0545 0.1199
EnQA-MSA 0.2550 0.2378 0.1036
VoroIF-GNN-score 0.0639 0.0873 0.1342
Average-VoroIF-GNN-residue-pCAD-score −0.0156 −0.0326 0.1499
VoroMQA-dark −0.0872 −0.0119 0.0860
GCPNet-EMA 0.3056 0.2567 0.0970
GCPNet-EMA w/o ESM embeddings 0.2592 0.1969 0.1292
GCPNet-EMA w/o plDDT 0.0853 0.0450 0.1337
  • Note: Results for methods performing best are listed in bold, and results for methods performing second-best are underlined. Note that all versions of GCPNet-EMA benchmarked for multimer structure EMA were pretrained using the AFDB, using the same structural denoising objective investigated in Table 1.
  • Abbreviations: Cor, Pearson's correlation coefficient; Loss, ranking loss defined as the target-averaged difference between the TM-score of a method's top-ranked decoy structure and that of the ground-truth top-ranked decoy structure for all decoys corresponding to a given target; SpearCor, Spearman's rank correlation coefficient.

For general PDB multimer structure EMA, Table 3 shows that GCPNet-EMA outperforms 4 single-model baseline methods (Jumper et al., 2021; Chen et al., 2023, 2023; Olechnovič & Venclovas, 2023) in terms of its per-target Pearson's and Spearman's correlation as well as its state of the art performance for ranking loss, for which it is tied only with AlphaFold-Multimer plDDT. Notably, without plDDT as an input feature, GCPNet-EMA still surpasses the Pearson's and Spearman's correlation of DProQA, a recent state-of-the-art method for protein multimer structure EMA. Overall, GCPNet-EMA offers 6% greater Spearman's correlation to ground-truth TM-scores for each decoy of a given multimer target compared to AlphaFold-Multimer, the second-best-performing method. Observing that GCPNet-EMA is successfully able to generalize from being trained for tertiary structure EMA to being evaluated for multimer structure EMA, these results suggest that GCPNet-EMA should be useful for a variety of tasks related to accuracy estimation of multimeric structures.

TABLE 3. A comparison of GCPNet-EMA against baseline methods for PDB protein multimer structure EMA.
Method Cor SpearCor Loss
AF2-plDDT 0.3654 0.2799 0.0563
DProQA 0.1403 0.1563 0.0816
EnQA-MSA 0.3303 0.2395 0.0577
VoroIF-GNN-score 0.1017 0.1213 0.0715
Average-VoroIF-GNN-residue-pCAD-score 0.0483 0.0355 0.1198
VoroMQA-dark 0.0099 0.1036 0.0835
GCPNet-EMA 0.3756 0.2971 0.0563
GCPNet-EMA w/o ESM embeddings 0.2920 0.2387 0.0799
GCPNet-EMA w/o plDDT 0.2176 0.1973 0.1082
  • Note: Results for methods performing best are listed in bold, and results for methods performing second-best are underlined. Note that all versions of GCPNet-EMA benchmarked for multimer structure EMA were pretrained using the AFDB, using the same structural denoising objective investigated in Table 1.
  • Abbreviations: Cor, Pearson's correlation coefficient; Loss, ranking loss defined as the target-averaged difference between the TM-score of a method's top-ranked decoy structure and that of the ground-truth top-ranked decoy structure for all decoys corresponding to a given target; SpearCor, Spearman's rank correlation coefficient.

Lastly, in Table 4, we compare the runtime of GCPNet-EMA to the runtime of EnQA-MSA using the 56 decoys comprising the tertiary structure EMA test dataset referenced in Table 1. The results here show that GCPNet-EMA offers 47% faster EMA predictions for arbitrary protein structure inputs compared to EnQA-MSA, highlighting real-world utility in incorporating GCPNet-EMA into modern protein structure prediction pipelines.

TABLE 4. A comparison of the runtime of GCPNet-EMA against the runtime of EnQA-MSA, using all 56 tertiary structure EMA test decoys as each model's inputs.
Method Average prediction speed ↓ $$ \downarrow $$
EnQA-MSA 15.3 s
GCPNet-EMA 8.1 s
  • Note: Results for the fastest method are listed in bold.

3 CONCLUSIONS

In this work, we introduced GCPNet-EMA for fast protein structure EMA. Our experimental results demonstrate that GCPNet-EMA offers state-of-the-art (competitive) estimation performance for per-residue (per-model) tertiary structural accuracy measures such as plDDT, while offering fast prediction runtimes within a publicly-available web server interface. Moreover, GCPNet-EMA achieves state-of-the-art PDB multimer structure EMA performance across all metrics and performs competitively for CASP15 multimer EMA. Consequently, as an open-source software utility, GCPNet-EMA should be widely applicable within the field of protein bioinformatics for understanding the relationship between predicted protein structures and their native structure counterparts. In future work, we believe it would be worthwhile to explore applications of GCPNet-EMA's predictions of protein structure accuracy to better understand the presence (or absence) of disordered regions in protein structures, to better characterize the potential protein dynamics in effect.

4 MATERIALS AND METHODS

In this section, we will describe our proposed method, GCPNet-EMA, in greater detail to better understand how it can learn geometric representations of protein structure inputs for downstream tasks.

Towards this end, we introduce our geometric neural network architecture which we refer to as the geometry-complete SE(3)-equivariant perceptron network (GCPNet). We illustrate the GCPNet algorithm in Figure 1 and outline it in Algorithm 1. Subsequently, we expand on our definition for GCP and GCPConv in Sections 4.1 and 4.2.1, respectively. As shown by Morehead and Cheng (2023a), by construction GCPNets possess the following three properties, which as we will discuss will be useful for predicting protein structure accuracy measurements.
  1. Property: GCPNets are SE(3)-equivariant, in that they preserve 3D transformations acting upon their vector inputs.
  2. Property: GCPNets are geometry self-consistent, in that they preserve rotation invariance for their scalar features.
  3. Property: GCPNets are geometry-complete, in that they encode direction-robust local reference frames for each node.

ALGORITHM 1. GCPNet for estimation of protein structure model accuracy

1: Input: h i ∈ H χ i ∈ χ $$ \left({h}_i\in \mathbf{H},{\chi}_i\in \boldsymbol{\chi} \right) $$ , e ij ∈ E ξ ij ∈ ξ $$ \left({e}_{ij}\in \mathbf{E},{\xi}_{ij}\in \boldsymbol{\xi} \right) $$ ,

x i ∈ X $$ {x}_i\in \mathbf{X} $$ , graph G $$ \mathcal{G} $$

2: Initialize X 0 = X C ← Centralize X $$ {\mathbf{X}}^0={\mathbf{X}}^C\leftarrow \mathbf{Centralize}\left(\mathbf{X}\right) $$

3: ℱ ij = Localize x i ∈ X 0 x j ∈ X 0 $$ {\mathrm{\mathcal{F}}}_{ij}=\mathbf{Localize}\left({x}_i\in {\mathbf{X}}^0,{x}_j\in {\mathbf{X}}^0\right) $$

4: Project h i 0 χ i 0 $$ \left({h}_i^0,{\chi}_i^0\right) $$ , e ij 0 ξ ij 0 ← GCP e h i χ i e ij ξ ij ℱ ij $$ \left({e}_{ij}^0,{\xi}_{ij}^0\right)\leftarrow {\mathbf{GCP}}_e\left(\left({h}_i,{\chi}_i\right),\left({e}_{ij},{\xi}_{ij}\right),{\mathrm{\mathcal{F}}}_{ij}\right) $$

5: for l = 1 $$ l=1 $$ to L $$ L $$ do

6: h i l χ i l $$ \left({h}_i^l,{\chi}_i^l\right) $$ , = GCPConv l h i l − 1 χ i l − 1 e ij 0 ξ ij 0 ℱ ij $$ ={\mathbf{GCPConv}}^l\left(\left({h}_i^{l-1},{\chi}_i^{l-1}\right),\left({e}_{ij}^0,{\xi}_{ij}^0\right),{\mathrm{\mathcal{F}}}_{ij}\right) $$

7: end for

8: Project h i L $$ {h}_i^L $$ , ← GCP p h i l χ i l e ij 0 ξ ij 0 ℱ ij $$ \leftarrow {\mathbf{GCP}}_p\left(\left({h}_i^l,{\chi}_i^l\right),\left({e}_{ij}^0,{\xi}_{ij}^0\right),{\mathrm{\mathcal{F}}}_{ij}\right) $$

9: Output: h i L $$ {h}_i^L $$

4.1 The geometry-complete perceptron module

GCPNet, as illustrated in Figure 1 and shown in Algorithm 1, represents the features for nodes within its protein graph inputs as a tuple h χ $$ \left(h,\chi \right) $$ to learn scalar features h ∈ ℝ h $$ \left(h\in {\mathrm{\mathbb{R}}}^h\right) $$ jointly with vector-valued features χ ∈ ℝ m × 3 $$ \left(\chi \in {\mathrm{\mathbb{R}}}^{m\times 3}\right) $$ . Likewise, GCPNet represents the features for edges in its protein graph inputs as a tuple e ξ $$ \left(e,\xi \right) $$ to learn scalar features e ∈ ℝ e $$ \left(e\in {\mathrm{\mathbb{R}}}^e\right) $$ jointly with vector-valued features ξ ∈ ℝ x × 3 $$ \left(\xi \in {\mathrm{\mathbb{R}}}^{x\times 3}\right) $$ . Hereon, to be concise, we refer to both node and edge feature tuples as s , V $$ \left(s,V\right) $$ . Lastly, GCPNet denotes each node's position in 3D space as a dedicated, translation-equivariant vector feature x ∈ ℝ 1 × 3 $$ x\in {\mathrm{\mathbb{R}}}^{1\times 3} $$ .

Defining notation for the GCP module. Let λ $$ \lambda $$ represent an integer downscaling hyperparameter (e.g., 3), and let ℱ ij ∈ ℝ 3 × 3 $$ {\mathrm{\mathcal{F}}}_{ij}\in {\mathrm{\mathbb{R}}}^{3\times 3} $$ denote the SO(3)-equivariant (i.e., 3D rotation-equivariant) frames constructed using the Localize operation in Algorithm 1, as previously described by Morehead and Cheng (2023a). We then use the local frames ℱ ij $$ {\mathrm{\mathcal{F}}}_{ij} $$ to define the GCP encoding process for 3D graph inputs. Specifically, for an optional time index t $$ t $$ , we define these frame encodings as ℱ ij t = a ij t b ij t c ij t $$ {\mathrm{\mathcal{F}}}_{ij}^t=\left({a}_{ij}^t,{b}_{ij}^t,{c}_{ij}^t\right) $$ , with a ij t = x i t − x j t ∥ x i t − x j t ∥ , b ij t = x i t × x j t ∥ x i t × x j t ∥ , $$ {a}_{ij}^t=\frac{x_i^t-{x}_j^t}{\parallel {x}_i^t-{x}_j^t\parallel },\kern0.45em {b}_{ij}^t=\frac{x_i^t\times {x}_j^t}{\parallel {x}_i^t\times {x}_j^t\parallel }, $$ and c ij t = a ij t × b ij t $$ {c}_{ij}^t={a}_{ij}^t\times {b}_{ij}^t $$ , respectively. Notably, Morehead and Cheng (2023a, 2023b) show how these frame encodings allow networks that incorporate them to effectively detect and leverage for downstream tasks the potential effects of molecular chirality on protein structure.

Using V $$ V $$ to express vector and frame representations within each GCP module. After initially projecting vector-valued input features ( χ ∈ ℝ m × 3 $$ \chi \in {\mathrm{\mathbb{R}}}^{m\times 3} $$ and ξ ∈ ℝ x × 3 $$ \xi \in {\mathrm{\mathbb{R}}}^{x\times 3} $$ ) to each be of hidden dimensionality ℝ r × 3 $$ {\mathrm{\mathbb{R}}}^{r\times 3} $$ and have their coordinates axes permuted to ℝ 3 × r $$ {\mathrm{\mathbb{R}}}^{3\times r} $$ , the GCP module separately expresses vector representations V $$ V $$ for nodes (edges) and local frames, the former of which is to have its representations downscaled by a factor of λ $$ \lambda $$ , using the following two equations, respectively.
z = v w d z w d z ∈ ℝ r × r / λ , $$ z=\left\{v{\boldsymbol{w}}_{d_z}|{\boldsymbol{w}}_{d_z}\in {\mathrm{\mathbb{R}}}^{r\times \left(r/\lambda \right)}\right\}, $$ ()
V s = v w d s w d s ∈ ℝ r × 3 × 3 . $$ {V}_s=\left\{v{\boldsymbol{w}}_{d_s}|{\boldsymbol{w}}_{d_s}\in {\mathrm{\mathbb{R}}}^{r\times \left(3\times 3\right)}\right\}. $$ ()
Expressing s ′ $$ {s}^{\prime } $$ as scalar representations for each GCP module. To express scalar representations, the GCP module computes two invariant sources of information from V $$ V $$ and combines them with s $$ s $$ , as follows:
q ij = V s ⋅ ℱ ij ∈ ℝ 9 , $$ {q}_{ij}=\left({V}_s\cdot {\mathrm{\mathcal{F}}}_{ij}\right)\in {\mathrm{\mathbb{R}}}^9, $$ ()
q = 1 | N i ∣ ∑ j ∈ N i q ij if V s represents nodes q ij if V s represents edges , $$ q=\left\{\begin{array}{ll}\frac{1}{\mid \mathcal{N}(i)\mid }{\sum}_{j\in \mathcal{N}(i)}{q}_{ij}& \mathrm{if}\kern0.5em {V}_s\;\mathrm{represents}\kern0.5em \mathrm{nodes}\\ {}{q}_{ij}& \mathrm{if}\kern0.5em {V}_s\;\mathrm{represents}\kern0.5em \mathrm{edges}\end{array}\right., $$ ()
s s , q , z = s ∪ q ∪ ∥ z ∥ 2 , $$ {s}_{\left(s,q,z\right)}=s\cup q\cup \parallel z{\parallel}_2, $$ ()
where N ⋅ $$ \mathcal{N}\left(\cdot \right) $$ denotes the neighbors of a node; where ⋅ $$ \cdot $$ represents the inner product; and where ∥ ⋅ ∥ 2 $$ \parallel \cdot {\parallel}_2 $$ indicates the L 2 $$ {L}_2 $$ norm of a vector. Subsequently, let s s , q , z ∈ ℝ t + 9 + r / λ $$ {s}_{\left(s,q,z\right)}\in {\mathrm{\mathbb{R}}}^{t+9+\left(r/\lambda \right)} $$ with hidden dimensionality t + 9 + r / λ $$ \left(t+9+\left(r/\lambda \right)\right) $$ be projected to s ′ $$ {s}^{\prime } $$ with hidden dimensionality t ′ $$ {t}^{\prime } $$ , with t $$ t $$ denoting the hidden dimensionality of s $$ s $$ :
s v = s s , q , z w s + b s w s ∈ ℝ t + 9 + r / λ × t ′ , $$ {s}_v=\left\{{s}_{\left(s,q,z\right)}{\boldsymbol{w}}_s+{\boldsymbol{b}}_s|{\boldsymbol{w}}_s\in {\mathrm{\mathbb{R}}}^{\left(t+9+\left(r/\lambda \right)\right)\times {t}^{\prime }}\right\}, $$ ()
s ′ = σ s s v . $$ {s}^{\prime }={\sigma}_s\left({s}_v\right). $$ ()
Computing V ′ $$ {V}^{\prime } $$ as updated vector representations within each GCP module. The GCP module lastly updates vector representations using the following equations:
V u = z w u z w u z ∈ ℝ r / λ × r ′ , $$ {V}_u=\left\{z{\boldsymbol{w}}_{u_z}|{\boldsymbol{w}}_{u_z}\in {\mathrm{\mathbb{R}}}^{\left(r/\lambda \right)\times {r}^{\prime }}\right\}, $$ ()
V ′ = V u ⊙ σ g σ + s v w g + b g w g ∈ ℝ t ′ × r ′ , $$ {V}^{\prime }=\left\{{V}_u\odot {\sigma}_g\left({\sigma}^{+}\left({s}_v\right){\boldsymbol{w}}_g+{\boldsymbol{b}}_g\right)|{\boldsymbol{w}}_g\in {\mathrm{\mathbb{R}}}^{t^{\prime}\times {r}^{\prime }}\right\}, $$ ()
where ⊙ $$ \odot $$ represents element-wise multiplication and the gating operation σ g $$ {\sigma}_g $$ is applied row-wise to V ′ $$ {V}^{\prime } $$ to preserve SO(3) equivariance for vector features.

To summarize, the GCP module learns tuples s , V $$ \left(s,V\right) $$ of scalar and vector features a total of ω $$ \omega $$ times to derive rich scalar and vector-valued features. The module does so by blending both feature types iteratively with the local geometric information provided by the chirality-sensitive frame encodings ℱ ij $$ {\mathrm{\mathcal{F}}}_{ij} $$ .

4.2 Learning from 3D protein graphs with GCPNet

In this section, we will describe how the GCP module can be used to perform 3D graph convolution with protein graph inputs, as illustrated in Algorithm 1.

4.2.1 A geometry-complete graph convolution layer

GCPNet defines a single layer l $$ l $$ of geometry-complete graph convolution ( GCPConv $$ \mathbf{GCPConv} $$ ) as
n i l = ϕ l n i l − 1 , A ∀ j ∈ N i Ω ω l n i l − 1 n j l − 1 e ij ℱ ij , $$ {n}_i^l={\phi}^l\left({n}_i^{l-1},\kern0.45em {\mathcal{A}}_{\forall j\in \mathcal{N}(i)}{\Omega}_{\omega}^l\left({n}_i^{l-1},{n}_j^{l-1},{e}_{ij},{\mathrm{\mathcal{F}}}_{ij}\right)\right), $$ ()
where n i l = h i l χ i l $$ {n}_i^l=\left({h}_i^l,{\chi}_i^l\right) $$ ; e ij = e ij 0 ξ ij 0 $$ {e}_{ij}=\left({e}_{ij}^0,{\xi}_{ij}^0\right) $$ ; N $$ \mathcal{N} $$ (i) represents the neighbors of node n i $$ {n}_i $$ , selected using a distance-based metric such as k-nearest neighbors or a radial distance cutoff; l $$ l $$ signifies the hidden dimensionality of the network; A $$ \mathcal{A} $$ is a permutation-invariant aggregation function; and Ω ω $$ {\Omega}_{\omega } $$ represents a message-passing function corresponding to the ω $$ \omega $$ th GCP message-passing layer.
At the start of each graph convolution layer, messages between source nodes i $$ i $$ and neighboring nodes j $$ j $$ are comprised as
m ij 0 = GCP n i 0 ∪ n j 0 ∪ e ij ℱ ij , $$ {m}_{ij}^0=\mathbf{GCP}\left({n}_i^0\cup {n}_j^0\cup {e}_{ij},{\mathrm{\mathcal{F}}}_{ij}\right), $$ ()
where ∪ $$ \cup $$ represents concatenation. Up to the ω $$ \omega $$ th iteration, each message is updated by the m $$ m $$ -th message update layer residually as
Ω ω l = ResGCP ω l m ij l − 1 ℱ ij , $$ {\Omega}_{\omega}^l={\mathbf{ResGCP}}_{\omega}^l\left({m}_{ij}^{l-1},{\mathrm{\mathcal{F}}}_{ij}\right), $$ ()
ResGCP η l z i l − 1 , ℱ ij = z i l − 1 + GCP η l z i l − 1 , ℱ ij . $$ {\mathbf{ResGCP}}_{\eta}^l\left({z}_i^{l-1},,,\kern0.35em ,{\mathrm{\mathcal{F}}}_{ij}\right)={z}_i^{l-1}+{\mathbf{GCP}}_{\eta}^l\left({z}_i^{l-1},,,\kern0.45em ,{\mathrm{\mathcal{F}}}_{ij}\right). $$ ()
Updated node features n ̂ l $$ {\hat{n}}^l $$ are derived residually using an aggregation of generated messages as
n ̂ l = n l − 1 ∪ f g e ω , v i l Ω e ω , v i l Ω ξ ω , v i l v i ∈ V , $$ {\hat{n}}^l={n}^{l-1}\cup f\left(\left\{\left({g}_{e^{\omega },{v}_i}^l{\Omega}_{e^{\omega },{v}_i}^l,\kern1em {\Omega}_{\xi^{\omega },{v}_i}^l\right)|{v}_i\in \mathcal{V}\right\}\right), $$ ()
where f $$ f $$ represents a summation or a mean function that is invariant to node order permutations; Ω e ω , v i l $$ {\Omega}_{e^{\omega },{v}_i}^l $$ denotes scalar message features collected for node i $$ i $$ ; Ω ξ ω , v i l $$ {\Omega}_{\xi^{\omega },{v}_i}^l $$ represents vector message features associated with node i $$ i $$ ; and g e ω l $$ {g}_{e^{\omega}}^l $$ represents the binary-valued (i.e., [0, 1]) output of a scalar message attention (gating) function, expressed as g e ω l = σ inf ϕ inf l Ω e ω l $$ {g}_{e^{\omega}}^l={\sigma}_{inf}\left({\phi}_{inf}^l\left({\Omega}_{e^{\omega}}^l\right)\right) $$ with ϕ inf : ℝ e → 0 , 1 1 $$ {\phi}_{inf}:{\mathrm{\mathbb{R}}}^e\to {\left[0,1\right]}^1 $$ mapping from high-dimensional scalar edge feature space to a single dimension and σ $$ \sigma $$ denoting a sigmoid activation function.
Each graph convolution layer then employs a node-specific feed-forward network to update node representations. In particular, a linear GCP function with shared weights ϕ f $$ {\phi}_f $$ is applied to n ̂ l $$ {\hat{n}}^l $$ , followed by r $$ r $$ GCP modules. Such operations are concisely portrayed:
n ˜ r − 1 l = ϕ f l n ̂ l , $$ {\tilde{n}}_{r-1}^l={\phi}_f^l\left({\hat{n}}^l\right), $$ ()
n l = GCP r l n ˜ r − 1 l . $$ {n}^l={\mathbf{GCP}}_r^l\left({\tilde{n}}_{r-1}^l\right). $$ ()

4.2.2 Designing GCPNet for estimation of protein structure model accuracy

In this remaining section, we discuss GCPNet-EMA—the overall GCPNet-based protein structure EMA algorithm (Algorithm 1).

Line 2 of Algorithm 1 uses the Centralize operation to remove the center of mass from each node (atom) position in a protein graph input to ensure that such positions are 3D translation-invariant for the remainder of the algorithm's execution.

Subsequently, the Localize operation on Line 3 crafts translation-invariant and SO(3)-equivariant frame encodings ℱ ij t = a ij t b ij t c ij t $$ {\mathrm{\mathcal{F}}}_{ij}^t=\left({a}_{ij}^t,{b}_{ij}^t,{c}_{ij}^t\right) $$ . As described in more detail in Morehead and Cheng (2023a), these frame encodings are chirality-sensitive and direction-robust for edges, imbuing networks that incorporate them with the ability to more easily detect the influence of molecular chirality on protein structure.

Notably, Line 4 uses GCP e $$ {\mathbf{GCP}}_e $$ to initially embed our node and edge feature inputs into scalar and vector-valued values, respectively, using encodings of geometric frames. Thereafter, Lines 5–7 show how each layer of graph convolution is applied iteratively via GCPConv l $$ {\mathbf{GCPConv}}^l $$ , starting from these initial node and edge feature embeddings. Important to note is that information flow originating from the geometric frames ℱ ij $$ {\mathrm{\mathcal{F}}}_{ij} $$ is always maintained to simplify the network's synthesis of information derived from its geometric local frames in each layer.

Lines 8 through 9 finalize the GCPNet-EMA algorithm for EMA by performing feature projections via GCP p $$ {\mathbf{GCP}}_p $$ to conclude the forward pass of GCPNet by returning its final node-specific scalar outputs.

4.2.3 Network outputs

To summarize, GCPNet-EMA receives a 3D graph input G $$ \mathcal{G} $$ with node positions x $$ \boldsymbol{x} $$ , scalar node and edge features, h $$ h $$ and e $$ e $$ , as well as vector-valued node and edge features, χ $$ \chi $$ and ξ $$ \xi $$ , where all of such features used are listed in Table 5. GCPNet then predicts scalar node-level properties while maintaining SE(3) invariance to estimate the per-residue and per-model accuracy of a given protein structure, to avoid imposing an arbitrary 3D reference frame on the model's final prediction.

TABLE 5. Features used by the GCPNet-EMA models with a k-NN (k = 16) C α $$ \alpha $$ protein graph representation.
Type Symmetry Feature name
Node Invariant Residue type
Node Invariant Positional encoding
Node Invariant Virtual dihedral and bond angles over the C α $$ \alpha $$ trace
Node Invariant Residue backbone dihedral angles
Node Invariant (Optional) residue-wise ESM embeddings
Node Invariant (Optional) residue-wise AlphaFold 2 plDDT
Node Equivariant Residue-sequential forward and backward (orientation) vectors
Edge Invariant Euclidean distance between connected C α $$ \alpha $$ atoms
Edge Equivariant Directional vector between connected C α $$ \alpha $$ atoms

4.2.4 Training, evaluating, and optimizing the network

As referenced in Table 6, we trained each GCPNet-EMA model on the tertiary structure EMA cross-validation dataset as discussed in Section 2, using its 80%–20% training and validation data splits for training and validation, respectively. Subsequently, for finetuning the afdb_rep_v4-pretrained GCPNet model weights, we performed a grid search for the best hyperparameters to optimize a model's performance on the EMA validation dataset, searching for the network's best combination of learning rate and weight decay rate within the intervals of [ 1 e − 5 $$ 1{e}^{-5} $$ , 4 e − 5 $$ 4{e}^{-5} $$ , 3 e − 4 $$ 3{e}^{-4} $$ , 1 e − 3 $$ 1{e}^{-3} $$ ] and [ 1 e − 5 $$ 1{e}^{-5} $$ , 1 e − 4 $$ 1{e}^{-4} $$ , 1 e − 3 $$ 1{e}^{-3} $$ ], respectively. The epoch checkpoint that yielded a model's best lDDT L1 loss value on the tertiary structure EMA validation dataset was then tested on the tertiary and multimer structure EMA test datasets as described in Section 2 for fair comparisons with prior methods. Note that we used the same training and evaluation procedure as well as hyperparameters in our ablation experiments with GCPNet-EMA. Moreover, pretraining was performed using Gaussian-noised afdb_rep_v4 structures with noised residue atom coordinates x ˜ i $$ {\tilde{x}}_i $$ defined as x ˜ i = x i + σε i $$ {\tilde{x}}_i={x}_i+{\sigma \varepsilon}_i $$ , where σ = 0.1 $$ \sigma =0.1 $$ and ε i ∼ N 0 I 3 $$ {\varepsilon}_i\sim \mathcal{N}\left(0,{I}_3\right) $$ . Notably, as shown by Zaidi et al. (2023), this corresponds to approximating the Boltzmann distribution with a mixture of Gaussian distributions.

TABLE 6. Specifications of each GCPNet-EMA model, where the learning rate and weight decay rate (for finetuning only) were determined by a grid search targeting the EMA dataset's validation split.
Specification Value
Number of GCP layers 6
Number of GCPConv operations per GCP layer 4
Hidden dimensionality of each GCP/GCPConv layer's embeddings 128
Optimizer Adam
Learning rate 1 e − 5 $$ 1{\mathrm{e}}^{-5} $$
Weight decay rate 1 e − 5 $$ 1{\mathrm{e}}^{-5} $$
Batch size 16
Number of trainable parameters 4 M
Pretraining runtime on afdb_rep_v4 (using 4 80GB NVIDIA GPUs) 5 days
Finetuning runtime on the tertiary structure EMA dataset (using one 24GB NVIDIA GPU) 8 h

4.3 Datasets

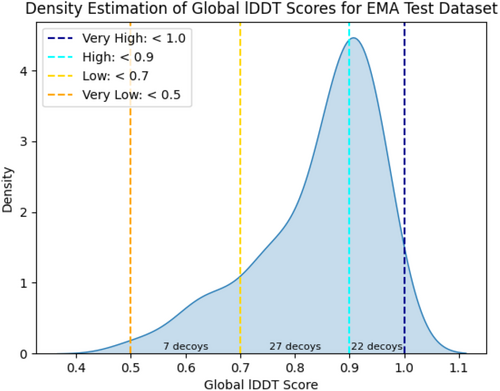
To evaluate the effectiveness of our proposed GCPNet-based EMA method (i.e., GCPNet-EMA) compared to baseline state-of-the-art methods for EMA, we adopted the experimental configuration of Chen et al. (2023). This configuration includes a standardized tertiary structure EMA cross-validation dataset for the training, validation, and testing of machine learning models, a dataset that we make publicly available at https://zenodo.org/record/8150859. As described by Chen et al. (2023), this cross-validation dataset is comprised of 4940 decoys (3906 targets) for training, 1236 decoys (1166 targets) for validation, and 56 decoys (49 targets) for testing, where such data splits are constructed such that no decoy (target) within the training or validation dataset belongs to the same SCOP family (Andreeva et al., 2014) as any decoy within the test dataset. Decoy structures were generated for each corresponding protein target using AlphaFold 2 for structure prediction (Jumper et al., 2021). We evaluate each method on the same 56 decoys (49 targets) contained in the test dataset to ensure a fair comparison between each method. Such test decoys, as illustrated in Figure 3, are predominantly ranked as “high” and “very high” quality decoys (i.e., lDDT values falling in the ranges of [0.7, 0.9] and [0.9, 1.0], respectively (Jumper et al., 2021; Varadi et al., 2021)), with the seven remaining decoys being of “low” structural accuracy as determined by having an lDDT value in the range of [0.5, 0.7]. We argue that evaluating methods in such a test setting is reasonable given that (1) the Continuous Automated Model EvaluatiOn (CAMEO) quality assessment category (Robin et al., 2021) employs a decoy quality distribution similar to that of the EMA test dataset; and (2) most protein structural decoys generated today are produced using high-accuracy methods such as AlphaFold 2.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
The distribution of global plDDT scores for each decoy in the tertiary structure EMA test dataset. This dataset, comprised of 56 decoys for 49 targets, consists of 22 very high quality decoys, 27 high quality decoys, and 7 low quality decoys, thereby closely resembling the data distributions used in similar benchmarks such as CAMEO.
Additionally, to rigorously evaluate the generalization capability and performance of GCPNet-EMA in the context of multimer structure EMA, we adopted a benchmark dataset of 100 hetero-multimer protein complexes from PDB entries released after AlphaFold-Multimer (i.e., between April 1, 2022 and December 9, 2022), which was previously compiled by (Liu et al., 2023b). Selected complexes, for each of which 350 decoy structures were generated by feeding 14 kinds of MSA paired $$ {\mathrm{MSA}}_{\mathrm{paired}} $$ in MULTICOM to AlphaFold-Multimer without any templates information, were meticulously filtered to ensure quality and non-redundancy via the following criteria.
  1. Sequence length: < 1,536 $$ <\mathrm{1,536} $$ residues.
  2. Resolution: < 4 $$ <4 $$ Å.
  3. Number of chains: < 8 $$ <8 $$ .
  4. Hetero-multimer definition: Sequence identity between chains < 0.9 $$ <0.9 $$ .
  5. Inter-chain contacts: At least 10 inter-chain residue-residue pairs with a minimum heavy atom distance of < 5 $$ <5 $$ Å.
  6. Sequence similarity to known structures: < 0.4 $$ <0.4 $$ sequence identity with monomer chains in the PDB prior to April 1, 2022 and no significant template hits (e.g., e-value >1) in the MULTICOM monomer template database (Liu et al., 2023a).
  7. Redundancy reduction: Clustering of subunits using MMseqs2 with a 0.3 sequence identity threshold and assigning the cluster ID of the hetero-multimer by the combination of the clusters of the subunits, followed by selection of the highest-resolution structure from each cluster ID of the hetero-multimers.

This general PDB multimer EMA dataset, characterized by its stringent filtering and focus on recently released hetero-multimers, provides a valuable benchmark for assessing the performance of multimer structure EMA methods, particularly in the context of challenging hetero-multimeric complexes. Furthermore, by way of its construction, it minimizes potential overlap between the tertiary structure EMA training and testing dataset, allowing for a meaningful assessment of each method's performance for multimer structure EMA. Note that the average TM-score of a decoy structure in this dataset is 0.7522, which as one might expect is slightly lower than that of the tertiary structure EMA dataset.

In conjunction with the PDB multimer EMA dataset, to compile a CASP15 multimer EMA test dataset we collected decoy structures generated by MULTICOM for the CASP15 assembly targets (Liu et al., 2023b). Note that 10 assembly targets (i.e., H1111, H1114, H1135, H1137, H1171, H1172, H1185, T1115o, T1176o, and T1192o) are not included due to various factors such as computational resource limitations and unavailable native structures or the presence of multiple conformations in native structures. As a result, this CASP15 MULTICOM multimer EMA dataset is comprised of an average of 254 decoy structures per target, all generated by AlphaFold-Multimer, across 31 assembly targets.

AUTHOR CONTRIBUTIONS

AM and JC conceived the project. AM designed the experiments. AM developed the source code. AM performed the primary experiments and data collection for tertiary structure quality assessment, and JL performed the experiments and data collection for multimer structure quality assessment. AM and JL analyzed the data. JC acquired the funding. AM, JL, and JC wrote the manuscript. AM, JL, and JC reviewed and edited the manuscript.

ACKNOWLEDGMENTS

This work was supported by one U.S. NSF grant (DBI2308699) and two U.S. NIH grants (R01GM093123 and R01GM146340).

    CONFLICT OF INTEREST STATEMENT

    The authors declare no conflicts of interest.

    DATA AVAILABILITY STATEMENT

    The source code, data, and instructions to train GCPNet-EMA, reproduce our results, or estimate the accuracy of predicted protein structures are freely available at https://github.com/BioinfoMachineLearning/GCPNet-EMA, and a public web server implementation is freely available at http://gcpnet-ema.missouri.edu.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.