Linking structural features of protein complexes and biological function
Abstract
Protein–protein interaction (PPI) establishes the central basis for complex cellular networks in a biological cell. Association of proteins with other proteins occurs at varying affinities, yet with a high degree of specificity. PPIs lead to diverse functionality such as catalysis, regulation, signaling, immunity, and inhibition, playing a crucial role in functional genomics. The molecular principle of such interactions is often elusive in nature. Therefore, a comprehensive analysis of known protein complexes from the Protein Data Bank (PDB) is essential for the characterization of structural interface features to determine structure–function relationship. Thus, we analyzed a nonredundant dataset of 278 heterodimer protein complexes, categorized into major functional classes, for distinguishing features. Interestingly, our analysis has identified five key features (interface area, interface polar residue abundance, hydrogen bonds, solvation free energy gain from interface formation, and binding energy) that are discriminatory among the functional classes using Kruskal-Wallis rank sum test. Significant correlations between these PPI interface features amongst functional categories are also documented. Salt bridges correlate with interface area in regulator-inhibitors (r = 0.75). These representative features have implications for the prediction of potential function of novel protein complexes. The results provide molecular insights for better understanding of PPIs and their relation to biological functions.
Introduction
Protein–protein interaction (PPI) is critical for molecular functions in living systems. PPIs are associated with catalysis, regulation, signaling, immunity, and inhibition, thereby playing a critical role in functional genomics.1 Extensive studies on the existing PPI complexes are the key to understanding cellular machinery as reviewed elsewhere.1-5 With modern experimental techniques such as two hybrid systems, protein fragment complementation, tandem affinity purification methods and protein arrays, several interacting protein pairs have been detected in large-scale studies,6 although their biological role may not be well characterized or known. Comprehensive homology modeling techniques of known interacting proteins combined with docking studies and PPI data helps in understanding structural assembly for functional preferences as shown for integrin αvβ6 heterodimer (two different protein subunits) complex.7 Thus, the analysis of PPIs is essential in predicting important biological functions.8, 9 It is well known that structure-based characterization of multimeric proteins is the key to ascribing biological functional annotation.10
The availability of protein–protein complexes at the Protein Data Bank (PDB)11 has enabled sequence and structural investigations on the existing complexes to decipher their recognition mechanisms and binding principles for decades.3, 12-15 The classical work by Chothia and Janin16 with three protein complexes defined ‘hydrophobicity’ (nonpolar interactions) as the major stabilizing factor in PPI, which has been affirmed with larger datasets of protein complexes.12, 14, 17-19 Conversely, shape complementarity, polar interactions, hydrogen bonding, and salt bridges are believed to primarily contribute to binding specificity and free energy of binding.20-23 Furthermore, a number of physicochemical factors known to govern protein–protein association include interface size, planarity, sphericity, complementarity, types of amino acid chemical groups, hydrophobicity, electrostatic interactions, H-bonds, distribution of binding energy, sequence conservation, and conserved residue clusters.12, 16, 21, 24-27 However, extensive surveys carried out thus far by various groups' typically average structural features over diverse datasets of protein–protein complexes, obscuring information on individual proteins' structural integrity. In an earlier study, we developed a homology model for integrin αvβ6 heterodimer7 where we found that the subunit interface in our model as well as the template X-ray structures clearly showed an increase of polar residues compared with the surface or the complex. Therefore, it is essential to revisit interface analysis to understand PPI binding principles, using a large nonredundant structural dataset.
The classification of protein–protein complexes based on their composition, affinity, interface stability, and lifetime association into different groups has gained momentum in the past decade,28-30 although the boundaries between these classes is often indefinite, based on physiological conditions.31 Alternatively, the classification of complexes into major functional groups can be valuable in relating structural data to biological functions for better understanding of PPIs.32 Moreover, the classification of protein–protein complexes based on functions and their usefulness in improving prediction accuracy has been observed recently.33 Therefore, for analyzing PPI primarily based on functions, a nonredundant set of complexes, with structural information, is essential.
Nonidentical protein subunits (or chains) noncovalently interact to form ‘heteromers’ with diverse functionality. Heterodimeric interactions are commonly found in enzyme-inhibitors, enzyme complexes, antibody–antigen, signal proteins and cell cycle proteins, and also include transient complexes. Dimeric interactions are amongst the strongest and most extensive in nature.12, 14 In this study, we have created a nonredundant dataset of 278 heteromeric protein structure dimers from the PDB, for characterization of their interface structural features to determine whether biochemical function is related to interface features. Several physico–chemical features such as interface size, interface area, hydrogen bonds (H-bonds), salt bridges, solvation free energy gain (ΔiG), binding energy (BE), and interface electrostatic energy (ΔΔGel) were investigated to study discriminatory features prevailing in different functional groups. Our analysis has identified key features [interface area, interface polarity abundance (P% − NP%), H-bonds, ΔiG, and BE] that are significantly different between the functional groups. This result has implications for function prediction for orphan proteins, where interacting partners are known and heteromeric complexes can be structurally modeled with high confidence.
Results and Discussion
Our nonredundant dataset (described in Materials and Methods: Heterodimer dataset) comprised 278 complexes (Table 1). Our previous dataset is 98.7% of the current dataset with only five new entries in the current dataset (underlined in Table 1). The dataset was then grouped into important functional groups and protein types to better understand PPIs among these divisions of complexes. The dataset comprises enzymes (40), regulators (144), enzyme-inhibitors (25), regulator-inhibitors (27) and immune (18) and biological assembly (24) complexes, of which 247 are globular and 31 membranous. The distribution of complexes under different functional classes is unbiased. Enzyme complexes are formed when two enzyme subunits interact to achieve a ‘catalytic’ function. For example, PDB ID: 1EUD succinyl coenzyme A (succinyl-CoA) synthetase is formed by the interaction between succinyl CoA synthetase α chain (311 AA) and succinyl-CoA synthetase β chain (396 AA). The succinyl-CoA synthetase (SCS) protein catalyses a reversible conversion of succinyl-CoA and succinate, coupled with phosphorylation/dephosphorylation. Enzyme complexes considered in this study do not include enzyme-inhibitor complexes. Enzyme-inhibitor complexes are formed when an enzyme and an inhibitor protein interact to achieve an ‘inhibitory’ function. For example, PDB ID: 1ARO is T7 RNA polymerase (883 AA) complexed to the transcriptional inhibitor T7 lysozyme (151 AA). The lysozyme binds at a site distant from the polymerase active site, suggesting an indirect mechanism of inhibition.
| Functional groups | Globular (247) | Membrane (31) | ||||||
|---|---|---|---|---|---|---|---|---|
| Enzymes (40) | 1EUD | 2APO | 2O2V | 3EP6 | 3O3O | 3REQ | 4HST | 3RGW |
| 1GK9 | 2BLF | 2QKL | 3FGR | 4EMJ | 3ZVQ | 4MRT | ||
| 1NME | 2CG5 | 3A8G | 3GA9 | 3L91 | 4BMP | 4NFU | ||
| 1VRA | 2GA9 | 3AON | 3JTQ | 3M7F | 4DBG | |||
| 1KA9 | 2XFG | 3AYH | 3DSS | 3ML1 | 4GED | |||
| 1SVD | 2ZIV | 3DRA | 3MWD | 3R07 | 4HNX | |||
| Regulators (144) | 1JEQ | 2G2S | 3B0C | 3LF4 | 4AT7 | 4G6T | 4IYP | 1FS0 |
| 1JKG | 2H9A | 3B0Z | 3MCB | 4AWX | 3VRD | 4JHP | 1H32 | |
| 1LSH | 2HRK | 3CPT | 3MKR | 4BJJ | 3W9C | 4KBM | 1NRJ | |
| 1N1J | 2IW5 | 3CX8 | 3MXN | 3O2P | 3ZNZ | 4KT1 | 1Z0J | |
| 1OF5 | 2VDB | 3DGP | 3NW0 | 3OG6 | 3ZYI | 1Z5Y | ||
| 1OO0 | 2P1M | 3DPL | 3GC3 | 3OJM | 4BL7 | 2GSK | ||
| 1ORY | 2QSF | 3EGV | 3HHM | 3SBT | 4C2A | 2PQN | ||
| 1US7 | 2QWO | 3CLS | 3KLD | 3THO | 4DVG | 2V6X | ||
| 1WQJ | 2V3B | 3D3B | 3KYJ | 3TU3 | 4GDX | 3AQF | ||
| 1YKH | 2VN6 | 3EI3 | 3MCA | 3VF0 | 4JE3 | 3BS5 | ||
| 2D74 | 2WD5 | 3F6Q | 3N1M | 4C9B | 4JEH | 4CXF | ||
| 1DJ7 | 2ZFD | 3FMO | 3NV0 | 4CBU | 4KHA | 4G1M | ||
| 1H2V | 2ZSI | 3FQD | 3OSS | 4CGY | 4KMO | 1ZHH | ||
| 1USU | 3ANW | 3GB8 | 3PGE | 4CT0 | 4L2I | 2FCW | ||
| 1WMH | 3AWU | 3F62 | 3Q87 | 4DEY | 4M69 | 2V8S | ||
| 1Z3E | 3AXJ | 3H7H | 3T5X | 4E4W | 4M6W | 3MP7 | ||
| 1ZBX | 3BEG | 3HZH | 3TBI | 4EGC | 4NQW | 3NY7 | ||
| 2CKL | 3A2F | 3IF8 | 3VZ9 | 4ETP | 4O8Y | 3OUN | ||
| 2DYO | 3ABE | 3K8P | 3ZET | 4EUK | 4FZV | 3V8X | ||
| 2FH5 | 3AU4 | 3KXC | 4A5U | 4EYY | 4GQ2 | 4G7X | ||
| Enzyme-inhibitors (25) | 1ARO | 1AY7 | 2OZN | 3QN1 | 3N4I | 4DRI | 4LV5 | |
| 1R0R | 1WPX | 3CKI | 2O3B | 3SHG | 4F9C | |||
| 1R8O | 1XG2 | 3DBO | 2VLQ | 4F6U | 4HT3 | |||
| 1UGH | 2B42 | 3IEY | 3R24 | 3FJU | 4I1S | |||
| Regulator-inhibitors (27) | 1A22 | 2FOM | 2QC1 | 3NVN | 3OQ3 | 4BI8 | 4GVB | 1E44 |
| 1M1E | 2HDI | 3N40 | 3ONA | 3QQ8 | 4GAF | 1T6B | ||
| 1JMA | 2F4M | 2RAW | 3AA7 | 3NYB | 4B8A | |||
| 1XOU | 2OMZ | 2VSM | 3BTP | 3OJA | 4G94 | |||
| Immune complexes (18) | 1Z92 | 2PTT | 3DLQ | 3PV6 | 4HFF | 4KT3 | 1T0P | |
| 2FHZ | 2Z64 | 3FPU | 3RNQ | 4J38 | 1V74 | |||
| 2P45 | 3DI3 | 3MJ7 | 3WA5 | 4K12 | ||||
| Biological assembly (24) | 1XEW | 2Z5B | 3K1R | 3LQC | 3W8I | 4H4K | 1GL4 | |
| 2FTX | 3CQC | 3KCP | 3VYR | 4AP2 | 4HPL | 1NPE | ||
| 2PA8 | 3FPN | 3KF6 | 3VU9 | 4F48 | 4IU2 | 3A4U | ||
| 3C5X | ||||||||
| 3LBX | ||||||||
| 3M1C | ||||||||
Regulatory complexes are formed between two protein subunits to achieve a ‘regulatory’ or ‘cellular’ function. For example, PDB ID: 1JEQ is a Ku heterodimer, formed by Ku70 (609 AA) and Ku80 (565 AA) subunits, contributing to genomic integrity by binding to DNA double-strand breaks and enabling repair by nonhomologous end-joining pathway. The regulatory complexes do not include regulator-inhibitor complexes, which are formed between a regulatory protein subunit and an inhibitor protein to achieve an ‘inhibitory’ function. For example, PDB ID: 1A22 is a complex between the G120R mutant (191 AA) of the human growth hormone and its cognate receptor, the human growth hormone receptor (238 AA). The G120R mutant of human growth hormone (hGH) is an antagonist binding to the growth hormone receptor. An example for each of these functional groups is shown in Figure 1.
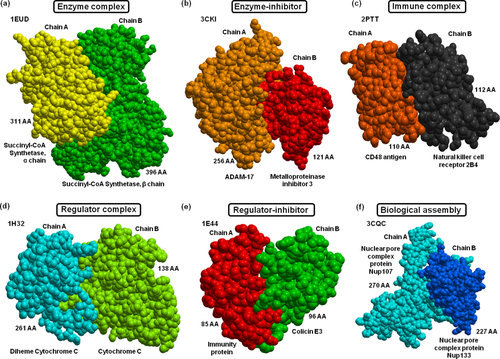
Examples of protein–protein complex structures from each functional group. (a) An enzyme complex (PDB: 1EUD) formed between succinyl-CoA synthetase α chain and succinyl-CoA synthetase β chain is shown in yellow and green colors, respectively. (b) TACE-N-TIMP-3 enzyme-inhibitor complex (PDB: 3CKI) with ADAM (a disintegrin and metalloproteinase) inhibition by TIMP-3 (tissue inhibitor of metalloproteinases 3) is shown in light brown and red, respectively. (c) An immune complex (PDB: 2PTT) between NK cell receptor 2B4 (CD244) bound to CD48 is shown in black and dark brown, respectively. (d) A regulatory SoxAX protein (involved in enzymatic oxidation of thiosulfate; PDB:1H32) of the diheme cytochrome C (in cyan colored) and cytochrome C (in light green) is shown. (e) A regulator–inhibitor (PDB:1E44) of the cytotoxic domain of colicin E3 in complex with its immunity protein is shown in green and red, respectively. (f) A biological assembly of the nuclear pore complex (NPC) between Nup107 and Nup133 (PDB: 3CQC) is shown in cyan and dark blue, respectively.
PPI features among functional groups
Of all the physicochemical features described in the Materials and Methods section, five were significant in discriminating between the functional categories. The results from these features, measured in terms of six parameters (Fig. 2), using a Kruskal-Wallis rank sum test (P-values in Table 2) are presented below, along with sets of correlated properties.
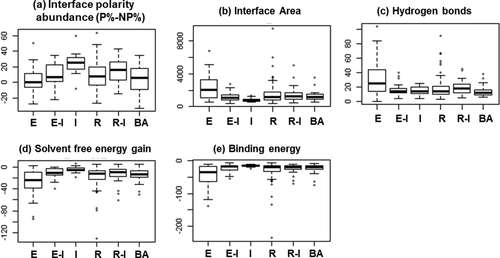
Discriminatory structural PPI features among functional groups. The interface polarity abundance (P% − NP%), interface area, hydrogen bonds, solvent free energy gain, and binding energies are significantly different among functional groups obtained using Kruskal-Wallis test (P-values shown in Table II). The functional classes include E, enzymes; E-I, enzyme-inhibitors; I, immune; R, regulators; R-I, regulator-inhibitors; BA, biological assembly.
| Functional groups | P-value | Q-value |
|---|---|---|
| Solvent free energy gain (ΔiG) | 7.08E−06 | 0.000128 |
| Interface area | 2.25E−05 | 0.000382 |
| Binding energy | 3.11E−05 | 0.000497 |
| Interface polarity abundance (P%−NP%) | 4.25E−05 | 0.000638 |
| Hydrogen bonds | 7.54E−04 | 0.009964 |
| Solvent free energy gain (ΔiG) P-value | 7.12E−04 | 0.009964 |
- Abbreviations: ΔiG, solvent free energy gain; ΔASA, interface area; ΔΔGel, interface electrostatic free energy calculation; BE, binding energy; H-bonds, hydrogen bonds; ICM, internal coordinate mechanics; NP, nonpolar residues; PDB, Protein Data Bank; P, polar residues; PPI, protein–protein interaction.
Interface area among complexes
The standard value reported by Lo Conte and colleagues for a protein interface is 1600 Å2 (±400).26 Bahadur and colleagues showed that the range of interface area (ΔASA) extends from 500 to 7000 Å2, with a mean of 1970 Å2,34 while Caffrey et al. showed that interface area ranges from 415 to 2361 Å2 for heterodimer complexes.35 Our analysis (described in Materials and Methods: Interface analysis) shows that the interface area per subunit (B/2) ranges from ∼350 to 9500 Å2 (±1100) and differs for each functional group as shown in Figure 2. The interface area is significantly different among functional groups with P = 2.25E−05 (Table 2).
Interface polarity abundance
The difference in percentages between interface polar residues and nonpolar residues (P% − NP%) gives the measure of the abundance of polar or nonpolar residues at the interface.32 The interface polarity abundance (P% − NP%) measure (described in Materials and Methods: Interface analysis) is significantly different among the different functional categories with P = 4.25E−05 (Table 2 and Fig. 2).
Hydrogen bonds among complexes
The stability of protein–protein binding depends on the number of hydrogen bonds (H-bonds) and salt bridges formed between the two interacting subunits. On an average, 10.1 H-bonds are formed at a protein–protein interface, with one H-bond per 170 Å2 interface area with an r value of 0.84 observed between H-bonds and interface area.26 The r value between H-bonds and interface area calculated using different dataset size and nature of data varies from 0.75 to 0.89,12, 14, 21, 26, 36, 37 with an average of 0.24 H-bonds per interface residue in heterodimers. High H-bond density per interface residue (0.64) with dominant charged and hydrophilic/polar residues at the heterodimer protein interfaces is also demonstrated.37 Our statistical analysis (described in Materials and Methods: Intermolecular hydrogen bonds calculation) shows that the total number of intermolecular H-bonds for each functional group is significantly different with P = 7.54E−04 (Table 2 and Fig. 2).
Solvent free energy gain upon interface formation
The solvation free energy gain upon interface formation (ΔiG)) [calculated as described in Materials and Methods: calculation of solvation free energy gain upon interface formation (ΔiG)] is significantly different among functional groups with P = 7.08E−06 04 (Table 2) as shown in Figure 2.
Binding energy at the interface
To study the strengths of binding among functional groups, we estimated the binding free energy (BE; also called binding affinity calculated as described in Materials and Methods: Binding energy calculation) of the dataset. The BEs are significantly different among functional groups with P = 3.11E−05 (Table 2) as shown in Figure 2.
Correlations amongst interface physiochemical features
Interface polarity abundance (P% − NP%) shows limited correlation with charged residues at the interface (r = 0.61) for the heterodimer dataset. However, this is not unexpected as charged residues are included in the polar residue set. Also, the protein complexes in our dataset show high correlation between intermolecular H-bonds and interface area (r = 0.90) as previously observed.12, 14, 21, 26, 36, 37 Moreover, H-bonds are correlated to BE (r = −0.70). Salt bridges (described in Materials and Methods: Intermolecular salt bridges calculation) across the interface do not show any significant correlation to all other features, which is in accord with another study.21 Although this parameter was not statistically significant between the different functional groups, it is correlated to interface area in regulator-inhibitor complexes (r = 0.75; see Supporting Information Fig. S1). This shows that intermolecular salt bridges are an important structural feature in some functional complexes.
The solvation free energy gain upon interface formation (ΔiG) shows high correlation with interface area in the heterodimer dataset (r = −0.88), suggesting ΔiG is an important feature in characterizing PPIs. Interestingly, biological assembly and immune complexes showed the least correlation of ΔiG with interface area (r = −0.67) as compared with other functional groups as shown in Supporting Information Figure S2. The ΔiG and BE are also highly correlated among the dataset (r = 0.88). Our analysis shows a high correlation between BE and interface area in the dataset (r = 0.96) as previously observed.38
The electrostatic component of binding free energy (ΔΔGel) was studied to quantify the electrostatic free energy favoring protein–protein interaction among functional groups of complexes (described in Materials and Methods: Interface electrostatic free energy calculation (ΔΔGel)). Interface electrostatic energy component of BE (Supporting Information Fig. S3) shows distribution of charges in the dataset with electrostatic energy contributing to destabilizing PPIs in a few complexes while stabilizing PPIs in the others, suggesting that quantification of accurate interface electrostatic component contributing to BE is often a nontrivial task. The frequency distribution also shows similar trends for interface electrostatic energy (Supporting Information Fig. S4). Although ΔΔGel values show limited correlation with interface area (r = −0.47), the enzymes complexes show correlation between ΔΔGel and interface area (r = −0.61), as opposed to other groups (r < 0.5).
These discriminatory PPI features hold significantly different among functional groups in globular proteins with P < 0.05 as shown in supplementary Supporting Information Table S1. Since there is insufficient information regarding all the functional groups in membrane proteins, the discriminatory features among functional groups in membrane proteins is not clear at this point. These observations corroborate the need for classification of complexes in determining their combinatorial features and drawing consensus for common patterns in protein–protein recognition. Incorporation of these combinatorial features among protein functional groups is necessary to develop models for residue-level protein–protein binding prediction and analysis, and also in utilizing PPI information for the prediction of potential protein functions in future studies.
Materials and Methods
Heterodimer dataset
We created a nonredundant protein heterodimer (comprising two different protein subunits) dataset, the 3D structures of which were determined by X-ray crystallography, from the PDB, using the RCSB's advanced search interface. The search criteria were: (i) resolution <= 3Å and (ii) protein size > 50 residues, as described in earlier studies (iii) limited to “experimental data” to obtain high resolution true structures and avoid short peptides, synthetic, or artificial complexes and (iv) the number of chains, entities, and oligomeric state is set at two to obtain dimers with two unique or different chains, (v) exclude DNA or RNA or a hybrid of such molecules with proteins or otherwise and (vi) sequence identity cut-off is set to 30% and (vii) the select parameter was set so that entries with mutations were not included in the dataset. The redundancy among heterodimer complexes was further removed using the USEARCH program39 at sequence identity cut-off of 20%, as this threshold eliminates remote homology of 25%40 seen in structures as well. The criteria set out are comparable with those of Janin and coworkers,41 who have used a resolution cutoff for X-ray structures (3.25Å) and chain length (minimum of 30 residues) for defining a benchmark dataset for complexes with experimental binding energies, toward developing a method for binding energy prediction.
Grouping based on function and protein type
The assembly of proteins into functional complexes is essential in biology. Therefore, the characterization of these functional complexes is an essential step in deciphering their binding principles. Hence, we have grouped the dataset into major functional groups such as enzymes (E), enzyme-inhibitors (EI), regulators (R), regulator-inhibitors (RI), immune (I), and biological assembly (BA) complexes, as described in the PDB header. In a few cases, where the complexes had more than one function, the functional group assigned is based on their primary role obtained from literature. The dataset comprised globular (247) and membranous (31) complexes.
Structural Analysis
Interface analysis
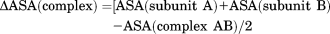 (1)
(1)The identified interface residues were further filtered based on the criteria that their ΔASA > 0.1Å2.44 The amount of polar, nonpolar, and charged residues at the interface was then estimated for the dataset. Polar residues considered in the analysis are R, N, D, E, Q, H, K, S, T, and Y.45 We have computed the relative abundance of polar or nonpolar residues [“interface polarity abundance (P% − NP%)”] compared with nonpolar residues at the interface as the difference between the percentage of interface polar residues and the percentage of interface nonpolar residues.
Intermolecular hydrogen bonds calculation
The hydrogen atoms covalently bound between two electronegative atoms and contributing to electrostatics was calculated using HBPLUS program.46 The output file of HBPLUS contains information on all donor and acceptor atoms, angles and distances within the distance of 4 Å and then filtered for intermolecular hydrogen bonds, where the hydrogen bond donor and acceptor atoms are from two different subunits.
Intermolecular salt bridges calculation
The salt bridges formed between two oppositely charged side-chain atoms, (i.e., basic and acidic amino acids) within a distance of 4 Å and contributing to the stability and electrostatics of the protein complex was calculated using the SBION program,47 and intermolecular salt bridges were then extracted such that the oppositely charged atoms are from two different subunits.
Calculation of solvation free energy gain upon interface formation (ΔiG)
The ΔiG of protein complex arises from the change in solvation energy as well as contact-dependent and electrostatic interactions of the subunits, quantifying the solvation free energy gained upon interface formation. The difference in total solvation energies between the isolated and complexed structure gives the solvation free energy gain at the interface (in kcal/mol), The PDBePISA webserver48 was used to calculate ΔiG for the heterodimer dataset.
Binding energy calculation (BE)
The interaction between two protein subunits can be characterized in terms of binding free energy. The BE term (comprising electrostatic, van der Waals, hydrophobic, and entropic terms) gives an indication of strong and weak intermolecular forces, with the most negative value considered the strongest. The binding free energy of 278 protein complexes was calculated using the DCOMPLEX program,49 which uses DFIRE-based potentials.50 DCOMPLEX is the most widely used program for calculating binding energies of protein complexes as it has been benchmarked to reproduce experimental binding free energy values.
Interface electrostatic free energy (ΔΔGel) calculation
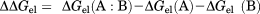 (2)
(2)Statistical analysis
The Kruskal-Wallis rank sum test, a nonparametric method,54 is used to test whether the mean ranks for the PPI features in all functional groups are the same. The discriminatory PPI features among functional groups were thus tested for statistical significance with P < 0.05 (for the Kruskal-Wallis rank sum test) in RStudio.55 Spearman's rank correlation coefficient has been used to measure of statistical dependence between the interface features, since it assesses how well the relationship between two properties can be described using a monotonic function.56
Acknowledgments
G.S. is the recipient of an iMQRES PhD scholarship from Macquarie University. The authors are grateful to Prof Pandjassarame Kangueane and Prof. Michael Gromiha for valuable discussions.