Pisum sativum has no competitive responses to neighbors: A case study in (non)reproducible plant biology
Abstract
Plant–plant competition is ubiquitous in nature. However, studying below ground behavior of roots has always posed certain difficulties. Pea (Pisum sativum L.) has become a common study species for questions about how plant roots respond to neighboring plant roots and barriers in soil. However, published results point in several different directions. This has sometimes been interpreted as pea having sophisticated context dependent responses that can change in complex ways depending on its surroundings, but it could also just point to small statistical power resulting in type I or II statistical errors. To explore this further, here, we combine the result of five new experiments with published results to examine 18 unique experiments from 10 different studies and 6 cultivars of pea for a total of 254 replicate plants. We used a Bayesian hierarchical meta-analysis approach to estimating the likely effect size from the available data, as well as quantify heterogeneity among different experiments, studies and cultivars. The posterior distributions show that, at the coarsest possible scale of total root production, it is unlikely that P. sativum root growth is influenced by either neighbors or pot volume that varies primarily by depth. We find no evidence of publication bias and conclude that this is simply due to statistical sampling error and the scientific method combined with frequentist statistics operating as intended. We suggest that further work on pea should consider repeating experiments that reported finer scale root plasticity at the rhizosphere scale or consider exploring different pot geometries such as volume that varies by depth or width. We also suggest that more diversity in study species are needed to better understand the neighbor-volume response.
1 INTRODUCTION
Plant–plant competition is ubiquitous in nature and influences individual plants, populations, communities, and ecosystems (Kraft et al., 2015; Tilman, 1982; Wilson, 1988). In addition, roots must navigate through a complex soil matrix that includes neighbors, enemies, mutualists, and barriers (De Deyn & Van der Putten, 2005; Falik et al., 2005). The mechanistic details of root plasticity below ground have always been more difficult to study than above ground for reasons that are somewhat obvious (Casper et al., 2003; Casper & Jackson, 1997; Schenk, 2006). These reasons include the difficulty in getting to roots through opaque soil, the fact that most roots of most species are visually identical (Mommer et al., 2011; Taggart et al., 2011), and debate about different experimental approaches and controls (Cahill, 2002; Chen et al., 2015, 2020, 2021; Gersani et al., 2001; Hess & de Kroon, 2007; Laird & Aarssen, 2005; McNickle, 2020; Semchenko et al., 2010).
The common pea (Pisum sativum L.) has emerged as one of the most-used plants for studying root plasticity in response to varied cues in the environment by ecologists. As far as we can tell, this was not a conscious choice by the research community but rather an organic process as different groups sought to build upon previous results in the literature. Pea is an attractive study species because it has a short life history of only 50–70 days depending on cultivar, reproduces by selfing, and it is relatively small in stature. Gregor Mendel used pea as his iconic first model for genetics for precisely this reason (Mendel & Bateson, 1901). Indeed, pea has been used to study many questions about root plasticity. For example, pea has a variety of mutants that allow researchers to toggle on and off both nitrogen fixing associations and arbuscular mycorrhizal fungus association and examine the consequences of different below ground mutualisms (Guinel & Geil, 2002; McNickle et al., 2020). Additionally, it has been shown in one study that pea roots can respond to barriers in soil, turning before contact by using exudates almost like a sonar (Falik et al., 2005). Pea roots have also been shown to be capable of discriminating self from nonself and exhibiting differences in root architecture when presented with self-roots or nonself-roots (Falik et al., 2003). In a similar study, pea was shown to preferentially proliferate into neighbor free soil volumes compared with regions of soil with more neighboring plants (Gersani et al., 1998). Another study that varied nutrient dynamics in time and space concluded that pea was capable of anticipating improving conditions in the future by pre-emptively proliferating roots before the improved conditions arrived (Shemesh et al., 2010). At the scale of total root growth, pea has also been shown to sometimes increase total root production in the presence of both a neighbor and larger pot volume compared with alone in a smaller pot (O'Brien et al., 2005) and sometimes decrease root production in the same varying neighbor-volume context (Chen et al., 2015) or exhibit no response at all (Jacob et al., 2017; McNickle et al., 2020; Meier et al., 2013). Combined, these myriad results give the impression that pea has sophisticated context dependent root growth plasticity that allows complex responses to different cues.
Precisely because of these wide-ranging and interesting results in the literature, we sought to further explore hypotheses about root growth plasticity and proliferation using pea as a study system. We performed five different experiments between 2013 and 2018 where we varied different aspects of the experiment that we thought would allow us to more closely repeat some of these previous findings noted above. These used the same basic experimental design as was most common in the literature where total nutrients per plant, total volume per plant, water per plant, and nutrient concentration were controlled across plants grown alone or with neighbors (Chen et al., 2015; Jacob et al., 2017; McNickle et al., 2020; Meier et al., 2013; O'Brien et al., 2005). However, our experiments were not exact replications. Rather, working from the hypothesis of context dependent responses, we continually fine-tuned experimental conditions in ways that we hypothesized were more similar to the conditions reported by previous authors because our prior expectation was that the published results were correct, and that we were somehow in error. We could never reproduce any previously published results.
Here, we do not focus on our five null result experiments (though the full details are given in the supporting information). Instead, we combine our five experiments with five published studies from the literature that used the same basic experimental approach and used a hierarchical Bayesian meta-analysis approach to synthesize the results. We ask what is the average response to simultaneously changing pot volume and the presence of neighboring plant roots across these many experiments. We also use these data to ask whether there is evidence of publication bias in the literature.
2 METHODS
2.1 Studies included in the meta-analysis
We sought experiments in the published literature that grew pea plants with neighbors in pots of volume and compared it to plants grown alone in pots of volume . This design controls total nutrients per plant, volume available per plant, water availability per plant, and soil nutrient concentration across the neighbor addition experiments but has been criticized because it simultaneously manipulates pot volume and neighbors. Thus, while this controls the entire resource environment, one cannot conclude whether the barriers imposed by restricting pot volume or neighbors were the cause of any significant results (Chen et al., 2015; Hess & de Kroon, 2007). We do not dispute this, but in the special case of no treatment effect of any kind, one can actually rule out both causes simultaneously. We identified five different studies in the literature that used this neighbor-volume experimental manipulation in pea (Chen et al., 2015; Jacob et al., 2017; McNickle et al., 2020; Meier et al., 2013; O'Brien et al., 2005). From these five studies we extracted the mean root and pod production within each treatment and their standard deviations to use as Bayesian priors. We also recorded the cultivar used and the pot volume used to define in the neighbor-volume manipulation. In addition to the neighbor-volume manipulation, some studies imposed additional factorial treatments. These additional treatments were not replicated among studies, and so we treated these as additional treatments as separate experiments performed within study and included them as a second level of random effects in a hierarchical random effect model. These means are recorded separately resulting in multiple data points for the following studies: (i) O'Brien et al. (2005) crossed the neighbor addition treatment with low and high nutrient addition, (ii) Chen et al. (2015) included three levels of soil nutrient concentration (see McNickle, 2020), and (iii) McNickle et al. (2020) grew plants with and without mycorrhizae. Two studies only collected root data and did not have pod data (Jacob et al., 2017; Meier et al., 2013), and one of these surprisingly did not report any estimates of variation (Jacob et al., 2017).
In addition, we performed five new supplementary experiments using the same basic neighbor-volume treatment as the rest of the studies. Since these are similar to the five published results, and since readers should treat our new data and previously published data equally, we detail the experiments in the supporting information. Briefly, one of our experiments implemented the basic neighbor-volume treatment where was 1 L. This experiment had resin bags in the soil, but they had no effect on pea growth (Tables S1 and S2 and Figures S1 and S2). When this did not allow us to repeat previous findings, we hypothesized that a larger rooting volume might be necessary to allow root responses. In addition, based on different approaches to allowing or preventing shoot interactions above ground by different groups (Chen et al., 2015; McNickle et al., 2020; O'Brien et al., 2005), we also hypothesized that shoot interactions might influence root interactions. Thus, the next four of our new experiments crossed the neighbor-volume treatment with the presence or absence of above ground shoot competition and increased the value of that defined pot volumes to 6.2 L. These 6.2 L pots were tall and narrow pots; thus, volume was added primarily by increasing depth, not by increasing horizontal rooting width. As above, we treated the presence or absence of shoot competition as separate studies nested within experiment as a hierarchical random effect and so there are actually eight data points from these four experiments. In these four experiments, we also explored different potting media in each case (Tables S1–S4 and Figures S1, S4, and S5).
2.2 Meta-analysis test statistic
We also generated funnel plots as a way of visualizing potential publication bias. A funnel plot is simply a plot of the observed hedges in versus the observed variance for each experiment overlaid on a funnel shape that demarcates the normal bounds of error expected from statistical sampling theory.
2.3 Hierarchical Bayesian linear mixed effects model
A hierarchical Bayesian linear mixed effects approach was implemented with brms (Bürkner, 2017, 2018) in the R statistical environment (v 4.1.1 R-Core-Team, 2021). To control for heterogeneity among studies, individual experiment was nested within study as a random effect. This allowed us to account for differences among both individual experiments (i.e., total nutrients (O'Brien et al., 2005), nutrient concentration (Chen et al., 2015; McNickle, 2020), with and without mycorrhizae (McNickle et al., 2020), with and without shoot competition (supporting Information), and individual research groups (e.g., soil media, fertilizer type, watering schedules, and timing). Since studies also did not always use the same cultivar and since cultivars represent a separate form of biologically interesting heterogeneity among studies in the form of genetic differences, we also included pea cultivar as another random effect. Finally, we included the pot volume used by each study as a continuous fixed effect to explicitly identify the effect of the value of in the neighbor-volume response. We present both the posterior mean for each study independent of value of and the linear relationship among studies accounting for the value of as a covariate. The posteriors were generated using four Markov chain Monte Carlo (MCMC) chains, 2,500 burn-ins, 5,000 iterations per chain, resulting in 10,000 estimates for each posterior distribution. No thinning was used as thinning has been shown to have no detectable effects on MCMC simulation other than increased computing time (Link & Eaton, 2012). To remain as unbiased as possible, our priors assumed that any value of or standard deviation was equally likely.
3 RESULTS
3.1 Root responses
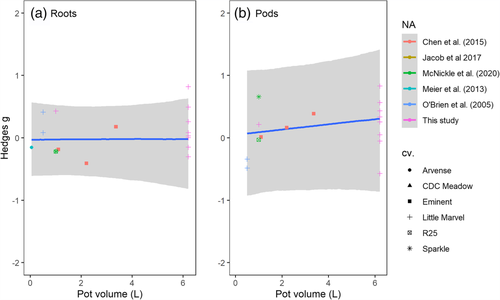
The meta-analysis included 18 unique experiments from 10 different studies for a total of 254 replicate alone-half and with neighbor-full pairs of plants. Additionally, six different cultivars of pea were used across the literature. The value of used by studies ranged from 50 ml (Meier et al., 2013) to 6.2 L (Figure S1), though these differed by depth more than by width to achieve increased volume.
The slope of the pot volume on effect size for roots was .00 (95%CI: −.12, .11) with an intercept of −.03 (95% CI: −.61, .58; Figure 1a). Unlike a frequentist approach that assigns a p-value to either accept or reject one hypothesis, the Bayesian framework allowed us use the posterior distributions to assign probabilities that any given outcome might be observed in a future study with peas. Here, the logical hypothesis to examine was the probability that the effect size was greater than zero (increased roots in the neighbor-full treatment) or less than zero (decreased roots in the neighbor-full treatment). Using the posterior distribution, there was a probability of .44 that the effect size for peas would be greater than zero and thus a probability of .56 that the effect size was less than zero. We interpret this as a null result.
With any meta-analysis, there are obviously differences among studies and here quantifying that heterogeneity was major motivation for our analysis. At its core, Bayesian statistics examine how many different ways the observed data could have been sampled and then combine these resampled outcomes into a posterior distribution. Thus, the hierarchical Bayesian mixed effects analysis is based on the assumption that each level of the random effect (experiment within study, study, and cultivar) has its own effect size which emerged from resampling and are averaged to get the global result. Accordingly, the Bayesian approach models each of these as a standard deviation around the random intercept. Furthermore, since each random effect was modeled with its own prior distribution, we can estimate this heterogeneity directly as standard deviations that also have 95% CIs (Table 1). The priors and posterior differences among studies are shown in Figure 2, and in general, all studies point towards a null response in the posterior distribution. Cultivar differences introduced an estimated standard deviation of .28 (95% CI: .01, .97) around the intercept; differences among studies produced an estimated standard deviation of .28 (95% CI: .01, 1.00) and differences among experiments but within a study had a standard deviation of .35 (95% CI: .2, .6). These should be interpreted as standard deviations around the random intercept of the model. So, since the intercept was -0.03, and the error was an order of magnitude higher, this highlights that a wide range of results might be possible with a small sample size.
| Tissue | Factor | Statistic | Estimate | Error | 95% CI |
|---|---|---|---|---|---|
| Roots | Mean effect size | Intercept | −.03 | .28 | (−.61, .58) |
| Pot volume | Slope | 0.00 | .06 | (−0.12, 0.11) | |
| Cultivar | StDev | .28 | .26 | (.01, .97) | |
| Study | StDev | .28 | .26 | (.01, 1.00) | |
| Study/experiment | StDev | .35 | 0.11 | (0.2, .6) | |
| Pods | Mean effect size | Intercept | 0.05 | .49 | (−.96, 1.07) |
| Pot volume | Slope | .04 | .07 | (−0.10, .19) | |
| Cultivar | StDev | .51 | .49 | (0.02, 1.85) | |
| Study | StDev | .49 | .52 | (.01, 1.00) | |
| Study/experiment | StDev | .37 | 0.13 | (.19, .70) |
- Note: Cultivar, study, and individual experiment nested within study were included as random effects. “Standard deviation” is abbreviated as “StDev.”
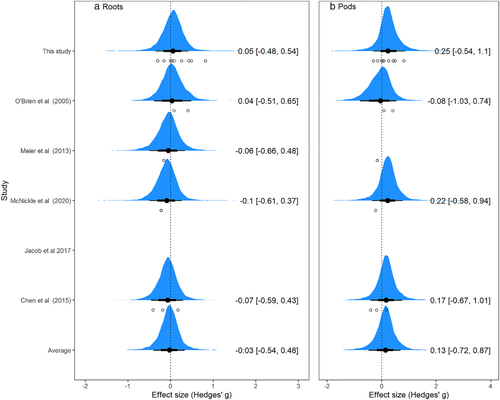
3.2 Pod responses
The estimated slope of relationship between pod mass and pot volume was weakly positive at .04 (95% CI: −.10, .19), and the intercept was .05 (95% CI: −.96, 1.07; Figure 1b). Thus, pot volume increased the expected neighbor-volume effect size by .04 standard deviations L−1 of pot volume. For example, a 1 L pot would have an estimated effect size of .09 standard deviations, a 2 L pot would have an estimated effect size of .13 standard deviations, and so on. The average posterior effect size for most studies was also slightly positive, indicating more pod mass in the neighbor-full treatment compared with the alone-half treatment (Figure 2b). As above, we can use the posterior distributions to assign probabilities to a given outcome in pea. Here, the average posterior distribution shows that there is a probability of .68 that the effect size could be greater than zero and thus, a probability of .32 that the effect size could be less than zero in a subsequent experiment.
As above, we estimated heterogeneity in the meta-analysis directly as standard deviations around the random intercept in the model with 95% CIs (Table 1). With pods, cultivar had an estimated standard deviation of .51 (95% CI: .02, 1.85), study had a standard deviation of .49 (95% CI: .02, 1.85), and differences among experiments but within a study had a standard deviation of .37 (95% CI: .19, .70). Thus, there is significant uncertainty that comes along with differences in experimental design, study, and cultivar used.
3.3 Publication bias
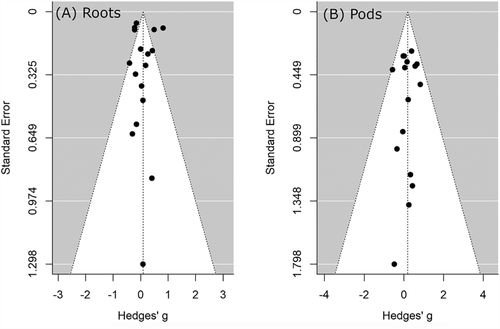
From the funnel plot comparing effect size and standard error in each study, all observed effect sizes for roots and pods fall roughly evenly on either side of the plot and primarily within the range of expected statistical error (Figure 3). Thus, we conclude that there is no evidence of publication bias in this literature, and differences among studies are simply statistical sampling errors.
4 DISCUSSION
Among ecologists, pea has become a sort of model species for the study of root plasticity in response to different external cues. This probably happened organically, as pea is an attractive model system, and because a number of studies had reported a variety of interesting and complex root behaviors (Chen et al., 2015, 2020; Falik et al., 2003; Falik et al., 2005; Gersani et al., 1998; Guinel & Geil, 2002; Jacob et al., 2017; McNickle, 2020; McNickle et al., 2020; Meier et al., 2013; O'Brien et al., 2005; Shemesh et al., 2010). After failing to reproduce some of these previous findings in five of our own experiments (supporting information), we combined our results with those from experiments that used the same treatments to gain a more holistic picture of pea root behavior that ultimately included 254 replicate pairs of plants grown in alone-half and neighbor full treatments. Since the literature is mostly populated by significant p-values, here we examined them in a Bayesian hierarchical meta-analysis that estimated the average posterior effect size of pea neighbor-volume effects as well as heterogeneity among studies and our priors assumed any result was equally likely. An absolute effect size of is considered small, and it corresponds to just 50%–58% of the treatment group being larger or smaller than the control and such a small effect would not be visually obvious. By this convention, for both roots and pods, the average effect size across studies was small (−.03 and .13 respectively; Figure 2). Furthermore, the 95% credible interval around estimates was so large that—as we already knew from the literature—effectively any result might be found for root responses in any given experiment that had a small sample size and therefore a large chance for statistical sampling error (Figure 2 and Table 1). These Bayesian posterior distributions suggest that if researchers take a frequentist approach to hypothesis testing with a relatively small sample size, then whether one finds a neighbor-volume root response in pea is essentially the same as flipping a coin (Figure 2a) and only slightly better than flipping a coin that a positive pod response would occur (Figure 2b). The coin flipping analogy does not mean that we conclude that the biology of pea is random, rather we mean that the root response to neighbors compared with alone has wide distribution centered on zero (Figure 2), and thus, when sample size is small, it is very easy to accidentally sample data points from the tails and make a type I statistical error (rejecting a true null hypothesis) with in a frequentist approach. Our original interpretation of the different results in the literature was that pea might have sophisticated context-dependent responses to many cues in the rhizosphere, and we sought to use this model system to explore these responses. However, based on this meta-analysis, we conclude that in general the current data suggest that pea has neither strong neighbor root responses nor strong responses to barriers imposed by halving pot volume when the treatments compared are two neighbor plants grown in a volume of and one plant grown in a pot of volume . A caveat on this conclusion is that it may only be valid for the genetics represented by the six cultivars included in our data.
In addition to the basic neighbor-full and alone-half comparison made within study, we could compare the pot volumes used among studies. The volume of the pot that peas were grown is varied from ml (Meier et al., 2013) to L (this study; supporting information) resulting in a wide range of potential constriction of root growth. However, for roots, the estimated posterior slope of this pot volume effect was .00 (95% CI: −.12, .11; Table 1 and Figure 1a). This means that one can expect the same effect size for roots at plant senescence whether or not peas are grown in 50 ml pots or 6.2 L pots. This is not the same as saying that plants did not have a growth response to pot volume (See Figure S5), only that the difference between plants in the two treatments (i.e., effect size) is zero standard deviations on average no matter the pot size that defines . The influence of pot volume used in a study on the effect size for pods on the other hand was weakly positive at .04 (95% CI: −.10, .19; Table 1 and Figure 1b). This means that the effect size ranged from 0.05 in a 50 ml pot to .30 in a 6.2 L pot for pods. Thus, we conclude that the neighbor-volume manipulation does begin to have an effect on pod production in a positive direction, even while the treatments seem to have no effect on total root biomass. Since these experiments confound neighbor addition and pot volume, it is impossible to determine which factor caused the increasing difference in pod production in neighbor-full pots relative to alone-half pots. For example, one could argue that pots of volume have more nutrients, water holding capacity, and space and that this lead to the increase in pod production relative to pots of volume and that neighbors had nothing to do with this (e.g., Hess & de Kroon, 2007). One could also argue that perhaps some kind of facilitation occurred between the two plants and that pot volume had nothing to do with the results (Callaway & Walker, 1997; Thorpe et al., 2011). One could also argue that both neighbor and volume effects simultaneously occurred, since there is no reason to think those two ideas are mutually exclusive. It would be difficult to design an experiment on just one genotype to solve the causal question of pot volume versus neighbors. We suggest that a quantitative trait locus (QTL) analysis might be a powerful way to attempt to elucidate mechanistic causes of root responses. Such an approach would explore the genetic basis of the root response to the neighbor-volume manipulation. Here, instead of attempting to address the problem with manipulations of volume and neighbors alone, one could map loci responsible for a root response. If the molecular basis for the loci identified could be elucidated (admittedly, not a small task), this might provide insight into what the plant is sensing and thus, what is causing the root response.
The weakly positive slope for the effect size on pod mass observed in our analysis (Figures 1b and 2b) should also be considered in the context of the heterogeneity among experiments, studies, and cultivars (Table 1). The Bayesian approach assumes that each individual experiment within study, combined with cultivar differences, has its own effect size that was sampled from the global population of possible effect sizes. Therefore, these random effects produce standard deviations with their own posterior distributions that should be interpreted as standard deviations around the intercept or mean effect. Interpreting these standard deviations is easiest when considering the posterior distribution of possible effect sizes for each study (Figure 2). For example, the tails of the posterior distribution for each study include effect sizes of 1 and −1 for both roots and pods and thus though the mean is centered on 0 and .14, respectively, there is a wide degree of uncertainty in these average estimates. For roots and pods, the uncertainty for cultivar was large which could indicate a genetic basis for the responses (Table 1). The differences among experiment performed within study indicate that other manipulations such as total nutrients (O'Brien et al., 2005), nutrient concentration (Chen et al., 2015; McNickle, 2020), manipulation of mycorrhizae (McNickle et al., 2020), and manipulation of shoot competition (supporting information) also introduce heterogeneity into the results, and none of this is surprising. We would direct interested readers to each individual study included in this meta-analysis to interpret the influence of these other treatments.
Importantly, we only studied the neighbor-volume response of pea roots at the coarsest possible scale: total root biomass. Pea might have other finer scale plastic root growth in space in relation to either neighbors or barriers such as pot walls (Cabal et al., 2020; Falik et al., 2003, 2005; O'Brien et al., 2007). These fine-scale behaviors of individual root tips as they navigate the rhizosphere are obviously not captured by studies of total root system size. For example, Falik et al. (2005) found that individual root tips of pea were able to adjust growth near barriers as small as .8 mm diameter nylon string. Such small-scale behaviors would be unlikely to be detectable at the coarse scale of a total root system mass but might still have important influences on lifetime survival and reproduction. Thus, it is still possible that finer-scale root navigation was responsible for the slight differences in pod mass we observed (Figures 1b and 2b), and it could be interesting to attempt to repeat those studies with pea as well. O'Brien et al. (2007) presented a model for finer-scale root responses to neighbors that might occur in regions of root system overlap relative to regions of soil where one plant is alone which could aide hypothesis development in future studies. Cabal et al. (2020) recently presented a very similar model which also makes spatially explicit predictions about intermingled root systems. If researchers want to continue to study pea responses to neighbors, we suggest that future experiments should attempt reproduce these finer-scale root responses at the scale of the rhizosphere and compare them with similar approaches on other species (e.g., Belter & Cahill, 2015; Downie et al., 2015). The GLO-roots imaging platform (sensu Rellán-Álvarez et al., 2015) is a relatively new tool that ecologists could use to explore such finer scale root responses. Finally, a caveat on our conclusion about volume (Figures 1 and S6) may only be valid for potting volume that varies primarily by depth and not by width. This is because, in general, the pots varied much more by depth than they did by width to achieve the gradient of volume analyzed here. Thus, there may be subtler effects of the geometry of pots with equal volume on root growth and proliferation that might emerge in future work.
We began the series of studies on pea described here in 2013 on the assumption that the published results in the literature were “true,” and variability was due to biologically interesting context dependent factors. However, what began as an honest approach to build upon these results and explore context dependency of root growth ultimately became a study in reproducibility as we failed time after time to be able to repeat previous findings. Since there is no evidence of publication bias (Figure 3), it is worth being clear how the standard approach to frequentist statistics, while working as intended, led us to the conclusion that previously published results were random sampling errors. Since statistics generally either accept an hypothesis or reject it, this creates a two-by-two simplex with four outcomes: (i) the null hypothesis is true but we incorrectly reject it, (ii) the null hypothesis is false but we incorrectly accept it, (iii) the null hypothesis is false and we correctly reject it, and (iv) the null hypothesis is true and we correctly accept it. Above, (i) and (ii) are known as type I and type II errors, respectively, where random chance has led to an erroneous conclusion based on the data, while (iii) and (iv) are what we are hoping to do as scientists: correctly use data to deduce reject false nulls and accept true ones. First, let us consider sample size and random sample error.
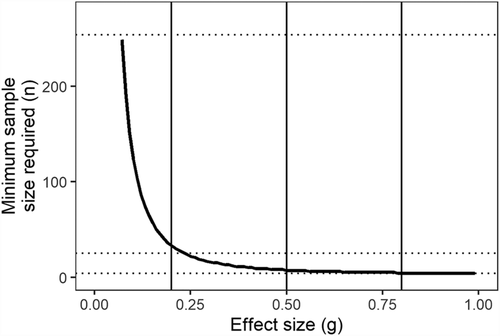
The type I error rate (i.e., rejecting a true null) is typically fixed in the frequentist approach at 5% or one in 20 (). The type II error rate (i.e., accepting a false null) is usually higher because it is considered less problematic as false nulls are thought to be more easily self-corrected in future research. The type II error rate is determined by the magnitude of the effect size from the treatments, the sample size of the experiment, and the type I error rate (Figure 4a). A commonly accepted type II error rate is 20% or one in five (). With and , we can calculate the sample size needed to correctly detect phenomena with small or large effect sizes (Figure 4). The fewest replicates among studies four (Jacob et al., 2017). A sample size of 4, assuming common type I and type II error rates of 0.05 and 0.2, respectively, is enough to just barely detect only the largest effect sizes (Figure 4). The most replicates among studies was 25 (Chen et al., 2015). A sample size of 25, again assuming common type I and type II error rates of 0.05 and 0.2, respectively, is enough to just barely detect medium and large effect sizes but not to correctly detect small effect sizes (Figure 4). Combined, the meta-analysis has 254 replicates which still is not enough to detect effect sizes smaller than .07 (Figure 4). Thus, if pea does exhibit some neighbor-volume response, it is a very small one that would require several thousand more data points to be statistically detectable without a type I or type II error.
This is just one case study in plant biology. However, we are aware of a similar example of a type I error ultimately being corrected by meta-analysis after years of research which also happened to involve plant root plasticity. For many years, there was a hypothesis that there should be a trade-off in a plant's ability to precisely place roots into nutrient rich zones of soil, compared with the ability of a plant to explore large spatial scales of soil volume (Campbell et al., 1991). This scale-precision trade-off hypothesis emerged from a study involving 10 species but only five replicates per species and shaped root plasticity research for decades (Hodge, 2004; Hodge, 2006). Ultimately, decades of work synthesized in a meta-analysis revealed that there was not really any evidence for this scale-precision trade-off and that the first paper was likely just a low statistical power type I error similar to the one we believe we have found here (de Kroon & Mommer, 2006; Kembel et al., 2008; Kembel & Cahill, 2005), but see Grime, 2007). It is not our goal to review every such case of a failure to replicate previously published results across the ecology literature, but the scale-precision hypothesis and the root over-proliferation hypothesis for pea specifically are two such examples which both happen to involve plant root plasticity. We surmise that these are unlikely to be the only such examples of a nonreproducible result across plant biology, and it is worth considering what it might mean if there are more nonreproducible results in the literature.
Indeed, similar failures to replicate results have caused many scientific fields to declare a reproducibility crisis (Ioannidis, 2005; Saltelli & Funtowicz, 2017). Our understanding is that the first field to declare a reproducibility crisis was psychology when a study reported evidence for psychic perception in humans (Bem, 2011; Pashler & Wagenmakers, 2012). Not surprisingly, this result was controversial, quickly criticized (Wagenmakers et al., 2011), and could not be repeated by subsequent studies (Galak et al., 2012). The mounting concerns about reproducibility led some in psychology to wonder how often any results could be repeated, and the crisis culminated in a large collaborative effort to try and reproduce 100 published results. This effort found that only 36 of these 100 previously published results were reproducible (Aarts et al., 2015). The cause was largely blamed on low statistical power and a culture that values novelty over replication (Hunter, 2001; Moonesinghe et al., 2007; Stanley et al., 2018). As far as we can tell, plant biology has not been drawn into the replication crisis like other fields such as psychology (Pashler & Wagenmakers, 2012), medicine (Ioannidis, 2005), and economics (Camerer et al., 2016). However, others have noted that true replications are relatively rare in related fields (Belovsky et al., 2004) and statistical power to detect all but the largest effect sizes can be low in many experiments (Steidl et al., 1997).
Given that just a few results were enough to spark fears of a replication crises in other fields (Pashler & Wagenmakers, 2012; Saltelli & Funtowicz, 2017), we might ask how other fields have approached a solution. One of the simplest solutions is to make data publically available in data repositories, and plant biologists seem to have already largely embraced this solution (GGM personal observation). In addition, some fields approach the problem by demanding very high power to detect small effect sizes by including very large numbers of replicates. For example, sample sizes in medicine are often in the thousands which serves to reduce the type II error rate. In medicine, human lives may literally depend on the ability to detect even small effect sizes and so the added expense of high statistical power can possibly be more easily justified. However, this added expense may not be a reasonable approach in plant biology. It is one thing to administer a medical intervention to thousands of people who then go off and live their lives during the experiment and another to care for thousands of replicate plants in a greenhouse or survey millions of hectares of forest. Funding agencies are acting rationally and in the interest of society by allocating more funding to save human lives than to understand plant biology.
Thus, if lowering the type II error rate with enormous sample sizes is not logistically feasible in plant science, perhaps we could consider reducing the type I error rate. Indeed, fields also differ in the cut-off they use for statistical significance. Most scientific fields, including biology, use a statistical significance cut-off of or a type I error rate of one in 20. In the language of confidence intervals, where a standard deviation is denoted by the symbol sigma, this statistical cut-off is also sometimes called two sigma. However, in physics, a five-sigma level of significance, which is or a type I error rate of one in 3.5 million, is required for a novel discovery to be believed (e.g., the detection of gravity waves: Abbott et al., 2016). Alternatively, three sigma, which is , or an error rate of one in about 370, is taken by physicists as weak evidence that a phenomena might exist and deserves further study (Lyons, 2013). Importantly, two, three, or five sigma has no theoretical basis, it is just a convenient and arbitrary cut-off based on a field's willingness to accept type I error (Colquhoun, 2017). Perhaps five sigma is unrealistic for plant biology, but when we look through our own past published results, three sigma seems frequently achievable, and perhaps erroneous conclusions in the literature at a rate of one in 370 are preferable to an error rate of one in 20.
4.1 Conclusion
Common pea has been studied by ecologists in the same basic neighbor-volume manipulation across 18 unique experiments from seven different studies for a total of 254 replicate alone-half and with neighbor-full pairs of plants. Positive, negative, and neutral results have all been published, and the interpretation of these results has been debated in the literature for more than a decade (Chen et al., 2015, 2020; Hess & de Kroon, 2007; Laird & Aarssen, 2005; McNickle, 2020). Here, we used a hierarchical Bayesian meta-analysis to generate posterior distributions from the published literature. We find that the six cultivars of pea which have been studied likely have no responses to a neighbor-volume manipulation at any pot volume ranging from 50 to 6,300 ml (varying mostly by depth). We conclude that this was simple statistical sampling error which is expected when science and frequentist statistics are operating as intended. We suggest that it might be valuable to attempt to replicate some of the finer scale results reported for pea (e.g., Falik et al., 2003; Falik et al., 2005), to further explore how increases in horizontal space to increase volume might affect pea, but for coarser-scale questions it might be worth expanding the diversity of species and genotypes for which we have data about root responses to the neighbor-volume manipulation.
ACKNOWLEDGMENTS
This work was supported by the USDA National Institute of Food and Agriculture Hatch project 1010722.
CONFLICT OF INTEREST
The authors declare no conflicts of interest.
AUTHOR CONTRIBUTIONS
GGM and MM designed the experiments. GGM performed supplemental experiment 1. MM performed supplemental experiments 2, 3, and 5 and frequentist statistical analyses. AK performed supplemental experiment 4 and frequentist statistical analyses. GGM performed the Bayesian meta-analysis. MM drafted the initial manuscript, and all authors contributed to revisions.




