High-Dimensional Disease Risk Score for Dealing With Residual Confounding Bias in Estimating Treatment Effects With a Survival Outcome
Funding: The authors received no specific funding for this work.
ABSTRACT
Purpose
Health administrative databases often contain no information on some important confounders, leading to residual confounding in the effect estimate. We aimed to explore the performance of high-dimensional disease risk score (hdDRS) to deal with residual confounding bias for estimating causal effects with survival outcomes.
Methods
We used health administrative data of 49 197 individuals in British Columbia to examine the relationship between tuberculosis infection and time-to-development of cardiovascular disease (CVD). We designed a plasmode simulation exploring the performance of eight hdDRS methods that varied by different approaches to fit the risk score model and also examined results from high-dimensional propensity score (hdPS) and traditional regression adjustment. The log-hazard ratio (log-HR) was the target parameter with a true value of log(3).
Results
In the presence of strong unmeasured confounding, the bias observed was −0.11 for the traditional method and −0.047 for the hdPS method. The bias ranged from −0.051 to −0.058 for hdDRS methods when risk score models were fitted to the full cohort and −0.045 to −0.049 when risk score models were fitted only to unexposed individuals. All methods showed comparable standard errors and nominal bias-eliminated coverage probabilities. With weak unmeasured confounding, hdDRS and hdPS produced approximately unbiased estimates. Our data analysis, after addressing residual confounding, revealed an 8%–11% higher CVD risk associated with tuberculosis infection.
Conclusions
Our findings support the use of selected hdDRS methods to address residual confounding bias when estimating treatment effects with survival outcomes. In particular, the hdDRS method using rate-based risk score modeling on unexposed individuals consistently exhibited the least bias. However, the hdPS method showed comparable performance across most evaluated scenarios. We share reproducible R codes to facilitate researchers' adoption and further evaluation of these methods.
Summary
- The high-dimensional disease risk score (hdDRS) method consistently outperformed the traditional methods in dealing with residual confounding when estimating treatment effects in comparative effectiveness studies with a survival outcome.
- In hdDRS, fitting the risk score model using unexposed individuals resulted in less bias compared to fitting the risk score model on the full cohort.
- The hdDRS with the rate-based risk score on unexposed individuals consistently produced the least bias and could better control for residual confounding bias than other hdDRS methods.
- The hdDRS with rate-based risk score on unexposed individuals had comparable results to those we obtained from hdPS, but the former consistently exhibited the least bias.
- After dealing with residual confounding bias, we observed an 8%–11% higher risk of cardiovascular disease associated with tuberculosis infection (hazard ratios: 1.08–1.11).
1 Introduction
Health administrative databases are increasingly common in exploring the relationship between a treatment/exposure and a survival outcome. Traditional methods for confounder adjustment, such as multivariable regression with the Cox proportional hazards model (Cox-PH), rely on investigators to identify, measure, and adjust for confounders available in the linked databases. However, health administrative databases often contain no information on many important confounders [1]. Therefore, traditional regression modeling often leads to biased effect estimates due to residual confounding [2]. For example, smoking, a strong confounder in the relationship between latent tuberculosis infection (TB infection) and cardiovascular disease (CVD), is often not included in administrative databases. This variable was therefore not included in previous studies based on such data [3, 4]. As a result, the observed relationship between TB infection and CVD adjusting for known measured confounders was likely to be biased due to unmeasured confounding by smoking.
In linked databases, many routinely collected healthcare variables are available that are external to the investigator-specified list of measured confounders. Usually, these healthcare variables are stored in the form of codes in the databases, which can be translated into proxy variables [5, 6]. Utilizing these empirically identified proxies with investigator-specified measured confounders, the high-dimensional propensity score (hdPS) and high-dimensional disease risk score (hdDRS) are proposed to reduce bias due to unmeasured confounding [5-7]. Although numerous studies have shown bias reduction via hdPS methods [8-12], we did not find any simulation or theoretical studies that explored the performance of hdDRS methods for reducing residual confounding bias. Two studies investigated the performance of hdDRS methods with a binary outcome, and both were based on empirical data, limiting generalizability due to an unknown true treatment effect [7, 13].
Two versions of the hdDRS methods exist in the literature; one fits the disease risk score (DRS) model only on the unexposed, while the other fits the DRS model on the full dataset [14, 15]. There are also multiple approaches to calculating DRS for a survival outcome, for example, treating the outcome as a binary, survival, or rate variable [15]. However, there is little exploration in the literature on the performance of different versions of hdDRS methods, particularly with a survival outcome.
In the present study, we compared the performance of various versions of the hdDRS for estimating causal effects with a survival outcome, and compared the results with those from the hdPS and traditional regression adjustment. We used plasmode simulations to generate data for a binary exposure (TB infection) and a survival outcome (time-to-CVD), while preserving the realistic relationships among the confounders.
2 Methods
2.1 Motivating Example: Tuberculosis Cohort in British Columbia
We utilized a retrospective population-based cohort of immigrants in British Columbia, Canada, between 1985 and 2019, who were tested for TB infection as coded in the provincial TB registry. The cohort was developed using linked immigration, TB Registry, and health administrative databases (Appendix-A) [4, 16]. The final analytical sample consisted of 49 197 individuals tested for TB infection, totalling 901 734 person-years of observation. Among these participants, 26 163 (53.2%) tested positive for TB infection, and 2114 (4.3%) developed CVD during the follow-up period. Fourteen measured confounders were considered for confounding adjustment (Appendix-A) [4].
2.2 Methods Compared
We focused on contrasting confounder adjustments using hdDRS, and also explored results from hdPS and multiple regression adjustments (Table 1). For the multiple regression analysis in a traditional way, the Cox-PH regression was fitted as the outcome model, adjusting for measured confounders. Compared to the traditional propensity score (PS) and DRS approaches that rely solely on investigator-specified measured confounders, hdPS and hdDRS methods systematically leverage high-dimensional healthcare databases to empirically identify and select additional proxy covariates that serve as surrogates for important, often unmeasured confounders.
| Method | Description | |
|---|---|---|
| (1) Traditional | We fitted Cox proportional hazards (PH) model, adjusting for measured confounders. | |
| (2) hdPS | There were seven major steps for hdPS: | |
| 2.1. |
Data sources: To identify the proxies, we considered the following data sources:
These codes/proxies were assessed in a one-year window prior to the index date. |
|
| 2.2. | Dimension reduction: To avoid double counting, we excluded codes that were part of any investigator-specified measured confounders. | |
| 2.3. | Define recurrence covariates: Proxies/codes from step 2.2 were converted into binary variables based on their recurrence. A maximum of three recurrence covariates (also known as empirical covariates) were created for each proxy/code: once (code is recorded ≥ once), sporadic (code is recorded ≥ the median), and frequent (code is recorded ≥ the 75th percentile). There were a total of 4,502 empirical covariates. | |
| 2.4. | Prioritization: To reduce overfitting and improve model prediction, we prioritize the recurrence covariates using LASSO regularization with the Cox-PH. All 4,502 empirical covariates were included in the model for modelling time-to-CVD survival outcome. The lambda hyperparameter of the model was selected using 5-fold cross-validation. | |
| 2.5. | Selection of recurrence covariates: The top 200 recurrence covariates from step 2.4 were selected based on the absolute log hazard ratio of the covariates. | |
| 2.6. | Estimating propensity score: To estimate the propensity score, we fitted logistic regression with investigator-specified measured confounders and the top 200 recurrence covariates. | |
| 2.7. | Outcome model: The Cox-PH model was fitted, adjusting for measured confounders and deciles of propensity score. White's robust sandwich estimator was used to calculate the standard error. | |
| (3) hdDRS | There are seven major steps for hdDRS, with 1–5 being identical to hdPS steps. | |
| 3.6. | Estimating disease risk score: To estimate the disease risk score (DRS), we considered the measured confounders specified by the investigator and the top 200 recurrence covariates. We calculated the score in eight different approaches:
|
|
| 3.7. | Outcome model: The Cox-PH model was fitted for each of the eight hdDRS methods, adjusting for measured confounders and deciles of DRS. White's robust sandwich estimator was used to calculate the standard error. | |
- Abbreviations: DRS, disease risk score; hdDRS, high-dimensional disease risk score; hdPS, high-dimensional propensity score; PH, proportional hazards.
There are seven steps in hdPS and hdDRS analyses, such as identifying the data sources for proxies, dimension reduction, defining recurrence covariates (‘empirical covariates’) from proxies, prioritizing empirical covariates, selecting top empirical covariates, estimating the PS or DRS, and outcome modelling [5-7, 13]. The steps are described in Table 1. Steps 1–5 are identical for both the hdPS and hdDRS methods; however, step 6 (score estimation) differs between them. Step 6 involved estimating the PS (the conditional probability of receiving the exposure given measured confounders) in the hdPS analysis, and the DRS (the conditional probability or rate of developing the outcome given measured confounders) in the hdDRS analysis. To estimate the PS or DRS, the measured confounders and the 200 empirical covariates identified using Cox-LASSO were used (Appendix-B). While logistic regression was used to estimate the PS, we calculated the DRS in eight different approaches: Full-Logistic, Full-Survival, Full-Hazard, Full-Rate, Unexposed-Logistic, Unexposed-Survival, Unexposed-Hazard, and Unexposed-Rate (Table 1) [14, 15]. Step 7 involved the outcome modelling, where the Cox-PH model was fitted, adjusting for the measured confounders and the deciles of the PS or DRS (Appendix-C). White's robust sandwich estimator was used to calculate the model-based standard error for both hdPS and hdDRS methods [17]. To demonstrate how to apply the compared methods in a given scenario, reproducible R codes on a simulated dataset are provided in the GitHub folder: https://github.com/belalanik/hdDRScausal.
2.3 Simulation Setup
2.3.1 Plasmode Simulation
To explore the performance of the methods, we designed a plasmode simulation based on our motivating example data (Appendix-D) [18]. We used the Cox-PH model to generate a survival outcome. The exposure of interest was binary. To generate the data, we used the following set of confounders with HRs from the motivating example data (Appendix-Table S1): the main effect of age, sex, neighbourhood income quintile, immigration status, tobacco use, CKD, Elixhauser comorbidity index, dyslipidemia, the quadratic effect of Elixhauser comorbidity index, and interactions between sex and CKD, and sex and Elixhauser comorbidity index. The true exposure effect on the outcome in terms of log-HR was .
2.3.2 Simulation Scenarios
To set up the simulation scenarios, we considered the true data-generating covariate set as , where B is the set of measured confounders, and U is a single unmeasured confounder. The empirical covariates were identified from the motivating example dataset, but they were not used to generate the simulated data. We considered two simulation scenarios: (i) strong unmeasured confounding by U and (ii) weak unmeasured confounding by U. Age was considered an unmeasured confounder with an HR of 4.62 for scenario (i), while dyslipidemia was considered an unmeasured confounder with an HR of 1.14 for scenario (ii). The association of age and dyslipidemia with TB infection exposure in terms of odds ratios were 0.75 and 1.35. For both simulation scenarios, we generated 1000 datasets, each comprising 10 000 individuals. The prevalence of exposure and event rate were approximately 30%.
2.3.3 Target Parameter
The log-HR was calculated as the target parameter of interest, a widely used measure of association for a survival outcome. The effect estimate was conditional on confounders for the traditional model, while conditional on confounders and PS in the hdPS, and conditional on confounders and DRS in the hdDRS analyses.
2.3.4 Performance Metrics
We assessed the performance of the methods in terms of bias, empirical standard error (SE), model-based SE, 95% confidence interval (CI) coverage probability, and bias-eliminated coverage probability (Appendix-D) [19]. We also calculated the Monte Carlo error to quantify the simulation uncertainty for all performance metrics [19].
2.3.5 Sensitivity Analyses
We conducted multiple sensitivity analyses to explore the robustness of our findings. First, we varied the event rate, which indirectly reflects the censoring rate under the assumption of non-informative right-censoring and no competing events. We explored three alternative scenarios compared to our primary analysis (which assumed 30% exposed and 30% event rate, i.e., 70% censoring rate): (i) 5% exposed and 30% event (70% censored), (ii) 30% exposed and 5% event (95% censored), and (iii) 5% exposed and 5% event (95% censored). Second, we conducted sensitivity analyses for the decision related to the hdPS and hdDRS parameters, including the number of empirical covariates and their ranking process. We performed analyses with only the top 500 empirical covariates [5], where covariates were identified using Cox-LASSO. To rank the empirical covariates, we used the Bross formula (a widely used approach) and random survival forest (see below). The hdPS and hdDRS analyses were performed with the measured confounders and the top 200 empirical covariates identified using the Bross formula [20] and random survival forest [21] (Appendix-E). We also performed the hdPS analysis with the inverse probability weighting (IPW) approach [6], where stabilized weight was used for increased precision of the estimate [22]. Third, we considered a null exposure effect (log-HR = 0). Fourth, we considered the misspecified PS, DRS, and outcome model. In that case, the quadratic effect of Elixhauser comorbidity index, and interactions between sex and CKD, and sex and Elixhauser comorbidity index were not considered in the outcome, PS, or DRS models. The effects of the non-linear and interaction terms on the outcome were weak in the data-generating mechanism and thus were expected to be associated with a small bias in the analysis. Fifth, we used regularized regression with LASSO to fit the PS and DRS models. The lambda hyperparameter in LASSO models was chosen using 5-fold cross-validation. Sixth, we used risk difference as a target parameter, which was calculated using g-computation [23]. The model-based SE was calculated using 200 bootstrap replicates [24]. Seventh, we explored the performance of the methods with smaller sample sizes, where we generated 1000 datasets of (i) 5000 individuals, (ii) 2000 individuals, and (iii) 1000 individuals. Eighth, we generated simulated datasets in which only age and sex were true confounders. The true exposure effect on the outcome remained log(3.00). In the traditional model, we adjusted only for sex. The hdPS and hdDRS methods adjusted for sex and the top 200 empirical covariates.
3 Results
When there was no unmeasured confounding, all methods produced an approximately unbiased estimate (Appendix-Figure S1), a comparable SE (~0.042), and a nominal coverage probability (~0.95).
3.1 Strong Unmeasured Confounding Present
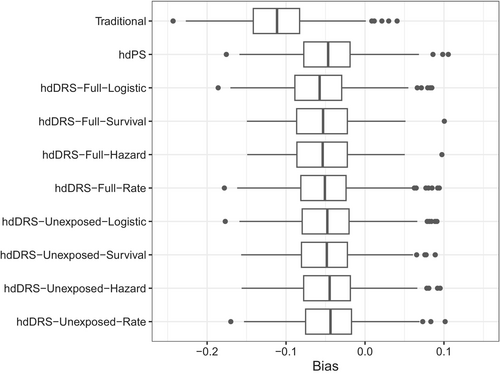
All methods produced a biased effect estimate for a strong unmeasured confounding scenario. The bias was −0.11 for all methods when only investigator-specified confounders were used in all analyses (Appendix-Figure S2). When empirical covariates were added to the investigator-specified confounders, the bias was significantly reduced for all hdDRS methods (Figure 1, Table 2). In contrast to all hdDRS methods, the hdDRS with rate-based DRS calculation on the unexposed cohort resulted in the lowest bias of −0.045, while the hdDRS with logistic-based DRS calculation on the full cohort had a bias of −0.058. The hdPS resulted in a bias of −0.047 in the same setting.
| Scenario | Bias | Empirical SE | Model-based SE | Coverage | Bias-eliminated coverage | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Estimate | MCE | Estimate | MCE | Estimate | MCE | Estimate | MCE | Estimate | MCE | |
| (A) Strong unmeasured confounding | ||||||||||
| Traditional | −0.111 | 0.001 | 0.043 | 0.001 | 0.041 | 0.000 | 0.220 | 0.013 | 0.943 | 0.007 |
| hdPS | −0.047 | 0.001 | 0.043 | 0.001 | 0.042 | 0.000 | 0.775 | 0.013 | 0.946 | 0.007 |
| hdDRS-full-logistic | −0.058 | 0.001 | 0.042 | 0.001 | 0.041 | 0.000 | 0.692 | 0.015 | 0.945 | 0.007 |
| hdDRS-full-survival | −0.054 | 0.003 | 0.042 | 0.002 | 0.041 | 0.000 | 0.682 | 0.034 | 0.964 | 0.014 |
| hdDRS-full-Hazard | −0.054 | 0.003 | 0.042 | 0.002 | 0.041 | 0.000 | 0.682 | 0.034 | 0.958 | 0.014 |
| hdDRS-full-rate | −0.051 | 0.001 | 0.042 | 0.001 | 0.041 | 0.000 | 0.735 | 0.014 | 0.956 | 0.006 |
| hdDRS-unexposed-logistic | −0.049 | 0.001 | 0.042 | 0.001 | 0.041 | 0.000 | 0.748 | 0.014 | 0.948 | 0.007 |
| hdDRS-unexposed-survival | −0.049 | 0.001 | 0.042 | 0.001 | 0.041 | 0.000 | 0.746 | 0.015 | 0.951 | 0.007 |
| hdDRS-unexposed-Hazard | −0.046 | 0.001 | 0.043 | 0.001 | 0.041 | 0.000 | 0.765 | 0.015 | 0.948 | 0.008 |
| hdDRS-unexposed-rate | −0.045 | 0.001 | 0.042 | 0.001 | 0.041 | 0.000 | 0.781 | 0.013 | 0.956 | 0.007 |
| (B) Weak unmeasured confounding | ||||||||||
| Traditional | −0.020 | 0.001 | 0.042 | 0.001 | 0.041 | 0.000 | 0.911 | 0.009 | 0.945 | 0.007 |
| hdPS | −0.006 | 0.001 | 0.043 | 0.001 | 0.042 | 0.000 | 0.935 | 0.008 | 0.944 | 0.007 |
| hdDRS-full-logistic | −0.014 | 0.001 | 0.042 | 0.001 | 0.041 | 0.000 | 0.925 | 0.008 | 0.940 | 0.008 |
| hdDRS-full-survival | −0.012 | 0.004 | 0.043 | 0.003 | 0.041 | 0.000 | 0.941 | 0.020 | 0.956 | 0.018 |
| hdDRS-full-Hazard | −0.012 | 0.004 | 0.043 | 0.003 | 0.041 | 0.000 | 0.941 | 0.020 | 0.956 | 0.018 |
| hdDRS-full-rate | −0.008 | 0.001 | 0.042 | 0.001 | 0.041 | 0.000 | 0.940 | 0.008 | 0.944 | 0.007 |
| hdDRS-unexposed-logistic | −0.004 | 0.001 | 0.042 | 0.001 | 0.041 | 0.000 | 0.939 | 0.008 | 0.943 | 0.007 |
| hdDRS-unexposed-survival | −0.005 | 0.001 | 0.042 | 0.001 | 0.041 | 0.000 | 0.945 | 0.008 | 0.944 | 0.008 |
| hdDRS-unexposed-Hazard | −0.002 | 0.001 | 0.043 | 0.001 | 0.041 | 0.000 | 0.944 | 0.008 | 0.939 | 0.008 |
| hdDRS-unexposed-Rate | −0.001 | 0.001 | 0.042 | 0.001 | 0.041 | 0.000 | 0.947 | 0.007 | 0.947 | 0.007 |
- Note: The results were derived from 1,000 sets of plasmode simulation data, each with a sample size of 10,000 and true effect estimate of log(3) in log hazard ratio scale. Here, ‘Unexposed’ denotes the disease risk score was calculated on the unexposed cohort, ‘Full’ denotes the disease risk score was calculated on the full cohort, and ‘Logistic’, ‘Survival’, ‘Hazard’, and ‘Rate’ indicates the approaches of calculating the disease risk score.
- Abbreviations: Bias-eliminated coverage, Bias-eliminated 95% confidence interval coverage probability; Coverage, coverage for nominal 95% confidence interval; EmpSE, empirical standard error; hdDRS, high-dimensional disease risk score; hdPS, high-dimensional propensity score; MCE, Monte Carlo error; ModSE, model-based standard error; MSE, mean squared error; Traditional, Cox proportional hazards model with adjusting for measured confounders.
The model-based and empirical SE were comparable for all methods (range: 0.041–0.043). As expected, all methods had poor coverage probabilities (0.22 for traditional, 0.68–0.78 for hdDRS methods, and 0.78 for hdPS). However, the bias-eliminated coverage probability was nominal for all methods (Table 2). Although all hdDRS methods had comparable SE and coverage probabilities, fitting the DRS models only on the unexposed individuals rather than the full cohort resulted in more bias reduction (range from −0.045 to −0.049 versus −0.051 to −0.058). All methods had a very small Monte Carlo error, with an error of 0.001–0.003 for bias, 0.001–0.002 for empirical SE, 0.000 for model-based SE, 0.013–0.034 for coverage, and 0.006–0.014 for bias-eliminated coverage.
3.2 Weak Unmeasured Confounding Present
For a weak unmeasured confounding scenario, the bias was small for all methods (Figure 2, Table 2). The bias was −0.020 for the traditional method, while it was −0.006 for the hdPS and ranged from −0.014 to −0.001 for the hdDRS methods. In contrast, the hdDRS methods with full-cohort DRS score calculation resulted in a bias between −0.008 and −0.014, while the hdDRS methods with unexposed-only DRS score calculation resulted in a bias between −0.001 and −0.005. The bias was −0.001 for the hdDRS with rate-based DRS calculation on the unexposed cohort.
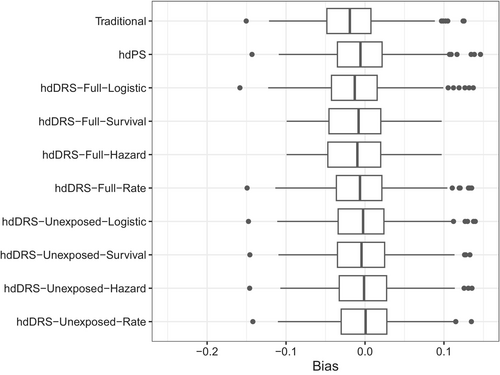
The model-based and empirical SE were comparable for all methods (0.041–0.043). The traditional method had a coverage probability of 0.91, while it was 0.94 for the hdPS and ranged from 0.93 to 0.95 for the hdDRS methods. The bias-eliminated coverage probability was nominal for all methods (Table 2). Again, the Monte Carlo error was small for all methods, such as 0.001–0.004 for bias, 0.001–0.003 for empirical SE, 0.000 for model-based SE, 0.007–0.020 for coverage, and 0.007–0.018 for bias-eliminated coverage.
3.3 Results for Sensitivity Analyses
The results of the sensitivity analyses were not materially different compared to the primary analysis (Appendix-F). Similar to the primary analysis with a strong unmeasured confounding, the hdDRS with rate-based DRS calculation on the unexposed cohort consistently produced the lowest bias for varying the event rate and exposure prevalence (Appendix-Table S2), with 500 empirical covariates or ranking the empirical covariates using the Bross formula or random survival forest (Appendix-Table S3), for a null exposure effect (Appendix-Table S4), misspecified DRS and PS models (Appendix-Table S5), LASSO for estimating scores (Appendix-Table S6), risk difference as the target parameter (Appendix-Table S7), and when data were generated for 5000 individuals (Appendix-Table S8), 2000 individuals (Appendix-Table S9), 1000 individuals (Appendix-Table S10), and age and sex as the only confounders (Appendix-Table S11). The hdDRS with rate-based DRS calculation on the unexposed cohort and the hdPS also produce approximately unbiased estimates with a weak unmeasured confounding.
3.4 Motivating Example Results
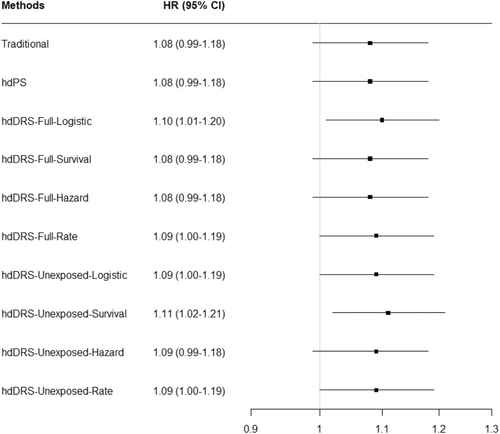
In exploring the relationship between TB infection and CVD, the traditional model had an adjusted HR of 1.08 (95% CI: 0.99–1.18). The HR was 1.08 (95% CI: 0.99–1.18) for the hdPS and 1.09 (95% CI: 1.00–1.19) for the hdDRS with rate-based DRS calculation on the unexposed cohort. The other hdDRS methods resulted in an HR ranging from 1.08 to 1.11 (Figure 3).
4 Discussion
4.1 Summary of the Findings
In a scenario with strong unmeasured confounding, the traditional method that relies on adjusting the model for only the measured confounders always produced a biased effect estimate. Adding empirically identified proxies to the investigator-specified measured confounders and fitting the hdDRS resulted in a significant bias reduction. The hdDRS with rate-based DRS calculation on the unexposed cohort consistently exhibited the least bias. The model-based and empirical SE were comparable for all methods. The bias-eliminated coverage probabilities also approached nominal levels across all methods. In a setting with weak unmeasured confounding, all methods performed well, demonstrating minimal bias, especially for the hdDRS with DRS calculation on the unexposed cohort. The hdPS also had results comparable to those we obtained from the hdDRS with DRS calculation on the unexposed cohort. Sensitivity analyses for varying the exposure prevalence and event rate, different hdDRS parameters, null exposure effect, model misspecifications, LASSO for estimating the scores, risk difference as the effect measure, smaller sample sizes, and specifying the true data-generating model with only age and sex revealed consistent trends; the hdDRS with rate-based DRS calculation on the unexposed cohort generally outperformed the other methods in reducing bias due to residual confounding. We applied all the methods in exploring the relationship between TB infection and CVD among people who immigrated to British Columbia and were tested for TB infection between 1985 and 2019. The method with only investigator-specified measured confounders showed an 8% higher risk of CVD among people who tested positive for TB infection than those who tested negative. Adding the empirically identified proxies with the investigator-specified measured confounders and fitting the hdPS and hdDRS methods showed an 8%–11% higher CVD risk associated with TB infection.
4.2 HdDRS to Deal With Residual Confounding Bias
The hdDRS methods with DRS calculation on the unexposed cohort had a comparatively smaller bias than the hdDRS methods with DRS calculation on the full cohort. Since DRS is used to balance baseline outcome risks, fitting the DRS models only among the unexposed and predicting the score on the full cohort could offer a stable estimate of the baseline risk of the outcome among the exposed and unexposed. This approach could also better capture the baseline risk of the outcome since control for confounding might otherwise be different in the exposed group [14]. Moreover, disentangling the risk of the outcome associated with proxies and exposure could be challenging when we include the exposure variable in the DRS calculation. Notably, the hdDRS-Unexposed-Logistic ignores the follow-up time in estimating the DRS; the hdDRS-Unexposed-Survival attempts to balance the survival probability of the outcome during the follow-ups; the hdDRS-Unexposed-Hazard attempts to balance the hazard during the follow-ups, while the hdDRS-Unexposed-Rate only attempts to balance the baseline outcome risks. The better balance of the baseline risk might be the reason for the consistently lower bias from the hdDRS with rate-based DRS calculation on the unexposed cohort than other hdDRS methods with DRS calculation on the unexposed cohort.
The hdPS is a popularly known method compared to the hdDRS in dealing with residual confounding bias in comparative effectiveness studies. Our study also found that the hdPS had comparable performance to the hdDRS with rate-based DRS calculation on the unexposed cohort in terms of reducing bias. However, the instability of an overfitted exposure model with a rare exposure in hdPS could fail to reduce significant bias [25]. The hdDRS methods with DRS calculation on the unexposed cohort could perform well in the same setting when the outcome of interest is not rare. Notably, both hdPS and hdDRS could perform poorly and overestimate the exposure effect when the PS and DRS models are overfitted, particularly with a rare exposure and a rare outcome, respectively [26, 27]. These methods also assume that the empirical covariates are potentially correlated with the variables that are unmeasured and these empirical covariates can be used as overall proxy measures to minimize bias due to residual confounding [5, 8, 28]. However, both approaches could be as good as the traditional method, even if there is strong or weak confounding or some confounders are misclassified. As we observed in our simulations, hdPS and hdDRS with rate-based DRS calculation on the unexposed cohort always resulted in approximately unbiased estimates under a weak unmeasured confounding scenario, while there were still some biases from the traditional method. In practice, rare outcomes are more common than rare exposures in comparative effectiveness studies with observational data. We recommend applying both hdPS and hdDRS with rate-based DRS calculation on the unexposed cohort. The analyst could come to a robust conclusion if both approaches result in a similar effect estimate.
4.3 HdDRS in Literature
Many previous studies explored the performance of PS and DRS methods developed with only investigator-specified measured confounders [15, 29-32]. The performance of the PS and DRS compared to that of a traditional method is not always superior, particularly when both exposure and outcome are non-rare [15, 29, 30]. Most of the hdPS work applies to continuous or binary outcomes, while only a few studies have been conducted with a survival outcome [9, 11, 33, 34]. However, the literature on hdDRS in dealing with residual confounding is limited. We found only two empirical studies on hdDRS, and both considered binary outcomes [7, 13]. One study showed that hdDRS using historical data improved confounding adjustment [7], while the other study concluded that hdDRS had similar or better confounding adjustment compared to the traditional method but worked slightly less well than hdPS [13]. However, both studies were empirical in nature without any simulations. The hdDRS was also applied in many applications, such as dealing with unmeasured/residual confounding in TB [4], cataract [35], fracture [36], CVD [37], diabetes [38], and multiple sclerosis research [39]. When exposure is time-dependent, or the outcome is being measured over time, implementing hdPS is challenging. In a recent study, we employed hdPS within the nested case–control design to simultaneously deal with time-dependent exposure and residual confounding [40]. The hdDRS methods can also be used in the same setting. With a longitudinally measured outcome, hdPS might not be implemented since each individual has multiple rows of data. However, the hdDRS methods with DRS calculation on the unexposed cohort could easily be applied in the same setting, which was also done in a recent work minimizing residual confounding bias with an outcome occurring over time [41].
4.4 Contextualize the Findings in TB Literature
Our results consistently showed that TB infection is associated with a modestly increased risk of CVD across methods. While the traditional model showed an 8% higher CVD risk (HR: 1.08, 95% CI: 0.99–1.18), the hdPS and hdDRS methods produced hazard ratios ranging from 1.08 to 1.11. The small variation across methods suggests relatively weak unmeasured confounding by smoking status, highlighting the robustness of the observed association. However, if the empirically identified proxies were poor surrogates for smoking, residual confounding may persist. We observed an 11% higher risk of CVD associated with TB infection in a previous study [4], where we conducted a sensitivity analysis by adjusting our model with investigator-specified confounders as well as tobacco use as a proxy for smoking. All these findings underscore the potential effect of TB infection on long-term CVD risk, while also demonstrating the importance of employing robust statistical methods to address residual confounding bias inherent in observational studies.
4.5 Limitations and Future Directions
Our study has some limitations. First, the hdPS and hdDRS methods might minimize residual confounding bias inherent in using health administrative data, while some residual confounding may remain. As we observed in our simulations, all methods produced a biased estimate with strong unmeasured confounding, while the bias was approximately zero in hdPS and hdDRS analyses with weak unmeasured confounding. Second, we considered the log-HR as the target parameter, which is a non-collapsible effect measure. Our analysis without unmeasured confounding revealed that all these methods resulted in a similar log-HR with a similar SE. The log-HR and associated SE were also similar for all methods when only the measured confounders were used in fitting the model. Moreover, our sensitivity analysis with the risk difference as a collapsible effect measure had similar trends to the results that we observed with the log-HR as the target parameter. This study estimated conditional (covariate-adjusted) effects of exposure rather than marginal (population-average) effects. Conditional estimates reflect the causal effect within subgroups defined by specific covariate patterns or strata and may not directly generalize to the entire target population. To obtain marginal effects, alternative methods such as inverse probability weighting or G-computation would be required. Therefore, caution is warranted when interpreting the current estimates as representative of the causal effect in the broader population. Third, we adjusted the outcome model for the deciles of the DRS, which is also commonly done in previous studies [7, 13, 29]. The stratification approach for hdPS and hdDRS, as well as hdPS with IPW, had similar effect estimates. Future studies could compare the methods with different modeling choices such as matching and weighting. Future studies could also combine PS and DRS in the same model and explore the performance with the separate hdPS and hdDRS methods [42]. Fourth, the inclusion of many covariates in hdPS may lead to a violation of the positivity assumption. The violation of the positivity assumption can result in a biased effect estimate as well as an inflated variance estimate [26, 43]. Trimming, overlap weighting, extrapolation beyond the overlap region, matching with a caliper, stratification, and estimating PS using machine learning dimension reduction techniques to reduce the dimension of covariates are often recommended to address the violation of the positivity assumption [44, 45]. Fifth, we considered the conventional methods for estimating PS or DRS. Future studies could estimate PS or DRS using machine learning methods. Since such approaches often result in poor coverage, recent literature has recommended using double robust methods, such as Targeted Maximum Likelihood Estimation [46-48]. However, we observed approximately nominal bias-eliminated coverage when PS or DRS was estimated using LASSO. Furthermore, the literature on machine learning methods for survival outcomes is limited [49], and the implementation details of double robust methods are somewhat unclear [50]. Sixth, we did not consider competing events in our analysis, while future studies could explore the performance of various versions of hdPS and hdDRS with a competing event. Given that hdDRS and hdPS are often specific to the data and covariates available, our results might not be generalizable. We recommend exploring the performance of hdPS and hdDRS in different research contexts by varying key hdPS/hdDRS parameters.
5 Conclusion
In conclusion, our simulation results indicate that selected hdDRS methods can effectively reduce residual confounding bias when estimating treatment effects for survival outcomes. While the hdDRS method employing rate-based DRS calculated on the unexposed cohort generally exhibited the lowest bias, the hdPS method performed comparably well across many scenarios. Both hdDRS and hdPS methods provided significant improvements over traditional regression adjustment. Thus, we recommend considering both hdDRS and hdPS approaches as viable methods for addressing residual confounding. Our sensitivity analyses further support these conclusions. While simulation findings indicated that hdDRS with rate-based modeling on the unexposed cohort achieved the least bias, the real-world TB analysis showed only modest variation in estimates across methods. This highlights that when unmeasured confounding is weak, the choice of adjustment method may have a limited impact on the final effect estimate.
5.1 Plain Language Summary
This study aimed to explore whether tuberculosis infection causes heart disease. People with tuberculosis have different characteristics than those without it. If we do not know some of these important factors, our exploration of the relationship can be biased. For example, we did not have smoking information in our data. The traditional approach only considers known, measurable factors, leading to a biased relationship. There are many healthcare variables available for patients. For example, diagnostic and procedure codes and drug dispensation can be useful. These variables can provide valuable information about smoking. We used these variables with advanced methods. This was to make up for the lack of data on smoking. A technique called the high-dimensional disease risk score was very effective. It worked best when the score calculation used data from uninfected people. Our method worked well even though some other important factors were unobserved. After fixing the bias, we found an 8% to 11% higher risk of heart disease from tuberculosis infection.
Acknowledgments
The study was conducted with support from the University of British Columbia Four-Year Doctoral Fellowship and Harry and Florence Dennison Fellowship in Medical Research.
Ethics Statement
Ethical approval was provided by the University of British Columbia (#H16-00265).
Conflicts of Interest
The authors declare no conflicts of interest.
Open Research
Data Availability Statement
The data from this study are held in a secure research environment managed by Population Data BC (https://www.popdata.bc.ca/). Access to data provided by the Data Stewards is subject to approval but can be requested for research projects through the Data Stewards or their designated service providers. The following data sets were used in this study: Vital Statistics, Tuberculosis registries, Medical Services Plan, Hospital Discharge Abstract Database, PharmaNet, Cancer Agency database, HIV registry, and Renal database. You can find further information regarding these data sets by visiting the PopData project webpage at https://my.popdata.bc.ca/project_listings/14-105/collection_approval_dates. All inferences, opinions, and conclusions drawn in this publication are those of the author(s), and do not reflect the opinions or policies of the Data Steward(s).




