Peridynamic simulations of rock indentation
Abstract
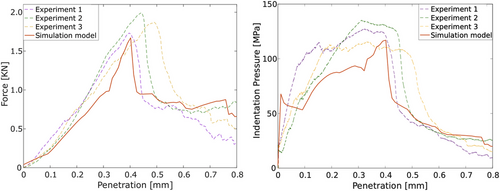
This paper presents an ordinary state-based peridynamic model to simulate failure in porous rocks and its application in the rock excavation processes. Rock indentation is a fundamental process for mechanical rock fracturing, which is frequently encountered in rock excavation. To model crushing occurring under high triaxial loads observed in the rock indentation experiments, peridynamic model has been extended to consider the pore-collapse phenomenon. Rock heterogeneity is considered in the simulations by sampling the strength parameters from a probability distribution function. The model is qualitatively validated using the acoustic emission data from the indentation experiments. The developed model is able to form a crushed zone, which serves as the point of initiation for tensile cracks, which split the specimen. Quantitative validation relies on the comparison of the force-penetration data as well as the indentation pressure-penetration data obtained from the simulations and experiments performed on Bentheim Sandstone specimens.
1 INTRODUCTION
Heterogeneous solids, such as rocks and concrete, contain a distribution of flaws. When subjected to tensile loads, cracks initiate from these flaws and propagate according to the linear elastic fracture mechanics (LEFM) criterion. This results in one or more cracks reaching a critical length, at which point the most critical crack propagates unstably, leading to failure. However, under compression, flaws in these materials undergo a complex sequence of failure processes. These include crack closure, pore-collapse, crack initiation in various modes, crack sliding, and the wing crack formation [1-4]. Due to the activation of these mechanisms, failure under compression results in diffused damage. This means that damage is observed at various locations, unlike in tensile failure where only a single crack localizes. The activation of these additional mechanisms under compression result in an order of magnitude higher dissipation as compared to the energy dissipated during tensile failure. This leads to significant variations in tensile and compressive strengths [5]. Hydrostatic pressure plays a crucial role in compressive failure by governing the activation of several of the aforementioned mechanisms. Therefore, it is a critical factor in the failure process.
In this paper, the standard ordinary state-based peridynamic simulation model [6-9] is extended to consider the additional dissipation due to the pore-collapse phenomenon and applied to the indentation test of a sandstone. Qualitative features of indentation are analyzed through acoustic emission (AE) data obtained from the experiments performed on Bentheim sandstone [10]. Quantitatively, the model is validated by comparison of force-penetration and indentation-penetration data obtained in the experiments by the simulation results.
2 PERIDYNAMIC CONTINUUM
Peridynamics continuum formulation [6] allows for the modeling of complex fragmentation processes. The reason is that the internal forces are computed, instead of a displacement gradient, from a displacement difference of material point x, with a set of material points 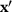 within a volume defined by a cutoff radius δ, known as the peridynamic horizon [11]. This notion of direct connectivity between the material points is referred to as a bond. Fracture processes are modeled by irreversibly deleting the bonds between the material points once they reach a critical value. Once a bond fails, it does not further contribute to the internal force calculation.
within a volume defined by a cutoff radius δ, known as the peridynamic horizon [11]. This notion of direct connectivity between the material points is referred to as a bond. Fracture processes are modeled by irreversibly deleting the bonds between the material points once they reach a critical value. Once a bond fails, it does not further contribute to the internal force calculation.
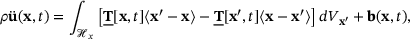 (1)
(1)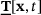 is the force state at x and
is the force state at x and 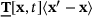 is the force, which a material point x exerts on
is the force, which a material point x exerts on 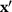 . Angular brackets are used to denote quantities that
. Angular brackets are used to denote quantities that 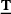 operates on.
operates on.The deformation state 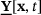 is defined as
is defined as 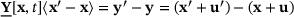 , where
, where 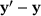 and
and 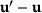 are the deformed relative position vector and the relative displacement vector of the bond
are the deformed relative position vector and the relative displacement vector of the bond  , respectively. Analogous to the deformation gradient of the classical continuum theory, it provides information on the change of relative positions in the neighborhood of a point x. In the following, the relative position vector is denoted as
, respectively. Analogous to the deformation gradient of the classical continuum theory, it provides information on the change of relative positions in the neighborhood of a point x. In the following, the relative position vector is denoted as 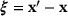 and the relative displacement vector is denoted as
and the relative displacement vector is denoted as 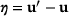 , which gives
, which gives 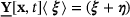 .
.
 for the ordinary state-based peridynamics is characterized by a magnitude, that is, a scalar state
for the ordinary state-based peridynamics is characterized by a magnitude, that is, a scalar state 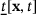 and a direction, provided by the unit vector state
and a direction, provided by the unit vector state 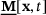 :
:
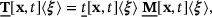 (2)
(2)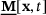 is a unit vector state, given by
is a unit vector state, given by
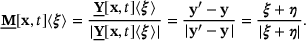 (3)
(3)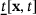 depends on a scalar stretch-like quantity, denoted as the extension state
depends on a scalar stretch-like quantity, denoted as the extension state 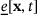 , which characterizes the kinematics of the model. Extension state
, which characterizes the kinematics of the model. Extension state 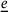 is defined as the difference of the length of the deformed and undeformed relative position vectors and can be further decomposed additively into an isotropic (
is defined as the difference of the length of the deformed and undeformed relative position vectors and can be further decomposed additively into an isotropic (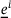 ) and a deviatoric (
) and a deviatoric (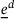 ) extension state, it is given by
) extension state, it is given by
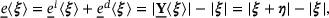 (4)
(4) =
= 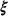 . The isotropic extension state can be represented in terms of a scalar-valued volume dilatation
. The isotropic extension state can be represented in terms of a scalar-valued volume dilatation 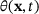 that is defined to match the volumetric strain of a classical continuum model under isotropic loading conditions.
that is defined to match the volumetric strain of a classical continuum model under isotropic loading conditions.
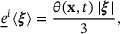 (5)
(5)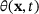 is defined as:
is defined as:
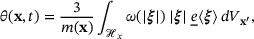 (6)
(6)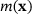 in known as the weighted volume, and is defined as:
in known as the weighted volume, and is defined as:
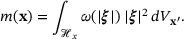 (7)
(7)2.1 Model extension to consider pore-collapse phenomenon
Ordinary state-based peridynamic model has been thoroughly investigated for the tension-dominated fracture problems, including failure strengths and crack dynamics [9, 12]. However, for cases where the dominant loading is in compression [13] and additional nonlinear dissipation phenomena, such as the pore-collapse, are present, the model underpredicts the failure strengths [14]. To this end, the standard ordinary state-based peridynamic model [7, 8] is extended to consider the pore-collapse phenomenon in porous materials.
The mechanical properties and the deformation characteristics of Bentheim sandstone were studied under triaxial loads by Klein et al. [4]. The material parameters for Bentheim sandstone are presented in Table 1. It is a relatively homogeneous porous rock, and these pores collapse under compressive loads leading to stiffening of the material, this effect can be seen by comparing the volumetric strain predicted by a constant bulk modulus with the one obtained in the experiments under hydrostatic compression, as shown in Figure 1. This stiffening under compressive pressure, due to pore-collapse, contributes to a significant increase in the total dissipated energy.
| Material parameter | Value |
|---|---|
| Young's modulus, E (Pa) | 9.5 × 109 |
| Poisson's ratio, ν | 0.18 |
| Density, ρ (Kg/m3) | 2011 |
Fracture energy, 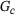 (J/m2) (J/m2) |
10 |
| Porosity, ϕ (%) | 24 |
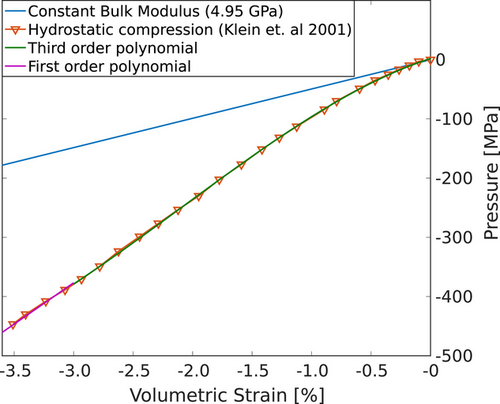
The material stiffening due to pore-collapse is modeled by using the experimental relationship between the hydrostatic compression and volumetric strain (Figure 1) instead of just using a constant Bulk modulus. According to Klein et al. [4], this relationship has one inflection point leading up to a compressive volumetric strain of 3.0% and after that, this relationship becomes linear again. So, the range of the volumetric strains from 0 to 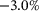 is fitted with a third-order polynomial and for compressive volumetric strain greater than 3.0%, a linear relationship is adapted. Additionally, these volumetric deformations are assumed to be irreversible, as pore-collapse is an irreversible process.
is fitted with a third-order polynomial and for compressive volumetric strain greater than 3.0%, a linear relationship is adapted. Additionally, these volumetric deformations are assumed to be irreversible, as pore-collapse is an irreversible process.
 (8)
(8) is the reversible elastic part of the volumetric strain and
is the reversible elastic part of the volumetric strain and 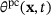 is the irreversible volumetric strain representing the pore-collapse under compression. The scalar force state
is the irreversible volumetric strain representing the pore-collapse under compression. The scalar force state 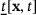 (Equation 2) is modified to consider only the elastic part of the dilatation as
(Equation 2) is modified to consider only the elastic part of the dilatation as
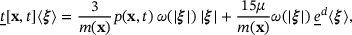 (9)
(9)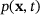 is the pressure which is computed according to
is the pressure which is computed according to
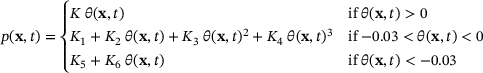 (10)
(10)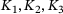 , and K4 are calibrated for a third-order polynomial and K5 and K6 are calibrated for a first-order polynomial using the experimental data from Klein et al.[4], as shown in Figure 1. The applicable range of volumetric strain for the third- and first-order polynomial are shown in Equation (10). For further details regarding the model, the interested reader is referred to Butt [14].
, and K4 are calibrated for a third-order polynomial and K5 and K6 are calibrated for a first-order polynomial using the experimental data from Klein et al.[4], as shown in Figure 1. The applicable range of volumetric strain for the third- and first-order polynomial are shown in Equation (10). For further details regarding the model, the interested reader is referred to Butt [14].2.2 Consideration of material heterogeneity
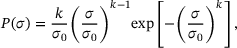 (11)
(11) for the shape parameter according to Liu et al. [16].
for the shape parameter according to Liu et al. [16].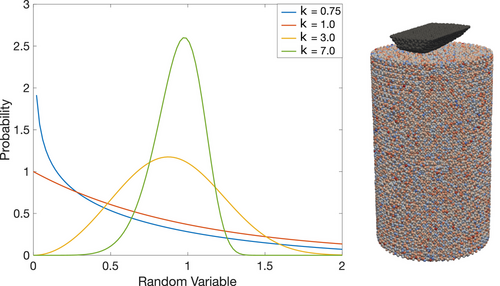
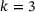 (right).
(right).The open-source software Peridigm [19, 20] was extended to consider the pore-collapse model as well as the distributed strengths in the simulation domain. This extended version of Peridigm is used to carry out the simulations presented in the next section.
3 ROCK INDENTATION SIMULATIONS
Numerical and experimental investigations [10, 21, 22] have shown that the rock fragmentation under indentation involves several progressive deformation mechanisms including the elastic deformations at an initial loading stage, then the volumetric compaction, plastic deformation, and finally the macro fracture. Thus, it is necessary for a simulation model to be able to reproduce these qualitative features observed in the indentation experiments.
Simulations performed in this study for the indentation tests cover a total of six specimen sizes, with a combination of three diameters 30, 50, and 84 mm and two heights 50 and 100 mm. For validating the current model, we use the experimental data from indentation tests on Bentheim Sandstone reported in Yang et al. [10]. The temporal evolution of fractures occurring due to the indentation load is presented in Figure 3 for a specimen with 30-mm diameter and 100-mm height. The simulation captures the experimental observation of the successive formation of the crushed zone and the initiation of a central macroscopic tensile fracture splitting the sample in half. Once the tensile stresses at the perimeter of this zone exceed a critical value, a tensile crack is formed which splits the specimen. As this tensile crack propagates, it exceeds a critical crack propagation velocity, at which the crack tip bifurcation takes place and the crack branches [12], as shown in the fourth column of Figure 3. Finally, the specimen splits into two main and several small fragments (fifth column of Figure 3).

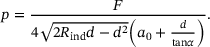 (12)
(12)
4 CONCLUSION
The standard constitutive framework of the ordinary state-based peridynamics was extended to include the pore-collapse phenomenon, which was modeled as permanent deformations. The extended model was validated through qualitative comparisons with the AE data and quantitative comparisons with the force-penetration and the pressure-penetration data from the indentation experiments performed on a Bentheim sandstone sample. These results suggest that the extended simulation model has a promising potential for modeling the indentation and excavation processes in porous rocks.
ACKNOWLEDGMENTS
The authors gratefully acknowledge the financial support provided by the German Science Foundation (DFG) in the framework of project C4 of the Collaborative Research Center SFB 837 Interaction modeling in mechanized tunneling (Grant-No. 77309832).
Open access funding enabled and organized by Projekt DEAL.




