Making a difference? The effects of Teach For America in high school
Abstract
Teach For America (TFA) selects and places graduates from the most competitive colleges as teachers in the lowest-performing schools in the country. This paper is the first study that examines TFA effects in high school. We use rich longitudinal data from North Carolina and estimate TFA effects through cross-subject student and school fixed effects models. We find that TFA teachers tend to have a positive effect on high school student test scores relative to non-TFA teachers, including those who are certified in field. Such effects offset or exceed the impact of additional years of experience and are particularly strong in science. © 2011 by the Association for Public Policy Analysis and Management.
Teach For America (TFA) recruits and selects graduates from some of the most selective colleges and universities across the country to teach in the nation's most challenging K−12 schools throughout the nation. TFA has grown significantly since its inception in 1990, when it received 2,500 applicants and selected and placed 500 teachers. In 2005, it received over 17,000 applicants and selected and placed a little over 2,000 new teachers, and the program anticipates expanding to over 4,000 placements in 2010. In total, the program has affected the lives of nearly 3 million students.
The growth of the program suggests that TFA is helping to address the crucial need to staff the nation's schools, a particularly acute need in high-poverty schools, but TFA is not without its critics. The criticisms tend to fall into two categories. The first is that most TFA teachers have not received traditional teacher training and therefore are not as prepared for the demands of the classroom as traditionally trained teachers. TFA corps members participate in an intensive five-week summer national institute and a two-week local orientation and induction program prior to their first teaching assignment.1 2 The second criticism is that TFA requires only a two-year teaching commitment, and the majority of corps members leave at the end of that commitment. The short tenure of TFA teachers is troubling because research shows that new teachers are generally less effective than more experienced teachers (Rivkin, Hanushek, & Kain, 2005; Rockoff, 2004).
The research reported here investigates the relative effectiveness (in terms of student tested achievement) of TFA teachers and examines the validity of the criticisms of TFA. Specifically, we look at TFA teachers in high schools, and especially in math and science, where considerable program growth is planned over the next few years. To the best of our knowledge, this is the first study of TFA at the high school level.
Using individual-level student data linked to teacher data in North Carolina, we estimate the effects of having a TFA teacher compared to a traditional teacher on student performance. The North Carolina data we employ are uniquely suited for this type of analysis because it includes end-of-course (EOC) testing for students across multiple subjects. This allows us to employ statistical methods that attempt to account for the nonrandom nature of student assignments to classes and teachers, which have been shown to lead to biased estimates of the impact of teacher credentials (Clotfelter, Ladd, & Vigdor, 2010; Goldhaber, 2007).
The findings show that TFA teachers are in general more effective, as measured by student exam performance, than traditional teachers. Moreover, they suggest that the TFA effect, at least in the grades and subjects investigated, offsets or exceeds the impact of additional years of experience, implying that TFA teachers are at least as effective as experienced high school teachers in math classes and more effective than experienced teachers in science classes.
PREVIOUS RESEARCH
Research examining the impact of TFA teachers on student performance is relatively limited given its rapid expansion and the attention that the program has received from the education policy community, college students, and school districts serving low-income communities.
We found no research on TFA at the high school level. Most work has focused on elementary school teachers and some on middle school teachers. Appendix Table A1 2 3 summarizes three recent studies that provide direct estimates of the TFA effect on student achievement. The most prominent study is the random assignment study conducted by Mathematica (Decker, Mayer, & Glazerman, 2006). The Mathematica study compares student achievement outcomes in grades 1 through 5 among students taught by TFA teachers and other teachers in the same schools and at the same grade levels. Students were randomly assigned to teachers prior to the beginning of the school year to ensure there were no systematic differences between the student groups at the outset of the study. The control group included all traditional teachers, representing the set of teachers who would likely have taught the students in the absence of TFA. The study found that TFA teachers outperformed traditional teachers in student math achievement by about 0.15 standard deviation on average. When TFA teachers were compared with inexperienced traditional teachers, the impact on math achievement was even larger. No significant difference was found between TFA teachers and traditional teachers in improving students' reading achievement.
Two other studies, both using large-scale data from New York City, also found significant positive TFA effects in math. In addition to using nonexperimental data, these two studies differ from the Mathematica study by focusing on reading and math performance of students in grades 4 though 8; both differentiated non-TFA teachers into multiple categories of teachers (e.g., in terms of certification), and both explicitly took experience into account.
Kane, Rockoff, and Staiger (2006) used six years of data and found a small positive effect for TFA on student math achievement (0.02 standard deviation) relative to certified teachers, controlling for years of teaching experience. The effect was somewhat smaller for elementary school teachers (0.015) and larger for middle school teachers (0.027). They also found that the returns to experience were greater for TFA teachers than for traditionally certified teachers, though not statistically significant. The experience differentials overall were small, such that even a small difference in effectiveness may offset turnover.
Boyd et al. (2006) compared the performance of teachers entering teaching in New York City from different pathways, including TFA. Compared with “college recommended” teachers—those who fulfilled certification requirements at a university-based program registered with the state—TFA teachers were found to have a positive effect of 0.05 standard deviation on students' middle school math performance and no effect on students' elementary school math performance.
In addition to these three studies, two smaller TFA studies were conducted using data from Houston (Raymond, Fletcher, & Luque, 2001; Darling-Hammond et al., 2005). Both found positive effects for TFA in math on the state test, though the second study found negative effects on other subjects and tests. The first study compared TFA teachers to other teachers in the district; the second study compared TFA teachers to other teachers holding standard certification. These two studies, however, are not as rigorous as the New York City studies.3 4
This study focuses on TFA effects in high school, where teacher academic qualifications are particularly important (Goldhaber & Brewer, 2000). Four sections follow. We first describe the data and the variables used in the analysis. The next section discusses the analytic strategy we employ. This is followed by a presentation of results. The final section discusses the implications for policy and practice.
DATA
We focus our analysis on North Carolina because of the rich administrative databases available through the North Carolina Education Research Data Center (NCERDC) at Duke University. Since the late 1990s, the state of North Carolina has required schools to administer subject-specific end-of-course (EOC) exams during the last two weeks of the school year.4 5 We estimate the effect of Teach For America teachers relative to traditional-route teachers on student achievement in high school using EOC exam outcomes.
NCERDC collects data from the North Carolina Department of Public Instruction (NCDPI) at the end of each school year and compiles the data into annual data sets at the student, teacher, classroom, and school levels. Student data contain information on ethnicity, gender, exceptionality status, grade level, district and school code, survey data on parent education and homework habits, and scale score achievement levels for any EOC exams taken by a student in a given year.5 6 Teacher data include salary, experience, licensure, educational attainment, PRAXIS test scores, and National Board Certification. Teach For America staff helped us construct a separate data set showing Teach For America corps members, which NCERDC later linked to their teacher data using Social Security numbers. Finally, the classroom data contain records for each activity that occurred in a North Carolina public school in a year. Records list course title, section number, semester, subject, grade level, student ethnicity and gender counts, and teacher experience, ethnicity and gender.
We limit our data to the 2000–2001 through 2006–2007 school years, the years of data available during which Teach For America corps members were teaching in North Carolina. We further limit our sample to the 23 Local Education Agencies (LEAs) that hired at least one TFA teacher at any point during this time period. Not all schools in these LEAs had TFA teachers during the study period. Since schools that hired TFA teachers may be different from those that did not in terms of school leadership, management, teacher support, and recruitment strategies, our final analytic samples are restricted to teachers and students in schools that hired at least one TFA teacher. We merge each annual student data set into a student longitudinal file. We apply the same method to the teacher and classroom data, so that we have three longitudinal files, one each at the student, teacher, and classroom levels.
To estimate the effect of a teacher on her students' testing outcomes, we must link students to their classroom instructor for the relevant EOC exam. This presents a challenge in North Carolina. The student data identify the proctor of each student's EOC exam, but the proctor is not necessarily the instructor for that student's class. In Goldhaber and Anthony (2004), the authors cite North Carolina state officials who say that at least 90 percent of the time, the students' proctor is the same person as the actual classroom teacher. They verify this information by contacting 20 large school districts and find that the proctor matches the students' classroom teacher 80 percent of the time at the elementary level. At the high school level, in Clotfelter, Ladd, and Vigdor (2010), the authors link classroom data to the student data using the classroom instructor code and the student exam proctor code and verify those matches using a fit statistic based on classroom demographics. They found a match in about 70 to 75 percent of the cases. Given the success of this method, we apply a matching and verification method similar to that used in Clotfelter, Ladd, and Vigdor, as described as follows.
First, individual students on the EOC file were aggregated into test classrooms by district and school code, year, test proctor, subject, and class period. Each resulting record is associated with one proctor and lists classroom-level demographic, exceptionality, and grade-level information. Next, we turn to the actual classroom data. We keep only course descriptors requiring EOC assessments as stipulated by the North Carolina Department of Public Instruction (Appendix Table A2) and collapse records for the same course meeting that differ only on the semester variable into one record per year.6 7 With both the EOC and classroom data aggregated into unique classroom-by-year-by-subject records, they can be matched. To do so, we link all exam classrooms in a school and year with all course activities related to the test subject in that school for that school year. Then we verify the matches using the teacher ID variable and a fit statistic similar to the one used by Clotfelter, Ladd, and Vigdor (2010). This statistic measures the expected squared deviations of total classroom membership count, number of white students, and number of male students between test classrooms and actual instructional classrooms.
We go through a number of steps to verify possible matches. First, we consider those classes matched by a uniquely identifiable teacher ID. If more than one exam classroom match occurred for an actual classroom teacher in the same section, course, school, and year, we keep the match with the lowest fit statistic (thus closer resemblance between the exam and actual classrooms). Among these retained matches, cases where the fit statistic is greater than or equal to 1.5 are deemed unreliable and hence discarded. The remaining cases are considered “good” matches with reasonable confidence. They constitute our first classroom and teacher subsample (sample A).
With those matches set aside, we use the fit statistic to verify classroom matches within school, year, and subject that do not match on teacher ID. The general idea is that, when an EOC exam is administered by a teacher other than the classroom instructor, if the test classroom sufficiently resembles the instruction classroom in terms of student demographic compositions, a classroom instructor can be reliably assigned to that group of students. The success of this strategy relies on the number of test classrooms within a school–year–subject combination and how distinctive they are. In our high school data set, the median number of test classrooms within each school, year, and subject is 6, and they appear to be sufficiently different from each other to be distinguished by demographic distributions. For each unique actual instructional classroom, we keep the test classroom that matched with the lowest fit statistic. Even after identifying the best match, if the fit statistic is equal to or greater than 1.5, we drop that classroom. The remaining matches constitute our second classroom and teacher subsample (sample B). We then combine those classrooms matched by teacher code and verified with those matched using only the fit statistic. In this data set, if a test proctor matches two actual classrooms, we keep the match with the lower fit statistic.
Once classroom instructors are identified, we attach them back to the student-level test data and link teacher characteristics data to the actual classroom instructor. Using this method, we are able to match about 84 percent of students to their teachers. For the purpose of model estimation, we use two alternative analytical samples to ensure estimated TFA effects are robust to matching methods. The first sample includes all teachers who are either matched on their ID and verified or matched by class demographic variables only. As we are less confident with cases where proctors and instructors are matched solely on the basis of class demographics, the second sample includes only those teachers who are matched on ID and verified by class demographics.
ANALYTIC STRATEGY
A key challenge to the estimation of TFA teacher effects is possible nonrandom sorting of teachers and students both across and within schools. Evidence has shown a matching between observed teacher qualifications (such as years of experience) and student achievement, possibly as a result of teacher preference and parent pressure (Clotfelter, Ladd, & Vigdor, 2010). When both teacher quality and student performance are systematically related to student ability and motivation, the relationship between teacher and student performance cannot be reliably estimated. In this particular study, if TFA teachers are assigned to students with greater needs, estimated TFA effects are likely to be downwardly biased; on the other hand, if TFA teachers are systematically assigned to less challenging classes, OLS estimates of TFA effects are likely to be biased upward.
 (1)
(1) (2)
(2)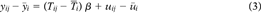 (3)
(3)As should be clear, whether or not the student-specific error term varies by subject is key to the validity of cross-subject fixed effects models. If the assignment of TFA teachers is based on subject-specific student ability that is multidimensional, the nonrandom matching of teachers to students remains unaccounted for in these fixed effects models.
Using the same North Carolina high school data, Coltfelter, Ladd, and Vigdor (2010) investigate this crucial question in great detail. They find that students with strong math ability and students with strong reading ability in the eighth grade have similar high school course track assignments (either in an advanced algebra course or in an advanced English course). Among students with different abilities in math and reading, those with relative strengths in one subject are no more likely than those relatively weak in the subject to be assigned to an advanced course. In addition, they find no relationship between the relative credentials of a student's algebra and English teachers and the student's ability in math relative to reading. Their investigation concludes that in North Carolina high schools, student ability varies little by subject; when schools assign students to classrooms, they appear to consider student ability to be “single dimensional.”
For further assurance, we conducted a direct examination of the eight core EOC subjects using an exploratory factor analysis. The results show that all eight tests are loaded predominantly on one single underlying factor, with factor loadings (representing the correlations between test scores in each subject and the factor) ranging from 0.74 to 0.87 (Figure 1). The analysis shows that a single underlying factor accounts for 67 percent of the variance in test scores across all eight subjects. None of the remaining factors accounts for more than 8 percent of the total variance. When we apply the same analysis separately for math subjects and science subjects (not shown in the figure), we find even stronger commonality between subjects that are within the same subject area (84 percent of the variance in all math subjects and 78 percent of the variance in all science subjects is accounted for by a single factor). These evidences lend further support to the assumption that students performing well in one subject are also likely to perform well in other subjects, and that any teacher–student sorting based on ability in one subject probably will follow similar patterns if such sorting were based on student ability in any other subjects.
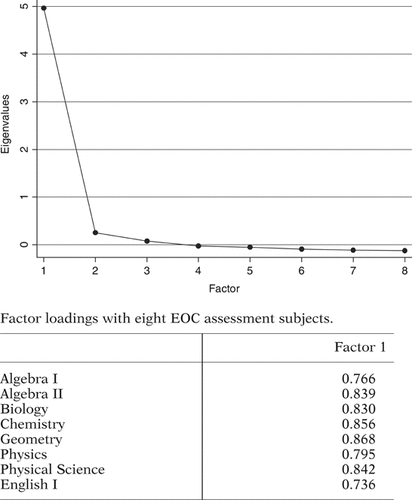
Screenplot of eigenvalues after exploratory factor analysis of eight EOC assessment subjects.
The lack of an initial student performance measure in a specific subject has another important implication for our cross-subject student fixed effects model. Since education is a cumulative process, academic performance depends not only on contemporaneous inputs but also on inputs from all previous time periods. Levels of academic performance at the beginning of the current time period capture students' cumulative education experiences up until that point. As a result, value-added models are typically used to estimate teacher effects on student performance. Without initial test scores for high school EOC subjects, we are not able to specify a model that controls for lagged student performance on the right-hand side of the equation (or the construction of a gain score).
In effect, our model without pretest information assumes complete “decay” of prior input; that is, initial academic preparation in a specific subject at the time of class enrollment has a negligible effect on EOC test scores. What the cross-subject model does account for is the overall level of performance across eight subjects. Clotfelter, Ladd, and Vigdor (2007) argue that a model with a missing lagged term leads to downward bias in estimates, and that the less the decay, the larger the downward bias.8 9 The TFA effect estimated using the cross-subject model, therefore, is likely to provide the lower bound of the true effects.
Variables and Model Specification
The North Carolina Department of Public Instruction requires students taking certain high school courses for credit to take end-of-course (EOC) tests on multiple subjects, including eight core subjects requiring testing for the entire span of years in our data set (Algebra I, Algebra II, Geometry, Physical Sciences, Physics, Chemistry, Biology, and English I9 10 ). Our dependent variable is standardized EOC test scores in these eight subjects. The scores are standardized by subject and year, with mean 0 and standard deviation 1. By this transformation, scores from different tests are put on the same scale.
As this study focuses on the overall effectiveness of TFA teachers as compared to non-TFA teachers, our key independent variable is an indicator variable of TFA membership. Because the primary research question of this study is whether or not the TFA program can provide effective teachers to supplement the existing teaching force, our main model does not include variables such as teacher experience, the selectivity of higher education institutions attended by teachers, or license test scores. The relative effectiveness of TFA teachers as compared with non-TFA teachers, however, may be the result of a couple of factors, such as differences in academic preparation in a subject area and in pedagogical training. Therefore, we also estimate several model specifications that include additional teacher variables to explore factors that might have been driving the effectiveness differentials.
All models are estimated with student fixed effects as well as subject-by-grade and year fixed effects. In all models we also include class size and peer average performance on 8th-grade math and reading (from North Carolina's end-of-grade exams that are administered to elementary and middle school students) to control for classroom environment. It should be noted that, due to the lack of survey data, we are unable to control for some unobserved factors that might affect the interpretation of our estimated TFA effect. For example, schools may provide additional support to TFA teachers. If this is the case, policymakers should take into account the added “cost” in hiring a TFA teacher above and beyond the cost of hiring a non-TFA teacher. As another example, a newly hired TFA teacher may be treated differently from a newly hired non-TFA teacher by her colleagues. Differences in collegial relationship, if they exist, could also affect how a TFA teacher performs relative to a non-TFA teacher.
RESULTS
Descriptive Findings
Tables 1–3 present comparisons of TFA teachers with all non-TFA teachers as well as novice non-TFA teachers in schools that had at least one TFA teacher. Novice teachers are defined as teachers with less than three years of experience. During our study period, there are an increasing number of TFA teachers in our sample over time, from seven in 2002 to 29 in 2007. All but three TFA teachers have two years of experience or less.
| TFA Teacher | Traditional Teacher | Novice Traditional Teachera | ||||
|---|---|---|---|---|---|---|
| Mean | SE | Mean | SE | Mean | SE | |
| Sex (percent) | ||||||
| Female | 65.31 | 4.30 | 67.68 | 0.39 | 71.78 | 0.86 |
| Male | 34.69 | 4.83 | 32.32 | 1.42 | 28.22 | 2.22 |
| Race (percent) | ||||||
| Black | 6.12 | 2.43 | 38.77* | 1.48 | 39.17* | 2.41 |
| Hispanic | 1.02 | 1.02 | 1.01 | 0.30 | 0.97 | 0.49 |
| White | 86.74 | 3.44 | 56.72* | 1.50 | 56.45 | 2.45 |
| Other | 6.12 | 2.43 | 3.50 | 0.56 | 3.41 | 0.90 |
| Overall teaching experience | 0.18 | 0.04 | 8.91* | 0.32 | 0.55* | 0.04 |
| Education attainment (percent) | ||||||
| Bachelor's | 97.96 | 1.44 | 71.28* | 1.40 | 85.89* | 1.72 |
| Master's | 2.04 | 1.44 | 26.43* | 1.36 | 13.87* | 1.71 |
| Advanced/doctorate | 0.00 | 0.00 | 2.20* | 0.45 | 0.24 | 0.24 |
| Selectivity of IHEb | ||||||
| Most selective | 17.35 | 3.85 | 2.28* | 0.46 | 2.19* | 0.72 |
| Very selective | 44.90 | 5.05 | 16.51* | 1.14 | 19.47* | 1.96 |
| Moderately selective | 37.76 | 4.92 | 54.27* | 1.54 | 54.75* | 2.46 |
| Not selective/not ranked | 0.00 | 0.00 | 26.95* | 1.37 | 23.60* | 2.10 |
| License test score (PRAXIS)c | 0.44 | 0.07 | −0.03* | 0.03 | −0.03* | 0.05 |
| Licensed in subject taughtd, e | ||||||
| Science | 88.00 | 3.78 | 84.38 | 1.21 | 82.92 | 2.43 |
| Math | 73.08 | 6.21 | 79.51 | 1.12 | 76.78 | 2.59 |
| English | 92.00 | 3.88 | 70.94* | 1.84 | 75.77* | 3.08 |
| Number of unique teachers | 98 | 1,087 | 413 | |||
| Number of teacher/year obs. | 149 | 2,423 | 595 | |||
- Note: Population is limited to teachers who were positively matched to their students.
- * * Significantly different from TFA teachers at 0.05 level.
- a a Novice teachers are those with fewer than three years' experience.
- b b Based on Petersons College Selectivity Rankings.
- c c There were 64 TFA teacher and year observations and 787 traditional teacher and year observations (248 novice ) with valid PRAXIS scores. Scores are standardized onto the same scale across years.
- d d Science licenses include: Biology (grades 9 to 12), Chemistry (grades 9 to 12), Earth Science (grades 9 to 12), Physical Science (grades 9 to 12), Physics (grades 9 to 12), and Science (grades 9 to 12). Math licenses include Mathematics (grades 9 to 12). English licenses include English (grades 9 to 12) and Reading (grades K to 12).
- e e Science classes are Biology, Chemistry, Physical Science, and Physics. Math classes are Algebra I, Algebra II, and Geometry. English includes only English I.
- Source: North Carolina Education Research Data Center.
| TFA Teacher | Traditional Teacher | Novice Traditional Teachera | ||||
|---|---|---|---|---|---|---|
| Mean | SE | Mean | SE | Mean | SE | |
| Average class size | 21.51 | 0.56 | 20.76 | 0.12 | 20.51 | 0.24 |
| Percent minority | 81.07 | 0.98 | 72.73* | 0.29 | 77.58* | 0.54 |
| Percent handicapped and learning disability | 9.65 | 1.09 | 10.59 | 0.26 | 12.23* | 0.59 |
| Percent LEP | 2.62 | 0.36 | 3.15 | 0.13 | 3.68* | 0.29 |
| Percent male | 47.70 | 0.79 | 48.47 | 0.19 | 49.54* | 0.38 |
| Percent achieving at level b | ||||||
| Algebra I | ||||||
| Superior performance | 12.61 | 2.53 | 11.90 | 0.43 | 10.77 | 0.81 |
| Consistent mastery | 46.24 | 3.83 | 39.00 | 0.54 | 38.57 | 1.11 |
| Inconsistent mastery | 28.55 | 3.22 | 37.89* | 0.58 | 38.55* | 1.15 |
| Insufficient mastery | 12.60 | 3.65 | 11.21 | 0.43 | 12.12 | 0.86 |
| Algebra II | ||||||
| Superior performance | 11.44 | 2.09 | 20.26* | 0.80 | 9.22 | 1.27 |
| Consistent mastery | 44.32 | 2.92 | 36.41* | 0.61 | 34.59* | 1.55 |
| Inconsistent mastery | 36.96 | 3.23 | 36.91 | 0.80 | 47.49* | 1.89 |
| Insufficient mastery | 7.28 | 1.79 | 6.42 | 0.39 | 8.70 | 1.11 |
| Biology | ||||||
| Superior performance | 6.06 | 1.08 | 7.85 | 0.35 | 4.93 | 0.54 |
| Consistent mastery | 36.75 | 2.01 | 34.78 | 0.58 | 30.67* | 1.14 |
| Inconsistent mastery | 39.97 | 1.90 | 35.27* | 0.53 | 37.43 | 0.98 |
| Insufficient mastery | 17.22 | 1.62 | 22.10* | 0.64 | 26.97* | 1.33 |
| Chemistry | ||||||
| Superior performance | 14.88 | 2.30 | 17.53 | 0.95 | 6.77* | 0.99 |
| Consistent mastery | 36.99 | 2.57 | 31.49* | 0.72 | 28.93* | 1.61 |
| Inconsistent mastery | 36.35 | 2.88 | 32.23 | 0.78 | 38.90 | 1.43 |
| Insufficient mastery | 11.79 | 1.76 | 18.75* | 0.82 | 25.40* | 1.74 |
| Geometry | ||||||
| Superior performance | 5.89 | 1.38 | 10.13* | 0.54 | 6.19 | 0.91 |
| Consistent mastery | 28.11 | 2.81 | 30.89 | 0.61 | 28.42 | 1.38 |
| Inconsistent mastery | 48.27 | 2.97 | 44.50 | 0.68 | 48.89 | 1.49 |
| Insufficient mastery | 17.73 | 2.86 | 14.49 | 0.53 | 16.51 | 1.27 |
| Physics | ||||||
| Superior performance | 13.87 | 3.44 | 25.53* | 2.18 | 5.55 | 2.53 |
| Consistent mastery | 50.77 | 5.83 | 40.68 | 1.69 | 50.94 | 7.11 |
| Inconsistent mastery | 26.43 | 5.97 | 24.50 | 1.59 | 27.64 | 5.40 |
| Insufficient mastery | 8.93 | 2.76 | 9.29 | 1.00 | 15.87 | 3.97 |
| Physical Science | ||||||
| Superior performance | 6.55 | 2.47 | 6.48 | 0.53 | 1.90 | 0.43 |
| Consistent mastery | 47.93 | 4.52 | 36.37* | 0.90 | 29.22* | 1.77 |
| Inconsistent mastery | 42.83 | 5.71 | 44.87 | 0.92 | 52.30 | 1.60 |
| Insufficient mastery | 2.69 | 1.22 | 12.28* | 0.72 | 16.58* | 1.62 |
| English I | ||||||
| Superior performance | 12.50 | 1.33 | 16.80* | 0.53 | 13.20 | 0.87 |
| Consistent mastery | 47.55 | 1.83 | 39.52* | 0.53 | 38.52* | 0.94 |
| Inconsistent mastery | 29.86 | 1.58 | 29.93 | 0.54 | 34.21* | 0.99 |
| Insufficient mastery | 10.09 | 1.18 | 13.75* | 0.52 | 14.07* | 0.85 |
| Number of classes | 440 | 8,447 | 1,848 | |||
- Note: Population is limited to teachers who were positively matched to their students.
- * * Significantly different from TFA teachers at 0.05 level.
- a a Novice teachers are those with fewer than three years' experience.
- b b These are achievement levels defined by the North Carolina Department of Public Instruction.
- Source: North Carolina Education Research Data Center.
| TFA Teacher | Novice Traditional Teacher | Traditional Teachera | ||||
|---|---|---|---|---|---|---|
| Mean | SE | Mean | SE | Mean | SE | |
| Sex (percent) | ||||||
| Female | 53.34 | 0.57 | 51.55* | 0.22 | 52.16 | 0.31 |
| Male | 46.66 | 0.57 | 48.45* | 0.22 | 47.85 | 0.31 |
| Race (percent) Black | 70.53 | 0.52 | 62.07* | 0.21 | 64.28* | 0.30 |
| Hispanic | 4.04 | 0.23 | 4.69* | 0.09 | 4.88* | 0.13 |
| White | 21.50 | 0.47 | 29.08* | 0.20 | 26.98* | 0.28 |
| Other | 3.92 | 0.22 | 4.17 | 0.09 | 3.85 | 0.12 |
| Exceptionality (percent) | ||||||
| Gifted | 7.28 | 0.30 | 6.16* | 0.10 | 5.65* | 0.14 |
| Learning disability | 4.26 | 0.23 | 4.66 | 0.09 | 4.49 | 0.13 |
| Handicapped | 2.48 | 0.18 | 3.27* | 0.08 | 2.96* | 0.11 |
| Non-exceptional | 85.99 | 0.40 | 85.91 | 0.15 | 86.91* | 0.21 |
| LEP students (percent) | 2.53 | 0.18 | 2.86 | 0.07 | 2.85 | 0.10 |
| Parents' education attainment | ||||||
| Less than high school | 9.66 | 0.36 | 8.90* | 0.13 | 8.99 | 0.19 |
| High school diploma | 32.11 | 0.57 | 28.27* | 0.21 | 28.85* | 0.30 |
| Some college | 34.91 | 0.58 | 32.74* | 0.21 | 32.80* | 0.31 |
| Bachelor's | 16.45 | 0.45 | 20.30* | 0.18 | 19.62* | 0.26 |
| Graduate degree | 5.15 | 0.27 | 7.60* | 0.12 | 6.99* | 0.17 |
| Achievement scoresb | ||||||
| Algebra I | −0.40 | 0.03 | −0.55* | 0.00 | −0.59* | 0.01 |
| Algebra II | −0.56 | 0.03 | −0.41* | 0.01 | −0.73* | 0.01 |
| Biology | −0.49 | 0.02 | −0.39* | 0.01 | −0.55* | 0.01 |
| Chemistry | −0.42 | 0.03 | −0.47 | 0.01 | −0.84* | 0.02 |
| Geometry | −0.61 | 0.03 | −0.50* | 0.01 | −0.67* | 0.01 |
| Physics | −0.68 | 0.05 | −0.47* | 0.02 | −0.78 | 0.06 |
| Physical Science | −0.27 | 0.06 | −0.40* | 0.01 | −0.70* | 0.02 |
| English I | −0.55 | 0.02 | −0.36* | 0.01 | −0.46* | 0.01 |
| Number of unique studentsc | 7,678 | 53,865 | 25,918 | |||
- Note: Population is limited to teachers who were positively matched to their students and unique students.
- * * Significantly different from TFA teachers at 0.05 level.
- a a Novice teachers are those with fewer than three years' experience.
- b b Standardized scores by subject and year.
- c c The total number of unique students in our sample is smaller than the sum of these numbers, as students may be taught by both TFA and traditional teachers.
- Source: North Carolina Education Research Data Center.
Compared with non-TFA teachers and novice non-TFA teachers, a smaller percentage of TFA teachers are from racial and ethnic minority groups (Table 1). About 13 percent of TFA teachers are nonwhite, compared with about 25 percent minorities among non-TFA teachers. TFA teachers are typically new college graduates. As a result, only 2 percent of them have a master's degree or higher. By contrast, 29 percent of all non-TFA teachers and 14 percent of novice non-TFA teachers have a graduate degree. However, significantly more TFA teachers have graduated from “most selective” or “very selective” higher education institutions than non-TFA teachers do (62 percent versus 19 percent). TFA teachers also have higher PRAXIS scores10 -8 on average than non-TFA teachers (about half a standard deviation higher).
TFA and non-TFA teachers are also assigned to classrooms and students with distinct characteristics and performance levels. Classes taught by TFA teachers on average have higher minority concentration (about 81 percent) as compared to those taught by non-TFA teachers (73 percent for all non-TFA teachers and 78 percent for novice non-TFA teachers) (Table 2). Students of TFA teachers are also less likely to have parents with bachelor's degrees or higher (Table 3). When compared with novice traditional teachers in schools that have had at least one TFA teacher, TFA teachers are assigned to higher-achieving students, both in terms of the average test scores and the percentage of students in a classroom who performed at the “superior performance” and the “consistent mastery” levels, as defined by the North Carolina Department of Public Instruction (Tables 2 and 3). When TFA teachers are compared with all traditional teachers, however, the pattern is less clear, with TFA teachers being assigned to lower-performing classrooms and students in some subjects and comparable or higher-performing classrooms and students in the others.
In short, TFA teachers differ significantly from non-TFA teachers (both novice and overall) in terms of their demographic characteristics, academic preparation, and experience, as well as the classes and students they teach. Such patterns are consistent with findings from earlier studies on TFA teachers using data from different states. Interestingly, when we compare TFA teachers and traditional teachers across all schools in districts that have hired at least one TFA teacher during the study period, we find that classrooms and students assigned to TFA teachers perform consistently worse than those assigned to traditional and novice traditional teachers in all subjects.11 -7 This indicates that TFA teachers, selected from the most competitive undergraduate institutions, are placed in the lowest-performing schools, but not necessarily the most challenging classrooms in those schools.
Analytic Findings
Such nonrandom assignment of TFA teachers to classrooms and students needs to be accounted for before reliable TFA effects can be estimated. Using the analytic strategy discussed in the previous section, student fixed effects models are estimated, with robust standard errors adjusted for the clustering of students within teachers. Results are presented in Tables 4, 5, and 6. Each table shows two models, with and without the teacher experience variables, in order to address the question of the effectiveness of TFA teachers from two perspectives. From the policymakers' perspective, it is important to learn whether TFA teachers' relatively short tenure is compensated for by their stronger academic preparation. In other words, it is important to learn how an average TFA teacher with one to two years of experience compares with an average traditional teacher with eight to nine years of experience. From the perspectives of school administrators and students, however, probably the more relevant question is whether TFA teachers are more or less effective than traditional teachers they need to hire—those with similar levels of experience—in the absence of TFA.
| Without Experience Variables | With Experience Variables | |||
|---|---|---|---|---|
| Independent Variables | Coef. | SE | Coef. | SE |
| TFA teacher | 0.084 | 0.019* | 0.134 | 0.020* |
| Other teacher characteristics | ||||
| Teacher experience (ref.: < 3 yrs.) | ||||
| 3 to 5 years | 0.072 | 0.015* | ||
| 6 to 10 years | 0.073 | 0.015* | ||
| 11 years or more | 0.081 | 0.012* | ||
| Male (ref.: female) | −0.049 | 0.014* | −0.050 | 0.014* |
| Race (ref.: other minorities) | ||||
| Black | 0.042 | 0.022 | 0.033 | 0.021 |
| White | 0.068 | 0.022* | 0.060 | 0.020* |
| Hispanic | 0.044 | 0.038 | 0.035 | 0.048 |
| Education attainment (ref.: BA) | ||||
| Master's degree | 0.013 | 0.013 | 0.003 | 0.013 |
| Doctorate/other advanced degrees | −0.060 | 0.039 | −0.084 | 0.040* |
| Classroom characteristics | ||||
| Average grade-8 math | 0.101 | 0.017* | 0.096 | 0.016* |
| Average grade-8 reading | 0.073 | 0.016* | 0.073 | 0.015* |
| Class size | 0.001 | 0.000* | 0.001 | 0.000* |
| Number of observations | 146,937 | 145,570 | ||
| Number of clusters | 1,088 | 1,078 | ||
- Note: Included EOC subjects are: Algebra I, Algebra II, Biology, Chemistry, Geometry, Physics, Physical Science, and English I.
- * * Significant at 0.05 level.
- All models include subject by grade fixed effects as well as year fixed effects.
| Without Experience Variables | With Experience Variables | |||
|---|---|---|---|---|
| Independent Variables | Coef. | SE | Coef. | SE |
| TFA teacher | 0.053 | 0.036 | 0.132 | 0.037* |
| Other teacher characteristics | ||||
| Teacher experience (ref.: < 3 yrs.) | ||||
| 3 to 5 years | 0.065 | 0.022* | ||
| 6 to 10 years | 0.125 | 0.017* | ||
| 11 years or more | 0.103 | 0.015* | ||
| Male (ref.: female) | −0.084 | 0.013* | −0.087 | 0.013* |
| Race (ref.: other minorities) | ||||
| Black | −0.002 | 0.025 | 0.006 | 0.027 |
| White | 0.045 | 0.025 | 0.056 | 0.024* |
| Hispanic | 0.075 | 0.070 | 0.119 | 0.064 |
| Education attainment (ref.: BA) | ||||
| Master's degree | 0.007 | 0.017 | 0.008 | 0.017 |
| Doctorate/other advanced degrees | 0.154 | 0.030* | 0.145 | 0.032* |
| Classroom characteristics | ||||
| Average grade-8 math | 0.071 | 0.023* | 0.065 | 0.023* |
| Average grade-8 reading | −0.003 | 0.023 | 0.003 | 0.023 |
| Class size | 0.002 | 0.001* | 0.002 | 0.001* |
| Number of observations | 64,252 | 63,594 | ||
| Number of clusters | 441 | 436 | ||
- Note: Included EOC subjects are: Algebra I, Algebra II, and Geometry.
- * * Significant at 0.05 level.
- All models include subject by grade fixed effects as well as year fixed effects.
| Without Experience Variables | With Experience Variables | |||
|---|---|---|---|---|
| Independent Variables | Coef. | SE | Coef. | SE |
| TFA teacher | 0.157 | 0.039* | 0.189 | 0.039* |
| Other teacher characteristics | ||||
| Teacher experience (ref.: < 3 yrs.) | ||||
| 3 to 5 years | 0.067 | 0.026* | ||
| 6 to 10 years | 0.104 | 0.032* | ||
| 11 years or more | 0.065 | 0.025* | ||
| Male (ref.: female) | −0.066 | 0.024* | −0.064 | 0.025* |
| Race (ref: other minorities) | ||||
| Black | 0.000 | 0.049 | −0.053 | 0.038 |
| White | 0.091 | 0.051 | 0.019 | 0.036 |
| Hispanic | 0.184 | 0.066* | 0.192 | 0.099 |
| Education attainment (ref.: BA) | ||||
| Master's degree | 0.017 | 0.024 | −0.004 | 0.026 |
| Doctorate/other advanced degrees | −0.082 | 0.043 | −0.142 | 0.042* |
| Classroom characteristics | ||||
| Average grade-8 math | 0.044 | 0.029 | 0.044 | 0.028 |
| Average grade-8 reading | 0.048 | 0.026 | 0.047 | 0.026 |
| Class size | 0.001 | 0.001 | 0.001 | 0.001 |
| Number of observations | 50,771 | 50,180 | ||
| Number of clusters | 350 | 346 | ||
- Note: Included EOC subjects are: Biology, Chemistry, Physics, and Physical Science.
- * * Significant at 0.05 level.
- All models include subject by grade fixed effects as well as year fixed effects.
Using variations in test scores across all eight EOC subjects, Table 4 shows that the net effect of having a TFA teacher is about 8.5 percent of a standard deviation in student test scores over traditional teachers. This implies that when all the perceived strengths and weaknesses are considered, TFA teachers are on average more effective than traditional teachers, including experienced teachers. When teacher experience is controlled, the effect of TFA teachers over non-TFA teachers is 13.5 percent of a standard deviation, almost twice the effect of having a teacher with three years or more experience relative to having a novice teacher. Evidence shows that, in terms of test scores, TFA teachers are able to more than offset their lack of teaching experience, either due to their better academic preparation in particular subject areas or due to other unmeasured factors such as motivation. Consistent with the literature, our estimates show that the first three years of teaching experience makes a significant difference in teacher effectiveness, but the experience effect diminishes after that point.
Table 5 and 6 present estimates for math subjects and science subjects separately. The net effect of TFA teachers is insignificant in math and 15.7 percent of a standard deviation in science. When teaching experience is controlled, TFA teachers are more effective than non-TFA teachers in both math and science subject areas (13.2 percent and 18.9 percent of a standard deviation, respectively). These estimates demonstrate that, compared with traditional teachers with similar levels of experience whom TFA teachers are likely to replace, TFA teachers have strong positive effects on student test scores. And despite the limitations of TFA teachers, they are no worse than average traditional teachers in teaching math subjects and much more effective in teaching science subjects.
Because we do not have additional information to verify the validity of the student–teacher matches where test proctor IDs and instructor IDs do not match and where the student–teacher link is established solely on the basis of classroom demographic distributions, we are not able to evaluate the scope of possible mismatches between students and teachers in those cases and its impact on model estimates.12 -15 In order to check the sensitivity of estimated TFA effects to our teacher–student linking methods, we reestimate our models by excluding those cases. These results are presented in Table 7. Using only those students whose classroom teachers and test proctors have the same uniquely identifiable IDs, and whose instructional classrooms sufficiently resemble the test classrooms in terms of demographic characteristics, we find slightly stronger positive TFA effects (controlling for experience) when all eight subjects are included (0.184) as well as when only high school science subjects are analyzed (0.217). Similar to the results obtained when using larger samples, TFA effects remain about 2 to 3 times the effect of having three to five years of teaching experience. By comparison, the TFA effect on math subjects decreased (0.090), with its magnitude comparable to the effect of having three to five years of experience (0.070), and is statistically insignificant. This indicates that the estimated effect of having TFA teachers is somewhat sensitive to our teacher– student matching strategy for math test scores.
| All Subjects | Math Subjects | Science Subjects | ||||
|---|---|---|---|---|---|---|
| Independent Variables | Coef. | SE | Coef. | SE | Coef. | SE |
| TFA teacher | 0.184 | 0.028* | 0.090 | 0.076 | 0.217 | 0.051* |
| Other teacher characteristics | ||||||
| Teacher experience (ref.: < 3 yrs.) | ||||||
| 3 to 5 years | 0.069 | 0.019* | 0.070 | 0.033* | 0.071 | 0.044 |
| 6 to 10 years | 0.070 | 0.020* | 0.141 | 0.029* | 0.081 | 0.040* |
| 11 years or more | 0.092 | 0.015* | 0.157 | 0.022* | 0.058 | 0.032 |
| Male (ref.: female) | −0.065 | 0.016* | −0.092 | 0.020* | −0.083 | 0.029* |
| Race (ref.: other minorities) | ||||||
| Black | 0.082 | 0.032* | 0.055 | 0.049 | 0.071 | 0.036* |
| White | 0.114 | 0.030* | 0.114 | 0.044* | 0.161 | 0.030* |
| Hispanic | 0.174 | 0.067* | 0.227 | 0.091* | 0.436 | 0.063* |
| Education attainment (ref.: BA) | ||||||
| Master's degree | 0.008 | 0.017 | −0.008 | 0.024 | 0.061 | 0.034 |
| Doctorate/other advanced degrees | −0.106 | 0.054* | 0.157 | 0.027* | −0.137 | 0.063* |
| Classroom characteristics | ||||||
| Average grade-8 math | 0.113 | 0.023* | 0.025 | 0.038 | 0.024 | 0.041 |
| Average grade-8 reading | 0.046 | 0.023* | 0.024 | 0.036 | 0.069 | 0.044 |
| Class size | 0.000 | 0.000 | 0.001 | 0.001* | 0.001 | 0.001 |
| Number of observations | 87,294 | 37,957 | 30,999 | |||
| Number of clusters | 805 | 320 | 260 | |||
- Note: Included EOC subjects are: Algebra I, Algebra II, Biology, Chemistry, Geometry, Physics, Physical Science, and English I.
- * * Significant at 0.05 level.
- All models include subject by grade fixed effects as well as year fixed effects.
Changing Comparison Groups
Next, we compare TFA teachers with non-TFA teachers with various qualifications in order to capture a more nuanced picture of the TFA effect. First, as shown in descriptive Table 1, different proportions of TFA and non-TFA teachers teach a subject within their license field. We are interested in whether TFA teachers are as effective as those non-TFA teachers who are licensed in the subjects they teach. Table 8 shows that the TFA effects remain similar to those when we compare TFA teachers with all non-TFA teachers. In-field TFA teachers retain an advantage of 0.138, 0.126, and 0.168 standard deviations over in-field non-TFA teachers in student performance across all EOC subjects, across math subjects, and across science subjects, respectively.
| All Subjects | Math Subjects | Science Subjects | ||||
|---|---|---|---|---|---|---|
| Independent Variables | Coef. | SE | Coef. | SE | Coef. | SE |
| TFA teacher | 0.138 | 0.020* | 0.126 | 0.041* | 0.168 | 0.038* |
| Other teacher characteristics | ||||||
| Teacher experience (ref.: < 3 yrs.) | ||||||
| 3 to 5 years | 0.073 | 0.016* | 0.056 | 0.024* | 0.058 | 0.026* |
| 6 to 10 years | 0.069 | 0.015* | 0.111 | 0.017* | 0.091 | 0.033* |
| 11 years or more | 0.072 | 0.012* | 0.094 | 0.017* | 0.034 | 0.023 |
| Male (ref.: female) | −0.055 | 0.013* | −0.095 | 0.013* | −0.070 | 0.024* |
| Race (ref.: other minorities) | ||||||
| Black | 0.048 | 0.022* | 0.040 | 0.028 | −0.050 | 0.043 |
| White | 0.068 | 0.021* | 0.081 | 0.025* | 0.012 | 0.041 |
| Hispanic | 0.126 | 0.046* | 0.145 | 0.060* | 0.175 | 0.089* |
| Education attainment (ref: BA) | ||||||
| Master's degree | 0.003 | 0.013 | 0.013 | 0.017 | −0.005 | 0.027 |
| Doctorate/other advanced degrees | −0.084 | 0.040* | 0.124 | 0.041* | −0.132 | 0.044* |
| Classroom characteristics | ||||||
| Average grade-8 math | 0.116 | 0.018* | 0.078 | 0.024* | 0.047 | 0.031 |
| Average grade-8 reading | 0.052 | 0.016* | −0.003 | 0.026 | 0.042 | 0.029 |
| Class size | 0.001 | 0.000 | 0.001 | 0.001* | 0.000 | 0.001 |
| Number of observations | 128,925 | 55,076 | 45,857 | |||
| Number of clusters | 848 | 334 | 290 | |||
- Note: Included EOC subjects are: Algebra I, Algebra II, Biology, Chemistry, Geometry, Physics, and Physical Science.
- * * Significant at 0.05 level.
- All models include subject by grade fixed effects as well as year fixed effects.
Tables 9 and 10 present comparisons of TFA teachers with non-TFA teachers holding two types of regular teaching licenses: the Standard Professional I license (SP I) and the Standard Professional/Continuing license (SP II). The SP I license is typically for teachers with less than three years of experience who have satisfied all state requirements for becoming a regular classroom teacher, whereas the SP II license is given to teachers with more experience (see http://www.dpi.state.nc.us/licensure/ for more details). Since levels of experience are implicitly controlled for in these subsamples, experience variables are excluded from these models. When compared with less experienced teachers with a regular teaching license, TFA teachers remain to be more effective across all subjects, for math subjects only, and for science subjects only. As expected, the TFA advantage is reduced when TFA teachers are compared with more experienced teachers holding SP II licenses. The TFA effect falls to about 0.055 for all subjects and to about 0.119 for science subjects only, but remains statistically significant in both cases. The TFA effect becomes insignificant for math subjects.
| All Subjects | Math Subjects | Science Subjects | |||||
|---|---|---|---|---|---|---|---|
| Independent Variables | Coef. | SE | Coef. | SE | Coef. | SE | |
| TFA teacher | 0.143 | 0.024* | 0.111 | 0.074 | 0.212 | 0.083* | |
| Other teacher characteristics | |||||||
| Male (ref.: female) | −0.033 | 0.024 | −0.184 | 0.058* | 0.083 | 0.115 | |
| Race (ref.: other minorities) | |||||||
| Black | −0.081 | 0.047 | −0.280 | 0.153 | −0.101 | 0.140 | |
| White | −0.021 | 0.042 | 0.035 | 0.150 | −0.426 | 0.068* | |
| Hispanic | 0.166 | 0.079* | 0.447 | 0.168* | — | — | |
| Education attainment (ref.: BA) | |||||||
| Master's degree | 0.033 | 0.025 | 0.143 | 0.073 | −0.163 | 0.113 | |
| Doctorate/other advanced degrees | 0.071 | 0.067 | 0.142 | 0.078 | 0.151 | 0.197 | |
| Classroom characteristics | |||||||
| Average grade-8 math | 0.042 | 0.044 | −0.024 | 0.091 | −0.154 | 0.143 | |
| Average grade-8 reading | 0.111 | 0.038* | 0.036 | 0.090 | 0.180 | 0.134 | |
| Class size | 0.000 | 0.001 | 0.002 | 0.002 | 0.003 | 0.002 | |
| Number of observations | 23,570 | 9,145 | 8,333 | ||||
| Number of clusters | 275 | 103 | 88 | ||||
- Note: Included EOC subjects are: Algebra I, Algebra II, Biology, Chemistry, Geometry, Physics, and Physical Science.
- * * Significant at 0.05 level.
- All models include subject by grade fixed effects as well as year fixed effects.
| All Subjects | Math Subjects | Science Subjects | ||||
|---|---|---|---|---|---|---|
| Independent Variables | Coef. | SE | Coef. | SE | Coef. | SE |
| TFA teacher | 0.055 | 0.021* | 0.009 | 0.042 | 0.119 | 0.049* |
| Other teacher characteristics | ||||||
| Male (ref.: female) | −0.034 | 0.016* | −0.085 | 0.018* | −0.081 | 0.029* |
| Race (ref.: other minorities) | ||||||
| Black | 0.042 | 0.031 | 0.052 | 0.032 | 0.032 | 0.052 |
| White | 0.062 | 0.029* | 0.104 | 0.033* | 0.119 | 0.043* |
| Hispanic | 0.005 | 0.055 | 0.199 | 0.069* | 0.149 | 0.106 |
| Education attainment (ref.: BA) | ||||||
| Master's degree | 0.004 | 0.015 | −0.003 | 0.018 | −0.012 | 0.032 |
| Doctorate/other advanced degrees | −0.114 | 0.053* | 0.138 | 0.038* | −0.247 | 0.061* |
| Classroom characteristics | ||||||
| Average grade-8 math | 0.098 | 0.019* | 0.098 | 0.028* | 0.030 | 0.038 |
| Average grade-8 reading | 0.092 | 0.019* | −0.014 | 0.029 | 0.073 | 0.039 |
| Class size | 0.000 | 0.000 | 0.002 | 0.001* | 0.000 | 0.001 |
| Number of observations | 108,553 | 48,657 | 36,288 | |||
| Number of clusters | 697 | 275 | 218 | |||
- Note: Included EOC subjects are: Algebra I, Algebra II, and Geometry.
- * * Significant at 0.05 level.
- All models include subject by grade fixed effects as well as year fixed effects.
Table 11 further restricts the comparison sample to teachers who are licensed to teach in North Carolina through the traditional training track; that is, these are the teachers who are licensed by completing an approved teacher education program at an accredited North Carolina institution of higher education. The TFA effects estimated with this comparison group range from 0.123 to 0.163 standard deviations and all remain statistically significant.
| All Subjects | Math Subjects | Science Subjects | |||||
|---|---|---|---|---|---|---|---|
| Independent Variables | Coef. | SE | Coef. | SE | Coef. | SE | |
| TFA teacher | 0.163 | 0.024* | 0.123 | 0.051* | 0.147 | 0.057* | |
| Other teacher characteristics | |||||||
| Teacher experience (ref: < 3 yrs.) | |||||||
| 3 to 5 years | 0.017 | 0.019 | −0.047 | 0.036 | −0.080 | 0.036* | |
| 6 to 10 years | 0.048 | 0.020* | 0.095 | 0.032* | −0.106 | 0.036* | |
| 11 years or more | 0.081 | 0.017* | 0.122 | 0.031* | 0.008 | 0.031 | |
| Male (ref.: female) | −0.041 | 0.013* | −0.058 | 0.020* | −0.160 | 0.035* | |
| Race (ref.: other minorities) | |||||||
| Black | 0.073 | 0.027* | 0.131 | 0.037* | −0.133 | 0.113 | |
| White | 0.101 | 0.025* | 0.157 | 0.036* | −0.019 | 0.101 | |
| Hispanic | −0.038 | 0.095 | 0.260 | 0.064* | — | — | |
| Education attainment (ref.: BA) | |||||||
| Master's degree | 0.039 | 0.017* | 0.019 | 0.026 | 0.017 | 0.039 | |
| Doctorate/other advanced degrees | 0.016 | 0.053 | 0.044 | 0.084 | −0.253 | 0.060* | |
| Classroom characteristics | |||||||
| Average grade-8 math | 0.108 | 0.022* | 0.076 | 0.038* | 0.045 | 0.054 | |
| Average grade-8 reading | 0.072 | 0.021* | 0.041 | 0.042 | 0.064 | 0.058 | |
| Class size | 0.000 | 0.000 | 0.003 | 0.001* | −0.001 | 0.001 | |
| Number of observations | 72,734 | 32,266 | 24,069 | ||||
| Number of clusters | 456 | 186 | 136 | ||||
- Note: Included EOC subjects are: Algebra I, Algebra II, Biology, Chemistry, Geometry, Physics, and Physical Science.
- * * Significant at 0.05 level.
- All models include subject by grade fixed effects as well as year fixed effects.
In short, the TFA effect remains mostly consistent no matter what our comparison group is. TFA teachers have particular strong positive effects on student science test scores. In all cases, the TFA effect is larger, sometimes several times larger than the effect of having three to five years of experience relative to no experience.13 -29
Our final table examines the effect of TFA teachers from another perspective. We are interested in whether TFA teachers are particularly effective for certain types of students. We focus on students' initial performance and divide them into quartiles (based on their 8th-grade math and reading scores). TFA effects are estimated for high-performing and low-performing students as well as students in the middle two performance quarters separately. Table 12 shows that having a TFA teacher is beneficial to all students regardless of their prior performance level. However, it seems that the TFA effect is strongest for students in the top quarter of the performance distribution and the weakest for students in the bottom quarter of the performance distribution.
| Top Quarter | Bottom Quarter | Middle Two Quarter | ||||
|---|---|---|---|---|---|---|
| Independent Variables | Coef. | SE | Coef. | SE | Coef. | SE |
| TFA teacher | 0.172 | 0.036* | 0.101 | 0.020* | 0.119 | 0.021* |
| Other teacher characteristics | ||||||
| Teacher experience (ref.: < 3 yrs.) | ||||||
| 3 to 5 years | 0.075 | 0.021* | 0.072 | 0.020* | 0.075 | 0.016* |
| 6 to 10 years | 0.113 | 0.024* | 0.049 | 0.017* | 0.070 | 0.016* |
| 11 years or more | 0.102 | 0.018* | 0.052 | 0.014* | 0.078 | 0.013* |
| Male (ref.: female) | −0.066 | 0.018* | −0.015 | 0.017 | −0.051 | 0.014* |
| Race (ref.: other minorities) | ||||||
| Black | 0.012 | 0.042 | −0.017 | 0.024 | 0.044 | 0.022* |
| White | 0.085 | 0.040* | −0.024 | 0.022 | 0.066 | 0.021* |
| Hispanic | 0.078 | 0.103 | −0.023 | 0.072 | 0.053 | 0.058 |
| Education attainment (ref.: BA) | ||||||
| Master's degree | 0.005 | 0.020 | 0.013 | 0.015 | 0.002 | 0.014 |
| Doctorate/other advanced degrees | −0.081 | 0.066 | −0.089 | 0.029* | −0.099 | 0.031* |
| Classroom characteristics | ||||||
| Average grade-8 math | 0.141 | 0.031* | −0.002 | 0.025 | 0.098 | 0.018* |
| Average grade-8 reading | 0.040 | 0.033 | 0.146 | 0.022* | 0.070 | 0.018* |
| Class size | 0.001 | 0.001 | 0.001 | 0.001* | 0.001 | 0.000* |
| Number of observations | 32,056 | 32,690 | 64,715 | |||
| Number of clusters | 941 | 1,046 | 1,047 | |||
- Note: Included EOC subjects are: Algebra I, Algebra II, Biology, Chemistry, Geometry, Physics, Physical Science, and English I. Performance quartiles are defined on student mean scores across subjects.
- * * Significant at 0.05 level.
- All models include subject by grade fixed effects as well as year fixed effects.
DISCUSSION
The research reported here is related to larger education policy and practice concerns about teacher quality, especially teacher quality for disadvantaged students. Teach For America taps into a nontraditional pool for teachers. The teachers TFA recruits and selects differ from traditional teachers, on average, in a number of ways. They tend to have stronger academic credentials; they have not been prepared in traditional teacher training programs; they are more likely to teach for only a few years (Boyd et al., 2006); and they are assigned to the most challenging schools in the country. Given these differences, the program has been controversial. Research providing guidance on the merits of the program to policymakers and to local education administrators has been limited at the elementary school level and nonexistent at the high school level. This study represents the first study at the high school level.
Our findings show that high school TFA teachers are more effective than the teachers who would otherwise be in the classroom in their stead. While these other teachers are a diverse group in terms of background and training, for policy purposes they are an appropriate comparison group. Other things being equal, the findings suggest that disadvantaged students taught by TFA teachers are better off than they would be in the absence of TFA.
But there are additional policy questions. Suppose we raised the bar on teacher qualifications and required that all high school teachers be fully licensed in their field, particularly teachers of math and science. Raising the bar may also mean we would have to raise salaries to attract sufficient numbers of qualified teachers. But under these conditions, would students be better or worse off with a TFA teacher? To examine this question we restricted the comparison to traditional teachers who were fully certified in field. The TFA advantage still held.
Or suppose we required that all teachers teaching disadvantaged high school students have, say, three years of prior experience. Would students be better or worse off with TFA teachers on average? The findings show that TFA status more than offsets any experience effects, particularly in teaching high school science subjects. Disadvantaged secondary students would be better off with TFA teachers than with fully licensed in-field teachers with similar or more years of experience.
We should note that the findings here do not necessarily mean that there is no value to teacher training. It is possible that the teachers that TFA recruits and selects would be even more effective with more pedagogical training. Our findings also do not mean that there is no value to teaching experience. As reported in Boyd et al. (2006), TFA teachers can become even more effective with experience at a rate that is comparable to the return to experience for non-TFA teachers.
The findings have important implications for the recruitment and selection aspects of human resource management in education, at least for high school teachers. They stress the likely importance of strong academic backgrounds for high school teachers: Once we control for PRAXIS scores and college selectivity, the estimated “TFA effect” is significantly reduced. For example, the TFA effect (controlling for experience and compared with all other teachers) is reduced from 0.132 to 0.035 in math subjects and from 0.189 to 0.151 in science subjects.14 -31 The findings also suggest that policymakers probably should focus more on issues of teacher selection, and less on issues of teacher retention, if the concern is the performance of disadvantaged high school students, especially in math and science. In short, they suggest that programs like TFA that focus on recruiting and selecting academically talented recent college graduates and placing them in schools serving disadvantaged students can help reduce the achievement gap, even if teachers stay in teaching only a few years.
Acknowledgements
We gratefully acknowledge support from the Steven L. Merrill Family Foundation and the Institute for Education Sciences, U.S. Department of Education. The research reported here is part of the activities of the National Center for the Analysis of Longitudinal Data in Education Research (CALDER). CALDER is supported by Grant R305AO60018 to The Urban Institute from the Institute for Education Sciences, U.S. Department of Education. We are indebted to Clara Muschkin and the staff at the North Carolina Education Research Data Center (NCERDC) for providing the data and to Cynthia Skinner, Teach For America, for helping to identify TFA teachers. The authors also thank Dan Goldhaber, Helen Ladd, Jacob Vigdor, three anonymous reviewers, and the editor of this journal for useful comments. The views expressed are those of the authors and should not be attributed to The Urban Institute, its trustees, or its funders. The research was completed when Colin Taylor was a research assistant at The Urban Institute, and it does not necessarily reflect the views of the Office of Maryland Governor Martin O'Malley, where he is currently employed.
APPENDIX
| Decker, Mayer, & Glazerman, 2006 | Kane, Rockoff, & Staiger, 2006 | Boyd et al., 2006 | |
|---|---|---|---|
| Methods | Random assignment | Fixed effects model | Fixed effects model |
| Data years | 2002–2003 | 2000–2005 | 1999–2004 |
| Comparison group | All other teachers | Certified teachers | “College recommended” teachers |
| Grades | Grades 1–5 | Grades 4–8 | Grades 4–8 |
| TFA effect (in standard deviations) | +0.15 in math | +0.02 ∼ 0.03 in math | +0.05 in math in grades 6–8 −0.03 ∼ 0.06 in English in the first year of teaching |
| Name of Course | End-of-Course Exam Required |
|---|---|
| English I | English I |
| Algebra IB | Algebra I |
| Algebra I | |
| Integrated Math II | |
| Geometry | Geometry |
| Integrated Math III | |
| Algebra II | Algebra II |
| Integrated Math III | |
| Biology | Biology |
| Biology II | |
| Chemistry | Chemistry |
| Chemistry II | |
| Physical Science | Physical Science |
| Physics | Physics |
| Physics II | |
| IB Physics III |
- Source: North Carolina Department of Public Instruction:
- http://www.ncpublicschools.org/docs/accountability/reporting/eoccreditcourses.pdf.
- Retrieved on March 3, 2008.
REFERENCES
- 2 In recent years, TFA corps members have also engaged in ongoing professional development activities provided by TFA and whatever other supports school districts provide new teachers.
- 3 All appendices are available at the end of this article as it appears in JPAM online. See the complete article at wileyonlinelibrary.com.
- 4 While not directly an examination of TFA, a recent study by Boyd et al. (2007) found that the improved teacher qualifications for the schools serving the most disadvantaged students—a result of recruitment strategies that target teachers with strong academic credentials, like Teach For America—led to improved student performance between 2000 and 2005. The improvement in academic credentials offset more than half of any deficit associated with being a first-year teacher. As with other studies, the effects in math were stronger than the effects in English language and the arts.
- 5 Subjects tested are Algebra, Algebra II, Geometry, Biology, Chemistry, Physics, Physical Science, English I, U.S. History, Civics and Economics, and Occupational Course of Study. We do not include U.S. History, Civics and Economics, or Occupational Course of Study because data for those tests are not available in all years. See Appendix Table A2 for a list of courses that require EOC testing. All appendices are available at the end of this article as it appears in JPAM online. See the complete article at wileyonlinelibrary.com.
- 6 Some students had multiple records in a year, with different EOC scores in each record. All observations for that student in that year were dropped. A very small number of students (less than 0.5 percent) had multiple valid scores on the same subject in one year, mostly a result of school change during the school year. An even smaller number of students (about 0.05 percent) had two identical scores on the same subject in one year with identical teachers associated with the scores. In both of these cases, we dropped those observations. On the other hand, some students took the same EOC subject exam multiple times throughout their high school years; in most cases, they had failed to reach the “proficient” level in earlier attempts. These cases account for 5 percent of all EOC students. Since repeated testing on the same subject may be a confounding factor in our estimation of teacher effect on student performance, we keep their first test scores only in our analysis.
- 7 Course activities in the classroom data are unique by district and school code, teacher code, year, subject, course number, and section number. These records are repeated for each semester or quarter of the course. All appendices are available at the end of this article as it appears in JPAM online. See the complete article at wileyonlinelibrary.com.
- 8 Dee and Cohodes (2008) use a similar strategy with the National Education Longitudinal Study (NELS) of 1988 (NELS: 88).
- 9 The authors acknowledge the insights from Rivkin (2006) and Hanushek, Kain, and Rivkin (2009) as the basis of this observation.
- 10 Not all eight subjects were tested in year 2006–2007. Chemistry, Physics, and Physical Science were excluded in 2006–2007 as the tests for these three subjects were changed in that year and were administered to select samples for field testing. The revised tests were planned to be implemented statewide in 2007–2008.
- -8 For initial certification in teaching in North Carolina, all candidates must pass the PRAXIS I test and one or more PRAXIS II subject tests. We calculate a teacher's PRAXIS performance by averaging her scores (normalized by test type) across all the PRAXIS tests that she took.
- -7 Results are available upon request.
- -15 For the 2006–2007 school year, NCERDC compiled a “course membership” file that provides a direct link between students and their classroom instructors for the first time. This file contains a large number of missing values on teacher ID (12 percent of the student records have missing teacher IDs). Nevertheless, this provides us with an opportunity to partially check the validity of our matching methods. We find that about 89 to 92 percent of students in our 2006–2007 analytic samples are correctly matched to their instructors.
- -29 Not all TFA teachers were assigned to classes that require EOC tests. Therefore, it is possible that only stronger TFA teachers were assigned to teach those higher-stakes classes. We compared various teacher characteristics including PRAXIS scores of TFA teachers in the analytic sample and other TFA teachers. No significant difference was found between these two groups of TFA teachers.
- -31 Details of these results are available upon request.




