Dynamical analysis of novel COVID-19 epidemic model with non-monotonic incidence function
Abstract
In this study, we developed and analyzed a mathematical model for explaining the transmission dynamics of COVID-19 in India. The proposed 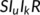 model is a modified version of the existing
model is a modified version of the existing  model. Our model divides the infected class
model. Our model divides the infected class 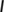 of
of  model into two classes:
model into two classes: 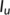 (unknown infected class) and
(unknown infected class) and 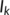 (known infected class). In addition, we consider
(known infected class). In addition, we consider 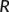 a recovered and reserved class, where susceptible people can hide them due to fear of the COVID-19 infection. Furthermore, a non-monotonic incidence function is deemed to incorporate the psychological effect of the novel coronavirus diseases on India's community. The epidemiological threshold parameter, namely the basic reproduction number, has been formulated and presented graphically. With this threshold parameter, the local and global stability analysis of the disease-free equilibrium and the endemic proportion equilibrium based on disease persistence have been analyzed. Lastly, numerical results of long-run prediction using MATLAB show that the fate of this situation is very harmful if people are not following the guidelines issued by the authority.
a recovered and reserved class, where susceptible people can hide them due to fear of the COVID-19 infection. Furthermore, a non-monotonic incidence function is deemed to incorporate the psychological effect of the novel coronavirus diseases on India's community. The epidemiological threshold parameter, namely the basic reproduction number, has been formulated and presented graphically. With this threshold parameter, the local and global stability analysis of the disease-free equilibrium and the endemic proportion equilibrium based on disease persistence have been analyzed. Lastly, numerical results of long-run prediction using MATLAB show that the fate of this situation is very harmful if people are not following the guidelines issued by the authority.
1 INTRODUCTION
The first case of the coronavirus pandemic was reported on January 30, 2020 in India (Zhu et al., 2020). India's response to COVID-19 has been graded, pro-active, and pre-emptive with high-level political commitment and a “whole government” approach to respond to the COVID-19 pandemic. Educational institutions, various Governments, and non-Government offices, and many commercial establishments have been shut down immediately. Government of India, exercise the Disaster Management Act, 2005, issued an order for State/UT's prescribing lockdown for containment of COVID-19 pandemic in the country for 21 days with effect from March 25, 2020, and announced to maintain mandatory physical distancing in India. Later Government extent the lockdown period up to May 3, 2020 as the number of active cases increases daily. The most common symptoms are dry cough, fever, and tiredness, but some infected people may have aches and pains, running nose, nasal congestion, sore throat, vomiting, or diarrhea. These symptoms usually are severe and begin gradually. Some people become infected, but neither has symptoms nor feels ill. Disease recovery is high without requiring special treatment. The guidelines for preventing the spreading of COVID-19 are wearing a face mask, staying more than 3 ft away from a sick person, washing hands with soap, or using alcohol-based hand rub, and so forth.
During an epidemic, reported cases of coronavirus disease are rising worldwide day by day due to human-to-human transmission; the study for prevention and control of infectious COVID-19 disease is essential. The modernized mathematical model is necessary to give a deeper understanding and perception of disease transmission mechanisms and find how to control the spread of the COVID-19 disease. Xiao and Ruan (2007) studied an epidemic model with a non-monotonic incidence rate, which describes the psychological effect of certain serious diseases on the community when the number of infectives is getting larger. Xu and Ma (2009) investigated a SIR epidemic model with nonlinear incidence rate and time delay. Yang et al. (2010) formulated a SIR model with vaccination and varying population. Sun and Hsieh (2010) investigated an susceptible exposed infected recovered (SEIR) model with varying population size and vaccination strategy. Zhou and Cui (2011) studied an SEIR epidemic model with a saturated recovery rate. Bai and Zhou (2012) proposed an SEIRS epidemic model with a general periodic vaccination strategy and seasonally varying contact rates. Khan et al. (2015) considered an SEIR model with nonlinear saturated incidence rate and temporary immunity. Elkhaiar and Kaddar (2017) studied the dynamics of an SEIR epidemic model with nonlinear treatment function that takes into account the limited availability of resources in the community. Wang et al. (2018) extended the incidence rate of an SEIR epidemic model with relapse and varying total population size to a general nonlinear form. Tiwari et al. (2017) investigated an SEIRS epidemic model with nonlinear saturated incidence rate. Lahrouz et al. (2012) studied the global dynamics of a SIRS epidemic model for infections with non-permanent acquired immunity. Tian and Wang (2011) discussed the global stability analysis for several deterministic cholera epidemic models. Samanta (2011) discussed the permanence and extinction of a non-autonomous HIV/AIDS epidemic model with distributed time delay. Cai et al. (2014) investigated an HIV/AIDS treatment model.
Gralinski and Menachery (2020) studied the return of novel coronavirus in 2019. Chen et al. (2020) developed a mathematical model for calculating the transmissibility of the novel coronavirus. Saldana et al. (2020) developed a compartmental epidemic model to study the transmission dynamics of the COVID-19 epidemic outbreak, with Mexico as a practical example. Silva et al. (2020) proposed a new SEIR agent-based COVID-19 model to simulate the pandemic dynamics using a society of agents emulating people, business, and government. Pal et al. (2020) proposed a COVID-19 model for stability analysis with five compartments. Lee et al. (2020) proposed a COVID-19 epidemic model for estimating the unidentified infected population in China. Maheshwari et al. (2020) forecasted the epidemic spread of COVID-19 in India using the ARIMA model. Zakharov et al. (2020) predicted the dynamics of the COVID-19 epidemic in real-time using the case-based rate reasoning model. Bonnas and Gianatti (2020) proposed a COVID-19 epidemic model where the population is partitioned into classes corresponding to ages. Roda et al. (2020) demonstrated the reasons for wide variations in numerous model predictions of the COVID-19 epidemic in China. Liu et al. (2020a) developed two differential equations models to account for the latency period of COVID-19 infection. Basnarkov (2021) studied a SEAIR epidemic spreading model of COVID-19. Yang and Wang (2020) proposed a mathematical model for the novel coronavirus epidemic in Wuhan, China. Wang, Lu, et al. (2020) performed the dynamical analysis of a COVID-19 epidemic model. Zlatic et al. (2020) developed a COVID-19 epidemics model spreading on the availability of tests for the disease. Xue et al. (2020) proposed a data-driven network model for the COVID-19 epidemics in Wuhan, Toronto, and Italy. Neves and Guerrero (2020) presented the A-SIR model to predict the evolution of the COVID-19 epidemic. Ndairou et al. (2020) proposed a mathematical model for COVID-19 epidemic with a case study of Wuhan.
Jiao and Huang (2020) proposed a SIHR COVID-19 epidemic model with effective control strategies. Zhao and Chen (2020) modeled the epidemic dynamics and control of the COVID-19 outbreak in China. Li et al. (2020) modeled the impact of mass influenza vaccination and public health interventions on COVID-19 epidemics. Pizzuti et al. (2020) investigated the prediction accuracy of the SIR model on networks for Italy. Wang, Zheng, et al. (2020) used the logistic model and machine learning technics to predict the COVID-19 epidemics. Pongkitivanichkul et al. (2020) estimated the size of the COVID-19 epidemic outbreak. Liu et al. (2020b) predicted the cumulative number of cases for the COVID-19 epidemic in China. Zhu and Zhu (2020) devised a method to analyze the COVID-19 epidemic. Kantner and Koprucki (2020) computed a strategy for the case that a vaccine is never found and complete containment is impossible. Engbert et al. (2021) presented a Stochastic SEIR epidemic model for regional COVID-19 dynamics by sequential data assimilation. Several researcher investigated the dynamics of COVID-19 using fractional order models (Askar et al., 2021; Awais et al., 2020; Rezapour et al., 2020). Rihan et al. (2020) analyzed a stochastic SIRC epidemic model with time-delay for COVID-19. Bambusi and Ponno (2020) explained the linear behavior in COVID-19 epidemic as an effect of lockdown. Alberti and Faranda (2020) presented statistical predictions of COVID-19 infections by fitting asymptotic distributions to actual data. Abbasi et al. (2020) discussed the Optimal control for Impulsive SQEIAR Epidemic model on COVID-19 epidemic. Lobato et al. (2020) identified an epidemiological model to simulate the COVID-19 epidemic. Khan and Atangana (2020) modeled the dynamics of novel coronavirus with fractional derivative. Alshammari and Khan (2021) analyzed the dynamics of modified SIR model with nonlinear incidence and recovery rates. Pal et al. (2021) presented a COVID-19 model with optimal treatment of infected individuals and the cost of necessary treatment. Khan et al. (2021) focused on the novel coronal virus model to understand its dynamics and possible control. Khajanchi and Sarkar (2020) developed a new compartment model that explains the transmission dynamics of COVID-19. Rai et al. (2021) studied the social media advertisements in combating the coronavirus pandemic in India. Tuncer (2020) explored globalization's effect on the spread of fear across the world by focusing on the case of COVID-19. Adekola et al. (2020) examined various forms of mathematical models relevant to the containment, risk analysis, and features of COVID-19.
This paper determines the fate of coronavirus infective individuals introduced into the population in India. The dynamics of the nonlinear system have been considered in the study with reinfection turned off. The basic reproduction number (BRN)  is estimated and analyzed as a threshold parameter for the stability analysis of the disease-free equilibrium (DFE) and endemic equilibrium. The uniform persistence of the disease near the threshold parameter is also determined.
is estimated and analyzed as a threshold parameter for the stability analysis of the disease-free equilibrium (DFE) and endemic equilibrium. The uniform persistence of the disease near the threshold parameter is also determined.
2 FORMULATION OF COVID-19 MATHEMATICAL MODEL
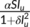 . Here
. Here  describes the infection force of the disease and
describes the infection force of the disease and 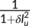 measures the inhibition effect from the behavioral change of the susceptible individuals when the number of infectious individuals increases. Some susceptible class individuals move to the reserved area, which is considered a safe zone during the pandemic. The known infected individuals entered the recovered class after recovered from the COVID-19. Here in this model, we consider the recovered class and the reserved class as the same and denote the density at time
measures the inhibition effect from the behavioral change of the susceptible individuals when the number of infectious individuals increases. Some susceptible class individuals move to the reserved area, which is considered a safe zone during the pandemic. The known infected individuals entered the recovered class after recovered from the COVID-19. Here in this model, we consider the recovered class and the reserved class as the same and denote the density at time 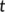 by
by 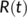 . The model of the study has been taken in the following form
. The model of the study has been taken in the following form
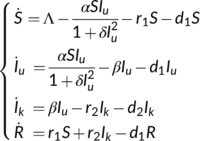 (1)
(1)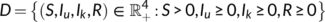 subject to initial conditions
subject to initial conditions
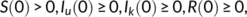 (2)
(2)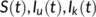 and
and 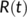 are the densities at the time
are the densities at the time 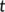 of susceptible population, unknown infected population (incubate the illness but do not have any symptoms and not identified), known infected population (in the isolated ward), and recovered or reserved population, respectively, and the parameters
of susceptible population, unknown infected population (incubate the illness but do not have any symptoms and not identified), known infected population (in the isolated ward), and recovered or reserved population, respectively, and the parameters 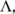
 ,
, 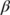 ,
, 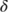 ,
, 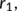
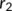 , and
, and  are all positive. Here,
are all positive. Here,  is defined as the total number of population under risk at the time
is defined as the total number of population under risk at the time 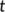 (Figure 1).
(Figure 1).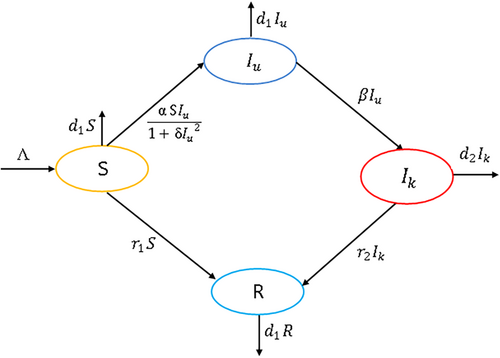
The biological meanings of the model parameters are listed below:
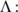 The recruitment rate at which new individuals enter the Indian population.
The recruitment rate at which new individuals enter the Indian population.
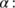 The homogeneous transmission coefficient from the susceptible population (
The homogeneous transmission coefficient from the susceptible population (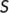 ) to the unknown infected population (
) to the unknown infected population (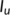 ). The rate of transmission of infection is given by
). The rate of transmission of infection is given by 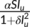 .
.
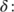 The parameter measures the psychological or inhibitory effect.
The parameter measures the psychological or inhibitory effect.
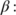 The transmission coefficient from the unknown infected population (
The transmission coefficient from the unknown infected population (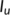 ) to the known infected population (treatment population) (
) to the known infected population (treatment population) (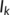 ).
).
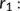 The transmission coefficient from the susceptible population (
The transmission coefficient from the susceptible population (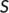 ) to the recovered or reserved population (
) to the recovered or reserved population (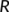 ).
).
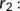 The transmission coefficient from the known infected population (treatment population) (
The transmission coefficient from the known infected population (treatment population) (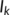 ) to the recovered population or reserved population (
) to the recovered population or reserved population (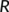 ).
).
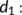 The natural death rate.
The natural death rate.
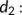 The death rate of the known infected class (
The death rate of the known infected class (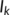 ).
).
- The susceptible population
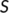 are those people who are not yet infected by the COVID-19 disease but may be infected when contacted with the unknown infected individuals
are those people who are not yet infected by the COVID-19 disease but may be infected when contacted with the unknown infected individuals 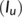 . One section of this susceptible population move directly to the reserved compartment which is also same as the recovered compartment (
. One section of this susceptible population move directly to the reserved compartment which is also same as the recovered compartment (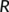 )
) - The unknown infected population (
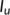 ) is composed of individuals who have COVID-19 infection without symptoms. These individuals are capable of infecting anyone who comes in contact with them.
) is composed of individuals who have COVID-19 infection without symptoms. These individuals are capable of infecting anyone who comes in contact with them. - The known infected population
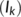 is composed of individuals who have COVID-19 disease with symptoms and undergo best available treatment in isolation ward. The individuals in this compartment undergo the supportive care treatment or treatment to support the vital organs of the body. These individuals do not spread the COVID-19 disease as they are in isolation.
is composed of individuals who have COVID-19 disease with symptoms and undergo best available treatment in isolation ward. The individuals in this compartment undergo the supportive care treatment or treatment to support the vital organs of the body. These individuals do not spread the COVID-19 disease as they are in isolation. - The recovered population and reserved population together named as
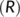 is composed of two kinds of individuals namely the individuals who are recovered from the COVID-19 disease after the best available treatment in the treatment compartment (
is composed of two kinds of individuals namely the individuals who are recovered from the COVID-19 disease after the best available treatment in the treatment compartment (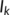 ) and those individuals who move to the reserved or safer areas from the susceptible compartment (
) and those individuals who move to the reserved or safer areas from the susceptible compartment (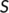 ).
).
3 ANALYSIS OF THE MODEL AND BASIC PROPERTIES
3.1 Non-negativity of solutions
Theorem 1.Every solution of the system (1) with initial conditions (2) are non-negative for every t 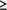 0.
0.
Proof.The right hand side of the dynamical system (1) is completely continuous and locally Lipschitzian on 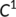 and hence the solution
and hence the solution 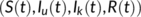 of the system (1) with the initial conditions (2) exists and is unique on the interval
of the system (1) with the initial conditions (2) exists and is unique on the interval 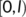 with
with 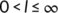 . From the first equation of the system (1) with initial condition
. From the first equation of the system (1) with initial condition 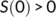 , we get
, we get
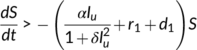
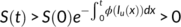
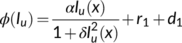
Integrating the second equation of the system (1) with initial condition  , the solution can be written in the form as
, the solution can be written in the form as
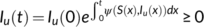
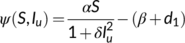
From the third and fourth equations of the system (1) with initial conditions  and
and 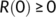 , we have
, we have
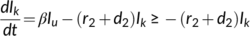
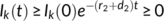
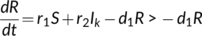
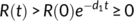
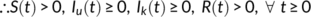 . This completes the proof of the theorem.■
. This completes the proof of the theorem.■
3.2 Boundedness of the system and invariant region
Theorem 2.All solutions of system (1) which lies in 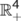 are uniformly bounded and are confined to the invariant region
are uniformly bounded and are confined to the invariant region 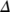 defined by
defined by  as t
as t 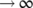 , where
, where 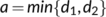
Proof.Let us assume that 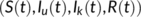 is a solution of (1). Since,
is a solution of (1). Since,
 (3)
(3)The time derivative of Equation (3) is
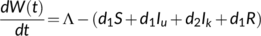
For each a 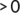 , we get
, we get
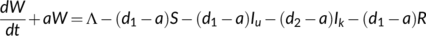
Assuming 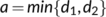 , we get
, we get
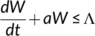
Applying the theory of differential inequality (Birkhoff & Rota, 1989), we find that
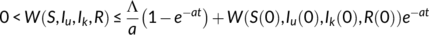
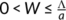 as
as  . Thus, all solutions of the COVID-19 system (1) which initiate in
. Thus, all solutions of the COVID-19 system (1) which initiate in 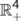 are uniformly bounded and confined to the region
are uniformly bounded and confined to the region 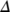 , where
, where  . Hence the feasible region
. Hence the feasible region 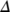 with initial conditions (2) is positively invariant region under the flow induced by the system (1) in
with initial conditions (2) is positively invariant region under the flow induced by the system (1) in 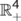 .■
.■Remark.All solutions of system (1) have non-negative components, given non-negative initial values in 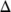 and stay in
and stay in 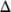 for t
for t 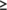 0 and globally attracting in
0 and globally attracting in 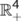 with respect to the system (1). Therefore, we restrict our attention to the dynamics of the system (1) in
with respect to the system (1). Therefore, we restrict our attention to the dynamics of the system (1) in 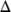 . Thus the system (1) with initial conditions (2) defined on
. Thus the system (1) with initial conditions (2) defined on  is well-posed mathematically and epidemiologically and it is sufficient to study the dynamics of the dynamical system (1) with initial conditions (2) defined on
is well-posed mathematically and epidemiologically and it is sufficient to study the dynamics of the dynamical system (1) with initial conditions (2) defined on 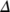 .
.
3.3 Equilibrium of system
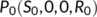 , where
, where 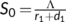 and
and  . Since the last equation of system (1) does not depend on other equations, we simply study the reduced system
. Since the last equation of system (1) does not depend on other equations, we simply study the reduced system
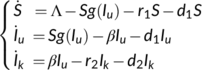 (4)
(4)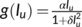 is increasing when
is increasing when 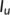 is small and decreasing when
is small and decreasing when 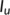 is large. The DFE point becomes
is large. The DFE point becomes  , where
, where 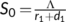 ,
, 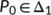 and
and 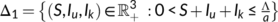 , where
, where 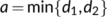 . The endemic equilibrium point of the system (4) is
. The endemic equilibrium point of the system (4) is 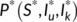 , where
, where 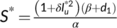 ,
, 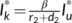 , and
, and 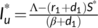 . The endemic equilibrium point exists if
. The endemic equilibrium point exists if 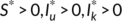 .
.4 DFE AND STABILITY ANALYSIS
To eradicate the disease from a varying size population, the more stringent way requires that the total number of the virus-infected population 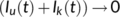 , while a weaker requirement is that proportion sum of the same tends to zero (Busenberg et al., 1991). Thus we need to find the conditions for the existence and stability of the DFE
, while a weaker requirement is that proportion sum of the same tends to zero (Busenberg et al., 1991). Thus we need to find the conditions for the existence and stability of the DFE 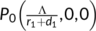 and the endemic equilibrium
and the endemic equilibrium 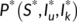 . Therefore,
. Therefore, 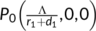 is the DFE of (4), which exists for all positive parameters.
is the DFE of (4), which exists for all positive parameters.
4.1 The basic reproduction number
The BRN is the average number of secondary infections generated by a single infection and is one of the most vital threshold quantities which mathematically represent the spreading of the virus infection.
The stability of 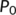 is equivalent to all the eigenvalues of the characteristic equation of
is equivalent to all the eigenvalues of the characteristic equation of 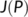 at
at  being with negative real parts, which can be assured by the BRN (
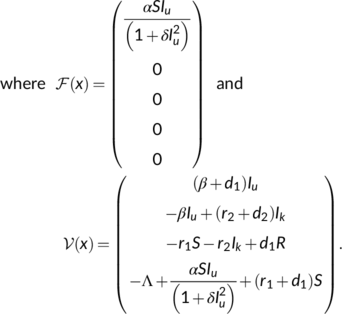
being with negative real parts, which can be assured by the BRN (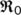 ) obtained by the next-generation matrix method (Van den Driessche & Watmough, 2002), where
) obtained by the next-generation matrix method (Van den Driessche & Watmough, 2002), where 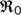 is the epidemiological threshold parameter.
is the epidemiological threshold parameter.
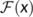 and
and 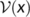 at the DFE
at the DFE 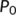 are given by
are given by
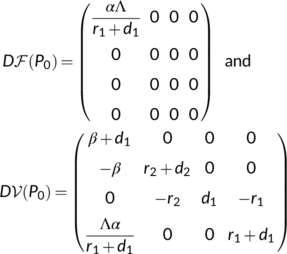
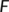 and
and 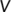 as below
as below
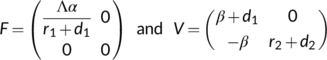
The next generation matrix for the system (1) is 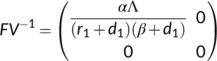 .
.
The spectral radius of the matrix 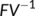 is
is  which is the BRN
which is the BRN 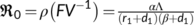 . Now, it has been observed that
. Now, it has been observed that 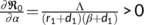 . From this observation, it is obvious that if the transmission coefficient
. From this observation, it is obvious that if the transmission coefficient  from the susceptible population (
from the susceptible population (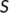 ) to unknown infected population (
) to unknown infected population (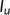 ) decreases, then the BRN
) decreases, then the BRN 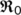 also decreases and therefore reduces the burden on the infection. Otherwise, if
also decreases and therefore reduces the burden on the infection. Otherwise, if  increase, then
increase, then 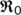 would also increase, and thus, the transmission of virus infection will also rise; therefore, the scenario will be very harmful to society.
would also increase, and thus, the transmission of virus infection will also rise; therefore, the scenario will be very harmful to society.
Now, the BRN 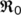 has been presented graphically in Figure 2 with respect to related estimated or hypothetical parameter values given in Table 1. From Figure 2, it is observed that as the value of
has been presented graphically in Figure 2 with respect to related estimated or hypothetical parameter values given in Table 1. From Figure 2, it is observed that as the value of  increases,
increases,  also increases simultaneously and become greater than unity after a certain value of
also increases simultaneously and become greater than unity after a certain value of  . Therefore, it is said that up to a certain value of
. Therefore, it is said that up to a certain value of  , the DFE point is stable (Theorem 3) and beyond that value of
, the DFE point is stable (Theorem 3) and beyond that value of  , the endemic equilibrium point is stable (Theorem 6).
, the endemic equilibrium point is stable (Theorem 6).
 with respect to
with respect to 
| Parameters | Value | Reference |
|---|---|---|

|
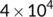
|
Estimated |

|
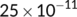
|
Estimated |
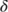
|
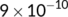
|
Assumed |
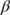
|
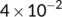
|
Estimated |
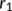
|
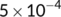
|
Assumed |
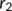
|
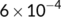
|
Estimated |
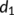
|
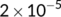
|
Estimated |
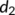
|
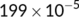
|
Estimated |
4.2 Local stability of the DFE
This section will discuss the parameter restrictions of the local stability of DFE.
Theorem 3.The disease free equilibrium 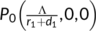 of the system (4) is locally asymptotically stable if
of the system (4) is locally asymptotically stable if 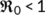 . Whereas, it is unstable if
. Whereas, it is unstable if 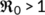 .
.
Proof.The variational matrix of the system (4) at 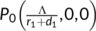 is given by
is given by
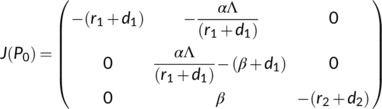 (6)
(6)The eigen values of the characteristic equation of 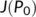 are
are
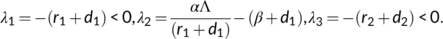
For stability, all eigen values must be negative. So, 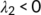 gives
gives
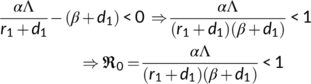
Hence, the DFE is locally asymptotically stable if 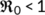 .■
.■
4.3 Global stability of the DFE
In this section, we will discuss the parameter restrictions of the global stability of DFE.
Theorem 4.When 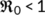 , the disease free equilibrium
, the disease free equilibrium 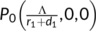 is globally asymptotically stable in
is globally asymptotically stable in 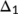 .
.
Proof.To prove the global stability of DFE 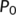 when
when 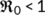 , we choose a suitable Lyapunov function
, we choose a suitable Lyapunov function 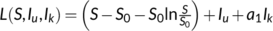 . Differentiating
. Differentiating 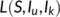 along (4), we obtain that
along (4), we obtain that
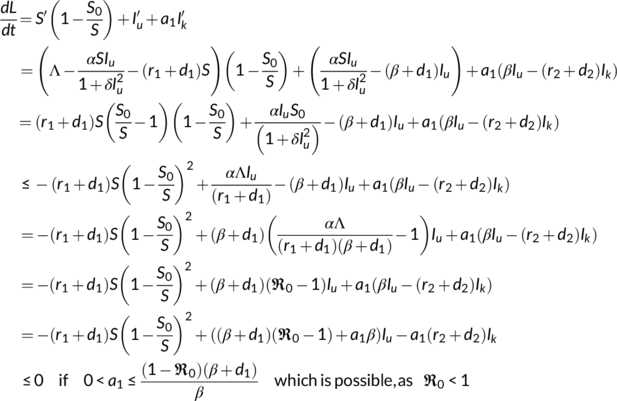
We observe that 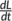 = 0 if and only if
= 0 if and only if  . Therefore, the maximum invariant set in
. Therefore, the maximum invariant set in 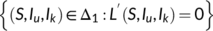 is the singleton set
is the singleton set 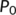 , when
, when 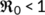 . By using Lasalle's invariance principle (LaSalle, 1976), the DFE
. By using Lasalle's invariance principle (LaSalle, 1976), the DFE 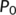 is globally asymptotically stable in
is globally asymptotically stable in 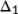 , when
, when 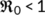 .■
.■
5 DISEASE PERSISTENCE
5.1 Uniformly persistence
In this subsection, an effort is made to understand the uniform persistence of the dynamical system (4) for the threshold parameter by applying the acyclicity theorem (Sun & Hsieh, 2010).
Definition 1.The system (4) is said to be uniformly persistent (Butler et al., 1986) if there exists a constant 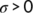 such that all solutions
such that all solutions 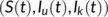 with positive initial
with positive initial 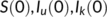 satisfy the following inequality
satisfy the following inequality
 (7)
(7)Let 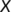 be a locally compact metric space with metric
be a locally compact metric space with metric 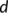 , and let
, and let 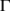 is a closed non-empty subset of
is a closed non-empty subset of 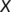 with the boundary
with the boundary 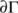 and interior
and interior 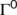 . Clearly,
. Clearly, 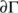 is a closed subset of
is a closed subset of 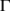 and let
and let 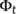 be a dynamical system on
be a dynamical system on 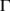 . Then set
. Then set 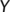 in
in 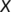 is said to be invariant if
is said to be invariant if 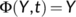 .
.
Theorem 5.Suppose the conditions 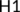 and
and 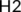 holds true for the dynamical system
holds true for the dynamical system 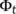
H1:.The system 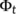 has a global attractor.
has a global attractor.
H2:.If 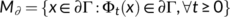 , then there exists a set
, then there exists a set
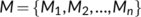 of disjoint, compact and isolated invariant sets in
of disjoint, compact and isolated invariant sets in 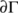 such that
such that
- There are no subsets of M which form a cycle on
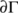 ;
; -
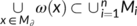 , where
, where 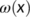 is the omega limit set of
is the omega limit set of 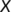
- Every set
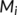 is isolated in
is isolated in 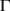 , 1
, 1 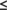 i
i 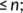
-
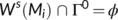 for
for 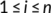 , where
, where 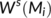 is a stable manifold of
is a stable manifold of 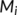 .
.
Then the dynamical system 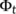 is uniformly persistent with respect to
is uniformly persistent with respect to 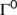 .
.
Proof.For the modified COVID-19 system (4), we assume that
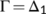 =
= 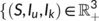 :
: 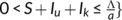 ,
, 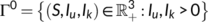 and
and 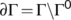 . Clearly,
. Clearly,  . On
. On 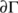 , the system (4) reduces to
, the system (4) reduces to 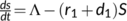 , in which
, in which  as
as 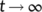 . So it is concluded that
. So it is concluded that 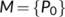 and
and  for all
for all 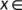
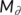 which proves (i) and (ii) of
which proves (i) and (ii) of 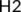 . From Theorem 3 the DFE
. From Theorem 3 the DFE 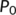 is unstable When
is unstable When 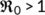 and also
and also 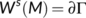 which indicates that (iii) and (iv) of
which indicates that (iii) and (iv) of 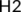 are satisfied. Since all system (4) solutions are uniformly bounded, a global attractor exists and hence
are satisfied. Since all system (4) solutions are uniformly bounded, a global attractor exists and hence 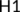 holds true for the system (4). Hence the system (4) is uniformly persistent with respect to
holds true for the system (4). Hence the system (4) is uniformly persistent with respect to 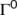 , when
, when 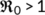 .■
.■
6 ENDEMIC EQUILIBRIUM AND STABILITY ANALYSIS
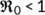 which implies that there is no endemic equilibrium when
which implies that there is no endemic equilibrium when 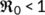 . To analyze the existence of nontrivial interior equilibrium of system (4), it should satisfy the following conditions:
. To analyze the existence of nontrivial interior equilibrium of system (4), it should satisfy the following conditions:
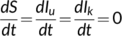 (8)
(8)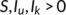 and the above Equations (9) leads to the following solutions as
and the above Equations (9) leads to the following solutions as 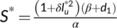 ,
, 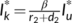 , and
, and 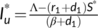 . Clearly
. Clearly 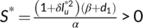 but
but 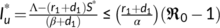 and
and 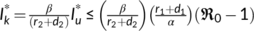 are positive if
are positive if 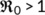 . Hence the nontrivial interior equilibrium
. Hence the nontrivial interior equilibrium 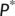 of system (4) exists if
of system (4) exists if 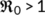 .
.6.1 Local stability analysis of the endemic equilibrium
Theorem 6.The endemic equilibrium 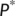 of the system (4) is locally asymptotically stable in
of the system (4) is locally asymptotically stable in 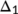 if
if 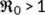 .
.
Proof.The variational matrix of the system (4) at 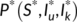 is
is
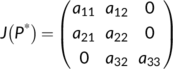
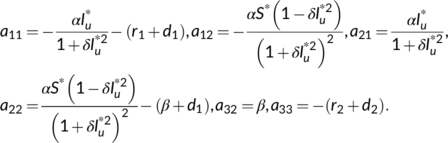
The characteristic equation of  is
is
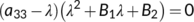 (9)
(9)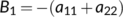 and
and  . One of the eigenvalues of
. One of the eigenvalues of 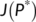 from the Equation (10) is
from the Equation (10) is 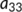 which is negative. The Routh–Hurwitz conditions state that the quadratic equation
which is negative. The Routh–Hurwitz conditions state that the quadratic equation 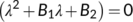 has negative roots or complex conjugates with negative real part if and only if
has negative roots or complex conjugates with negative real part if and only if 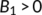 and
and 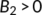 . But after simplification, we get
. But after simplification, we get
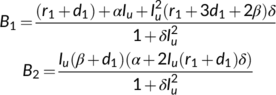
Obviously 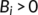 for
for 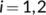 . Hence, the positive equilibrium point
. Hence, the positive equilibrium point 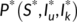 is locally asymptotically stable if
is locally asymptotically stable if 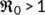 .■
.■
6.2 Global stability analysis of the endemic equilibrium
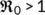 , we apply here a geometric approach (Li & Muldowney, 1996). We begin the preliminary discussion on the geometric approach by formulating the local version of the
, we apply here a geometric approach (Li & Muldowney, 1996). We begin the preliminary discussion on the geometric approach by formulating the local version of the 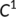 closing lemma of Pugh (Hirsch, 1991). Consider the differential equation
closing lemma of Pugh (Hirsch, 1991). Consider the differential equation
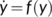 (10)
(10)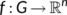 ,
,  open set, simply connected and
open set, simply connected and 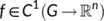 .
.Let 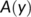 be an
be an 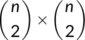 matrix valued function which is
matrix valued function which is  in
in  and
and 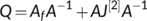 , where
, where 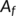 is the matrix obtained by replacing each entry
is the matrix obtained by replacing each entry 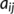 in
in 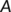 by its directional derivative in the direction of
by its directional derivative in the direction of 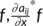 . Let
. Let 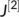 be the second additive compound matrix of
be the second additive compound matrix of 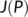 and
and 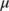 be the Lozinskii measure (Coppel, 1965) with respect to a vector norm
be the Lozinskii measure (Coppel, 1965) with respect to a vector norm  on
on 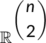 defined as
defined as 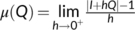 , I is the unit matrix.
, I is the unit matrix.
The following quantity 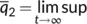
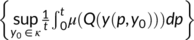 is well defined. If there exists a compact absorbing set
is well defined. If there exists a compact absorbing set  and the system (11) has a unique equilibrium
and the system (11) has a unique equilibrium 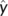 in
in 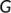 , then the unique equilibrium
, then the unique equilibrium  of (11) is globally asymptotically stable in
of (11) is globally asymptotically stable in 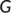 if
if 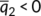 .
.
Theorem 7.Assume that 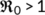 . Then there exist
. Then there exist 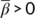 such that the unique endemic equilibrium
such that the unique endemic equilibrium 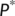 is globally asymptotically stable in the interior of
is globally asymptotically stable in the interior of 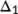 when
when 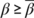 .
.
Proof.To prove this result, we find the second additive compound matrix 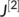 from the Jacobian matrix
from the Jacobian matrix 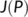 of (5) for the reduced system (4) at
of (5) for the reduced system (4) at 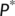 in the following form:
in the following form:
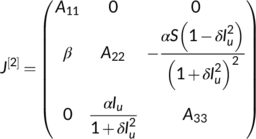 (11)
(11)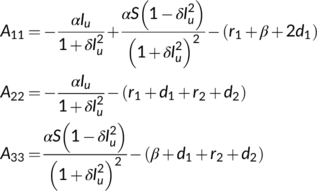
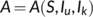 is defined by
is defined by  with
with 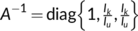 . Then
. Then 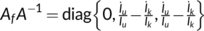 . Therefore, the matrix
. Therefore, the matrix 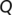 can be written in the following block form as
can be written in the following block form as
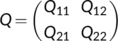
 ,
, 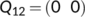 ,
, 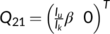 and
and
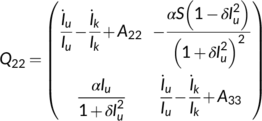
The vector norm  of the vector
of the vector 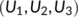 in
in 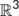 can be defined as
can be defined as  . Suppose
. Suppose 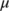 be the Lozinskii measure with the above defined norm, so as described in (Martin, 1974) and it follows the condition as
be the Lozinskii measure with the above defined norm, so as described in (Martin, 1974) and it follows the condition as  , where
, where 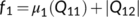 ,
,  ,
, 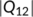 , and
, and 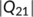 are the matrix norm with respect to the
are the matrix norm with respect to the 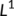 vector norm. If
vector norm. If 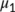 denotes the Lozinskii measure with respect to
denotes the Lozinskii measure with respect to 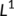 norm. Using the second equation of system (4), we have
norm. Using the second equation of system (4), we have
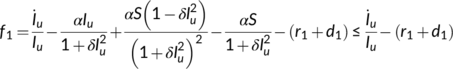
Using the third equation of system (4), we have
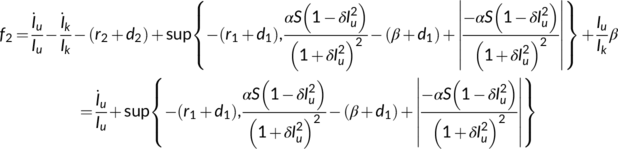
Since system (4) is uniformly persistent when 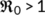 , there exist
, there exist 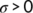 and
and 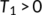 such that
such that 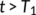 implies
implies 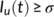 ,
, 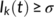 , and
, and 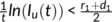 for all
for all 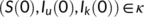 . If
. If 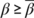 , where
, where 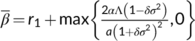 , then
, then 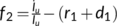 . Therefore, we get
. Therefore, we get 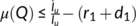 . Hence,
. Hence,
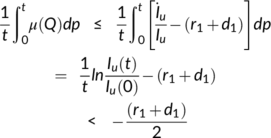
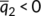 . Thus, the endemic equilibrium
. Thus, the endemic equilibrium 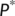 of the reduced system (4) is globally asymptotically stable, when
of the reduced system (4) is globally asymptotically stable, when 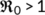 .■
.■7 DISCUSSION AND SIMULATIONS
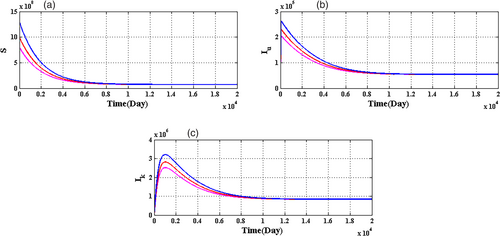
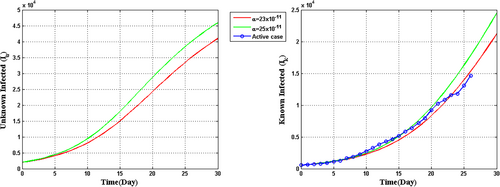
In this section, firstly we consider the case when the BRN 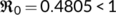 by utilizing the parameter values as in Table 1. For different initial conditions, the dynamics of the system (4) is represented in Figure 3. These figures illustrate that the susceptible population (
by utilizing the parameter values as in Table 1. For different initial conditions, the dynamics of the system (4) is represented in Figure 3. These figures illustrate that the susceptible population (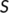 ) persists and tends to
) persists and tends to 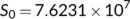 as
as 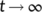 and the unknown infected population (
and the unknown infected population (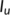 ) and the known infected population (
) and the known infected population (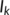 ) tends to zero as
) tends to zero as 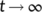 , that is, the system (4) approaches the DFE
, that is, the system (4) approaches the DFE 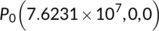 . This numerical simulation supports the result stated in Theorem 4. Next, we consider the case when
. This numerical simulation supports the result stated in Theorem 4. Next, we consider the case when  by utilizing the values of parameter from Table 1 with
by utilizing the values of parameter from Table 1 with 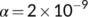 . For various initial conditions, the dynamics of the system (4) is represented in Figure 4. These figures illustrate that the susceptible population (
. For various initial conditions, the dynamics of the system (4) is represented in Figure 4. These figures illustrate that the susceptible population (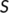 ), the unknown infected population (
), the unknown infected population (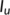 ) and the known infected population (
) and the known infected population (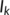 ) all persist, that is, the system (4) tends to endemic equilibrium
) all persist, that is, the system (4) tends to endemic equilibrium 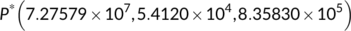 .
.
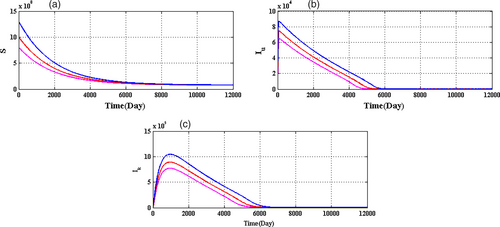
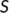 (a),
(a), 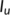 (b),
(b), 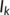 (c) when
(c) when 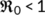 for different initial conditions using parameter values from Table 1
for different initial conditions using parameter values from Table 1
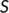 (a),
(a), 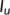 (b),
(b), 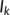 (c) when
(c) when 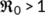 for different initial conditions with parameter values from Table 1 with
for different initial conditions with parameter values from Table 1 with 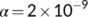
To determine the outbreak of infected individuals of COVID-19 disease in the Indian population, we present the numerical simulation of the proposed dynamical system (1), using MATLAB for simulation experiments, based on the SARS-CoV-2 virus-infected cases in the time frame in India. Here, we employ the nonlinear least-squares curve fitting method with the help of “fminsearch” function from the MATLAB Optimization Toolbox to obtain the best-fit parameters for INDIA. The procedure looks for the set of initial guesses and pre-estimated parameters for the model whose solutions best fit or pass through all the data points by reducing the sum of the square difference between the observed data and the model solution, that is, If a theoretical model 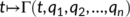 is attained and depend on a few unknown parameters
is attained and depend on a few unknown parameters 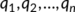 and a sequence of actual data points
and a sequence of actual data points 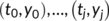 is also at hand then the aim is to obtain values of the parameters so that the error
is also at hand then the aim is to obtain values of the parameters so that the error 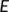 calculated can attain a minimum, where
calculated can attain a minimum, where 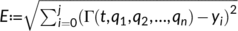 .
.
For simulation, we assume the initial values are 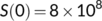 ,
, 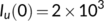 ,
, 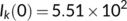 from March 25 to April 14, 2020 and
from March 25 to April 14, 2020 and 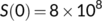 ,
, 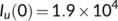 ,
, 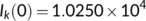 from April 15 to April 20, 2020.
from April 15 to April 20, 2020.
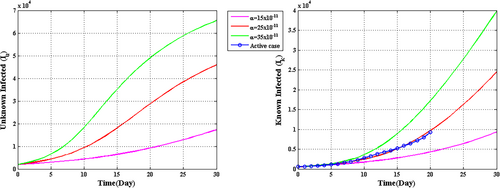
Figures 5-8 are drawn based on the parameter values (shown in Table 1). The values of the parameters are fixed based on the following real-time data of India, as shown in Table 2, the spread of the COVID-19 disease during the lockdown period is recorded as follows (MoHFW, 2021)
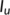 ) and known infected population (
) and known infected population (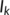 ) for
) for 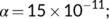
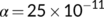 , and
, and 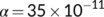
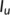 ) and known infected population (
) and known infected population (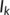 ) for
) for 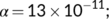
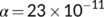 , and
, and 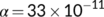
 ) and known infected population (
) and known infected population ( ) for
) for 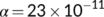 and
and 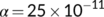
 ) and known infected population (
) and known infected population (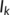 ) for
) for 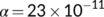 and
and 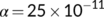
| Date | 
|
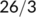
|
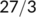
|
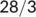
|
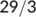
|
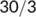
|
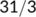
|
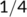
|
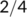
|
| Active cases | 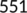
|

|
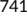
|
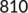
|

|
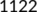
|

|

|

|
| Date | 
|
|
|
|
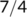
|
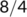
|
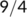
|
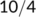
|
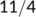
|
| Active cases | 
|
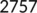
|
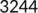
|

|

|

|
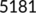
|

|
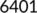
|
| Date | 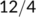
|
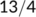
|
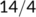
|
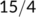
|

|
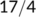
|
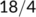
|

|
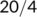
|
| Active cases | 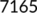
|

|
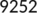
|

|
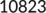
|

|
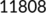
|

|

|
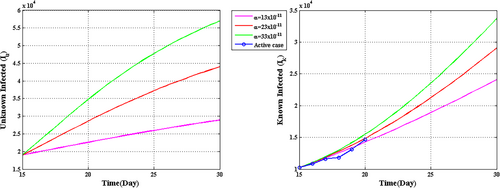
Figure 5 has been drawn for the unknown infected population (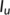 ) and known infected population (
) and known infected population (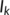 ) for
) for 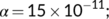
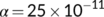 , and
, and 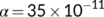 for the specified period from March 25 to April 14, 2020 during the first lockdown. This figure is fascinating because it is observed that for
for the specified period from March 25 to April 14, 2020 during the first lockdown. This figure is fascinating because it is observed that for 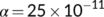 , the known infected population curve of our proposed system fits to the curve of the real confirmed infected individuals in India during the above said period.
, the known infected population curve of our proposed system fits to the curve of the real confirmed infected individuals in India during the above said period.
Figure 6 shows the time history of the unknown infected population (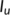 ) and known infected population (
) and known infected population (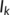 ) for
) for 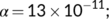
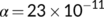 , and
, and 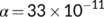 for the period from April 15 to April 20, 2020 during the second lockdown situation. Figure 10 is very interesting because it is observed that for
for the period from April 15 to April 20, 2020 during the second lockdown situation. Figure 10 is very interesting because it is observed that for 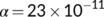 , the known infected population curve of our proposed COVID-19 system fits to the curve of the real confirmed infected individuals in India during the above said period.
, the known infected population curve of our proposed COVID-19 system fits to the curve of the real confirmed infected individuals in India during the above said period.
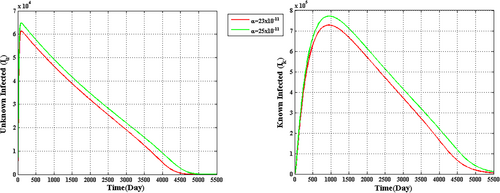
Figure 7 shows that the time history of the unknown infected (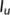 ) and known infected (
) and known infected (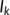 ) populations of the proposed system corresponding to
) populations of the proposed system corresponding to 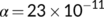 and
and 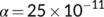 fits to the curve of the real confirmed infected individuals in India during the lockdown period from March 25 to April 20, 2020.
fits to the curve of the real confirmed infected individuals in India during the lockdown period from March 25 to April 20, 2020.
It is also clear that  as a representative of lack of following the good practices such as proper hand wash, sanitizing the places, nasal, and oral covering with a mask, social distancing has an effect in the proposed coronavirus model and an increase in
as a representative of lack of following the good practices such as proper hand wash, sanitizing the places, nasal, and oral covering with a mask, social distancing has an effect in the proposed coronavirus model and an increase in  means many individuals are not following the good practices as said above and as a result, many individuals gets infected and move to the unknown infected population (
means many individuals are not following the good practices as said above and as a result, many individuals gets infected and move to the unknown infected population (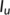 ). Long run prediction of the time history of the known infected population (
). Long run prediction of the time history of the known infected population (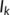 ) for
) for 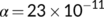 and
and 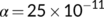 is drawn in Figure 8, which shows that the disease gets diminished may be due to the availability of a Vaccine.
is drawn in Figure 8, which shows that the disease gets diminished may be due to the availability of a Vaccine.
From Figure 8, it is observed that the active cases will decrease and the COVID-19 disease will persist in the society for a long period. Furthermore, it is noticed that the COVID-19 disease diminishes after a long period if people do not strictly follow the government guidelines and vaccination is not found at the earliest as we have considered that geographical and climatic factors do not have any impact on this virus infection.
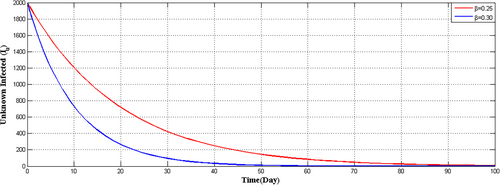
From Figure 9, it is noticed that if 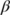 increases, which is a representative of the identification process of the infected individuals, then the unknown infected population reduces and hence we can identify the individuals for quarantine. Thus, the lockdown period can be reduced and people can come back to a normal situation.
increases, which is a representative of the identification process of the infected individuals, then the unknown infected population reduces and hence we can identify the individuals for quarantine. Thus, the lockdown period can be reduced and people can come back to a normal situation.
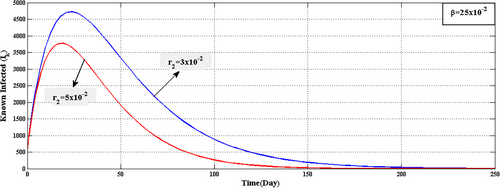
 ) with time for corresponding the value of
) with time for corresponding the value of 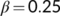 and
and 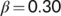
Figure 10 shows that if the recovery rate  increases, which representing the quality of treatment and cooperation of the patient to the treatment, then the known infected population (
increases, which representing the quality of treatment and cooperation of the patient to the treatment, then the known infected population ( ) tends to zero in the long run. Hence, the rapid spread of COVID-19 disease is reduced drastically.
) tends to zero in the long run. Hence, the rapid spread of COVID-19 disease is reduced drastically.
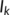 ) with time with the recovery rate
) with time with the recovery rate 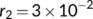 and
and 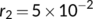
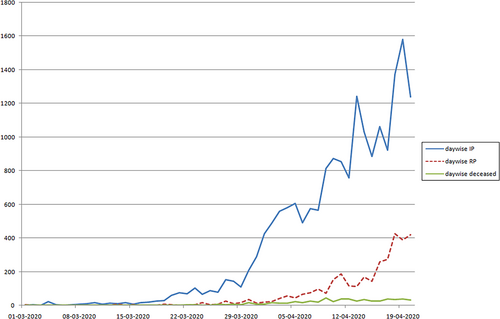
Figure 11 represents the graphical representation of the day-wise increase of infected, recovered, and deceased population from March 1 to March 20, 2020 in India (COVID19 tracker, 2021). It is observed that active infected cases start to increase from the third week of March because many have already been infected, failed to be in isolation, not strictly adhering to the rules imposed by the Government and ICMR at the time of the second week of March, and hence the active cases increases but in control during the first lock downstage. It is also observed that the day-wise recovered cases are also increasing and day-wise deceased cases are very low. From the above discussions, it can be said that SARS-COV-2 is threatening to the society, but not deadly dangerous until now in Indian perspective.
8 CONCLUSION
The proposed model has determined the outbreak of COVID-19 disease in the Indian population. The BRN 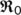 is the threshold limit that determines the dynamical proliferation. The reproduction number
is the threshold limit that determines the dynamical proliferation. The reproduction number 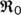 decreases if the transmission coefficient
decreases if the transmission coefficient  decreases. If
decreases. If  increases, then the transmission of COVID-19 disease increases and is very harmful to society. The system has a unique DFE
increases, then the transmission of COVID-19 disease increases and is very harmful to society. The system has a unique DFE 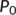 , which is globally stable if
, which is globally stable if 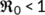 which symbolizes that the disease diminishes eventually. When
which symbolizes that the disease diminishes eventually. When 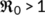 , the system is uniformly persistent under some conditions, a unique endemic equilibrium is globally stable. The study shows that the infected population who incubate the illness of our proposed system fits well to the real confirmed infected individuals in India during the lockdown period.
, the system is uniformly persistent under some conditions, a unique endemic equilibrium is globally stable. The study shows that the infected population who incubate the illness of our proposed system fits well to the real confirmed infected individuals in India during the lockdown period.
By observing the time graph of the known infected class (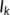 ) for various values of
) for various values of  , we conclude that if people do not strictly follow the guidelines and lockdown measures imposed by the Government of India to prevent the rapid spread of the infection, the situation will be out of control.
, we conclude that if people do not strictly follow the guidelines and lockdown measures imposed by the Government of India to prevent the rapid spread of the infection, the situation will be out of control.
ACKNOWLEDGMENTS
We are grateful to the editor and anonymous referees for their careful reading, valuable comments, and helpful suggestions which have helped us to improve the presentation of this work significantly.
CONFLICT OF INTEREST
The authors declare no conflicts of interest.
AUTHOR CONTRIBUTIONS
Analysis and draft the paper: R. Prem Kumar and Sanjoy Basu. Collected the data, conceived and designed the analysis, perform the analysis tool for the paper: D. Ghosh and P. K. Santra. Supervised, designed the analysis and wrote the paper: G. S. Mahapatra.
CONSENT TO PARTICIPATE
This article does not contain any studies involving animals or human participants performed by any authors. Anyone can read material published in the Journal.
CONSENT FOR PUBLICATION
We, the undersigned, give our consent for the publication of identifiable details, which can include figures and details within the text (“Material”) to be published in the above Journal and Article. Therefore, anyone can read material published in the Journal.
NOMENCLATURE
-
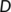
-
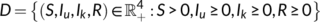 is the set on which the dynamical system is defined
is the set on which the dynamical system is defined -
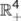
-
- 4-dimensional positive real space
-
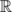
-
- the set of all real numbers
-
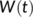
-
- the total number of population at time t
-
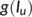
-
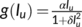 is the non-monotonic incidence function
is the non-monotonic incidence function -
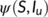
-
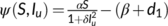 used for simplifying big expressions in Theorem 1
used for simplifying big expressions in Theorem 1
-
-
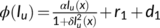 used for simplifying big expressions in Theorem 1
used for simplifying big expressions in Theorem 1
-
-
 which is positively invariant region in
which is positively invariant region in 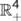 for the system (1)
for the system (1) -

-
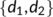
-
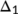
-
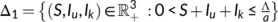 which is positively invariant region in
which is positively invariant region in 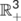 for the reduced system (4)
for the reduced system (4) -
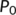
-
- the disease free equilibrium of the reduced system (4)
-
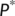
-
- the endemic equilibrium of the reduced system (4)
-
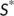 ,
, 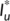 ,
, 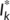
-
- the coordinates of the endemic equilibrium point
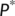 of the reduced system (4)
of the reduced system (4) - the coordinates of the endemic equilibrium point
-
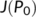
-
- the Jacobian or variational matrix of the system (4) evaluated at the disease free equilibrium point
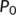
- the Jacobian or variational matrix of the system (4) evaluated at the disease free equilibrium point
-
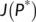
-
- the Jacobian or variational matrix of the system (4) evaluated at the endemic equilibrium point
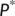
- the Jacobian or variational matrix of the system (4) evaluated at the endemic equilibrium point
-
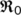
-
- basic reproduction number
-
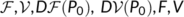
-
- these standard symbols are used in the calculation of the basic reproduction number
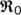 as per the cited reference used for calculation
as per the cited reference used for calculation - these standard symbols are used in the calculation of the basic reproduction number
-
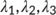
-
- the eigen values of the characteristic equation of
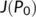
- the eigen values of the characteristic equation of
-
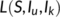
-
- Lyapunov function chosen to prove the global stability of the disease free equilibrium
-
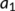
-
- the positive constant in Lyapunov function
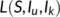
- the positive constant in Lyapunov function
-
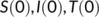
-
- the initial conditions for the reduced system (4)
-
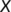
-
- locally compact metric space used in the introduction of the uniform persistence theorem
-
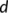
-
- the metric for the metric space X
-
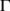
-
- a closed non-empty subset of
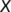 used in the introduction of the uniform persistence theorem
used in the introduction of the uniform persistence theorem - a closed non-empty subset of
-
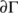
-
- the boundary of

- the boundary of
-
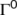
-
- the interior of
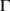
- the interior of
-
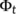
-
- it is a dynamical system
-
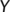
-
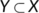
-
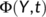
-
- the solution space of the dynamical system
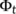
- the solution space of the dynamical system
-
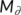
-
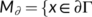 :
: 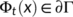 ,
, 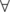 t
t 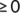 }
} -
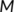
-
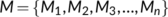 is compact, pairwise disjoint, isolated invariant subsets in
is compact, pairwise disjoint, isolated invariant subsets in 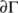
-
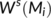
-
- the stable manifold of
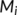
- the stable manifold of
-
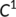
-
- the class
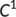 consists of all differentiable functions whose derivative is continuous. Those functions are called continuously differentiable functions
consists of all differentiable functions whose derivative is continuous. Those functions are called continuously differentiable functions - the class
-
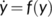
-
- the dynamical system used in the introduction of the geometric approach method used to investigate the global stability of the endemic equilibrium
-

-
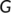 is the domain of
is the domain of 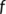 used in the introduction of the geometric approach method used to investigate the global stability of the endemic equilibrium
used in the introduction of the geometric approach method used to investigate the global stability of the endemic equilibrium -
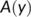
-
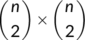 matrix valued function which is
matrix valued function which is 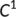 in
in 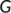
-
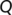
-
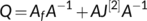 , which is used in accordance with the geometric approach method to investigate the global stability of the endemic equilibrium
, which is used in accordance with the geometric approach method to investigate the global stability of the endemic equilibrium -
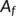
-
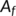 is the matrix obtained by replacing each entry of the matrix
is the matrix obtained by replacing each entry of the matrix 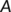 by its directional derivative in the direction of
by its directional derivative in the direction of 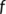
-
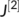
-
- the second additive compound matrix obtained from the jacobian matrix
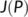
- the second additive compound matrix obtained from the jacobian matrix
-
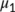
-
- the Lozinskii measure with respect to
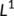 norm
norm - the Lozinskii measure with respect to
-
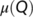
-
- Lozinskii measure of the matrix
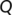 which is given by
which is given by 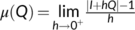 , I is the unit matrix
, I is the unit matrix - Lozinskii measure of the matrix
-
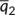
-

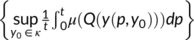 . This quantity is defined as per the Geometric approach method to investigate the global stability of the endemic equilibrium
. This quantity is defined as per the Geometric approach method to investigate the global stability of the endemic equilibrium -

-
- it is a compact absorbing set in the interior of
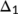 which is absorbing for the reduced system (4)
which is absorbing for the reduced system (4) - it is a compact absorbing set in the interior of
-
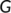
-
 is an open and simply connected set used in the introduction of Geometric approach method
is an open and simply connected set used in the introduction of Geometric approach method -
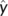
-
- the unique endemic equilibrium in G of the dynamical system
 used in the introduction of the Geometric approach to investigate the global stability of the endemic equilibrium
used in the introduction of the Geometric approach to investigate the global stability of the endemic equilibrium - the unique endemic equilibrium in G of the dynamical system
-
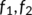
-
- these symbols are used as per the Geometric approach to investigate the global stability of the endemic equilibrium
-

-
- used in the definition of uniform persistence
Biographies
Mr. R. Prem Kumar is an Assistant Professor of Mathematics at Avvaiyar Government College for Women, Karaikal-609602 in the Union Territory of Puducherry. He is pursuing his Ph.D at National Institute of Technology Puducherry, Karaikal-609609.
Dr. Sanjoy Basu is an Assistant Professor of Mathematics at Arignar Anna Government Arts and Science College, Karaikal, Puducherry, India. He obtained M.Sc. and Ph.D. in Mathematics from Jadavpur University, Kolkata, India. Dr. Basu has been involved in teaching and research for more than twelve years and has published more than seven research articles in various International, National journals and proceedings to his credit. His fields of interest in research work are Solid Mechanics, Soft Computing, and Mathematical Biology.
Dipankar Ghosh holds the dual degrees of M.Sc. in Applied Mathematics and M.Sc. in Statistics from the University of Burdwan, Burdwan, India, and Ph.D. persuing from National Institute of Technology, Puducherry, India. Mr. Ghosh has been involved in research for more than four and half years and has published more than five research articles in various international journals and proceedings to his credit. His research interest field is Mathematical Biology.
Prasun Kumar Santra holds the degrees of M.Sc. in Applied Mathematics from Bengal Engineering and Science University, Shibpur, presently IIEST Shibpur, India, and Ph.D. from Maulana Abul Kalam Azad University of Technology, West Bengal, India. Dr. Santra has been involved in research for more than five years and has published more than twelve research articles in various international journals and proceedings to his credit. His research interest field is Mathematical Biology.
Dr. G. S. Mahapatra is an Associate Professor at National Institute of Technology Puducherry, India. He obtained M.Sc. and Ph.D. in Applied Mathematics from Bengal Engineering and Science University, Shibpur, presently IIEST Shibpur, India. Dr. Mahapatra has been involved in teaching and research for more than seventeen years and has published more than ninety research articles in various International, National journals and proceedings to his credit. His fields of interest in research work are Inventory Management, Reliability, Optimization, Fuzzy Set theory, Soft Computing, and Mathematical Biology.
Open Research
DATA AVAILABILITY STATEMENT
Available at https://www.who.int, www.mohfw.gov.in, www.covid19india.org



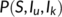 becomes
becomes
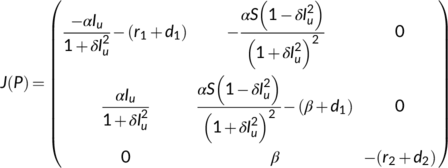
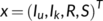 . Then the system (
. Then the system (
 closing lemma for 3-dimensional systems
closing lemma for 3-dimensional systems
