Physiology of the weight-loss plateau in response to diet restriction, GLP-1 receptor agonism, and bariatric surgery
Abstract
Objective
The objective of this study was to investigate why different weight-loss interventions result in varying durations of weight loss prior to approaching plateaus.
Methods
A validated mathematical model of energy metabolism and body composition dynamics was used to simulate mean weight- and fat-loss trajectories in response to diet restriction, semaglutide 2.4 mg, tirzepatide 10 mg, and Roux-en-Y gastric bypass (RYGB) surgery interventions. Each intervention was simulated by adjusting two model parameters affecting energy intake to fit the mean weight-loss data. One parameter represented the persistent shift of the system from baseline equilibrium, and the other parameter represented the strength of the feedback control circuit relating weight loss to increased appetite.
Results
RYGB surgery resulted in a persistent intervention magnitude more than threefold greater than diet restriction and about double that of tirzepatide and semaglutide. All interventions except diet restriction substantially weakened the appetite feedback control circuit, resulting in an extended period of weight loss prior to the plateau.
Conclusions
These preliminary mathematical modeling results suggest that both glucagon-like peptide 1 (GLP-1) receptor agonism and RYGB surgery interventions act to weaken the appetite feedback control circuit that regulates body weight and induce greater persistent effects to shift the body weight equilibrium compared with diet restriction.
Study Importance
What is already known?
- All weight-loss interventions eventually result in a weight plateau, with no further weight loss despite continued intervention.
- The timing of the weight plateau varies among interventions, with some interventions requiring substantially more than 1 year to approach the plateau.
What does this study add?
- Mathematical modeling was used to simulate body weight trajectories, body composition, and energy balance dynamics of diet restriction, glucagon-like peptide 1 (GLP-1) receptor agonism, and bariatric surgery interventions.
- The timing of the weight plateau was mainly determined by the intervention's ability to alter the strength of the feedback control circuit relating weight loss to increased appetite.
How might these results change the direction of research or the focus of clinical practice?
- These results emphasize that weight-loss interventions need to be considered within the context of a dynamic physiological system controlling both energy intake and expenditure.
- Basic research and clinical practice may be influenced by attaining a greater appreciation for the physiological resistance to weight-loss interventions and how they play out over time.
INTRODUCTION
Every obesity intervention eventually results in a body weight plateau, after which no further weight loss occurs. The timing of the plateau is a subject of great interest, especially in the context of the recently introduced glucagon-like peptide 1 (GLP-1) receptor agonists that exhibit ongoing weight loss without an obvious plateau until well after 12 months [(1, 2)]. Similarly, bariatric surgery often results in a prolonged period of weight loss, whereas diet interventions typically exhibit plateaus within ~12 months. What explains these differing weight trajectories?
Here, I used a validated mathematical model of energy balance and body composition dynamics [(3)] to simulate the mean weight-loss kinetics in response to a variety of interventions within the context of a physiological system that regulates body weight via feedback control of both energy intake and expenditure [(4, 5)]. Specifically, I sought to quantify the magnitude of interventions involving diet restriction, semaglutide, tirzepatide, and Roux-en-Y gastric bypass (RYGB) surgery by simulating mean responses in published studies. Preliminary results suggest that, unlike diet restriction, semaglutide, tirzepatide, and RYGB weaken the appetite feedback control circuit by ~40% to 70%, thereby resulting in an extended period of weight loss prior to the plateau.
METHODS
Mathematical model simulations were initialized using mean baseline anthropometric data from published studies on intensive calorie restriction [(7)], dietary macronutrient restriction [(8)], RYGB surgery [(9)], semaglutide [(2)], and tirzepatide [(1)] assuming a mean baseline free-living physical activity level of 1.65 [(10)]. Each intervention was simulated by fitting the parameters P(t) and k such that the modeled body weight time courses matched the observed mean weight trajectories. Body fat was measured by dual-energy x-ray absorptiometry in all published intervention studies, and mean body fat loss data were compared to model simulations that assumed nonlinear partitioning between lean and fat tissues, originally described by Forbes [(11)].
To simulate RYGB surgery and intensive calorie restriction, P(t) was assumed to be single parameter value for time, t > 0. Given the similar weight-loss trajectories for the low-carbohydrate and low-fat diet restriction groups, I combined the diet restriction groups from the Diet Intervention Examining The Factors Interacting with Treatment Success (DIETFITS) trial and used a constant effect for P(t) = P0 for the first 3 months, followed by a gradual reduction of diet adherence to match the mean self-reported intake changes [(8)]. Specifically, I assumed a linear reduction from month 3 to 0.86 × P0 at 6 months, followed by a linear reduction to 0.78 × P0 at 12 months. To simulate escalating doses of semaglutide and tirzepatide, P(t) = P0 + (Pmax-P0)t/T until t = T, where P0 is the initial drug effect and time t = T is the end of the dose escalation period, after which P(t) = Pmax, indicating the maximum drug effect. Predicted changes in energy intake and total energy expenditure were compared with mean data at corresponding time points, where available. For each intervention, a single value for the appetite feedback control parameter k was fit to the data.
A linearized version of the mathematical model used in the present study has been previously described [(3)], and the characteristic exponential time scale of the linear system is , where ρ is the effective energy density of the weight change and ε defines the change in energy expenditure per unit weight change and includes the metabolic adaptation to weight loss. Values for ρ and ε were determined from the baseline anthropometrics and physical activity, as previously described [(3)]. The long-term change in body weight in the linearized model is given by , where P(∞) is the long-term value of the parameter defining the magnitude of the intervention to shift the system from the baseline equilibrium.
RESULTS
To simulate the intensive calorie restriction intervention in the Comprehensive Assessment of Long Term Effects of Reducing Intake of Energy (CALERIE) phase 2 study [(7)], the best fit model parameters were k = 82 kcal/day per kilogram and P(t) = 830 kcal/day, resulting in a body weight change trajectory that plateaued after about 12 months, with simulated body fat being slightly greater than the mean observed values (Figure 1A). Figure 1B shows a substantial initial decline of energy intake at the onset of the intervention, followed by an increase over time that closely matched observed mean energy intake changes obtained using the intake balance method [(12)]. Simulated total energy expenditure rapidly decreased after the intervention onset and thereafter maintained an approximately constant level over the remainder of the 24-month intervention and matched the mean energy expenditure data reasonably well.
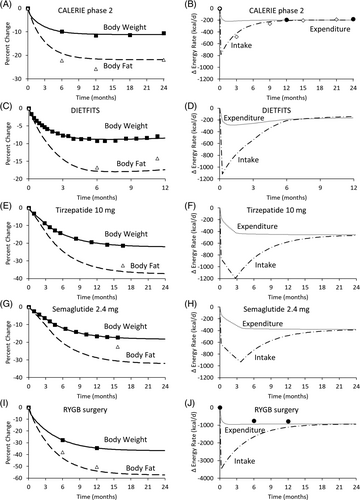
Diet restriction in the DIETFITS study [(8)] was simulated by the best fit parameters k = 101 kcal/day per kilogram and P0 = 1200 kcal/day after accounting for waning diet adherence assessed by self-reported intake changes. This resulted in a body weight-change plateau within 12 months, with slightly more simulated body fat loss than was observed (Figure 1C). Figure 1D illustrates the simulated changes in energy intake and expenditure.
Tirzepatide therapy was simulated using best fit parameters k = 48 kcal/day per kilogram, P0 = 830 kcal/day, and Pmax = 1560 kcal/day after the 12-week dose escalation period [(1)], resulting in an expected mean weight-change plateau after about 24 months (Figure 1E). Tirzepatide therapy resulted in changes in mean values for body fat that were only slightly higher than the simulated values. Tirzepatide simulations resulted in a rapid initial decrease in energy intake and further declined during the dose escalation period, after which intake increased until approaching the simulated energy expenditure toward the end of the 24-month simulation (Figure 1F).
Simulation of semaglutide therapy [(2)] was achieved using best fit parameters k = 49 kcal/day per kilogram, P0 = 610 kcal/day, and Pmax = 1300 kcal/day after the 16-week dose escalation period, resulting in an expected weight-change plateau about 24 months after the intervention onset (Figure 1G). Energy intake decreased at the onset of the intervention and further declined during the dose escalation period, after which intake increased until approaching the simulated energy expenditure toward the end of the 24-month simulation (Figure 1H). Unlike the simulations of the other weight-loss interventions, the model predicted substantially lower levels of body fat than the mean values observed following the semaglutide intervention. This indicated a possible semaglutide-induced alteration in energy partitioning. To account for this effect, I fit both the observed mean body weight and body fat changes during semaglutide therapy (not shown), which required adjusting the energy partitioning parameter by approximately threefold from its baseline value, originally described by Forbes [(11)]. The revised best fit model parameters after making this adjustment in energy partitioning were k = 31 kcal/day per kilogram, P0 = 535 kcal/day, and Pmax = 1040 kcal/day after the 16-week dose escalation period.
RYGB surgery was simulated using best fit parameters k = 58 kcal/day per kilogram and P = 3600 kcal/day, which resulted in the greatest weight loss and a plateau at 24 months, with measured mean body fat changes that were only slightly greater than the simulated values (Figure 1I) [(9)]. Energy intake decreased by a very large amount after the surgery, corresponding to almost no food intake immediately after the surgery, followed by an increase over time to approach total energy expenditure after about 24 months. Modeled total energy expenditure decreased by ~150-kcal/day more than was measured using a respiratory chamber (Figure 1J).
Table 1 summarizes the best fit model parameters P and k used to match the observed mean body weight trajectories, as well as the estimated long-term body weight change calculated using the linearized model parameters ρ, ε, and τ, assuming that physical activity was maintained and the final value of the parameter P continued indefinitely.
| Calorie restriction | Diet restriction | Tirzepatide 10 mg | Semaglutide 2.5 mg (baseline energy partitioning) | Semaglutide 2.5 mg (adjusted energy partitioning) | RYGB surgery | |
|---|---|---|---|---|---|---|
| Parameters adjusted to fit to the observed mean body weight trajectories | ||||||
| P0 | 830 | 1200 | 830 | 610 | 535 | 3600 |
| Pmax (kcal/d) | 830 | 1200 | 1560 | 1300 | 1040 | 3600 |
| k (kcal/d per kg) | 82 | 101 | 48 | 49 | 31 | 58 |
| Linearized model parameters determined by baseline anthropometrics and physical activity | ||||||
| ρ (kcal/g) | 9.6 | 10.3 | 10.9 | 10.8 | 8.8a | 11.3 |
| ε (kcal/d per kg) | 24 | 21 | 19 | 19 | 24a | 19 |
| τ (d) | 91 | 85 | 162 | 160 | 161 | 147 |
| Long-term weight change (kg) | −7.8 | −7.7 | −23.2 | −19.1 | −19.1 | −47.2 |
- Abbreviation: RYGB, Roux-en-Y gastric bypass.
- a Adjusting the energy partitioning parameter affected the linearized model parameters ρ and ε.
DISCUSSION
Weight-loss interventions should be considered within the context of the dynamic physiological system controlling both energy intake and expenditure. Each intervention simulated by the mathematical model assumed persistent effects to decrease energy intake from baseline, but energy intake subsequently increased to eventually match energy expenditure, resulting in a weight plateau. The magnitude of the persistent intervention that shifts the system from its baseline equilibrium was more than threefold greater following RYGB surgery compared with diet restriction and about double that of tirzepatide, which was slightly larger than semaglutide at the doses studied. Although intensive calorie restriction achieved the smallest intervention magnitude, the study participants exerted a substantial persistent effort to cut ~800 kcal/day from their baseline diet. The approximately exponential rise in energy intake after the start of the intervention shows that the same amount of effort to cut calories was met with increasing resistance as ongoing weight loss increasingly activated the feedback control circuit, stimulating appetite. Within 12 months, this resistance, together with decreased total energy expenditure, matched the persistent effort to cut calories, and weight loss plateaued. In the macronutrient diet restriction study, gradual loss of diet adherence was superimposed on the feedback control circuit, thereby resulting in an earlier body weight plateau. Thus, the timing of the weight-loss plateau is determined by both the strength of the feedback circuit controlling appetite together with the (perhaps waning) effect of the intervention magnitude to shift the system from its baseline equilibrium.
Why did the other interventions result in prolonged weight-loss periods with plateaus well after 12 months? Interestingly, the mathematical model suggests that the time to reach a weight plateau has nothing to do with the magnitude of the intervention, P, after it reaches a constant value. Rather, a linearized version of the mathematical model used in the present study shows that the characteristic time scale of the system is given by , where ρ is the effective energy density of the weight change, ε defines the change in energy expenditure per unit weight change (including metabolic adaptation to weight loss), and k is the appetite feedback gain parameter [(4)]. If k decreases because of the drug and surgery interventions, representing a weakening of the appetite feedback control circuit, then τ increases, indicating an extension of the time to reach the weight plateau. Furthermore, the linearized model estimates that the amount of weight lost at the plateau is given by , indicating that a decrease in the appetite feedback control parameter k acts along with the parameter defining the long-term magnitude of the intervention to shift the system from the baseline equilibrium, P(∞), to decrease body weight.
The preliminary estimate of k = 95 kcal/day per kilogram weight loss derived using data from SGLT2 inhibition [(5)] was reasonably close to the best fit value of k = 83 kcal/day per kilogram weight loss achieved by calorie restriction in the CALERIE phase 2 trial, as well as the k = 101 kcal/day per kilogram weight loss in the DIETFITS macronutrient restriction trial, and resulted in the weight plateaus within 12 months. However, RYGB surgery, semaglutide, and tirzepatide all resulted in much lower values of k of ~30 to 60 kcal/day per kilogram, suggesting that these interventions weakened the feedback control of appetite by ~40% to 70% and thereby resulted in a prolonged period of weight loss prior to the plateau.
Another way to increase the characteristic time τ to approach a weight plateau or the magnitude of weight lost at the plateau would be to decrease the value of the parameter ε, defining how energy expenditure changes per unit weight loss. However, there is a limited ability to decrease ε because the values were less than ~25 kcal/day per kilogram. Because the model simulations reasonably matched the mean energy expenditure data, there was no indication that ε was changed from its baseline value, and the observed prolongation of the time to approach a reduced weight plateau with RYGB surgery, tirzepatide, and semaglutide is most likely due to a weakening of the feedback control of appetite rather than an alteration of energy expenditure.
The mathematical model of energy partitioning depends on body fat and the magnitude of weight change, as previously described [(3)]. The simulated body fat changes generally matched the data quite well, except for the semaglutide intervention, in which mean loss of body fat was substantially less than that predicted by the model. Thus, a greater-than-expected proportion of fat-free mass was lost with semaglutide treatment, indicating a potential effect on energy partitioning. More research is needed to investigate body composition changes during semaglutide treatment and whether the composition of fat-free mass lost has functional implications.
Simulated free-living energy intake and expenditure changes with calorie restriction matched the observations reasonably well, but mean changes in energy expenditure following RYGB surgery measured using respiratory chambers were slightly less than predicted by the model. This may be indicative of an effect of bariatric surgery to preserve energy expenditure, or perhaps the respiratory chamber data did not fully capture the changes in energy expenditure in free-living people. Unfortunately, model simulations of energy intake and expenditure for tirzepatide and semaglutide treatment could not be compared with data because such measurements are not yet available.
This study has several limitations. First, its focus was on group average responses, ignoring substantial individual variability characteristic of all weight-loss interventions. Previous attempts to mathematically model energy balance dynamics in individuals during diet restriction have revealed that the imprecision of energy expenditure and body composition measurements results in insufficient model constraints at the individual level [(6)]. Thus, mechanistic determinants of individual long-term weight loss and body composition variability are presently unclear and beyond the scope of the current study. Another limitation is the lack of specificity regarding the modeled feedback control of appetite, which does not presently account for its molecular mechanisms or whether these appetite signals are associated with loss of body fat, fat-free mass, or something else. Furthermore, I have assumed a linear feedback control of appetite as weight is perturbed away from its baseline equilibrium, which may be overly simplistic.
In conclusion, varying model parameters P and k that affect energy intake alone was sufficient to simulate body weight trajectories during a variety of weight-loss interventions. The simulations indicated that RYGB surgery, tirzepatide, and semaglutide interventions substantially weakened the feedback control of appetite unlike diet restriction interventions. The persistent magnitudes of these interventions to shift the system from its baseline equilibrium were quantified and varied by more than threefold, but even the intensive calorie restriction intervention corresponded to a persistent effect to cut energy intake by ~800 kcal/day over the 2-year simulations. Our previous modeling analyses of obesity pharmacotherapies illustrated that, after an early reduction in energy intake, an approximately exponential increase over time is the expected result of a constant magnitude intervention superimposed on a physiological system with proportional feedback control of appetite [(4, 13)]. However, our previous analyses did not address the question of the timing of the weight-loss plateau or its implications regarding the effect of the interventions on the appetite feedback control circuit. Interestingly, the model simulations do not predict any weight regain when assuming fixed values of the model parameters during the latter stages of the interventions. This suggests that explaining weight regain requires additional assumptions regarding waning adherence to the interventions, tachyphylaxis, or changes in physiology or the environment beyond the scope of the present study.
FUNDING INFORMATION
This work was supported by the Intramural Research Program of the National Institutes of Health, National Institute of Diabetes and Digestive and Kidney Diseases.
CONFLICT OF INTEREST STATEMENT
The author declared no conflict of interest.





