Effects of household composition and income security on body weight in working-age men
Disclosure: The authors declared no conflict of interest.
Abstract
Objective
Many recent studies have provided evidence suggesting that increases in body weight may spread via social networks. The mechanism(s) by which this might occur have become the subject of much speculation, but to date little direct evidence has been available. Building on evidence from economics, anthropology, and behavioral biology, within-household peers might influence body weight via implicit provision of income security was hypothesized.
Design and Methods
Using a sample of 2,541 working-age men from the National Longitudinal Survey of Youth (1979), the effect of cohabitation on weight gain over a 6-year period was estimated. The potential confound caused by the joint determination of economic insecurity and cohabitation status with instrumental variables that exploit variation in local and state-level macroeconomic conditions and the presence of children in the home was addressed.
Results
The marginal effect of cohabitation with adults on body weight is negative. Moreover, the magnitude of the effect is more than six times greater when the cohabitant is engaged in paid employment.
Conclusions
Income insecurity may play an important role in peer-to-peer transmission of weight gain.
It-s a long, long road from which there is no return. While we're on the way to there, why not share.—The Hollies
Introduction
Several recent studies have examined the possibility that obesity might be a product of one-s social environment. In particular, studies of social networks have provided evidence suggesting that obesity is more likely when one has friends who are obese. These results appear to be somewhat robust to alternative econometric specifications, and have been reported in both adolescent and adult populations ((1-3); but see also (4-6)). Although many plausible relational mechanisms such as the propagation of body weight norms, unhealthy eating habits, smoking, and participation in sports have been suggested, none has been tested directly.
In this article, we provide empirical support for an alternative mechanism that has gone unmentioned in the social networks literature, but which might plausibly explain the peer effects that have been reported. In particular, we explore the possibility that peers can provide a network of financial or economic support, which could then affect body weight via deep-seated psychological stress–response mechanisms. A broad interdisciplinary literature supports this putative relationship between economic insecurity and obesity [see Smith (7) and Wisman and Capehart (8) for recent reviews].
Considerable evidence suggests that social networks play an important role in the modulation of financial security through risk sharing and income pooling (9-11). The availability of effective social support networks, moreover, may significantly decrease the likelihood of a household evaluating its food, economic, and housing conditions as vulnerable (12). At the level of the household (the locus of our analysis), a potentially important component of financial security is likely to be risk-sharing among household members. One way to buffer against labor market risk or labor lost to illness, for instance, is through intra-household labor substitution, where large households with more workers can more easily compensate for lost income (13, 14). Indeed, extended households are often formed to cope with the destructive consequences of poverty (15) and to buffer against the economic effects of labor market risk (16).
There is also considerable evidence of food-sharing in response to risky foraging outcomes among modern hunter-gatherers (17-19), suggesting that the practice may have originated in human evolutionary history, a necessary precondition to the innate psychological stress–response we posit. This is important because it opens up the possibility that the mechanism might hold (in modern environments) even when financial resources are not in fact pooled. If the link between economic insecurity and obesity is indeed an evolutionary vestige, we would expect body weight to be affected by environmental cues that were strongly correlated with food security over the course of evolutionary history. The anthropological evidence referenced above suggests that such cues may well have included information about the social or material well-being of close friends or relatives.
To test for such a “peer effect” at the household level, we estimate the effect of household composition – roughly measured as the number of workers and nonworkers in the home – on individual weight, via its effect on financial insecurity. We do so using regression analysis to estimate the relationship between body weight and income characteristics, including both household composition and income insecurity measures, while controlling for other important personal and household factors.
Section Household Composition and Obesity discusses hypotheses about the relationship between obesity and income characteristics. Section Empirical Model, develops an empirical model. Section Data and Estimation, describes the data and discuss estimation issues. Section Results includes the results and discussion. Section Conclusion concludes.
Household Composition and Obesity
An individual household member may affect body weights of others in a household via effects on in-home production and consumption patterns within the home, as well as via effects on the level and risk profile of household income. Employment status is likely to play a key role in such effects, though the direction of impact is somewhat ambiguous.
Consider the effect of having an additional adult resident in the home who does not have paid employment and relies at least partly on the household for financial support. Assuming economies of scale in meal preparation that the new addition contributes effort to meal preparation and other household chores, it is likely to be easier for other household members to enjoy healthy, freshly prepared meals (20). However, given a limited budget and another mouth to feed, it might become more difficult to budget for healthy, balanced meals (21). In contrast, if the additional resident is fully employed, his contribution to household income could be used to purchase healthier foods, but it is more likely that he will be unable to contribute substantially to household work.
As noted in the Introduction, there is a third mechanism by which an additional household member might affect body weights: by bolstering (or diminishing) income security. Assuming that income is at least partly shared during periods of crisis, the impact of an additional member on household income security will depend on his employment status. If employed, and assuming the risk of job loss is at least partly independent of the risk faced by other household members, the additional income can be viewed as a source of diversification of total household income, thus reducing the level of risk faced by all. A nonworking and financially dependent resident, on the contrary, could represent a heavy burden in the event that other household members experience job loss.
Empirical Model
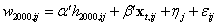 (1)
(1)Equation 1 is linear in parameters, and in principle can be estimated via ordinary least squares (OLS). However, OLS as an estimator will be biased if weight is endogenously related to one or more of the independent variables. Reverse causality and unobserved personal characteristics that are correlated with body weight are both likely causes of endogeneity in our model. Reverse causation is present when weight exerts an influence on one of the right-hand side variables. Cawley (22), for example, finds that higher body weight corresponds to lower wages for women. If true, the OLS estimate for income not only includes the effect of wages on weight, but also the effect of weight on wages, making the estimate upward-biased. Bias relating to unobserved personal characteristics is present when weight gain is endogenously related to a right-hand side variable. It could be, for example, that an individual who suffers from economic insecurity will gain weight, while also inviting others to live with him in an attempt to alleviate the effects of financial insecurity. In this case, OLS estimates of α incorrectly include the effect of the latent variable “economic insecurity” and therefore will not represent the unbiased, causal effect of household composition on weight.
We correct for potential endogeneity bias in two ways. First, we include weight in 1994 in the model. Including 1994 weight in the model partially controls for permanent unobserved characteristics unique to the individual, as well as pre-1994 economic insecurity that may introduce bias into the estimates if omitted. The 1994 weight is used because it allows us to examine the effects of household composition and other individual-level measures on changes in weight over a 6-year time span. Also, 1994 is the most recent year that is not included in any of the other variables used in our regression (data from 1995 and later were used to construct the employment insecurity measures). Controlling for 1994 weight, however, does not eliminate bias occurring from events after 1994, nor for personal characteristics that change over time.
Second, to address the remaining potential for bias and inconsistency, we apply a Generalized Method of Moments (GMM) estimator, which uses instrumental variables to compensate for remaining endogeneity directly. This also facilitates the ability to flexibly address potential heteroskedasticity in the regression disturbances. For our instruments to be valid they must be: (1) highly correlated with the endogenous RHS variable of interest, (2) asymptotically uncorrelated with the errors, and (3) correctly excluded from the equation of interest (i.e., have no direct effects on weight). To test whether the instruments are highly correlated with the endogenous variables, we performed a test of instrument relevance (also known as a weak instruments test). This test is based on the Kleibergen–Paap rk LM statistic (23). The null hypothesis is that the model is under-identified, or that the smallest canonical correlation between the linear combinations of the independent variables and the instrument(s) is zero. Rejecting the test statistic indicates that the instruments pass the weak instruments test and are valid in this respect.
The other important instrument characteristic is that it be asymptotically uncorrelated with the regression disturbance (i.e., the instrument itself is exogenous). The Hansen J-statistic (24) is applied to test for exogeneity (equivalently, that the instruments are orthogonal to the regression disturbances). This test statistic is the GMM criterion function evaluated at the efficient GMM estimator, and it has a Chi-square distribution with degrees of freedom equal to the number of excluded instruments minus endogenous variables. This test is actually a joint test of the two requirements: exogeneity of the instrument and correct model specification (i.e., that the instruments are justly excluded). A large test statistic leads to rejecting the null hypothesis and indicates that the instruments do not satisfy the orthogonality conditions and are not valid.
Data and Estimation
The data used in our analysis come from the National Longitudinal Survey of Youth, 1979 cohort (NLSY79). This survey follows an initial cohort of 12,686 men and women born between 1957 and 1964. It was administered annually until 1993, and biennially since then. Although our study incorporates data from 1994 to 2000, the analysis is cross-sectional in nature. The nature of the dataset allows a comprehensive study of different measures of household composition for the respondent in 2000 as well as their personal experience with unemployment over the 5-year period previous to 2000, and other individual level data.
Although women are included as members of the household in our analysis, they are not included as the measure of observation (the dependent variable) because the women in our sample are ages 29-42, peak child-bearing years. Fertility decisions may be related to any economic insecurity women face, and this complication would be difficult or impossible to address given our data limitations.
The primary variables of interest relate to financial insecurity. Three measures of personal unemployment are used: the posterior probability of unemployment in 2000, a dummy variable indicating whether the individual was unemployed at the time of interview in 2000, and a dummy variable indicating whether the individual was unemployed at any time in 2000. The posterior probability of unemployment is a proxy for an individual-s perceived economic insecurity. This variable is formed using the last 5 years of weekly unemployment history and represents an individual-s perception of whether they will be unemployed the following year (for details see 25). Previous evidence suggests that higher levels of insecurity correspond to weight gain (25). “Unemployed at the time of the survey” and “unemployed anytime during the year” are expected to have two distinct effects on weight as they measure different aspects of unemployment. An individual who is in fact unemployed on the day of the survey likely has a relatively low opportunity cost of healthy living because individuals who are not employed have more time to exercise and prepare healthy foods, and thus might be expected to weigh less (26-28). We treat this variable as exogenous because, controlling for one-s underlying risk (over the course of a year) of being unemployed, the chances of being unemployed on the particular day the individual happens to be interviewed should not be related to unobserved personal characteristics. The underlying risk itself, however, is captured by the variable “unemployed anytime during the year,” and we treat it as endogenous. The economic insecurity hypothesis predicts that individuals facing prospective unemployment risk will be expected to weigh more, ceteris paribus. Means and standard deviations for all NLSY79 variables included in the analysis are presented in Table 1.
| Characteristica | Mean | SDb |
|---|---|---|
| Weight (in lbs) in 2000 | 197.121 | 39.069 |
| Number of workers in the home | 0.75 | 0.732 |
| Number of nonworkers in the home | 1.528 | 1.469 |
| Ratio of working adults to adults | 0.301 | 0.254 |
| Number of children in the home | 1.299 | 1.321 |
| Family income | 57.163 | 53.245 |
| Posterior probability of unemployment | 0.03 | 0.076 |
| Unemployed at any time in 2000 | 0.119 | – |
| Unemployed at time of interview in 2000 | 0.026 | – |
| currently smoke | 0.309 | – |
| Weight (in lbs) in 1994 | 187.708 | 35.872 |
| Height in 1985 (in inches) | 69.659 | 2.586 |
| Height squared in 1985 | 4859.127 | 358.576 |
| Age | 38.846 | 2.264 |
| Black | 0.274 | – |
| Hispanic | 0.184 | – |
| White | 0.542 | – |
| Married | 0.605 | – |
| Divorce or separated | 0.185 | – |
| Widowed | 0.004 | – |
| Never married | 0.206 | – |
| BA | 0.219 | – |
| Some college | 0.216 | – |
| High school graduate | 0.447 | – |
| High school dropout | 0.117 | – |
| Live within a Metropolitan area | 0.728 | – |
- a N = 2880.
- b Variance for proportions of the binary variables is p(1 − p), where p is the reported mean of the binary variable.
Our data include several measures of household composition. As explained above, we propose that these measures play a role in risk management as well as decreasing the relative price of healthy living. The household composition variables include: the number of workers in the home, the number of nonworkers in the home, and the ratio of working adults to (all) adults. Subsets of these variables are included in different estimation specifications because the same instruments are used to estimate various measures of household composition and including them in the same regression makes it impossible to identify the distinct effects of these measures on weight.
The relationship of most interest is that between household income, income uncertainty, and weight, but several other personal characteristics that are expected to play a role in determining weight are included in the regressions as controls. They are: 1994 weight, height in 1985, height squared in 1985, age, race, marital status, years of schooling, a dummy variable indicating whether the respondent lives in a metropolitan area, and a dummy variable indicating whether the respondent smokes daily. Because NLSY79 uses self-reported heights and weights, we correct for reporting error using NHANES III data, which includes a subsample of individuals for whom both stated and measured heights and weights were recorded. Correction factors from NHANES III (generated by regressing measured height/weight on stated height/weight for each demographic group of interest) were applied, as described in Cawley (22). Unless otherwise specified, variables are measured in the year 2000.
Approximately 75% of the individuals in our sample live with other people. The average weight for people who live with others is 198.1 pounds, compared with 194.1 for individuals that live alone. Nearly 61% of individuals in our sample live with someone who works. The average weight of people that live with someone who works is 199.8 pounds, whereas 192.9 is the average weight of people that do not live with workers. The average number of workers in the home in addition to the respondent is 0.75, with some homes having as many as five additional workers. The average number of workers in the sample for obese individuals is 0.82, whereas the average for nonobese people is 0.72. Furthermore, the average number of people in the home (in addition to the respondent) for obese people is 2.37, whereas the average for nonobese is 2.24. These statistics indicate that on average, higher weights correspond to more workers and more people in the home. Without correcting for endogeneity and controlling for other covariates, these raw correlations may incorrectly suggest that increasing the number of workers in the home causes weight gain, whereas in reality the relationship may be the other way around.
To further investigate the relationship between various measures of household composition and weight and economic security, we consider the Pearson Correlation Coefficients for these relationships. The correlation coefficients between changes in weight to changes in measures of household composition (including the number of workers in the home and the number of people in the home) from 1998 to 2000 are less than 4%. The correlation coefficients between changes in unemployment and the same measures of household composition are 1% or less over the same time period. These statistics suggest that there is little statistical evidence that households invite additional workers (or nonworkers) into the home to alleviate economic insecurity in the short term, implying that any bias relating to this aspect of endogeneity is likely very small.
Potentially endogenous variables include family income, unemployment risk, smoking, and household composition, and instrumental variables are used to address the endogeneity problem. State- and MSA-level instruments are used whenever possible to ensure that the instruments are exogenous to the errors and that they do not have an independent effect on weight. Because of limited data availability, however, we cannot rely solely on state- or MSA-level instruments to identify the effect of various measures of household composition on weight, so individual-level instruments are used as well. The use of individual-level instruments allows us to consistently estimate the effects of household composition on weight. Our instruments are as follows: state median household income from the US Census Bureau is used as an instrument for family income. A time series of local unemployment rates in the respondent-s MSA of residence are used as instruments for unemployment risk. A series of cigarette taxes (see 29) are used as instruments for smoking. State median home prices from the US Census Bureau, as well as the total number of adults in the home, are used to estimate the causal effect of the number of workers in the home on weight. The number of children in the home is used to identify the effect of nonworkers in the home (although fertility may be dependent on unobserved personal characteristics and economic insecurity, the number of children in the home is arguably not affected by weight at any given time). Finally, county ethnicity percentages and the number of children in the home are used to identify the effects of adult nonworkers on weight because evidence suggests that certain ethnicities are more likely to have more adults (e.g., grandparents and extended family members) in the home (15, 16). The results of instrument validity tests are discussed in the next section along with the rest of the results.
Results
To provide a more complete examination of the relationships between household composition and weight, we perform regression analysis on several different model specifications. Results are presented in Table 2. Each column represents a different specification, differing from each other only in the variable(s) that are used to measure household composition and unemployment.3
| Variables | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| Family income (in $1,000) | 0.0476a | 0.0472 | 0.0471 | 0.0604c |
| (0.028) | (0.034) | (0.033) | (0.019) | |
| Unemployed at any time during the year | 23.8274c | – | – | – |
| (5.346) | ||||
| Unemployed at time of interview | –13.9714c | – | – | – |
| (4.389) | ||||
| Posterior probability of unemployment | – | 59.7271c | 63.504c | 67.8946c |
| (23.098) | (23.499) | (9.801) | ||
| Number of workers in the home | – | –3.1469c | –2.7316c | – |
| (1.051) | (1.038) | |||
| Number of nonworkers in the Home | – | – | –0.4212b | – |
| (0.172) | ||||
| Ratio of working adults to adults | – | – | – | –9.8802c |
| (2.907) | ||||
| Smoke daily | –14.5259c | –7.6233 | –7.5824 | 1.5167 |
| (3.998) | (5.303) | (5.228) | (3.031) | |
| Weight in 1994 (in pounds) | 0.9385c | 0.9352c | 0.9362c | 0.9453c |
| (0.012) | (0.013) | (0.013) | (0.010) | |
| Height (in inches) | 0.4234 | –0.4199 | –1.1735 | 3.2031 |
| (4.307) | (3.900) | (3.913) | (2.435) | |
| Height (in inches) squared | 0.0016 | 0.0086 | 0.014 | –0.0188 |
| (0.031) | (0.029) | (0.029) | (0.018) | |
| Age | –0.2291a | –0.0984 | –0.1271 | –0.1980a |
| (0.133) | (0.138) | (0.135) | (0.114) | |
| Black | 2.6963c | 3.0563c | 3.068c | 2.9989c |
| (0.804) | (0.846) | (0.854) | (0.542) | |
| Hispanic | –1.7962c | –0.7697 | –0.5805 | –0.8109 |
| (0.629) | (0.659) | (0.670) | (0.570) | |
| Married | –0.3542 | 2.2664 | 2.6581 | 3.8241c |
| (1.624) | (1.903) | (1.891) | (0.885) | |
| Divorced or separated | –1.4264 | –1.3403 | –1.2634 | –1.2387 |
| (0.920) | (0.967) | (0.962) | (0.794) | |
| Widow | 1.9894 | 5.8011 | 6.2007 | 3.025 |
| (4.870) | (4.478) | (4.439) | (4.223) | |
| BA degree | –7.7437b | –5.3397 | –5.3652 | –1.4322 |
| (3.550) | (4.146) | (4.113) | (2.074) | |
| Some college | –3.131 | –1.4408 | –1.5713 | 1.2403 |
| (2.186) | (2.257) | (2.239) | (1.173) | |
| High school graduate | –1.4331 | –0.0729 | –0.187 | 1.7692b |
| (1.475) | (1.594) | (1.581) | (0.882) | |
| Live within a Metropolitan area | 0.5428 | –0.1992 | –0.1671 | 0.4515 |
| (0.631) | (0.512) | (0.514) | (0.379) | |
| N | 2541 | 2541 | 2541 | 2532 |
| Adjusted R2 | 0.729 | 0.759 | 0.759 | 0.752 |
- Robust standard errors (adjusted for within-state clustering) in parentheses.
- a *significant at 10%,
- b **significant at 5%,
- c ***significant at 1%
Instruments are as follows:
| Variable | Instrument(s) |
| Family income | State median household income |
| Posterior probability of unemployment | Local unemployment rates, 1988–2000 |
| Unemployed any time during 2000 | Local unemployment rates, 1988–2000 |
| Smoke | Cigarette taxes, 1988–2000 |
| Number of household workers | State median home prices, number of adults in the home |
| Number of household non-workers | Number of children in the home |
We fail to reject the Hansen J-Statistic in every specification, suggesting that the instruments used are unrelated to the error term, as required for consistent estimation. Results for this test are found in Table 3. We estimated preliminary OLS regressions (not reported) for each of these specifications. Most of our endogenous variables switch signs from the expected (biased) sign in the OLS regression to the expected (unbiased) sign in the GMM regression, suggesting that the instruments used are likely valid (30). However, because multiple endogenous variables are used in each regression this may not necessarily be the case.
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Tests of over-identification (instrument exogeneity) | ||||
| Null: Over-identifying restrictions are valid (Note: “Fail to Reject the Null” implies valid instruments) | ||||
| Hansen J-statistic | 16.36 | 24.14 | 23.56 | 28.03 |
| χ2 distribution p-value | 0.56 | 0.19 | 0.21 | 0.3 |
| Tests of under-identification (instrument relevance) | ||||
| Null: Equations are under-identified (Note: “Fail to Reject the Null” implies invalid instruments) | ||||
| Full set of instruments | ||||
| Kleibergen–Paap rk LM statistic | 18.39 | 21.26 | 21.1 | 32.95 |
| χ2 distribution p-value | 0.49 | 0.38 | 0.39 | 0.16 |
| Treating sources of under–identification as exogenous | ||||
| Kleibergen–Paap rk LM statistic | 32.772 | 23.89 | 24.33 | 30.49 |
| χ2 distribution p-value | 0.02 | 0.01 | 0.01 | <0.01 |
- Columns index specifications as reported in Table 2.
- Sources of under-identification, and their corresponding specifications: Family Income (1), Smoke (2–4).
Our full suite of instruments, however, fails to pass the weak instruments test, implying that as a group they are not highly correlated with the endogenous variables and could imply biased coefficient estimates. Family income was found to be the source of under-identification in the first specification, and smoking was found to be the source of under-identification (with cigarette taxes as the instruments) in regressions (2-4). Therefore, Table 3 reports the Kleibergen–Paap rk LM test statistics with corresponding p-values for two sets of regressions: regressions that treat these two sources of under-identification as endogenous, and test statistics for the regressions where the source of under-identification is treated as exogenous. The Hansen J-Statistic is not rejected at α = 0.05 in any specification where the source of under-identification is treated as exogenous. We therefore report regressions that contain the original variables (rather than instrumented variables) in the regressions in which the instruments identifying the variable (family income and smoking, respectively) are weak. However, regardless of whether we utilize the weak instruments or use the original variables for income and smoking, respectively, the coefficients relating to our hypotheses about household composition and weight engender the same conclusions; they retain the same sign, retain statistical significance at conventional levels, and are different in magnitude by at most 29% of the value reported in Table 2 (The signs on the parameters associated with family income and smoking switch between the exogenous and endogenous treatment only once: for smoking in regression (4). Of all the other parameters in all four regressions combined, only five parameter estimates switch sign, but none of them were statistically significant in either regression, and none were directly related to the hypotheses regarding household composition on which this article focuses).
Given the richness of the available data relating to household composition of workers, nonworkers, children, and adults, there are many possible regression specifications that could be reported. We present here a limited set that illustrates and reflects the general nature of these relationships. We begin our discussion of the regression results by focusing on the estimates for family income and the various measures of unemployment. Family income has a small but marginally significant effect on weight. Increasing income by $1,000 increases weight by anywhere between 0.04 and 0.06 pounds, indicating that individuals are more likely to gain (not lose) weight as current income rises. Increasing an individual-s posterior probability of unemployment by 0.01 increases weight by nearly a pound in some specifications. This result might appear to contradict Ruhm (26), Ruhm (27), who finds that employment rates and body weight are positively related. Specification (1), however, reconciles these findings as we see that being currently unemployed has a negative effect on weight (the opportunity cost of time effect), while having been unemployed at any time over the year has a positive effect on weight (the insecurity effect). These findings suggest that weight is a function of both time costs and economic insecurity, as previously established. They also relate directly to the relationship between various measures of household composition and weight as workers are expected to affect weight through an increased security effect and contributors are expected to affect weight through a decreased time cost effect. We now study the effects of these and other measures of household composition on weight.
Specification (2) indicates that increasing the number of workers in the household by one person decreases weight by just over three pounds. We hypothesize that the increased security that accompanies more workers in the home is the mechanism driving the negative relationship with weight. As noted above, household workers serve as a financial safety net as intra-household labor substitutions minimize the effects of adverse economic shocks caused by illness, job loss, or many other factors.
Specification (3) indicates that both workers and nonworkers have a negative effect on weight. The effect of workers is larger than the effect of nonworkers, presumably because of a larger relative importance of income and/or income security effects over time cost effect. (One might hypothesize that these results are driven by the presence of a working [or nonworking] spouse. To test this, we replicated specification (3), omitting spouses from our counts of working and non-working adults; the results [available from the authors upon request] were virtually unchanged.) It should be noted that the effect of workers in this specification is smaller in magnitude (−2.73) than the effect in specification (2) (−3.14), implying that missing variable bias may exist in the second specification because nonworkers were not included. These results are consistent with our findings in specification (1), where various measures of unemployment are estimated. Specification (1) indicates that the effect of decreasing the relative cost of healthy living (being currently unemployed) decreases weight, while increasing insecurity (being unemployed anytime during the year) increases weight. In this regression, increasing the number of workers (increasing security) decreases weight, as does increasing the number of nonworkers, or contributors to household production (perhaps by decreasing the relative cost of healthy eating).
Finally, specification (4) indicates that increasing the ratio of working adults to adults by one decreases weight by over nine pounds. This would seem to provide further confirmation that employment status is of critical importance in determining the direction of the effects of cohabitation on body weight.
These empirical results offer insights into the effect of household composition on weight. First, living with others (having a social network in your home) decreases fattening. Evidence also suggests that in general, both workers and non-workers have a negative effect on weight. The effect of workers on weight is large and supports earlier findings (25, 31) that economic insecurity can be an important determinant of body weight.
Limitations
Our results should be interpreted in light of several important limitations. First, the validity of our instruments relies on the assumption that each is (causally) related to the independent variable of interest, but unrelated to the dependent variable (body weight in 2000). For example, if the number of children in the household (which we use as an instrument for “number of household nonworkers” in Table 2, specification 3) causes, on average, the body weight of the survey respondent to change, then the coefficient we report for the endogenous variable will be biased.
Data limitations preclude us from knowing whether workers actually pool income (though the literature we cite in the Introduction suggests many do), nor to specifically test the hypothesis that nonworking adults contribute to household production and decrease the cost of eating healthy foods. Thus, our estimates of the effects of household composition on body weight do not measure the effects of risk sharing or decreasing the relative price of a healthy lifestyle directly, but rather measure the combined effects of our specific measures of household composition on weight. To the extent that these effects work in opposite directions, our estimates will underestimate the income insecurity effects of household composition on body weight.
Another important limitation is the restriction of our sample to working-age males. Reports in the literature suggest that female body weight is more sensitive to both peer effects and income and food insecurity than is male body weight (2, 32). Our findings might therefore underestimate the effects of household composition on body weight in the general population.
Conclusion
The medical and epidemiological literature has examined the relationship between body weight and social networks, but has largely ignored the role that social networks play in the modulation of socioeconomic stressors such as income insecurity that are likely to have direct effects on body weight. Our results suggest that the reported peer effects on obesity in social networks could be an artifact, at least in part, of the underlying economic relationships between the individuals in question.
Given the increasing attention being focused on obesity as a public health problem, studies like ours should be understood as underscoring the scientific uncertainties that remain about the causes of the modern obesity epidemic (33). Many possibilities have been proposed, but the complexity of the phenomenon necessarily requires that most be studied in isolation, and this study is no exception.
There is suggestive evidence, however, that economic insecurity may have large effects on obesity. The evidence is most striking when viewed across countries over time: Offer et al. (34), for instance, find in a panel of developed countries that obesity rates are more sensitive to economic insecurity than to income inequality or fast food prices, while Smith (35) notes that obesity rates have risen most rapidly in countries that have most aggressively adopted policies that weaken worker protections and social insurance programs. Given this evidence, it should not be too surprising if it turns out that the social transmission of obesity among peers is reflective of the deeper social and economic bonds that are the fabric of society.





