Superconvergence and gradient recovery for a finite volume element method for solving convection-diffusion equations

Corresponding Author

Tie Zhang

Department of Mathematics and State Key Laboratory of SAPI Technology and Research Center of National Metallurgical Automation, Northeastern University, Shenyang, 110004 China

Correspondence to: Tie Zhang, Department of Mathematics, Northeastern University, Shenyang, 110004, China, (e-mail: [email protected]) Search for more papers by this author

Ying Sheng,

Ying Sheng

Department of Mathematics and State Key Laboratory of SAPI Technology and Research Center of National Metallurgical Automation, Northeastern University, Shenyang, 110004 China

Search for more papers by this author

Tie Zhang,

Corresponding Author

Tie Zhang

Department of Mathematics and State Key Laboratory of SAPI Technology and Research Center of National Metallurgical Automation, Northeastern University, Shenyang, 110004 China

Correspondence to: Tie Zhang, Department of Mathematics, Northeastern University, Shenyang, 110004, China, (e-mail: [email protected]) Search for more papers by this author

Ying Sheng,

Ying Sheng

Department of Mathematics and State Key Laboratory of SAPI Technology and Research Center of National Metallurgical Automation, Northeastern University, Shenyang, 110004 China

Search for more papers by this author

First published: 13 February 2014

https://doi.org/10.1002/num.21862

Citations: 2

Share a link

Email
Wechat
Bluesky

Abstract

We study the superconvergence of the finite volume element (FVE) method for solving convection-diffusion equations using bilinear trial functions. We first establish a superclose weak estimate for the bilinear form of FVE method. Based on this estimate, we obtain the H¹-superconvergence result: 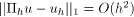$urn:x-wiley::media:num21862:num21862-math-0001$ . Then, we present a gradient recovery formula and prove that the recovery gradient possesses the 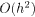$urn:x-wiley::media:num21862:num21862-math-0002$ -order superconvergence. Moreover, an asymptotically exact a posteriori error estimate is also given for the gradient error of FVE solution.Copyright © 2014 Wiley Periodicals, Inc. Numer Methods Partial Differential Eq 30: 1152–1168, 2014

References

1 Z. Q. Cai, On the finite volume element method Numer Math 58 (1991), 713–735.
10.1007/BF01385651
Web of Science® Google Scholar
2 E. Süli, Convergence of finite volume schemes for poission's equation on nonuniform meshes, SIAM J Numer Anal 28 (1991), 1419–1430.
10.1137/0728073
Web of Science® Google Scholar
3 R. Lavarov, I. Michev, and P. Vassilevski, Finite volume methods for convection-diffusion problems, SIAM J Numer Anal 33 (1996), 31–55.
10.1137/0733003
Web of Science® Google Scholar
4 Z. Y. Chen, R. H. Li, and A. H. Zhou, A note on the optimal L²-estimate of the finite volume element method Adv Comput Math 16 (2002), 291–303.
10.1023/A:1014577215948
Web of Science® Google Scholar
5 R. E. Ewing, T. Lin, and Y. P. Lin, On the accuracy of the finite volume element method based on piecewise linear polynomials SIAM J Numer Anal 39 (2002), 1865–1888.
10.1137/S0036142900368873
Web of Science® Google Scholar
6 T. Zhang, T. P. Lin, and R. J. Tait, On the finite volume element version of Ritz-Volterra projection and applications to related equations, J Comput Math 20 (2002), 491–504.
Web of Science® Google Scholar
7 H. J. Wu and R. H. Li, Error estimate for finite volume element methods for general second order elliptic problem, Numer Methods Partial Differential Equations 19 (2003) 693–708.
10.1002/num.10068
Web of Science® Google Scholar
8 S. H. Chou and X. Ye, Superconvergence of finite volume methods for the second order elliptic problem Comput Methods Appl Mech Eng 196 (2007), 3706–3712.
10.1016/j.cma.2006.10.025
Web of Science® Google Scholar
9 J. C. Xu and Q. S. Zou, Analysis of linear and quadratic simplical finite volume methods for elliptic equations, Numer Math 111 (2009) 469–492.
10.1007/s00211-008-0189-z
Web of Science® Google Scholar
10 L. Chen, A new class of high order finite volume element methods for second order elliptic equations, SIAM J Numer Anal 47 (2010) 4021–4023.
10.1137/080720164
Web of Science® Google Scholar
11 R. H. Li and P. Q. Zhu, Generalized difference methods for second order elliptic partial differentil equations I, The case of a triangular mesh, Numer Math A J Chin Univ 4 (1982) 140–152.
Google Scholar
12 Z. Y. Chen, L² estimate of linear element generalized difference schemes, Acta Sci Nat Univ Sunyatseni 33 (1994) 22–28.
Google Scholar
13 Z. Y. Chen, Superconvergence of generalized difference methods for elliptic boundary value problem, Numer Math, A J of Chin Univ(English Ser) 3 (1994) 163–171.
Web of Science® Google Scholar
14 R. H. Li, Z. Y. Chen, and W. Wu, Generalized difference methods for differential equations: numerical analysis of finite volume methods, Marcel, New York, 2000.
10.1201/9781482270211
Google Scholar
15 R. E. Bank and D. J. Rose, Some error estimates for the box method, SIAM J Numer Anal 24 (1987) 777–787.
10.1137/0724050
Web of Science® Google Scholar
16 T. Schmidt, Box schemes on quadrilateral meshes, Computing 51 (1993) 271–292.
10.1007/BF02238536
Web of Science® Google Scholar
17 S. H. Chou and Q. Li, Error estimates in $urn:x-wiley::media:num21862:num21862-math-0308$ in covolume methods for elliptic and parabolic problem: a unified approach, Math Comp 69 (2000) 103–120.
10.1090/S0025-5718-99-01192-8
Web of Science® Google Scholar
18 J. L. Lv and Y. H. Li, L² error estimates and superconvergence of the finite volume element methods on quadrilateral meshes, Adv Comput Math 37 (2012), 393–416.
10.1007/s10444-011-9215-2
Web of Science® Google Scholar
19 Q. D. Zhu and Q. Lin, The superconvergence theory of finite elements, Hunan Science and Technology Publishing House, Changsha 1989.
Google Scholar
20 Q. Lin and Q. D. Zhu, The preprocessing and postprocessing for the finite element methods, Shanghai Sci & Tech Publishing, Shanghai, China, 1994.
Google Scholar
21 T. Zhang, Finite element methods for evolution integro-differential equations, Northeastern University Publishing House, Shenyang, 2001.
Google Scholar

Citing Literature

Volume30, Issue4

July 2014

Pages 1152-1168

Superconvergence and gradient recovery for a finite volume element method for solving convection-diffusion equations

Abstract

References

Citing Literature

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Superconvergence and gradient recovery for a finite volume element method for solving convection-diffusion equations

Abstract

References

Citing Literature

References

Related

Information