Disasters are catastrophic events that can severely affect the life conditions of entire communities. Disaster-related issues are usually dealt with according to the Disaster Operations Management framework, which is composed of four phases: mitigation, preparedness, response, and recovery. This work focuses on two crucial operations belonging to the response phase: shelter location and evacuation of endangered populations. Specifically, the ultimate scope of this paper is to present some applications of a scenario-based mixed-integer two-stage linear program which integrates shelter location with two different types of evacuation, self- (or car-based) evacuation and supported- (or bus-based) evacuation, namely the Scenario-Indexed Shelter Location and Evacuation Routing (SISLER) model. The SISLER model is solved using an off-the-shelf optimization software, whose performance is improved through the addition of some valid inequalities which are added at the root node of the solution tree to improve the lower bound. Computational results are reported for both testbed instances and a realistic case study (Sioux Falls network). The analysis of the solutions provides some useful managerial insights for relevant stakeholders working within the shelter location and evacuation planning area, such as emergency management practitioners and public service providers.

1 INTRODUCTION

Disasters are calamitous occurrences that threaten the everyday life of many communities around the globe. Disasters are usually categorized into two main groups, depending on what prompted them: natural disasters (i.e., due to nature) and man-made disasters (i.e., due to human beings). Examples of the former are geophysical (i.e., earthquake), meteorological (i.e., cyclone), climatological (i.e., drought), and hydrological (i.e., flood) events while examples of the latter are terroristic and cyber-attacks. For example, the storm surge of Hurricane Katrina of 2005 led to 1200 casualties in the State of Louisiana and yielded a $108 billion property damage. The population of New Orleans at that time was more than 480 000 people however, tens of thousands were evacuated but many others stayed in New Orleans, especially the elderly and those with lack of access to transportation [17]. Another example is the Great East Japan earthquake of 2011 and the resulting tsunami. The occurrence of this calamitous event led to 20 000 deaths and a $300 billion estimated material damage [11]. Currently, in 2019, there are still 54 000 people who are displaced but, luckily, more than 20 000 people have moved from provisional accommodations to permanent homes during 2018 [30]. All these events clearly demonstrate the urgency of developing novel research in the area of disaster management. Disaster-related operations are usually classified according to the Disaster Operations Management framework [2], which is composed of four phases: mitigation and preparedness, which address pre-disaster activities, and response and recovery, which address post-disaster ones. Risk assessment, communication systems set-up, casualty rescue, and debris clean-up are examples of activities belonging to the mitigation, preparedness, response, and recovery phases, respectively.

This paper focuses on two crucial operations within disaster response: shelter location and evacuation routing. A shelter is a facility where people experiencing perilous circumstances can be supplied with services such as first-aid, drinkable water, food, and/or beds [26]. The aim of shelter location problems is to identify the best location of these facilities, given a pool of candidate sites, so as to maximize accessibility from the disaster affected zones (e.g., minimize the total traveling distance or time between affected zones and shelters). Depending on aspects such as the transportation mode (e.g., foot, car, bus, train, boat, and helicopter) and the disaster type (e.g., earthquake, flood, and hurricane), different types of evacuation can occur such as self-evacuation and supported-evacuation [26]. The former evacuation type concerns those people who can autonomously drive a vehicle while the latter type of evacuation is related to special-needs populations such as the elderly, the medically homebound, and so on [35]. The scope of evacuation routing problems is to optimally identify the evacuee routes so as to minimize the total evacuation time.

Different types of disasters require a diverse evacuation process: preventive evacuation is usually arranged for wildfires and hurricanes while immediate evacuation is required for floods and earthquakes. Nevertheless, inefficient evacuation plans can lead to life losses as well as evacuees being resentful towards governmental organizations [9]. Renne and Mayorga [32] report that, since the occurrence of Hurricane Katrina in 2005 which showed inefficiency, especially in relation to special-needs population, many cities in the United States are still lagging behind and do not have an evacuation plan in place. Among other aspects, Renne and Mayorga [32] highlight the need to account for vulnerable evacuees and multimodal evacuation (i.e., different transportation modes at the same time) when planning emergency response. These are complex and critical issues that should be captured in efficient evacuation plans.

1.1 Problem overview

A recent paper by Esposito Amideo et al. [14] identified the emerging challenges in the shelter location and evacuation routing research field through: (a) the analysis and cross-comparison of recent disaster operations management surveys; (b) the analysis of all the recent optimization models combining shelter location and evacuation routing problems; and (c) a questionnaire to the authors of such models. This meticulous review process has led to the definition of five macro-categories of challenges: (1) stakeholder involvement, (2) evacuation modes, (3) clear definition of modeling inputs and parameters, (4) evacuee behavior, and (5) system behavior. Stakeholder involvement covers all aspects aimed at including relevant stakeholders through the optimization model development process (e.g., problem definition, data collection, experimentation, and calibration). Evacuation modes refer to the types of evacuation to be considered (e.g., self- and supported-evacuation). Clear definition of modeling inputs focuses on all those features that help to devise a more realistic model (e.g., are shelters existing building such as schools or open spaces? what is the amount of square meters available to set up a shelter facility?). Evacuee behavior tackles all those aspects that could affect the way evacuees react to and perform during the evacuation process such as the time of day during which the evacuation takes place, potential route diversions (e.g., to pick-up children at school), demographics, route preference, and warning signal dissemination. Finally, system behavior includes aspects such as shelter capacity availability, different types of shelters, network congestion, infrastructure disruption, and fairness of the evacuation process.

The model here discussed, namely the Scenario-Indexed Shelter Location and Evacuation Routing (SISLER) model [13], contributes to the emergency response literature by addressing challenges belonging to the evacuation modes (2), evacuee behavior (4), and system behavior (5) categories. Specifically, SISLER combines shelter location, car- and bus-based evacuations decisions through an integrated user-system perspective while accounting for fairness among self- and supported-evacuees and road network disruptions due to disastrous occurrences. The adoption of a combined approach between users (evacuees) and system (public authorities arranging shelter locations and bus-based evacuation) and the appreciation of network disruptions clearly distinguishes SISLER from the Comprehensive Evacuation Problem (CEP) of Goerigk et al. [18] that, to the best of the authors' knowledge, is the only other optimization model currently combining shelter location with self- and supported-evacuations and, hence, addressing an evacuation modes-based challenge. Specifically, SISLER overcomes the limitations of one of the assumptions underpinning CEP related to the adoption of a system optimal approach where a planning authority is in charge of shelter location, car- and bus-based evacuation decisions. It may be argued that this assumption is not very realistic given that self-evacuees usually attempt to travel the shortest available route and enforcing a specific route for each evacuee may be impractical. SISLER assumes that all self-evacuees, even the furthest ones, are able to reach a shelter within a traveling time threshold and, based on how strict or loose this threshold is (i.e., how much self-evacuees are willing to travel either a shorter or lengthier route), they are free to decide which path to take. On the other side, the system planner is in charge of opening shelter sites and arranging supported-evacuation. This assumption tackles challenges belonging to both categories (4) and (5). In fact, self-evacuee willingness to travel either shorter or lengthier routes allows to account for evacuee behavior (4) while, imposing that all self-evacuees, despite their position, are able to reach a shelter within a traveling time threshold, attempts to address equity issues, which are system behavior-related challenges (5). Moreover, SISLER deploys scenario-based programming, which is a modeling technique that has already been successfully deployed within the disaster management field (see e.g., [31] for emergency relief supply pre-positioning and [25] in the specific shelter location and evacuation routing research area). It may be argued that, during disaster response, given that the disaster has occurred, the specific scenario to deal with is known. However, within a restricted time frame to put into action an evacuation plan, it is fundamental to know in advance how to proceed. Therefore, under uncertain circumstances and based on disaster-specific historical data of the areas under consideration, a scenario-based formulation is an efficient tool to obtain a solution that is robust across different disastrous conditions: shelter locations need to be known in advance (being those strategic decisions) while routes can be identified when the scenario is revealed (being those operational decisions). Real-time travel times can be obtained through GIS-based tools (i.e., Google Maps) and evacuees from a given affected area can be given instructions related to which shelter they should go to through the use of social media and other communication channels [3, 15, 37]. Furthermore, the scenario-based formulation of SISLER accounts for road network infrastructure disruptions in a direct way, which is another system behavior-related challenge (5). In Goerigk et al. [18], infrastructure disruption was only addressed indirectly through the inclusion of a risk exposure measure into a multiobjective formulation where the evacuation time, the number of shelters to be opened, and the risk exposure of the evacuees are combined.

The contribution of this paper is fourfold. First, a critical review of optimization models combining shelter location and evacuation routing problems based on typical objectives, constraints, and applications is presented. Second, a scenario-based mixed-integer two-stage linear program, namely the SISLER model, addressing shelter location, car- and bus-based evacuations together is described, as preliminary introduced by Esposito Amideo and Scaparra [13]. Third, some valid inequalities are identified to improve the lower bound and facilitate the solution of SISLER to optimality through a commercial optimization software, specifically IBM ILOG CPLEX 12.6. Finally, managerial insights for relevant stakeholders working within the shelter location and evacuation planning area, such as emergency management practitioners and public service providers, are provided based on the application of SISLER to test instances as well as the realistic case study of the Sioux Falls network.

The outline of this paper is as follows. Section 2 provides a state-of-the-art literature review for combined shelter location and evacuation routing problems. Section 3 details the SISLER model in terms of underpinning assumptions and model formulation. Section 4 describes the solution methodology adopted to solve SISLER, based on the addition of valid inequalities. Section 5 presents applications of SISLER to both testbed instances and a realistic case study. Finally, Section 6 offers conclusive remarks along with future research directions.

2 LITERATURE REVIEW

Over the years, researchers have developed various optimization models for shelter location (strategic decisions), car-based evacuation, and bus-based evacuation (tactical decisions) as separate problems. However, the decisions arising from one of the two problems directly affect the other one and vice-versa (e.g., budgetary resources availability, road network utilization). The focus of this section is to briefly review optimization models combining shelter opening and evacuation of endangered populations (either by car or bus), which will demonstrate that there is little evidence of the three problems combined together. An extensive survey on optimization for shelter location and evacuation routing is provided by Esposito Amideo et al. [14]. Table 1 briefly summarizes the main features of shelter location, car-based evacuation, and bus-based evacuation as combined problems in terms of objectives, constraints, and case studies.

TABLE 1. Features of shelter location, car-based evacuation, and bus-based evacuation as combined problems

Problem	Authors	Total evacuation time	Total number of evacuees	Total number of shelters	Total resources	Total risk	Total shelter opening cost	Total travel distance	Flow conservation	Maximum number of evacuees	Minimum number of evacuees	Number of shelters	Shelter capacity	Shelter capacity expansion	Shelter utilization	Vehicle capacity	Bomb disposal	Bushfire	Earthquake	Fire	Flood	Generic man-made threat	Hurricane
		Objectives							Constraints								Case study
Shelter location and car-based evacuation	Kongsomsaksakul et al. [22]	×						×	×												×
	Alçada-Almeida et al. [1]	×				×		×		×	×	×								×
	Ng et al. [29]	×						×														×
	Li et al. [24]	×										×											×
	Coutinho-Rodrigues et al. [12]			×		×		×		×	×	×								×
	Li et al. [25]	×										×											×
	Bayram et al. [5]							×				×							×
	Kılcı et al. [20]						×								×				×
	Gama et al. [16]							×				×									×
	Heßler and Hamacher (2016)						×		×								×
	Bayram and Yaman [4]							×				×							×
Shelter location and bus-based evacuation	Shahparvari et al. [33]		×		×								×	×				×
Shelter location, car- and bus-based evacuations	Goerigk et al. [18]	×		×		×			×				×			×	×		×

Integrated models can address three possible combinations of the aforementioned problems: (a) shelter location and self-evacuation; (b) shelter location and supported-evacuation; and (c) shelter location, self-, and supported-evacuation. Combination (a) has been the most widely investigated. Kongsomsaksakul et al. [22] introduced a bi-level program under flood circumstances solved with a genetic algorithm and provided an application to the Logan network, Utah (USA). Alçada-Almeida et al. [1] developed a multiobjective optimization model, addressing evacuee traveling distance and risk, in case of a fire disaster for the city of Coimbra (Portugal). Ng et al. [29] presented a bi-level program solved with a Simulated Annealing algorithm and applied it to the Sioux Falls network (USA) hypothesizing a generic man-made threat. Coutinho-Rodrigues et al. [12] extended the model proposed by Alçada-Almeida et al. [1] by including two additional criteria in the objective function: total evacuation time and total number of shelters to be opened. Li et al. [24, 25] produced a scenario-based bi-level program under hurricane circumstances addressing driver route-choice behavior and applied it to the state of North Carolina (USA). Bayram et al. [5] introduced a nonlinear mixed-integer program based on a Constrained System Optimal approach, solved by using a second-order cone programming approach and applied to both test and realistic case studies, such as the Istanbul European and Istanbul Anatolian networks under earthquake circumstances. Kılcı et al. [20] addressed shelter location and self-evacuation with the ultimate goal of improving the Turkish Red Crescent (TRC) approach; the model is solved through a commercial solver and applied to two realistic case studies, the Kartal district of Istanbul and the province of Van (Turkey), under earthquake circumstances. Gama et al. [16] detailed a multi-period mixed-integer program, including warning signals dissemination under flood circumstances; the model was solved with a Simulated Annealing algorithm and tested on the Wake County, North Carolina (USA). Heßler and Hamacher [19] proposed different models based on a sink location problem, solved through adaptations of source location heuristics and applied to both random and realistic instances (i.e., the evacuation of the city of Kaiserslautern, Germany, under a bomb disposal scenario). Bayram and Yaman [4] extended the work of Bayram et al. [5] by addressing the uncertainty affecting evacuation demand as well as potential alteration to the network structure (both roads and shelter sites) due to the disaster occurrence; the authors develop a scenario-based two-stage stochastic nonlinear mixed-integer program solved with ad hoc exact solution approach based on both Benders decomposition and the cutting plane method.

To the best of the authors' knowledge, only one paper has addressed each of the combinations (b) and (c). For combination (b), Shahparvari et al. [33] dealt with evacuation under bushfire circumstances and focus on late evacuees that require the support of public authorities to evacuate under short notice scenario; the authors present a multiobjective integer program solved with an ϵ-constraint approach and applied to the 2009 Black Saturday bushfire in Victoria (Australia). Finally, for combination (c), which is also the one of interest to this paper, Goerigk et al. [18] proposed a multi-period, multi-criteria mixed-integer program, called the CEP, solved with a genetic algorithm and tested on two realistic case studies: the evacuation of the city of Kaiserslautern (Germany) due to a bomb defusion and the evacuation of the city of Nice (France) due to an earthquake with a subsequent flood. The reason for so few contributions in categories (b) and (c) is that the seminal paper for bus-based evacuation [6] only appeared in 2011 thus requiring some years prior to provide either combination (b) or (c). SISLER aims to contribute to combination (c), as it will be detailed in the next section.

3 THE SISLER MODEL

SISLER is a scenario-based mixed-integer two-stage linear program. The decisions are divided into first-stage decisions and recourse (or second-stage) decisions. Specifically, shelter openings are first-stage decisions while, once uncertainties are revealed (in our case, these are the network conditions after potential disruptions), self-evacuees-to-shelters allocations and supported-evacuees route decisions are made and, as such, they are recourse decisions.

Self-evacuation and supported-evacuation include those evacuees who can autonomously drive a vehicle and those who cannot (e.g., the elderly, the medically homebound), respectively. More precisely, self-evacuation involves people evacuating with their own vehicles towards a shelter (people moving towards other destinations are not considered) while supported-evacuation is arranged by public authorities and relies on buses which are stored and dispatched from a depot. In the following, self-evacuation is also referred to as car-based evacuation (or mode (a)) and supported-evacuation as bus-based evacuation (or mode (b)).

Several disruption scenarios are considered, each differing in terms of road network arc availability and occurring with a given probability. Hence, the objective of SISLER is to minimize the supported-evacuation completion time, accounting for all the disruption scenarios, weighted by their own probability. The following subsections illustrate the model assumption (Section 3.1) and its formulation (Section 3.2), respectively.

3.1 Model assumptions

The assumptions underpinning the SISLER model are as follows.

The area affected by the disaster is divided in different evacuation zones. Both self-evacuation and supported-evacuation start at the centroid of each zone. In fact, prior to plan for the evacuation of a certain area, a process named zoning is carried out, which divides the region under study in different zones. Then, for each zone, the point where all evacuees are assumed to depart for evacuation is identified, namely the centroid.
For each zone, the number of self-evacuees and supported-evacuees (i.e., evacuation demand) is known.
Both shelters and buses have a limited capacity. In fact, when planning for shelters, the amount of space available to each evacuee as well as to vehicles taking them to safe sites should be accounted for (guidelines can be found from agencies such as the TRC, as outlined by Kılcı et al. [20]). Similarly, buses can only carry a limited number of passengers.
Setting up a shelter requires a given amount of resources. To be operative, in fact, shelters need to be equipped with items such as first-aid kits, drinkable water, food stocks, emergency beddings/blankets, and personnel. The level of expenditure to open a shelter varies according to the shelter size and type (e.g., pre-existing buildings such as schools, gyms, or open spaces) [20]. It is assumed that there is a limited amount of resources available to set up the shelters, which cannot be exceeded.
Split delivery of supported-evacuees is possible (i.e., more than one bus may collect people from the same area and bring them to different shelters). However, all self-evacuees from the same zone go to the same shelter. From a practical point of view, in fact, it would be difficult to direct self-evacuees from the same zone to different shelters.
To ensure an efficient and egalitarian evacuation of self-evacuees, each car-based evacuation zone must be assigned to a shelter located within a traveling time threshold (i.e., the shortest travel time between each evacuation zone and its designated shelter cannot exceed a specified threshold). Note that, because of the shelter capacity restrictions, self-evacuees are not necessarily allocated to their closest shelter.
Contraflow lane reversal [28] has been assumed on the network arcs whose destination node is a shelter site, which means that those arcs can be traveled only in one direction (i.e., towards the shelter). Contraflow lane reversal consists of blocking all traffic into the affected area, thus increasing the amount of lanes available for evacuation. This approach has been adopted in various evacuation processes in the United States [8] to reduce congestion on outgoing routes and allow evacuees to leave dangerous zones quickly.
Each bus performs a single trip to collect evacuees from the evacuation zones. This is a realistic assumption for some kind of disasters, such as floods. When a flood strikes, in fact, there is a central zone that is initially affected. Then the flood starts to propagate in neighboring areas. From an evacuation perspective, once a bus has departed from the depot, it collects the evacuees, takes them to a shelter and stops there, without returning to the dangerously affected area, which may no longer be reachable. This assumption also follows from the contraflow lane reversal.

3.2 Model formulation

The SISLER model can be described as follows.

Sets and indices
G(N, A)	directed network
o	depot node where all the buses are stored
N_a	set of zones where evacuation mode (a) starts, indexed by i
N_b	set of zones where evacuation mode (b) starts, indexed by i. Note that N_a ∩ N_b ≠ ∅ hence, some zones may have both evacuations (mode (a) and (b)) occurring
N_t	set of transit nodes of the transportation network, indexed by i
N_s	set of potential shelter sites, indexed by j
D	set of network disruption scenarios, indexed by d
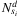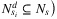$urn:x-wiley:00283045:media:net22058:net22058-math-0001$ ( $urn:x-wiley:00283045:media:net22058:net22058-math-0002$	set of potential shelter sites to which a zone i, i ∈ N_a, can be assigned in scenario d, d ∈ D
A	set of network arcs
A_d (A_d ⊆ A)	set of available arcs under disruption scenario d
K	set of buses stored and dispatched from a depot node o, indexed by k

The entire set of network nodes N is equal to {o ∪ N_a ∪ N_b ∪ N_t ∪ N_S}. In the following, for the sake of readability, we will consider N ′ = {N_b ∪ N_t ∪ N_S} and N′′ = {N_b ∪ N_t}.

Parameters
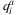$urn:x-wiley:00283045:media:net22058:net22058-math-0003$	expected number of mode (a) evacuees in zone i, i ∈ N_a
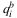$urn:x-wiley:00283045:media:net22058:net22058-math-0004$	expected number of mode (b) evacuees in zone i, i ∈ N_b
C_j	capacity of a shelter at site j, j ∈ N_s
r_j	amount of resources to set up a shelter at site j, j ∈ N_s
R	total amount of available resources

B_k	capacity of bus k, k ∈ K
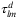$urn:x-wiley:00283045:media:net22058:net22058-math-0005$	bus-based evacuation traveling time from node l to node m in scenario d, with l, m ∈ N′, d ∈ D such that (l, m) ∈ A_d
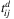$urn:x-wiley:00283045:media:net22058:net22058-math-0006$	car-based evacuation shortest traveling time from zone i, i ∈ N_a, to site 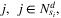$urn:x-wiley:00283045:media:net22058:net22058-math-0007$ in scenario d, d ∈ D
p_d	probability of occurrence of scenario d, d ∈ D

Decision variables
γ_d	bus-based evacuation maximum completion time in scenario d, d ∈ D
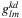$urn:x-wiley:00283045:media:net22058:net22058-math-0008$	number of evacuees traveling from node l to node m with bus k in scenario d, with l, m ∈ N′, k ∈ K, d ∈ D, such that (l, m) ∈ A_d
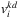$urn:x-wiley:00283045:media:net22058:net22058-math-0009$	number of evacuees starting evacuation at node i, i ∈ N_b, with bus k, k ∈ K, in scenario d, d ∈ D
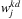$urn:x-wiley:00283045:media:net22058:net22058-math-0010$	number of evacuees ending evacuation at site j, j ∈ N_s, with bus k, k ∈ K, in scenario d, d ∈ D
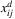$urn:x-wiley:00283045:media:net22058:net22058-math-0011$	1 if the evacuees in zone i, i ∈ N_a, are assigned to shelter 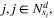$urn:x-wiley:00283045:media:net22058:net22058-math-0012$ in scenario d, d ∈ D, 0 otherwise
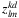$urn:x-wiley:00283045:media:net22058:net22058-math-0013$	1 if bus k travels from node l to node m in scenario d, with k ∈ K, l ∈ {N′ ∪ o}, m ϵ N′, d ∈ D, such that (l, m) ∈ A_d, 0 otherwise
y_j	1 if a shelter is opened at site j, j ∈ N_s, 0 otherwise

To build the set $urn:x-wiley:00283045:media:net22058:net22058-math-0014$ for each zone i, i ∈ N_a, we define T^d as the self-evacuees traveling time threshold in scenario d, d ∈ D, and let α, α ∈ [0; 1], be a parameter representing the car-based evacuees willingness to travel. Then, $urn:x-wiley:00283045:media:net22058:net22058-math-0015$ is defined as follows:

$urn:x-wiley:00283045:media:net22058:net22058-math-0016$

On this basis, the mathematical formulation of SISLER is the following.

$urn:x-wiley:00283045:media:net22058:net22058-math-0017$ (1)

$urn:x-wiley:00283045:media:net22058:net22058-math-0018$

$urn:x-wiley:00283045:media:net22058:net22058-math-0019$ (2)

$urn:x-wiley:00283045:media:net22058:net22058-math-0020$ (3)

$urn:x-wiley:00283045:media:net22058:net22058-math-0021$ (4)

$urn:x-wiley:00283045:media:net22058:net22058-math-0022$ (5)

$urn:x-wiley:00283045:media:net22058:net22058-math-0023$ (6)

$urn:x-wiley:00283045:media:net22058:net22058-math-0024$ (7)

$urn:x-wiley:00283045:media:net22058:net22058-math-0025$ (8)

$urn:x-wiley:00283045:media:net22058:net22058-math-0026$ (9)

$urn:x-wiley:00283045:media:net22058:net22058-math-0027$ (10)

$urn:x-wiley:00283045:media:net22058:net22058-math-0028$ (11)

$urn:x-wiley:00283045:media:net22058:net22058-math-0029$ (12)

$urn:x-wiley:00283045:media:net22058:net22058-math-0030$ (13)

$urn:x-wiley:00283045:media:net22058:net22058-math-0031$ (14)

$urn:x-wiley:00283045:media:net22058:net22058-math-0032$ (15)

$urn:x-wiley:00283045:media:net22058:net22058-math-0033$ (16)

$urn:x-wiley:00283045:media:net22058:net22058-math-0034$ (17)

$urn:x-wiley:00283045:media:net22058:net22058-math-0035$ (18)

$urn:x-wiley:00283045:media:net22058:net22058-math-0036$ (19)

The objective function (1) minimizes the expected bus-based evacuation maximum completion time over the different network scenarios. Constraints (2) guarantee that γ_d is the completion time (i.e., the longest bus route) in scenario d. Constraints (3-9) model the bus-based evacuation. For each bus k and scenario d, constraints (3) ensure that each bus departs from the depot o (if it departs); constraints (4), (5), (6), and (7) are flow conservation constraints: specifically, (4), (5), and (6) explicitly define the flow conservation that applies to each evacuation zone, transit node, and shelter, respectively; constraints (8) impose that people travel an arc only if a bus, whose capacity cannot be exceeded, serves that arc; constraints (9) guarantee that all the people of zone i ∈ N_b evacuate to some shelter. Constraints (10) model the car-based evacuation. For each scenario d, constraints (10) ensure that every evacuation zone i ∈ N_a is assigned to exactly one shelter. Constraints (11) link together both self-evacuation and supported-evacuation variables by imposing that the shelter capacity cannot be exceeded. Constraint (12) states that the total amount of resources available to set up shelters cannot be exceeded. Constraints (13-19) are non-negativity and binary constraints.

Note that transit nodes can be omitted from the formulation if we perform a preprocessing phase where, for each scenario d, d ∈ D, the shortest traveling time for each couple of nodes (l, m), l, m ϵ {N_b ∪ N_s}, on the basis of the available arcs A_d, is computed. However, we preferred to show the formulation with the transit nodes due to its generality and, hence, wider applicability: in fact, the current formulation can be easily adapted to varying disastrous conditions and unforeseen scenarios (potentially high in number) and/or integrated with additional node/arc capacity constraints. Moreover, the knowledge of the actual routing on the transportation network is paramount for an efficient on-field operations management.

Also note that SISLER's objective function can yield multiple optimal solutions, some of which are inefficient from the car-based evacuation perspective. To guarantee an efficient allocation of self-evacuees to shelters, a lexicographic objective function is deployed by adding a second term (car-based evacuation total duration time across all the scenarios) to the objective function (1) (as adopted by Bish [6]). In particular, the lexicographic objective formulation is the following:

$urn:x-wiley:00283045:media:net22058:net22058-math-0037$ (20)

where $urn:x-wiley:00283045:media:net22058:net22058-math-0038$ is the total car-based evacuation duration time for scenario d ∈ D, and $urn:x-wiley:00283045:media:net22058:net22058-math-0039$ is a lexicographic constant which ensures that the supported-evacuation maximum completion time dominates the self-evacuation total duration time. The objective function (1) can be easily modified so as to solve a min–max problem for each scenario: specifically, instead of minimizing the expression $urn:x-wiley:00283045:media:net22058:net22058-math-0040$ , it is possible to minimize only p_dγ_d which means to minimize the maximum bus-based evacuation time for the single scenario d. The experimental section will provide results in both cases (i.e., single scenario and combined scenarios instances).

An interesting feature of SISLER is that it allows to identify a trade-off between self-evacuation and supported-evacuation oriented solutions, by changing the parameters α and T^d which represent the route length that car-based evacuees are willing to accept. This permits to balance the bus-based evacuation completion time objective and the car-based evacuation equity requirement.

Figure 1 displays two different solutions, where triangle, square, and round shapes represent, respectively, the depot, candidate shelter sites, and evacuation zone centroids. Selected shelters are marked with a cross and centroids are identified with the acronyms of the evacuees departing from there (i.e., SES = self-evacuees who move towards a shelter, SE = supported evacuees who move towards a shelter, and M = mixed demand, which is a combination of SES and SE). Normal and dashed arrow lines represent SES assignments and SE routes, respectively. A tighter threshold (Figure 1A) favors self-evacuation by inducing the opening of shelters close to self-evacuees or mixed evacuation zones; if the threshold becomes looser (Figure 1B), the supported-evacuation maximum completion time decreases while the self-evacuation total duration time increases. For the sake of simplicity, the network in the example does not include transit nodes. Note that, even if the SISLER formulation directly assigns each SES node to a shelter, the picture displays the actual path from each SES node to its assigned shelter, since this better represents a real evacuation process along the transportation network.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Self-evacuation oriented solution (A) and supported-evacuation oriented solution (B)

4 SOLUTION METHODOLOGY

The SISLER model has been optimally solved through an off-the-shelf optimization software, the IBM ILOG CPLEX 12.6. Valid inequalities have been identified and added at the root node of the solution tree so as to improve the lower bound.

4.1 Valid inequalities for SISLER

Valid inequalities for SISLER have been identified based on the subproblems SISLER is composed of which are: the bus evacuation problem (BEP), the capacitated facility location problem (CFLP), and the multi-commodity flow problem (MCFP).

First, the literature on the BEP is little given that this problem has been introduced fairly recently [6]. However, the BEP is related to the well-known vehicle routing problem. The routing aspect of SISLER is not pure given that the buses, once they start the journey from the depot, stop at a shelter destination without returning to the depot due to the contraflow lane reversal assumption (Section 3.1, point 7). Moreover, a flood-like disaster was considered while devising SISLER, hence, even if the contraflow lane reversal assumption was relaxed, it would be safer to assume that buses do not return to the depots. In fact, bus depots were subject to flooding in the aftermath of Hurricane Katrina in 2005 [6]. Finally, SISLER is a static model in its current version and, as such, evacuation occurs within a single time period during which buses drop supported-evacuees at shelter sites. Given the usage of buses, the following round-up constraints [7] are introduced to SISLER

$urn:x-wiley:00283045:media:net22058:net22058-math-0041$ (21)

which impose a lower bound on the number of buses that can be used for each scenario, assuming that B_k = B, ∀ k ∈ K.

Second, the literature on inequalities for the CFLP [21, 23] presents three main categories of inequalities:

Aggregated capacity constraints such as

$urn:x-wiley:00283045:media:net22058:net22058-math-0042$ (22)

which, given facilities with equal capacity restrictions (i.e., C_j = C ∀ j ∈ N_s), impose a lower-bound on the number of facilities that should be opened.

Residual capacity (RC) constraints such as

$urn:x-wiley:00283045:media:net22058:net22058-math-0043$ (23)

where 1 ≤ RC ≤ C, having assumed C_j = C ∀ j ∈ N_s. These constraints identify the customer demand that the last available facility should satisfy. In the case of SISLER, evacuees are seen as customers (hence, evacuee demand as customer demand), and shelters as facilities.

Variable upper bounds constraints such as

$urn:x-wiley:00283045:media:net22058:net22058-math-0044$ (24)

which require that a customer can be assigned to a facility only if the facility is open. For SISLER, it means that self-evacuees move towards a shelter site in a certain scenario only if the shelter has been opened.

Finally, the literature for the MCFP presents various inequalities; however, those which could be easily deployed for SISLER are the strong inequalities introduced by Chouman et al. [10] for the Multi-Commodity Capacitated Fixed-Charge Network Design problem, which is based on the MCFP. The concept underpinning this set of constraints is the following: if a network arc is deployed, then the amount of flow of a certain commodity traversing that arc should be less than or equal to the demand of the commodity itself. This set of constraints, given that the two categories of evacuees (i.e., self-evacuees and supported-evacuees) can be seen as two different commodities, has been adopted and used for supported-evacuees. The adapted valid inequalities are the following:

$urn:x-wiley:00283045:media:net22058:net22058-math-0045$ (25)

Specifically, for each scenario d, the amount of supported-evacuees leaving evacuation zone i ∈ N_b with bus k should not exceed the total evacuation demand of that zone and travel only an arc (i, m) which is available.

Among all the aforementioned valid inequalities, (21) and (25) have demonstrated to yield an improvement in the value of the linear relaxation of SISLER, when considered separately or in combination, while the remaining valid inequalities did not affect the value of the linear relaxation of SISLER. Therefore, (21) and (25) have been embedded as valid inequalities at the root node of the decision tree within the IBM ILOG CPLEX 12.6.2 Branch-and-Cut framework.

It has been possible to appreciate which are the cuts that CPLEX adopts to solve SISLER instances and in which amount (based on average values): flow cover cuts (61%), mixed integer rounding (MIR) cuts (25%), lift-and-project cuts (8%), implied bound cuts (3%), cover and Gomory fractional cuts (both at 1%), and clique, zero-half, and GUB cuts (that together constitute 1%). The in-depth description of the aforementioned cuts is out of the scope of this paper. However, an interesting observation can be drawn on the first two categories of cuts added by CPLEX (i.e., flow cover and MIR cuts, which represent the majority of the cuts) and the nature of SISLER. In fact, flow cover cuts are defined based on constraints containing continuous variables whose upper bound varies between zero and a positive value according to the corresponding binary variables, while MIR cuts are produced by imposing integer rounding on the coefficient of integer decisional variables as well as the corresponding right-hand side constraint. This is in line with the flow problem component of SISLER, which contributes to model the bus-based evacuation.

5 EXPERIMENTAL RESULTS

SISLER is a mixed-integer linear programming model which was implemented using IBM ILOG OPL modeling language and solved with CPLEX Branch-and-Cut algorithm (default setting), version 12.6, enriched with additional valid inequalities, as described in Section 5.1, on a computer with an Intel® Core™ i5-5200U CPU @ 2.20 GHz and 8.00 GB of RAM.

5.1 Testbed instances generation

Two testbed instances of different density have been deployed to test SISLER: one of 25 nodes and 56 arcs (25 × 56) and another one of 25 nodes and 165 arcs (25 × 165). Both instances have been generated as follows. A 100 × 100 square study area like the one displayed in Figure 2 has been considered, where the black area represents the central zone of the disaster (i.e., where the disaster starts), the gray area the region where the disaster can propagate, and the white area the safety zone (i.e., the disaster cannot reach that area). The coordinates of evacuation zones, transit nodes, and shelter sites were generated at random in the black, light gray, and white areas, respectively.

Specifically, evacuation zones where only self-evacuation occurs account for 25% of the network nodes (i.e., six nodes), evacuation zones where only supported-evacuation occurs account for 15% of the network nodes (i.e., four nodes), evacuation zones where both self-evacuation and supported-evacuation occur account for 15% of the network nodes (i.e., four nodes), transit nodes account for 15% of the network nodes (i.e., four nodes), shelter sites account for the remaining 25% of the network nodes (i.e., six nodes), and the remaining 5% of the network nodes constitutes the depot node. Arcs were also generated at random and Euclidean distances were used as a proxy for traveling times. In accordance with the contraflow lane reversal assumption, it was assumed that arcs from transit nodes to candidate shelter sites can be traveled only in one direction (i.e., towards the shelter). Scenarios of increasing disaster magnitude have been considered, such as small-scale, medium-scale, and large-scale disruption circumstances, so as to account for disaster propagation. Nevertheless, different type of scenarios could be considered. In particular, three scenarios have been considered: (1) a small disruption scenario, where all network arcs are available, (2) a medium disruption scenario, where some network arcs connecting evacuation nodes (i.e., within the black area), accounting for 20% of the network arcs, are affected by the disaster, and (3) a large disruption scenario where some arcs connecting evacuation and transit nodes (i.e., from the black to the gray area), accounting for 10% of the network arcs, are disrupted in addition to the arcs already inoperative in the medium disruption scenario. Arcs to be disrupted were decided at random; however, when advancing from the medium to the large scenario, within a level of proximity. This choice of scenarios was motivated having in mind a specific disaster such as flooding where the off-set of the disaster occurs in certain points of networks and then propagates from there within a certain degree of proximity.

Results are reported for two cases: where only one of the three scenarios is considered (i.e., single scenario instances) and where all the three scenarios are considered (i.e., combined scenario instances).

In terms of model parameters, the following settings were adopted.

Evacuation demand (measured in number of households) was assumed to be a random integer uniformly distributed between 50 and 550, as in [16].
A homogeneous bus fleet was assumed (i.e., B_k = B ∀ k ∈ K) and the number of buses was computed as the round-up ratio (total bus-based evacuation demand/bus capacity),:
$urn:x-wiley:00283045:media:net22058:net22058-math-0046$
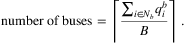
Shelter capacities were computed as reported by Gama et al. [16], based on Lorena and Senne [27], as the round-up ratio (total evacuation demand/maximum number of shelters that can be opened):
$urn:x-wiley:00283045:media:net22058:net22058-math-0047$
where, more specifically, p is the maximum number of shelters that can be opened based on the budget constraint (12) and β is a weighting parameter set equal to 0.8. Shelter capacities are assumed to be the same for each shelter (i.e., C_j = C ∀ j ∈ N_s).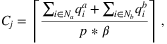
For each scenario and car-based evacuation zone, the shortest traveling time and the time threshold were computed in a preprocessing phase. Self-evacuee shortest traveling times for each scenario (i.e., 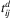$urn:x-wiley:00283045:media:net22058:net22058-math-0048$ ) were computed through a shortest path algorithm, while the self-evacuee traveling time threshold for each scenario (i.e., T^d) was computed through an auxiliary capacitated p-center model. In particular, the p-center model aims at minimizing the self-evacuee maximum traveling time to reach shelter sites. In this case, shelter capacities are still computed as based on Lorena and Senne [27] however, only the total self-evacuee evacuation demand is considered (i.e., $urn:x-wiley:00283045:media:net22058:net22058-math-0049$ ) to compute the reduced shelter capacity. Moreover, taking into account the trade-off between car- and bus-based evacuees, we have also considered all the values from 0 to 1 with step size 0.1 for the parameter α,introduced in Section 3.2.
A decreasing probability distribution was used to combine the three different scenarios (p₁ = 0.5, p₂ = 0.3, and p₃ = 0.2). This choice is based on the assumption that a large-scale disastrous circumstance (i.e., scenario 3) is less likely than a medium-scale one (i.e., scenario 2), which in turn is less likely than a small-scale disruption leaving transport links unaffected (i.e., scenario 1).

5.1.1 Computational results for the 25 × 56 network

The network with 25 nodes and 56 arcs was used as a proof of concept to demonstrate the validity of the problem and to preliminary test the SISLER formulation. Given its dimensions, even without adding the inequalities found for SISLER, both single and combined scenario instances were solved in a matter of a few seconds.

The results for the 25 × 56 network are displayed in Table 2 for the small, medium, large scenarios, and their combination, respectively. The table reports the bus-based evacuation maximum completion time (Bus time), the car-based evacuation total duration time (Car time), and the open shelters for different values of α ranging from 0 to 1 (note that the potential shelter sites for the 25 × 56 network are nodes 19, 20, 21, 22, 23, and 24).

TABLE 2. Computational results for the 25 × 56 network

Scenario	α	Bus time	Car time	Shelters
Scenario 1 (small)	0–0.1	212	282	{19,20,23,24}
	0.2–0.4	143	301	{19,21,23,24}
	0.5–1	138	323	{19,22,23,24}
Scenario 2 (medium)	0–0.4	175	347	{19,21,23,24}
	0.5–0.6	168	427	{20,22,23,24}
	0.7–1	168	421	{19,20,22,24}
Scenario 3 (large)	0–1	211	447	{19,20,22,24}
All scenario (mix)	0–0.1	216	322.4	{19,20,23,24}
	0.2–0.4	166.2	361.2	{20,21,23,24}
	0.5–1	161.6	415.2	{20,22,23,24}

From the analysis of the table, it is possible to infer the trade-off between the bus-based evacuation maximum completion time and the car-based evacuation total duration time. For example, in the small scenario when α increases from 0.1 to 0.2, the supported-evacuation maximum completion time drops by nearly 33% (from 212 to 143), while the self-evacuation total duration time increases by around 7% (from 282 to 301), which also implies a change in the shelter location decisions (from node 20 to node 21). Another change in both evacuation times and shelter locations can be observed when α rises from 0.4 to 0.5. In this case, the bus-based evacuation maximum completion time decreases by nearly 3% (from 143 to 138), while the car-based evacuation total duration time raises by around 7% (from 301 to 323), and node 22 is open instead of node 21. Other examples can be appreciated from the analysis of the medium scenario. When α increases from 0.4 to 0.5, the supported-evacuation maximum completion time drops by nearly 4% (from 175 to 168), while the self-evacuation total duration time increases by around 23% (from 347 to 427), leading to a shift in shelter location decisions (two nodes are changed among four, specifically, nodes 20 and 22 are preferred over nodes 19 and 21). Conversely, when α rises from 0.7 to 0.8, the bus-based evacuation time does not change. However, the car-based evacuation completion time decreases by nearly 1% (from 427 to 421) and there is a change in shelter location decisions (from node 20 to node 19). This is motivated by the fact that the more α increases, the more the self-evacuation traveling time threshold becomes looser, thus allowing allocations that were infeasible for lower values of α. Differently from the small and medium scenarios, no trade-off between the bus-based evacuation maximum completion time and the car-based evacuation total duration time can be appreciated for the large scenario. In this case, the solution is always the same, irrespective of the value of α. However, the trade-off can still be observed when combining the three scenarios. In fact, when α increases from 0.1 to 0.2, the supported-evacuation maximum completion time drops by nearly 23% (from 216 to 166.2), while the self-evacuation total duration time rises by around 12% (from 322.4 to 361.2), and this implies a change in the shelter location decisions (from node 19 to node 21). Another change in both evacuation times and shelter locations can be noted when α raises from 0.4 to 0.5. In this case, the bus-based evacuation maximum completion time decreases by nearly 3% (from 166.2 to 161.6), while the car-based evacuation total duration time rises by around 15% (from 361.2 to 415.2), and node 22 is opened instead of node 21. A visual representation of the trade-off between the bus-based evacuation maximum completion time and the car-based evacuation total duration time when α varies between 0 and 1 for the small, medium and combined scenarios is displayed in Figure 3A, B, and C, respectively.

Moreover, the comparison of the results across the table highlights the importance of considering multiple scenarios. The solutions found when all the three scenarios are taken into account can differ quite significantly from the solutions obtained for a single scenario. For example, the optimal set of shelters in the solution obtained when α = 0.2, 0.3 and 0.4, which is composed of nodes 20, 21, 23, and 24, is different from the optimal set selected in the single scenario instances for the same values of α (i.e., 19, 21, 23, and 24 for both the small and medium scenarios and 19, 20, 22, and 24 for the large scenario), and so are the bus routes and self-evacuee to shelter allocations.

Table 3 reports the values of the linear relaxation of SISLER without any inequality (LR), with the addition of inequalities (21) (LR + BUS), (25) (LR + FLOW), and both inequalities (21) and (25) (LR + BUS + FLOW) for the small (S), medium (M), large (L) scenarios, and their combination (MIX), respectively.

TABLE 3. Computational results for the 25 × 56 network—linear relaxation values

Scenario	LR	LR + BUS	LR + FLOW	LR + BUS + FLOW
S	103.83	111.83	113.9	120.83
M	113.18	121.98	137.9	145.9
L	117.98	132.38	141.7	153.57
MIX	109.47	118.99	126.66	134.9

From the analysis of the table, it is possible to appreciate the improvement in the value of the linear relaxation of SISLER. In fact, the presence of inequalities (21), (25), and their combination increases, respectively, the value of the linear relaxation by around: 8% (from 103.83 to 111.83), 10% (from 103.83 to 113.9), and 16% (from 103.83 to 120.83) in the small scenario; 8% (from 113.18 to 121.98), 22% (from 113.18 to 137.9), and 29% (from 113.18 to 145.9) in the medium scenario; 12% (from 117.98 to 132.38), 20% (from 117.98 to 141.7), and 30% (from 117.98 to 153.57) in the large scenario; and 9% (from 109.47 to 118.99), 16% (from 109.47 to 126.66), and 23% (from 109.47 to 134.9) in the combined scenario. The value of the linear relaxation is the same whichever value of α, indicating that the choice of α is not relevant to this matter. Usually, an improvement in the value of the linear relaxation results in a reduction of the computing time required to solve the instances. As mentioned previously, it was not possible to appreciate the benefits of the additional inequalities in terms of computational performance on the 25 × 56 network. However, the positive contribution of the additional inequalities will be demonstrated through the analysis of the experimental results of the 25 × 165 network, specifically when it comes to combined scenario instances.

5.1.2 Computational results for the 25 × 165 network

Following the same scheme for instance generation, computational results are now reported for a more dense network with 25 nodes and 165 arcs. In particular, it is demonstrated how the inclusion of the ad hoc inequalities within the IBM ILOG CPLEX Branch-and-Cut framework makes a clear difference and allows to always obtain an integer solution, which would have not been possible otherwise, within the pre-fixed computational time limit set equal to 3600 s. The reason for this tight time limit is due to the fact that, in order to effectively deploy SISLER during the Disaster Operations Management framework response phase, it has to provide solutions in a reasonable amount of time.

Results are displayed in Table 4 for the small, medium, and large scenarios. These instances have been solved in matter of seconds and, as such, the table reports only the bus-based evacuation maximum completion time (Bus time), the car-based evacuation total duration time (Car time), and the open shelters for different values of α ranging from 0 to 1 (note that the potential shelter sites for the 25 × 165 network are nodes 19, 20, 21, 22, 23, and 24) without any insight on the CPU time, which will be relevant for the combined scenario instances.

TABLE 4. Computational results for the 25 × 165 network—Scenarios 1, 2, and 3

Scenario	α	Bus time	Car time	Shelters
Scenario 1 (small)	0	133	402	{20,21,24}
Scenario 1 (small)	0.1–1	132	407	{20,23,24}
Scenario 2 (medium)	0	133	402	{20,21,24}
Scenario 2 (medium)	0.1–1	133	401	{20,23,24}
Scenario 3 (large)	0	139	409	{20,22,24}
	0.1	137	416	{22,23,24}
	0.2–1	133	420	{20,21,24}

Similarly to the 25 × 56 network, it is possible to infer the trade-off between the bus-based evacuation maximum completion time and the car-based evacuation total duration time. For example, in the small scenario when α increases from 0 to 0.1, the supported-evacuation maximum completion time drops by nearly 1% (from 133 to 132), while the self-evacuation total duration time increases by around 1% (from 402 to 407). This entails a change in the shelter location decisions where node 23 is open instead of node 21. Another example can be appreciated from the analysis of the medium scenario. When α increases from 0 to 0.1, the bus-based evacuation maximum completion time does not change however, the car-based evacuation total duration time decreases slightly (from 402 to 401). This is motivated by the fact that the more α increases, the more the self-evacuation traveling time threshold becomes looser, thus allowing allocations that were infeasible for lower values of α. This also entails a change in the shelter location decisions where node 23 is open instead of node 21. Further examples emerge in the analysis of the large scenario. When α increases from 0 to 0.1, the supported-evacuation maximum completion time drops by nearly 1% (from 139 to 137), while the self-evacuation total duration time increases by around 2% (from 409 to 416), and there is a change in shelter locations (from node 20 to node 23). Another change in both evacuation times and shelter sites can be observed when α rises from 0.1 to 0.2. In this case, the bus-based evacuation maximum completion time decreases by nearly 3% (from 137 to 133), while the car-based evacuation total duration time raises by around 1% (from 416 to 420), and the optimal set of shelter locations changes from 22, 23, and 24 to 20, 21, and 24.

Table 5 details results for combined scenario instances. The table reports the CPU time spent at the root node in seconds (Time at the root node) and the total CPU time spent to solve an instance in seconds (Total CPU time) without any inequality (I), with the addition of inequalities (21) (I + BUS), (25) (I + FLOW), and both inequalities (21) and (25) (I + BUS + FLOW) for different values of α ranging from 0 to 1. The tables also report the solution details in terms of bus-based evacuation maximum completion time (Bus max time), the car-based evacuation total duration time (Car tot time), and the open shelters (note that the potential shelter sites for the 25 × 165 network are nodes 19, 20, 21, 22, 23, and 24) for all the different values of α.

TABLE 5. Computational results for the 25 x 165 network—all scenarios (mix)

All scenarios (mix)
	I		I + BUS		I + FLOW		I + BUS + FLOW		Solution details
α	Time at root node	Total CPU time	Time at root node	Total CPU time	Time at root node	Total CPU time	Time at root node	Total CPU time	Bus max time	Car tot time	Open shelters
0	—	—	—	—	—	—	—	—	—	—	—
0.1	4.04	3600^a	5.41	3600^a	2.06	143.69	2.18	522.67	135	395.3	{22,23,24}
0.2	3.32	3600^a	4.04	3600^a	3.06	623.74	2.50	474.41	132.5	411.2	{20,23,24}
0.3	3.60	3600^a	2.93	3600^a	3.38	736.04	2.54	2769.05	132.5	411.2	{20,23,24}
0.4	3.32	3600^a	4.74	3408	3.11	3600^a	2.31	282.14	132.5	411.2	{20,23,24}
0.5	3.09	3600^a	3.12	3600^a	3.95	947.85	2.89	1922.12	132.5	411.2	{20,23,24}
0.6	3.84	3600^a	4.15	3600^a	2.80	630.01	2.68	855.87	132.5	411.2	{20,23,24}
0.7	3.32	3600^a	3.21	3600^a	3.34	1194.53	2.25	253.8	132.5	411.2	{20,23,24}
0.8	3.14	3600^a	3.56	3600^a	2.42	1707.12	2.28	534.18	132.5	411.2	{20,23,24}
0.9	5.23	3600^a	5.04	3600^a	2.96	2409.87	2.34	418.72	132.5	411.2	{20,23,24}
1	3.48	3600^a	3.20	3600^a	3.31	3600^a	2.62	440.56	132.5	411.2	{20,23,24}
AVG	3.6	3600	3.9	3580.8	3	1559.3	2.5	847.4	132.8	409.6	N/A

Note: —, no solution has been found; N/A, not applicable.
a Instance not been solved to optimality within the pre-fixed time limit of 3600 s.

The trade-off can also be inferred when the three scenarios are combined together (i.e., Table 6). In fact, when α rises from 0.1 to 0.2, the supported-evacuation maximum completion time decreases by around 2% (from 135 to 132.5), while the car-based evacuation total duration time rises by nearly 4% (from 395.3 to 411.2), and node 20 is opened instead of node 22. Table 6 reports the values of the linear relaxation of SISLER without any inequality (LR), with the addition of inequalities (21) (LR + BUS), (25) (LR + FLOW), and both inequalities (21) and (25) (LR + BUS + FLOW) for the small (S), medium (M), large scenarios (L), and their combination (MIX), respectively.

TABLE 6. Computational results for the 25 × 165 network—linear relaxation values

Scenario	LR	LR + BUS	LR + FLOW	LR + BUS + FLOW
S	64.86	68.36	86.86	90.30
M	64.86	68.36	95.36	98.61
L	64.86	68.36	95.36	98.61
MIX	64.86	68.36	91.11	94.46

Further observations can be drawn from the combined analysis of Tables 5 and 6 that concern the value of the linear relaxation of SISLER, the total CPU time spent to solve an instance, and the number of instances that have not been solved to optimality within the pre-fixed time limit (this applies exclusively to combined scenario instances). Table 6 shows that the addition of inequalities (21), (25), as well as their combination, leads to an improvement of the value of the linear relaxation of SISLER by around, respectively: 5% (from 64.86 to 68.36), 34% (from 64.86 to 86.86), and 39% (from 64.86 to 90.30) in the small scenario; 5% (from 64.86 to 68.36), 47% (from 64.86 to 95.36), and 52% (from 64.86 to 98.61) in both the medium and large scenarios; and 5% (from 64.86 to 68.36), 40% (from 64.86 to 91.11), and 46% (from 64.86 to 94.46) in the combined scenario. These values are correlated to the time spent at the root node as well as the total CPU time spent to solve an instance and, specifically in case of combined scenario instances (i.e., Table 5), to the number of instances that have been solved within the pre-fixed time limit of 3600 s. Based on average computed values (AVG), the time spent at the root node increases by around 8% (from 3.6 to 3.9) when adding inequalities (21), while decreases by nearly 16% (from 3.6 to 3) when adding inequalities (25), and 32% (from 3.6 to 2.5) when combining them. On the other side, the total CPU time decreases by around 3% (from 3600 to 3508.8), 57% (from 3600 to 1559.3), and 76% (from 3600 to 847.4) when adding inequalities (21), (25), and their combination, respectively. These results are in line with the increase in the value of the linear relaxation previously reported. Furthermore, the presence of inequalities allows to solve instances to optimality within the pre-fixed time limit and to reduce the average gap for those that were not solved to optimality, as displayed in Table 7. In particular, Table 7 reports the lower bound value (LB), the upper bound value (UB), which is the best found integer, and the resulting gap (GAP) for combined scenario instances without any inequality (I), with the addition of inequalities (21) (I + BUS), (25) (I + FLOW), and both inequalities (21) and (25) (I + BUS + FLOW) when α varies from 0 to 1.

TABLE 7. Computational results for the 25 × 165 network—all scenarios (mix)—gap analysis

α	LB	UB	GAP	LB	UB	GAP	LB	UB	GAP	LB	UB	GAP
	I			I + BUS			I + FLOW			I + BUS + FLOW
0	—	—	—	—	—	—	—	—	—	—	—	—
0.1	131.54	137	3.99%	131.17	137	4.26%	135	135	0%	135	135	0%
0.2	113.09	133	14.97%	129.14	133	2.90%	132.5	132.5	0%	132.5	132.5	0%
0.3	126.63	133	4.79%	123.94	133	6.81%	132.5	132.5	0%	132.5	132.5	0%
0.4	123.99	133	6.77%	132.5	132.5	0%	132.24	132.5	0.20%	132.5	132.5	0%
0.5	132.5	133	0.38%	123.64	133	7.04%	132.5	132.5	0%	132.5	132.5	0%
0.6	123.04	133	7.49%	132.5	133	0.38%	132.5	132.5	0%	132.5	132.5	0%
0.7	125.13	133	5.92%	127.87	133	3.86%	132.5	132.5	0%	132.5	132.5	0%
0.8	125.43	133	5.69%	129.13	133	2.91%	132.5	132.5	0%	132.5	132.5	0%
0.9	128.54	133	3.35%	130.83	133	1.63%	132.5	132.5	0%	132.5	132.5	0%
1	128.74	133	3.20%	126.54	133	4.86%	130	132.5	1.89%	132.5	132.5	0%
AVG	125.86	133.4	5.65%	128.73	133.35	3.46%	132.474	132.75	0.21%	132.75	132.75	0

Note: —, no solution has been found; N/A, not applicable.

The addition of inequalities (21), which yielded the lowest increase of the linear relaxation value, did not help solving any of the combined scenario instance to optimality. Conversely, the addition of inequalities (25), corresponding to a higher increase of the linear relaxation value, led to solve to optimality 8 out of 10 combined scenario instances. Finally, the combination of inequalities (21) and (25), resulting in the best improvement in the value of the linear relaxation, yielded to close to optimality all the combined scenario instances. Moreover, a decrease in the average gap by around 39% (from 5.65% to 3.46%) and 96% (from 5.65% to 0.21%) can be appreciated for the addition of inequalities (21) and (25), respectively.

5.2 Case study: Sioux Falls network

5.2.1 Case study description

In addition to testbed instances, SISLER has also been tested on a realistic case study, which is the Sioux Falls network (network data are available at Transportation Network, which is a network repository for transportation research [34]). The Sioux Falls network has been quite used in the transportation literature, including evacuation planning studies [29]. The network is composed of 24 nodes and 76 arcs and it is displayed in Figure 4.

For experimentation purposes: nodes 4, 7, 8, 14, 19, and 21 are assumed to be car-based evacuation only zones; nodes 3, 9, 15, and 22 are assumed to be bus-based evacuation only zones; nodes 5, 11, 16, and 23 are assumed to be mixed-evacuation zones; nodes 1, 2, 13, 18, and 20 are assumed to be candidate shelter sites; node 12 is assumed to be the depot; and the remaining network nodes are assumed to be transit nodes. Note that, based on SISLER assumptions, arcs whose final destination is a candidate shelter location are traveled only towards the shelter (hence, the arc that is traveled in the opposite direction is not considered) and, given that buses are not returning to the depot, all the network arcs originally having node 12 as a terminal point have been discarded. This has led to a reduced version of the Sioux Falls network with 24 nodes and 58 arcs, as reported in Figure 5.

Network nodes are categorized in Figure 5 as follows: blue, red, and brown round shapes represent car-based only, bus- based only, and mixed-evacuation demand zones, respectively; green square shapes are shelter candidate locations; and the yellow triangle is the depot.

Evacuation demand and traveling times were computed based on the Sioux Falls network data that have been found (Transportation Networks). Model parameter settings (e.g., bus fleet, number of buses, shelter capacity, self-evacuees traveling time threshold, and scenario probability distribution) were computed exactly as described for the testbed instances. The three different scenarios were designed as follows: for the small scenario (Scenario 1), it is assumed that all network arcs are available, which is the network displayed in Figure 5; for the medium scenario (Scenario 2), it is assumed that arcs (4,5), (5,4), (8,16), (14,15), (15,14), and (16,8) are disrupted; and for the large scenario (Scenario 3), it is assumed that arcs (10,11), (10,17), (11,10), (17,10), (21,24), and (24,21) are disaster-affected, in addition to the arcs already unavailable in the medium scenario. Figures 6 and 7 display the Sioux Falls network under Scenario 2 and Scenario 3, respectively.

5.2.2 Computational results

Results are displayed in Table 8 for the small, medium, and large scenarios. These instances have been solved in matter of seconds and, as such, the tables report only the bus-based evacuation maximum completion time (Bus time), the car-based evacuation total duration time (Car time), and the open shelters for different values of α ranging from 0 to 1 (remember that the potential shelter sites for the Sioux Falls network are nodes 1, 2, 13, 18, and 20).

TABLE 8. Computational results for the Sioux Falls network—Scenarios 1, 2, and 3

Scenario	α	Bus time	Car time	Shelters
Scenario 1 (small)	0–0.1	25	83	{2,18,20}
Scenario 1 (small)	0.2–1	25	74	{13,18,20}
Scenario 2 (medium)	0–0.2	41	75	{1,18,20}
Scenario 2 (medium)	0.3–1	31	79	{13,18,20}
Scenario 3 (large)	0–0.4	44	88	{1,2,20}
	0.5–0.6	44	88	{2,13,18}
	0.7	44	88	{1,2,20}
	0.8–1	44	88	{2,13,18}

From the analysis of the table, it is possible to infer the trade-off between the bus-based evacuation maximum completion time and the car-based evacuation total duration time. For example, in the small scenario when α increases from 0.1 to 0.2, the supported-evacuation maximum completion time does not change while the self-evacuation total duration time reduces by around 11% (from 83 to 74). This is motivated by the fact that the more α increases, the more the self-evacuation traveling time threshold becomes looser, thus allowing allocations that were infeasible for lower values of α and, in this specific case, it also implies a change in the shelter location decisions (from node 2 to node 13). A change in both evacuation times and shelter locations can be observed from the analysis of the medium scenario. When α increases from 0.2 to 0.3, the bus-based evacuation maximum completion time drops by nearly 23% (from 41 to 31), while the car-based evacuation total duration time increases by around 5% (from 75 to 79), leading to a shift in shelter location decisions (node 13 is opened instead of node 1). Moreover, regarding the large scenario, neither the supported-evacuation maximum completion time nor the self-evacuation total duration time change however, there are some changes in the shelter location decisions (e.g., when α increases from 0.4 to 0.5). The reason for this can be the presence of multiple optimal solutions. In fact, the objective function considers the supported-evacuation maximum completion time and the self-evacuation total duration time in its lexicographic form. However, the shelter location decisional variables are not present in the objective function. Single scenario instances were solved in matter of few seconds. Results of combined scenario instances are reported in Table 9. The table reports the CPU time spent at the root node in seconds (Time at the root node) and the total CPU time spent to solve an instance in seconds (Total CPU time) under four different circumstances which are without any inequality (I), with the addition of inequalities (21) (I + BUS), (25) (I + FLOW), and both inequalities (21) and (25) (I + BUS + FLOW) for different values of α ranging from 0 to 1. The table also reports the solution details in terms of bus-based evacuation maximum completion time (Bus max time), the car-based evacuation total duration time (Car tot time), and the open shelters for all the different values of α.

TABLE 9. Computational results for the Sioux Falls network—all scenarios (mix)

All scenarios (mix)
	I		I + BUS		I + FLOW		I + BUS + FLOW		Solution details
α	Time at root node	Total CPU time	Time at root node	Total CPU time	Time at root node	Total CPU time	Time at root node	Total CPU time	Bus max time	Car tot time	Open shelters
0	1.25	949.75	1.28	800.71	1.58	2099.81	1.39	267.28	36	73	{1,18,20}
0.1	1.20	3002.2	1.29	2797.32	1.76	783.81	1.45	826.6	36	73	{1,18,20}
0.2	1.20	344.19	1.26	512.7	1.69	638.98	2.06	817.54	36	73	{1,18,20}
0.3	1.09	105.19	1.11	65.26	1.78	94.71	1.97	52.88	33	75.4	{1,18,20}
0.4	1.23	66.69	1.36	60.79	1.95	58.41	1.70	141.8	31	81.9	{1,18,20}
0.5	1.01	337.77	1.34	130.96	1.53	401.61	1.33	349.96	31	76.9	{13,18,20}
0.6	1.31	175.19	1.29	186.03	1.34	595.89	1.42	433.37	31	76.9	{13,18,20}
0.7	1.34	369.83	1.11	214.92	1.64	229.43	1.39	433.64	30.6	83.1	{2,18,20}
0.8	1.11	229.73	1.14	119.47	1.67	144.77	1.62	80.09	30.6	83.1	{2,18,20}
0.9	1.00	143.32	1.19	401.25	1.39	92.56	1.37	326.09	30.6	83.1	{2,18,20}
1	1.19	338.47	1.08	233.19	1.68	128.5	1.53	75.49	30.6	83.1	{2,18,20}
AVG	1.17	551.12	1.22	502.05	1.64	478.95	1.58	345.85	32.4	78.4	N/A

A visual representation of the trade-off between the bus-based evacuation maximum completion time and the car-based evacuation total duration time when α varies between 0 and 1 for the medium scenario, which is the most interesting among the single scenarios in terms of objective function variations, and for the combined scenarios is displayed in Figure 8A and B, respectively.

Moreover, the comparison of the results across all the tables highlights the importance of considering multiple scenarios. In fact, the solutions found when all the three scenarios are taken into account can differ quite significantly from the solutions obtained for a single scenario. For example, the optimal set of shelters in the solution obtained when α = 0.7, 0.8, 0.9, and 1, which is composed of nodes 2, 18, and 20, is different from the optimal set selected in each individual scenario for the same values of α (i.e., 13, 18, and 20 for both the small and medium scenarios and 2, 13, and 18 for the large scenario), and so are the bus routes and self-evacuee to shelter allocations. Table 10 reports the values of the linear relaxation of SISLER without any inequality (LR), with the addition of inequalities (21) (LR + BUS), (25) (LR + FLOW), and with both inequalities (21) and (25) (LR + BUS + FLOW) for the small (S), medium (M), large scenarios (L), and their combination (MIX), respectively.

TABLE 10. Computational results for the Sioux Falls network—linear relaxation values

Scenario	LR	LR + BUS	LR + FLOW	LR + BUS + FLOW
S	19.31	19.31	19.57	19.57
M	19.82	19.82	20.09	20.09
L	24.42	24.42	24.68	24.68
MIX	20.48	20.48	20.75	20.75

Further observations can be drawn from the combined analysis of Tables 9 and 10 from a computational perspective. A slight improvement in the value of the linear relaxation of SISLER can be appreciated. The presence of inequalities (21) does not yield any improvement while inequalities (25) increase the value of the linear relaxation by around 1% in each single scenario (from 19.31 to 19.57 in the small scenario, from 19.82 to 20.09 in the medium scenario, and from 24.42 to 24.68 in the large scenario). The combination of inequalities (21) and (25) does not produce any improvement. The reason for this result may be due to either the specific network under consideration or the scenario settings. Based on average computed values (AVG), the presence of additional inequalities entails an increase in the time spent at the root node by around 3% (from 1.17 to 1.22), 39% (from 1.17 to 1.64), and 33% (from 1.17 to 1.58), for inequalities (21), (25), and their combination, respectively. Inversely, the total CPU time decreases by around 9% (from 551.12 to 502.05), 13% (from 551.12 to 478.95), and 37% (from 551.12 to 345.85) for inequalities (21), (25) and their combination, respectively. This is in line with the increase in the value of the linear relaxation (from 20.48 to 20.75) that can be appreciated for (21), (25), and their combination, respectively. Hence, this demonstrates the positive contribution deriving from additional inequalities. Obviously, there are some instances for specific values of α, where the addition of inequalities may actually delay the completion of an instance. However, the above statements hold on average terms, and single instances should be studied separately for each network.

6 CONCLUSIONS AND FUTURE RESEARCH DIRECTIONS

This paper has extended the preliminary work of Esposito Amideo and Scaparra [13] by presenting some applications of a scenario-based mixed-integer two-stage linear program which integrates shelter location with two different types of evacuation, self- (or car-based) evacuation and supported- (or bus-based) evacuation, namely the SISLER model. The model combines both user and system perspectives, whereby users are in charge of their routes while the system arranges shelter sites and evacuation for special-needs populations. Trade-off solutions between the two perspectives can be appreciated through the willingness of self-evacuees to travel paths that are lengthier than their shortest ones. The model was solved through an off-the-shelf optimization software, the IBM ILOG CPLEX 12.6. Nevertheless, some valid inequalities were identified and added at the root node of the solution tree so as to improve the lower bound. Experimentation was carried out on both testbed instances and a realistic case study. Results showed user-system trade-off solutions and also highlighted the importance of considering different disruption scenarios. In fact, in some cases, the solution obtained for combined scenarios can be quite different from the solutions of the related single scenario instances. Moreover, it has been proven that the addition of further inequalities has positively contributed to the model solution from a computational perspective. In fact, for the larger testbed networks, it allowed the solution of instances within the pre-fixed time limit and sped up the total CPU time needed to solve instances on an average basis (this was appreciated also for the realistic case study). Overall, the obtained results demonstrate that the approach is able to find robust and efficient evacuation plans, thus providing local governments and emergency planners with a valuable decision support tool.

Nevertheless, SISLER is not exempt from limitations based on its underpinning assumptions. First, SISLER is a deterministic model with respect to input data because it assumes that the evacuation demand is known. However, evacuees may not be willing to leave their own houses despite warning signals thus requiring adjustments to the evaluation of the evacuation demand. This shortcoming may be tackled through the use of robust optimization methodologies able to address uncertainties in the evacuation demand. Second, SISLER is a static model however, a dynamic variant of the model could capture aspects that currently have been either partially addressed or neglected; these include, for example: the disaster propagation rate, independently from the different disruption scenarios, the resource availability (e.g., shelter supplies, buses), and the traveling times, which could be considered as dependent upon the number of vehicles traveling on the network (i.e., traveling times as functions of the flow variables). Third, SISLER was devised thinking of a flood-like disaster; however, an integrated evacuation framework shall be able to address also other types of calamities. SISLER's adaptation to other types of disasters certainly warrants further investigation. Fourth, contraflow lane reversal is currently one of the major assumptions underpinning SISLER in line with some real-world evacuations. However, in other applications, this assumption may need to be relaxed and the model changed accordingly (i.e., by allowing buses to perform multiple trips). These changes will undoubtedly increase the model complexity, thus requiring new solution approaches. In addition, congestion-related issues may need to be addressed more explicitly by incorporating them directly into the model. This represents in itself another interesting area for future research. Fifth, SISLER could be embedded in a GIS-based decision support system to facilitate its use in practice. Finally, from a computational perspective, SISLER has been tested on networks whose node cardinality is around 25 and whose arc cardinality ranges from 56 to 165; also, only three possible scenarios have been considered (i.e., small-like disruption, medium-like disruption, and large-like disruption). With these settings, additional inequalities proved to be successful. However, an increase in the number of disruption scenarios and/or network dimensions will require the development of new ad hoc cuts, to be identified through polyhedral theory. Alternatively, other approaches could be devised such as Benders decomposition, deploying some forms of relaxation to obtain bounds to speed up the resolution process, or defining a path-based formulation of the model to be tackled through a branch-and-price approach. Finally, Soft OR approaches [36] could be used to facilitate the engagement with disaster management stakeholders, such as emergency management practitioners, civil protection agencies, and public authorities. The use of such approaches would ensure that stakeholders take ownership of the model and, consequently, would increase the likelihood that the model is used in practice to inform evacuation decisions in real disaster situations. In conclusion, despite the successful and encouraging results so far obtained, enhancements of SISLER from both a modeling and algorithmic perspectives will have to be considered to increase its potential as a realistic model and its scalability in terms of applications to larger real-life networks.

ACKNOWLEDGMENT

Open access funding provided by IReL.

Open Research

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.

REFERENCES

1L. Alçada-Almeida, L. Tralhao, L. Santos, and J. Coutinho-Rodrigues, A multiobjective approach to locate emergency shelters and identify evacuation routes in urban areas, Geogr. Anal. 41(1) (2009), 9–29.
10.1111/j.1538-4632.2009.00745.x
Web of Science® Google Scholar
2N. Altay and W. G. Green, OR/MS research in disaster operations management, Eur. J. Oper. Res. 175(1) (2006), 475–493.
10.1016/j.ejor.2005.05.016
Web of Science® Google Scholar
3S. K. Aros and D. E. Gibbons, Exploring communication media options in an inter-organizational disaster response coordination network using agent-based simulation, Eur. J. Oper. Res. 269(2) (2018), 451–465.
10.1016/j.ejor.2018.02.013
Web of Science® Google Scholar
4V. Bayram and H. Yaman, Shelter location and evacuation route assignment under uncertainty: A Benders decomposition approach, Transp. Sci. 51(2) (2017), 416–436.
10.1287/trsc.2017.0762
Web of Science® Google Scholar
5V. Bayram, B. Ç. Tansel, and H. Yaman, Compromising system and user interests in shelter location and evacuation planning, Transp. Res. B: Methodol. 72 (2015), 146–163.
10.1016/j.trb.2014.11.010
Web of Science® Google Scholar
6D. R. Bish, Planning for a bus-based evacuation, OR Spectr. 33(3) (2011), 629–654.
10.1007/s00291-011-0256-1
Google Scholar
7M. Boccia, T. G. Crainic, A. Sforza, and C. Sterle, Multi-commodity location-routing: Flow intercepting formulation and branch-and-cut algorithm, Comput. Oper. Res. 89 (2018), 94–112.
10.1016/j.cor.2017.08.013
Web of Science® Google Scholar
8M. Brachman and R. Church, Planning for disaster: A review of the literature with a focus on transportation related issues (FiRST report), Geotrans Laboratory, UCSB, Santa Barbara, CA, 2009.
Google Scholar
9 Camp Coordination and Camp Management (CCCM) Cluster, The MEND Guide, 2014, available at https://cccmcluster.org/resources/mend-guide.
Google Scholar
10M. Chouman, T. G. Crainic, and B. Gendron, A cutting-plane algorithm for multicommodity capacitated fixed-charge network design, CIRRELT, Montreal, 2009.
Google Scholar
11 CNN, 2011 Japan Earthquake – Tsunami Fast Facts, 2019, available at https://edition.cnn.com/2013/07/17/world/asia/japan-earthquake---tsunami-fast-facts/index.html (accessed July 12, 2019).
Google Scholar
12J. Coutinho-Rodrigues, L. Tralhão, and L. Alçada-Almeida, Solving a location-routing problem with a multiobjective approach: The design of urban evacuation plans, J. Transp. Geogr. 22 (2012), 206–218.
10.1016/j.jtrangeo.2012.01.006
Web of Science® Google Scholar
13A. Esposito Amideo and M. P. Scaparra, A scenario planning approach for shelter location and evacuation routing, in Optimization and Decision Science: Methodologies and Applications. ODS 2017. Springer proceedings in Mathematics & Statistics, Vol 217, A. Sforza and C. Sterle, Eds., Springer, Cham, 2017, 567–576.
10.1007/978-3-319-67308-0_57
Google Scholar
14A. Esposito Amideo, M. P. Scaparra, and K. Kotiadis, Optimising shelter location and evacuation routing operations: The critical issues, Eur. J. Oper. Res. 279(2) (2019), 279–295.
10.1016/j.ejor.2018.12.009
Web of Science® Google Scholar
15J. Fry and J. M. Binner, Elementary modelling and behavioural analysis for emergency evacuations using social media, Eur. J. Oper. Res. 249(3) (2016), 1014–1023.
10.1016/j.ejor.2015.05.049
Web of Science® Google Scholar
16M. Gama, B. F. Santos, and M. P. Scaparra, A multi-period shelter location-allocation model with evacuation orders for flood disasters, EURO J. Comput. Optim. 4(3–4) (2016), 299–323.
10.1007/s13675-015-0058-3
Web of Science® Google Scholar
17S. Gibbens, Hurricane Katrina, explained, 2019, available at https://www.nationalgeographic.com/environment/natural-disasters/reference/hurricane-katrina/ (accessed July 12, 2019).
Google Scholar
18M. Goerigk, K. Deghdak, and P. Heßler, A comprehensive evacuation planning model and genetic solution algorithm, Transp. Res. E: Logist. Transp. Rev. 71 (2014), 82–97.
10.1016/j.tre.2014.08.007
Web of Science® Google Scholar
19P. Heßler and H. W. Hamacher, Sink location to find optimal shelters in evacuation planning, EURO J. Comput. Optim. 4(3–4) (2016), 325–347.
10.1007/s13675-015-0054-7
Web of Science® Google Scholar
20F. Kılcı, B. Y. Kara, and B. Bozkaya, Locating temporary shelter areas after an earthquake: A case for Turkey, Eur. J. Oper. Res. 243(1) (2015), 323–332.
10.1016/j.ejor.2014.11.035
Web of Science® Google Scholar
21A. Klose and A. Drexl, Lower bounds for the capacitated facility location problem based on column generation, Manag. Sci. 51(11) (2005), 1689–1705.
10.1287/mnsc.1050.0410
Web of Science® Google Scholar
22S. Kongsomsaksakul, C. Yang, and A. Chen, Shelter location-allocation model for flood evacuation planning, J. East. Asia Soc. Transp. Stud. 6 (2005), 4237–4252.
Google Scholar
23J. M. Leung and T. L. Magnanti, Valid inequalities and facets of the capacitated plant location problem, Math. Program. 44(1–3) (1989), 271–291.
10.1007/BF01587093
Web of Science® Google Scholar
24A. C. Li, N. Xu, L. Nozick, and R. Davidson, Bilevel optimisation for integrated shelter location analysis and transportation planning for hurricane events, J. Infrastruct. Syst. 17(4) (2011), 184–192.
10.1061/(ASCE)IS.1943-555X.0000067
Web of Science® Google Scholar
25A. C. Li, L. Nozick, N. Xu, and R. Davidson, Shelter location and transportation planning under hurricane conditions, Transp. Res. E: Logist. Transp. Rev. 48(4) (2012), 715–729.
10.1016/j.tre.2011.12.004
Web of Science® Google Scholar
26 London Resilience Team, London Resilience Partnership Mass Evacuation Framework Version 2.0, 2014, available at https://www.london.gov.uk/sites/default/files/gla_migrate_files_destination/London%20Mass%20Evacuation%20Framework%20V2%200.pdf.
Google Scholar
27L. A. Lorena, and E. L. Senne, A column generation approach to capacitated p-median problems, Comput. Oper. Res. 31(6) (2004), 863–876.
10.1016/S0305-0548(03)00039-X
Web of Science® Google Scholar
28P. Murray-Tuite and B. Wolshon, Evacuation transportation modeling: An overview of research, development, and practice, Transp. Res. C: Emerg. Technol. 27 (2013), 25–45.
10.1016/j.trc.2012.11.005
Web of Science® Google Scholar
29M. Ng, J. Park, and S. T. Waller, A hybrid bilevel model for the optimal shelter assignment in emergency evacuations, Comput. Aided Civ. Inf. Eng. 25(8) (2010), 547–556.
10.1111/j.1467-8667.2010.00669.x
Web of Science® Google Scholar
30 Nippon.com, The state of recovery in Tohoku eight years after 3/11, 2019, available at https://www.nippon.com/en/japan-data/h00404/the-state-of-recovery-in-tohoku-eight-years-after-311.html (accessed July 12, 2019).
Google Scholar
31C. G. Rawls and M. A. Turnquist, Pre-positioning and dynamic delivery planning for short-term response following a natural disaster, Socio Econ. Plan. Sci. 46(1) (2012), 46–54.
10.1016/j.seps.2011.10.002
Google Scholar
32J. L. Renne and E. Mayorga, What has America learned since Hurricane Katrina? Evaluating evacuation plans for carless and vulnerable populations in 50 large cities across the United States (no. 18-03079), 2018.
Google Scholar
33S. Shahparvari, P. Chhetri, B. Abbasi, and A. Abareshi, Enhancing emergency evacuation response of late evacuees: Revisiting the case of Australian black Saturday bushfire, Transp. Res. E: Logist. Transp. Rev. 93 (2016), 148–176.
10.1016/j.tre.2016.05.010
Web of Science® Google Scholar
34 Transportation Network for Research Core Team, Transportation Networks for Research, available at https://github.com/bstabler/TransportationNetworks (accessed August 24, 2018).
Google Scholar
35 Transportation Research Board, The role of transit in emergency evacuation: Special report 294, Transportation Research Board, 2008.
Google Scholar
36L. N. Van Wassenhove and M. Besiou, Complex problems with multiple stakeholders: How to bridge the gap between reality and OR/MS? J. Bus. Econ. 83(1) (2013), 87–97.
10.1007/s11573-012-0643-3
Google Scholar
37Z. Wang and X. Ye, Social media analytics for natural disaster management, Int. J. Geogr. Inf. Sci. 32(1) (2018), 49–72.
10.1080/13658816.2017.1367003
Web of Science® Google Scholar

Citing Literature

Volume78, Issue1

Special Issue on Freight Transportation and Logistics

July 2021

Pages 46-68

An integrated user-system approach for shelter location and evacuation routing

Abstract

1 INTRODUCTION

1.1 Problem overview

2 LITERATURE REVIEW

3 THE SISLER MODEL

3.1 Model assumptions

3.2 Model formulation

4 SOLUTION METHODOLOGY

4.1 Valid inequalities for SISLER

5 EXPERIMENTAL RESULTS

5.1 Testbed instances generation

5.1.1 Computational results for the 25 × 56 network

5.1.2 Computational results for the 25 × 165 network

5.2 Case study: Sioux Falls network

5.2.1 Case study description

5.2.2 Computational results

6 CONCLUSIONS AND FUTURE RESEARCH DIRECTIONS

ACKNOWLEDGMENT

Open Research

DATA AVAILABILITY STATEMENT

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

An integrated user-system approach for shelter location and evacuation routing

Abstract

1 INTRODUCTION

1.1 Problem overview

2 LITERATURE REVIEW

3 THE SISLER MODEL

3.1 Model assumptions

3.2 Model formulation

4 SOLUTION METHODOLOGY

4.1 Valid inequalities for SISLER

5 EXPERIMENTAL RESULTS

5.1 Testbed instances generation

5.1.1 Computational results for the 25 × 56 network

5.1.2 Computational results for the 25 × 165 network

5.2 Case study: Sioux Falls network

5.2.1 Case study description

5.2.2 Computational results

6 CONCLUSIONS AND FUTURE RESEARCH DIRECTIONS

ACKNOWLEDGMENT

Open Research

DATA AVAILABILITY STATEMENT

REFERENCES

Citing Literature

Figures

References

Related

Information