INTRODUCTION

Effective species conservation and management relies on accurate assessments of population abundance and how abundance changes over time. Although many management programs rely on indices of abundance as indicators of change, estimates of true abundance are critical in many cases. Decisions concerning endangered species rely on assessments of the likelihood that the species abundance of representative subpopulations is reduced below a specified quasi-extinction threshold (Gilpin and Soulé 1986; Fagan and Holmes 2006), whereas recovery targets often focus, in part, on abundance of the subpopulations exceeding a specified threshold before recovery can be claimed (e.g., Colorado Pikeminnow Ptychocheilus lucius, U.S. Fish and Wildlife Service [USFWS] 2002; pygmy rabbit Brachylagus idahoensis, Washington Department of Fish and Wildlife 1995; Sierra Nevada bighorn sheep Ovis canadensis sierrae, USFWS 2007). For harvested species, the accurate assessment of total abundance is useful in evaluating harvest levels that are sustainable (Rughetti and Festa-Bianchet 2014; Nichols et al. 2015; Ohlberger et al. 2019). In each of these situations, biased estimates of total abundance can have substantial management and conservation implications. Overestimating abundance may suggest successful recovery of endangered species that are still below target thresholds (Johansson et al. 2020) or make unsustainably large harvest levels appear to be sustainable for targeted species (Sinclair et al. 1985; Walters and Maguire 1996; Wiedenmann and Jensen 2019). Conversely, underestimates may cause the implementation of unnecessary conservation actions and regulation (Scheerer 2007; Vallecillo et al. 2021). Therefore, identifying assessment tools that provide accurate estimates of population abundance is critical to the effective and sustainable management of species.

Mark–recapture methods have a long history of use for estimating the abundance of fish and wildlife populations (Chapman 1951; Cormack 1968; Otis et al. 1978; see Thomson et al. 2009 for a collection of modern mark–recapture methods on abundance estimation and use). Mark–recapture methods rely on randomly marking a subset of the population (via capture and subsequent release with marks) and then estimating abundance based on capture and recapture probabilities during subsequent sampling occasions (Otis et al. 1978; Schwarz and Arnason 1996). Here we focus on closed-capture mark–recapture methods, where sampling occurs over a relatively short period such that changes from births, deaths, immigration, and emigration are minimal (Otis et al. 1978; Kendall et al. 1995). Although these methods can provide robust estimates of population abundance, the process of capturing and marking individuals can be expensive and require extensive field sampling. It may be difficult to sample the entire population, and capture probabilities can be low even when sampling the entire population. We address the first issue in this article, but when the entire population is randomly sampled and capture probabilities are low (e.g., <0.10), as can be the case for rare and aquatic species, estimates are unreliable and often biased high (Otis et al. 1978; Rosenberg et al. 1995; Kéry and Royle 2015). We do not address this second issue in this article.

Passive, remote detection methods such as antennas for animals with passive integrated transponder (PIT) tags (Gibbons and Andrews 2004) or camera traps for animals that have been marked or have unique marks (O’Connell et al. 2011; Alonso et al. 2015) have been developed in recent decades. Remote detection systems can greatly improve our ability to estimate abundance by increasing capture and recapture probabilities (Gibbons and Andrews 2004; Gilbert et al. 2020). However, remote systems detect (capture) only marked animals and the unmarked animals typically have a much different initial capture probability than the marked animals. If unaccounted for, heterogeneity in capture probability results in biased estimates of abundance, which has led to development of models that can deal with heterogeneity from unknown causes (Chao 1987; Pledger 2000). Methods have also been developed to deal with known heterogeneity in capture probabilities due to capture methods (e.g., physical capture vs. antenna detection; Conner et al. 2020; Dzul et al. 2022) or individual characteristics (e.g., age, sex, size; White 1982).

A further assumption of mark–recapture models is that the population is randomly sampled, which encompasses many issues (e.g., certain age-classes may not be large enough to be captured, some animals have behaviors that make them uncatchable, etc.) Here, we focus on the random sampling assumption that all individuals are available for capture (Otis et al. 1978; Pollock et al. 1990), and we refer to this as the available-for-capture assumption in this article. Meeting the available-for-capture assumption may be feasible for animals that are already marked because remote detection systems can operate continuously and can be placed throughout the area of interest, but they may be difficult for unmarked animals that must be physically captured initially during the closed-capture sampling period. This is because physical sampling can be limited in space, time, or the ability to capture a certain class of animal (e.g., small or stationary animals missed). In this study, we focus on this issue of some individuals being unavailable for physical capture, which results in a nonrandom sample.

Many fishes of conservation concern make predictable migrations to distinct spawning habitats, so antennas are increasingly being applied to assess the population dynamics of imperiled migratory species (Bottcher et al. 2013; Cathcart et al. 2015; Pearson et al. 2016; Dzul et al. 2022). Endangered fish recovery programs often rely in part on supplementing wild populations with individuals that are reared in hatcheries or translocated from alternative locations with self-sustaining populations (Rasmussen et al. 2009; Spurgeon et al. 2015; Day et al. 2017; Fonken et al. 2023). These stocking and translocation events provide valuable opportunities to PIT-tag (i.e., mark) a large number of individuals, which can be detected later with antennas at relevant locations (e.g., within spawning tributaries), and these remote systems can operate almost continuously (excepting technical problems). Although these remote systems can provide accurate estimates of population size of marked individuals, they are estimates (and not a census) because not all fish are detected; some may move out of the study area or may not move over the antenna, and if the study occurs over multiple periods, some may not survive. We use the term “marked population” to refer to estimates of population size of marked individuals or as the collection of all marked individuals.

When fish populations are supplemented, the marked population often represents primarily hatchery-raised or translocated individuals and wild individuals need to be physically captured and marked to estimate total abundance. Limited management resources for physical capture surveys can leave a portion of the wild, unmarked individuals unavailable for capture. For example, a population with an 8-week spawning period may only be sampled for physical capture and marking during part of each day and/or for only a part of the spawning period (Scoppettone and Vinyard 1991). Additionally, physical capture methods may not sample from the entire population due to the inability to sample certain habitats effectively (Cone et al. 1988; Bernard et al. 1993). In such situations, a portion of the unmarked population is unavailable for sampling and not counted in the estimate of population size; thus, sampling of the unmarked population is nonrandom. In this situation, estimates of the abundance of marked individuals can be highly precise and accurate, whereas estimates for unmarked individuals will be biased low, yielding estimates of total abundance that are also biased low.

Here, we present a simple alternative abundance estimator that can be used to determine whether nonrandom sampling (i.e., failure to meet the available-for-capture assumption) of the unmarked population is causing bias in total abundance estimates from closed-capture models using mixed physical and remote capture data. Using a simulation approach, we examine the bias and precision of abundance estimates from two modeling approaches: (1) estimating total population abundance using closed-capture models that incorporate mixed data from physical captures of previously unmarked individuals and remote detections from previously marked individuals and (2) estimating abundance of only marked individuals using closed-capture models and then dividing abundance estimates for the marked population by an estimate of the proportion of population that is marked to obtain an estimate of total abundance (our simple alternative estimator). We assume that a random sample is used to estimate the proportion that is marked, which is predicated on the assumption that marked individuals are randomly distributed across the population and that marked individuals behave the same way as unmarked individuals. If marked individuals meet these assumptions, a random sample of the population should provide an unbiased estimate of the proportion of individuals in the population that have a mark. We compare the bias and precision of abundance estimates derived from the two approaches across a range of scenarios (i.e., physical- and antenna-capture probabilities, proportion marked, sample size) to bracket most field sampling situations. Finally, we compare the abundance estimates for spawning fish from the two approaches for two case studies representing fishes of conservation concern with different life history expressions: spawning adfluvial June Sucker Chasmistes liorus and spawning fluvial Bull Trout Salvelinus confluentus. Both species are listed as threatened under the Endangered Species Act (USFWS 2015, 2021). These two case studies are representative of common, but quite different, field situations, and our results are widely applicable to populations with mixed data.

METHODS

Simulation methods

To determine the effect of deviating from meeting the available-for-capture assumption for the unmarked population on population estimates, we simulated data sets with encounter histories from physical captures and remote antenna detections (captures) of PIT-tagged individuals across a range of scenarios to encompass various possible field-sampling conditions (Table 1). Within the modeling framework, we refer to antenna detections as captures and recaptures to maintain the terminology of closed-capture models but we use the term “antenna capture” when there is ambiguity of the type of capture. The population of sampled fish are from a closed population, and a specified proportion of those fish are available for physical capture; that is, if the proportion unavailable for physical capture (prop_miss) = 0, the entire population is available to be physically sampled; if prop_miss > 0, then that proportion of unmarked fish is not available for sampling. Note that our simulation approach assumes that the same population of fish is sampled physically and by the antenna during a closed-capture period. That is, the physical capture location and antenna locations are close enough that fish are vulnerable to both physical capture (for marked and unmarked individuals) and antenna detection (for marked individuals only). We used the same simulated data set from the same population to compare abundance estimates between two modeling approaches: (1) a mixed-data approach that incorporates both antenna detections and physical captures and (2) a proportional approach using antenna detections only, described in detail below.

TABLE 1. Simulation input parameter values for closed-capture models mixed-data (physical capture and antenna detections) for two approaches to estimate population abundance. These input values were used in simulations to randomly generate input data files (encounter histories). We used the same simulated data set from the same population for each approach but dealt with the data differently for the two approaches.

Simulation inputs	Values
Population abundance (N)	10,000
Probability of initial physical capture (pcap)	0.05–0.20 by 0.05
Probability of initial capture by antenna detection (pdet) and antenna detection probability of recapture (c)a, b	0.1–0.30 by 0.1
Proportion of fish marked at start of the closed capture sampling period (propmark)	0.05–0.30 by 0.05
Number of fish sampled to estimate proportion marked (nsamp)	50–300 by 50
Proportion of the unmarked population that was missed for physical capture (propmiss)	0–0.95 by 0.05

• ^a Probability of recapture (c) was always equal to p_det.
• ^b Probability of capture (p_cap and p_det) and recapture (c) were simulated and modeled as constant—for example, p_det (.) = c(.)—where “.” indicates the same (i.e., constant) p and c for all four encounters.

For all the simulation scenarios (Table 1), we used four sampling occasions (i.e., encounter histories had four encounters; for example, 0110, 1000, etc., where 0 = not captured or detected in a capture period and 1 = captured and/or detected in a sampling period). We first generated a population of marked and unmarked individuals based on the scenario of population size (N) and proportion marked (prop_mark; Figure 1, step 1). We then simulated encounter histories for both antenna detections and physical captures for each individual within the population (Figure 1, step 2). A marked (PIT-tagged) fish could only be initially captured by detection on an antenna with probability p_det. Individuals not having a PIT tag could only be initially captured physically with probability p_cap. After initial capture, all simulated recaptures were from the antenna only with the same probability as initial capture by the antenna; therefore, recapture probability (c) was equal to p_det for all fish. We note that in the field, fish that were already marked could be captured either physically or detected by the antenna, which should result in a cumulative initial capture and/or recapture probability slightly higher than what we used in the simulations. However, to facilitate the interpretation and presentation of the results, we did not combine initial capture and recapture probabilities. We assumed a closed population during the sampling period (no births, deaths, immigration, or emigration were included in the model) and 100% tag retention, and we did not include individual heterogeneity in our simulations.

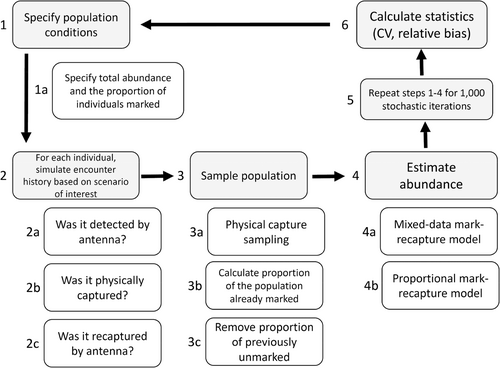
After encounter histories were generated for each simulated population, we applied two random sampling events (Figure 1, step 3). First, we conducted an independent random sample of the simulated population (sample size specified as n_samp) to estimate the proportion of the population that was previously marked (p̂rop_mark) in the physical samples (Figure 1, step 3a). Then, after the proportion marked was estimated we randomly removed a specified proportion of unmarked individuals (prop_miss) from the simulated data for a model iteration (Figure 1, step 3bc), as these individuals would never be physically captured or captured on antennas because they never receive a mark. For example, if N = 10,000, prop_mark = 0.25, and prop_miss = 0.10, then we removed 10,000 × (1 – 0.25) × 0.10 = 750 individuals from the available unmarked portion of the population. We assumed that the marked individuals were randomly distributed throughout the population and that, therefore, p̂rop_mark from our sample in step 3a would not be affected by prop_miss. Thus, we assumed that the estimates of p̂rop_mark were unbiased. We generated all the simulations in program R (R Core Team 2023; code included in Supplemental Material available in the online version of this article).

To estimate population abundance, we analyzed the data using the Huggins formulation (Huggins 1989, 1991) of a closed-capture model (Figure 1, step 4; Otis et al. 1978; see Cooch and White 2019 for a clear explanation of the closed-capture likelihood equations for both methods). For the mixed-data approach (Figure 1, step 4a), we used an individual covariate, which we call PrevCap, to account for the fact that once PIT-tagged the probability of being “captured” by an antenna detection was different (typically higher) than that for physical captures (Conner et al. 2020; Dzul et al. 2022). All the estimating models had constant initial capture probability (p, which was p_cap or p_det) and c—that is, p_cap(.) = c(.) or p_det(.) = c(.)—where “.” indicates a constant p or c (i.e., same for the four encounters). Specifically, the model for the mixed-data approach was p(. + PrevCap) = c(.), where p was constant and equal to c with an additive effect on p for previously captured fish (i.e., fish whose initial capture is via antenna detection). For the proportional approach, we used the model p_det(.) = c(.). We note that c was not used in the estimation of N in the closed-capture models, so c could be any value (including 0 as in a removal model), although it needs to be properly modeled so that the estimate of initial capture (p_cap or p_det) is unbiased. Because modeling c was not important for our comparison, we used simple models that matched how the data were generated. For all the simulations, we analyzed each simulated data set using the program MARK (White and Burnham 1999; White et al. 2001; White 2008) via R package RMARK (Laake 2013), estimating abundance N and its standard error (SE).

For the proportional approach, total population abundance was estimated by dividing the closed-capture abundance estimates for marked fish only by estimates of p̂rop_mark (Figure 1, step 4b). We calculated the variance of these abundance estimates using the delta method (Seber 1982; Powell 2007). For each mixed-data and proportional model simulation, we calculated percent CV($\widehat{N}$) as [SE($\widehat{N}$) / $\widehat{N}$] × 100 to represent precision and percent relative bias [($\widehat{N}$- N) / N] × 100 to represent bias. We ran 1000 iterations for each scenario (Table 1; Figure 1) and report the mean of the estimates, CV($\widehat{N}$), and relative bias across the simulations.

RESULTS

Simulation experiments

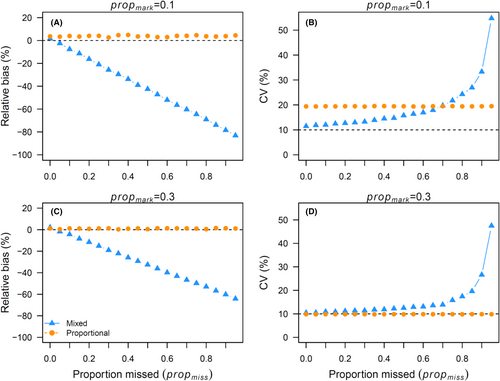
As the proportion of the population that was not available to be physically captured during closed-capture sampling (prop_miss) increased, abundance estimates for the mixed-data approach became increasingly negatively biased, whereas there was almost no bias for the proportional approach when prop_mark ≥ 0.1 (Figure 2A shows two cases). For the mixed-data approach, the relationship between relative bias and prop_miss was not 1:1 but depended on the proportion of the population that was marked. When the marked proportion was 0.1, the bias was greater than when the marked proportion was 0.3 for the same proportion missed (Figure 2A). The CV was less directly related to the proportion missed for the mixed-data approach, yet a threshold was apparent after which precision decreased (CV increased) in an exponential manner, with a very high prop_miss (>~0.65; Figure 2B). The proportion approach was not related to prop_miss (Figure 2B).

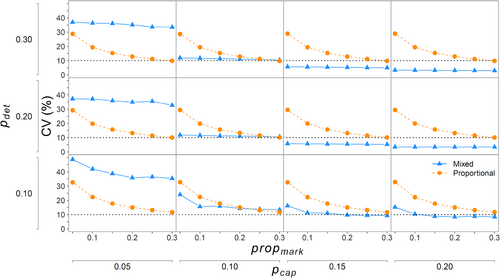
When all the fish were available for capture (prop_miss = 0), there were differences in bias and precision between the two approaches. Because the proportional approach did not use physical captures to estimate abundance in the closed-capture model, changes in initial capture probability (p_cap) did not affect relative bias or CV of $\widehat{N}$ (Figures 3 and 4). Similarly, because the mixed-data approach did not use prop_mark to estimate N, prop_mark did not contribute to relative bias or CV of $\widehat{N}$ from the mixed-data approach (Figures 3 and 4). For the mixed-data approach, the CV demonstrated a large decrease when p_cap increased from 0.05 to 0.10 and smaller decreases thereafter (Figure 4). For the proportional approach, relative bias and CV of abundance estimates were mainly related to prop_mark, with both metrics decreasing exponentially as prop_mark increased. In fact, relative bias and CV changed little as p_det increased because both were so strongly related to prop_mark. However, for the relative bias, the decrease was diminished when prop_mark was >0.15 and still retained low positive bias, whereas the CV decreased for the entire range of prop_mark (Figures 3 and 4).

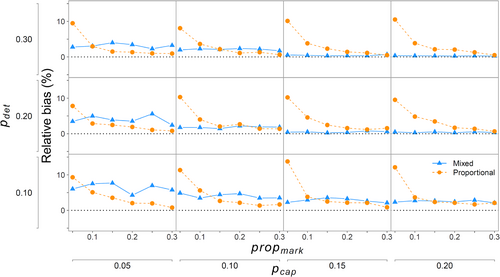
On average, when all the fish were available for capture (prop_miss = 0), there was some positive relative bias for both methods in simulations where initial capture probabilities (p_cap and p_det) were low (Figure 3). Although positive bias was generally low (≤5%), the proportional method had higher positive bias than the mixed-data approach when p_cap ≥ 0.15 and p_det ≥ 0.20. Relative bias was almost 0 for both approaches when p_cap ≥ 0.15, p_det ≥ 0.20, and prop_mark ≥ ~0.15 (Figure 3). However, the proportional approach can have a positive bias of up to 10% (1.1×; Figure 3) when prop_mark is very low (0.05–0.10), even when p_cap ≥ 0.15 and p_det ≥ 0.20.

Case studies

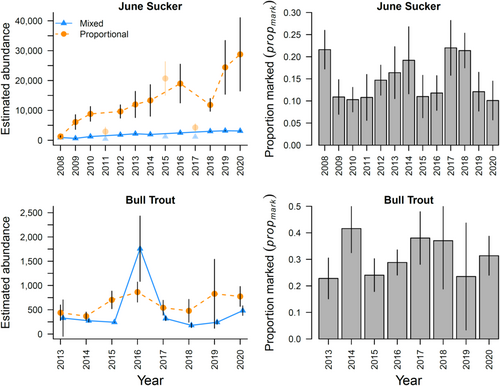
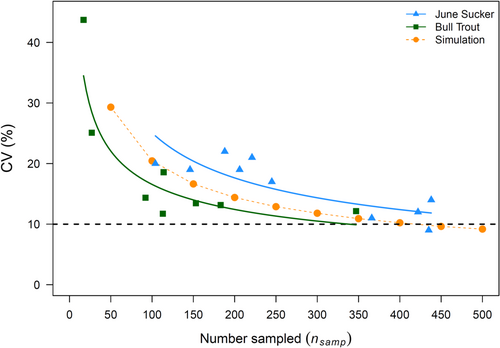
Our two case study results demonstrated different magnitudes of deviation between abundance estimates for the proportional and mixed-data approaches. The difference between abundance estimates from the two approaches were much greater for June Sucker than they were for Bull Trout (Figure 5A). The abundance estimates from the proportional data approach averaged approximately 6× greater for June Sucker (range = 1.4–9.5×) and 2× greater for Bull Trout (range = 1.3–3.4×). The proportion of marked fish was higher for Bull Trout than for June Sucker across all survey years (Figure 4B), where Bull Trout averaged 0.31 (range = 0.23–0.42) and June Sucker averaged 0.15 (range = 0.10–0.22). Although a higher proportion of Bull Trout than June Sucker was PIT-tagged, the CV of abundance estimates from the proportional approach was lower for June Sucker for all the sample sizes that were used to estimate prop_mark (Figure 6). This is likely due to the difference in sample sizes of physically captured individuals that were used to estimate prop_mark and number of unique individuals that was used to estimate N for PIT-tagged fish. For estimating prop_mark, the sample size for June Suckers was 1.9× greater (mean = 248, range = 104–438) than that for Bull Trout (mean = 131, range = 17–347). The difference was even greater for unique individuals (number of fish with encounter histories) that were used to estimate N for PIT-tagged fish. The mean value for number of unique individuals per year for June Sucker (mean = 1713, range = 230–2906) was 12.0× that for Bull Trout (mean = 143, range = 84–181). However, the simulations and both case study results showed an exponentially decreasing trend in CV values for abundance estimates with increasing numbers of individuals sampled to estimate prop_mark (Figure 6).

DISCUSSION

Accurately estimating abundance for populations of management or conservation concern is a critical component of effective decision making (Nichols 2014). Increasingly, mark–recapture analytical methods are capable of integrating mixed-data processes to improve the precision and robustness of population estimates (e.g., Boulanger et al. 2008; Alonso et al. 2015; Dzul et al. 2022). However, our results demonstrate that closed-capture models are subject to substantial negative bias when a segment of the population of interest is not available for physical capture, and physical captures therefore do not represent a random subset of the population.

Lack of population closure and heterogeneity (from unknown sources) in capture probability can also cause bias in estimates of abundance (Pollock et al. 1990; Link 2004; Boulanger et al. 2004), but these issues can be resolved. Population closure can be tested (Stanley and Burnham 1999) and open population models used when the closure assumption is not met (Jolly 1965; Arnason and Schwarz 1995; Link and Barker 2005). Furthermore, unknown heterogeneity can be modeled (Pledger 2000). Although these violations have remedies, there is no generalized test to identify the bias due to animals that are not available for capture, regardless of whether mixed data or data of only one type are used. Using an open population model, such as the Jolly–Seber (Jolly 1965) or multistate with an unobservable state (Horton et al. 2011), does not remedy the problem of not sampling a proportion of the population. Although these models include animals that enter and exit the study site during the sampling period (open population models) or animals that are not observable for a portion of the sampling period, if an animal is not ever available for capture during the sampling period, estimates of population size will still be biased low.

In situations where physical captures and antenna detections from antennas that are operating relatively continuously during the closed-capture sampling period are used to estimate N, we recommend that practitioners compare the outputs of mixed-data probability models with those from the simpler proportional model presented herein to determine whether their population estimates are biased. If estimates from the mixed-data approach are ≤10% lower than those from the proportional approach, it is likely that the entire population was sampled (prop_miss = 0) because the proportional approach has some positive bias. However, even small proportions of the population being unavailable for sampling renders the mixed-data approach estimates more biased, though in the opposite direction. That is, if estimates from the mixed-capture model are substantially lower than those from the proportional approach (>10% lower), it is likely that physical capture efforts are missing a segment of the population.

Diagnosing whether the entire population is available for physical capture during the closed-capture sampling period is a matter of scale. For example, if the entire population were sampled, using the lowest estimated proportion marked for Bull Trout from 2012 to 2020 of prop_mark = 0.23 and using p_cap = 0.19 and p_det = 0.24 (means from field data), the simulations indicate that the estimates of population size from the proportional approach should be biased approximately 1.02–1.03× high (2–3% relative bias; see the two upper-right panels in Figure 3) relative to those from the mixed-data approach. Based on field data, estimates from the proportional approach were 1.3–3.4× greater than those from the mixed-data approach (except for 2016, which had an anomaly that is not relevant to this discussion). This indicates that most of the issue is due to a proportion of the population not being available for physical capture during the closed-capture sampling period. The situation is similar, but more dramatic, for June Sucker estimates. Comparing the abundance estimates for marked animals divided by the proportion marked with other closed-capture estimates is a relatively straightforward way to determine whether this important bias exists. However, if not all individuals are available for sampling to estimate the proportion that is marked, there can still be undetected bias, as we discuss below.

Management decisions for populations of management or conservation concern are often informed by whether population abundance meets certain thresholds such as escapement goals (e.g., Cunningham et al. 2019), stock targets used in harvest control rules (e.g., Punt et al. 2010), or abundance targets for endangered species recovery (e.g., USFWS 2001). The precision of abundance estimates is therefore critical to informing management decisions, as more precise estimates will improve confidence in whether a population is meeting management targets. Analytical approaches that have been developed over the past several decades have improved our ability to generate more precise estimates of abundance when using detections from remote sources (e.g., Pearson et al. 2016; Conner et al. 2020; Dzul et al. 2022). Indeed, when the entire population is sampled (random sampling; prop_miss = 0) our simulation analyses highlight how mixed-data models produce more precise (i.e., lower CV) and less positively biased estimates of abundance than are produced via the simple proportional model, except when the probability of initial capture (via physical and antenna detection) is very low (<0.1). Thus, in scenarios where marked individuals can be reliably recaptured by remote methods and physical capture efforts during closed-capture can randomly sample large proportions of the population, mixed-data models can provide estimates that are superior to those that are obtained with the simple proportional model. Populations that undergo predictable seasonal migrations and become concentrated along migration routes (e.g., diadromous/potamodromous fishes) represent ideal scenarios. However, the benefit of applying these models to such populations erodes if the whole population is not available for physical sampling (i.e., p_cap = 0 for a portion of the population and p_cap > 0 for the rest of the population).

Random sampling of the population is an underlying assumption of many mark–recapture models. However, acquiring truly random samples of fish and wildlife populations can be challenging due to logistical and economic issues such as inability to access the full range of the population's habitat or limited personnel or funding availability to sample throughout an entire closed-capture period. Our simulation model results demonstrate that the negative bias of abundance estimates is proportional to the percentage of the population that is unavailable for physical sampling. Individuals that are already marked are available for passive recapture for the duration of the closed-capture period, whereas physical sampling captures and recaptures are periodic. As mixed-data closed-capture models assume that all individuals that are available for passive recapture are also available for physical capture, any part of the population that is unavailable for physical capture will bias abundance estimates low. The negative bias that is produced by nonrandom sampling has been observed previously in closed-capture models (Cone et al. 1988; Bernard et al. 1993; Thompson et al. 1998) but has not been considered in mixed-data approaches. Thus, our simulation results highlight a potential pitfall of using mixed-data closed-capture models if practitioners do not test for bias. The reduced variance in the abundance estimates derived from the mixed-data models is an attractive property, but more precise estimates that are biased can result in inappropriate management decisions.

The potential for negative bias first came to our attention when estimating spawning abundance for June Sucker with closed-capture models. Annual estimates of spawning abundance increased across the period of the study, suggesting successful ongoing stocking efforts. However, our estimates of total abundance were not much greater than our estimates of the abundance of marked fish only, even though only a relatively small proportion of the total population was marked. The issue for June Sucker appears to arise from physical sampling occurring during a small proportion of the spawning migration period and over a small portion of habitat. Utah Lake's three largest tributaries, the Provo River, Hobble Creek, and Spanish Fork, contain approximately 16 river kilometers of spawning habitat. Although we restrict our inference to the population of spawning June sucker in the three primary tributaries of Utah Lake to account for the spatial issue, even for the spawning population, sampling all the available fish that spawn is infeasible due to limited financial resources and logistical issues (difficult to sample 24 h/day for 2 months), leaving a large proportion of the spawning population unavailable for physical capture. Consequently, mixed-data model estimates are severely negatively biased. Although the trend that is estimated from the mixed-data model depicts the increasing abundance of the spawning population across the period of study, the accuracy of the abundance estimates is very low and suggests a much smaller spawning population than is present. Accurately characterizing the abundance of spawning June Sucker is critical to conservation efforts that are directed at identifying the relationship between stocking and total abundance of spawning individuals.

Although abundance estimates from the mixed-data models for both case studies were negatively biased relative to those from the proportional approach, the estimates for spawning June Sucker were, on average, 3× more negatively biased than those for Bull Trout. In contrast to the relatively sparse physical sampling of June Sucker, spawning Bull Trout were captured at a weir that spans the full river channel, so all the Bull Trout that were migrating to summer rearing and spawning habitat would have to pass through the weir and, theoretically, should be available for physical capture. However, the population estimates from the mixed-data model still averaged 50% lower than those for the proportional model, suggesting that a proportion of the population is not available for physical capture. Logistical challenges of weir installation during high-water periods following spring runoff as well as variance in migration timing among individuals make a proportion of the spawning population unavailable for sampling during the closed-capture period, as some Bull Trout move upstream before the weir is installed and are not available for physical capture. This proportion can be quite large in years with large snowpack and thus larger magnitude and duration of high-flow periods. In addition, the Imnaha River weir and trapping facility are designed to physically capture spring Chinook Salmon for hatchery broodstock. Bull Trout can volitionally pass through the weir using slots at the bottom of the weir panels that are sized to pass all but the largest fluvial fish. We note that the problem of underestimating abundance was similarly documented in a recent study of returning Chinook Salmon on the Columbia River from 2016 to 2019 (Coykendall et al. 2022). The detection rate for returning PIT-tagged fish was assumed to be 100% through Granite Dam, yet another technique (parentage-based tagging) showed that abundance based on the returning PIT tags was biased low by 35%, which meant that almost 50,000 fish were missed each year.

The strong negative bias in the mixed-data approach motivates the following question: if you have marked animals in the population at the start of a closed-capture sampling period, why not always use the proportional approach? There are three potential drawbacks; the primary drawback of the proportional approach is that abundance estimates may have lower precision (higher CV) unless a large sample is taken to estimate the proportion marked (prop_mark). The CV for a mixed-data approach is ≤10% once p_cap ≥ 0.1 and p_det ≥ 0.2, attainable values in both case studies and for many species migrating through a restricted area. In contrast, achieving a CV of 10% for the same p_cap and p_det as in the example above requires sampling at least 400 animals if prop_mark = 0.10 and sampling at least 250 for a relatively high prop_mark = 0.30. There is a second drawback if prop_mark is low (≤~0.05); there can be a positive bias in population size estimates even if all the population is available for capture. In general, we recommend against using the proportional approach if prop_mark is low. However, even small proportions of the population being unavailable for sampling renders the mixed-data approach estimates more biased, though in the opposite direction. This brings us to the third drawback: in scenarios where marked individuals are not evenly distributed among the population and marked and unmarked individuals are not equally vulnerable to capture, bias can also plague the estimation of the proportion marked.

For the proportional approach, ensuring a random sample of the population is of paramount importance for unbiased estimates of the proportion marked. If the distribution and behavior of marked individuals is not representative of the entire population, there can still be bias. We evaluated this assumption for June Sucker. We compared estimates for the proportion of marked individuals among physical captures that were collected from locations considered spawning staging areas in Utah Lake from 2008 to 2023 with those for the proportion of marked individuals among physical captures from the Provo River (where, on average, 84% of the marked fish are detected). We found no pattern in the differences in proportion marked, and only 2 of 16 years had significant differences in proportions; we combined the data to estimate the proportion marked and assumed that it was representative for spawning June Sucker (Landom et al. 2024).

Although similarity in the distribution and behavior of marked and unmarked fish is reasonable for spawning June Sucker, where most marks come from stocked fish, it may not be for Bull Trout. There may be a segment of the Bull Trout population that always spawns early, before the weir is installed, and may not be available to be sampled during the spawning sampling period. In this situation and if fish that spawn early always spawn early, there may be a high bias in prop_mark and abundance would be biased low for the proportional approach (as well as for the mixed-data approach). To counter this possibility for Bull Trout, the monitored population could be defined as Bull Trout that spawn during June and July rather than the population of spawning Bull Trout, with prop_mark estimated only from fish that are physically captured in June and July.

Beyond temporal or spatial availability issues, if there is a behavioral response of fish that have been marked, then the estimate of prop_mark can be biased. For example, if marked fish were trap shy, prop_mark would be biased low and the estimate of total population abundance would be biased high. Size-selective capture methods could also lead to differential bias in estimates across size-classes within the population. This could be accounted for by analyzing different size-classes separately or by defining the population as those that are fully recruited to physical capture gears, as would be the situation in our case studies examining the abundance of adult fish that are making spawning migrations. Finally, negative bias in PIT tag estimates may arise from entirely different sources, such as PIT tag shedding or PIT-tagging-related mortality. This was the case for the abundance estimates of returning Chinook Salmon in the Snake River; Coykendall et al. (2022) found that PIT tag estimates of abundance were 35% lower than parentage-based tagging estimates. Although bias due to mortality or tag loss would not be detected with our approach, Coykendall et al. (2022) recommend a second method, parentage-based tagging, to evaluate bias due to PIT tag shedding or loss.

Finally, as found in other closed-capture simulation studies (Minta and Mangel 1989; Conner et al. 2020; Dzul et al. 2022), when initial capture probability (i.e., the cumulative probability of p_cap and p_det for mixed-data models) is low, there was small positive bias in the estimates of abundance for both approaches examined here. The positive bias occurs because when the estimates of initial capture probability are very low (close to 0), estimates of abundance become extremely high (Otis et al. 1978; Rosenberg et al. 1995; Kéry and Royle 2015). The same positive bias occurs when prop_mark is low for the same reason. That is, when the estimate of prop_mark is very low (close to 0), estimated abundance will be high, as seen when prop_mark was 0.05 (Figure 3; also see the Supplemental Material). Thus, when sampling intensity and/or the proportion of the population that is marked is low, both the proportional and mixed-data approaches may contain undiagnosed high, positive biases.

Accurate and precise estimates of population abundance are critical to the effective management of fish and wildlife populations (Nichols 2014). Although mixed-data closed-capture models can provide highly precise and accurate estimates of abundance when all assumptions are met, nonrandom sampling because not all individuals are available for physical capture, a relatively common deviation from model assumptions, causes mixed-data closed-capture models to produce highly negatively biased abundance estimates. The simple proportional model that we present here can easily be applied to check for bias in abundance results from these models. We suggest focusing on expanded sampling to get an accurate estimate of the proportion of the population that is marked. Sampling to estimate the proportion that is marked is more tractable than trying to ensure that the entire population is available for physical capture during a limited closed-capture sampling period. Sampling to meet the assumption that all individuals are available for physical capture during a closed-capture period is limited by resources and logistics (hard to sample all day and all night every day to get a thorough representative sample) and the relatively short time that is required for closed-capture sampling. Using ancillary data, using different methods than those that are used for the closed-capture sample, or expanding sampling times or areas can help produce a random and representative sample of proportion marked. If sampling for the proportion of the population that is marked is random and representative of the whole population, then dividing the estimate of N of the marked population, sampled during the closed-capture period, by the accurate estimate of proportion marked will provide an unbiased (accurate) estimate of total population abundance.

CONFLICT OF INTEREST STATEMENT

The authors declare there are no conflicting interests.

ETHICS STATEMENT

There were no ethical guidelines applicable to this study.