To introduce the dipolectric antenna: a novel RF coil design for high-field MRI using a combination of a dipole antenna with a loop-coupled dielectric resonator antenna.

Methods

Simulations in human voxel model Duke involving 8-, 16-, and 38-channel dipolectric antenna arrays for brain MRI were conducted. An 8-channel dipolectric antenna for occipital lobe MRI at 7 T was designed and constructed. The array was built of four dielectric resonator antennas (dielectric constant = 1070) and four segmented dipole antennas. In vivo MRI experiments were conducted in one subject, and the SNR performance was benchmarked against a commercial 32-channel head coil.

Results

A 38-channel dipolectric antenna array provided the highest whole-brain SNR (up to a 2.3-fold SNR gain in the center of the Duke's head vs. an 8-channel dipolectric antenna array). Dipolectric antenna arrays driven in dipole-only mode (with dielectric resonators used as receive-only) yielded the highest transmit performance. The constructed 8-channel dipolectric antenna array provided up to threefold higher in vivo peripheral SNR when compared with a 32-channel commercial head coil.

Conclusion

Dipolectric antenna can be considered a promising approach to enhance SNR in human brain MRI at 7 T. This strategy can be used to develop novel multi-channel arrays for different high-field MRI applications.

1 INTRODUCTION

Despite a considerable SNR gain provided by ultrahigh-field (UHF) MRI, that is, at 7 T and above, a continuous pursuit for higher sensitivity remains valid and is of high interest for neuroscientists who explore the anatomy, function, connectivity, and chemical composition of human brain in vivo at the macroscopic scale.^{1, 2} A standard approach to increase whole-brain SNR in high-field MRI is to use multi-channel RF coil arrays.³ Conventional RF arrays are constructed using conductive loop elements with lumped components (capacitors, inductors) required for tuning, decoupling (e.g., by overlapping³ or with additional capacitive⁴ and/or inductive circuits⁵), and power matching. Although this strategy can lead to an increase in peripheral SNR, it is not expected to improve SNR in deep brain: Decreasing a loop's diameter leads to higher resistive losses and reduced quality factor. This effect was experimentally verified at 3 T by Wiggins et al., who developed a 96-channel array for brain MRI,⁶ and recently confirmed by Uğurbil et al. for a 64-channel array for 7 T.⁷ However, there are promising alternatives that can provide considerable receive gains in periphery and in deep brain at 7 T and above. Unlike at 1.5 or 3 T, RF coils at UHF operate at the interface of near and far field of electromagnetic radiation.⁸ This makes different types of antennas particularly suitable for UHF-MRI, and some of them can be intrinsically complementary to each other, which brings potential performance gains.

As mentioned above, increasing SNR in the center of human brain can be considered more challenging because it is not expected to be achieved simply by increasing the number of loop coil elements in a receive array.^{6, 7} To address this issue, multi-channel dipole antenna arrays seem to be particularly promising. Dipole antennas were first used to enhance transmit efficiency in body MRI at 7 T,^{8, 9} and recent reports focused on novel designs for brain MRI at different B₀ field strengths: 7 T,¹⁰ 9.4 T,¹¹ and 10.5 T.¹² Those findings were further supported by theoretical work from Lattanzi et al.,¹³ who demonstrated that dipole antennas can capture curl-free currents, which contribute to the ultimate intrinsic SNR, and their significance is expected to grow with the sample size and the Larmor frequency. The theory prescribes that a combination of dipole antennas with standard loop coils is essential to approach the ultimate intrinsic SNR.¹³ This was first experimentally verified by Wiggins et al. in a cylindrical phantom¹⁴; then by Ertürk et al. for body applications¹⁵; and recently by Avdievich et al., who developed a 32-channel loop–dipole array for brain MRI at 7 T.¹⁶

A very effective approach, which was proposed to enhance receive performance of standard RF coils at UHF, was to combine them with dielectric materials with high ε_r (high-permittivity materials [HPM]¹⁷). HPMs can be either used as passive (also known as dielectric pads) or active elements, that is, dielectric resonator antennas (DRA). Although dielectric pads were introduced to address ${\mathrm{B}}_1^{+}$ inhomogeneities, they were also found suitable to improve SNR in human brain MRI at 7 T.¹⁸ Development of DRAs is still an active area of research, and there is an evidence showing that they can be considered an encouraging alternative to loop coil arrays at 7 T and above.^19-22 DRA can be designed as a ceramic block with a desired dielectric constant ε_r and low loss tangent (or electrical conductivity σ). A small coupling loop can be used to excite different dielectric modes within the dielectric block. The geometry and ε_r of the DRA can be freely adjusted, thereby providing extra degrees of freedom to tailor the electromagnetic field distribution for particular application.

The interplay between dipole antennas and dielectric materials was studied by other authors. In particular, the New York University group^{23, 24} showed that integration of HPMs could be a practical method to improve RF shimming performance of a dipole antenna array and SNR. Furthermore, Brink et al. provided preliminary evidence that using a dielectric “sleeve” can help to improve transmit/receive (TXRX) performance of a dipole antenna array.²⁵ Different modes, which can be induced by a short dipole antenna in direct contact with rectangular dielectric blocks, were studied by Ipek et al.²⁶ as well as by Wenz and Gruetter.²⁷ Nevertheless, a combination of a dipole antenna with an HPM with the latter acting as an active element (in fact, a DRA) was not considered so far. It was only demonstrated in a preliminary simulation study²⁸ that mixing loop-coupled DRAs with dipole antennas should be feasible because both elements produce orthogonal electromagnetic field patterns: By aligning a dipole antenna along the central axis of a loop-coupled DRA, a very high level of isolation between these two elements can be achieved. However, until now there was no experimental validation for the idea of mixing dipole antennas with loop-coupled DRAs.

Therefore, in this work we aim to investigate potential advantages of combining two types of elements: a dipole antenna and a loop-coupled dielectric resonator antenna for brain MRI at 7 T. It is hypothesized that by using the combined approach with a higher number of elements, which are complementary to each other, an SNR increase could be achieved. Moreover, the interaction between dipole antennas and HPM could have a beneficial effect on the transmit performance of dipole antennas. Recognizing this opportunity, we here introduce a novel concept of dipolectric antenna (dipole + dielectric), which is a combination of dipole antenna with a loop-coupled, rectangular DRA. To further explore this strategy, electromagnetic simulations involving 8-, 16-, and 38-channel arrays were performed, and an 8-channel dipolectric antenna array was constructed and used in in vivo study at 7 T.

2 METHODS

2.1 Electromagnetic field simulations

Numerical electromagnetic field and specific absorption rate (SAR) simulations were performed using the finite-difference time-domain solver of Sim4Life V7.0 (Zurich Medtech, Zurich, Switzerland). In the simulations, a spherical phantom (radius = 85 mm, ε_r = 77, σ = 1.09 S/m) and the human voxel model “Duke” from the Virtual Family were used.²⁹ Copper elements were modeled as perfect electrical conductors. The excitation signal was of Gaussian type (center frequency = 297.2 MHz, bandwidth = 500 MHz). The grid was manually adjusted for all the components in the simulation. The smallest mesh cell was 2 mm (“Duke” conductors, dielectric blocks, ports), whereas for the spherical phantom it was 4 mm. In each simulation, a hollow cylinder (radius = 200 mm, length = 300 mm) mimicking the head gradient insert of our MR scanner was included. The simulation data were exported as Touchstone files and used in Advanced Design System 2019 (Keysight Technologies, CA) to design the tuning/matching circuits. Subsequently, the same RF circuits were reproduced in the MATCH module of Sim4Life. The B₁ data for each channel were normalized to 0.02 W input power per channel, exported, and used for the SNR calculation and ${\mathrm{B}}_1^{+}$ optimization,³⁰ ensuring an appropriate power normalization (see Supplementary materials). SNR was calculated using the Roemer's approach³ combined with the scattering parameter formalism proposed by Kühne.^{30, 31} The SAR_10g for each phase setting was normalized to 1 W total input power. ${\mathrm{B}}_1^{+}$ efficiency was defined as ${\mathrm{B}}_1^{+}$ /√P, where P is total input power; and SAR efficiency was defined as ${\mathrm{B}}_1^{+}$ /√pSAR_10g, where pSAR_10g is peak SAR averaged over a mass of 10 g for given transmit mode.

2.2 Dipolectric antenna

Dipolectric antenna was designed as a combination of a loop-coupled DRA and a dipole antenna (Figure 1). In this proof-of-principle study, a similar rectangular DRA (HyQ Research Solutions, PA) to the one in O'Reilly et al.²¹ was used, but with a 7.5-times lower σ value (ε_r = 1070, σ = 0.2 S/m). DRA dimensions were 90 × 44 × 5 mm. For the dipole antenna (length = 250 mm, conductor width = 6 mm, conductor thickness = 36 μm), a “segmented” approach (a similar one to the “bumped” dipole antenna³²) was used: The antenna's feeding point along with the tuning inductors was placed 20 mm above the top of the DRA and physically connected with the antenna's arms positioned below (Figure 1).

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Schematics of dipolectric antennas (top and side view) consisting of a loop-coupled DRA and a dipole antenna: For an 8-channel and a 16-channel array, a rectangular DRA (green) was used, whereas for a 38-channel array it was a cylindrical DRA (blue). To excite a transverse electric mode, a small loop coil (diameter = 18 mm, tuned to 297.2 MHz and matched to 50 Ω) was placed above each DRA. The RF feed of the dipole antenna along with the inductors L_D were located 20 mm above the top layer of the DRA (8- and 16-channel arrays), whereas for a 38-channel array the inductors were positioned in the same plane as the RF feed. DRA, dielectric resonator antenna.

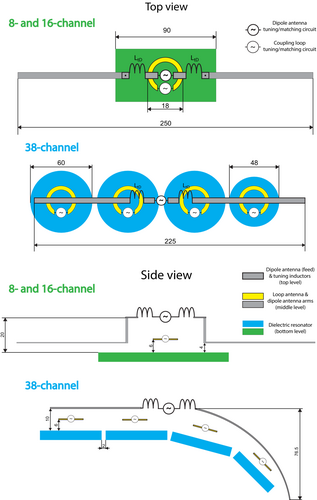
An individual dipolectric antenna was studied in simulations and MR phantom experiments (Figure 2) and was compared to a loop–dipole combined antenna; for this purpose, the DRA was replaced with a rectangular loop coil identical to that in Ref. 21: 90 × 44 mm, copper width = 5 mm. The distance between the loop coil and the dipole element for the loop–dipole antenna was the same as between the bottom surface of the DRA and the dipole element for the dipolectric antenna. The dipole element in the loop–dipole combined antenna was tuned to the Larmor frequency using two inductors L = 51 nH, and three capacitors (C = 7.5 pF) and a single capacitor with variable capacitance were used for the loop element. Several different transmit modes (see section 2.5: Transmit modes) were investigated for the dipolectric antenna. These modes correspond to the following ones for the loop–dipole antenna: loop-only, dipole-only (LD), and loop–dipole (LD). Furthermore, both combined approaches were compared to the “standalone” designs: a rectangular DRA (identical as for the dipolectric antenna), a rectangular loop coil (identical as for the loop–dipole antenna), and a segmented dipole antenna; Additionally, a cylindrical DRA and a circular loop coil of the same outer diameter as the cylindrical DRA (three capacitors with C = 10 pF; copper width = 5 mm) were studied in simulations only. The distance between each element and a spherical phantom was 5 mm.

2.3 8- and 16-channel dipolectric antenna array

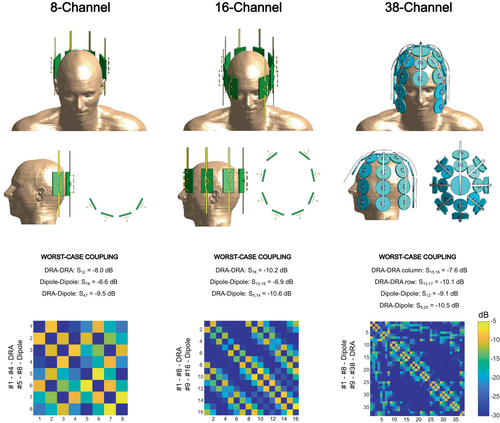
Dipolectric antenna, such as in Figure 1, was studied in two multi-channel array configurations: 8- and 16-channel. Both arrays were loaded with the head of Duke (including the shoulders). The elements of the 8-channel array were positioned at the back of the Duke's head (Figure 3) with the intent to use it for occipital lobe imaging. For the 8-channel array, the distance between the DRA was 20 mm. The elements of the 16-channel array were distributed around the Duke's head: Eight elements at the back of the head were aligned similarly to the 8-channel array, whereas the other eight were distributed such that vision through the array was feasible (Figure 3). The distance between each DRA and the surface of Duke's head for the 8-channel array was 5 mm for the two inner DRA elements and 10 mm for the two outer DRA elements (to enable fitting larger heads). The distance between each DRA and Duke's head for the 16-channel array was kept constant (5 mm). Additionally, a 16-channel dipolectric antenna array was compared with two other array designs: an 8-channel “straight” dipole antenna array (no segmentation) and an 8-channel folded dipole antenna.³³ Each “straight” dipole antenna was positioned at the same distance from the surface of Duke model as distance between the surface of Duke and bottom part of DRAs. Folded dipole antenna was reproduced from the previous work³³: Simulations were performed with a superior RF shield, but no passive elements for decoupling were included.

2.4 38-channel dipolectric antenna array

A different design was used for a 38-channel dipolectric antenna array (Figures 1 and 3). In this case, cylindrical DRAs replaced rectangular DRAs that were used for 8- and 16-channel arrays. Two different cylindrical geometries were used: radius₁ = 30 mm, radius₂ = 24 mm, thickness (both) = 5 mm. A total of 30 DRAs were positioned around the head of human voxel model Duke and distributed in eight columns (7 columns: 4 DRAs per column, and 1 column next to the forehead with 2 DRAs) and in 4 rows (top row: 8 DRAs with radius₂, second row from the top with 8 DRAs with radius₁, and the other two rows with 7 DRAs per row to enable vision through the array). The distance between the bottom of a DRA and the surface of the Duke's head was not constant: For two top rows, the distance was approximately 5 to 15 mm, and for two bottom rows it was approximately 20 to 30 mm. The variations in distance between particular DRAs and Duke's head arise from the fact that the array was designed to fit different head sizes. On the top of the array there was a passive dielectric block (identical to the DRA with radius₁). An identical coupling loop as in Figure 1 was placed above each DRA (6 mm distance from the DRA). Eight dipole antennas were positioned so that each dipole antenna was above a single DRA column. The distance between each dipole antenna and a DRA was 10 mm. Dipole antenna length was identical as the one for 8- and 16-channel arrays, but it was bent to conform to the geometry of the array defined by the DRAs. In receive (RX) mode, all 38 of the elements (dipole antennas and DRAs) were used, whereas in TX, only dipole antennas (driven in a circularly polarized mode) were used.

2.5 Transmit modes

In simulations, 16-channel dipolectric antenna array was driven in four different (TX) modes:

Dipolectric: Both DRAs and dipole antennas actively transmit RF,
Dipole-only: Dipole antennas actively transmit, and DRAs are terminated to 50 Ω,
Dipole-only (DRA-open): Dipole antennas actively transmit, and the DRAs ports are defined as open circuits (this mode is supposed to mimic a scenario in which DRAs elements are detuned during TX and used as receive-only),
DRA-only (DRAs actively transmit, and dipole antennas are terminated to 50 Ω).

16-channel array was used for this purpose because all of the elements are distributed such that a standard circularly polarized mode (45° phase increment per element) could be used. Simulations were benchmarked against: an 8-channel dipole antenna and an 8-channel DRA array. All of the simulations were also performed for the DRAs with higher electrical conductivity (σ = 1.5 S/m), which was reported previously.²¹

Throughout this study, when any dipolectric antenna is included in a receive performance (SNR) comparison, it is always used in “dipolectric mode”; that is, all of the elements are receiving.

2.6 8-channel dipolectric array construction

The 8-channel dipolectric antenna array was constructed, and bench measurements were performed using a 4-channel vector network analyzer (Agilent Keysight Technologies, CA). Each dipole antenna and coupling loop was etched from a 36-μm copper layer on a 1-mm thick FR4 board. Both components (the DRA and the dipole antenna) of the dipolectric antenna were tuned to 297.2 MHz and matched to 50 ohm using standard capacitive tuning/matching networks. Three nonmagnetic variable capacitors were used per one dipolectric antenna: one for the dipole antenna, and the other two for the coupling loop. In the simulations, an inductance L_D (55 nH) was used for tuning of dipole antennas. In the experimental setup, L_D was realized using a hand-wound inductor with an isolated copper wire (0.5 mm-radius), number of turns (n = 3), inner diameter = 9 mm, length = 10 mm, fill factor = 3.13. The constructed 8-channel dipolectric antenna was driven in dipole-only mode. ${\mathrm{B}}_1^{+}$ efficiency was optimized using an algorithm, which was developed earlier in our laboratory.³⁴ For ${\mathrm{B}}_1^{+}$ optimization, a small, hand-drawn circle-like (radius = 15 mm) mask close to the center of Duke's head was defined. The algorithm yielded a phase setting, which was later used in MR experiments: (127°, 85°, 0°, 0°).

2.7 RF interface

An RF interface was built of a two-stage 1:4 power divider (MRI.TOOLS, Berlin, Germany) and 8 TX/RX switches (MR CoilTech, Glasgow, UK). In all of the experiments, all eight DRA/dipole elements were actively receiving the signal (8 TXRX switches were used). To reduce common modes on the cables, bazooka cable traps were built. Bazooka baluns were made using a cylindrical tube of Teflon (length = 5 cm, diameter = 8 mm), including a fixed capacitor (14 pF), covered with copper tape (35 mm) over the coaxial cable (K_02252_D-08; Huber & Suhner, Naenikon, Switzerland). For the 8-channel dipolectric antenna array, two bazooka baluns per element were used.

2.8 Phantom and in vivo experiments

The 8-channel dipolectric antenna array was evaluated in phantom (spherical; radius = 85 mm; ε_r = 77, σ = 1.09 S/m; Siemens Healthineers, Erlangen, Germany) and in vivo experiments. All scans were performed on a Magnetom 7 T/680 mm human scanner (Siemens Healthineers, Erlangen, Germany) with a head-gradient insert (max 80 mT/m and 333 T/m/s). Informed consent was obtained from a subject according to a procedure approved by the local ethics committee. ${\mathrm{B}}_1^{+}$ mapping was performed using SA2RAGE³⁵: TR/TE = 2400/0.78 ms, FOV = 256 × 256 mm, number of slices = 64, slice thickness = 2.5 mm. Anatomical MR images were acquired using a 3D gradient echo (GRE) sequence: (TR/TE = 6.5/2.82 ms, slice thickness = 1 mm, FOV = 256 × 240 mm). In vivo SNR was evaluated using the Kellman approach.³⁶ For this purpose, two separate 2D GRE scans (signal and noise-only) were acquired: TR/TE = 1000/3.37 ms, flip angle (FA) = 48°, matrix = 192 × 192, number of slices = 1 (transversal; isocenter), slice thickness = 1 mm. The noise-only data was acquired using the same parameters but with TX voltage set to 0. The resulting SNR maps were corrected for FA variations by obtaining corresponding ${\mathrm{B}}_1^{+}$ maps (SA2RAGE: TR/TE = 2400/0.78 ms, FOV = 256 × 256 mm, number of slices = 64, slice thickness = 2.5 mm) and applying them in the following equation⁵: $\mathrm{SNR}={\mathrm{SNR}}_{\mathrm{raw}}\frac{1-\cos \alpha \cdot {e}^{- TR/T1}}{\left(1-{e}^{- TR/T1}\right)\cdot \sin \alpha }$ , where α is the spatially varying FA as determined by the SA2RAGE measurement and normalized for the GRE sequence; TR is the repetition time (1 s); and T₁ is the longitudinal relaxation time (assumed 2.3 s for the whole brain).

3 RESULTS

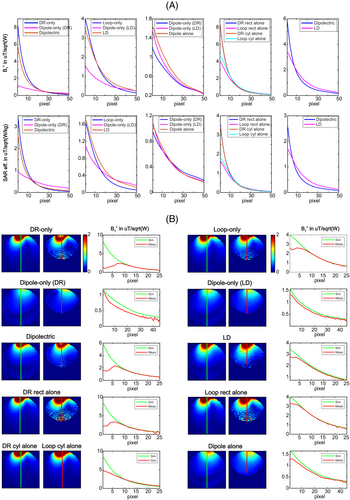
Dipolectric antenna was simulated and ${\mathrm{B}}_1^{+}$ , and SAR efficiency in a spherical phantom for different TX modes (DR-only, dipole-only [DR], and dipolectric) was compared to the those obtained for a loop–dipole combined antenna (loop-only, dipole-only (LD), LD). Furthermore, transmit performance for the “standalone” designs: A rectangular/cylindrical DRA, a rectangular/circular loop coil, and a segmented dipole antenna were evaluated (Figure 2A). The highest ${\mathrm{B}}_1^{+}$ efficiency in the center was found for: LD (0.34 μT/√W, pSAR_10g = 4.03 W/kg), standalone dipole (0.32 μT/√W, pSAR_10g = 2.49 W/kg), and dipole-only (LD) and dipole-only (DR): both 0.30 μT/√W [pSAR_10g = 2.05 and 1.57 W/kg]. These data resulted in the highest SAR efficiency in the center for: dipole-only (DR) (0.24 μT/√[W/kg]), dipole-only (LD) (0.21 μT/√[W/kg]), standalone dipole (0.20 μT/√[W/kg]), and LD (0.17 μT/√[W/kg]) (Figure 2A). The highest ${\mathrm{B}}_1^{+}$ and SAR efficiency in the periphery (up to ∼2 cm depth) was found when all of the RF power was fed to the DRAs, that is for the DR-only mode as well as for the standalone rectangular and cylindrical DRAs. ${\mathrm{B}}_1^{+}$ and SAR efficiency for the DRAs was lower in the center of the phantom when compared to their corresponding loop elements: loop-only versus DR-only (0.20 vs. 0.16 μT/√W; pSAR_10g = 5.99 vs. 5.90 W/kg), rectangular loop coil versus rectangular DRA (0.20 vs. 0.18 μT/√W; pSAR_10g = 5.99 vs. 5.88 W/kg), and cylindrical loop coil versus cylindrical DRA (0.18 vs. 0.15 μT/√W; pSAR_10g = 6.66 vs. 6.22 W/kg). The data obtained from simulations agreed well with the phantom experiments (Figure 2B).

In simulations, 8-, 16-, and 38-channel dipolectric antenna arrays were loaded with the Duke's head, and S-matrices were obtained (Figure 3). For the 8-channel array, coupling between adjacent dipole antennas (dipole–dipole) was between −6.5 and −9.0 dB; coupling between adjacent DRAs (DRA–DRA): from −8.1 to −10.4 dB; coupling between adjacent DRAs and dipole (DRA–dipole) antennas: from −9.6 to −12.5 dB. For the 16-channel array, dipole–dipole coupling was between −7.4 and −12.5 dB; DRA–DRA: from −10.2 to −20.3 dB; DRA-dipole: from −10.7 to −19.3 dB. For the 38-channel array, dipole–dipole coupling was between −9.1 and −11.5 dB; DRA–DRA (in a single column): from −7.6 to −11.1 dB; DRA–DRA (in a single row): from −9.6 to −23.8 dB; DRA–dipole: from −10.5 to −34.5 dB.

To evaluate SNR performance of a dipolectric antenna, 8- and 16-channel arrays (for two different DRA's σ: 1.5 S/m [σ₁] and 0.2 S/m [σ₂]) were compared with their standalone counterparts: DRA and dipole antenna arrays (Figure 4A,B). It was found that 8-channel dipolectric antenna array (σ₂) provided the highest SNR in the center (the 60th pixel along profile V was considered) as well as in peripheral regions of the Duke's head. In the center, it was: 1.12-fold higher versus 4-channel dipole antenna array; 1.19-fold higher versus 8-channel dipolectric antenna array (σ₁); twofold and 3.2-fold higher versus 4-channel DRA array for σ₂ and σ₁, respectively (Figure 4A). Similarly, SNR performance of a 16-channel dipolectric antenna array (σ₂) was superior in the periphery and in the center of Duke's head. In the center, it was 1.23-fold higher versus 16-channel dipolectric antenna array (σ₁); 1.27-fold higher versus 8-channel dipole antenna array; 1.43- and 2.38-fold higher versus 8-channel DRA antenna array for σ₂ and σ₁, respectively (Figure 4B). A peripheral SNR was compared for one point (10th pixel along profile V) in the brain behind the skull. It was found that SNR for 8-channel dipolectric array was between 1.22 and 2.3-fold higher than other designs (Figure 4A), whereas the SNR for 16-channel dipolectric array was between 1.23- and 2.54-fold higher than its counterparts (Figure 4B). Finally, 8- and 16-channel dipolectric antenna arrays (0.2 S/m) were compared with a 38-channel dipolectric antenna array (Figure 4C). For the latter, a substantial SNR gain in the center of Duke's head was found: 1.27-fold and 2.3-fold versus 16- and versus 8-channel array, respectively.

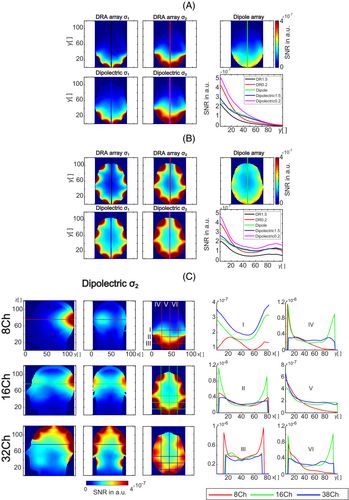
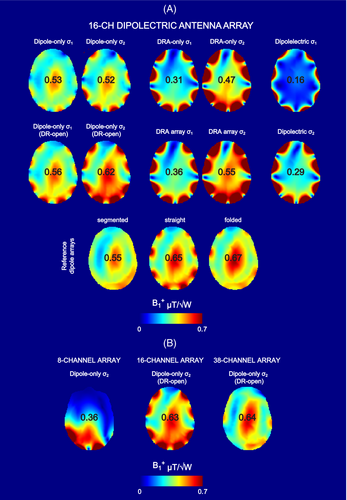
To evaluate transmit performance of a dipolectric antenna, different TX modes were investigated for a 16-channel dipolectric antenna array. For σ₂ (excluding the dipole-only for which a minimal loss was observed), significant ${\mathrm{B}}_1^{+}$ gains compared with σ₁ were observed (Figure 5A). The reference 8-channel folded and 8-channel “straight” dipole antenna array provided the highest peak ${\mathrm{B}}_1^{+}$ efficiency in the center of Duke's head: 0.67 and 0.65 μT/√W, respectively. Dipole-only σ₂ (DR-open) was the mode that provided the third highest peak ${\mathrm{B}}_1^{+}$ efficiency (0.62 μT/√W) when compared with the other ones: dipole-only (0.52 μT/√W), DRA-only (0.47 μT/√W), and dipolectric (0.29 μT/√W). Furthermore, it was found that ${\mathrm{B}}_1^{+}$ efficiency for dipole-only σ₂ (DR-open) was higher when compared with an 8-channel dipole antenna array (0.55 μT/√W), and 8-channel DRA arrays (σ₁ and σ₂): 0.36 and 0.55 μT/√W, respectively. The highest averaged ${\mathrm{B}}_1^{+}$ efficiency across the central axial slice was found for the dipolectric antenna array driven in dipole-only (DR-open) mode: 0.48 ± 0.17 μT/√W. However, the highest ${\mathrm{B}}_1^{+}$ homogeneity was observed for the reference dipole arrays: 8-channel straight (0.44 ± 0.11 μT/√W), folded (0.42 ± 0.09 μT/√W), and segmented dipole antenna array (0.38 ± 0.09 μT/√W). Finally, ${\mathrm{B}}_1^{+}$ efficiency for all three dipolectric antenna arrays—8-, 16-, and 38-channel—were compared, and significant increase for 16- and 38-channel dipolectric antennas arrays versus 8-channel counterpart was observed (Figure 5B). To further investigate transmit performance of the 16-channel dipolectric antenna, SAR efficiency was estimated for different TX modes and summarized in Table 1 (see Figure S1 for the SAR efficiency distribution).

TABLE 1. Transmit performance of different TX modes for the 16-channel dipolectric antenna array: peak

{\mathrm{B}}_1^{+}

in the center of Duke's head, along with

{\mathrm{B}}_1^{+}

homogeneity in the investigated slice. In addition, SAR efficiency in the center of Duke's head and corresponding peak SAR_10g values obtained from simulations.

TX mode	max ${\mathrm{B}}_1^{+}$ center μT/√W	avg ${\mathrm{B}}_1^{+}$ slice μT/√W	SAR efficiency μT/√(W/kg)	pSAR_10g (W/kg)
Dipole array (folded)	0.67	0.42 ± 0.09	0.96	0.49
Dipole array (straight)	0.65	0.44 ± 0.11	0.99	0.43
Dipole-only σ₂ (DR-open)	0.62	0.48 ± 0.17	0.97	0.42
Dipole-only σ₁ (DR-open)	0.56	0.39 ± 0.10	1.00	0.32
Dipole array (segmented)	0.55	0.38 ± 0.09	0.91	0.38
DRA array σ₂	0.55	0.70 ± 0.50	0.55	0.49
Dipole-only σ₁	0.53	0.34 ± 0.08	1.00	0.29
Dipole-only σ₂	0.52	0.37 ± 0.12	0.99	0.28
DRA-only σ₂	0.47	0.62 ± 0.47	0.73	0.43
DRA array σ₁	0.36	0.45 ± 0.33	0.80	0.20
DRA-only σ₁	0.31	0.40 ± 0.31	0.71	0.20
Dipolectric σ₂	0.29	0.48 ± 0.39	0.50	0.33
Dipolectric σ₁	0.16	0.23 ± 0.22	0.40	0.17

Abbreviations: avg, average; DR, dielectric resonator; DRA, dielectric resonator antennas; max, maximum; pSAR, peak specific absorption rate; SAR, specific absorption rate; TX, transmit.

To investigate performance of the constructed 8-channel dipolectric antenna, bench measurements were performed (Figure 6). It was found that for the 8-channel dipolectric antenna array, coupling between particular channels when the array was loaded with a spherical phantom was between −9.8 and −12.0 dB for the adjacent DR elements, between −6.8 and −10.3 dB for the neighboring dipole elements, and within the range of −11.1 and −16.6 dB between the adjacent DR elements and dipole antennas. Additionally, scattering parameter matrix measurements were performed at the bench in three different subjects (Figure S2). The worst-case reflection coefficient was found to be −10.5 dB.

To validate electromagnetic field simulations, ${\mathrm{B}}_1^{+}$ mapping in the spherical phantom was performed for each channel of the 8-channel dipolectric antenna array (Figure 7). The same procedure was conducted for the dipole-only phase setting (used in the final in vivo experiments). A good agreement between the simulations and measurements was observed. The simulation data did not include 1.25 dB power loss per channel, which could explain minor quantitative differences. Dipole-only phase setting (127°, 85°, 0°, 0°) with the maximum SAR_10g of 0.53 W/kg (normalized to 1 W total forward power) was used in the study. An explicit 50% margin of safety was considered to determine the conversion factor (k-factor) for in vivo experiments. There was also an implicit safety margin (25% power loss per channel on the way between the coil plug and the coil). The same TX mode was used to obtain exemplary anatomical images (Figure 8).

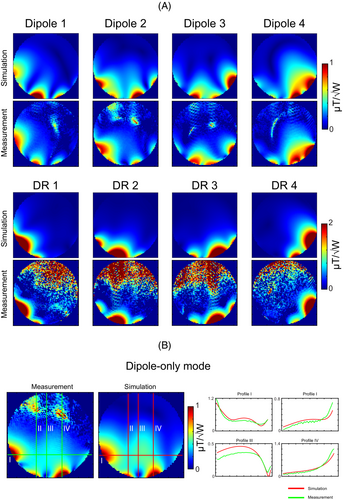
To determine SNR performance of the constructed 8-channel dipolectric array, in vivo experiments were conducted. To evaluate how significantly different types of elements (dipole antennas and DRAs) contribute to the overall SNR in different brain regions, the 2D GRE data were reconstructed, and SNR ratio maps were provided. It was found that in deeper located regions, dipolectric array contributed to an SNR increase of 1.1- to 1.2-fold versus four dipole antennas, and 1.5- to 2-fold versus four DRAs. In the periphery, it was 1.3- to 2.2-fold higher versus four dipole antennas and up to 1.2-fold higher than four DRAs (Figure 9A). The data obtained for the dipolectric array was benchmarked against a commercial head coil with 32 RX channels, and apparent (up to threefold) peripheral SNR gains were observed (Figure 9B) with an SNR ratio map highlighting the sensitivity region of the 8-channel array for which the SNR is greater or equal than the one for 32-channel coil. The SNR for the 8-channel array decreases when approaching the center of the subject's brain: approximately 0% to 40% drop (along the central horizontal profile, Hor2; see Figure 9C) versus the commercial coil. The central SNR, which was evaluated for a circular region of interest in the center of the subject's head (Figure 9C), was higher by 31.9% ± 13.2% for the commercial coil.

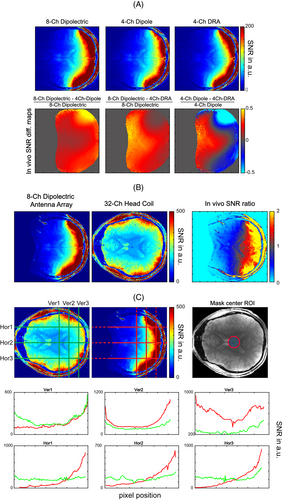
4 DISCUSSION

In this work, a novel RF coil design for ultrahigh-field MRI—dipolectric antenna—was introduced. Dipolectric antenna is based on the principle of mixing a dipole with a loop-coupled DRA: By aligning these two elements together such that electromagnetic fields produced by them are orthogonal to each other, a very low interchannel coupling can be achieved. Using this strategy, high-channel count RF arrays can be developed; here, we investigated dipolectric antennas that were built of 8-, 16-, and 38-channels. Finally, an 8-channel array was designed, constructed, evaluated, and benchmarked against a 1 TX/32 RX Nova coil in in vivo MRI experiments at 7 T.

In simulations, 8-channel and 16-channel dipolectric antenna arrays were loaded with human head (Duke), and the SNR for several types of arrays (dipole array, DRA array [σ₁, σ₂], and dipolectric antenna arrays [σ₁, σ₂]) was evaluated (Figure 4). It was demonstrated that 8-channel dipolectric antenna array can provide considerable SNR gains verus other designs: between 1.12- and 3.2-fold in the center and between 1.22- and 2.3-fold in the periphery. Similar gains were observed when 16-channel dipolectric antenna array was compared with other designs: between 1.23- and 2.38-fold in the center and between 1.16- and 2.1-fold in the periphery. The data showed that substantial SNR gains (center and periphery) are achievable when dipolectric antenna arrays with lower σ values are used.

It was also found that higher number of elements in a dipolectric antenna array can lead to a substantial SNR increase in the center of the Duke's brain. For this purpose, three designs (all σ₂)—8-, 16-, and 38-channel—were compared (Figure 4C). The data indicate that the highest SNR in the center of the brain can be obtained with the 38-channel array: 1.27-fold higher than the one for the 16-channel array, and even up to 2.3-fold higher than for the 8-channel array.

In TX, it was shown that dipole-only σ₂ (DR-open) mode should be considered as the one that is the most suitable for whole-brain MRI. This was possible because for the dipole-only mode, dipole antennas coupled with DRAs (the coupling loops were terminated to 50 ohm in TX), whereas in dipole-only mode (DR-open) that coupling was significantly reduced (an open circuit in each coupling loop during TX), which turned out to be advantageous in TX (Figure S3). This mode provided the highest ${\mathrm{B}}_1^{+}$ efficiency (0.62 μT/√W) and one of the highest SAR efficiencies (0.97 μT/√[W/kg]) in the center of the Duke's head for 16-channel dipolectric antenna array; ${\mathrm{B}}_1^{+}$ efficiency was 1.12-fold higher and SAR efficiency was 1.06-fold higher (pSAR_10g was 16% lower) than the ones for a standalone, 8-channel dipole antenna array (Table 1). However, ${\mathrm{B}}_1^{+}$ homogeneity in the analyzed slice was lower in the case of dipolectric antenna array (0.48 ± 0.17 μT/√W vs. 0.38 ± 0.09 μT/√W). In receive mode, when all elements were active (dipolectric mode), 1.28-fold (center) and 1.7-fold gains were observed versus the dipole antenna array. The data indicate that dipolectric antenna arrays for whole-brain MRI should be driven such that dipole antennas act as TXRX elements and DRAs as receive-only. This approach is expected to maximize TX and RX performance of a dipolectric antenna array.

An experimental SNR was evaluated for the constructed 8-channel dipolectric antenna array and compared with a commercial 32-channel receive-only array, demonstrating significant peripheral SNR gain (even up to threefold) and a lower central SNR by 31.9% ± 13.2%, which was estimated for a small ROI in the center of the brain (Figure 9B,C). In vivo SNR ratio maps revealed a large region in the subject's brain where SNR for the dipolectric array is equal or greater than the one for the Nova coil (even in the vicinity of the center of the brain). We also investigated the SNR contribution from different types of elements in the 8-channel dipolectric antenna array (Figure 9A). We found that the experimental data stays in a very good agreement with our simulation data provided for the same array (Figure 4A), indicating that our SNR calculations are valid and can be used to draw conclusions related to the receive performance of dipolectric antenna arrays with a higher number of channels. Note that the number of receive channels is fourfold lower for the constructed dipolectric antenna array; and for a fair comparison, a 38-channel dipolectric antenna array would be a more suitable candidate. The fact that such an array was not developed yet can be considered a limitation of our study. However, simulations showed that the central SNR for 38-channel array can be even up to 2.3-fold higher than the one for the 8-channel dipolectric array. A simple extrapolation of our results (assuming that central SNR for the 38-channel array is 2.3-fold higher vs. the 8-channel array) would result in a 1.6-fold SNR gain versus the Nova coil. Recently, Avdievich¹⁶ reported a 20% SNR gain in the center of human brain using their 32-channel loop–dipole array versus the Nova coil. This would mean that the 38-channel dipolectric antenna array could provide a 1.4-fold gain versus the Avdievich design. Unfortunately, due to variations in loading (Duke vs. the subject) and losses that were not included in the simulations (cables, etc.), our results cannot be directly extrapolated. If a similar loss factor (25%), as for transmit field mapping for the 8-channel array (Figure 7), is considered for the 38-channel dipolectric antenna array, the SNR gains would be reduced to 1.35- and 1.15-fold versus the Nova head coil and the Avdievich's approach, respectively. To summarize, the observed SNR gains can be considered significant, and sufficiently promising to consider the development of a 38-channel array.

Although ${\mathrm{B}}_1^{+}$ homogeneity estimated for the 16-channel dipolectric antenna array driven in dipole-only (DR-open) mode was lower, it was found to be a more efficient transmitter than the reference 8-channel segmented dipole antenna array (26% higher slice averaged ${\mathrm{B}}_1^{+}$ efficiency and 10% higher SAR efficiency). However, in this work we also simulated an 8-channel folded dipole antenna array,³³ which was proposed earlier for brain MRI at 7 T, showing superior TX performance versus 8 TX/32 RX Nova coil. This comparison is even more relevant because a very similar design was used in a 32-channel loop–dipole combined array for brain MRI at 7 T published very recently.¹⁶ Peak ${\mathrm{B}}_1^{+}$ efficiency (0.67 μT/√W) in the center of Duke's head was found to be 8% higher for the 8-channel dipole antenna as well as ${\mathrm{B}}_1^{+}$ homogeneity (0.42 ± 0.09 μT/√W), but an averaged ${\mathrm{B}}_1^{+}$ efficiency across the central axial slice was higher for the 16-channel dipolectric antenna array driven in dipole-only (DR-open) mode: 0.48 ± 0.17 μT/√W. Due to higher pSAR_10g for the 8-channel folded dipole antenna, SAR efficiency in the center of Duke's head was slightly lower when compared with the 16-channel dipolectric antenna array (0.96 vs. 0.97 μT/√[W/kg]). Also, note that TX performance provided by the folded and “straight” dipole elements was comparable (Figure 5) (Table 1). Nevertheless, the data indicate that dipolectric antenna arrays can be also considered as efficient RF transmitters for brain MRI at 7 T. We also estimated an optimal SNR for the 8-channel folded dipole antenna array (Figure S4) and found that it was outperformed by the 16-channel and 38-channel dipolectric antenna arrays; the data indicate that the 38-channel dipolectric antenna array can provide more than 50% higher central SNR, along with a massive peripheral SNR increase versus the 8-channel folded dipole antenna array. Interestingly, in the case of loop–dipole combination, receive-only loops can have a detrimental effect on TX performance of a dipole antenna array.^{10, 16} In the case of a dipolectric antenna, on the contrary, the DRAs have a beneficial effect on TX performance (what can be tentatively called a “dielectric pad effect”), and this can be considered an advantageous feature of dipolectric antenna.

In all of our simulations, the DRAs with a lower electrical conductivity (σ₂ = 0.2 S/m) provided significantly higher transmit and receive performance when compared with the DRAs with a higher σ₁ = 1.5 S/m. The higher value was reproduced from previous work,²¹ which reported on a very low coupling between array's elements when σ₁ was used. Our data indicate that losses within the DRA, which can be associated with a 7.5-fold higher σ (σ₁), are more dominant than losses due to increased interelement coupling for lower σ (σ₂). This led to substantially diminished performance of DRA arrays and dipolectric antenna arrays (σ₁ vs. σ₂) (Figures 4 and 5).

Dipolectric antenna is a novel approach that can be tailored for a wide range of applications: The geometry of DRA as well as its electrical properties can be also optimized for imaging of different anatomical structures. Furthermore, ceramic materials can be currently developed in an impressively wide range of dielectric constants and electrical conductivities, and this should provide a motivation to explore such structures in the context of novel RF concepts tailored for different B₀ field strengths. Also, note that the dielectric block does not necessarily have to be designed as a homogeneous structure³⁷; mixing dielectric materials of different electrical properties could be considered as promising aspect of the future DRA optimizations. The same applies to the geometry of the dipole antenna and the distribution of the lumped components on the antenna. Preliminary simulations indicate that an optimal DRA ε_r value might be different than the one that was used in this study (Figure S5). The data obtained for a single, loop-fed rectangular DRA, which was loaded with a spherical phantom, indicate that to achieve higher ${\mathrm{B}}_1^{+}$ efficiency in the center, higher ε_r values can be considered. The ε_r value (1070), which was used for the purpose of this study, seems to be a good compromise between high peripheral and central ${\mathrm{B}}_1^{+}$ efficiency. Note, however, that these data do not take into account RF interactions between (non-) neighboring dipole antennas and DRAs, which would be crucial to fully evaluate TX and RX performance of multi-channel dipolectric antenna arrays. This can be addressed by performing more time-consuming simulations involving high-channel count arrays (e.g., 38-channel) with the DRA's ε_r set as a variable. To summarize, further, application-oriented optimizations of the DRA and dipole antenna are not only possible but are expected to bring additional performance gains.

To conclude, we introduced the concept of dipolectric antenna, and we showed that it can be a promising approach for ultrahigh-field MRI applications.

ACKNOWLEDGMENTS

The authors would like to thank Jeremie Clement (currently at Siemens Healthineers) for valuable discussions on multi-channel SNR reconstruction. The authors acknowledge access to the facilities and expertise of the Center for Biomedical Imaging (CIBM), a Swiss research center of excellence founded and supported by Lausanne University Hospital (CHUV), University of Lausanne (UNIL), Ecole polytechnique fédérale de Lausanne (EPFL), University of Geneva (UNIGE), and Geneva University Hospitals (HUG). Open access funding provided by Ecole Polytechnique Federale de Lausanne.

Supporting Information

Filename

Description

mrm29719-sup-0001-Supporting_figures.docxWord 2007 document , 1.7 MB

Figure S1. (A) SAR efficiency obtained for different TX modes of the 16-channel dipolectric antenna array and the reference dipole antenna arrays from Figure 5 (B) SAR efficiency comparison of three different dipolectric antenna arrays (8-, 16-, 38-channel).

Figure S2. An averaged scattering matrix obtained from 3 subjects: #1-#4 – DRA elements, #5-#8 – dipole antennas. Dipole antennas were more sensitive to different loadings, yet the worst case reflection coefficient was found to be −10.5 dB.

Figure S3. Scattering parameter matrices which were obtained for different TX modes for 8- and 16-channel dipolectric antenna arrays.

Figure S4. ${\mathrm{B}}_1^{+}$ efficiency, SAR efficiency and optimal SNR for the selected dipolectric and dipole antenna arrays. The 16- and 38-channel dipolectric antenna arrays driven in Dipole-only (DR-open) mode can provide a comparable ${\mathrm{B}}_1^{+}$ and SAR efficiency when compared with an 8-channel folded dipole antenna array (the only significant difference is the reduced SAR efficiency for the 38-channel array). Optimal SNR calculated for 16- and 38-channel dipolectric antenna arrays was 14% and more than 50% higher in the center than the one for an 8-channel folded dipole antenna array along with a massive SNR gain in the periphery. To put it in a perspective, in the recent work of Avdievich et al., it was experimentally showed that the central SNR contribution from the 8-channel folded dipole antenna array was near 60% what seems to stay in a good agreement with our simulations (the SNR contribution from segmented dipole antennas is lower in the center than the one for the folded dipole antenna array). Note on SNR calculations: Independent of the approach used (Z- or S-matrix domain), the optimum SNR reconstruction is concerned with finding a superposition that maximizes the ratio ${\mathrm{B}}_1^{-}/\sqrt{{\mathrm{P}}_{\mathrm{abs}}}$ where P_abs is the power absorbed in the sample. For the Z-Matrix approach³, this is $\max \left(\left({\mathrm{B}}_{\mathrm{z}}\mathrm{I}\right)/\sqrt{\left({\mathrm{I}}^{\mathrm{H}}\mathrm{ZI}\right)}\right)$ with the (column) coil current vector I and B_z being the row vector of ${\mathrm{B}}_1^{-}$ values produced at the voxel of interest for unit currents. For the S-Matrix approach, this results in calculating $\max =\left(\left({\mathrm{B}}_{\mathrm{s}}\mathrm{a}\right)/\left({\mathrm{a}}^{\mathrm{H}}\left(\mathrm{I}-\mathrm{S}{\mathrm{S}}^{\mathrm{H}}\right)\mathrm{a}\right)\right)$ , where I is the identity matrix, B_s is the ${\mathrm{B}}_1^{-}$ vector created by unit power excitations, and a is the forward power vector used. For a system where only losses in the sample occur, ${\mathrm{Q}}_{\mathrm{abs}}=\mathrm{I}-{\mathrm{SS}}^{\mathrm{H}}$ (note that we have here chosen a normalization where P_fwd = 1). In the real setting, it is not Q_abs which is relevant for power correlation matrix for the noise, but rather all losses, that is,e. Q_abs + Q_lmp + Q_rad = Q_fwd−Q_ref. Here, to calculate the relevant loss matrix for SNR estimation, Q_fwd−Q_ref, i.e. ( $\mathrm{I}-{\mathrm{SS}}^{\mathrm{H}}$ ) was used. ${\mathrm{B}}_1^{-}/{\mathrm{Q}}_{\mathrm{abs}}$ is essentially the maximum possible SNR for a specific array when discounting all losses besides the sample.

Figure S5. (A) Transmit field distribution (central axial slice) in a spherical phantom for different ε_r values of a loop-coupled rectangular DRA (90 × 44 × 5 mm). (B) ${\mathrm{B}}_1^{+}$ and SAR efficiency along the central profiles from (A): in the periphery (pixels 1–10) and in the center of a spherical phantom (pixel 43) assuming loss tangent = 0 for all DRAs. (C) ${\mathrm{B}}_1^{+}$ and SAR efficiency along the central profiles from (A): in the periphery (pixels 1–10) and in the center of a spherical phantom (pixel 43) assuming loss tangent = 0.011 (corresponding to σ = 0.2 S/m for ε_r = 1070) for all DRAs.

Please note: The publisher is not responsible for the content or functionality of any supporting information supplied by the authors. Any queries (other than missing content) should be directed to the corresponding author for the article.

REFERENCES

1Dumoulin SO, Fracasso A, van der Zwaag W, Siero JCW, Petridou N. Ultra-high field MRI: advancing systems neuroscience towards mesoscopic human brain function. Neuroimage. 2018; 168: 345-357.
10.1016/j.neuroimage.2017.01.028
PubMed Web of Science® Google Scholar
2Sclocco R, Beissner F, Bianciardi M, Polimeni JR, Napadow V. Challenges and opportunities for brainstem neuroimaging with ultrahigh field MRI. Neuroimage. 2018; 168: 412-426.
10.1016/j.neuroimage.2017.02.052
PubMed Web of Science® Google Scholar
3Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phased array. Magn Reson Med. 1990; 16: 192-225.
10.1002/mrm.1910160203
CAS PubMed Web of Science® Google Scholar
4von Morze C, Tropp J, Banerjee S, et al. An eight-channel, nonoverlapping phased array coil with capacitive decoupling for parallel MRI at 3 T. Concepts Magn Reson Part B Magn Reson Eng. 2007; 31B: 37-43.
10.1002/cmr.b.20078
Web of Science® Google Scholar
5Shajan G, Kozlov M, Hoffmann J, Turner R, Scheffler K, Pohmann R. A 16-channel dual-row transmit array in combination with a 31-element receive array for human brain imaging at 9.4 T: a transmit and receive array combination for human brain MRI at 9.4 T. Magn Reson Med. 2014; 71: 870-879.
10.1002/mrm.24726
CAS PubMed Web of Science® Google Scholar
6Wiggins GC, Polimeni JR, Potthast A, Schmitt M, Alagappan V, Wald LL. 96-channel receive-only head coil for 3 tesla: design optimization and evaluation. Magn Reson Med. 2009; 62: 754-762.
10.1002/mrm.22028
PubMed Web of Science® Google Scholar
7Uğurbil K, Auerbach E, Moeller S, et al. Brain imaging with improved acceleration and SNR at 7 Tesla obtained with 64-channel receive array. Magn Reson Med. 2019; 82: 495-509.
10.1002/mrm.27695
PubMed Web of Science® Google Scholar
8Raaijmakers AJE, Ipek O, Klomp DWJ, et al. Design of a radiative surface coil array element at 7 T: the single-side adapted dipole antenna. Magn Reson Med. 2011; 66: 1488-1497.
10.1002/mrm.22886
CAS PubMed Web of Science® Google Scholar
9Raaijmakers AJE, Italiaander M, Voogt IJ, et al. The fractionated dipole antenna: a new antenna for body imaging at 7 Tesla. Magn Reson Med. 2016; 75: 1366-1374.
10.1002/mrm.25596
PubMed Web of Science® Google Scholar
10Clément J, Gruetter R, Ipek Ö. A combined 32-channel receive-loops/8-channel transmit-dipoles coil array for whole-brain MR imaging at 7T. Magn Reson Med. 2019; 82: 1229-1241.
10.1002/mrm.27808
PubMed Web of Science® Google Scholar
11Avdievich NI, Solomakha G, Ruhm L, Henning A, Scheffler K. Unshielded bent folded-end dipole 9.4 T human head transceiver array decoupled using modified passive dipoles. Magn Reson Med. 2021; 86: 581-597.
10.1002/mrm.28711
PubMed Web of Science® Google Scholar
12Lagore RL, Moeller S, Zimmermann J, et al. An 8-dipole transceive and 24-loop receive array for non-human primate head imaging at 10.5 T. NMR Biomed. 2021; 34:e4472.
10.1002/nbm.4472
CAS PubMed Web of Science® Google Scholar
13Lattanzi R, Wiggins GC, Zhang B, Duan Q, Brown R, Sodickson DK. Approaching ultimate intrinsic signal-to-noise ratio with loop and dipole antennas. Magn Reson Med. 2018; 79: 1789-1803.
10.1002/mrm.26803
CAS PubMed Web of Science® Google Scholar
14Wiggins GC, Zhang B, Cloos M, et al. Mixing loops and electric dipole antennas for increased sensitivity at 7 Tesla. In Proceedings of the 21st Annual Meeting of IS MRM, Salt Lake City, UT, 2013. Abstract 2737
Google Scholar
15Ertürk MA, Raaijmakers AJE, Adriany G, Uğurbil K, Metzger GJ. A 16-channel combined loop-dipole transceiver array for 7 Tesla body MRI. Magn Reson Med. 2017; 77: 884-894.
10.1002/mrm.26153
PubMed Web of Science® Google Scholar
16Avdievich NI, Nikulin AV, Ruhm L, et al. A 32-element loop/dipole hybrid array for human head imaging at 7 T. Magn Reson Med. 2022; 88: 1912-1926.
10.1002/mrm.29347
PubMed Web of Science® Google Scholar
17Haines K, Smith NB, Webb AG. New high dielectric constant materials for tailoring the B 1 + distribution at high magnetic fields. J Magn Reson. 2010; 203: 323-327.
10.1016/j.jmr.2010.01.003
CAS PubMed Web of Science® Google Scholar
18Teeuwisse WM, Brink WM, Webb AG. Quantitative assessment of the effects of high-permittivity pads in 7 Tesla MRI of the brain: assessment of the effects of high-permittivity pads. Magn Reson Med. 2012; 67: 1285-1293.
10.1002/mrm.23108
PubMed Web of Science® Google Scholar
19Aussenhofer SA, Webb AG. Design and evaluation of a detunable water-based quadrature HEM ₁₁ mode dielectric resonator as a new type of volume coil for high field MRI: design and evaluation of a detunable quadrature HEM ₁₁. Magn Reson Med. 2012; 68: 1325-1331.
10.1002/mrm.24451
PubMed Web of Science® Google Scholar
20Aussenhofer SA, Webb AG. An eight-channel transmit/receive array of TE01 mode high permittivity ceramic resonators for human imaging at 7T. J Magn Reson. 2014; 243: 122-129.
10.1016/j.jmr.2014.04.001
CAS PubMed Web of Science® Google Scholar
21O'Reilly TPA, Ruytenberg T, Webb AG. Modular transmit/receive arrays using very-high permittivity dielectric resonator antennas: very-high permittivity DRA arrays. Magn Reson Med. 2018; 79: 1781-1788.
10.1002/mrm.26784
PubMed Web of Science® Google Scholar
22Wenz D, Dardano T. Multi-feed, loop-dipole combined dielectric resonator antenna arrays for human brain MRI at 7 T. Magn Reson Mater Phys Biol Med. 2023; 36: 227-243.
10.1007/s10334-023-01078-y
CAS Google Scholar
23Haemer GG, Vaidya M, Collins CM, Sodickson DK, Wiggins GC, Lattanzi R. Approaching ultimate intrinsic specific absorption rate in radiofrequency shimming using high-permittivity materials at 7 Tesla. Magn Reson Med. 2018; 80: 391-399.
10.1002/mrm.27022
PubMed Web of Science® Google Scholar
24Lakshmanan K, Carluccio G, Walczyk J, et al. Improved whole-brain SNR with an integrated high-permittivity material in a head array at 7T. Magn Reson Med. 2021; 86: 1167-1174.
10.1002/mrm.28780
CAS PubMed Web of Science® Google Scholar
25Brink WM, Paska J, Dai J, et al. Dielectric enhanced dipoles for MRI—approaching the ideal current pattern. In Proceedings of the 2017 International Conference on Electromagnetics in Advanced Applications (ICEAA), Verona, Italy, 2017. p. 1220-1223.
Google Scholar
26Ipek O, Raaijmakers A, Lagendijk J, Luijten P, van den Berg C. Optimization of the radiative antenna for 7-T magnetic resonance body imaging. Concepts Magn Reson Part B Magn Reson Eng. 2013; 43B: 1-10.
10.1002/cmr.b.21224
Web of Science® Google Scholar
27Wenz D, Gruetter R. Dipole-fed rectangular dielectric resonator antennas for magnetic resonance imaging at 7 T: the impact of quasi-transverse electric modes on transmit field distribution. Front Phys. 2021; 9:675509.
10.3389/fphy.2021.675509
Web of Science® Google Scholar
28Wenz D, Gruetter R. Dielectric resonators and dipole antennas combined: new approach in radio frequency coil design for Ultrahigh Field MRI. In Proceedings of the 28th Annual Meeting of ISMRM, Virtual Conference, 2020. p. 4086.
Google Scholar
29Christ A, Kainz W, Hahn EG, et al. The virtual family-development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys Med Biol. 2010; 55: N23-N38.
10.1088/0031-9155/55/2/N01
PubMed Web of Science® Google Scholar
30Kuehne A, Goluch S, Waxmann P, et al. Power balance and loss mechanism analysis in RF transmit coil arrays. Magn Reson Med. 2015; 74: 1165-1176.
10.1002/mrm.25493
PubMed Web of Science® Google Scholar
31Kühne A. Parallel transmission in MRI-electromagnetic considerations and advances in signal chain hardware. Dissertation. Magdeburg, Germany: Otto-von-Guericke-Universität; 2016.
Google Scholar
32Sadeghi-Tarakameh A, Adriany G, Metzger GJ, et al. Improving radiofrequency power and specific absorption rate management with bumped transmit elements in ultra-high field MRI. Magn Reson Med. 2020; 84: 3485-3493.
10.1002/mrm.28382
PubMed Web of Science® Google Scholar
33Avdievich NI, Solomakha G, Ruhm L, Nikulin AV, Magill AW, Scheffler K. Folded-end dipole transceiver array for human whole-brain imaging at 7 T. NMR Biomed. 2021; 34:e4541.
10.1002/nbm.4541
CAS PubMed Web of Science® Google Scholar
34Clément JD, Gruetter R, Ipek Ö. A human cerebral and cerebellar 8-channel transceive RF dipole coil array at 7T. Magn Reson Med. 2019; 81: 1447-1458.
10.1002/mrm.27476
PubMed Web of Science® Google Scholar
35Eggenschwiler F, Kober T, Magill AW, Gruetter R, Marques JP. SA2RAGE: a new sequence for fast ${\mathrm{B}}_1^{+}$ −mapping. Magn Reson Med. 2012; 67: 1609-1619.
10.1002/mrm.23145
CAS PubMed Web of Science® Google Scholar
36Kellman P, McVeigh ER. Image reconstruction in SNR units: a general method for SNR measurement. Magn Reson Med. 2005; 54: 1439-1447.
10.1002/mrm.20713
CAS PubMed Web of Science® Google Scholar
37Sadeghi-Tarakameh A, Jungst S, Lanagan M, et al. A nine-channel transmit/receive array for spine imaging at 10.5 T: introduction to a nonuniform dielectric substrate antenna. Magn Reson Med. 2022; 87: 2074-2088.
10.1002/mrm.29096
CAS PubMed Web of Science® Google Scholar

Citing Literature

Volume90, Issue4

October 2023

Pages 1695-1712

Dipolectric antenna for high-field MRI