Optimized bias and signal inference in diffusion-weighted image analysis (OBSIDIAN)
Abstract
Purpose
Correction of Rician signal bias in magnitude MR images.
Methods
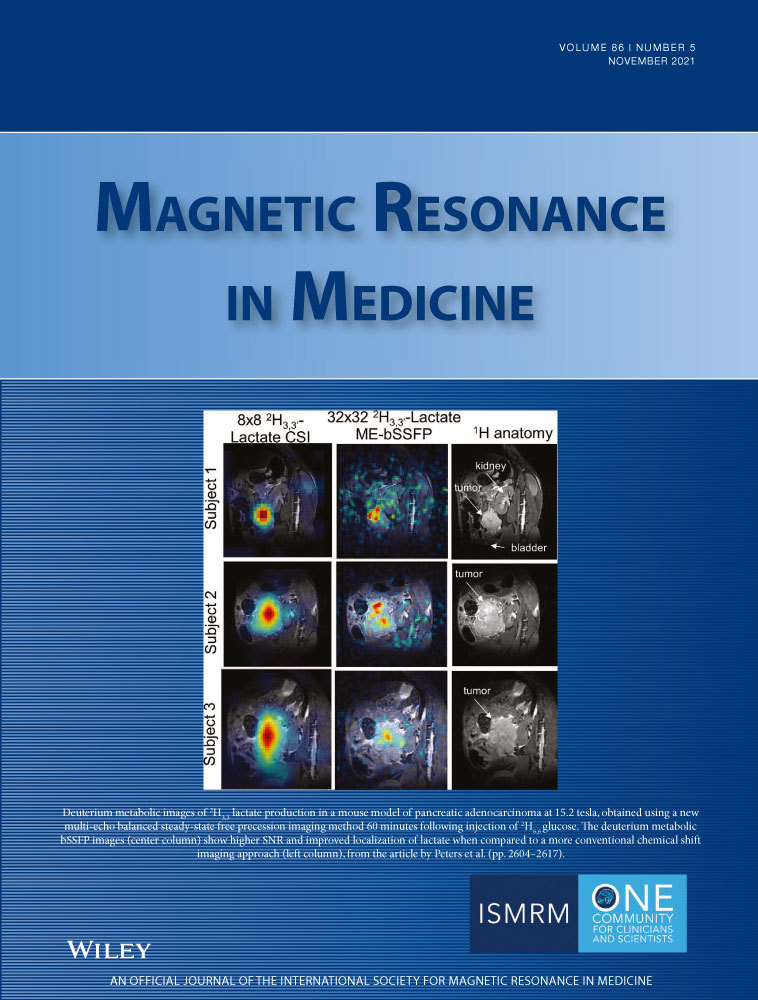
A model-based, iterative fitting procedure is used to simultaneously estimate true signal and underlying Gaussian noise with standard deviation 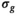 on a pixel-by-pixel basis in magnitude MR images. A precomputed function that relates absolute residuals between measured signals and model fit to
on a pixel-by-pixel basis in magnitude MR images. A precomputed function that relates absolute residuals between measured signals and model fit to 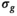 is used to iteratively estimate
is used to iteratively estimate  . The feasibility of the method is evaluated and compared to maximum likelihood estimation (MLE) for diffusion signal decay simulations and diffusion-weighted images of the prostate considering 21 linearly spaced b-values from 0 to 3000 s/mm2. A multidirectional analysis was performed with publically available brain data.
. The feasibility of the method is evaluated and compared to maximum likelihood estimation (MLE) for diffusion signal decay simulations and diffusion-weighted images of the prostate considering 21 linearly spaced b-values from 0 to 3000 s/mm2. A multidirectional analysis was performed with publically available brain data.
Results
Model simulations show that the Rician bias correction algorithm is fast, with an accuracy and precision that is on par to model-based MLE and direct fitting in the case of pure Gaussian noise. Increased accuracy in parameter prediction in a low signal-to-noise ratio (SNR) scenario is ideally achieved by using a composite of multiple signal decays from neighboring voxels as input for the algorithm. For patient data, good agreement with high SNR reference data of diffusion in prostate is achieved.
Conclusions
OBSIDIAN is a novel, alternative, simple to implement approach for rapid Rician bias correction applicable in any case where differences between true signal decay and underlying model function can be considered negligible in comparison to noise. The proposed composite fitting approach permits accurate parameter estimation even in typical clinical scenarios with low SNR, which significantly simplifies comparison of complex diffusion parameters among studies.
1 INTRODUCTION
Sensitizing the MR signal to the thermal motion of the water molecules allows an abundant wealth of information on the tissue micro-structure to be encoded into the MR image.1 Extracting this information often requires advanced modeling, which has been of great interest in the past years.2, 3 While many modeling efforts show promising prospects for improved disease and cancer detection, implementation in clinical routines is hindered by the low signal-to-noise ratio (SNR) available.
The high motion sensitivity of the motion probing gradients, introduces random phase variations. As these phase variations are difficult to account for, phase information is commonly removed by applying the magnitude operator. However, this nonlinear operation alters the noise characteristics with respect to the original complex signal. The resulting signal bias, also known as Rician bias, is particularly severe for low SNR. The Rician bias problem has been known for many decades4, 5 and many methods have been suggested to deal with it.6-16 With the more recent advent of parallel imaging and multicoil acquisition, spatial variability of noise is another obstacle for bias removal. In this context, new methods have been developed that take this complication into account.17-24 Furthermore, in the interest of short acquisition times, it is often not possible to repeat measurements at the same parameter setting. Simultaneous estimation of signal and spatially variable noise without repeated acquisition has been suggested by only a few authors. Some of these methods are outlined in the next paragraph.
Landman et al19 propose an estimation technique using a biophysical model in combination with a regularization procedure for increased robustness. As the estimation technique is based on a Gaussian noise assumption, it is suggested that the noise level for low SNR voxels, where this assumption is violated, is extrapolated from regions with sufficiently high SNR observations. In the work by Veraart et al,21 noise estimation by wavelet decomposition is compared to simultaneous estimation of the signal and the noise field using a maximum likelihood estimation (MLE) approach. A model-driven approach using maximum a posteriori estimation (MAP) was introduced by Poot and Klein.22 In this work, regularization was found to improve the noise field estimation in a similar manner as in the work by Andersson.18 A more recent model-free approach is the MP-PCA method by Veraart et al23, 24 that uses principal component analysis (PCA) in combination with random matrix theory25 to decompose the signal in true signal and noise components.
In the present work, we have implemented a model-driven approach that works on a pixel-by-pixel basis using another parameter dimension, as for example a range of b-values in DWI. Both the signal intensity and the underlying noise standard deviation are estimated simultaneously by iterative model fitting and bias removal with no need for repeated acquisition. The methods presented in the previous paragraph focus on diffusion tensor imaging (DTI). The present method, meanwhile, has been primarily developed for diffusion measurements over a large range of b-values with only a few different encoding directions (usually 3). However, as also shown in this work, there is no fundamental obstacle in applying the method to multidirectional data for fiber architecture exploration. With simulations, the OBSIDIAN method including variants, which also exploit inter-pixel correlation of slowly varying noise, are evaluated and compared to the analysis without bias correction, the analysis of bias-free data, and to the analysis with established methods24, 26 in terms of precision, accuracy and speed of parameter estimation. Findings are confirmed with the analysis of actual image data.
2 THEORY
2.1 Rician distribution
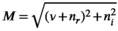 (1)
(1)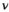 is the signal intensity, and
is the signal intensity, and 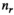 and
and 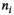 are independent Gaussian random variables with zero mean and standard deviation
are independent Gaussian random variables with zero mean and standard deviation 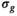 describing the noise in the real and imaginary channel, respectively.4 Without loss of generality, we assume that the signal intensity
describing the noise in the real and imaginary channel, respectively.4 Without loss of generality, we assume that the signal intensity 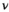 is real. The magnitude signal M follows a Rician distribution with an expectation value
is real. The magnitude signal M follows a Rician distribution with an expectation value 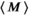 given by:
given by:
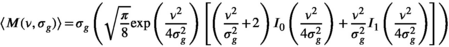 (2)
(2)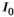 and
and 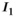 are the zeroth- and first-order modified Bessel function, respectively. In Figure 1A, Rician probability distribution functions are depicted for several
are the zeroth- and first-order modified Bessel function, respectively. In Figure 1A, Rician probability distribution functions are depicted for several  values. Note, that a Rician distribution for
values. Note, that a Rician distribution for  is known as a Rayleigh distribution, whereas for higher
is known as a Rayleigh distribution, whereas for higher  values the distribution converges toward a Gaussian distribution. From the Rician nature of the signal distribution follows that in the case of low
values the distribution converges toward a Gaussian distribution. From the Rician nature of the signal distribution follows that in the case of low  , there is a noticeable difference between the actual signal intensity
, there is a noticeable difference between the actual signal intensity 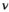 and the expectation value
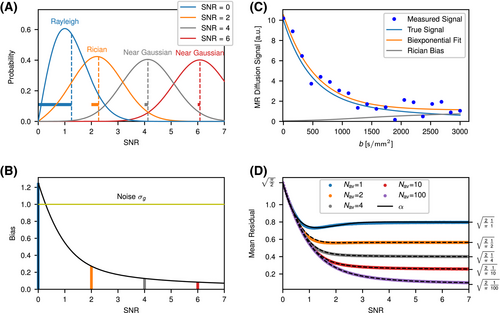
and the expectation value 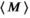 , which is expressed in the Rician bias
, which is expressed in the Rician bias  (Figure 1B):
(Figure 1B):
 (3)
(3)
 values up to around 3 the bias is large enough to cause a visible increase in the mean signal, also known as rectified noise floor. C, Simulated biexponential signal decay for
values up to around 3 the bias is large enough to cause a visible increase in the mean signal, also known as rectified noise floor. C, Simulated biexponential signal decay for  =10 at b=0. A biexponential fit applied to the measured, that is, biased signal, results in increasing overestimation of the diffusion signal with rising diffusion weighting. In this example, Rician bias exceeds the true signal at the highest diffusion weighting. D, Numerically determined mean absolute residual in function of SNR for different amounts of averaging. Thin lines represent approximate analytical functions
=10 at b=0. A biexponential fit applied to the measured, that is, biased signal, results in increasing overestimation of the diffusion signal with rising diffusion weighting. In this example, Rician bias exceeds the true signal at the highest diffusion weighting. D, Numerically determined mean absolute residual in function of SNR for different amounts of averaging. Thin lines represent approximate analytical functions 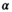 of the mean absolute residual for the respective amount of averaging
of the mean absolute residual for the respective amount of averagingMany common operations on the complex raw signal, as for example Fourier transform, preserve its Gaussian noise characteristics. This is also true for various commonly employed reconstructions filters, as for example the Hamming filter.27 Parallel imaging techniques also preserve the Gaussian noise characteristics, provided the raw signal from various radio-frequency coils is combined linearly.
3 METHODS
3.1 OBSIDIAN algorithm
The idea behind the OBSIDIAN algorithm is to use a series of data points 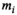 (
(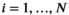 ) measured at parameter settings
) measured at parameter settings 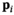 to estimate the true signals
to estimate the true signals 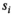 and the Gaussian noise standard deviation
and the Gaussian noise standard deviation 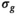 by iteratively fitting and correcting for Rician bias using an assumed underlying model for the data. In the case of diffusion-weighted imaging (DWI), the data points
by iteratively fitting and correcting for Rician bias using an assumed underlying model for the data. In the case of diffusion-weighted imaging (DWI), the data points 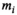 could be taken at different b-values (
could be taken at different b-values (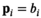 ) and the model of choice could for example be a biexponential model. The source code is publically available at https://github.com/dMRI-GU/OBSIDIAN.
) and the model of choice could for example be a biexponential model. The source code is publically available at https://github.com/dMRI-GU/OBSIDIAN.
3.1.1 Algorithm workflow
 ) and an iterative part (cycle
) and an iterative part (cycle  ). In the initial part a first estimate
). In the initial part a first estimate 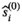 of the true signal
of the true signal 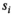 is obtained by fitting the model function
is obtained by fitting the model function 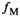 to the data points
to the data points 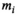 yielding the estimates
yielding the estimates 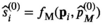 , where
, where 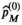 are the free parameters of the model that result from the fit. The estimation of
are the free parameters of the model that result from the fit. The estimation of 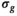 is given by the Root Mean Square Error (
is given by the Root Mean Square Error (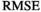 ) of the fit:
) of the fit:
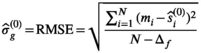 (4)
(4) is the the number of free fit parameter in the model. For linear regression,
is the the number of free fit parameter in the model. For linear regression, 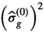 is an unbiased estimator for
is an unbiased estimator for  under certain conditions (see 28, chapter 3]). For nonlinear regression as used here, this relation is more complicated and often discussed in the context of the degrees of freedom of the fitting procedure.29, 30 In the present work, however, Equation (4) has proven to be useful for an initial estimate of
under certain conditions (see 28, chapter 3]). For nonlinear regression as used here, this relation is more complicated and often discussed in the context of the degrees of freedom of the fitting procedure.29, 30 In the present work, however, Equation (4) has proven to be useful for an initial estimate of 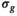 .
.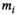 given by
given by
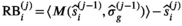 (5)
(5)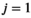 , which is the first cycle of the iterative part,
, which is the first cycle of the iterative part,  is used as a guess for the true signal intensity at each data point
is used as a guess for the true signal intensity at each data point 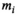 and
and 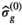 as a guess for
as a guess for 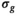 in order to calculate the Rician bias as given by Equation (3). Subsequently, the Rician bias is subtracted from the measured signal
in order to calculate the Rician bias as given by Equation (3). Subsequently, the Rician bias is subtracted from the measured signal 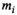 and a bias-corrected signal is obtained
and a bias-corrected signal is obtained
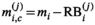 (6)
(6)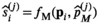 (7)
(7)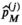 are the free parameters of the model from the fit in cycle j. Finally, as described in the next subsection, a new estimate
are the free parameters of the model from the fit in cycle j. Finally, as described in the next subsection, a new estimate 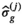 for of the underlying Gaussian standard deviation is calculated by considering the absolute residuals. The iteration is continued until one of the two following break criteria is meet at cycle
for of the underlying Gaussian standard deviation is calculated by considering the absolute residuals. The iteration is continued until one of the two following break criteria is meet at cycle 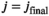 :
:
- the cycle number j exceeds a certain value:
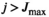 (8)
(8)- the absolute relative change in
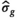 for two subsequent cycles is smaller than a given value
for two subsequent cycles is smaller than a given value 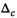 , ie,
, ie,
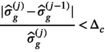 (9)
(9)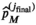 , while the final estimate for
, while the final estimate for 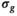 is given by
is given by 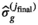 . A flowchart of the algorithm is presented in Figure 2.
. A flowchart of the algorithm is presented in Figure 2.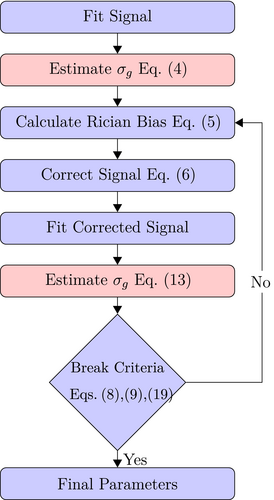
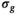 the
the 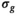 estimation steps (red background) are not applicable. Break criteria are Equation (8) and either Equation (9) (
estimation steps (red background) are not applicable. Break criteria are Equation (8) and either Equation (9) (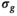 unknown) or Equation (19) (
unknown) or Equation (19) (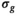 known). Choosing the absolute residuals for the second and subsequent estimations of
known). Choosing the absolute residuals for the second and subsequent estimations of 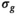 according Equation (13), as explained in Section 3.1.2, is only one of many options. Taking, for example, the square of the residuals could lead to simpler expressions for the
according Equation (13), as explained in Section 3.1.2, is only one of many options. Taking, for example, the square of the residuals could lead to simpler expressions for the 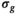 estimation
estimation3.1.2 Estimating 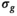 by absolute residuals
by absolute residuals
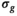 is estimated via the absolute value of the residuals
is estimated via the absolute value of the residuals
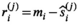 (10)
(10) can be expressed as the product of
can be expressed as the product of 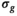 and a function
and a function 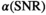 , which only depends on
, which only depends on  :
:
 (11)
(11)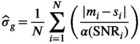 (12)
(12)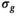 . As such, Equation (12) is not practical, since the calculation of the
. As such, Equation (12) is not practical, since the calculation of the  requires the knowledge of
requires the knowledge of 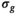 , that is, the quantity to be estimated. However, in the iterative process, in each cycle j,
, that is, the quantity to be estimated. However, in the iterative process, in each cycle j, 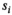 and
and 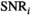 are approximated by
are approximated by 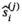 and
and 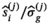 , respectively. Moreover, it was found that the divisor 1/N in Equation (12) has to be modified to
, respectively. Moreover, it was found that the divisor 1/N in Equation (12) has to be modified to 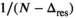 in the same spirit as for the RMSE (see Equation 4) due to the effective degrees of freedom from the fitting process. As shown later,
in the same spirit as for the RMSE (see Equation 4) due to the effective degrees of freedom from the fitting process. As shown later, 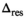 , the delta degrees of freedom, is smaller than the actual number of free parameters in the model and has to be determined for each model individually. Without this correction, the
, the delta degrees of freedom, is smaller than the actual number of free parameters in the model and has to be determined for each model individually. Without this correction, the 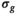 estimation would be biased. Finally, one arrives at the following equation for the sigma estimation in cycle j:
estimation would be biased. Finally, one arrives at the following equation for the sigma estimation in cycle j:
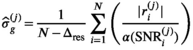 (13)
(13)3.1.3 Derivation of the mean absolute residual function 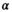
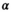 (see Equation 3 in Supporting Information) is difficult and extensive literature search did not reveal any prior report about such function. For
(see Equation 3 in Supporting Information) is difficult and extensive literature search did not reveal any prior report about such function. For 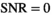 ,
, 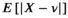 (Equation 11) is identical to the mean of a Rayleigh distribution, hence,
(Equation 11) is identical to the mean of a Rayleigh distribution, hence, 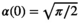 . For
. For 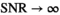 ,
, 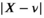 converges toward a folded normal distribution meaning that
converges toward a folded normal distribution meaning that 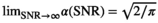 . In order to estimate
. In order to estimate 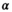 between these two extreme cases,
between these two extreme cases, 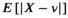 was derived numerically for different
was derived numerically for different  values and
values and  (see Figure 1D). An analytical expression for
(see Figure 1D). An analytical expression for 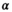 is more practical with respect to the algorithm, as any positive real number can be expected as input. As evident in the function plot of Figure 1D,
is more practical with respect to the algorithm, as any positive real number can be expected as input. As evident in the function plot of Figure 1D,
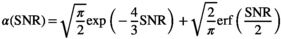 (14)
(14) independent and identically distributed Rician random variables
independent and identically distributed Rician random variables 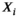 , that is,
, that is,
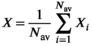 (15)
(15)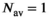 case formulated in Equation (11)
case formulated in Equation (11)
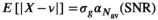 (16)
(16)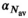 indicating the number of averages. In a similar manner as for
indicating the number of averages. In a similar manner as for  ,
, 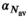 was determined numerically different
was determined numerically different 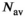 values. The results for
values. The results for 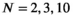 and 100 are presented in Figure 1D. Again, the limiting cases,
and 100 are presented in Figure 1D. Again, the limiting cases, 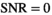 and
and 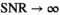 , can be calculated analytically, giving
, can be calculated analytically, giving 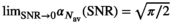 and
and 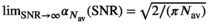 .
.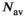 , in accordance with the central limit theorem, X converges toward a Gaussian random variable with a mean given by Equation (2) and a standard deviation of
, in accordance with the central limit theorem, X converges toward a Gaussian random variable with a mean given by Equation (2) and a standard deviation of 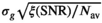 , with
, with 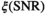 being the correction factor as defined by17:
being the correction factor as defined by17:
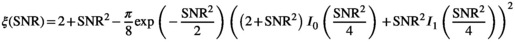 (17)
(17)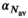 :
:
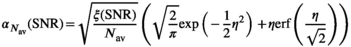 (18)
(18)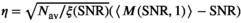 . As can be seen in Figure 1D there is already good agreement for
. As can be seen in Figure 1D there is already good agreement for  and
and 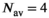 , while the curve matches perfectly for
, while the curve matches perfectly for 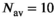 and
and 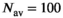 .
.3.1.4 OBSIDIAN with known 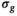
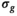 is known a priori a simplified version of the algorithm can be used, where the
is known a priori a simplified version of the algorithm can be used, where the 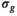 estimation steps are removed (see Figure 2). The only further difference to the full OBSIDIAN algorithm is a different break criterion. Instead of monitoring relative changes in the estimated
estimation steps are removed (see Figure 2). The only further difference to the full OBSIDIAN algorithm is a different break criterion. Instead of monitoring relative changes in the estimated 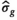 (see Equation 9), the decision is based on relative changes in the signal value at one or multiple values in
(see Equation 9), the decision is based on relative changes in the signal value at one or multiple values in 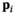 with indices in
with indices in 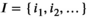 :
:
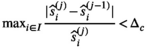 (19)
(19)3.2 Models and fitting algorithm
The following 1D signal decay models are considered in this work: biexponential, kurtosis, gamma distribution, and stretched exponential. The models have been discussed extensively in literature3, 31-34 and are briefly described in the Supporting Information Section 2 along with a DTI approach for multidirectional data.
Nonlinear least-squares fitting was performed using the “trf” (Trust Region Reflective algorithm) method in the optimize.curve_fit SciPy package. A summary of all starting parameters and bounds is given in Supporting Information Table S1.
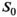 . In the case of the biexponential model, the components of the modified, 3D fitting function
. In the case of the biexponential model, the components of the modified, 3D fitting function 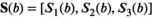 are given by:
are given by:
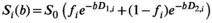 (20)
(20)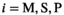 being the direction index.
being the direction index.3.3 Algorithm implementation
 values below 20. For higher values, the following approximation is used35 to avoid numerical overflow for the Bessel functions:
values below 20. For higher values, the following approximation is used35 to avoid numerical overflow for the Bessel functions:
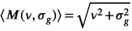 (21)
(21)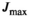 is always set to 100 in this work.
is always set to 100 in this work. 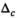 was 0.02 if not stated otherwise.
was 0.02 if not stated otherwise.A description of the implementation of the alternative MLE and MP-PCA methods is found in the Supporting Information Section 3. For MLE, prior knowledge about the statistical distribution of the noise is included in the parameter optimization procedure. MP-PCA is a more recent approach, that unlike OBSIDIAN and MLE can correct for Rician bias without the need for a model. Due to their widespread use in the MRI community, both methods are interesting for comparison.
3.4 Simulations
3.4.1 Simulation of tissue water diffusion signal
As a simulation model, a biexponential model with two tissue types was considered, that is, one labeled “normal” for normal prostate tissue and one labeled “cancer” for cancerous prostate tissue. Model parameters were selected in approximate accordance to literature reference values without the influence of intravoxel incoherent motion (IVIM).3 For both tissue types the fast diffusion parameter 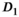 was set to the same value of 2.2 μm2/ms. Meanwhile, simulation values for the slow diffusion parameter
was set to the same value of 2.2 μm2/ms. Meanwhile, simulation values for the slow diffusion parameter 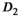 and fast signal fraction f for normal and cancer were different, that is,
and fast signal fraction f for normal and cancer were different, that is, 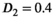 μm2/ms and
μm2/ms and 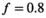 for normal tissue and
for normal tissue and 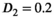 μm2/ms and
μm2/ms and 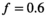 for cancerous tissue. The range of SNR values evaluated was between 5 and 100. For all simulations, data consisted of signals at
for cancerous tissue. The range of SNR values evaluated was between 5 and 100. For all simulations, data consisted of signals at 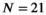 b-values, linearly spaced in the range of 0 to
b-values, linearly spaced in the range of 0 to 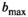 . If not stated otherwise,
. If not stated otherwise, 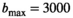 s/mm2, in agreement with the patient scan protocol described in Section 3.6.
s/mm2, in agreement with the patient scan protocol described in Section 3.6.
Rician noise was added to the model data. As Gaussian distributed data does not have a bias, it can be regarded as a benchmark for the bias correction algorithm. Consequently, data sets were also generated with added Gaussian noise. Without loss of generality, 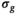 was set to 1 for all simulations, meaning that
was set to 1 for all simulations, meaning that 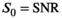 .
.
3.4.2 Comparison of model functions
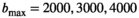 , and 5000 s/mm2 with the normal tissue as base model. Gaussian noise was added to generate decays with
, and 5000 s/mm2 with the normal tissue as base model. Gaussian noise was added to generate decays with 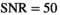 . Direct fitting of each decay profile with the model function f(b, p), resulted in parameters sets
. Direct fitting of each decay profile with the model function f(b, p), resulted in parameters sets 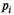 and a mean fitted signal
and a mean fitted signal
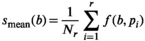 (22)
(22) from the true signal
from the true signal 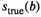 , one can estimate at which
, one can estimate at which  value,
value,  , differences between the actual biexponential model and the assumed model become significant. A significant limit can be considered when
, differences between the actual biexponential model and the assumed model become significant. A significant limit can be considered when 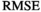 equals the
equals the 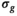 of the underlying Gaussian noise distribution, as expressed in the following equation:
of the underlying Gaussian noise distribution, as expressed in the following equation:
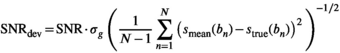 (23)
(23)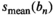 with respect to the
with respect to the  is assumed.
is assumed.3.4.3 Determination of 
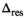 for the absolute residual expectation value was determined numerically with model parameters as listed in Table 1. The analysis was performed at
for the absolute residual expectation value was determined numerically with model parameters as listed in Table 1. The analysis was performed at 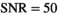 . From the noisy signal decay profiles, the Rician bias (Equation 3) was subtracted and then a direct function fit was applied to each profile. The resulting fit parameters were used to calculate the signal estimates
. From the noisy signal decay profiles, the Rician bias (Equation 3) was subtracted and then a direct function fit was applied to each profile. The resulting fit parameters were used to calculate the signal estimates 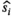 . An estimation of
. An estimation of 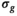 was then performed using Equation (13), however, with
was then performed using Equation (13), however, with 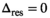 . The mean of the estimated sigma
. The mean of the estimated sigma 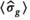 permitted the determination of
permitted the determination of 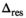 as follows:
as follows:
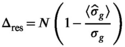 (24)
(24)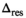 with encoding along a single (1D) and three (3D) directions
with encoding along a single (1D) and three (3D) directions| Function | Parameter | Value | 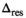 1D 1D |
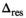 3D 3D |
|---|---|---|---|---|
| Biexponential |
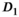
|
2.2 | 2.3 (4) | 5.4 (10) |
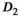
|
0.4 | |||
| f | 0.8 | |||
| Kurtosis |
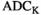
|
2.2 | 1.7 (3) | 3.7 (7) |
| K | 0.5 | |||
| Gamma distribution |
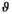
|
2.4 | 1.8 (3) | 3.7 (7) |
| k | 1.2 | |||
| Stretched exponential |
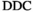
|
1.5 | 1.9 (3) | 3.9 (7) |
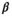
|
.7 |
-
Notes: The actual number of free parameters is given in parentheses. The parameters for the biexponential model are identical to the normal-tissue model. The parameters for the other models are chosen to generate signal decays that closely resemble the biexponential reference model. Diffusion coefficients and
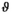 are in μm2/ms.
are in μm2/ms.
3.4.4 OBSIDIAN performance testing
The different scenarios tested are described in Table 2. Denoising with the MP-PCA method is described in Section 6 of the Supporting Information.
| Method | Noise distribution | Realizations |
|---|---|---|
| OBSIDIAN | Rician | 106 |
| Direct Fit | Rician | 104 |
| Gauss Direct Fit | Gaussian | 104 |
| OBSIDIAN K Composite | Rician | 105/K |
| Direct Fit K Composite | Rician | 106/K |
| Gauss Direct Fit K Composite | Gaussian | 106/K |
| OBSIDIAN K Average | Rician | 106/K |
| MLE | Rician | 104 |
| MLE K Composite | Rician | 105/K |
-
Notes: For the approaches “Direct Fit” and “Gauss Direct Fit,” fitting was performed without bias correction. The
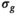 estimation in these cases was done using the RMSE formula given in Equation (4). For the approach “OBSIDIAN K Composite,” a two-step procedure resembling the patient data analysis explained in Section 3.6 was used. In the first step, K realizations were fitted individually with the OBISIDIAN method resulting in K estimates for
estimation in these cases was done using the RMSE formula given in Equation (4). For the approach “OBSIDIAN K Composite,” a two-step procedure resembling the patient data analysis explained in Section 3.6 was used. In the first step, K realizations were fitted individually with the OBISIDIAN method resulting in K estimates for 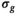 . In the second step, the same K realizations collectively served as input for OBSIDIAN with known
. In the second step, the same K realizations collectively served as input for OBSIDIAN with known 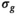 , whereby the fixed
, whereby the fixed 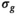 was the average from the first step. This means that for each b-value there were a total of K input signal values. For “MLE K Composite,” the procedure was equivalent, however, based on the corresponding MLE algorithm. The approaches “Direct Fit K Composite” and “Gauss Direct Fit K Composite,” K realizations underwent collectively a direct fit. For the approach “OBSIDIAN K Average,” K realizations were averaged prior to applying the OBSIDIAN algorithm. This means that for each b-value there was one averaged input signal value and the OBSIDIAN algorithm was applied with the mean absolute residual function
was the average from the first step. This means that for each b-value there were a total of K input signal values. For “MLE K Composite,” the procedure was equivalent, however, based on the corresponding MLE algorithm. The approaches “Direct Fit K Composite” and “Gauss Direct Fit K Composite,” K realizations underwent collectively a direct fit. For the approach “OBSIDIAN K Average,” K realizations were averaged prior to applying the OBSIDIAN algorithm. This means that for each b-value there was one averaged input signal value and the OBSIDIAN algorithm was applied with the mean absolute residual function 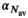 , where
, where 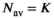 .
. 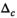 was set to 0.002 for the second step in “OBSIDIAN K Composite”,
was set to 0.002 for the second step in “OBSIDIAN K Composite”, 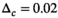 in all other cases. OBSIDIAN and MLE refer to the direct application of the OBSIDIAN and the comparative MLE algorithm to each of the n realizations, respectively.
in all other cases. OBSIDIAN and MLE refer to the direct application of the OBSIDIAN and the comparative MLE algorithm to each of the n realizations, respectively.
3.5 MRI acquisition of multi-b data in patients
A clinical multiparametric prostate imaging protocol was performed on a Philips Ingenia CX 3T equipped with a 32 element dS Torso 3.0T coil. In addition, diffusion-weighted images for a wide range of b-values were obtained with the standard single-shot echo-planar imaging sequence. Scan parameters were as follows: two-fold multicoil acceleration, 280 mm  233 mm field-of-view,
233 mm field-of-view, 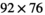 acquisition matrix,
acquisition matrix, 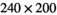 reconstruction matrix, 10% of slice thickness for inter-slice spacing, 21 evenly spaced b-values ranging from 0 to 3000 s/mm2, 3 encoding directions (M, P, and S),
reconstruction matrix, 10% of slice thickness for inter-slice spacing, 21 evenly spaced b-values ranging from 0 to 3000 s/mm2, 3 encoding directions (M, P, and S), 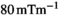 gradient strength (“enhanced” mode),
gradient strength (“enhanced” mode), 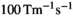 slew rate,
slew rate, 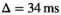 ,
, 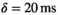 , 70 ms TE (70% partial Fourier encoding), no averaging. To gain better insight into the effect of noise, both a scan with 3 mm (4 minutes scan time, 3860 ms TR) and 6 mm (2 minutes scan time, 1920 ms TR) slice thickness was performed. In the internal postprocessing, a Riesz filter was applied, without influence on the Rician nature of the signal according to Dietrich et al.27
, 70 ms TE (70% partial Fourier encoding), no averaging. To gain better insight into the effect of noise, both a scan with 3 mm (4 minutes scan time, 3860 ms TR) and 6 mm (2 minutes scan time, 1920 ms TR) slice thickness was performed. In the internal postprocessing, a Riesz filter was applied, without influence on the Rician nature of the signal according to Dietrich et al.27
Details about the patient population, selected from the Göteborg-2 screening trial (G2),36 and region of interest selection are found in the Supporting Information. The G2 study has been approved by the Swedish ethical board.
3.6 Multi-b data analysis
Images reconstructed with the vendor-installed scanner software were transferred for off-line post-processing. To avoid signal decays caused by blood perfusion, the lowest b-value, that is, 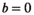 was excluded from subsequent fitting. Fits were performed pixel-wise, except for the approach termed “Direct Fit ROI Composite,” where instead all signal decay profiles within the ROI were collectively fitted.
was excluded from subsequent fitting. Fits were performed pixel-wise, except for the approach termed “Direct Fit ROI Composite,” where instead all signal decay profiles within the ROI were collectively fitted.
The following steps only applied to the processing with the OBSIDIAN and MLE algorithm, but not to any of the direct fit approaches. A 2D Gaussian filter with a standard deviation of 12 pixels was used to low-pass filter the resulting 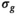 -maps. This removed evident uncertainties in the estimation of
-maps. This removed evident uncertainties in the estimation of 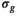 and enforced a more realistic spatial dependence of
and enforced a more realistic spatial dependence of 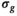 , such as it can be expected with a coil array. Subsequently, another fit was performed with a fixed value for
, such as it can be expected with a coil array. Subsequently, another fit was performed with a fixed value for 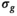 . For the approaches termed “OBSIDIAN” and “MLE,” this was done pixel-wise with the
. For the approaches termed “OBSIDIAN” and “MLE,” this was done pixel-wise with the 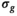 value at the corresponding location of the low-pass filtered
value at the corresponding location of the low-pass filtered  map. Meanwhile, for the approaches termed “OBSIDIAN ROI Composite” and “MLE ROI Composite,” the fixed
map. Meanwhile, for the approaches termed “OBSIDIAN ROI Composite” and “MLE ROI Composite,” the fixed 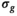 was based on an ROI average, generally spanning over multiple slices, of the low-pass filtered
was based on an ROI average, generally spanning over multiple slices, of the low-pass filtered 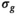 maps. Subsequently, all signal decay profiles within this ROI were collectively fitted using bias correction based on this fixed
maps. Subsequently, all signal decay profiles within this ROI were collectively fitted using bias correction based on this fixed 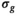 with
with 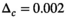 .
.
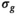 maps. For all approaches, the 3 diffusion encoding direction-dependent values of each model parameter were averaged and used as final result. Moreover, average
maps. For all approaches, the 3 diffusion encoding direction-dependent values of each model parameter were averaged and used as final result. Moreover, average  was computed as mean
was computed as mean 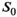 over mean
over mean 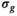 . The effective SNR, that is,
. The effective SNR, that is, 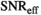 over the ROI is given by:
over the ROI is given by:
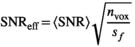 (25)
(25)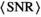 is the average SNR over the ROI,
is the average SNR over the ROI, 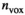 the number of voxels in the ROI and
the number of voxels in the ROI and 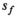 the ratio between the reconstructed and acquisition voxel volume, which equals
the ratio between the reconstructed and acquisition voxel volume, which equals 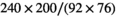 for the present patient study.
for the present patient study.Finally, the MP-PCA algorithm was evaluated with identical parameter settings as applied in the simulations.
3.7 Multidirectional data
For several combinations of two nonzero b-shells of the publically available MASSIVE brain dataset,37 OBSIDIAN with a single tensor and dual tensor model (see also Supporting Information 9) was applied to each pixel of a small region in the central section of the corpus callosum. The shells consisted of 250, 500, 500, 500, and 600 gradient orientations with a b-value of 500, 1000, 2000, 3000, and 4000 s/mm2, respectively. Only EPI phase encoding in the anterior-posterior (AP) direction was considered.
4 RESULTS
4.1 Model function comparison
The OBSIDIAN approach relies on model functions that describe the signal decay sufficiently well, so that observed residuals are predominantly noise related. In Figure 3, the average difference between fits with the different model functions and the true normal-tissue model, 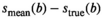 , is shown for different
, is shown for different 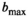 values. Trivially, the biexponential model function attains ideally a perfect fit to the true model data. For the kurtosis model function (Equation 6), there are only minor deviations for the b-value range 0 to 2000 s/mm2. However, deviations increase markedly with increasing b-value range. For the gamma distribution model function (Equation 8), deviations remain minor over all investigated b-value ranges. A similar behavior is observed for the stretched exponential model function (Equation 7), albeit with larger deviations. Finally, the monoexponential model function (Equation 9) shows the largest deviations of all model functions. The values for the signal-to-noise ratio
values. Trivially, the biexponential model function attains ideally a perfect fit to the true model data. For the kurtosis model function (Equation 6), there are only minor deviations for the b-value range 0 to 2000 s/mm2. However, deviations increase markedly with increasing b-value range. For the gamma distribution model function (Equation 8), deviations remain minor over all investigated b-value ranges. A similar behavior is observed for the stretched exponential model function (Equation 7), albeit with larger deviations. Finally, the monoexponential model function (Equation 9) shows the largest deviations of all model functions. The values for the signal-to-noise ratio 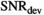 at which differences between the models become significant are shown in Table 3.
at which differences between the models become significant are shown in Table 3.
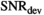 ) for different
) for different 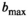 at which the mean residual between the mean of the fitted model and the true biexponential model equals noise
at which the mean residual between the mean of the fitted model and the true biexponential model equals noise 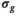 (see Equation 23)
(see Equation 23)Model   (s/mm2) (s/mm2) |
2000 | 3000 | 4000 | 5000 |
|---|---|---|---|---|
| Kurtosis | 870 | 185 | 96 | 69 |
| Gamma distribution | 183 | 136 | 134 | 146 |
| Stretched exponential | 71 | 55 | 53 | 56 |
| Monoexponential | 34 | 27 | 26 | 26 |
-
Notes: For the kurtosis model, an SNR value in the vicinity of 1000 is necessary to reach this limit at
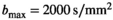 . For higher
. For higher 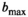 , the effect of truncation to a second-order polynomial in b is evident and accordingly values
, the effect of truncation to a second-order polynomial in b is evident and accordingly values 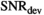 are considerably lower. For the gamma distribution model,
are considerably lower. For the gamma distribution model, 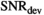 values are around 150 and for the stretched exponential model around 60. As expected, the monoexponential model is the easiest to distinguish from the biexponential model with
values are around 150 and for the stretched exponential model around 60. As expected, the monoexponential model is the easiest to distinguish from the biexponential model with  values of around 30.
values of around 30.
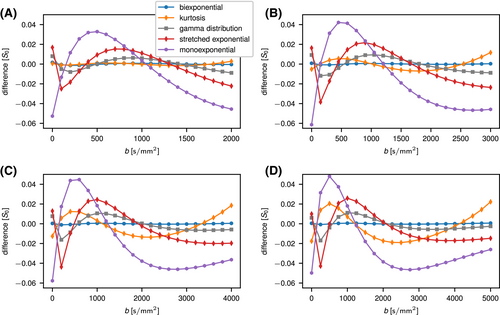
 values (A: 2000, B: 3000, C: 4000, and D: 5000 s/mm2). Base data were normal tissue at
values (A: 2000, B: 3000, C: 4000, and D: 5000 s/mm2). Base data were normal tissue at  with Gaussian noise added. Solid lines serve as guides for the eye
with Gaussian noise added. Solid lines serve as guides for the eye4.2 Determination of 
The results for the determination of the delta degrees of freedom 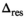 can be found in Table 1.
can be found in Table 1.
4.3 OBSIDIAN performance in a simulated scenario
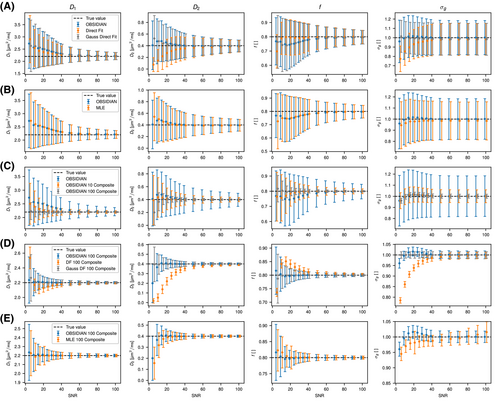
Generally, for all fit approaches, the estimates of model parameters become both more accurate and precise at higher  values. In Figure 4A, results obtained with the OBSIDIAN algorithm, the direct fit and the direct fit with Gaussian noise are shown for the normal prostate tissue simulation scenario. For the fast diffusion component
values. In Figure 4A, results obtained with the OBSIDIAN algorithm, the direct fit and the direct fit with Gaussian noise are shown for the normal prostate tissue simulation scenario. For the fast diffusion component 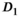 , all 3 algorithms show a similar behavior both with respect to mean and standard deviation. There is a systematic overestimation of
, all 3 algorithms show a similar behavior both with respect to mean and standard deviation. There is a systematic overestimation of 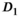 for
for 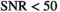 , with a large standard deviation relative to the true value of
, with a large standard deviation relative to the true value of 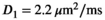 . For the slow diffusion component
. For the slow diffusion component 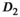 and the fast diffusion signal fraction f, results obtained with direct fitting at
and the fast diffusion signal fraction f, results obtained with direct fitting at 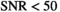 differ from results obtained with OBSIDIAN or direct fitting with Gaussian noise. For
differ from results obtained with OBSIDIAN or direct fitting with Gaussian noise. For 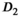 , direct fitting underestimates the true coefficient, while both the mean of the OBSIDIAN and Gaussian case are close to the actual value. For f the opposite is true, that is, the mean is more accurate for the direct fitting case. Meanwhile, for OBSIDIAN and a direct fit with Gaussian noise, estimation of
, direct fitting underestimates the true coefficient, while both the mean of the OBSIDIAN and Gaussian case are close to the actual value. For f the opposite is true, that is, the mean is more accurate for the direct fitting case. Meanwhile, for OBSIDIAN and a direct fit with Gaussian noise, estimation of 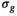 exhibits uniform precision and consistently high accuracy over the entire SNR range. In contrast, a direct fit with Rician noise results in increasing underestimation of
exhibits uniform precision and consistently high accuracy over the entire SNR range. In contrast, a direct fit with Rician noise results in increasing underestimation of 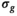 with decreasing SNR.
with decreasing SNR.
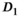 ,
, 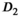 , and f) and noise (
, and f) and noise (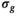 ) as function of SNR and for different fitting approaches. A, OBSIDIAN vs Direct Fit vs Gauss Direct Fit. B, OBSIDIAN vs MLE. C, OBSIDIAN vs OBSIDIAN 10 Composite vs OBSIDIAN 100 Composite. D OBSIDIAN 100 Composite vs DF (Direct Fit) 100 Composite vs Gauss DF (Direct Fit) 100 Composite. Although no results are shown, it should be noted that applying a single fit to K averaged signal decays yielded the same results as the approach Direct Fit K Composite. E, OBSIDIAN 100 Composite vs MLE 100 Composite. For a detailed explanation of the different fitting approaches see Table 2
) as function of SNR and for different fitting approaches. A, OBSIDIAN vs Direct Fit vs Gauss Direct Fit. B, OBSIDIAN vs MLE. C, OBSIDIAN vs OBSIDIAN 10 Composite vs OBSIDIAN 100 Composite. D OBSIDIAN 100 Composite vs DF (Direct Fit) 100 Composite vs Gauss DF (Direct Fit) 100 Composite. Although no results are shown, it should be noted that applying a single fit to K averaged signal decays yielded the same results as the approach Direct Fit K Composite. E, OBSIDIAN 100 Composite vs MLE 100 Composite. For a detailed explanation of the different fitting approaches see Table 2The composite method (Figure 4C) leads to better predictions for 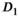 both in terms of precision and accuracy. For very low SNR values, the means of the composite method deviate slightly more from the true value for
both in terms of precision and accuracy. For very low SNR values, the means of the composite method deviate slightly more from the true value for 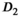 , f and
, f and  . In Figure 4D, the OBSIDIAN 100 Composite approach is compared to direct fitting of both Rician and Gaussian composite signal decays. It is apparent that the OBSIDIAN algorithm is almost on par with the Gaussian direct fit case, while direct fit estimates in the Rician composite case deviate more for
. In Figure 4D, the OBSIDIAN 100 Composite approach is compared to direct fitting of both Rician and Gaussian composite signal decays. It is apparent that the OBSIDIAN algorithm is almost on par with the Gaussian direct fit case, while direct fit estimates in the Rician composite case deviate more for 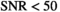 , in particular for
, in particular for 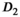 and f.
and f.
For a more concise interpretation of the results in Figure 4, the underlying distributions of the estimated parameters have to be considered. From the histograms shown in Figures 5A, B, and C, which correspond to the results shown in Figure 4A, it is obvious that for  values up to 50 the underlying parameter distributions are far from Gaussian. The only exception is the estimated noise
values up to 50 the underlying parameter distributions are far from Gaussian. The only exception is the estimated noise 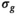 . For example, at
. For example, at 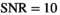 , a large number of parameter estimates equals either the lower or upper bound of the fit routine (see Table S1). Truly Gaussian characteristics are only attained for
, a large number of parameter estimates equals either the lower or upper bound of the fit routine (see Table S1). Truly Gaussian characteristics are only attained for 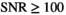 . In contrast, for the composite approach with 10 signal decays (Figure 5D), Gaussian characteristics are observed for
. In contrast, for the composite approach with 10 signal decays (Figure 5D), Gaussian characteristics are observed for  30 and upwards, whereas for the composite approach with 100 signal decays (Figure 5E) distributions are narrow for all studied
30 and upwards, whereas for the composite approach with 100 signal decays (Figure 5E) distributions are narrow for all studied  values. However, there is a systematic deviation for
values. However, there is a systematic deviation for 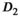 for
for 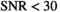 , as already seen in Figure 4A. Finally, in Figure 5F histograms are presented for the “OBSIDIAN 100 Average” approach. Compared to the “OBSIDIAN 100 Composite” approach, parameter estimates for
, as already seen in Figure 4A. Finally, in Figure 5F histograms are presented for the “OBSIDIAN 100 Average” approach. Compared to the “OBSIDIAN 100 Composite” approach, parameter estimates for 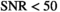 appear more scattered with broader and seemingly multimodal distributions. For higher SNR, results are more accurate, however, lack precision for
appear more scattered with broader and seemingly multimodal distributions. For higher SNR, results are more accurate, however, lack precision for 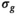 when compared to the composite approach with the same number of aggregate signal decays.
when compared to the composite approach with the same number of aggregate signal decays.
 (2.0, [0, 4]),
(2.0, [0, 4]), 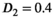 (0.5, [0, 1]),
(0.5, [0, 1]), 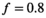 (0.5, [0.1, 0.9]) and
(0.5, [0.1, 0.9]) and 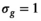 (starting values and fitting bounds given in parenthesis, see also Supporting Information Table S1). Units for
(starting values and fitting bounds given in parenthesis, see also Supporting Information Table S1). Units for 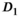 and
and 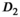 are
are 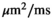
The different fit algorithms were also applied to the prostate tumor tissue simulation scenario (see Supporting Informmation Figures S2 and S3). In general, results were somewhat less affected by Rician noise. Moreover, different model functions were fitted to the biexponential signal decays of both tissue simulation scenarios. In agreement with biexponential fits, OBSIDIAN-based approaches yielded superior results that were comparable to fits of signals contaminated by Gaussian noise. These results are not documented in further detail.
For the MLE approach, results match those found with OBSIDIAN (Figure 4B and Supporting Informmation Figure S1A), but OBSIDIAN provides a more accurate estimate of 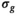 . In the composite fitting case (Figure 4E and Supporting Informmation Figure S1B) for
. In the composite fitting case (Figure 4E and Supporting Informmation Figure S1B) for 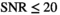 , the OBSIDIAN algorithm produces parameters with higher accuracy than the MLE approach. For the MLE composite approaches, convergences failed for a small number of cases (less than 0.5%). For the MP-PCA denoising approach, an underestimation of
, the OBSIDIAN algorithm produces parameters with higher accuracy than the MLE approach. For the MLE composite approaches, convergences failed for a small number of cases (less than 0.5%). For the MP-PCA denoising approach, an underestimation of 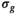 of about 10% in the center of the image, where the
of about 10% in the center of the image, where the  was lowest, was observed.
was lowest, was observed.
Typical computation time with parallelization for a quad-core Intel(R) Core(TM) i7-6700 CPU @ 3.40GHz was around 5 minutes for 105 decay profiles for OBSIDIAN. In the case of the 1D model functions, computation times for MLE and OBSDIAN were similar, but OBSDIAN was about 3 times faster for the 3D model function (Equation (20)).
4.4 Multi-b prostate data
Multi-b diffusion scans were successfully completed in all 25 enrolled patients. Various image examples that result with OBSIDIAN processing, including images that document the denoising or signal inference capability of OBSIDIAN, are presented in Figure 6. An overview of biexponential fitting results for different algorithms, ROIs, and section thickness are given in Table 4.
| Method |
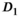
|
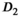
|
f | SNR |
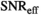
|
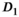
|
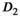
|
f | SNR |
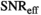
|
|---|---|---|---|---|---|---|---|---|---|---|
| Slice Thickness: 3 mm | Normal PZ (Volume:  , Number of Cases: 21) , Number of Cases: 21) |
Normal TZ (Volume:  , Number of Cases: 21) , Number of Cases: 21) |
||||||||
| Direct Fit |
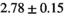
|
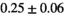
|
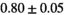
|
20 ± 5 | 332 |
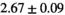
|
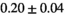
|
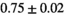
|
14 ± 2 | 395 |
| Direct Fit ROI Composite |
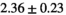
|
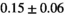
|
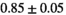
|
12 ± 2 | 197 |
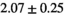
|
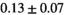
|
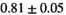
|
9 ± 1 | 255 |
| MLE |
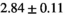
|
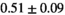
|
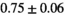
|
19 ± 5 | 315 |
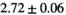
|
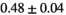
|
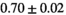
|
13 ± 2 | 358 |
| MLE ROI Composite |
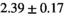
|
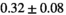
|
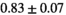
|
18 ± 5 | 304 |
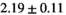
|
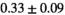
|
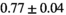
|
12 ± 2 | 343 |
| OBSIDIAN |
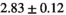
|
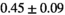
|
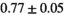
|
19 ± 5 | 318 |
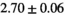
|
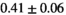
|
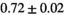
|
13 ± 2 | 361 |
| OBSIDIAN ROI Composite | 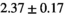 *** *** |
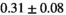
|
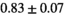 ** ** |
18 ± 5 | 307 | 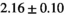 *** *** |
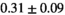
|
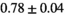 ** ** |
12 ± 2 | 345 |
| Reference Values3 |
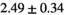
|
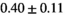 *** *** |
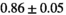
|
- | - |
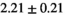
|
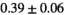 *** *** |
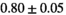
|
- | - |
| Slice Thickness: 6 mm | Normal PZ (Volume: 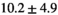 , Number of Cases: 23) , Number of Cases: 23) |
Normal TZ (Volume: 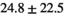 , Number of Cases: 24) , Number of Cases: 24) |
||||||||
| Direct Fit |
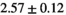
|
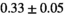
|
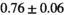
|
26 ± 6 | 324 |
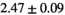
|

|
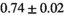
|
21 ± 4 | 386 |
| Direct Fit ROI Composite |
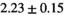
|
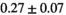
|
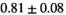
|
14 ± 2 | 168 |
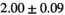
|
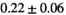
|
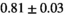
|
12 ± 2 | 216 |
| MLE |
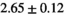
|
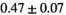
|
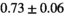
|
26 ± 6 | 319 |
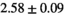
|
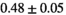
|
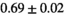
|
19 ± 4 | 363 |
| MLE ROI Composite |
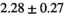
|
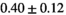
|
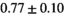
|
25 ± 6 | 309 |
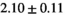
|
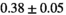
|
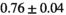
|
19 ± 4 | 352 |
| OBSIDIAN |
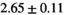
|

|
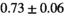
|
26 ± 6 | 319 |
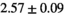
|
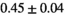
|
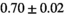
|
19 ± 4 | 363 |
| OBSIDIAN ROI Composite | 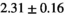 *** *** |
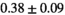
|
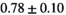
|
25 ± 6 | 311 | 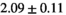 *** *** |
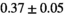
|

|
19 ± 4 | 352 |
| Significance to 3 mm | ** | * | - | - | * | ** | - | - | ||
| Reference Values3 | 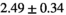 * * |
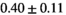
|
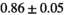 *** *** |
- | - | 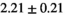 * * |
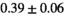
|
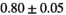 ** ** |
- | - |
| Slice Thickness: 3 mm | Tumor PZ (Volume: 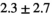 , Number of Cases: 5) , Number of Cases: 5) |
Tumor TZ (Volume: 1.1, Number of Cases: 1) | ||||||||
| Direct Fit |
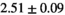
|
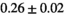
|
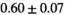
|
14 ± 3 | 97 | 2.46 | 0.27 | 0.58 | 11 | 68 |
| Direct Fit ROI Composite |
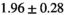
|
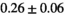
|
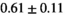
|
11 ± 3 | 75 | 1.83 | 0.28 | 0.57 | 9 | 56 |
| MLE |

|
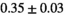
|
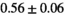
|
14 ± 3 | 97 | 2.41 | 0.37 | 0.52 | 11 | 66 |
| MLE ROI Composite |
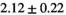
|
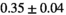
|
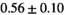
|
13 ± 3 | 94 | 2.10 | 0.41 | 0.49 | 11 | 63 |
| OBSIDIAN |
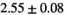
|
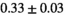
|
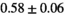
|
14 ± 3 | 98 | 2.48 | 0.34 | 0.56 | 11 | 66 |
| OBSIDIAN ROI Composite |
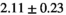
|
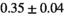
|

|
14 ± 3 | 95 | 2.10 | 0.41 | 0.49 | 11 | 63 |
| Significance to Normal | * | *** | - | - | - | - | ||||
| Reference Values3 |
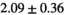
|
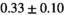
|
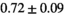 ** ** |
- | - |
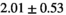
|
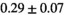
|
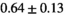
|
- | - |
| Slice Thickness: 6 mm | Tumor PZ (Volume: 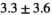 , Number of Cases: 5) , Number of Cases: 5) |
Tumor TZ (Volume: 2.0, Number of Cases: 1) | ||||||||
| Direct Fit |
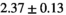
|
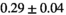
|
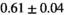
|
21 ± 5 | 131 | 2.26 | 0.30 | 0.57 | 17 | 94 |
| Direct Fit ROI Composite |

|
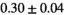
|
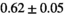
|
15 ± 5 | 87 | 1.68 | 0.34 | 0.56 | 9 | 49 |
| MLE |
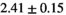
|
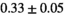
|
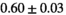
|
22 ± 5 | 133 | 2.27 | 0.42 | 0.52 | 16 | 88 |
| MLE ROI Composite |
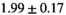
|
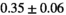
|
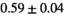
|
21 ± 5 | 130 | 1.81 | 0.41 | 0.50 | 15 | 86 |
| OBSIDIAN |
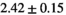
|
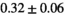
|
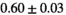
|
22 ± 5 | 133 | 2.29 | 0.39 | 0.55 | 16 | 89 |
| OBSIDIAN ROI Composite |
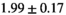
|
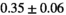
|
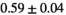
|
21 ± 5 | 130 | 1.81 | 0.40 | 0.50 | 15 | 86 |
| Significance to Normal | *** | *** | - | - | - | - | ||||
| Reference Values3 |
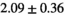
|
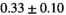
|
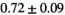 ** ** |
- | - |
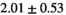
|
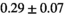
|
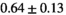
|
- | - |
-
Notes: The number of patients represented in both 3 and 6 mm data was 19 for PZ, 20 for Normal TZ, 5 for Tumor PZ, and 1 for Tumor TZ. Significances indicated next to OBSIDIAN ROI Composite values are between PZ and TZ values, while significances indicated next to reference values are between OBSIDIAN ROI Composite and reference values. For Tumor PZ, no significant differences between 3 and 6 mm were observed. For Tumor TZ, no significances could be computed, as only data of one patient was available. Reference values are taken from Table 2 (
 =250 s/mm2) of.3 The PI-RADS and biopsy Gleason scores of the 6 lesions analyzed were 3 and 3+3, 3 and 3+3, 4 and 3+4 with post-surgical score 3+4, 5 and 3+4, 5 and 4+3, and 5 and 4+5, respectively. Values are given as mean ± standard deviation. Volume given in ml; Diffusion coefficients in
=250 s/mm2) of.3 The PI-RADS and biopsy Gleason scores of the 6 lesions analyzed were 3 and 3+3, 3 and 3+3, 4 and 3+4 with post-surgical score 3+4, 5 and 3+4, 5 and 4+3, and 5 and 4+5, respectively. Values are given as mean ± standard deviation. Volume given in ml; Diffusion coefficients in 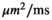 . Significance levels: *
. Significance levels: *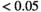 , **
, **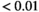 , ***
, ***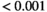 .
.
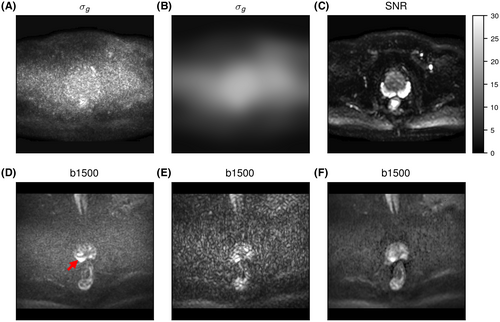
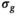 generated with the OBSIDIAN algorithm. B, After applying a 2D Gaussian filter with standard deviation of 12 pixels on the
generated with the OBSIDIAN algorithm. B, After applying a 2D Gaussian filter with standard deviation of 12 pixels on the 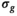 map shown in (A), the spatial noise characteristics of the coil array become evident. C, Signal-to-noise ratio map with the prostate in the center and absolute SNR values indicated along the gray scale. D, Clinical data(
map shown in (A), the spatial noise characteristics of the coil array become evident. C, Signal-to-noise ratio map with the prostate in the center and absolute SNR values indicated along the gray scale. D, Clinical data(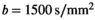 , 3 directions, 6 averages) shows prominent tumor lesion (red arrow). E, Multi-b scan raw data (
, 3 directions, 6 averages) shows prominent tumor lesion (red arrow). E, Multi-b scan raw data (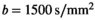 , 3 directions, no averaging). F, The signal map (
, 3 directions, no averaging). F, The signal map (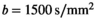 , 3 directions) that results with OBSIDIAN fitting exhibits overall image quality and lesion conspicuity that matches or even rivals the clinical scan data. Slice thickness for all data shown, including clinical data, was 3 mm
, 3 directions) that results with OBSIDIAN fitting exhibits overall image quality and lesion conspicuity that matches or even rivals the clinical scan data. Slice thickness for all data shown, including clinical data, was 3 mmFor the MP-PCA denoising algorithm, most of the principle components (>80%) were identified as signal components resulting in estimates for 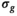 about a factor 10 lower than what was observed for the OBSIDIAN and MLE methods.
about a factor 10 lower than what was observed for the OBSIDIAN and MLE methods.
4.5 Multidirectional brain data
Diffusion tensor analysis resulted in estimated 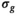 that were similar irrespective of b-shell and model. The
that were similar irrespective of b-shell and model. The 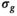 values were also considerably smaller than originally assessed by the authors of the MASSIVE data set. Resulting FA values were slightly higher with Rician bias correction. For details, see Supporting Information Tables S2 and S3.
values were also considerably smaller than originally assessed by the authors of the MASSIVE data set. Resulting FA values were slightly higher with Rician bias correction. For details, see Supporting Information Tables S2 and S3.
5 DISCUSSION
The best choice for the tissue diffusion signal decay model is often a matter of dispute.3, 38, 39 The monoexponential model can readily be distinguished at relative low  , obviously due to the lower amount of complexity in this model. But as shown in Table 3, high
, obviously due to the lower amount of complexity in this model. But as shown in Table 3, high  values would be required to observe significant differences among the other models. Such high SNR is typically not attainable, unless a considerable sacrifice is made in spatial resolution or the object is close to the radiofrequency receiver coil, for example, when an endorectal coil is used in a prostate exam.3 On a pixel-by-pixel basis, without signal averaging, even an
values would be required to observe significant differences among the other models. Such high SNR is typically not attainable, unless a considerable sacrifice is made in spatial resolution or the object is close to the radiofrequency receiver coil, for example, when an endorectal coil is used in a prostate exam.3 On a pixel-by-pixel basis, without signal averaging, even an  of 50, that is, an SNR value where the parameter estimation of models with 3 or 4 parameters tends to be reliable, is hard to achieve with clinical imaging protocols. Thus, distinguishing models on the basis of single voxels is impractical in a clinical setting. For composite fitting on the other hand, very high effective
of 50, that is, an SNR value where the parameter estimation of models with 3 or 4 parameters tends to be reliable, is hard to achieve with clinical imaging protocols. Thus, distinguishing models on the basis of single voxels is impractical in a clinical setting. For composite fitting on the other hand, very high effective  values can be attained if ROIs are sufficiently large (see Table 4). In this situation, the proper choice of a fitting model could be more important.
values can be attained if ROIs are sufficiently large (see Table 4). In this situation, the proper choice of a fitting model could be more important.
The delta degrees of freedom 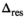 were always smaller than the actual number of free parameters of the respective model. A general assumption of a 1:2 ratio between the 2 numbers for all fit functions appears not unreasonable. Using the number of free parameters instead of the simulated values as
were always smaller than the actual number of free parameters of the respective model. A general assumption of a 1:2 ratio between the 2 numbers for all fit functions appears not unreasonable. Using the number of free parameters instead of the simulated values as 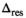 would have lead to an overestimation of
would have lead to an overestimation of 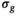 of around 10%.
of around 10%.
Application of OBSIDIAN to simulated data shows that resulting parameter estimations are on par with those from directly fitting measured signal decays with Gaussian noise. This constitutes a significant accomplishment, since it essentially eliminates the disadvantage of using magnitude data instead of the otherwise preferable complex data. It should nonetheless be recognized that even under such ideal conditions, accuracy, and precision of the parameter estimations below  are low and deteriorate further with decreasing SNR levels. In direct fits, as one can expect, the presence of Rician bias at
are low and deteriorate further with decreasing SNR levels. In direct fits, as one can expect, the presence of Rician bias at 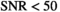 leads to an underestimation of
leads to an underestimation of 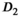 (Figure 4A). The better accuracy for f in the direct fit case should be interpreted with care, as standard deviations are relatively large. This observation is further augmented by the non-Gaussian characteristics of the parameter distributions that resulted for
(Figure 4A). The better accuracy for f in the direct fit case should be interpreted with care, as standard deviations are relatively large. This observation is further augmented by the non-Gaussian characteristics of the parameter distributions that resulted for 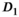 ,
, 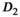 , and f (see histograms in Figures 5A, B, and C). This also highlights the role of fit boundaries, as they at low SNR can have an effect on the final parameter distribution and the resulting mean value. In many diffusion MRI applications, as is also the case in the present work, there is a priori knowledge about the expected parameters, so setting fitting boundaries can be regarded reasonable.
, and f (see histograms in Figures 5A, B, and C). This also highlights the role of fit boundaries, as they at low SNR can have an effect on the final parameter distribution and the resulting mean value. In many diffusion MRI applications, as is also the case in the present work, there is a priori knowledge about the expected parameters, so setting fitting boundaries can be regarded reasonable.
In order to improve precision and accuracy of the prediction, multiple signal decays with same or at least very similar characteristics can be taken into account. With respect to MR images, these profiles might originate from an ROI with the same tissue type. In accordance with the central limit theorem, post hoc averaging of estimated coefficients obtained with any of the fit algorithms only leads to a trivial improvement in precision, but not in accuracy. Composite fitting (Figure 4C), on the other hand, improves both precision and accuracy. Here a two-step procedure was chosen, as it is more practical with respect to clinical data, where variations in 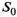 over the ROI can corrupt the noise estimation. Still, for simulated data with only noise-related variations of
over the ROI can corrupt the noise estimation. Still, for simulated data with only noise-related variations of 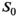 it was found that composite fitting also works in a single-step procedure. However, for optimal results at low SNR, a more restrictive, that is, lower choice of the break parameter
it was found that composite fitting also works in a single-step procedure. However, for optimal results at low SNR, a more restrictive, that is, lower choice of the break parameter 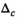 is necessary. Averaging multiple signal decays is akin to a preprocessing step that involves smoothing. Averaging followed by the application of OBSIDIAN with the modified
is necessary. Averaging multiple signal decays is akin to a preprocessing step that involves smoothing. Averaging followed by the application of OBSIDIAN with the modified 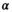 -function appears to yield correct results, but was found to be numerically unstable and needs further investigation (Figure 5F). Note, that for a particular smoothing kernel, e.g. Gaussian kernel with a certain width, a corresponding
-function appears to yield correct results, but was found to be numerically unstable and needs further investigation (Figure 5F). Note, that for a particular smoothing kernel, e.g. Gaussian kernel with a certain width, a corresponding 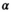 -function needs to be computed. Averaging the multiple signal decays before the application of a direct fit was equivalent to performing a composite direct fit.
-function needs to be computed. Averaging the multiple signal decays before the application of a direct fit was equivalent to performing a composite direct fit.
Application of the OBSIDIAN method to patient data leads to 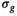 maps with high-frequency random fluctuations in the image space as shown in Figure 6A. The low-pass filtered
maps with high-frequency random fluctuations in the image space as shown in Figure 6A. The low-pass filtered 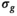 map, depicted in Figure 6B, is a more realistic representation of the actual spatially dependent noise in a multicoil scenario. Such noise maps are useful for coil testing and protocol planning.
map, depicted in Figure 6B, is a more realistic representation of the actual spatially dependent noise in a multicoil scenario. Such noise maps are useful for coil testing and protocol planning.
The pixel-wise SNR values of the present study are well below 50 and therefore pixel-wise estimations of the diffusion model parameter exhibit low precision and can be expected to be affected by similar errors as predicted by simulation. In order to achieve more reliable estimates for different tissue types, it is indispensable to simultaneously fit multiple signal decays over an entire ROI. Considering the reference values as gold standard, the comparison of the composite fitting strategies shown in Table 4 reveals that OBSIDIAN ROI Composite is superior to Direct Fit ROI Composite (or direct fitting of beforehand averaged data), which is also predicted by the simulation results.
All significances reported in Table 4 relate to the approach OBSIDIAN ROI Composite. There are significant differences due to slice thickness. As expected 3 mm measurements exhibit lower SNR than 6 mm measurements. That SNR does not scale with slice thickness (in-plane resolution was identical) can be explained with the different TR (3860 ms vs 1920 ms) and the resulting 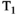 weighting. Baur et al40 report for 3T relatively long median
weighting. Baur et al40 report for 3T relatively long median 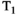 values of 1666 -1759 ms for the PZ and 1486-1508 ms for the TZ, which would explain a sizeable effect from using the shorter TR. The absence of any slice thickness related significant differences in tumor tissue may be explained by the different signal decay in tumor, which is much less prone to signal bias, even with the lower per pixel
values of 1666 -1759 ms for the PZ and 1486-1508 ms for the TZ, which would explain a sizeable effect from using the shorter TR. The absence of any slice thickness related significant differences in tumor tissue may be explained by the different signal decay in tumor, which is much less prone to signal bias, even with the lower per pixel  at
at 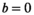 . Another reason for lack of significance may be the small number of tumor cases.
. Another reason for lack of significance may be the small number of tumor cases.
In agreement with the reference study,3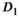 in the normal PZ was significantly higher than in the normal TZ, whereas
in the normal PZ was significantly higher than in the normal TZ, whereas 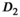 showed no significant difference between normal zones. Also in agreement with the reference study, the parameter f was slightly higher in the PZ than in the TZ. Moreover, parameter differences between normal tissue and tumor in the PZ were in agreement with the reference study for
showed no significant difference between normal zones. Also in agreement with the reference study, the parameter f was slightly higher in the PZ than in the TZ. Moreover, parameter differences between normal tissue and tumor in the PZ were in agreement with the reference study for 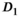 and f, as both were significantly reduced in tumor tissue. For
and f, as both were significantly reduced in tumor tissue. For  , a reduction, which is in agreement with the reference study, was only observed for the 6 mm data set, but did not reach significance.
, a reduction, which is in agreement with the reference study, was only observed for the 6 mm data set, but did not reach significance.
Finally, the comparison of all OBSIDIAN ROI Composite and reference values revealed no significant differences for 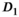 and
and 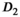 with the exception of a slightly lower OBSIDIAN ROI Composite
with the exception of a slightly lower OBSIDIAN ROI Composite 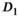 for normal tissue at 6 mm slice thickness and a markedly lower OBSIDIAN ROI Composite
for normal tissue at 6 mm slice thickness and a markedly lower OBSIDIAN ROI Composite 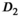 for normal tissue at 3 mm slice thickness. The OBSIDIAN ROI Composite f values were lower for all performed comparisons and this difference was invariably significant except for the 3 mm normal-tissue case. These lower fast diffusion signal fractions were most pronounced in tumor tissue and seem not explainable by low SNR or methodological deficiencies. A plausible explanation are the different echo times used, that is, 70 ms for the present study and 100 ms for the reference study. The longer echo time of the reference study would de-emphasize slow-diffusing solid tumor components with shorter
for normal tissue at 3 mm slice thickness. The OBSIDIAN ROI Composite f values were lower for all performed comparisons and this difference was invariably significant except for the 3 mm normal-tissue case. These lower fast diffusion signal fractions were most pronounced in tumor tissue and seem not explainable by low SNR or methodological deficiencies. A plausible explanation are the different echo times used, that is, 70 ms for the present study and 100 ms for the reference study. The longer echo time of the reference study would de-emphasize slow-diffusing solid tumor components with shorter  relaxation times. An earlier pilot study 41 that was performed with the same equipment, same pulse sequence and
relaxation times. An earlier pilot study 41 that was performed with the same equipment, same pulse sequence and 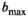 as the reference study, attained a shorter echo time of 85 ms through concurrent driving of magnetic field gradients. Indeed, in agreement with the echo time-dependence hypothesis, signal fraction values observed in this pilot study were lower than in the reference study, that is,
as the reference study, attained a shorter echo time of 85 ms through concurrent driving of magnetic field gradients. Indeed, in agreement with the echo time-dependence hypothesis, signal fraction values observed in this pilot study were lower than in the reference study, that is, 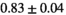 and
and 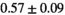 for normal PZ and tumor PZ, respectively. Other protocol parameters that could contribute to altered signal fractions, are a different diffusion encoding time
for normal PZ and tumor PZ, respectively. Other protocol parameters that could contribute to altered signal fractions, are a different diffusion encoding time 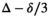 , that is, 27 ms for the present study and 35 ms for the reference study, and a slightly different range of diffusion encoding. Finally, for the present study, the mix of lesion grades and associated diffusion properties may be different.
, that is, 27 ms for the present study and 35 ms for the reference study, and a slightly different range of diffusion encoding. Finally, for the present study, the mix of lesion grades and associated diffusion properties may be different.
With respect to MLE, we obtain for simulations as well as patient data almost identical results as with OBSIDIAN. But at very low SNR with a composite approach OBSIDIAN outperformed MLE. Since MLE relies on the computation of modified Bessel functions within the fit routine, there is a potential computational performance advantage for OBSIDIAN. In particular, OBSIDIAN provided a clear speed advantage once multiple directions with identical 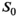 were fitted in a single step. Both methods require prior selection of a decay model. Using a maximum a posteriori method in conjunction with regularization as presented by Poot and Klein22 could improve accuracy and precision of the MLE results. Furthermore, Veraart et al21 found that motion and eddy current correction has a negative impact on the MLE procedure. No such corrections were applied in the current study. For a future study, it might be of interest to see if OBSIDIAN can better cope with this situation.
were fitted in a single step. Both methods require prior selection of a decay model. Using a maximum a posteriori method in conjunction with regularization as presented by Poot and Klein22 could improve accuracy and precision of the MLE results. Furthermore, Veraart et al21 found that motion and eddy current correction has a negative impact on the MLE procedure. No such corrections were applied in the current study. For a future study, it might be of interest to see if OBSIDIAN can better cope with this situation.
In terms of MP-PCA denoising, good results were observed for simulation data. However, for patient data, the MP-PCA noise estimates were far too low in comparison to the other methods. A dataset for testing purposes is available in the Supporting Information.
The application of OBSIDIAN to the MASSIVE data set demonstrates that the method also can be useful to estimate noise and correct Rician noise in a multidirectional scenario. Further testing with more complex models is warranted.
Finally, it shall be pointed out that there is no theoretical obstacle for OBSIDIAN in going from Rician to noncentral 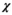 distributed noise, as it results from certain multicoil reconstruction schemes.42, 43 In particular, the Rician expectation value in Equation (11) has to be replaced with the corresponding expectation value for a noncentral
distributed noise, as it results from certain multicoil reconstruction schemes.42, 43 In particular, the Rician expectation value in Equation (11) has to be replaced with the corresponding expectation value for a noncentral 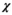 distributed random variable.
distributed random variable.
6 CONCLUSION
Direct model fitting of magnitude signal decays that exhibit significant Rician bias produces coefficient estimations with substantial errors. Commonly performed prior averaging of such magnitude signal decays or post hoc averaging of the parameters derived from individual fits does not remedy this error and even results in distinctly different false estimations. The proposed model-driven OBSIDIAN approach allows for Rician bias correction on a pixel-by-pixel basis, hence, is not relying on a uniform noise distribution. As underpinned by simulations and experimental data, concurrent application of this method over many pixels with similar signal decays allows for significant improvement in both accuracy and precision of the coefficient estimation. Therefore, OBSIDIAN effectively permits for universal study comparison, as potential SNR dependent biases in the parameter estimation are minimized. It was further shown that the proposed method produces equivalent results as a maximum likelihood approach. The proposed method is an alternative that potentially exhibits advantages in terms of computational speed and convergence and is likely of interest in other contexts, even beyond the field of MRI.
ACKNOWLEDGEMENTS
We thank Maria Ljungberg and Göran Starck from the Sahlgrenska MR center and Nicolas Geades from Philips Healthcare for assistance with protocol setup.



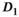 and
and 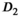 are
are 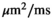 . For fitting bounds and starting values see Supporting Information Table S1. Actual model values were
. For fitting bounds and starting values see Supporting Information Table S1. Actual model values were 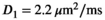 ,
, 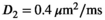 ,
, 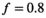 and
and 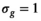
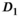 ,
,  , and f) and noise (
, and f) and noise (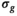 ) as function of SNR and for different fitting approaches. A, OBSIDIAN vs Direct Fit vs Gauss Direct Fit. B, OBSIDIAN vs OBSIDIAN 10 Composite vs OBSIDIAN 100 Composite. C, OBSIDIAN 100 Composite vs DF (Direct Fit) 100 Composite vs Gauss DF (Direct Fit) 100 Composite. Although no results are shown, it should be noted that applying a single fit to K averaged signal decays yielded the same results as the approach Direct Fit K Composite. For a detailed explanation of the different fitting approaches see Section
) as function of SNR and for different fitting approaches. A, OBSIDIAN vs Direct Fit vs Gauss Direct Fit. B, OBSIDIAN vs OBSIDIAN 10 Composite vs OBSIDIAN 100 Composite. C, OBSIDIAN 100 Composite vs DF (Direct Fit) 100 Composite vs Gauss DF (Direct Fit) 100 Composite. Although no results are shown, it should be noted that applying a single fit to K averaged signal decays yielded the same results as the approach Direct Fit K Composite. For a detailed explanation of the different fitting approaches see Section 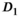 and
and 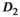 are
are 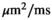 . For fitting bounds and starting values see Supporting Information Table S1. Actual model values were
. For fitting bounds and starting values see Supporting Information Table S1. Actual model values were 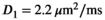 ,
, 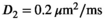 ,
, 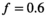 and
and 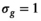
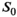 in the simulation was set to
in the simulation was set to 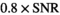 . For maximum likelihood estimation (MLE),
. For maximum likelihood estimation (MLE), 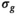 bounds were set to [0.001, 10]. For patient data, signal decays were pixel-wise normalized prior to fitting with a pixel-specific normalization factor
bounds were set to [0.001, 10]. For patient data, signal decays were pixel-wise normalized prior to fitting with a pixel-specific normalization factor 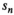 . Consequently a constant starting value of 1 was used for
. Consequently a constant starting value of 1 was used for 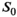 . The bounds for
. The bounds for 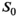 were
were 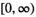 in all cases. In the MLE case, the
in all cases. In the MLE case, the 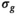 bounds were set pixel-dependent to
bounds were set pixel-dependent to 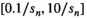 in order to account for the normalization
in order to account for the normalization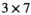 pixels) for two models and different combinations of b-shells as given by the table matrix. Single tensor refers to Equation (10), while dual tensor refers to Equation (11). In the case of the dual tensor model, the average angle between the eigenvectors belonging to the largest eigenvalues for
pixels) for two models and different combinations of b-shells as given by the table matrix. Single tensor refers to Equation (10), while dual tensor refers to Equation (11). In the case of the dual tensor model, the average angle between the eigenvectors belonging to the largest eigenvalues for 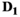 and
and 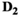 was
was 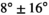
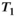 relaxation time in prostate cancer and benign prostate tissue using a modified look-locker inversion recovery sequence
relaxation time in prostate cancer and benign prostate tissue using a modified look-locker inversion recovery sequence