A simplified framework to optimize MRI contrast preparation
Corresponding Author
Eric Van Reeth
CNRS, Inserm, CREATIS UMR 5220, U1206, Univ Lyon, INSA-Lyon, Université Claude Bernard Lyon 1, UJM-Saint Etienne, Lyon, France
Correspondence
Eric Van Reeth, Creatis, CPE 3 rue Victor Grignard, 69100, Villeurbanne, France.
Search for more papers by this authorHélène Ratiney
CNRS, Inserm, CREATIS UMR 5220, U1206, Univ Lyon, INSA-Lyon, Université Claude Bernard Lyon 1, UJM-Saint Etienne, Lyon, France
Search for more papers by this authorKevin Tse Ve Koon
CNRS, Inserm, CREATIS UMR 5220, U1206, Univ Lyon, INSA-Lyon, Université Claude Bernard Lyon 1, UJM-Saint Etienne, Lyon, France
Search for more papers by this authorMichael Tesch
Department of Chemistry, Technical University of Munich, Munich, Germany
Search for more papers by this authorDenis Grenier
CNRS, Inserm, CREATIS UMR 5220, U1206, Univ Lyon, INSA-Lyon, Université Claude Bernard Lyon 1, UJM-Saint Etienne, Lyon, France
Search for more papers by this authorOlivier Beuf
CNRS, Inserm, CREATIS UMR 5220, U1206, Univ Lyon, INSA-Lyon, Université Claude Bernard Lyon 1, UJM-Saint Etienne, Lyon, France
Search for more papers by this authorSteffen J. Glaser
Department of Chemistry, Technical University of Munich, Munich, Germany
Search for more papers by this authorDominique Sugny
ICB, CNRS UMR5209, Université de Bourgogne, France
Institute for Advanced Study, Technical University of Munich, Garching, Germany
Search for more papers by this authorCorresponding Author
Eric Van Reeth
CNRS, Inserm, CREATIS UMR 5220, U1206, Univ Lyon, INSA-Lyon, Université Claude Bernard Lyon 1, UJM-Saint Etienne, Lyon, France
Correspondence
Eric Van Reeth, Creatis, CPE 3 rue Victor Grignard, 69100, Villeurbanne, France.
Search for more papers by this authorHélène Ratiney
CNRS, Inserm, CREATIS UMR 5220, U1206, Univ Lyon, INSA-Lyon, Université Claude Bernard Lyon 1, UJM-Saint Etienne, Lyon, France
Search for more papers by this authorKevin Tse Ve Koon
CNRS, Inserm, CREATIS UMR 5220, U1206, Univ Lyon, INSA-Lyon, Université Claude Bernard Lyon 1, UJM-Saint Etienne, Lyon, France
Search for more papers by this authorMichael Tesch
Department of Chemistry, Technical University of Munich, Munich, Germany
Search for more papers by this authorDenis Grenier
CNRS, Inserm, CREATIS UMR 5220, U1206, Univ Lyon, INSA-Lyon, Université Claude Bernard Lyon 1, UJM-Saint Etienne, Lyon, France
Search for more papers by this authorOlivier Beuf
CNRS, Inserm, CREATIS UMR 5220, U1206, Univ Lyon, INSA-Lyon, Université Claude Bernard Lyon 1, UJM-Saint Etienne, Lyon, France
Search for more papers by this authorSteffen J. Glaser
Department of Chemistry, Technical University of Munich, Munich, Germany
Search for more papers by this authorDominique Sugny
ICB, CNRS UMR5209, Université de Bourgogne, France
Institute for Advanced Study, Technical University of Munich, Garching, Germany
Search for more papers by this authorAbstract
Purpose
This article proposes a rigorous optimal control framework for the design of preparation schemes that optimize MRI contrast based on relaxation time differences.
Methods
Compared to previous optimal contrast preparation schemes, a drastic reduction of the optimization parameter number is performed. The preparation scheme is defined as a combination of several block pulses whose flip angles, phase terms and inter-pulse delays are optimized to control the magnetization evolution.
Results
The proposed approach reduces the computation time of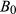 
-robust preparation schemes to around a minute (whereas several hours were required with previous schemes), with negligible performance loss. The chosen parameterization allows to formulate the total preparation duration as a constraint, which improves the overall compromise between contrast performance and preparation time. Simulation, in vitro and in vivo results validate this improvement, illustrate the straightforward applicability of the proposed approach, and point out its flexibility in terms of achievable contrasts. Major improvement is especially achieved for short-T2 enhancement, as shown by the acquisition of a non-trivial contrast on a rat brain, where a short-T2 white matter structure (corpus callosum) is enhanced compared to surrounding gray matter tissues (hippocampus and neocortex).
Conclusions
This approach proposes key advances for the design of optimal contrast preparation sequences, that emphasize their ability to generate non-standard contrasts, their potential benefit in a clinical context, and their straightforward applicability on any MR system.
References
- 1Nitz WR, Reimer P. Contrast mechanisms in MR imaging. Eur Radiol. 1999; 9: 1032–1046.
- 2Kim SG, Hu X, Ugurbil K. Accurate T1 determination from inversion recovery images: application to human brain at 4 Tesla. Magn Reson Med. 1994; 31: 445–449.
- 3Hetherington HP, Pan JW, Mason GF, Adams D, Vaughn MJ, Twieg DB, et al. Quantitative 1H spectroscopic imaging of human brain at 4.1 T using image segmentation. Magn Reson Med. 1996; 36: 21–29.
- 4de Graaf RA, Brown PB, McIntyre S, Nixon TW, Behar KL, Rothman DL. High magnetic field water and metabolite proton T1 and T2 relaxation in rat brain in vivo. Magn Reson Med. 2006; 56: 386–394.
- 5Ratiney H, Noworolski SM, Sdika M, Srinivasan R, Henry RG, Nelson SJ, et al. Estimation of metabolite T1 relaxation times using tissue specific analysis, signal averaging and bootstrapping from magnetic resonance spectroscopic imaging data. Magn Reson Mater Phys Biol Med.2007; 20: 143–155.
- 6Ganji SK, Banerjee A, Patel AM, Zhao YD, Dimitrov IE, Browning JD, et al. T2 measurement of J-coupled metabolites in the human brain at 3T. NMR Biomed. 2012; 25: 523–529.
- 7Dieringer MA, Deimling M, Santoro D, Wuerfel J, Madai VI, Sobesky J, et al. Rapid parametric mapping of the longitudinal relaxation time T1 using two-dimensional variable flip angle magnetic resonance Imaging at 1.5 Tesla, 3 Tesla, and 7 Tesla. PLOS ONE 2014; 9: 1–8.
- 8Hajnal JV, De Coene B, Lewis PD, Baudouin CJ, Cowan FM, Pennock JM, et al. High signal regions in normal white matter shown by heavily T2-weighted CSF nulled IR sequences. J Comput Assisted Tomography. 1992; 16: 506–513.
- 9Brittain JH, Hu BS, Wright GA, Meyer CH, Macovski A, Nishimura DG. Coronary angiography with magnetization-prepared T2 contrast. Magn Reson Med. 1995; 33: 689–696.
- 10Dyvorne H, Balchandani P. Slice-selective adiabatic magnetization T2-preparation (SAMPA) for efficient T2-weighted imaging at ultrahigh field strengths. Magn Reson Med. 2016; 76: 1741–1749.
- 11Nezafat R, Stuber M, Ouwerkerk R, Gharib AM, Desai MY, Pettigrew RI. B1-insensitive T2 preparation for improved coronary magnetic resonance angiography at 3T. Magn Reson Med. 2006; 55: 858–864.
- 12Obara M, Kuroda K, Wang J, Honda M, Yoneyama M, Imai Y, et al. Comparison between two types of improved motion-sensitized driven-equilibrium (iMSDE) for intracranial black-blood imaging at 3.0 tesla. J Magn Reson Imaging. 2014; 40: 824–831.
- 13Larson PEZ, Conolly SM, Pauly JM, Nishimura DG. Using adiabatic inversion pulses for long-T2 suppression in ultrashort echo time (UTE) imaging. Magn Reson Med. 2007; 58: 952–961.
- 14Du J, Ma G, Li S, Carl M, Szeverenyi NM, VandenBerg S, et al. Ultrashort echo time (UTE) magnetic resonance imaging of the short T2 components in white matter of the brain using a clinical 3T scanner. Neuroimage. 2014; 87: 32–41.
- 15Weiger M, Wu M, Wurnig MC, Kenkel D, Boss A, Andreisek G, et al. ZTE imaging with long-T2 suppression. NMR Biomed. 2015; 28: 247–254.
- 16Gatehouse PD, Bydder GM. Magnetic resonance imaging of short T2 components in tissue. Clinical Radiol. 2003; 58: 1–19.
- 17Vidarsson L, Conolly SM, Lim KO, Gold GE, Pauly JM. Echo time optimization for linear combination myelin imaging. Magn Reson Med. 2005; 53: 398–407.
- 18Rahmer J, Börnert P, Groen J, Bos C. Three-dimensional radial ultrashort echo-time imaging with T2 adapted sampling. Magn Reson Med. 2006; 55: 1075–1082.
- 19Sussman MS, Pauly JM, Wright GA. Design of practical T2-selective RF excitation (TELEX) pulses. Magn Reson Med. 1998; 40: 890–899.
- 20Larson PEZ, Gurney PT, Nayak K, Gold GE, Pauly JM, Nishimura DG. Designing long-T2 suppression pulses for ultrashort echo time imaging. Magn Reson Med. 2006; 56: 94–103.
- 21Rahmer J, Blume U, Bornert P. Selective 3D ultrashort TE imaging: omparison of “dual-echo” acquisition and magnetization preparation for improving short-T2 contrast. Magn Reson Mater Phys Biol Med. 2007; 20: 83.
- 22Brittain JH, Olcott EW, Szuba A, Gold GE, Wright GA, Irarrazaval P, et al. Three-dimensional flow-independent peripheral angiography. Magn Reson Med. 1997; 38: 343–354.
- 23Liu CY, Wieben O, Brittain JH, Reeder SB. Improved delayed enhanced myocardial imaging with T2-Prep inversion recovery magnetization preparation. J Magn Reson Imaging. 2008; 28: 1280–1286.
- 24Van Reeth E, Ratiney H, Tesch M, Grenier D, Beuf O, Glaser SJ, et al. Optimal control design of preparation pulses for contrast optimization in MRI. J Magn Reson. 2017; 279: 39–50.
- 25Lapert M, Zhang Y, Janich M, Glaser S, Sugny D. Exploring the physical limits of saturation contrast in magnetic resonance imaging. Sci Rep. 2012; 2.
- 26Schwendinger M, Quant J, Schleucher J, Glaser S, Griesinger C. Broadband Heteronuclear–Hartmann–Hahn sequences. J Magn Reson Ser A. 1994; 111: 115–120.
- 27Suter D, Mahesh TS. Spins as qubits: quantum information processing by nuclear magnetic resonance. J Chem Phys. 2008; 128: 052206.
- 28Skinner TE, Gershenzon NI. Optimal control design of pulse shapes as analytic functions. J Magn Reson. 2010; 204: 248–255.
- 29Pontryagin LS. Mathematical theory of optimal processes. Boca Raton, FL: CRC Press; 1987.
- 30Conolly S, Nishimura D, Macovski A. Optimal control solutions to the magnetic resonance selective excitation problem. IEEE Trans Med Imaging. 1986; 5: 106–115.
- 31Skinner TE, Reiss TO, Luy B, Khaneja N, Glaser SJ. Application of optimal control theory to the design of broadband excitation pulses for high-resolution NMR. J Magn Reson. 2003; 163: 8–15.
- 32Liu H, Matson GB. Radiofrequency pulse designs for three-dimensional MRI providing uniform tipping in inhomogeneous B1 fields. Magn Reson Med. 2011; 66: 1254–1266.
- 33Janich MA, Schulte RF, Schwaiger M, Glaser SJ. Robust slice-selective broadband refocusing pulses. J Magn Reson. 2011; 213: 126–135.
- 34Janich MA, McLean MA, Noeske R, Glaser SJ, Schulte RF. Slice-selective broadband refocusing pulses for the robust generation of crushed spin-echoes. J Magn Reson. 2012; 223: 129–137.
- 35Kobzar K, Ehni S, Skinner TE, Glaser SJ, Luy B. Exploring the limits of broadband 90. and 180. universal rotation pulses. J Magn Reson. 2012; 225: 142–160.
- 36Skinner TE, Gershenzon NI, Nimbalkar M, Glaser SJ. Optimal control design of band-selective excitation pulses that accommodate relaxation and RF inhomogeneity. J Magn Reson. 2012; 217: 53–60.
- 37Skinner TE, Gershenzon NI, Nimbalkar M, Bermel W, Luy B, Glaser SJ. New strategies for designing robust universal rotation pulses: application to broadband refocusing at low power. J Magn Reson. 2012; 216: 78–87.
- 38Vinding MS, Maximov II, Tošner Z, Nielsen NC. Fast numerical design of spatial-selective RF pulses in MRI using Krotov and quasi-Newton based optimal control methods. J Chem Phys. 2012; 137: 054203.
- 39Maximov II, Vinding MS, Desmond H, Nielsen NC, Shah NJ. Real-time 2D spatially selective MRI experiments: comparative analysis of optimal control design methods. J Magn Reson. 2015; 254: 110–120.
- 40Aigner CS, Clason C, Rund A, Stollberger R. Efficient high-resolution RF pulse design applied to simultaneous multi-slice excitation. J Magn Reson. 2016; 263: 33–44.
- 41Xu D, King KF, Zhu Y, McKinnon GC, Liang ZP. Designing multichannel, multidimensional, arbitrary flip angle RF pulses using an optimal control approach. Magn Reson Med. 2008; 59: 547–560.
- 42Grissom WA, Xu D, Kerr AB, Fessler JA, Noll DC. Fast large-tip-angle multidimensional and parallel RF pulse design in MRI. IEEE Trans Med Imaging. 2009; 28: 1548–1559.
- 43Massire A, Cloos MA, Vignaud A, Bihan DL, Amadon A, Boulant N. Design of non-selective refocusing pulses with phase-free rotation axis by gradient ascent pulse engineering algorithm in parallel transmission at 7 T. J Magn Reson. 2013; 230: 76–83.
- 44Sbrizzi A, Hoogduin H, Hajnal JV, van den Berg CA, Luijten PR, Malik SJ. Optimal control design of turbo spin-echo sequences with applications to parallel-transmit systems. Magn Reson Med. 2017; 77: 361–373.
- 45Gras V, Vignaud A, Amadon A, Mauconduit F, Bihan D, Boulant N. In vivo demonstration of whole-brain multislice multispoke parallel transmit radiofrequency pulse design in the small and large flip angle regimes at 7 tesla. Magn Reson Med. 2017; 78: 1009–1019.
- 46Vinding MS, Brenner D, Tse DHY, Vellmer S, Vosegaard T, Suter D, et al. Application of the limited-memory quasi-Newton algorithm for multi-dimensional, large flip-angle RF pulses at 7T. Magn Reson Mater Phys Biol Med. 2017; 30: 29–39.
- 47Gras V, Vignaud A, Amadon A, Le Bihan D, Boulant N. Universal pulses: a new concept for calibration-free parallel transmission. Magn Reson Med. 2017; 77: 635–643.
- 48Lefebvre PM, Van Reeth E, Ratiney H, Beuf O, Brusseau E, Lambert SA, et al. Active control of the spatial MRI phase distribution with optimal control theory. J Magn Reson. 2017; 281: 82–93.
- 49Bonnard B, Cots O, Glaser SJ, Lapert M, Sugny D, Zhang Y. Geometric optimal control of the contrast imaging problem in nuclear magnetic resonance. IEEE Trans Auto Control. 2012; 57: 1957–1969.
- 50Assémat E, Lapert M, Sugny D, Glaser SJ. On the application of geometric optimal control theory to nuclear magnetic resonance. Math Control Related Fields. 2013; 3: 375–396.
- 51Bonnard B, Cots O. Geometric numerical methods and results in the contrast imaging problem in nuclear magnetic resonance. Math Models Methods Appl Sci. 2014; 24: 187–212.
- 52Chang Y, Wei D, Glaser SJ, Yang X. Optimized phase-sensitive inversion recovery for MRI contrast manipulation. Appl Magn Reson. 2015; 46: 203–217.
- 53Van Reeth E, Ratiney H, Tesch M, Glaser SJ, Sugny D. Optimizing MRI Contrast with B1 pulses using optimal control theory. In IEEE 13th International Symposium on Biomedical Imaging (ISBI). Prague: IEEE; 2016.
10.1109/ISBI.2016.7493271 Google Scholar
- 54Lapert M, Zhang Y, Braun M, Glaser SJ, Sugny D. Singular extremals for the time-optimal control of dissipative spin
particles. Phys Rev Lett. 2010; 104: 083001.
- 55Khaneja N, Brockett R, Glaser SJ. Time optimal control in spin systems. Phys Rev A. 2001; 63: 032308.
- 56Khaneja N, Glaser SJ, Brockett R. Sub-Riemannian geometry and time optimal control of three spin systems: quantum gates and coherence transfer. Phys Rev A. 2002; 65: 032301.
- 57Khaneja N, Reiss T, Luy B, Glaser SJ. Optimal control of spin dynamics in the presence of relaxation. J Magn Reson. 2003; 162: 311–319.
- 58Bonnard B, Chyba M, Marriott J. Singular trajectories and the contrast imaging problem in nuclear magnetic resonance. SIAM J Control Optim. 2013; 51: 1325–1349.
- 59Garon A, Glaser S, Sugny D. Time-optimal control of SU(2) quantum operations. Phys Rev A. 2013; 88: 043422.
- 60Khaneja N, Reiss T, Kehlet C, Schulte-Herbrüggen T, Glaser SJ. Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms. J Magn Reson. 2005; 172: 296–305.
- 61Glaser JS, Boscain U, Calarco T, Koch PC, Köckenberger W, Kosloff R, et al. Training Schrödinger's cat: quantum optimal control. Eur Phys J D. 2015; 69: 1–24.
- 62de Fouquieres P, Schirmer SG, Glaser SJ, Kuprov I. Second order gradient ascent pulse engineering. J Magn Reson. 2011; 212: 412–417.
- 63Squire W, Trapp G. Using complex variables to estimate derivatives of real functions. SIAM Rev. 1998; 40: 110–112.
- 64Wansapura JP, Holland SK, Dunn RS, Ball WS. NMR relaxation times in the human brain at 3.0 tesla. J Magn Reson Imaging. 1999; 9: 531–538.
10.1002/(SICI)1522-2586(199904)9:4<531::AID-JMRI4>3.0.CO;2-L CAS PubMed Web of Science® Google Scholar
- 65Parry A, Clare S, Jenkinson M, Smith S, Palace J, Matthews PM. White matter and lesion T1 relaxation times increase in parallel and correlate with disability in multiple sclerosis. J Neurol. 2002; 249: 1279–1286.
- 66Redpath TW, Smith F. Use of a double inversion recovery pulse sequence to image selectively grey or white brain matter. British J Radiol. 1994; 67: 1258–1263.
- 67Wattjes M, Lutterbey G, Gieseke J, Träber F, Klotz L, Schmidt S, et al. Double inversion recovery brain imaging at 3T: diagnostic value in the detection of multiple sclerosis lesions. Am J Neuroradiol. 2007; 28: 54–59.
- 68Jochimsen TH, von Mengershausen M. ODIN—Object-oriented development interface for NMR. J Magn Reson. 2004; 170: 67–78.
- 69Jochimsen TH, Schäfer A, Bammer R, Moseley ME. Efficient simulation of magnetic resonance imaging with Bloch–Torrey equations using intra-voxel magnetization gradients. J Magn Reson. 2006; 180: 29–38.
- 70Black S, Gao F, Bilbao J. Understanding white matter disease. Stroke 2009; 40: 48–52.
- 71Hittmair K, Mallek R, Prayer D, Schindler EG, Kollegger H. Spinal cord lesions in patients with multiple sclerosis: comparison of MR pulse sequences. Am J Neuroradiol. 1996; 17: 1555–1565.
- 72Turetschek K, Wunderbaldinger P, Bankier AA, Zontsich T, Graf O, Mallek R, et al. Double inversion recovery imaging of the brain: initial experience and comparison with fluid attenuated inversion recovery imaging. Magn Reson Imaging. 1998; 16: 127–135.
