A comparison of optimization algorithms for localized in vivo B0 shimming
Abstract
Purpose
To compare several different optimization algorithms currently used for localized in vivo B0 shimming, and to introduce a novel, fast, and robust constrained regularized algorithm (ConsTru) for this purpose.
Methods
Ten different optimization algorithms (including samples from both generic and dedicated least-squares solvers, and a novel constrained regularized inversion method) were implemented and compared for shimming in five different shimming volumes on 66 in vivo data sets from both 7 T and 9.4 T. The best algorithm was chosen to perform single-voxel spectroscopy at 9.4 T in the frontal cortex of the brain on 10 volunteers.
Results
The results of the performance tests proved that the shimming algorithm is prone to unstable solutions if it depends on the value of a starting point, and is not regularized to handle ill-conditioned problems. The ConsTru algorithm proved to be the most robust, fast, and efficient algorithm among all of the chosen algorithms. It enabled acquisition of spectra of reproducible high quality in the frontal cortex at 9.4 T.
Conclusions
For localized in vivo B0 shimming, the use of a dedicated linear least-squares solver instead of a generic nonlinear one is highly recommended. Among all of the linear solvers, the constrained regularized method (ConsTru) was found to be both fast and most robust. Magn Reson Med 79:1145–1156, 2018. © 2017 International Society for Magnetic Resonance in Medicine.
INTRODUCTION
B0 shimming is crucial for magnetic resonance spectroscopy and imaging, as an inhomogeneous B0 field introduces several artifacts such as geometric distortion, loss of signal-to-noise ratio, signal dropout, and loss of resolution as a result of blurring in imaging applications 1-5 and line broadening, localization problems, and loss of spectral resolution in spectroscopy applications 6. The problem becomes even worse at higher field strengths.
The task of B0 shimming is usually accomplished by measuring the magnetic field and calculating the required currents that have to be applied to a set of shim coils to cancel the nonuniformities of the original field. Many different methods have been proposed to find the optimal shim currents. Ideally, one should find an automated B0 shimming algorithm that is robust, numerically stable, and applicable to any arbitrary volume of interest. This algorithm should also handle the hardware limits of the shim system. Finally, it should be able to take the real shim field models into account in case the imperfections in the design cause the generated shim fields to deviate from the ideal spherical harmonics model 7-9.
The need for a reliable B0 shimming algorithm becomes even more important in the case of small regions of interests (ROIs) or when the ROI lies somewhere off-center relative to the iso-center of the magnet, where the shim fields are no longer orthogonal. In both of these cases, solving the shimming problem is tricky, as the problem becomes increasingly ill-conditioned, and unless a robust shimming algorithm is used, one may end up with unreasonably high shim values that are prone to noise in the input 19.
Over the years, different approaches for B0 shimming have been proposed. These methods can be classified into two general categories: projection and volumetric mapping methods. Projection mapping methods like FASTMAP, FASTERMAP, FASTESTMAP, or Pencil Beam 10-14 only measure a few linear projections, and hence have the advantage of being less time-consuming. The drawback, however, is that the localization techniques used to acquire these projections make it impossible to apply them to disjoint regions of interest such as in multivoxel spectroscopy. Moreover, because only a limited number of projections are acquired, they cannot always capture all of the local inhomogeneities.
Alternatively, the volumetric image-based mapping methods require longer acquisition times, but provide a full 3D map of the field. These B0 shimming routines then use a range of optimization algorithms to calculate the optimal shim values. Some approaches just calculate the required shim currents by simple matrix inversion, which provides the minimum-norm solution that minimizes residual B0 inhomogeneity in a least-squares sense 15-19. However, simple inversion is inherently unconstrained and cannot take the limits of the shim system into account. Although Juchem et al. 16, Wen and Jaffer 17, and Webb and Macovski 18 report that exceeding shim values never happened in their in vivo applications, there is no guarantee that this will hold for all other shim applications or different systems. Wen and Jaffer 17 proposed a method based on Powell 20, in which the simple matrix inversion is combined with an additional step in which they clip the shim currents that exceed their limit and recalculate new first-order values that compensate for the clipped higher-order shim values. However, this method is also not guaranteed to yield the best possible shim, as some inhomogeneities by nature cannot be compensated by only first-order terms. Adalsteinsson et al. 19 proposed a truncated singular value decomposition (TSVD) to regularize the problem. However, the constraints of the system are not directly taken into account, and it is not clear how the threshold for truncating the singular values should be chosen.
Another common trend is to use a constrained minimization algorithm to solve the problem. Klassen and Menon 21 used a linear least-squares optimization method based on the MATLAB (The MathWorks, Natick, MA) lsqlin function, and removed shim coils from the computation when the ROI is small, to prevent ill-conditioning. Both van Gelderen et al. 22 and Weiger et al. 23 used a least-squares optimization method but did not mention the specific algorithm or implementation. Hetherington et al. 24 proposed a three-step shimming method that would “minimize the possibility of becoming trapped in a high-order local solution.” In this method they start by fitting only the first-order shim terms and then use this as a starting value for the fit of higher-order shims in each step. Recently, more and more groups 8, 25-27 have used a Levenberg-Marquardt nonlinear least-squares minimization routine 28. Fillmer et al. 27 built upon this method by performing a multiple starting value search and including a region of less interest to avoid “local minimum traps.”
As shown by this brief literature review, several different methods are used by different groups on a range of B0 shimming applications. However, there is still a need for a systematic comparison of these algorithms. The aim of this work is to evaluate and compare the performance of 10 optimization algorithms in a range of B0 shimming applications in human brain on both a 7T and a 9.4T scanner.
THEORY
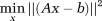 ()
()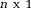 vector (n is the number of voxels in the ROI) that holds all of the unshimmed B0 field map voxels stacked column-wise to convert from a 2D or 3D ROI to a single vector; and A is a nxc matrix (c is the number of shim terms). The columns of A hold the fields produced by different shim coils, whereas the rows correspond to different voxels. Finally, x is a
vector (n is the number of voxels in the ROI) that holds all of the unshimmed B0 field map voxels stacked column-wise to convert from a 2D or 3D ROI to a single vector; and A is a nxc matrix (c is the number of shim terms). The columns of A hold the fields produced by different shim coils, whereas the rows correspond to different voxels. Finally, x is a
 vector of the unknown shim currents that need to be calculated.
vector of the unknown shim currents that need to be calculated.The hardware limitations of the shim system can be included as box-constraints
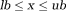 .
.
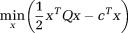 ()
()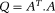 and
and
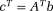 . This is a quadratic programming problem, and hence convex. Therefore, any solution to this problem is a global minimum. This means that the algorithm should not depend on a starting value and should always converge to the same global minimum.
. This is a quadratic programming problem, and hence convex. Therefore, any solution to this problem is a global minimum. This means that the algorithm should not depend on a starting value and should always converge to the same global minimum.
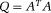 . is always positive semidefinite. In case it becomes positive definite, there is a unique solution to this problem. However, even when the matrix is only positive semidefinite, even though there are multiple solutions, they all yield the same global minimum. Note that this is true for all shimming applications, and having the box constraints does not change this fact.
. is always positive semidefinite. In case it becomes positive definite, there is a unique solution to this problem. However, even when the matrix is only positive semidefinite, even though there are multiple solutions, they all yield the same global minimum. Note that this is true for all shimming applications, and having the box constraints does not change this fact.
However, depending on the shimming application, the problem can become very ill-posed. In this case, the shim fields produced by the shim coils no longer form an orthogonal basis, and the columns of the matrix A will be nearly linearly dependent. By definition, an ill-posed problem is a problem in which the solution does not depend continuously on the input 29, meaning that arbitrary small perturbations can cause arbitrary large changes in the solution 19. According to the perturbation theory 19, even a small amount of noise in measuring the B0 field or estimating the sensitivity of the shim coils, or even precision round-off errors, can drastically change the results.
It is important to note that the ill-conditioning does not mean that a meaningful approximate solution cannot be computed. Rather, it implies that standard optimization methods cannot be used in a straightforward manner. Instead, more sophisticated methods must be applied to ensure the computation of a meaningful solution. This is the essential goal of regularization methods.
What is usually mistaken for local minima traps 27 or high-order local solutions 24 are actually the unstable behavior of the global solution that is typically physically meaningless and can change drastically by perturbing the input data.
Considering the theory behind this problem, even though it is a conventional linear least-squares minimization problem, extra care should be taken in choosing an algorithm that calculates stable solutions independent of the shimming application at hand.
METHODS
Algorithms
- 1.
Unconstrained pseudo-inversion (pinv): If the shimming problem in Equation [1] was unconstrained, the obvious solution to it would be
where A† is the pseudo-inverse of the matrix A. This solution always yields the best shim quality achievable when the system is not bound by constraints. Therefore, the unconstrained pseudo-inversion algorithm (pinv) using the MATLAB pinv function was considered as the benchmark for comparison purposes.
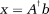 ()
() - 2–5. Generic constrained nonlinear optimization methods using the MATLAB fmincon function with three methods: active-set (nonlin-as) 30, interior-point (nonlin-ip) 31 and sequential quadratic programming (sqp) 30, and another one using Levenberg-Marquardt's algorithm implemented in IDL (levMar) (28).
- 6. A dedicated quadratic programming solver using the interior-point-convex method (QP) 32 using the MATLAB quadprog function.
- 7. A dedicated linear least-squares solver using the MATLAB lsqlin function.
- 8.
A constrained inversion algorithm in which the system is iteratively inverted and the values that exceed the limits are clipped to their maximum (Clipped-it). This method handles the constraints in an iterative manner while still keeping the problem at each step essentially unconstrained. Let us assume that in the first iteration we calculate the solution to the shim problem as
And suppose that the calculated values for two of the shim terms (xi, xj) exceeded their limits (xi > ui, xj > uj). These two terms are clipped to their maximum value (set xi = ui, xj = uj) and the b vector is updated by subtracting their contribution from the measured field vector as follows:
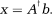 ()In the next iteration, the updated b vector
()In the next iteration, the updated b vector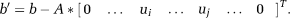 ()
()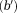 , and an updated matrix A that is obtained by eliminating the rows corresponding to shim terms i and j, form the updated problem
This is repeated until all constraints are satisfied.
, and an updated matrix A that is obtained by eliminating the rows corresponding to shim terms i and j, form the updated problem
This is repeated until all constraints are satisfied.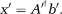 ()
() - 9. Similar to method 8, except that before starting the iterative inversion, the singular values of matrix A are truncated to a fixed and empirically chosen threshold (0.003) (Fixed-tsvd).
- 10.
A new method (constrained TSVD inversion method, or ConsTru) in which we simply solve the shim problem by pseudo-inverting the matrix A, but if any of our hardware limit constraints are violated, we truncate the smallest singular value of the matrix A and re-invert the new matrix. We continue doing this by truncating the next smallest singular value in each step until the calculated solution does not violate any hardware constraints. The rationale behind this algorithm is that if we consider the singular value decomposition of the matrix A
where
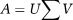 ()
() is a diagonal matrix with the singular values of the matrix A as its nonzero elements, then we can write the pseudo-inverse of the matrix A as
where
is a diagonal matrix with the singular values of the matrix A as its nonzero elements, then we can write the pseudo-inverse of the matrix A as
where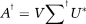 ()
()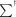 is calculated by taking the reciprocal of each nonzero element on the diagonal and transposing the matrix. This equation shows that if matrix A has small singular values (which is the case when the shim problem is ill-conditioned), the reciprocal of these values on the diagonal of
is calculated by taking the reciprocal of each nonzero element on the diagonal and transposing the matrix. This equation shows that if matrix A has small singular values (which is the case when the shim problem is ill-conditioned), the reciprocal of these values on the diagonal of
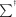 would contribute significantly to the norm of the solution
would contribute significantly to the norm of the solution
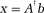 . This is problematic not only because this high norm solution would most probably violate the hardware limits, but also because according to the perturbation theory 19, these high values will amplify any input noise and result in numerically unstable solutions. It is therefore clear why truncating the small singular values of the matrix A before inverting it would help condition the problem and result in a minimum norm solution. A more comprehensive mathematical description of this can be found in Appendix A.
. This is problematic not only because this high norm solution would most probably violate the hardware limits, but also because according to the perturbation theory 19, these high values will amplify any input noise and result in numerically unstable solutions. It is therefore clear why truncating the small singular values of the matrix A before inverting it would help condition the problem and result in a minimum norm solution. A more comprehensive mathematical description of this can be found in Appendix A.
Data Acquisition
For this study, a total of 66 in vivo data sets from the brains of healthy volunteers were considered. Half of these data sets were acquired on a 7T magnet, and the other half on a 9.4T system. All participating volunteers gave written informed consent in accordance with local ethics regulations. Whole-brain B0 maps covering the entire cerebrum, cerebellum, and brain stem were acquired.
The 7T data sets were acquired on a 7T Achieva system (Philips Healthcare, Cleveland, OH) with a Nova Medical 32-channel Tx/Rx coil using a 2D gradient echo (GRE) sequence with repetition time (TR) = 6.86 ms; echo time (TE) = 3.1/4.1 ms; field of view (FOV) = 240 × 240 mm2; in-plane resolution = 2 × 2 mm2; 110 slices and slice thickness = 2 mm.
The 9.4T data sets were acquired on a 9.4T human whole-body Siemens scanner (Siemens, Erlangen, Germany) with an in-house-developed 8-channel transmit/receive coil 33. The B0 maps were acquired with a 2D GRE sequence with TR of 100 ms; TE = 4.01/4.77 ms; FOV = 200 × 200 mm2; in-plane resolution = 1.56 × 1.56 mm2; 50 slices and slice thickness = 4 mm.
Tests
For each volunteer, the performance of the algorithms for up to third-order shimming in five different shim volumes were studied (Fig. 1): (i) a whole-brain region covering the entire cerebrum, cerebellum, and brain stem; (ii) another global application covering the whole brain minus the medulla and the cervical spine; (iii) a single slice positioned off-center and going through the frontal sinus air cavity; (iv) a single voxel (2 × 2 × 2 cm3) located in the frontal cortex; and (v) in the visual cortex. The hardware limits of the shim system given in Table 1 were taken into account. The algorithms were tested against the following criteria.
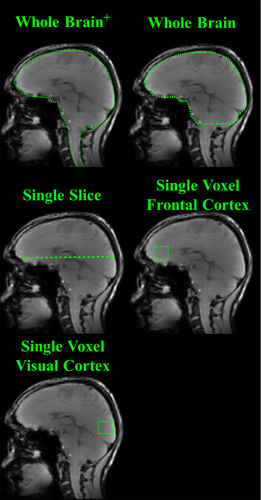
Anatomical image overlaid with five different shim volumes chosen for this study: (i) a whole-brain global shimming application for a region covering the entire cerebellum, cerebrum, and brain stem indicated as whole brain+; (ii) another whole-brain global shimming application covering the whole cerebellum minus the medulla and the cervical spine; (iii) a single-slice shimming application for a slice positioned off-center relative to the iso-center of the magnet; (iv) a single-voxel shimming application for a voxel located in the frontal cortex; and (v) another one in the visual cortex.
| Shim term | Spherical harmonic function | Sensitivity (Hz/cmn/A) | Maximum (mT/mn) |
|---|---|---|---|
| X | x | 42.15 | 0.99 |
| Y | y | 42.15 | 0.99 |
| Z | z | 42.15 | 0.99 |
| Z2 | z2 − 1/2*(x2 + y2) | 1.97 | 4.63 |
| ZX | Zx | 3.35 | 7.88 |
| ZY | Zy | 3.30 | 7.75 |
| C2 | x2 − y2 | 3.20 | 7.52 |
| S2 | 2xy | 3.13 | 7.35 |
| Z3 | z(z2 − 3/2*(x2 + y2)) | 0.012 | 2.82 |
| Z2X | x(z2 − 1/4*(x2 + y2)) | 0.016 | 3.76 |
| Z2Y | y(z2 − 1/4*(x2 + y2)) | 0.016 | 3.76 |
| ZC2 | z(x2 − y2) | 0.1 | 23.72 |
| ZS2 | 2zxy | 0.099 | 23.25 |
| C3 | x(x2 − 3y2) | 0.045 | 10.57 |
| S3 | y(3x2 − y2) | 0.044 | 10.33 |
- Note: The maximum available current for each shim channel was 10 A.
Sensitivity to Starting Values
Out of the 10 algorithms, four of them (namely, the generic nonlinear solvers (Algorithms [2] to [5])), require a starting value. Because these are numerical algorithms, they might not always converge within the given number of iterations; hence, the announced solution might well depend on where the search starts. Therefore, in this test the robustness of each of these algorithms is evaluated against the starting values. For each volunteer and shimming application, 1000 random starting point values were generated.
Numerical Stability
As the shimming problem becomes increasingly ill-conditioned, it becomes more and more challenging to calculate a meaningful and numerically stable solution; hence, the shim algorithm should be robust against any kind of perturbations by means of better-conditioning the problem. In this test, the robustness of each of the 10 algorithms was tested against noisy inputs. For each volunteer, 1000 different noisy B0 maps were generated by adding random white noise to the measured maps. The maximum amplitude of the noise was kept within ±1% of the original measured value.
Speed
Any time spent on calculating a stable solution for B0 shimming is an overhead to the scan time. Hence, in this test the speed of each of these algorithms was tested. The run times were calculated based on a 2.3-GHz 6-core Intel CPU with 16 GB of RAM.
Overall Performance in Different Shimming Applications
As mentioned previously, the theoretical limit on how well the shimming can do for the least-squares objective function, given a certain number of shim terms, is always given by the pinv algorithm. In practice, the shimming problem is always bound by hardware limits. Therefore, it may be impossible to achieve this theoretical limit. In this test, we evaluate how close the result of each of these algorithms gets to the theoretical limit. The test was performed on all volunteers and in all shimming applications for both second and third order.
Only the in vivo data sets acquired at 7 T were used for these four tests.
Overall Performance on 7T versus 9.4T Data Sets
It is well-known that B0 field homogeneity becomes more problematic at higher field strengths. Therefore, it would be interesting to evaluate how well each of the algorithms would handle the higher inhomogeneity in the B0 fields measured at 9.4 T compared with those measured at 7 T, and to compare the best shim quality one can achieve on each of them. So, in this test we compared the best shim quality achievable given the hardware limits of the shim system in all shimming application on both 7T and 9.4T data sets. For this test the best shimming algorithm (judged by the results of all of these performance tests) was used. For the comparison to be purely about the field strength and not the shim system specifications, the same hardware constraints (as stated in Table 1) were used in simulation on both 7T and 9.4T data sets.
Application in In Vivo Single-Voxel Spectroscopy
One of the most challenging shimming applications (in the sense of robustly finding the optimal shim solution) is single-voxel spectroscopy (such as in the frontal cortex of the brain). The shim quality directly affects the linewidth of the peaks in the spectrum. The purpose of this test was to apply the best shimming algorithm (judged by the results of all these performance tests) to shim a single voxel located in the frontal cortex of the brain, acquire non-water suppressed spectra, and evaluate the shim quality by calculating the linewidth of the unsuppressed water peak. The results were compared with those of shimming the same region with the vendor-implemented shimming routine. The effect of higher-order shimming was also studied by shimming the same volume with incremental second, third, fourth, and partial fifth/sixth-order spherical harmonic shim terms.
This test was performed on a 9.4T whole-body Siemens scanner with an in-house-developed eight-channel transmit/receive coil 33. To perform higher-order B0 shimming, an insert shim (MX10W-28) from Resonance Research Inc (Billerica, MA) was used. Twenty-eight channels including complete second, third, and fourth-degree spherical harmonics (and partial fifth and sixth-degree harmonics) were available. The sensitivities of each shim channel can be found in Table 2. A total of 10 healthy volunteers were scanned for this test. A STEAM sequence was used to acquire non-water-suppressed spectra with the following parameters: voxel size 2 × 2 × 2 cm3, 16 averages, TR of 5 s, TE of 11 ms, flip angle of 90 °, 1024 complex points, and spectral bandwidth of 8 kHz. The maximum shim current for each shim channel was limited to 2 A, and a total of 20 A was dedicated to the positive and negative rails (10 A each).
| Shim term | Spherical harmonic function | Sensitivity (Hz/cmn/A) | Maximum (mT/mn) |
|---|---|---|---|
| Z0 | 1 | 6058 | 0.28 |
| Z2 | z2−1/2*(x2+y2) | 6.942 | 3.26 |
| ZX | zx | 24.15 | 11.34 |
| ZY | zy | 24.15 | 11.34 |
| C2 | x2-y2 | 3.64 | 1.71 |
| S2 | 2xy | 3.64 | 1.71 |
| Z3 | z(z2−3/2*(x2+y2)) | 0.4923 | 23.12 |
| Z2X | x(z2−1/4*(x2+y2)) | 1.0 | 46.97 |
| Z2Y | y(z2−1/4*(x2+y2)) | 1.0 | 46.97 |
| ZC2 | z(x2−y2) | 1.77 | 83.14 |
| ZS2 | 2zxy | 1.77 | 83.14 |
| C3 | x(x2−3y2) | 0.188 | 8.83 |
| S3 | y(3x2−y2) | 0.188 | 8.83 |
| Z4 | z4−3z2(x2+y2)+3/8*(x2+y2) | 0.04206 | 197.57 |
| Z3X | zx(z2−3/4*(x2+y2)) | 0.123 | 577.78 |
| Z3Y | zy(z2−3/4*(x2+y2)) | 0.123 | 577.78 |
| Z2C2 | z(x2−y2)(z2−1/6*(x2+y2)) | 0.093 | 436.86 |
| Z2S2 | 2z(xy)(z2−1/6*(x2+y2)) | 0.093 | 436.86 |
| ZC3 | x(x2−3y2)(z2−1/8*(x2+y2)) | 0.121 | 568.38 |
| ZS3 | x(x2−3y2) (z2−1/8*(x2+y2)) | 0.121 | 568.38 |
| C4 | x4−6x2y2+y4 | 0.0187 | 87.84 |
| S4 | 4xy(x2−y2) | 0.0187 | 87.84 |
| ZC4 | z(x4−6x2y2+y4) | 5.71E-3 | 2682.20 |
| ZS4 | 4zxy(x2−y2) | 5.71E-3 | 2682.20 |
| C5 | x(x4−10x2y2+5y4) | 9.9E-4 | 465.04 |
| S5 | y(y4−10x2y2+5x4) | 9.9E-4 | 465.04 |
| ZC5 | zx(x4−10x2y2+5y4) | 3.21E-4 | 15078.56 |
| ZS5 | zy(y4−10x2y2+5x4) | 3.21E-4 | 15078.56 |
- Note: The maximum shim current for each shim channel was limited to 2 A, and a total of 20 A was dedicated to the positive and negative rails (10 A each).
RESULTS
Sensitivity to Starting Values
To evaluate the quality of the shim and how dependent it is on the starting values, the standard deviation of the frequency shifts (σB0) in the shimmed map was chosen as a metric. Figure 2 shows the results for a single voxel shimming application located in the frontal cortex. The results are shown only for the four algorithms that require a starting point value to operate. Each box in the box plot contains 33000 σB0 values, which are the results of applying the corresponding algorithm to all 33 volunteers (the ones acquired on the 7T magnet) with all 1000 different randomly generated starting point values. For comparison purposes, the best shim quality achievable through an unconstrained inversion (pinv) is also shown. On each box, the central mark (–) indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The mean value is shown with a cross symbol (†), and the whiskers span from 9 to 91% of the data. To better visualize how the outcome of the algorithms changes depending on the starting value, the results of the first 50 test cases are plotted in Figure 2b for a representative volunteer.
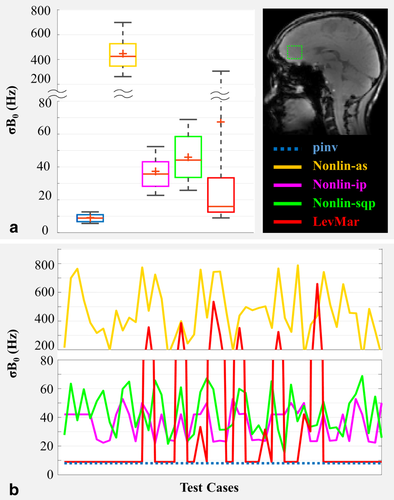
Starting-value sensitivity test results for a single voxel located in the frontal cortex. a: Box plot of the σB0 (standard deviation of the frequencies in the shimmed B0 map) resulting from applying each shimming algorithm to all 33 of the 7T in vivo data sets for all 1000 starting-point test cases. The best shim quality achievable through an unconstrained pinv algorithm is also shown for comparison purposes. b: Results of the same test in one representative in vivo data set (only 50 out of 1000 test cases are shown for better visualization).
These results, and those for single-slice and whole-brain applications, are summarized in Supporting Table S1.
The results show that the LevMar method gets closest to the best theoretical shim in most cases. All four algorithms depend heavily on the value of the starting point. However, as shown in Figure 2b, the LevMar method is the most robust against changes in the starting-point value except for cases in which it completely fails to converge. Note that the ill-conditioned problem has caused the nonlin-as method to result in unreasonably high values of the solution.
Numerical Stability
Figure 3a shows the box plot of the results of applying the 10 algorithms to all 33 volunteer data sets on 1000 noisy B0 maps each. For comparison purposes, the results of the unconstrained pinv algorithm is shown in the first column. Figure 3b shows the same results but only for the first 50 test cases on a representative volunteer for better visualization. The results shown in this figure, as well as those for single-slice and whole-brain applications are summarized in Supporting Table S1.
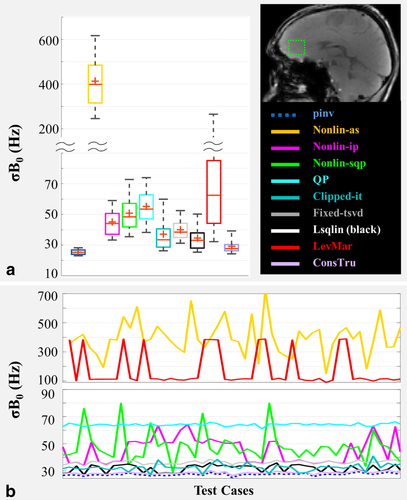
Numerical stability test results for a single voxel located in the frontal cortex. a: Box plot of the of the σB0 (standard deviation of the frequencies in the shimmed B0 map) resulting from applying each shimming algorithm to all 33 of the 7T in vivo data sets for all 1000 noisy test cases. The best shim quality achievable through an unconstrained pinv algorithm is also shown for comparison purposes. b: Results of the same test in one representative in vivo data set (only 50 out of 1000 test cases are shown for better visualization).
It is evident that the ConsTru algorithm follows the best theoretical shim quality most closely and is most robust against the noisy inputs. All other algorithms are more sensitive to the perturbations in the input; hence, their optimal convergence in the case of ill-conditioned problems is not guaranteed.
Speed
The average runtimes of the 10 algorithms across all volunteers are shown in Figure 4. The four nonlinear optimization methods (LevMar, Nonlin-as, Nonlin-ip, Nonlin-SQP) are orders of magnitude slower than the rest, and the Clipped-it, Fixed-tsvd, ConsTru and the QP methods prove to be the fastest. The results are summarized in Supporting Table S2.
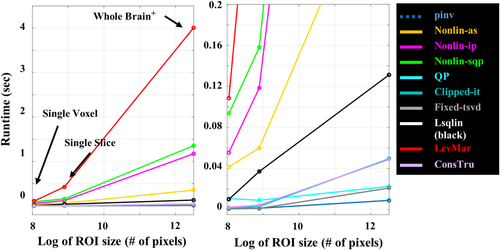
Comparison of the average runtime of the algorithms across all 33 of the 7T in vivo data sets as a function of the ROI size (shown on a log scale) on the left. A more zoomed in view is found on the right.
Overall Performance in Different Shimming Applications
Figure 5 shows the overall performance of these algorithms in three of the five shimming applications (the other two are shown in Supporting Fig. S1). Each algorithm was applied to all 33 volunteer data sets acquired at a 7T field strength. The average shim quality across all volunteers is shown in Supporting Table S3 for both second-order and third-order shimming. It can be seen that in the case of bigger ROIs, all of the algorithms (except for Nonlin-as and Nonlin-ip) perform similarly. This is expected, as the problem is well-conditioned in these cases. The differences start to show more as we move on to smaller ROIs. It can be seen that the ConsTru algorithm consistently gets closest to the best shim quality possible and is less prone to differences in the input data.
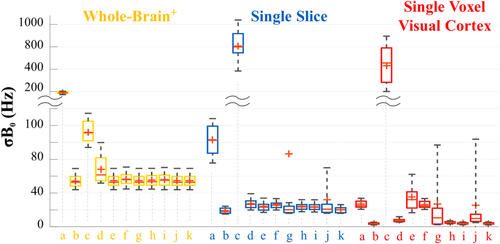
The overall performance of the different shimming algorithms in three different shimming applications. Each box contains the σB0 (standard deviation of the frequencies in the shimmed B0 map) resulting from applying each of the corresponding shimming algorithm to all 33 of the 7T in vivo data sets. The best shim quality achievable through an unconstrained pinv algorithm is also shown for comparison purposes. The different algorithms are indicated as follows: (a) unshimmed, (b) pinv, (c) nonlin-as, (d) nonlin-ip, (e) nonlin-sqp, (f) QP, (g) Clipped-it, (h) Fixed-tsvd, (i) Lsqlin, (j) LevMar, and (k) ConsTru.
Furthermore, to visualize how the σB0 values translate into shim quality, Figure 6 shows the resulting shimmed B0 map for a representative volunteer in a single-voxel shimming application. It can be seen that the ill-conditioned problem has caused some of these algorithms to result in unreasonable solutions. Once again, the ConsTru algorithm proves to have the best performance by getting closest to the best theoretical shim quality achievable.
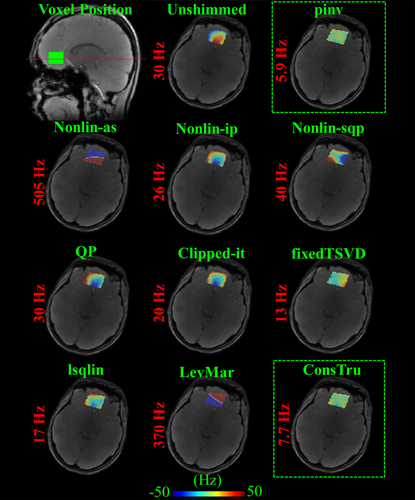
The resulting shim quality of 10 different shimming algorithms for a single-voxel shimming region located in the frontal cortex. B0 maps from a representative volunteer are shown along with the resulting standard deviation of the frequencies in the ROI. All B0 maps are displayed between −50 and 50 Hz.
From the results of the performance tests so far, it is evident that the ConsTru algorithm consistently performs most robust and among the fastest.
Overall Performance on 7T versus 9.4T Data
Figure 7 shows a comparison of the overall performance of the ConsTru algorithm on 7 T versus 9.4 T in five shimming applications. For each field strength, 33 in vivo data sets were available.
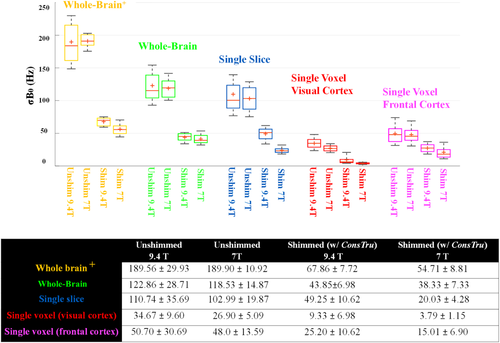
Comparison of the performance of the ConsTru shimming algorithms on a 7 T versus 9.4 T magnet in five different shimming applications. Each box contains the results of applying the ConsTru shimming algorithm to all 33 in vivo data sets. The average ( ± standard deviation) shim quality across all 33 volunteers for each algorithm is summarized in the table below the box plot.
Application in In Vivo Single-Voxel Spectroscopy
Figure 8a shows the box plot of the linewidth of the unsuppressed water peak in a single voxel in the frontal cortex after applying the vendor-implemented second-order shimming routine as well as those for the ConsTru algorithm for up to second, third, fourth, and partial fifth/sixth-order shimming. Each box contains the values obtained on 10 volunteers at 9.4 T. The total amount of current needed to achieve the shim (excluding the first-order terms) are shown in the accompanying table.
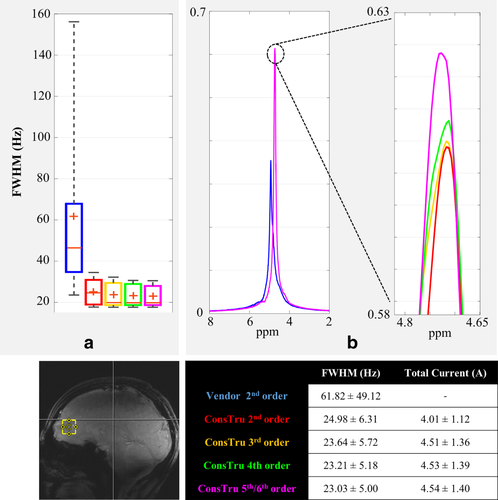
Comparison of the vendor-implemented second-order shim and the ConsTru algorithm for shimming up to second, third, fourth, and partial fifth/sixth order for single-voxel spectroscopy in the frontal cortex at 9.4 T. a: Box plot of the full width at half maximum of the unsuppressed water. Each box contains the results of applying the corresponding algorithm to 10 volunteers. The average ( ± standard deviation) of the results averaged across 10 volunteers, along with the amount of current needed to achieve the shim results, are summarized in the table below the plots. Same color codes as the table are used in the box plot. b: Representative unsuppressed water spectrum from one volunteer along with the voxel position. The magnified version of the tip of the peak is shown on the right, for better visualization of the differences between incremental higher orders of shimming.
Figure 8b shows the unsuppressed water peaks from a representative volunteer acquired with different shimming methods. Although the difference between the vendor-implemented second-order shim and ConsTru's second-order shim is clear, the difference between the ConsTru's second, third, fourth, and partial fifth/sixth order is not as big and is only visible when we magnify the top portion of the peak.
DISCUSSION
The task of B0 shimming can be very tricky when the shimming problem becomes ill-conditioned. Noise or error in the input data can be present for a number of reasons, such as limited spatial resolution, errors in the measurement of the reference field map, motion artifacts, limited signal-to-noise ratio and residual phase wrapping errors (in case multi-echo B0 mapping sequences 16, 34 are not used), and deviation of the shim fields generated by the coils from the ideal spherical harmonic functions. Additionally, there is always a limit on the maximum amount of shim currents. Considering all of this, the shimming algorithm should be robust and able to tolerate certain levels of noise and uncertainty in the input data, and yet result in reasonably low values of the solution.
The sensitivity to the starting-point-value test demonstrates that any nonlinear least-squares optimization method that requires a starting point to operate is prone to numerical instability. The next choice would be dedicated quadratic solvers that do not require a starting-point value. However, the results of the numerical stability test also show that unless some measure is taken to better condition the problem, unstable and suboptimal solutions are inevitable.
Typically, the way shim routines are designed to handle the ill-conditioned problem or errors in the input is either by preventing the problem from becoming ill-conditioned (by excluding certain shim fields) 18, 21, or by performing multiple iterations of the shim algorithm to ensure convergence 19, 27. The first method cannot be easily applied to any arbitrary ROI, because depending on the shape, size, or angulation of the ROI, different shim terms contribute differently to the shim; hence, direct operator supervision is required to exclude the correct shim terms. The second method, which either performs multiple iterations by measuring the reference field and solving the problem multiple times 19 or by feeding multiple starting values to the algorithm to get rid of the instability in the results 27, is also not ideal, because in the interest of reducing the overhead time, the algorithm should be fast and ideally require only one iteration.
The third option to better condition the problem is to regularize the shim matrix using methods such as SVD truncation or Tikhonov regularization methods 35, 19. Both of these are essentially minimum-norm solution methods and have the advantage of being noniterative, ROI-independent, fast, and robust. For the purposes of this study, the TSVD method was chosen (a more formal discussion is presented in Appendix B).
There will always be a trade-off between regularization and data fidelity; therefore, extra care should be taken in choosing the regularization parameter. The reason is that after regularization, we are no longer solving the original problem, but rather an approximated version of it. The regularization parameter can either be chosen empirically (Fixed-tsvd) or adaptively (ConsTru). It is always possible that by choosing an unnecessarily high value of the regularization parameter, we do not get as close to the best shim quality achievable (Fig. 6), or the measured shim quality in practice would be worse than the predicted one. Therefore, the adaptive regularization method (ConsTru) is preferable.
After sufficiently regularizing the matrix, finding the solution reduces to a simple matrix inversion. The only remaining issue is finding a way to constrain the solution. Two different methods were considered in this study: clipping the exceeding values and projecting the remaining inhomogeneities on other shim terms iteratively (Clipped-it, Fixed-tsvd), or adaptively choosing the regularization parameter that will satisfy the constraints while maintaining as much data fidelity as possible (ConsTru). The results of the overall performance test proved that the latter method on average got closest to the best theoretical shim quality.
Another advantage of the ConsTru algorithm is its flexibility in handling arbitrary constraints. This is because cost functions are directly calculated in each iteration, and more regularization is applied in the next step if constraints are being violated. This is of particular interest in cases in which the shim system has both limits on the maximum shim current of each channel and the total amount of positive and negative shim currents that the amplifiers can provide as a whole.
Although there are inherent differences between the levels of B0 inhomogeneities on a 7T versus 9.4T magnet, the ConsTru algorithm was able to successfully shim both data sets (Fig. 7). The residual differences between the shimmed maps on 7 T versus 9.4 T can be explained by noting that the same hardware constraints were used to shim both sets of data.
Applying the ConsTru algorithm to a single-voxel ROI in the frontal cortex at 9.4 T resulted in reproducible spectral linewidths that were much better than the vendor-implemented shim routine (Fig. 8). Increasing the number of orders decreased the mean linewidth; however, the improvement was not statistically significant (paired t-test). Additionally, despite the ill-conditioning, the ConsTru algorithm was always able to shim without requiring high amounts of currents ( < 4.5 A in total) because of its regularized nature.
In summary, this study showed in simulation that the proposed method (ConsTru) enabled successful and robust B0 shimming for a range of shimming applications, shimming orders, and field strengths. The method proved to be most robust and among the fastest compared with a wide range of algorithms derived from diverse concepts. The effectiveness of the algorithm was demonstrated in vivo for single-voxel spectroscopy. Because this algorithm calculates the analytical closed-form solution, it is very easy to implement. Furthermore, it is easily applicable to any arbitrary ROI, including multivoxel or multi-object shimming applications, and can be used to enable dynamic shimming.
CONCLUSIONS
For localized in vivo B0 shimming, the use of a dedicated linear least-squares solver instead of a generic nonlinear solver is highly recommended. The reason is that these solvers do not depend on a starting value and converge much faster. Among the linear least-squares solvers, the constrained TSVD inversion method (ConsTru) was found to be the most robust and among the fastest ones. The algorithm is easy to implement and applicable to any arbitrary ROI or shim system. The proposed method was used in a single-voxel spectroscopy application at 9.4 T, where it enabled the acquisition of high-quality spectra in the frontal cortex of the brain.