Polymerization Reactor Modeling in Industry†
Dedicated to the memory of the late Dr. George A. Kalfas of DuPont.
Abstract
This paper provides an industrial perspective for the development of polymer reaction engineering models and their application to create new materials, products, and improved or novel processes. The challenges specific to polymer reactor modeling are discussed in the context of articles and books that the authors have found useful. Four components of a polymer reactor model (kinetics, thermodynamics, transport effects, and particle dynamics) are discussed with illustrative examples. Finally typical outputs of polymer reactor models are shown to demonstrate that a first principles model supported and validated by experiments can be a very powerful tool for fundamental understanding of polymer reactors and is a recommended alternative to empirical methods and experimentation alone.
Introduction
Industrial polymer production represents a large investment resulting in significant sales volume. Therefore, it is the job of the engineer in collaboration with the polymer scientist, to produce the most efficient, economical and quality processes possible, which are required in a highly competitive multinational world. Traditionally experiments and empirical methods have been used to design and operate these polymer processes. However, with recent advances in theory, computational software, and hardware it is now possible to complement experiments and empiricism with sound mathematical models. These mathematical models, which are constructed on a first principles basis and have been validated with experimental data, may be used as a surrogate of the real process for a variety of applications where it may be costly, inconvenient, impractical, or unsafe to use the actual process. These applications include mechanistic investigation, design, control, simulation, operator training, safety screening, recipe checkout, and sensitivity analyses. In addition many difficult or impossible to measure quantities can be obtained from a well validated model.
It is well known that constructing models of polymerization reactors can be a challenging task. The difficulty involved in polymerization reactor models, as opposed to traditional small molecule reactor models, is primarily due to the disperse nature of the reactor products. The polymer products are characterized by a number of distributions, since the polymer is a collection of chains rather than a small molecule. These distributions typically include the molecular mass distribution, the copolymer composition and sequence distribution, and branching distributions (BD). The product itself may be produced in a reactor with multiple phases such as continuous, polymer-rich and other liquid phases and possibly a vapor phase. It is worth noting that monomers are usually partitioned between all existing phases in a reactor. The polymer phase may consist of solvent and chains as one phase or this phase may be composed of particles. This then also leads to a particle size distribution (PSD) in the case of emulsion, dispersion, precipitation, or suspension polymerizations. Prediction of these distributions is critical for the prediction of the final product properties, which are important to the customer. It is also important to know where all the species are and in what phase of the reactor they are in order to calculate the yields and conversions. The presence of a catalyst represents an additional modeling challenge both in terms of kinetic complexity and reactor configurations as is particularly the case in the modeling of polyolefin reactors.
The purpose of this paper is to show by examples how these models are categorized, constructed from component submodels and solved. It is not meant to be an exhaustive literature review but to provide a flavor of how these problems are attacked and solved from our industrial viewpoint. We are expanding here on some of the ideas presented in the conference proceedings article by Mueller et al.1
In this paper we first review some of the more recent literature of the last 40 years or so particularly illustrating review articles and books that have been useful to the industrial practitioner. We then show how we classify our polymers by chemistry and physics. Then the elements of polymerization models are discussed with examples. The particular problem of parameter estimation once the chemistry, mechanism, and physical structure of the model are elucidated is also discussed. Some aspects of model implementation are shown. Finally, we attempt to draw some conclusions based on literature approaches and our own experience. Since we are quite familiar with heterogeneous free-radical polymerization systems, we cannot help but overemphasize this area. But suffice it to say other areas such as catalytic polymerization (e.g., using Ziegler–Natta or metallocene based catalysts) are equally important but we will leave their discussion to other reviews. The reader should forgive us if we include many of our own former papers in this review, but nevertheless they should still serve as examples for our purpose.
Literature Review
Polymer Reaction Engineering Articles
The earliest review that we examine is that of Ray2 in 1972. This review is an excellent starting point for one who wants to understand relatively quickly some of the aspects of the mathematical modeling of polymerization reactors. It also serves as a fair review of much of the previous decade's progress with 125 references to some of the early classic works in polymer reaction engineering. The mathematical techniques as well as some of the distributions that are necessary as well as numerical methods for solving the polymerization kinetic equations were reviewed along with some practical examples that are still applicable today. In a more recent and shorter review Ray, Soares, and Hutchinson3 also provided a very interesting historical retrospective of the early years (1930 and 1940 s) and the developing years of the field (1950–1980 s) and concluded with the current challenges and thoughts for the future.
An early paper on the dynamic modeling of emulsion polymerization reactors is that of Penlidis, MacGregor, and Hamielec.4 This survey paper discussed the dynamic and steady-state modeling of emulsion polymerizations of homo and copolymers in a variety of reactor types including batch, semi-batch, and continuous reactors and showed how these models can be used for reactor design optimization and online state estimation and control. In an award lecture delivered in 1993, Penlidis5 further elaborated on the results obtained in his laboratory from systematic studies of polymer reaction engineering and polymer production technology problems.
A paper which illustrates the use of a polymerization model for reactor control was published in 1989 by Congalidis, Richards and Ray.6 A hierarchical control system was designed for a solution copolymerization reactor using a combination of feedforward, ratio, and feedback control to regulate polymer production rate, copolymer composition, molecular weight, and reactor temperature. The model of methyl methacrylate and vinyl acetate copolymerization was based upon one used in industry. This particular reactor model has served as a benchmark problem for many studies using alternative control strategies and techniques that have been performed since its original publication, the most recent example being that of Lima et al.7
A fairly complex emulsion polymerization model which includes multiphase and PSD was proposed by Richards, Congalidis, and Gilbert.8 This particular model included several types of particle nucleation and multiphase species material balances to calculate the time evolution of the concentration, size, and colloidal characteristics of the latex particles, as well as the monomer conversions, copolymer composition, and average molecular weight in the emulsion system. This paper among others served as a good starting point for subsequent emulsion polymerization models of increasing complexity including the full PSD as well as molecular weight distributions (MWD) (e.g., Immanuel et al.9). Saldívar and Ray10 and Saldívar, Dafniotis, and Ray11 also discussed their comprehensive modeling approach of emulsion copolymerization with emphasis on the numerical techniques which were necessary to solve the partial differential equations describing the PSD and the molecular weight moments of the bulk polymer.
Another class of heterogeneous polymerization is suspension polymerization where one or more water insoluble monomers containing oil soluble initiators are dispersed in the continuous aqueous phase by using strong stirring and stabilizers. This process has been practiced for decades in industry and some of the underlying important issues namely the dependence of the final PSD on the operating parameters, the stabilizer mode of action, and the dispersion mechanisms were discussed in a review by Yuan, Kalfas, and Ray.12 In a subsequent review Vivaldo-Lima et al.13 provided an update on suspension polymerization stressing the time period from 1991 to 1995, as well as research articles or reports not considered in previous reviews. Their review emphasized all the major phenomena that affect the particle size distribution and the experimental validation of their model with the styrene/divinylbenzene copolymerization system.
A fairly comprehensive review of polymer reactor modeling by Kiparissides14 appeared in 1996. The author explained the chemistries and categories of reaction mechanisms and processes involved in producing polymers. He also explained how to develop these comprehensive mathematical models which are capable of predicting molecular and morphological properties as functions of reactor configuration and operating conditions. He presented an overview of these different polymerization processes and modeling approaches.
The review paper by Dubé et al.15 outlined a common model framework which is applicable to many multicomponent systems for monomer conversion, multivariable distributions of concentrations of monomers bound in the polymer chains and molecular weights, long- and short-chain branching frequencies, chain microstructure, and crosslinked gel content. The free volume theory was used to account for diffusion-controlled termination, propagation, and initiation. Various comonomer systems such as benzene/meta- (or para-) divinylbenzene16 were used to illustrate the development of practical semibatch and continuous reactor operational policies for the manufacture of copolymers with high quality and productivity.
A short but nevertheless interesting paper by Chen17 appeared in 2002. The author discussed the challenges of polymer process modeling in general as well as some unsolved problems and future opportunities. He also discussed the various submodels that are used in constructing polymer reactor models such as polymer thermodynamics, transport properties, structure–property relationships, mass transfer, computational chemistry, and computational fluid dynamics.
Another short but important paper appeared by Hungenberg18 in 2004. He described the article as a “non-exhaustive and somehow arbitrary review on actual trends and remaining challenges for a model based process development”. He discussed some of the challenges that are still important in this field as well as some of the unsolved problems. He also showed how various submodels support the entire model in the process of model building.
A review by Choi et al.19 discussed recent developments in modeling techniques for the calculation of polymer properties including molecular weight distribution, copolymer composition distribution, sequence length distribution, and long chain branching. The application of process models to the design of model-based reactor optimizations and controls was also discussed with some examples. Some of these concepts were further elaborated in a subsequent publication by Choi20 with special emphasis on the modeling, analysis, and control of polymer microstructure as illustrated in the heterogeneous catalyzed alpha-olephin polymerization.
The investigation of the polymerization of ethylene under high pressure (up to 3 000 bar) has been an important area of research because of the complexity of the kinetic mechanisms and the industrial significance of the process. This area was recently reviewed by Bauer et al.21 with special emphasis on the techniques that were used to elucidate and characterize the underlying kinetic mechanisms. An important industrial example of the mathematical modeling of free radical ethylene copolymerization in high-pressure tubular reactors was illustrated in Kiparissides et al.22 in 2005. Here some of the previous work in this extensive area were also reviewed. A detailed kinetic mechanism, which can become quite complex, was the basis of the equations derived for the various molecular species as well as the total mass, energy, and momentum in the polymerization reactor. The thermodynamics and transport properties were also introduced in the solution of the model. The model is capable of calculating the number and weight average molecular weights and polymer composition averages as well as the short and long chain branching frequencies. The model was compared with industrial experimental data for several copolymerization grades. Further discussion of some of the industrial aspects of polyolefin production was provided in the review paper by Villa.23. In particular he illustrated some of his modeling concepts with a catalytic Ziegler–Natta autoclave reactor for low density polyethylene (LDPE) production. Constrained geometry catalysts as an alternative to the Ziegler–Natta catalysts were mentioned. He also discussed some aspects of living polymerization as a more efficient process technology. Another example he used was the ring opening polymerization of glycidol as a polyol polymerization. His conclusion was that reaction engineers have an important role in new polymer developments, because they are able to exploit molecular architecture that a new reaction mechanism is capable of producing.
A review article on the measurement and control of polymerization reactors was published by Richards and Congalidis24 in 2006, which surveyed the instrumentation technologies of particular interest in polymerization reactors with emphasis on the measurement of viscosity, composition, molecular weight, and particle size. This paper presented a hierarchical approach to the control system design and reviewed traditional regulatory as well as advanced control strategies for batch, semibatch, and continuous reactors. These approaches were illustrated by focusing on the control of a commercial multiproduct continuous emulsion polymerization reactor. Finally, the paper captured some of the trends in the polymer industry, which may impact future development in measurement and reactor control.
Kiparissides25 discussed the challenges of particulate polymerization reactor modeling from a population balance perspective. The analysis of these processes is a rather complex problem due to the highly coupled kinetics, thermodynamics, heat and mass transfer phenomena, taking place in a heterogeneous process. Here some mathematical techniques for the solution of the dynamic population balances were discussed. Examples of theoretical and experimental results were shown on the PSD in a suspension polymerization reactor. Two specific numerical techniques, the orthogonal collocation on finite elements and the fixed pivot technique, were applied to a free radical batch polymerization reactor to calculate the molecular weight distribution. Future directions in multidimensional population balance models, multicompartment models and issues on optimization and control were also discussed.
When these models are constructed and mechanisms elucidated, the problem still remains of specifying all the numerous parameters in the model. Careful experiments can be done to estimate some of them independently such as pulse laser polymerization (PLP) studies. A review on finding rate coefficients for free-radical polymerization using PLP was given by Beuermann and Buback.26 The pulsed laser polymerization technique coupled with size exclusion chromatography (SEC) yields the propagation rate coefficient. The single pulse SP–PLP method which combines PLP with time resolved NIR spectroscopy also yields the termination rate coefficient. A new trend is to attempt to calculate these parameters from first principles. Deglmann et al.27 illustrated the problem of calculating the propagation rate coefficients in free radical solution polymerization based on in situ quantum chemical methods. They concluded that a predictive calculation of chemical reactive kinetics in solution is a highly promising approach for obtaining rate coefficients and elucidation of reaction mechanisms. The important task of a careful evaluation of kinetic and other model parameters will be addressed later in this work.
One additional element of complexity is that the distributions which are important in polymer reactor modeling are not always necessarily univariate, but there are occasions when they can be bivariate or multivariate. They may be, for example, the joint molecular weight distribution (MWD) and composition distribution (CD). In other cases the two-dimensional radical distributions can be the MWD and BD. Another example of a two-dimensional radical distribution is shown in the article by Nikitin et al.,28 that discusses a long chain branch point formed by monomer addition to radicals Ri,j with distinct values of fragment lengths i and j. Finally, another example of this type of multivariate species distribution is the evaluation of the chain length distribution (CLD) in an emulsion polymerization. The three dimensional distribution Ni,n,m is defined as the number of particles with i radicals containing a pair of radicals with chain lengths n and m and can be computed as shown in the paper by Butté et al.29 In these cases the search for the multivariate distribution becomes computationally intensive.
Polymer Reaction Engineering Books
There are many books available to the engineer who is interested in practicing polymer reaction engineering. This section reviews those books, which we have found helpful in our work. In fact many of these books have already been reviewed by authorities in the field, so we benefit here from a few of their thoughts. Although the seasoned expert in the field may find this section superfluous and decide to skip it, we believe it is of value to practitioners entering the field especially those with experience of modeling of only small molecule reaction systems.
We may divide these books into two categories. The first category is that of a general polymer chemistry and physics text whereas the second category is more specific to polymer reactors themselves. Among the former we find the books by Flory,30 Rodriguez et al.31 and Odian.32 Of course there are several other polymer chemistry books which could be mentioned here to complement these three, as for example the book Polymer Chemistry by Hiemenz and Lodge33 in 2007 and the latest edition of the Polymer Handbook34 in 1999.
Although Flory's book Principles of Polymer Chemistry,30 is over a half century old it still is a valuable source for original work up until that time in polymer chemistry. Huggins35 wrote “The coverage of the field is thorough and accurate. Although a large proportion of the treatment is based on Professor Flory's own work, that of others is not neglected. Quantitative relationships are expressed mathematically, as they should be, but the mathematics is kept as simple as reasonably possible. Throughout the book, the author shows his gift for making complex subjects understandable.” This work is a good reference for the origin of many of the commonly used kinetic mechanisms.
Of the book Principles of Polymer Systems by Rodriguez,31 Pearce36 wrote “Professor Rodriguez has produced a fine revision of his textbook. This book fills a real need for a basic polymer textbook for individuals with an engineering orientation. As such, it is an excellent first textbook for courses on polymers, and can be used as a basis reference textbook, and is recommended also as a basic desk copy reference.” The books which are more specialized to PRE itself will now be addressed.
Of the book Principles of Polymerization by Odian,32 Immanuel37 wrote “This is a comprehensive book on the mechanisms and kinetics of the different types of polymerization, with the latest (fourth) edition including topics of ongoing research interest. A typical course on polymers to students in (chemical) engineering in this integrative climate would comprise the following: polymers, their function, and its characterization in the context of typical applications; polymerization chemistry and kinetics; polymerization reaction engineering; dynamic modeling, and optimization/control. This book will be an invaluable textbook for the polymerization chemistry, kinetics, and reactor dynamics part of such a course.”
Of Polymer Chemistry by Hiemenz and Lodge,33 Barner-Kowollik and Junkers38 wrote “The second edition of Polymer Chemistry, updated by Timothy Lodge, is a book designed for the beginner in polymer science and addresses advanced undergraduate students and may even find some use in postgraduate polymer courses. We have not used the book before in our undergraduate teaching, but were immediately taken by clear and concise language as well as the overall structure. Each chapter features a chapter summary as well as a relatively extensive problem section. The chapters are assembled in a logical fashion going from the various polymerization protocols to polymer structure, conformations, thermodynamics to viscoelasticity. A separate chapter is dedicated to the important technique of light scattering. Overall, the strengths of the book lie in the physical aspects of polymer science.”
We would be remiss if we did not at least mention the Polymer Handbook34 which we have used extensively. Royappa39 wrote “There is not a polymer scientist alive, I wager, who has not at one point or another had to refer to the Polymer Handbook. This venerable compendium of polymer-related information, now in its fourth edition and its fourth decade, is absolutely indispensable to anyone with a serious interest in polymer chemistry and physics. The compilers of this enormous mountain of polymer data have brought on board some new editors and associate editors, and the results of their labors are laudable.” However, Gilbert40 reminded us of a general caution of the use of rate coefficients taken from the Polymer Handbook and the literature in general. He illustrated his point by constructing a plot (Figure 2.7 of Gilbert40) of the propagation rate coefficients for methyl methacrylate at 25 and 30 °C from the data tabulated in the Polymer Handbook, which show a wide range of values under ostensibly the same conditions. He observed that “while the scatter of values of rate coefficients in Figure 2.7 of Gilbert40 might be seen in a single set of measurements and so represent statistical fluctuations, one would hope that each of the literature data shown in this figure is itself a proper average over a number of individual measurements and should therefore show little variation between different workers using different techniques if the results were what they purport to be.”
Of Principles of Polymerization Engineering by Biesenberger and Sebastian,41 Platzer42 wrote “This is a very comprehensive and well-written book that covers the kinetics of polymerization processes in an excellent way. The authors deal with the concepts of addition homo- and copolymerization, branching, initiation, termination, mixing, thermal effects, flow phenomena, and viscosity changes. They present numerous mathematical models for reaction equilibria, reactor design, and recovery of polymer by devolatilization.”
Of Reaction Engineering of Step Growth Polymerization by Gupta and Kumar,43 Jenkins44 wrote “Basic studies of chemical reactions are carried out under conditions very different from those necessary in commercial processes, leaving a gap which must be bridged by the chemical engineer. Polymerization is one of the largest scale chemical operations. Recent years have seen a substantial increase in the number of books dealing with polymerization reaction engineering. The present text restricts itself to polymerization processes of the step-growth type, typified by polyesterification, and polyamidification.”
Of Control of Polymerization Reactors by Schork et al.,45 Chylla46 wrote “Control of Polymerization Reactors is a book that fills a niche for a treatment of automatic control of polymerization reactors. Polymer reactor engineering and the control of polymer reactors have developed into core chemical engineering technologies of great commercial importance. Yet, few books on polymer reactor engineering and fewer still on the control of polymer reactors exist. This book treats the subject of polymer reactors more broadly than the title suggests” and “Overall, Control of Polymerization Reactors is a well-written, comprehensive book on the subject of polymer reactor engineering and control. The authors provide readers with a firm foundation in the principles of polymer reactor engineering to develop a broad background for understanding the challenges in polymer reactor control.”
Of Polymer Reaction Engineering edited by McGreavy,47 Ryan48 wrote “The academic world and, more importantly, the chemical industry needs a well written book on polymer reactor engineering which would unify the subject bringing out the key fundamental issues whilst leaving the tedious detail to the more specialized literature. Considering the vast amount of economic activity emanating from reactors there is a surprisingly poor coverage of the area. Most of the texts which purport to fill this void are either conference proceedings or edited contributions. This book is an improvement on most of its predecessors being a typeset collection of contributed chapters which have been edited to give some consistency of style.”
Of Emulsion Polymerization: A mechanistic approach by Gilbert,40 Warson49 wrote “The author criticizes some published work in which the number of variable parameters of unknown value exceeds the number which can be obtained from limited sets of data, and stresses that sufficient independent data must be available to pinpoint unambiguously the mechanism of a process.” and “This is probably the most comprehensive book yet published on emulsion polymerization, using a critical but useful approach to a highly complex subject, which, after 70 years of study, still has many problems unsolved theoretically, even if there have been enormous advances in theory and technical practice.”
Of Polymerization Process Modeling by Dotson et al.,50 Brooks51 wrote “In their preface, the authors say that this book is based on material that can be used for senior students or graduate students and it is not intended as a review book for the practising polymerization engineer. There are seven chapters which cover many important aspects of polymerization processes. Each chapter includes a substantial, up-to-date, list of references and a set of problems for the reader.” and “Readers with a basic grasp of chemistry and mathematics, will find this book a useful aid in coming to terms with the essentials of polymerization processes. There are a few points of detail with which the reviewer did not agree, but that does not detract from the value of the book. It can be recommended to students, by teachers of university courses in materials and chemical engineering, because it provides a treatment that is not found in many other books.”
Of Chemistry and Technology of Emulsion Polymerization edited by van Herk,52 Cunningham53 wrote “Originating from a course on emulsion polymerization taught at Eindhoven for many years, the book's target audience includes graduate students as well as industrial practitioners interested in furthering their fundamental and practical understanding of emulsion polymerization. A stated objective of the book is to provide a readily comprehensible framework for coupling theory to the issues encountered in industrial latex production.” He goes on to say “Industrial practitioners seeking to teach themselves about emulsion polymerization should find it strikes a good balance between depth and breadth. While not as exhaustive in detail as other available books on emulsion polymerization, its comparative conciseness (coupled with extensive references) makes it an excellent source for learning the key principles of emulsion polymerization.”
Of the Handbook of Polymer Reaction Engineering edited by Meyer and Keurentjes54 the publisher stated “This first book dedicated to all aspects of the field presents our current knowledge in its entirety, covering the necessary disciplines and processes involved – from the monomer to the final product. With an international editor and author team from academia and such leading chemical companies as Bayer, BASF, and DuPont, the text adopts a multidisciplinary approach and a practical point of view. Starting with polymer chemistry and thermodynamics, the book goes on to deal with measurement, control, and characterization, before tackling process development, safety issues, scale-up, and modeling. It concludes with emerging processes. With its unparalleled depth of coverage, this will be the definitive reference on this topic for years to come.” We tend to agree with this view; two of us contributed to the book a chapter entitled “Measurement and Control of Polymerization Reactors”.55
Of the book Polymer Reaction Engineering edited by Asua56 the author stated that “Polymers are “product-by-process” whose microstructure, and hence their final properties, are mostly determined in the reactor. Therefore, the understanding of the processes occurring in the reactor is crucial to achieve an efficient, consistent, safe, and environmentally-friendly production of polymer materials with improved performance. This book provides the link between fundamentals of polymerization kinetics and the polymer microstructure achieved in the reactor. The aim is to instill a firm understanding of the effect of polymerization kinetics on both reactor performance and polymer quality, learning how to manipulate the process variables to achieve the process goals.”
Polymer Classification
Polymers can be classified in various ways. For example, depending on the source, they are natural polymers (e.g., protein, rubber, cellulose) or synthetic polymers (plastics). Depending on number and arrangement of monomers they can be classified into homopolymers, copolymers (e.g., random, block, graft), terpolymers etc. Amorphous, semicrystalline, and crystalline polymers differ with respect to their chain order (cf. Figure 1).
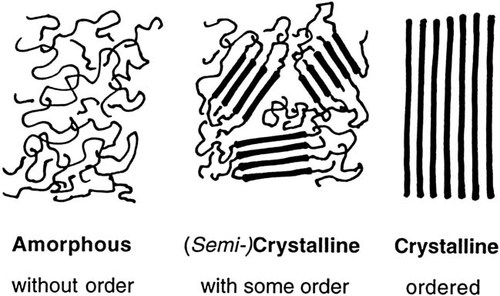
Classification of polymers with respect to their chain order.
Synthetic polymers can be classified with respect to the dominant kinetic mechanism that results in long chain growth. In condensation or step-growth polymerization monomers can react with other monomers and also with polymer chains of any length to build up molecular weight. Typical condensation polymers are polyesters like polyethylene terephthalate (PET), and polyamides like nylon 6,6. In addition or chain-growth polymerization growing chains add on monomers to build up molecular weight and there are live and dead polymer chains. For addition or chain-growth polymerization subtypes can be identified with respect to the active site (free-radical, cationic, anionic, or coordination polymerization). Typical addition polymers are polyethylene, poly(propylene), ethylene copolymers, polystyrene, or poly(methyl methacrylate) (PMMA).
Classifying a given polymerization system is usually the first step in polymerization modeling, and will help to decide how to attack the problem. In this work, we show some concepts and tools that are used in industry to solve polymer reaction engineering problems using mathematical modeling. Rather than elaborating on an example of a specific polymerization system we will review some typical kinetic, thermodynamic, and mass transfer models that we use to analyze and solve our commercial polymerization processes which are oftentimes complex in nature.
Elements of Polymerization Models
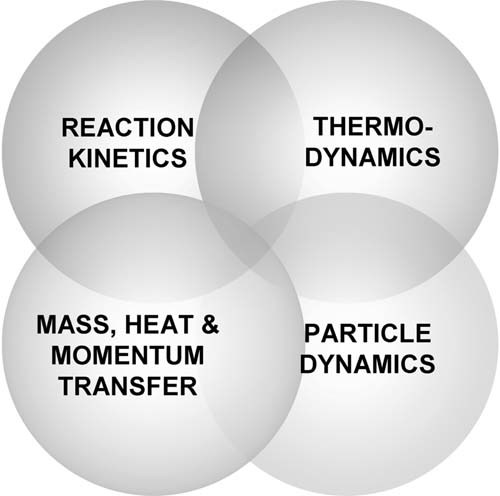
During the model development stage usually multiple submodels or elements are treated and eventually combined to yield the final global polymerization models. Figure 2 shows the four typical elements of a polymerization model namely the reaction kinetics, the thermodynamics, the particle dynamics, and the mass, heat, and momentum transfer. The level of complexity in each submodel is a strong function of the model application. For example in many cases it may be appropriate to use a lumped approach in describing particle dynamics in terms of an average particle diameter whereas in other cases it may be imperative to include the full PSD calculations. Furthermore there are additional elements of a model that have not been explicitly included in Figure 2 such as mixing, which is well known to be of importance in high pressure polyolefin reactors for instance.
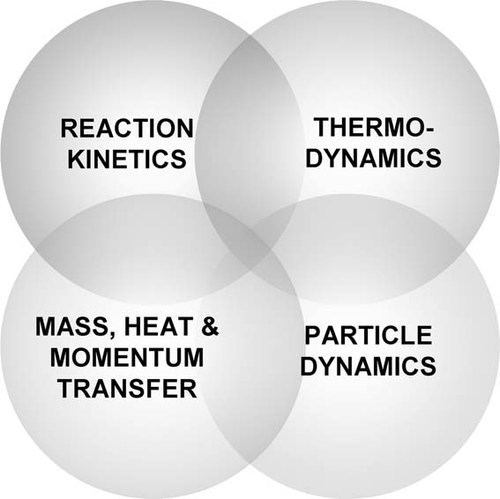
Elements (submodels) of polymerization models.
The Reaction Kinetics submodel consists of mass and population balance equations, which are derived based on elementary reactions proposed in the reaction mechanism.50 This usually yields a system of differential and/or algebraic equations that can be solved using various numerical methods (e.g., method of moments or numerical discretization).
Regarding the thermodynamics of a polymerization system, there are several approaches with different levels of complexity to describe phase behavior and phase partitioning of a polymerization mixture, ranging from simple partition coefficients to complex equations of state or activity coefficient models. Typical equations of state are Peng-Robinson (for small molecules), and Sanchez-Lacombe57, 58 or PC-SAFT59, 60 which are appropriate when a polymer phase is also present in the reactor. The thermodynamic submodel usually consists of a set of non-linear algebraic equations that is solved simultaneously with the differential mass balances.
Many polymerization systems are characterized by the existence of a separate polymer-rich phase which often appears in the form of polymer particles. In these systems, a submodel describing the particle dynamics needs to be developed. It usually contains the description of particle formation (nucleation), particle growth, particle coagulation, and sometimes also particle breakage. There are various approaches to describe the particle kinetics in a polymerization system. Simple ones, for example, assume instantaneous nucleation (seeded polymerization) yielding equal-sized spherical particles of constant number (no coagulation). More detailed ones include particle formation by homogeneous and heterogeneous nucleation followed by particle coagulation where particles can be described as equal-sized spheres or as a distribution of a range of sizes. Particle coagulation is promoted by Brownian motion (perikinetic), shearing stresses (orthokinetic), or sedimentation. There are also models that account for the role of surfactants or stabilizer, for example, by using the DLVO theory.8
Finally, mass transport effects are important in many polymerization systems. Diffusion limitations usually affect both chemical rate coefficients and interphase mass transport. The latter can be described by film theory with the help of correlations for mass transfer coefficients. Typical diffusion limitations on polymerization reactions are the cage, glass, and gel effects. The cage effect describes the decrease of initiator efficiency whereas glass and gel (or Trommsdorff) effects denote the reduction of propagation and termination reaction coefficients, respectively. Models to evaluate diffusion coefficients of monomers and polymer chains are usually needed to accurately describe mass transport effects (cf. section Parameter Evaluation).
It is worth noting that today commercial software packages are available that can be used to solve submodels of any of the types shown in Figure 2 (cf. discussion in section Model Implementation). Unfortunately, most of the commercially available packages are specialized and may not be able to address all model elements with the desired depth. In this case, derived equations for all submodels need to be solved using user-defined algorithms, the solution of which may be a challenge even for nowadays high-performance computers. Some recent efforts have been focused on the coupling of commercial packages to simultaneously solve two or more of the elements shown in Figure 2 as discussed with some more detail in section Model Implementation.
Parameter Evaluation
The estimation of the large number of model parameters is a critical task when developing fundamental mathematical models. For most reliable model predictions and highest predictability the number of adjustable or “free” parameters should be kept to a minimum. Parameters can be obtained from literature sources or by fitting to experimental data.
Figure 3 shows that as model complexity increases (e.g., by the incorporation of additional kinetic mechanisms) the ability of the model to predict system behavior is enhanced. Although the increased number of parameters may make it easier to match the experimental observations with the model, there is an increased effort to evaluate these parameters from independent experiments. Therefore, there is an optimum which balances model complexity and parameter estimation. Improvements in experimental capabilities may shift the minimum toward more complex models. The following subsections show some examples of typical types of parameters and how they can be estimated by fitting independent experimental data.
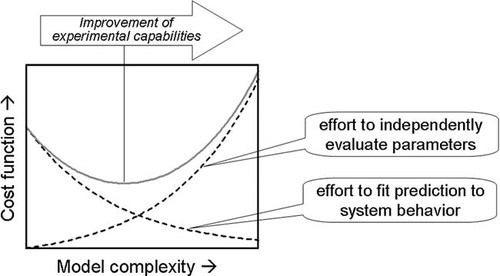
Cost function showing effort to independently evaluate model parameters and effort to fit model results to system behavior as a function of model complexity.
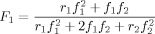 ((1))
((1))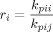 ((2))
((2))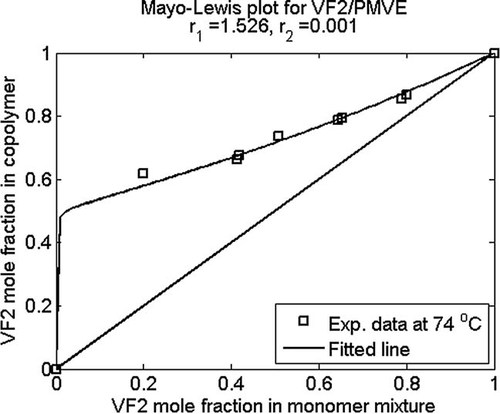
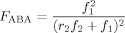 ((3))
((3))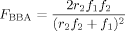 ((4))
((4))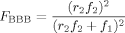 ((5))
((5))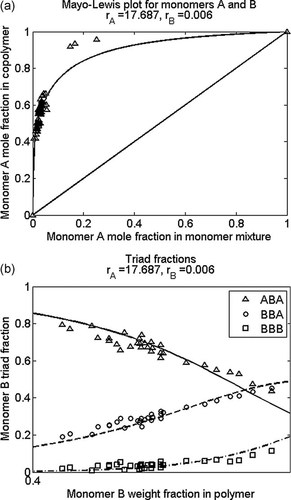
Calculated (line) and experimental (symbols) (a) mole fraction of monomer A in A/B copolymer as a function of A mole fraction in monomer mixture and (b) triad fractions as a function of monomer B weight fraction; fitted values of reactivity ratios are given in the figure title.
Another class of parameters is thermodynamic parameters. Thermodynamic models usually require a number of pure component or molecular parameters and, depending on the mixing rules used, one or more binary interaction parameters. For example, the Sanchez–Lacombe equation of state uses three temperature independent molecular parameters per component. Figure 6 and 7 show results of estimating such parameters for propylene and poly(vinylidene fluoride) using experimental data of density as a function of temperature and pressure and in the case of propylene also saturated vapor pressure as a function of temperature. It is worth noting that the method used to obtain the parameter values shown in Figure 6 uses both types of experimental data simultaneously.
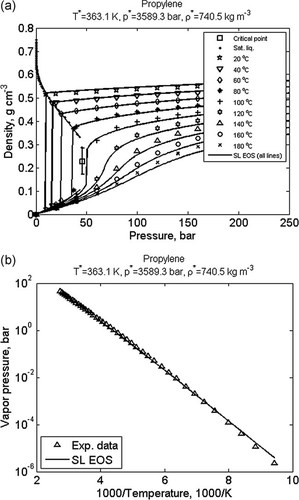
Calculated (lines) and experimental (symbols) (a) PVT-data for propylene and (b) propylene vapor pressure as a function of temperature; fitted values of Sanchez–Lacombe molecular parameters are given in the figure titles; experimental data are from DIPPR database (saturated liquid density and vapor pressure,65 critical point66) and from NIST Chemistry WebBook (density vs. pressure).67
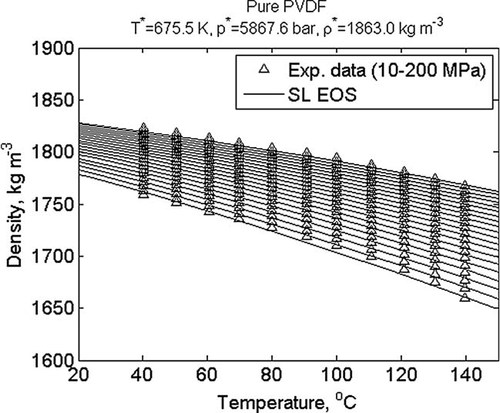
Calculated (lines) and experimental (symbols) PVT-data for poly(vinylidene fluoride) from 10 (bottom) to 200 MPa (top); fitted values of Sanchez–Lacombe molecular parameters are given in the figure titles; experimental data.68
Mixing rules are used to relate pure component properties with mixture behavior. Usually, for a given equation of state many different mixing rules are available in the literature, some requiring one, others more than one binary interaction parameter per component pair. The results of the evaluation of the binary interaction parameter between 1,3-propanediol and water using binary VLE data is shown in Figure 8 for the Sanchez–Lacombe equation of state. It is worth noting that very similar results are obtained when using the PC-SAFT model. Unlike the pure component parameters for some equations of state, the binary interaction parameters are usually temperature dependent.
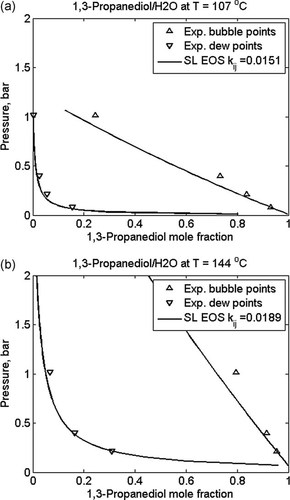
Calculated (lines) and experimental (symbols) bubble and dew point pressures at (a) 107 and (b) 144 °C as a function of composition for a mixture of 1,3-propanediol and water; experimental data;69 fitted values of binary interaction parameter for Sanchez Lacombe EOS are given in the figure legends.
 ((6))
((6))Here kt0 denotes the termination rate constant of short chains in diluted phase, rxy the reaction radius (i.e., the distance at which two chains of length x and y react instantaneously), Dx,com the center-of-mass diffusion coefficient of a chain of length x, kp the propagation rate constant, [M] the monomer concentration, a the root mean square end-to-end distance divided by the square root of the number of monomer units in the chain, and NA the Avogadro constant. Figure 9 shows a typical behavior of the termination rate constant as a function of chain length and polymer weight fraction evaluated from the expression above. It can be seen that kt is a strong function of both chain length and polymer weight fraction.
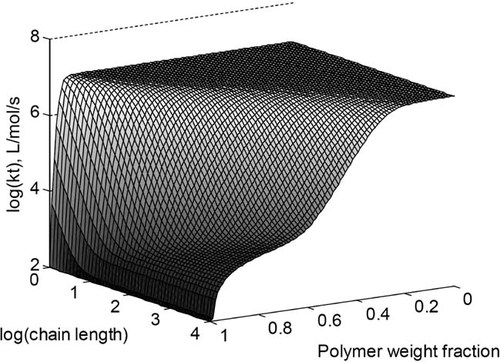
Bimolecular termination rate constant as a function of chain length and polymer weight fraction in the reaction mixture.
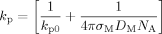 ((7))
((7))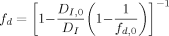 ((8))
((8))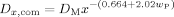 ((9))
((9))The expressions given in Equation (6) to (8) are sometimes referred to as the “parallel” approach as opposed to the “serial” approach, in which the overall rate coefficients are calculated by simple summation of reaction and diffusion contributions as discussed by Dubé et al.15
Regarding the measurement of the termination rate coefficient, we would like to refer to the work by Beuermann and Buback26 on pulsed laser experiments and by Barner-Kowollik et al.78 who recently reviewed and evaluated experimental methods that have been used for the determination of termination rate coefficients in free-radical polymerization.
Model Implementation
After formulating the model in terms of a set of equations, which could in principle include algebraic, integral, difference, partial, and ordinary differential equations, various numerical methods are used to solve the entire model as they are typically too complex for analytical solution. Some software platforms used to solve numerically model equations are briefly discussed in this section.
A number of commercial software packages are now available to model polymer reactors. Aspen Polymers (formally Aspen Polymers Plus) offered by Aspen Technology is a commercial software solving specific types of popular polymer reaction processes. Aspen Polymers is a layered product built on top of Aspen Plus developed for small molecule chemical processes. Aspen Technology claims that “Aspen Polymers is a market-leading, first-principles polymer modeling technology for accurate and reliable simulation and optimization of polymer processes. It is fully integrated with industry-standard simulators, including Aspen Plus, Aspen Plus Dynamics, and Aspen Custom Modeler.” A good example of the use of Aspen Polymers Plus and Aspen Dynamics is in the article by Khare et al.79 from 2004 which studied the steady-state and dynamic modeling of polypropylene stirred bed reactors.
Another commercial simulation package called PREDICI is described in the work by Wulkow80 in 2008. This package has evolved from a solver for population balances describing MWD in polymer reaction kinetics into a flexible tool for many kinds of polymer processes. This program is capable of modeling complex reaction mechanisms as well as multiphase behavior in various types of reactors and the author discusses the mathematical techniques and algorithms used. In particular the Galerkin h-p-method is used extensively as a numerical method to solve the discrete population balance equations arising in polymerization kinetics. Many industrial practitioners are now using this program in constructing polymer reactor models. A very recent example of the complexity that PREDICI can handle is given by Wang and Hutchinson81 in 2011. This mechanistic terpolymerization model, which is implemented in PREDICI, includes methacrylate depropagation, acrylate backbiting, chain scission, and macromonomer propagation, as well as penultimate chain-growth and termination kinetics. Another example of the use of PREDICI is that of Nikitin et al.28 studying the effect of intramolecular transfer to polymer on stationary free-radical polymerization of alkyl acrylates. It is worth noting that the developers of PREDICI also offer a software tool called PARSIVAL that has been designed for the description and simulation of particle dynamics in dispersed systems. Another application of PREDICI was discussed by Schütte and Wulkow82 where a hybrid approach was used to combine the deterministic population balance approach with a stochastic Monte-Carlo approach based on chemical master equations.
In addition to the above mentioned commercial software, academic researchers have also been active in this area. For example, the dynamic flow sheeting package POLYRED, developed by the University of Wisconsin Polymerization Reaction Engineering Laboratory (UWPREL), can be used to model polymerization processes and to estimate model parameters from both batch and continuous process data.83 In a series of papers Gao and Penlidis84, 85 discussed the development of a comprehensive simulator database package (referred to as “Watpoly”) for bulk and or solution terpolymerization and its validation with butyl acrylate/methyl methacrylate/vinyl acetate data. The authors claim that “after almost two decades of continuous effort in refining and testing this bulk/solution multicomponent simulation model/package/database, it is strongly believed that the package can provide a very flexible and useful tool that could guide academic and industrial research and development.” In a subsequent paper Gao and Penlidis86 presented a simulator/database package for the more challenging case of emulsion homo- and copolymerization under a wide range of reaction and operation conditions (e.g., batch, semi-batch, seeded, or unseeded). One of the attractiveness of their simulator is that their component database contains physical/chemical data for many components of an emulsion polymerization process such as monomers, initiators, and surfactants. Polic et al.87 presented a framework for parameter estimation within the Watpoly framework and illustrated it with a homopolymer system (styrene) and a copolymer one (styrene/methyl methacrylate). Finally in a series of papers the group at the Chemical Process Research Institute at the University of Thessaloniki88, 89 presented the development of a computer aided design platform for the simulation, parameter estimation, and optimization of industrial polymer processes. One of the features of their approach is that the simulator was constructed in an object-oriented programming environment using CapeOpen system specifications which allows the integration of different models obtained from different sources. The use of the simulator was illustrated by three examples indicative of the extensive industrial experience of the authors namely a low-density polyethylene high pressure tubular reactor process, gas-phase, and slurry phase olefin catalytic polymerization processes, and a poly(vinyl chloride) batch suspension process.
In some cases the complexity of the physicochemical picture of a polymerization system, the level of information that needs to be retained by a model, the implementation of sophisticated process control strategies, or a combination of the afore mentioned still requires the development of user-defined models from scratch using “lower level” platforms such as FORTRAN or MATLAB. Such user-defined models can also be combined with commercial software packages as reported recently by Pohn et al.90 for the development of a computational framework consisting of a computational fluid dynamics model (POLY3D, Rheosoft Inc.) coupled to a population balance model (programmed in FORTRAN) that solves the PSD in a high solids latex reactor. The coupling of multiple submodels can also be done using commercial software packages only as recently shown by Boettger and Hergeth91 who presented a new approach to simulate complex kinetic mechanism combined with complex multicomponent phase equilibria for an emulsion polymerization process. In their approach the thermodynamic modeling was done using PC-SAFT solved in MULTIFLASH and the kinetic modeling was performed in PREDICI. The models have been coupled via CapeOpen interface. Finally, we would like to mention that DuPont TMODS is an in-house proprietary dynamic simulator that can be used to transfer a validated model to plant sites as discussed in the article by Cox et al.92
Model implementation always involves making careful choices. The complexity of the implementation is always related to the types of predictive capabilities that are desired. Use of FORTRAN, MATLAB or Aspen Customer Modeler may be justified when full control over the derivation and solution methods of the appropriate kinetic and reactor equations is desired. However, the development time may be considerable and this may be justified in the case of very unusual polymerization kinetics or complex heterogeneous reactors. The use of the object oriented packages discussed above, which provide various degrees of control over the polymerization mechanism and the method of solution, reduces the model development time. In industry short model development times are desirable so that the benefits can be quickly realized. A factor which influences the decision of which specific commercial package to use for model implementation is whether a library of parameters for the monomers of interest is available or whether these would have to be estimated. An additional factor is whether the commercial package has been extensively validated with the class of systems that the user is interested in modeling (e.g., polyolefins) because in this case the development time can be even shorter.
In the next subsection some examples are shown of typical outputs of polymerization models. Figure 10 shows the cumulative copolymer composition average as a function of reaction time for a free-radical emulsion polymerization with four monomers. Composition number and weight distributions for the same polymerization are given in Figure 11. The CD has been obtained by counting the number (or mass) of polymer chains of a given instantaneous composition. The integration over reaction time yields the total number (or mass) of chains with that composition. The entire distribution is obtained by repeating the counting and integration for all possible compositions.
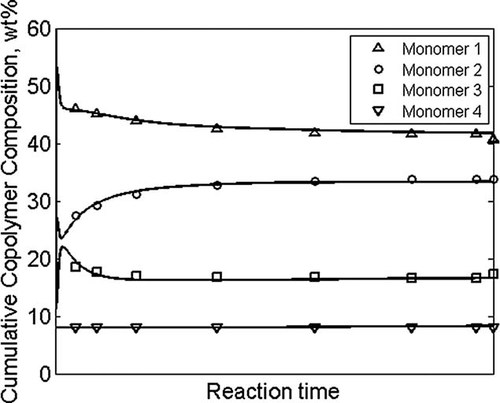
Calculated (lines) and experimental (symbols) cumulative copolymer composition as a function of reaction time for an emulsion polymerization with four monomers.
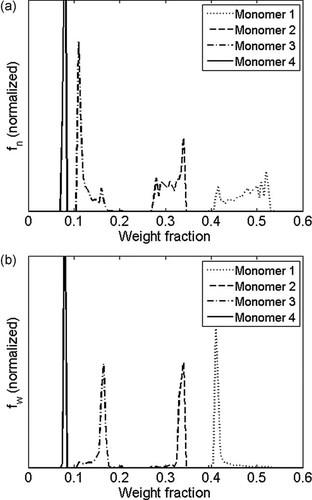
Calculated normalized CD for the same emulsion polymerization as shown in Figure 10: (a) number and (b) weight distribution.
Another example of model output is liquid water concentration, evaporation rate, molecular weight, and endgroup concentration as a function of reaction time for a condensation polymerization. The simulation results and experimental data shown in Figure 12 are for the sulfuric acid catalyzed polymerization of 1,3-propanediol described in more detail by Mueller et al.93 It is seen that in this particular polymerization run a lot of water is being formed early in the batch, which is rapidly removed from the reaction mixture by evaporation. Number and weight average molecular weights increase almost linearly with reaction time for the duration shown here. At the same time unsaturated endgroups are formed as shown in Figure 12d. A more detailed discussion of the results shown in Figure 12 is given in the reference.93
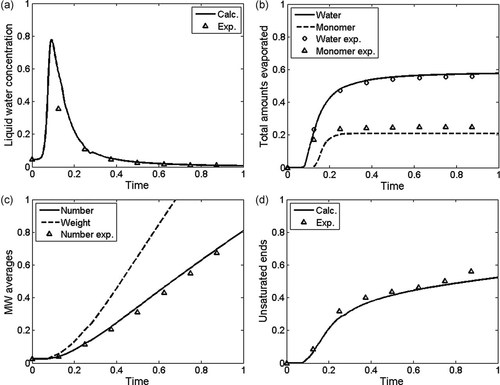
Calculated (lines) and experimental data as a function of reaction time for the sulfuric acid catalyzed condensation polymerization of 1,3-propanediol: (a) liquid water concentration, (b) evaporated amounts of water and monomer, (c) molecular weight averages, and (d) unsaturated endgroup concentration.
Various model outputs for a heterogeneous polymerization are given in Figure 13. In particular, conversion, molecular weight average, particle number, and particle diameter are shown as a function of process time for the dynamic startup of a styrene emulsion polymerization in a CSTR.8 This model uses a lumped particle balance to describe the PSD. Full particle size distributions may also, with considerably more effort, be computed and compared to this lumped particle balance approach as is done by Immanuel et al.9 The aim of this study was to elucidate the degree of disparity of model predictions for batch operation, and to elucidate the ability of the simple lumped models to predict oscillatory dynamics for continuous operation.
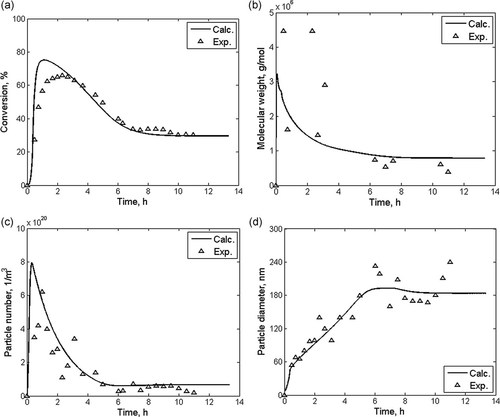
Comparison of model outputs (lines) and experimental data (symbols) for a continuous styrene emulsion polymerization as a function of reaction time:8 (a) monomer conversion, (b) number average molecular weight, (c) particle number, and (d) particle diameter.
A common characteristic in the examples that we discussed is the fact that several independent model outputs are compared to available experimental results rather than a single model output like monomer conversion which results in greater confidence in the underlying model structure and parameters.
Conclusion
With the tools and concepts available today, some of which have been briefly discussed in the present article, detailed polymerization models can be developed and used to address important problems in industry. Polymerization models may be applied to different stages of process and product development. The support of early lab investigations focuses mainly on getting an improved understanding of underlying mechanisms and also model-guided optimization of product quality. At an intermediate scale, process and product development in pilot plants are supported by models. An optimization of recipe and conditions can be achieved by combining modeling and experimental efforts. Finally, for existing processes, models can be developed and implemented at plant sites where they can be used for operator training, process optimization, monitoring, and control. In some cases, models are even used in real time in parallel with the process to aid in troubleshooting and process control.
Even though the development of fundamental polymerization models can be very laborious and time consuming, we have found that, just like well planned experiments, the model building activity can be very profitable. In fact, it is preferable that the model development is done based upon and in combination with good experiments. Using models and experiments together in combination offers a very powerful tool and is a recommended alternative to empirical methods and experimentation alone.
Acknowledgements
The authors gratefully acknowledge the helpful conversations, encouragement, and support of some of our Polymer Reaction Engineering colleagues including Prof. Robin A. Hutchinson, Prof. Costas Kiparissides, Dr. Kenneth W. Leffew, Dr. Tony W. Liu, Prof. Massimo Morbidelli, Prof. W. Harmon Ray, Prof. Giuseppe Storti, Dr. Paul E. M. Wijnands, Dr. Michael Wulkow, and the late Dr. W. David Smith, Jr.
Biographical Information
Philipp A. Mueller is a Senior Research Engineer at DuPont where he has worked on various processes employing fundamental mathematical models of the kinetics and thermodynamics of polymerization reactions. He has published a number of refereed journal articles in the field of polymer reaction engineering and a book chapter on Heterogeneous Polymerization in Supercritical Carbon Dioxide. He received his MS in Chemical Engineering in 2001 and his Doctor of Natural Sciences in 2005 from ETH Zurich, Switzerland.
Biographical Information
John R. Richards is a Research Fellow at DuPont and has worked on processes employing polymerization modeling and process control. He has developed polymerization models and control systems for a broad spectrum of products including polymers, monomers, and biological systems. He received his BS in Biochemical Engineering and AB in Psychology from Rutgers University in 1976 and his MS from Cornell University in 1978. He then joined DuPont and received his PhD from the University of Delaware in Chemical Engineering in 1994. He is an affiliated faculty member at the University of Delaware and is a Fellow of the AIChE.
Biographical Information
John P. Congalidis is a Research Planning Fellow with DuPont Central Research and Development. His career with DuPont included assignments in advanced process control systems implementation, polymer products development and manufacturing, kinetic modeling, and research management. He has published several refereed journal articles and book chapters in the area of polymerization reactor modeling and control. His contributions to DuPont resulted in three Engineering Excellence Awards. He was the 2010 AICHE Annual Meeting Program Chair for Systems and Control. He received his Diploma in Chemical Engineering from the National Technical University of Athens and his Doctorate in Chemical Engineering from MIT.