RESEARCH ARTICLE
Positive ground state solutions for fractional Kirchhoff type equations with critical growth
Wentao Huang,
Xiao Luo,
Corresponding Author
Wentao Huang
School of Science, East China Jiaotong University, Nanchang, China
Correspondence
Wentao Huang, School of Science, East China JiaoTong University, Nanchang 330013, China.
Email: [email protected]
Communicated by: K. Chelminski
Search for more papers by this authorXiao Luo
School of Mathematics, Hefei University of Technology, Hefei, China
Search for more papers by this authorWentao Huang,
Xiao Luo,
Corresponding Author
Wentao Huang
School of Science, East China Jiaotong University, Nanchang, China
Correspondence
Wentao Huang, School of Science, East China JiaoTong University, Nanchang 330013, China.
Email: [email protected]
Communicated by: K. Chelminski
Search for more papers by this authorXiao Luo
School of Mathematics, Hefei University of Technology, Hefei, China
Search for more papers by this authorAbstract
We study the existence of positive ground state solutions for the following fractional Kirchhoff type equation
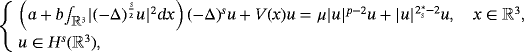
with
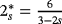and s ∈ (0,1). Under suitable assumptions on V(x), by using a monotonicity trick and a global compactness principle, we prove that the equation admits a positive ground state solution if
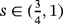and μ > 0 large enough.
REFERENCES
- 1Fiscella A, Valdinoci E. A critical Kirchhoff type problem involving a nonlocal operator. Nonlinear Anal. 2014; 94: 156-170.
- 2Kirchhoff G. Mechanik. Leipzig: Teubner; 1883.
- 3Arosio A, Panizzi S. On the well-posedness of the Kirchhoff string. Trans Amer Math Soc. 1996; 348: 305-330.
- 4D'Ancona P, Spagnolo S. Global solvability for the degenerate Kirchhoff equation with real analytic data. Invent Math. 1992; 108: 247-262.
- 5He X, Zou W. Existence and concentration behavior of positive solutions for a Kirchhoff equation in
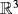. J Differ Equations. 2012; 2: 1813-1834.
- 6Li G, Ye H. Existence of positive ground state solutions for the nonlinear Kirchhoff type equations in
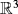. J Differ Equations. 2014; 257: 566-600.
- 7Guo Z. Ground states for Kirchhoff equations without compact condition. J Differ Equations. 2015; 259: 2884-2902.
- 8He Y, Li G. Standing waves for a class of Kirchhoff type problems in
involving critical Sobolev exponents. Calc Var Partial Differ Equations. 2015; 54: 3067-3106.
- 9Deng Y, Peng S, Shuai W. Existence and asympototic behavior of nodal solutions for the Kirchhoff-type problems in
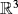. J Funct Anal. 2015; 269: 3500-3527.
- 10He X, Zou W. Ground states for nonlinear Kirchhoff equations with critical growth. Ann Mat Pura Appl. 2014; 193(4): 473-500.
- 11Li G, Ye H. Existence of positive solutions for nonlinear Kirchhoff type problems in
with critical Sobolev exponent. Math Methods Appl Sci. 2014; 37: 2570-2584.
- 12Lü D, Xiao J. Ground state solutions for a coupled Kirchhoff-type system. Math Methods Appl Sci. 2015; 38: 4931-4948.
- 13Tang X, Chen S. Ground state solutions of Nehari-Pohozaev type for Kirchhoff-type problems with general potentials. Calc Var Partial Differ Equations. 2017; 56: 25.
- 14Bucur C, Valdinoci E. Nonlocal Diffusion and Applications, Lecture Notes of the Unione Matematica Italiana, 20. Cham: Springer; 2016. Unione Matematica Italiana, Bologna.
10.1007/978-3-319-28739-3 Google Scholar
- 15Dávila J, del Pino M, Dipierro S, Valdinoci E. Concentration phenomena for the nonlocal Schrödinger equation with Dirichlet datum. Anal PDE. 2015; 8: 1165-1235.
- 16Fiscella A, Pucci P. Kirchhoff-Hardy fractional problems with lack of compactness. Adv Nonlinear Stud. 2017; 17: 429-456.
- 17Autuori G, Fiscella A, Pucci P. Stationary Kirchhoff problems involving a fractional elliptic operator and a critical nonlinearity. Nonlinear Anal. 2015; 125: 699-714.
- 18Nyamoradi N. Existence of three solutions for Kirchhoff nonlocal operators of elliptic type. Math Commun. 2013; 18: 489-502.
- 19Xiang M, Zhang B, Ferrara M. Existence of solutions for Kirchhoff type problem involving the non-local fractional p-Laplacian. J Math Anal Appl. 2015; 424: 1021-1041.
- 20Pucci P, Saldi S. Critical stationary Kirchhoff equations in
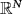involving nonlocal operators. Rev Mat Iberoam. 2016; 32: 1-22.
- 21Ambrosio V, Isernia T. A multiplicity result for a fractional Kirchhoff equation in
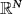with a general nonlinearity. Commun Contemp Math. 2017; 20:1750054.
- 22Xiang M, Zhang B, Zhang X. A critical Kirchhoff type problem involving the fractional p-Laplacian in
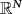. Complex Var Elliptic Equ. 2018; 63: 652-670.
- 23Autuori G, Pucci P. Elliptic problems involving the fractional Laplacian in
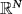. J Differ Equations. 2013; 255: 2340-2362.
- 24Caffarelli L, Salsa S, Silvestre L. Regularity estimates for the solution and the free boundary of the obstacle problem for the fractional Laplacian. Invent Math. 2008; 171: 425-461.
- 25Chang X, Wang Z. Ground state of scalar field equations involving a fractional Laplacian with general nonlinearity. Nonlinearity. 2013; 26: 479-494.
- 26Deng Y, Shuai W. Sign-changing solutions for non-local elliptic equations involving the fractional Laplacian. Adv Differ Equations. 2018; 23: 109-134.
- 27Dipierro S, Medina M, Valdinoci E. Fractional Elliptic Problems with Critical Growth in the Whole of
, Appunti Scuola Normale Superiore di Pisa (Nuova Serie), vol. 15. Pisa: Edizioni della Normale; 2017.
10.1007/978-88-7642-601-8 Google Scholar - 28Fiscella A, Pucci P. p-fractional Kirchhoff equations involving critical nonlinearities. Nonlinear Anal Real World Appl. 2017; 35: 350-378.
- 29Pucci P, Xiang M, Zhang B. Multiple solutions for nonhomogeneous Schrödinger-Kirchhoff type equations involving the fractional p-Laplacian in
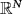. Calc Var Partial Differ Equations. 2015; 54: 2785-2806.
- 30Secchi S. Ground state solutions for nonlinear fractional Schrödinger equations in
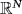. J Math Phys. 2013; 54: 17.
- 31Xiang M, Wang F. Fractional Schrödinger-Poisson-Kirchhoff type systems involving critical nonlinearities. Nonlinear Anal. 2017; 164: 1-26.
- 32Jeanjean L. On the existence of bounded Palais-Smale sequences and application to a Landesman-Lazer-type problem set on
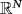. Proc Roy Soc Edinburgh Sect A. 1999; 129: 787-809.
- 33Jeanjean L. Existence of solutions with prescribed norm for semilinear elliptic equations. Nonlinear Anal. 1997; 28: 1633-1659.
- 34Cotsiolis A, Tavoularis NK. Best constants for Sobolev inequalities for higher order fractional derivatives. J Math Anal Appl. 2004; 295: 225-236.
- 35Di Nezza E, Palatucci G, Valdinoci E. Hitchhiker's guide to the fractional Sobolev spaces. Bull Sci Math. 2012; 136: 521-573.
- 36Willem M. Minimax Theorems, Progr. Nonlinear Differential Equations Appl, vol. 24. Boston, MA: Birkhäuser Boston, Inc; 1996.
- 37Silvestre L. Regularity of the obstacle problem for a fractional power of the Laplace operator. Comm Pure Appl Math. 2007; 60: 67-112.
