Characterisation of multiple conducting permeable objects in metal detection by polarizability tensors
Abstract
Realistic applications in metal detection involve multiple inhomogeneous-conducting permeable objects, and the aim of this paper is to characterise such objects by polarizability tensors. We show that, for the eddy current model, the leading order terms for the perturbation in the magnetic field, due to the presence of N small conducting permeable homogeneous inclusions, comprises of a sum of N terms with each containing a complex symmetric rank 2 polarizability tensor. Each tensor contains information about the shape and material properties of one of the objects and is independent of its position. The asymptotic expansion we obtain extends a previously known result for a single isolated object and applies in situations where the object sizes are small and the objects are sufficiently well separated. We also obtain a second expansion that describes the perturbed magnetic field for inhomogeneous and closely spaced objects, which again characterises the objects by a complex symmetric rank 2 tensor. The tensor's coefficients can be computed by solving a vector valued transmission problem, and we include numerical examples to illustrate the agreement between the asymptotic formula describing the perturbed fields and the numerical prediction. We also include algorithms for the localisation and identification of multiple inhomogeneous objects.
1 INTRODUCTION
There is considerable interest in being able to locate and characterise multiple conducting permeable objects from measurements of mutual inductance between a transmitting and a receiving coil, where the coupling is inductive. An obvious example is in metal detection where the goal is to identify and locate the multiple objects present in a low conducting background. Applications include security screening, archaeological digs, ensuring food safety as well as the search for land mines, and unexploded ordnance and land mines. Other applications include magnetic induction tomography for medical imaging applications and monitoring of corrosion of steel reinforcement in concrete structures.
In all these practical applications, the need to locate and distinguish between multiple conducting permeable inclusions is common. This includes benign situations, such as coins and keys accidentally left in a pocket during a security search or a treasure hunter becoming lucky and discovering a hoard of Roman coins, as well as threat situations, where the risks need to be clearly identified from the background clutter. For example, in the case of searching for unexploded land mines, the ground can be contaminated by ring-pulls, coins, and other metallic shrapnel, which makes the process of clearing them very slow as each metallic object needs to be dug up with care. Furthermore, conducting objects are also often inhomogeneous and made up of several different metals. For instance, the barrel of a gun is invariably steel while the frame could be a lighter alloy, jacketed bullets have a lead shot and a brass jacket, and modern coins often consist of a cheaper metal encased in nickel or brass alloy. Thus, in practical metal detection applications, it is important to be able to describe both multiple objects and inhomogeneous objects.
Magnetic polarizability tensors (MPTs) hold considerable promise for the low-cost characterisation in metal detection. An asymptotic expansion describing the perturbed magnetic field due to the presence of a small conducting permeable object has been obtained by Ammari, Chen, Chen, Garnier, and Volkov,1 which characterises the object in terms of a rank 4 tensor. Ledger and Lionheart have shown that this asymptotic expansion simplifies for orthonormal coordinates and allows a conducting permeable object to be characterised by a complex symmetric rank 2 MPT with an explicit expression for its six coefficients.2 Ledger and Lionheart have also investigated the properties of this tensor,3 and they have written the article4 to explain these developments to the electrical engineering community as well as to show how it applies in several realistic situations. In a previous study,5 they have obtained a complete asymptotic expansion of the magnetic field, which characterises the object in terms of a new class of generalised magnetic polarizability tensors (GMPTs); the rank 2 MPT being the simplest case. The availability of an explicit formula for the MPT's coefficients, and its improved understanding, allows new algorithms for object location and identification to be designed, eg, in an existing study.6
Electrical engineers have applied MPTs to a range of practical metal detection applications, including walk through metal detectors, in line scanners, and demining, eg, previous studies,7-13 see also our article4 for a recent review but without knowledge of the explicit formula described above. Engineers have made a prediction of the form of the response for multiple objects, eg, existing study14 but without an explicit criteria on the size or the distance between the objects in order for the approximation to hold. Grzegorczyk, Barrowes, Shubitidze, Fernández, and O'Neill have applied a time domain approach to classify multiple unexploded ordinance using descriptions related to MPTs.15 Davidson, Abel-Rehim, Hu, Marsh, O'Toole, and Peyton have made measurements of MPTs for inhomogeneous US coins16 and Yin, Li, Withers, and Peyton have also made measurements to characterise inhomogeneous aluminium/carbon-fibre reinforced plastic sheets.17 But, in all cases, without an explicit formula.
Our work has the following novelties: Firstly, we characterise rigidly joined collections of different metals (ie, metals touching or held in that configuration by a nonconducting material) by MPTs overcoming a deficiency of our previous work. Secondly, we find that the frequency spectra of the eigenvalues of the real and imaginary parts of the MPT for an inhomogeneous object exhibit multiple nonstationary inflection points and maxima, respectively, and the number of these gives an upper bound on the number of materials making up the object. To achieve this, we revisit the asymptotic formula of Ammari et al1 and our previous work2 and extend it to treat multiple objects by describing the perturbed magnetic field as a sum of terms involving the MPTs associated with each of the inclusions. We also provide a criteria based on the distance between the objects, which determines the situations in which the expression will hold. We derive a second asymptotic expansion that describes the perturbed magnetic field in the case of inhomogeneous objects and, as a corollary, this also describes the magnetic field perturbation in the case of closely spaced objects. In each case, we provide new explicit formulae for the MPTs. We also present algorithms for the localisation and characterisation of objects, which extends those for the isolated object case.1
The paper is organised as follows: In Section 2, the characterisation of a single homogeneous object is briefly reviewed. Section 3 presents our main results for characterising multiple and inhomogeneous objects by MPTs. Sections 4 and 5 contain the details of the proofs for our main results. In Section 6, we present numerical results to demonstrate the accuracy of the asymptotic formulae and presents results of algorithms for the localisation and identification of multiple (inhomogeneous) objects.
2 CHARACTERISATION OF A SINGLE CONDUCTING PERMEABLE OBJECT
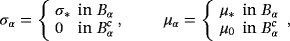
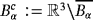 . For metal detection, the relevant mathematical model is the eddy current approximation of Maxwell's equations since σ∗ is large and the angular frequency ω = 2πf is small (see Ammari, Buffa, and Nédélec18 for a detailed justification). Here, the electric and magnetic interaction fields, Eα and Hα, respectively, satisfy the curl equations
. For metal detection, the relevant mathematical model is the eddy current approximation of Maxwell's equations since σ∗ is large and the angular frequency ω = 2πf is small (see Ammari, Buffa, and Nédélec18 for a detailed justification). Here, the electric and magnetic interaction fields, Eα and Hα, respectively, satisfy the curl equations
 (1)
(1) and decay as O(|x|−1) for |x|→∞. In the above equation, J0 is an external current source with support in
and decay as O(|x|−1) for |x|→∞. In the above equation, J0 is an external current source with support in
 . In absence of an object, the background fields E0 and H0 satisfy 1 with α = 0. The task is to find an economical description for the perturbed magnetic field (Hα − H0)(x) due to the presence of Bα, which characterises the object's shape and material parameters by a small number of parameters separately to its location z. For x away from Bα, the leading order term in an asymptotic expansion for (Hα − H0)(x) as α→0 has been derived by Ammari et al.1 We have shown that this reduces to the simpler form2, 4
*
. In absence of an object, the background fields E0 and H0 satisfy 1 with α = 0. The task is to find an economical description for the perturbed magnetic field (Hα − H0)(x) due to the presence of Bα, which characterises the object's shape and material parameters by a small number of parameters separately to its location z. For x away from Bα, the leading order term in an asymptotic expansion for (Hα − H0)(x) as α→0 has been derived by Ammari et al.1 We have shown that this reduces to the simpler form2, 4
*
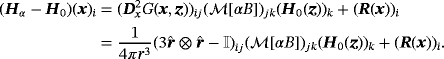 (2)
(2)In the above, G(x,z): = 1/(4π|x−z|) is the free space Laplace Green's function, r:=x−z, r = |r| and
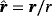 and
and
 is the rank 2 identity tensor. The term R(x) quantifies the remainder, and it is known that
is the rank 2 identity tensor. The term R(x) quantifies the remainder, and it is known that
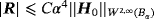 . The result holds when ν: = σ∗μ0ωα2 = O(1) (this includes the case of fixed σ∗, μ∗, ω as α→0) and requires that the background field be analytic in the object. Note that 2 involves the evaluation of the background field within the object (usually at it's centre), ie, H0(z).
. The result holds when ν: = σ∗μ0ωα2 = O(1) (this includes the case of fixed σ∗, μ∗, ω as α→0) and requires that the background field be analytic in the object. Note that 2 involves the evaluation of the background field within the object (usually at it's centre), ie, H0(z).
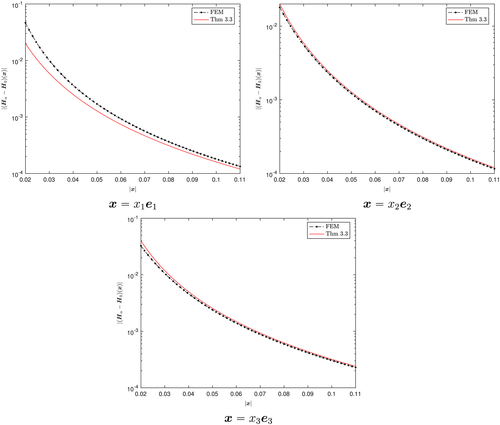
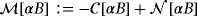 in this asymptotic expansion, which depends on ω, σ∗, μ∗/μ0, α and the shape of B, but is independent of z, is the MPT, and its coefficients can be computed from
in this asymptotic expansion, which depends on ω, σ∗, μ∗/μ0, α and the shape of B, but is independent of z, is the MPT, and its coefficients can be computed from
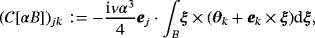 (3a)
(3a)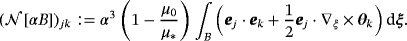 (3b)
(3b)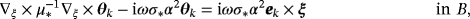 (4a)
(4a) (4b)
(4b)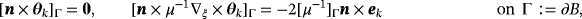 (4c)
(4c) (4d)
(4d) for a variety of simply and multiply connected objects. These have been obtained by applying an hp-finite element method to solve (4) for θk, k = 1,2,3 and then to compute
for a variety of simply and multiply connected objects. These have been obtained by applying an hp-finite element method to solve (4) for θk, k = 1,2,3 and then to compute
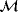 using (3). Our previously presented results have exhibited excellent agreement with for MPTs previously presented in the electrical engineering literature. Pratical applications of the asymptotic formula have been discussed in another study.4
using (3). Our previously presented results have exhibited excellent agreement with for MPTs previously presented in the electrical engineering literature. Pratical applications of the asymptotic formula have been discussed in another study.43 MAIN RESULTS
The asymptotic formula given in 2 is for a single isolated homogenous object. But, as described in the introduction, for realistic metal detection scenarios, measurements of the perturbed magnetic field often relate to field changes caused by the presence of multiple objects or inhomogeneous objects. The purpose of this work is to extend the description to the cases of well separated multiple homogeneous objects and inhomogeneous objects. As a result of corollary, our second main result also describes the case of objects that of objects that are closely spaced. Below, we summarise the main results of our paper.
3.1 Multiple homogeneous objects that are sufficiently well spaced
We consider N homogenous-conducting permeable objects of the form
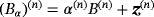 †with Lipschitz boundaries where, for the nth object, B(n) denotes a corresponding unit sized object located at the origin, α(n) denotes the object's size, and z(n) the object's translation from the origin. The union of all objects is
†with Lipschitz boundaries where, for the nth object, B(n) denotes a corresponding unit sized object located at the origin, α(n) denotes the object's size, and z(n) the object's translation from the origin. The union of all objects is
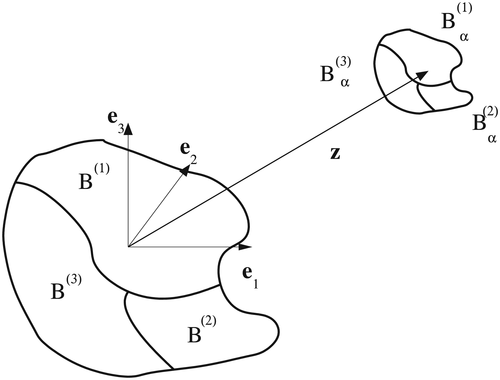
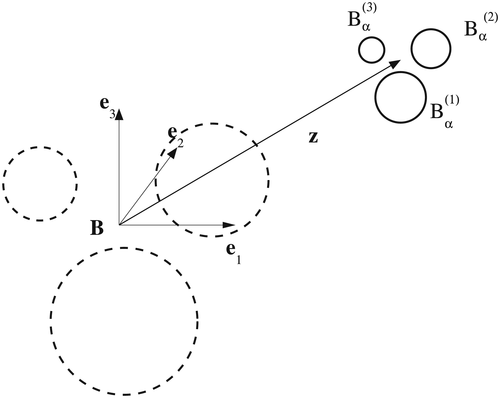
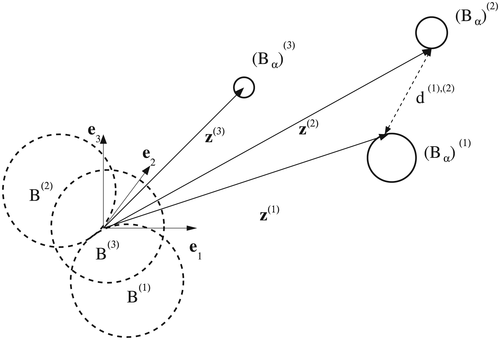
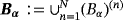 where we use a bold subscript α to denote the possibility that each object in the collection can have a different size. We also employ the same notation for the fields Eα and Hα, which satisfy 1. An illustration of a typical configuration is shown in Figure 1. In this figure, there are N = 3 objects, which are the spheres
where we use a bold subscript α to denote the possibility that each object in the collection can have a different size. We also employ the same notation for the fields Eα and Hα, which satisfy 1. An illustration of a typical configuration is shown in Figure 1. In this figure, there are N = 3 objects, which are the spheres
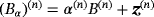 , n = 1,2,3, where, for the nth object, α(n) is its size (here its radius), and z(n) is its translation from the origin. In the presented case, B = B(1) = B(2) = B(3) is a unit sphere located at the origin although, in practice, the objects do not need to have the same shape.
, n = 1,2,3, where, for the nth object, α(n) is its size (here its radius), and z(n) is its translation from the origin. In the presented case, B = B(1) = B(2) = B(3) is a unit sphere located at the origin although, in practice, the objects do not need to have the same shape.
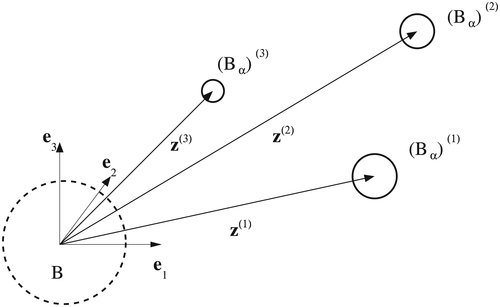
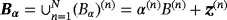 such that they are not closely spaced where each object (Bα)(n) is a sphere, α(n) is the radius of the nth sphere, z(n) describes the translation of the nth sphere from the origin, and B = B(1) = B(2) = B(3) is a unit sphere positioned at the origin
such that they are not closely spaced where each object (Bα)(n) is a sphere, α(n) is the radius of the nth sphere, z(n) describes the translation of the nth sphere from the origin, and B = B(1) = B(2) = B(3) is a unit sphere positioned at the origin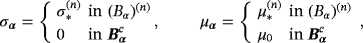
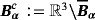 and set
and set
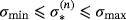 and
and
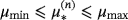 for n = 1,…,N. We introduce
for n = 1,…,N. We introduce
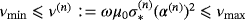 and set
and set
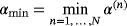 ,
,
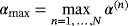 and require that the parameters of the inclusions be such that
and require that the parameters of the inclusions be such that
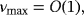
The task is then to provide a low-cost description of (Hα − H0)(x) for x away from Bα. This is accomplished through the following result.
Theorem 3.1.For the arrangement Bα of N homogeneous conducting permeable objects
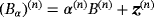 with
with
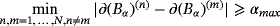 and parameters such that ν(n) = O(1) , the perturbed magnetic field at positions x away from Bα satisfies
and parameters such that ν(n) = O(1) , the perturbed magnetic field at positions x away from Bα satisfies
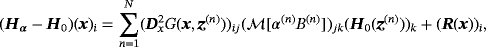 (5)
(5)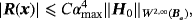
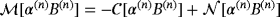 , n = 1,…,N, can be computed independently for each of the objects α(n)B(n) using the expressions
, n = 1,…,N, can be computed independently for each of the objects α(n)B(n) using the expressions
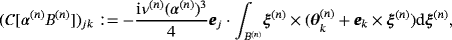 (6a)
(6a)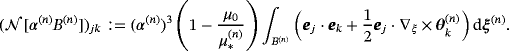 (6b)
(6b)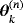 , k = 1,2,3, to the transmission problem
, k = 1,2,3, to the transmission problem
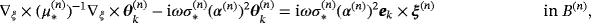 (7a)
(7a) (7b)
(7b) (7c)
(7c)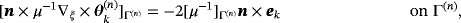 (7d)
(7d) (7e)
(7e)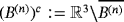 , Γ(n): = ∂B(n) and ξ(n) is measured from an origin chosen to be in B(n).
, Γ(n): = ∂B(n) and ξ(n) is measured from an origin chosen to be in B(n).
Proof.The result follows from by using a tensor representation of the asymptotic formula in Theorem 4.8, which is an extension of Theorem 3.2 obtained in a previous work1 for N sufficiently well-spaced objects. A tensor representation of this result leads to each of the N objects being characterised by a rank 4 tensor. Then, by considering each object in turn and repeating the same arguments as in Theorem 3.1 in another study,2 which exploits the skew symmetries of the tensor coefficients, the result stated in 5 is obtained. The symmetry of
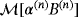 follows from repeating the arguments in Lemma 4.4 in the previous study.2□
follows from repeating the arguments in Lemma 4.4 in the previous study.2□
3.2 Single inhomogeneous object
In this case,
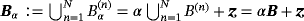 describes a single object comprised of N constitute parts,
describes a single object comprised of N constitute parts,
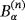 , such that there is a single common size parameter α, the configuration B contains the origin, and z is a single translation, as illustrated in Figure 2. Notice that for the inhomogeneous case, we use
, such that there is a single common size parameter α, the configuration B contains the origin, and z is a single translation, as illustrated in Figure 2. Notice that for the inhomogeneous case, we use
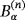 rather than (Bα)(n) as α is the same for all n, and we revert to the use of nonbold α subscripts for the fields Eα and Hα, which satisfy 1.
rather than (Bα)(n) as α is the same for all n, and we revert to the use of nonbold α subscripts for the fields Eα and Hα, which satisfy 1.

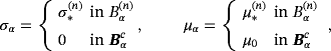
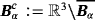 , and we drop the subscript α on μ and σ when considering the object B. We redefine
, and we drop the subscript α on μ and σ when considering the object B. We redefine
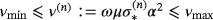 with the same requirements on
with the same requirements on
 as before.
as before.The task is then to provide a low-cost description of (Hα − H0)(x) for x away from Bα. This is accomplished through the following result.
Theorem 3.3.For an inhomogeneous object, Bα = αB+z made up of N constitute parts with parameters such that
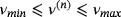 the perturbed magnetic field at positions x away from Bα satisfies
the perturbed magnetic field at positions x away from Bα satisfies
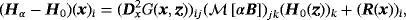 (8)
(8)
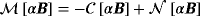 are given by
are given by
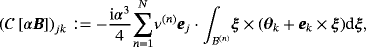 (9a)
(9a)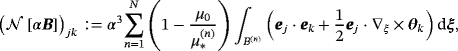 (9b)
(9b)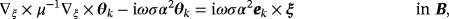 (10a)
(10a) (10b)
(10b)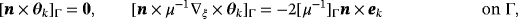 (10c)
(10c) (10d)
(10d)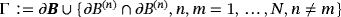 .
.
Proof.The result follows from by using a tensor representation of the asymptotic formula in Theorem 5.3, which is an extension of Theorem 3.2 obtained in the previous research1 for an homogeneous object to the inhomogeneous case. Using a tensor representation of this result leads to the object being characterised in terms of a rank 4 tensor. Then, by repeating the same arguments as in Theorem 3.1 in another study,2 which exploits the skew symmetries of the tensor coefficients, the result stated in 8 is obtained. The symmetry of
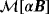 follows from repeating the arguments in Lemma 4.4 in the previous study.2□
follows from repeating the arguments in Lemma 4.4 in the previous study.2□
Corollary 3.4.For the case of N = 1 then Bα becomes Bα and Theorem 3.3 reduces to the case of a single homogenous object as obtained in existing works1, 2 and described in Section 2.
Corollary 3.5.Theorem 3.3 also immediately applies to objects that are closely spaced and, in this case, Bα = αB+z implies a single size parameter α and a single translation z for the configuration B. An illustration of a typical configuration is shown in Figure 3. In this figure, there are N = 3 objects consisting of three spheres configured such that they scale and translate together according to α and z, respectively, and, in this case, B is the combined configuration of three (larger) spheres with different radii and with centres located away from the origin.
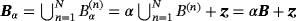 where each object is a sphere, α is a single scaling parameter, z describes their translation of the configuration from the origin
where each object is a sphere, α is a single scaling parameter, z describes their translation of the configuration from the origin
Remark 3.6.The applicability of Theorem 3.3 to closely spaced objects is expected to be limited since, in order to compute the characterisation, prior knowledge of the multiple object configuration (ie, location and orientation with respect to each other) is required, which, in practice, will not be the case. The formula also requires that the objects be closely spaced as there is a single scaling parameter and single translation that describes the configuration, but prior knowledge of the location of the configuration is not required. Instead, this result is expected to be of more practical value in the description of inhomogeneous objects where the configuration of the different regions of an object will be known in advance.
4 RESULTS FOR THE PROOF OF THEOREM 3.1
4.1 Elimination of the current source
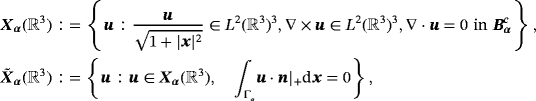
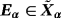 such that
such that
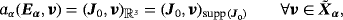
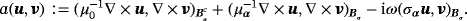
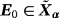 such that
such that
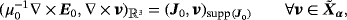
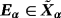 such that
such that
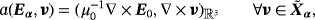
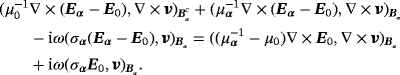 (11)
(11)4.2 Energy estimates
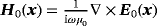 is analytic where the expansion is applied. We extend this to the multiple object case by requiring that J0 be supported away from Bα and introduce the following for n = 1,…,N
is analytic where the expansion is applied. We extend this to the multiple object case by requiring that J0 be supported away from Bα and introduce the following for n = 1,…,N
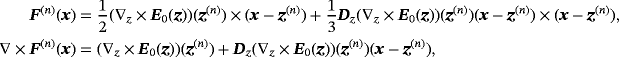
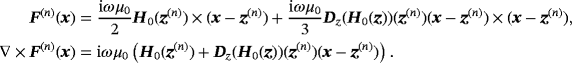
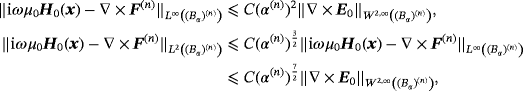 (12)
(12)
Remark 4.1.Higher order Taylor series could be considered (as previously in another study5 for the case of a single object) and lead to a more accurate representation of the field in terms of GMPTs. However, in order for such a representation to apply, there will be further implications in the allowable distance between the objects.
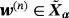 such that
such that
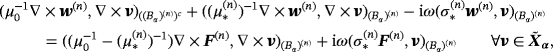 (13)
(13)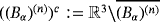 . By the addition of such problems, we have
. By the addition of such problems, we have
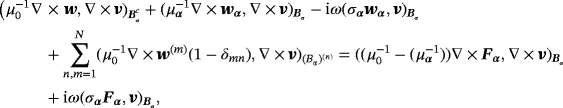 (14)
(14)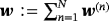 ,
,
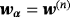 in (Bα)(n) and
in (Bα)(n) and
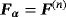 in (Bα)(n).
in (Bα)(n).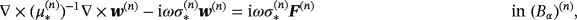 (15a)
(15a) (15b)
(15b) (15c)
(15c) (15d)
(15d)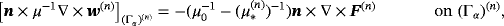 (15e)
(15e) (15f)
(15f)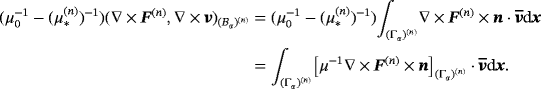
Lemma 4.2.For objects (Bα)(n) and (Bα)(m) with n ≠ m, we have that
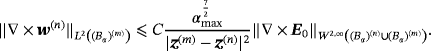
Proof.Introducing
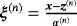 , which, without loss of generality, we assume the origin to be in B(n). We set
, which, without loss of generality, we assume the origin to be in B(n). We set
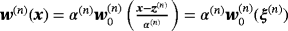 and so
and so
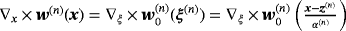 . Note that
. Note that
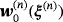 satisfies
satisfies
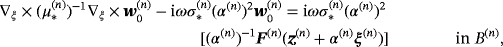 (16a)
(16a) (16b)
(16b) (16c)
(16c) (16d)
(16d)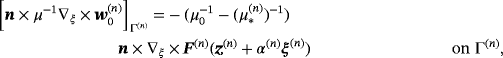 (16e)
(16e) (16f)
(16f)From the above, we have that
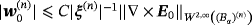 for sufficiently large |ξ(n)| and so we estimate that
for sufficiently large |ξ(n)| and so we estimate that
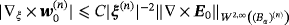 for the same case. Thus, for m ≠ n,
for the same case. Thus, for m ≠ n,
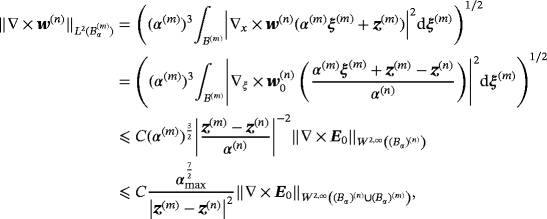
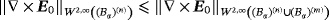 .□
.□
Corollary 4.3.Given the description
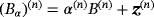 , we are free to configure B(n) in different ways provided that the origin lies at a point in B(n) (similarly with
, we are free to configure B(n) in different ways provided that the origin lies at a point in B(n) (similarly with
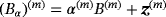 ) . Thus, |z(m) − z(n)| will be smallest when the origin lies in the boundaries of the objects, as illustrated in Figure 4. Requiring that
) . Thus, |z(m) − z(n)| will be smallest when the origin lies in the boundaries of the objects, as illustrated in Figure 4. Requiring that
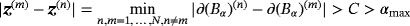 then Lemma 4.2 implies that
then Lemma 4.2 implies that
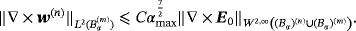
The following Lemma extends Ammari et al's Lemma 3.21 to the case of N multiple objects, when they are sufficiently well spaced.
Lemma 4.4.Provided that
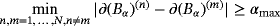 , there exists a constant C such that
, there exists a constant C such that
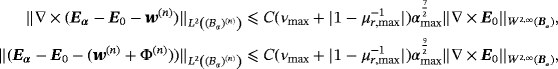
Proof.We start by proceeding along the lines presented in1 and introduce
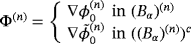 where
where
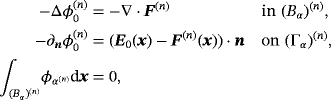
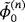 being the solution of an exterior problem in an analogous way to
being the solution of an exterior problem in an analogous way to
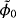 in the previous study.1 Using 11 and 14 (and after multiplying by μ0), we can deduce that
in the previous study.1 Using 11 and 14 (and after multiplying by μ0), we can deduce that
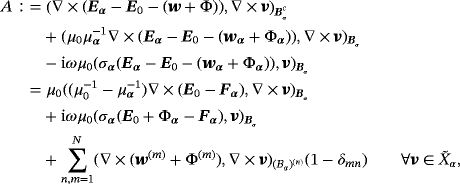 (17)
(17)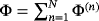 and
and
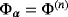 in (Bα)(n). Choosing v=Eα − E0 − (wα + Φα) then we have that
in (Bα)(n). Choosing v=Eα − E0 − (wα + Φα) then we have that
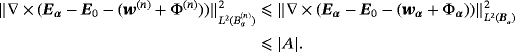
Also, by application of the Cauchy-Schwartz inequality, we can check that
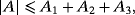 (18)
(18)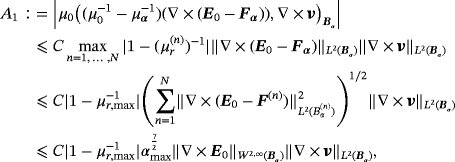 (19)
(19)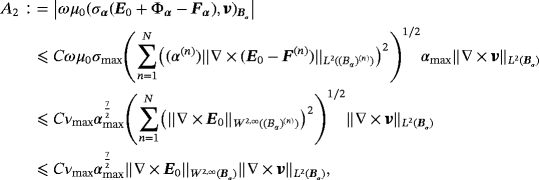 (20)
(20)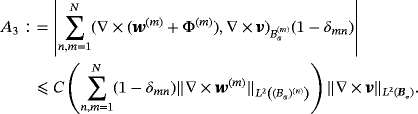 (21)
(21)To bound A1 and A2 we have used 12,
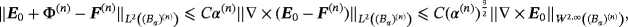 (22)
(22)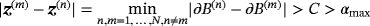 and applying Corollary 4.3 then
and applying Corollary 4.3 then
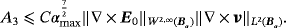 (23)
(23)Using 19-20, and 23 in 18 we find that

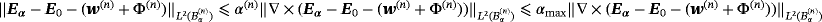 , this completes the proof.□
, this completes the proof.□By recalling the definition of
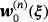 stated in Lemma 4.2, Ammari's et al's Theorem 3.11 in the case of multiple sufficiently well spaced objects becomes
stated in Lemma 4.2, Ammari's et al's Theorem 3.11 in the case of multiple sufficiently well spaced objects becomes
Theorem 4.5.Provided that
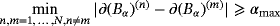 , there exists a constant C such that
, there exists a constant C such that
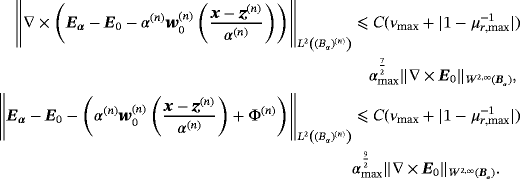
Proof.The result immediately follows from Lemma 4.4 and the definition of
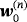 .□
.□
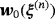 are obtained by extending in an obvious way the expressions in given in (3.13) and (3.14) in the previous study1 where the latter is now written in terms of
are obtained by extending in an obvious way the expressions in given in (3.13) and (3.14) in the previous study1 where the latter is now written in terms of
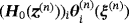 as well as
as well as
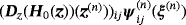 where
where
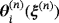 and
and
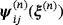 satisfy the transmission problems
satisfy the transmission problems
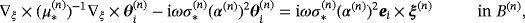 (24a)
(24a) (24b)
(24b) (24c)
(24c) (24d)
(24d)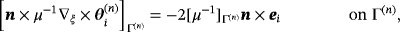 (24e)
(24e) (24f)
(24f)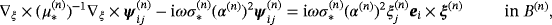 (25a)
(25a) (25b)
(25b) (25c)
(25c) (25d)
(25d)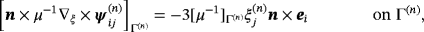 (25e)
(25e) (25f)
(25f)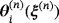 and
and
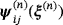 are analogues to the single object case presented in the previous research.1
are analogues to the single object case presented in the previous research.14.3 Integral representation formulae
Repeating the proof of Lemma 3.3 in the previous study1 for the multiple object case, it extends in an obvious way to
Lemma 4.6.Let
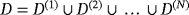 be the union of N bounded domains each with Lipschitz boundaries
be the union of N bounded domains each with Lipschitz boundaries
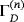 whose outer normal is n. For any
whose outer normal is n. For any
 satisfying ∇ × ∇×E=0, ∇·E=0 in
satisfying ∇ × ∇×E=0, ∇·E=0 in
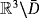 , we have, for any
, we have, for any
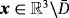
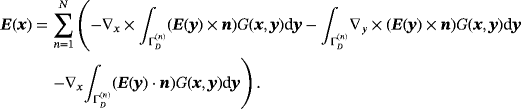
In a similar way, repeating the proof of their Lemma 3.4 for multiple objects it extends in an obvious way to
Lemma 4.7.Let
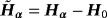 . Then for
. Then for
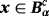
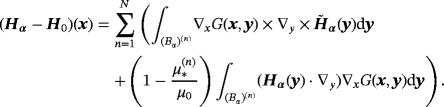
4.4 Asymptotic formulae
Ammari et al's Theorem 3.21 presents the leading order term in asymptotic expansion for (Hα − H0)(x) for a single inclusion Bα as α→0. In the case of multiple objects that are sufficiently well spaced, this extends to
Theorem 4.8.For a collection of N objects such that ν(n) is order one, α(n) is small and
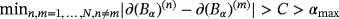 then for x away from Bα we have
then for x away from Bα we have
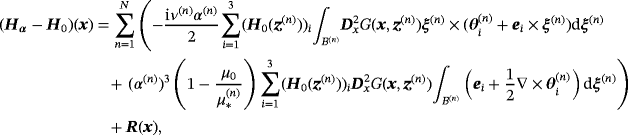 (26)
(26) is the solution of (24) and
is the solution of (24) and
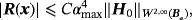 (27)
(27)
Proof.The proof uses as its starting point Lemma 4.7 and considers each object (Bα)(n) in turn. It applies very similar arguments to the proof of Ammari et al's Theorem 3.21 except Theorem 4.5 is used in place of their Theorem 3.1, 22 is used in place of their (3.6) and note that
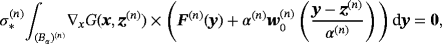 (28)
(28)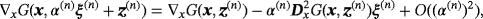 (29)
(29)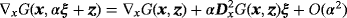 as α→0, which leads to the wrong sign in their first term, as previously reported for the single homogenous object case.2□
as α→0, which leads to the wrong sign in their first term, as previously reported for the single homogenous object case.2□
5 RESULTS FOR THE PROOF OF THEOREM 3.3
Recall that in this case, the object is inhomogeneous and is arranged as
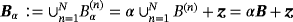 where α is a single small scaling parameter and z a single translation.
where α is a single small scaling parameter and z a single translation.
5.1 Elimination of the current source
The results presented in Section 4.1 hold also in the case when the object is inhomogeneous except the subscript α is replaced by α.
5.2 Energy estimates
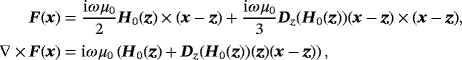
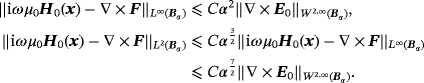 (30)
(30)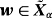 such that
such that
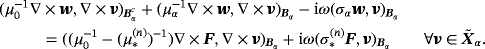 (31)
(31)The following Lemma extends Ammari et al's Lemma 3.21 to the case of an inhomogeneous object.
Lemma 5.1.For an inhomogeneous object Bα , there exists a constant C such that
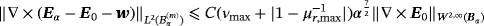 (32)
(32)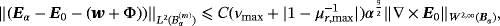 (33)
(33)
Proof.Here we introduce
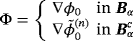 where
where
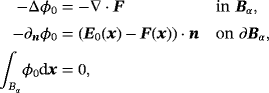
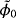 being the solution of an exterior problem in an analogous way to.1 Then, by writing
being the solution of an exterior problem in an analogous way to.1 Then, by writing
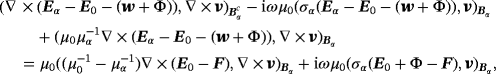
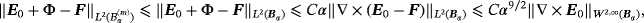 (34)
(34)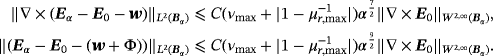
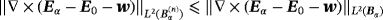 and
and
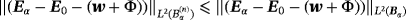 , which holds for n = 1,…,N.□
, which holds for n = 1,…,N.□
 so that
so that
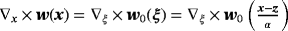 we find that w0(ξ) satisfies
we find that w0(ξ) satisfies
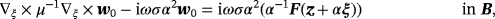 (35a)
(35a) (35b)
(35b) (35c)
(35c) (35d)
(35d)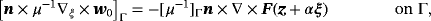 (35e)
(35e)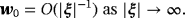 (35f)
(35f)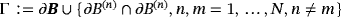 .
.In this case, Ammari et al's Theorem 3.11 becomes
Theorem 5.2.There exists a constant C such that
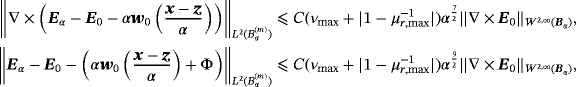
Proof.The result immediately follows from Lemma 5.1 and the definition of w0.□
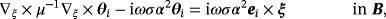 (36a)
(36a) (36b)
(36b) (36c)
(36c) (36d)
(36d)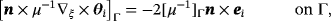 (36e)
(36e) (36f)
(36f)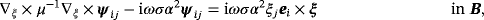 (37a)
(37a) (37b)
(37b) (37c)
(37c) (37d)
(37d)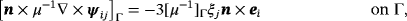 (37e)
(37e) (37f)
(37f)5.3 Integral representation formulae
The integral representation formulae presented in Section 4.3 only require (Bα)(n) to be replaced by
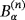 and Hα to be replaced by Hα for an inhomogeneous object.
and Hα to be replaced by Hα for an inhomogeneous object.
5.4 Asymptotic formulae
Ammari et al's Theorem 3.21 presents the leading order term in asymptotic expansion for (Hα − H0)(x) for a single homogenous inclusion Bα = αB+z as α→0. In the case of an inhomogeneous inclusion, this becomes
Theorem 5.3.For an inhomogeneous object Bα such that ν(n) is order one and α is small then for x away from Bα, we have
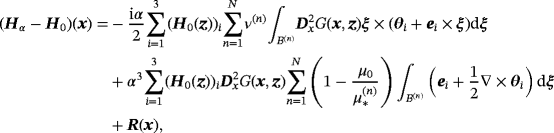 (38)
(38)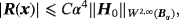 (39)
(39)
Proof.The proof uses as its starting point Lemma 4.7 and considers each region
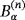 in turn. It applies similar arguments to the proof of Ammari et al's Theorem 3.21 except that our Theorem 5.2 is used in place of their Theorem 3.1 and our 34 instead of their (3.6). Furthermore, note that by summing contributions, we have that
in turn. It applies similar arguments to the proof of Ammari et al's Theorem 3.21 except that our Theorem 5.2 is used in place of their Theorem 3.1 and our 34 instead of their (3.6). Furthermore, note that by summing contributions, we have that
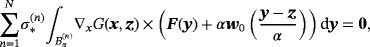 (40)
(40)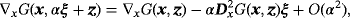 (41)
(41)6 NUMERICAL EXAMPLES AND ALGORITHMS FOR OBJECT LOCALISATION AND IDENTIFICATION
In this section, we consider an illustrative numerical application of the asymptotic formulae 5 and 8, numerical examples of the frequency spectra of the MPT coefficients, and propose algorithms for multiple object localisation and inhomogeneous object identification as extensions of those in another study.6
6.1 Numerical illustration of asymptotic formulae for (Hα − H0)(x)
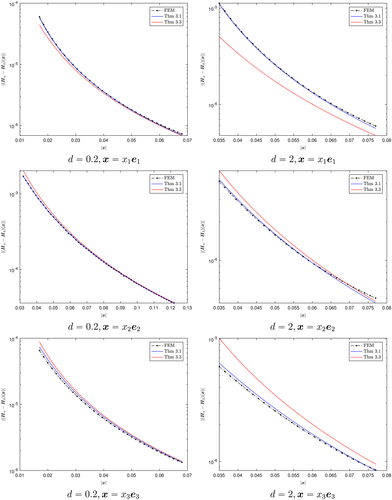
To illustrate the results in Theorems 3.1 and 3.3, comparisons of (Hα − H0)(x) ‡will be undertaken with a finite element method (FEM) solver19 for multiple objects and for inhomogeneous objects. We first show comparisons for two spheres, then comparisons for two tetrahedra followed by comparisons for an inhomogeneous parallelepiped.
6.1.1 Two spheres
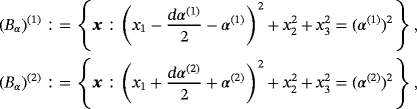
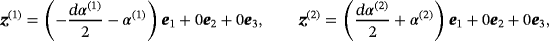
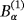 and
and
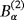 , respectively. Thus, the objects (Bα)(n), n = 1,2, are centered about the origin with
, respectively. Thus, the objects (Bα)(n), n = 1,2, are centered about the origin with
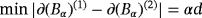 . The material properties of the spheres are
. The material properties of the spheres are
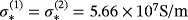 ,
,
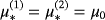 , we use ω = 133.5rad/s and the object sizes are chosen as α = α(1) = α(2) = 0.01m and hence
, we use ω = 133.5rad/s and the object sizes are chosen as α = α(1) = α(2) = 0.01m and hence
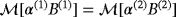 , independent of their separation, which will be used in Theorem 3.1. For closely spaced objects, we expect Theorem 3.3 to be applicable, and in this case,we set
, independent of their separation, which will be used in Theorem 3.1. For closely spaced objects, we expect Theorem 3.3 to be applicable, and in this case,we set
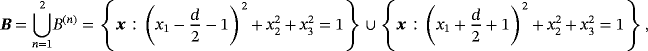
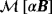 must be recomputed for each new d.
must be recomputed for each new d.Comparisons of (Hα − H0)(x) obtained from the asymptotic formulae 5 and 8 in Theorems 3.1 and 3.3 as well as a full FEM solution are made in Figure 5 for d = 0.2 and d = 2 along three different coordinates axes. To ensure the tensor coefficients were calculated accurately, a p = 3 edge element discretisation and an unstructured mesh of 6581 tetrahedra are used for computing
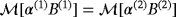 and meshes of 8950, and 11940 unstructured tetrahedral elements are used for computing
and meshes of 8950, and 11940 unstructured tetrahedral elements are used for computing
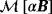 for d = 0.2 and d = 2, respectively. In addition, curved elements with a quadratic geometry resolution are used for representing the curved surfaces of the spheres. For these, and all subsequent examples, the artificial truncation boundary was set to be 100|B|. To ensure an accurate representation of (Hα − H0)(x) for the FEM solver, the same discretisation, suitably scaled, as used for
for d = 0.2 and d = 2, respectively. In addition, curved elements with a quadratic geometry resolution are used for representing the curved surfaces of the spheres. For these, and all subsequent examples, the artificial truncation boundary was set to be 100|B|. To ensure an accurate representation of (Hα − H0)(x) for the FEM solver, the same discretisation, suitably scaled, as used for
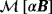 is employed.
is employed.
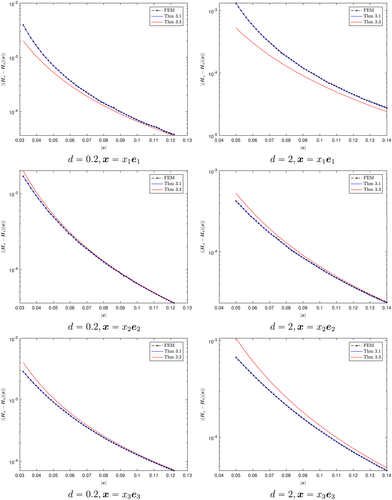
For the closely spaced objects, with d = 0.2, we observe good agreement between Theorem 3.3 and the FEM solution in Figure 5, with all three results tending to the same result for sufficiently large |x|. The improvement for larger |x| is expected as the asymptotic formulae 5 and 8 are valid for x away from Bα≡Bα. For objects positioned further apart, with d = 2, we observe that the agreement between Theorem 3.1 and the FEM solution is best. This agrees with what our theory predicts, since, for d = 2,
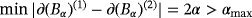 and so this theorem applies.
and so this theorem applies.
6.1.2 Two tetrahedra
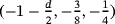 ,
,
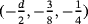 ,
,
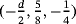 ,
,
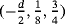 , and
, and
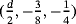 ,
,
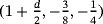 ,
,
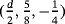 ,
,
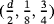 , scaled by α(1) and α(2) respectively. Thus, the objects (Bα)(n), n = 1,2, are centered about the origin with
, scaled by α(1) and α(2) respectively. Thus, the objects (Bα)(n), n = 1,2, are centered about the origin with
 and we determine B(n) from
and we determine B(n) from
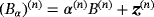 by setting
by setting
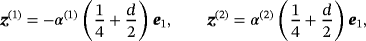
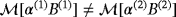 due to their different shapes, although the MPTs are independent of d. However, note that (Bα)(2) = α(2)Rx((Bα)(1))/α(1) and B(2) = Mx(B(1)), where
due to their different shapes, although the MPTs are independent of d. However, note that (Bα)(2) = α(2)Rx((Bα)(1))/α(1) and B(2) = Mx(B(1)), where
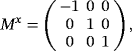
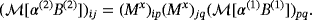 (42)
(42)
 [Colour figure can be viewed at wileyonlinelibrary.com]
[Colour figure can be viewed at wileyonlinelibrary.com]For
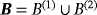 , we instead choose B(1) = (Bα)(1)/α(1), B(2) = (Bα)(2)/α(2) and set z=0.
, we instead choose B(1) = (Bα)(1)/α(1), B(2) = (Bα)(2)/α(2) and set z=0.
Comparisons of (Hα − H0)(x) for this case are made in Figure 7 for d = 0.2 and d = 2 along three different coordinates axes. To ensure the tensor coefficients are calculated accurately, a p = 3 edge element discretisation and unstructured meshes of 15617 and 15488 tetrahedra are used for computing
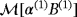 and
and
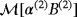 ,
§ respectively, and meshes of 15837 and 22045 unstructured tetrahedral elements are used for computing
,
§ respectively, and meshes of 15837 and 22045 unstructured tetrahedral elements are used for computing
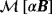 for d = 0.2 and d = 2, respectively. To ensure an accurate representation of (Hα − H0)(x) for the FEM solver, the same mesh, suitably scaled, as used for
for d = 0.2 and d = 2, respectively. To ensure an accurate representation of (Hα − H0)(x) for the FEM solver, the same mesh, suitably scaled, as used for
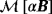 is employed with p=6.
is employed with p=6.
As in Section 6.1.1, we observe good agreement between Theorem 3.3 and the FEM solution for the closely spaced objects in Figure 7, with all three results tending to the same result for sufficiently large |x|. For objects positioned further apart, with d = 2, we observe that the agreement between Theorem 3.1 and the FEM solution is again best, which again agrees with what our theory predicts, since, for d = 2,
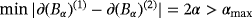 , and so this theorem applies.
, and so this theorem applies.
6.1.3 Inhomogeneous parallelepiped
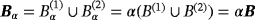 with
with

 ,
,
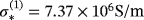 , and
, and
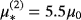 ,
,
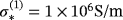 , respectively.
, respectively.Comparisons of (Hα − H0)(x) obtained from using the asymptotic expansion 8 in Theorem 3.3 and a full FEM solution are made in Figure 8 along three different coordinates axes. To ensure the tensor coefficients are calculated accurately, a p = 3 edge element discretisation and an unstructured mesh of 13121 tetrahedra are used for computing
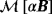 . To ensure an accurate representation of (Hα − H0)(x) for the FEM solver, the same mesh, suitably scaled, as used for
. To ensure an accurate representation of (Hα − H0)(x) for the FEM solver, the same mesh, suitably scaled, as used for
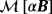 is employed with p=5. We observe a good agreement between Theorem 3.3 and the FEM solution for sufficiently large |x|.
is employed with p=5. We observe a good agreement between Theorem 3.3 and the FEM solution for sufficiently large |x|.
6.2 Frequency spectra
The frequency response of the coefficients of
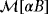 for a range of single homogeneous objects has been presented in existing studies3, 4 where the real part was observed to be sigmoid with respect to
for a range of single homogeneous objects has been presented in existing studies3, 4 where the real part was observed to be sigmoid with respect to
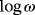 and the imaginary part had a distinctive single maxima. Rather than consider the coefficients, it is in fact better to split
and the imaginary part had a distinctive single maxima. Rather than consider the coefficients, it is in fact better to split
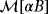 in to the real part
in to the real part
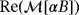 and an imaginary part
and an imaginary part
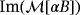 , which are both real symmetric rank 2 tensors, and to compute the eigenvalues of these. Indeed, many of the objects previously considered had rotational and/or reflection symmetries such that the eigenvalues coincide with the real and imaginary parts of the diagonal coefficients.
, which are both real symmetric rank 2 tensors, and to compute the eigenvalues of these. Indeed, many of the objects previously considered had rotational and/or reflection symmetries such that the eigenvalues coincide with the real and imaginary parts of the diagonal coefficients.
A theoretical investigation of
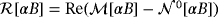 and
and
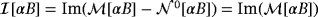 , where
, where
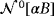 corresponds to the real symmetric rank 2 tensor describing the limiting response in the case of ω→0, and agrees with the Póyla-Szegö tensor for a homogenous permeable object, has been undertaken.20 In this, we prove results on the eigenvalues of these tensors.
corresponds to the real symmetric rank 2 tensor describing the limiting response in the case of ω→0, and agrees with the Póyla-Szegö tensor for a homogenous permeable object, has been undertaken.20 In this, we prove results on the eigenvalues of these tensors.
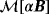 for an inhomogeneous object Bα, the coefficients of
for an inhomogeneous object Bα, the coefficients of
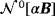 are given by
are given by
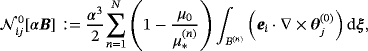 (43)
(43) (44a)
(44a) (44b)
(44b) (44c)
(44c)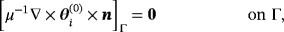 (44d)
(44d)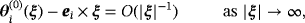 (44e)
(44e)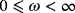 , the eigenvalues of
, the eigenvalues of
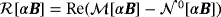 and
and
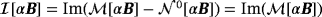 have the properties
have the properties
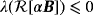 and
and
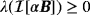 (this also applies to a homogenous objects where Bα reduces to Bα).20
(this also applies to a homogenous objects where Bα reduces to Bα).20To illustrate how the behaviour of
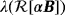 and
and
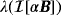 changes for an inhomogeneous object, we consider the geometry of the parallelepiped described in Section 6.1.3 placed at the origin so that
changes for an inhomogeneous object, we consider the geometry of the parallelepiped described in Section 6.1.3 placed at the origin so that
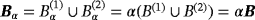 with α = 0.01m. Note that, although
with α = 0.01m. Note that, although
 and
and
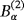 have different properties, the object B still reflectional symmetries in the e1 and e3 axes and a π/2 rotational symmetry about e1 so that the independent coefficients of
have different properties, the object B still reflectional symmetries in the e1 and e3 axes and a π/2 rotational symmetry about e1 so that the independent coefficients of
 are
are
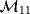 and
and
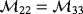 (and hence
(and hence
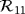 ,
,
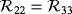 are the independent coefficients of
are the independent coefficients of
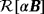 and
and
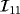 ,
,
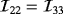 are the independent coefficients of
are the independent coefficients of
 ). In Figure 9, we show the computed results for
). In Figure 9, we show the computed results for
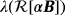 and
and
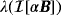 for the case where
for the case where
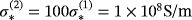 and
and
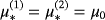 , and in Figure 10, we show the corresponding result for
, and in Figure 10, we show the corresponding result for
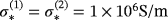 and
and
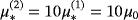 . For this, we use similar discretisations to those stated previously. In the former case,
. For this, we use similar discretisations to those stated previously. In the former case,
 vanishes but not in the latter case.
vanishes but not in the latter case.
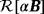 and
and
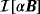 : inhomogeneous object parallelepiped up of two cubes with
: inhomogeneous object parallelepiped up of two cubes with
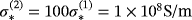 and
and
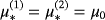 [Colour figure can be viewed at wileyonlinelibrary.com]
[Colour figure can be viewed at wileyonlinelibrary.com]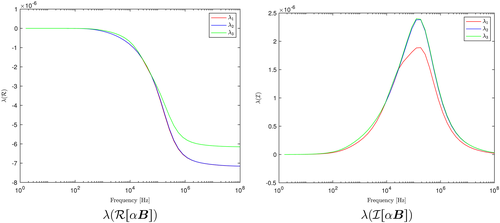
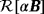 and
and
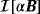 : inhomogeneous parallelepiped made up of two cubes with
: inhomogeneous parallelepiped made up of two cubes with
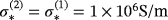 and
and
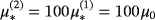 [Colour figure can be viewed at wileyonlinelibrary.com]
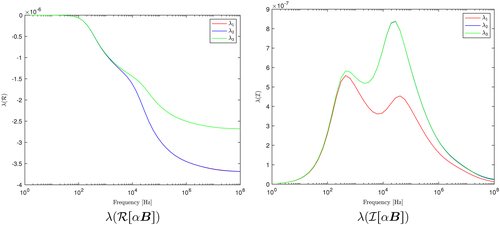
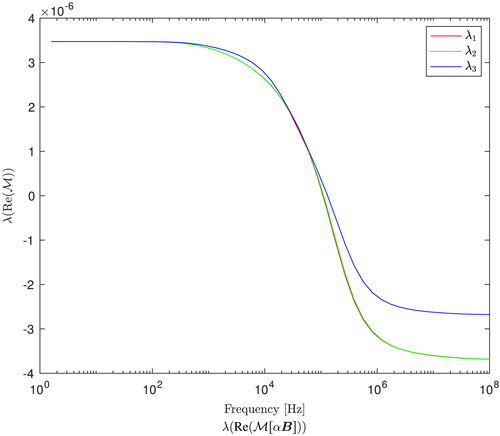
[Colour figure can be viewed at wileyonlinelibrary.com]We observe, in Figure 9, that although
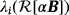 , i = 1,… ,3 are still monotonically decreasing with
, i = 1,… ,3 are still monotonically decreasing with
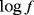 , it is no longer sigmoid for an inhomogeneous object with varying σ and constant μ and has multiple nonstationary inflection points. Furthermore, rather than a single maxima,
, it is no longer sigmoid for an inhomogeneous object with varying σ and constant μ and has multiple nonstationary inflection points. Furthermore, rather than a single maxima,
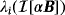 , i = 1,… ,3 has two distinct local maxima. However, the results shown in Figure 10 illustrate for an inhomogeneous object with varying μ and constant σ,
, i = 1,… ,3 has two distinct local maxima. However, the results shown in Figure 10 illustrate for an inhomogeneous object with varying μ and constant σ,
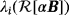 , i = 1,… ,3, that the behaviour is quite different, and in this case,
, i = 1,… ,3, that the behaviour is quite different, and in this case,
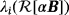 , i = 1,…,3 is still sigmoid and the curves for
, i = 1,…,3 is still sigmoid and the curves for
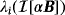 , i = 1,…,3 still have a single maxima. In the limiting case of ω→0,
, i = 1,…,3 still have a single maxima. In the limiting case of ω→0,
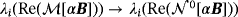 , i = 1,…,3 and, for the latter case with a contrast in μ, the behaviour is as shown in Figure 11, which is quite different to a homogenous object of the same size.
, i = 1,…,3 and, for the latter case with a contrast in μ, the behaviour is as shown in Figure 11, which is quite different to a homogenous object of the same size.
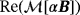 : inhomogeneous parallelepiped made up of two cubes with
: inhomogeneous parallelepiped made up of two cubes with
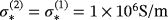 and
and
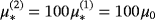 [Colour figure can be viewed at wileyonlinelibrary.com]
[Colour figure can be viewed at wileyonlinelibrary.com]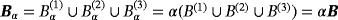 with
with
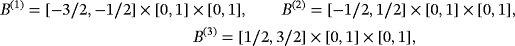
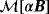 , an unstructured mesh of 15 109 tetrahedral elements is generated and p = 4 elements employed. The independent coefficients of
, an unstructured mesh of 15 109 tetrahedral elements is generated and p = 4 elements employed. The independent coefficients of
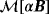 are again
are again
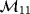 and
and
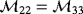 .
.In Figure 12, we show
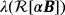 and
and
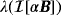 for the case where
for the case where
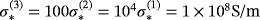 and
and
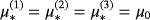 , and in Figure 13, we show the corresponding result for
, and in Figure 13, we show the corresponding result for
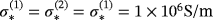 and
and
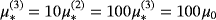 . In the former case,
. In the former case,
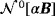 vanishes, but not in the latter case.
vanishes, but not in the latter case.
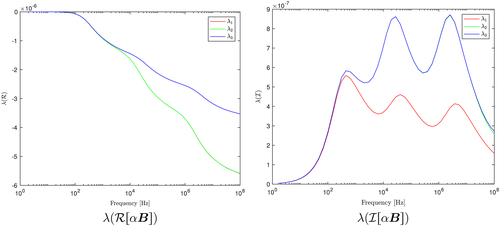
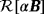 and
and
 : inhomogeneous parallelepiped made up of three cubes with
: inhomogeneous parallelepiped made up of three cubes with
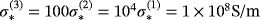 and
and
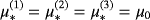 [Colour figure can be viewed at wileyonlinelibrary.com]
[Colour figure can be viewed at wileyonlinelibrary.com]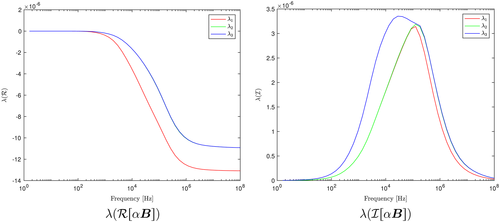
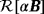 and
and
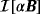 : inhomogeneous parallelepiped made up of three cubes with
: inhomogeneous parallelepiped made up of three cubes with
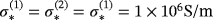 and
and
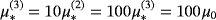 [Colour figure can be viewed at wileyonlinelibrary.com]
[Colour figure can be viewed at wileyonlinelibrary.com]We observe, in Figure 12, that
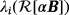 , i = 1,…,3 is still monotonically decreasing with multiple nonstationary points of inflection, and
, i = 1,…,3 is still monotonically decreasing with multiple nonstationary points of inflection, and
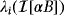 , i = 1,…,3 now has three distinct local maxima. In Figure 13, we see that
, i = 1,…,3 now has three distinct local maxima. In Figure 13, we see that
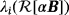 , i = 1,…,3 is sigmoid, and
, i = 1,…,3 is sigmoid, and
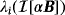 , i = 1,…,3 has only a single maxima. Unlike Figure 11, we see in Figure 14 that the low frequency response of λi(Re(M[αB])), i = 1,…,3 are different. This is probably due to the fact that the chosen contrasts in μ imply that one of the three cubes no longer has a dominant effect over the other two.
, i = 1,…,3 has only a single maxima. Unlike Figure 11, we see in Figure 14 that the low frequency response of λi(Re(M[αB])), i = 1,…,3 are different. This is probably due to the fact that the chosen contrasts in μ imply that one of the three cubes no longer has a dominant effect over the other two.
 : inhomogeneous parallelepiped made up of three cubes with
: inhomogeneous parallelepiped made up of three cubes with
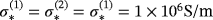 and
and
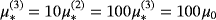 [Colour figure can be viewed at wileyonlinelibrary.com]
[Colour figure can be viewed at wileyonlinelibrary.com]
Remark 6.1.The results shown in Figures 9 and 12 indicate that the number of points of nonstationary inflection in
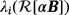 and the number of local maxima in
and the number of local maxima in
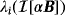 can potentially be used to determine an upper bound on the number of regions with varying σ that make up an inhomogeneous object Bα. Note, that contrasts in σ between the regions making up the inhomogeneous object have deliberately chosen as large in these examples and we acknowledge that, for small contrasts, detecting such peaks would be more challenging.
can potentially be used to determine an upper bound on the number of regions with varying σ that make up an inhomogeneous object Bα. Note, that contrasts in σ between the regions making up the inhomogeneous object have deliberately chosen as large in these examples and we acknowledge that, for small contrasts, detecting such peaks would be more challenging.
6.3 Object localisation
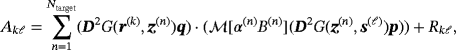
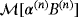 as 3 × 3 matrices.
¶ Assuming that the data is corrupted by measurement noise and is sampled using Hadamard's technique, as in the previous study,6 then the MSR matrix can be written in the form
as 3 × 3 matrices.
¶ Assuming that the data is corrupted by measurement noise and is sampled using Hadamard's technique, as in the previous study,6 then the MSR matrix can be written in the form
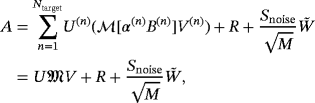
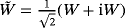 and W is a K × L matrix with independent and identical Gaussian entries with zero mean and unit variance, and Snoise is a positive constant. In addition, U is a matrix of size K × 3Ntarget
and W is a K × L matrix with independent and identical Gaussian entries with zero mean and unit variance, and Snoise is a positive constant. In addition, U is a matrix of size K × 3Ntarget
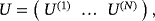
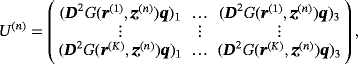
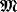 is of size 3Ntarget × 3Ntarget and is block diagonal in the form
is of size 3Ntarget × 3Ntarget and is block diagonal in the form
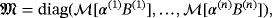
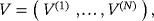
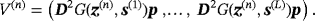 (45)
(45)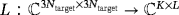 as
as
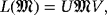 (46)
(46)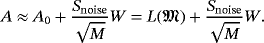
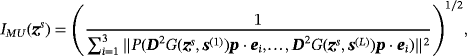 (47)
(47)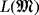 .
.
Proposition 6.2.Suppose that
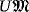 has full rank. Then
has full rank. Then
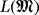 has 3Ntarget non-zero singular values. Furthermore, IMU will have Ntarget peaks at the object locations z=zs.
has 3Ntarget non-zero singular values. Furthermore, IMU will have Ntarget peaks at the object locations z=zs.
- 1. The number and locations of the measurement and excitor pairs. In practice, the number of each will be limited to powers of 4 for practical reasons.1
- 2.
The noise level, which we define as the reciprocal of the signal to noise ratio in terms of the n + 3(n − 1)th singular value of A0 (ordered as S1(A0) > S2(A0)…
In other studies,1, 6 the SNR was based instead on the largest singular value S1(A0).
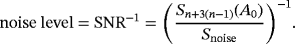 (48)
(48) - 3. The frequency of excitation.
Remark 6.3.From the examination of the frequency dependence of the coefficients of
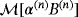 we have seen that the real and imaginary parts for different objects
we have seen that the real and imaginary parts for different objects
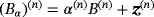 are different. Moreover, in general, their imaginary components exhibit resonance behaviour at different (possibly multiple) frequencies. Consequently, different objects, in general, correspond to different singular values of A0. The presence of multiple objects with the same shape and size, but with different locations, will result in multiplicities of the singular values (in the absence of noise). If only a single frequency is considered and Snoise is chosen based on the largest singular value S1(A0), then it will generate a W with Gaussian statistics that are associated with only one of the objects possibly present. If the singular values associated with the other objects are much smaller than S1(A0), it may be difficult to detect the other objects present. In particular, to locate those objects with smaller MPT coefficients (and hence smaller singular values) at that frequency under consideration.
are different. Moreover, in general, their imaginary components exhibit resonance behaviour at different (possibly multiple) frequencies. Consequently, different objects, in general, correspond to different singular values of A0. The presence of multiple objects with the same shape and size, but with different locations, will result in multiplicities of the singular values (in the absence of noise). If only a single frequency is considered and Snoise is chosen based on the largest singular value S1(A0), then it will generate a W with Gaussian statistics that are associated with only one of the objects possibly present. If the singular values associated with the other objects are much smaller than S1(A0), it may be difficult to detect the other objects present. In particular, to locate those objects with smaller MPT coefficients (and hence smaller singular values) at that frequency under consideration.
We explore this through the following experiment. We simulate excitations and measurements taken at regular intervals on the plane [ − 1,1] × [ − 1,1] × {0} such that L = K = 256. The dipole moments are chosen as p=q=e3 so that the plane of all measurement, and excitation coils are parallel to this horizontal surface. With these measurements, the location identification of a coin
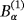 of radius 0.01125m and thickness 3.15 × 10−3m with
of radius 0.01125m and thickness 3.15 × 10−3m with
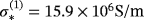 and
and
 and a tetrahedron
and a tetrahedron
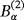 with vertices (5.77 × 10−3,0,0)m, ( − 2.88,5,0) × 10−3m, ( − 2.88, − 5,0) × 10− 3m and (0,0, − 8.16 × 10−3)m and material properties
with vertices (5.77 × 10−3,0,0)m, ( − 2.88,5,0) × 10−3m, ( − 2.88, − 5,0) × 10− 3m and (0,0, − 8.16 × 10−3)m and material properties
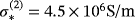 and
and
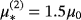 will be considered. The true locations of these objects are assumed to be
will be considered. The true locations of these objects are assumed to be
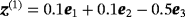 and
and
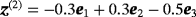 , respectively. To perform the imaging, noise is added to the simulated A0 to create A, and the image functional IMU is evaluated for different positions zs. To do this, we compute
, respectively. To perform the imaging, noise is added to the simulated A0 to create A, and the image functional IMU is evaluated for different positions zs. To do this, we compute
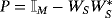 where WS are the first 3N singular vectors of A, which are chosen based on the magnitudes of the singular values and thereby allows us to also predict the number of objects N present.
where WS are the first 3N singular vectors of A, which are chosen based on the magnitudes of the singular values and thereby allows us to also predict the number of objects N present.
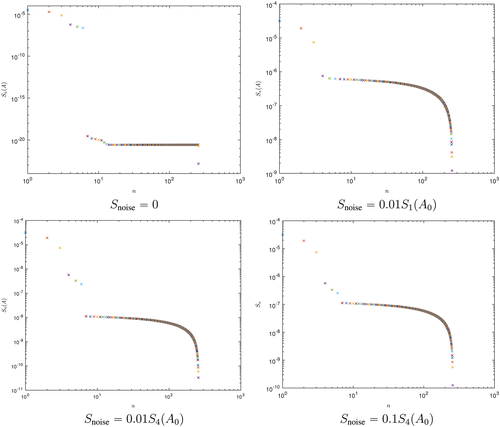
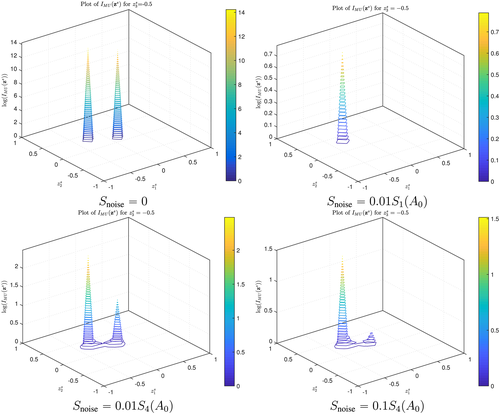
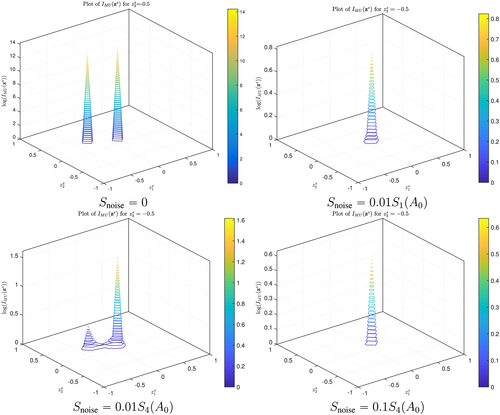
We first consider location identification at a frequency f = 1 × 105Hz, which is close to the resonance peaks for the two objects, and consider the singular values of A0 and A in Figure 15. At this frequency, Sn(A0), n = 1,2,3 are associated with the coin and Sn(A0), n = 4,5,6 with the tetrahedron. Without noise, A = A0 and the six physical singular values are clearly distinguished, but, by considering a noise level of 1% so that Snoise = 0.01S1(A0), it is no longer possible to distinguish Sn(A), n = 4,5,6 from the noisy singular values. On the other hand, by setting Snoise = 0.01S4(A0), or even Snoise = 0.1S4(A0), we can distinguish all 6 singular values from the noise. This means that with Snoise = 0.01S1(A0) we expect to only locate the coin, but with Snoise = 0.01S4(A0),0.1S4(A0) we expect to find both objects. This is confirmed in Figure 16 where we plot IMU on the plane −0.5e3. We observe that for Snoise = 0.01S1(A0), we can only locate the coin, for Snoise = 0.01S4(A0) we can locate both the coin and the tetrahedron and even by increasing the noise level to 10% and setting Snoise = 0.1S4(A0) both objects can still be identified. On the other hand, choosing the frequency f = 132Hz, such that Sn(A0), n = 1,2,3 are associated with the tetrahedron and Sn(A0), n = 4,5,6 with the coin, Figure 17 shows that the phenomena is reversed, and with a 10% noise level and Snoise = 0.1S4(A0), only the tetrahedron can be identified at this frequency.
6.4 Object identification
A dictionary-based classification technique for individual object identification has been proposed by Ammari et al6 and this easily extends to the identification of multiple inhomogeneous objects. We propose a slight variation on that proposed by Ammari et al, which uses the eigenvalues of the real and imaginary parts of the MPT as a classifier as opposed to its singular values at a range of frequencies. The motivation for this is the richness of the frequency spectra of the eigenvalues, as shown in Section 6.2 and that it provides an increased number of values to classify each object. We also propose a strategy in which objects are put in to canonical form before forming the dictionary. The algorithm comprises of two stages as described below.
6.4.1 Offline stage
 , i = 1,…,Ncandidate by ensuring that the origin for ξ(i) in B(i) coincides with the centre of mass of B(i) and the object's size α(i) is chosen such that
, i = 1,…,Ncandidate by ensuring that the origin for ξ(i) in B(i) coincides with the centre of mass of B(i) and the object's size α(i) is chosen such that
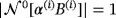 #where
#where
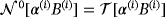 in the case of a homogenous object and corresponds to the Póyla-Szegö tensor as well as being the characterisation for σ∗ = 0 for this object.
∥ In the case of an object with homogenous materials, the coefficients of
in the case of a homogenous object and corresponds to the Póyla-Szegö tensor as well as being the characterisation for σ∗ = 0 for this object.
∥ In the case of an object with homogenous materials, the coefficients of
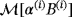 are computed by solving the transmission problem (7) using FEM and then applying (6), and in the case of an inhomogeneous object, (10) and (9) are used. In each case, the eigenvalues
are computed by solving the transmission problem (7) using FEM and then applying (6), and in the case of an inhomogeneous object, (10) and (9) are used. In each case, the eigenvalues
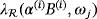 and
and
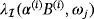 are obtained for a range of frequencies ωj and
are obtained for a range of frequencies ωj and
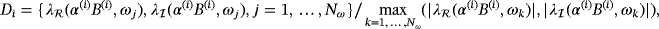
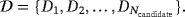
6.4.2 Online stage
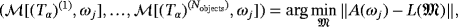
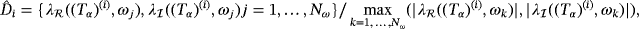
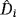 within the dictionary
within the dictionary
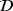 .6 Notice the target could also be inhomogeneous in which case (Tα)(i) is replaced by
.6 Notice the target could also be inhomogeneous in which case (Tα)(i) is replaced by
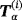 .
.6.4.3 Numerical example
As a challenging object identification example, we consider a dictionary consisting of parallelepipeds described in Section 6.2, which consist of either two regions
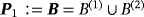 with
with
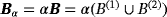 or three regions
or three regions
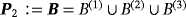 with
with
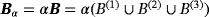 , and vary the material properties according to the descriptions previously described. We also consider the limiting case where the two (three) regions have the same parameters. The dictionary for these objects is generated according to the off-line stage with ω ∈ 2π(2,300,4 × 103,5 × 104,2 × 105)rad/s, arbitrarily chosen over the frequency spectrum.
, and vary the material properties according to the descriptions previously described. We also consider the limiting case where the two (three) regions have the same parameters. The dictionary for these objects is generated according to the off-line stage with ω ∈ 2π(2,300,4 × 103,5 × 104,2 × 105)rad/s, arbitrarily chosen over the frequency spectrum.
For the online stage, take
 , i = 1,2, j = 1,…,Nω = 5 to be given by considering targets
, i = 1,2, j = 1,…,Nω = 5 to be given by considering targets
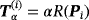 where R is an arbitrary rotation and adding noise. In Figure 18, we illustrate the algorithms ability to differentiate between these similar objects. The red bars indicate the predicated classification, which is correct for the examples presented (it was also found to be correct for the cases of the other parallelepipeds). We can observe that greatest similarity in terms of the classification is between the two homogeneous parallelepipeds and between the two parallelepipeds with contrasting σ, and in each case, the classification becomes more challenging as the noise level is increased.
where R is an arbitrary rotation and adding noise. In Figure 18, we illustrate the algorithms ability to differentiate between these similar objects. The red bars indicate the predicated classification, which is correct for the examples presented (it was also found to be correct for the cases of the other parallelepipeds). We can observe that greatest similarity in terms of the classification is between the two homogeneous parallelepipeds and between the two parallelepipeds with contrasting σ, and in each case, the classification becomes more challenging as the noise level is increased.
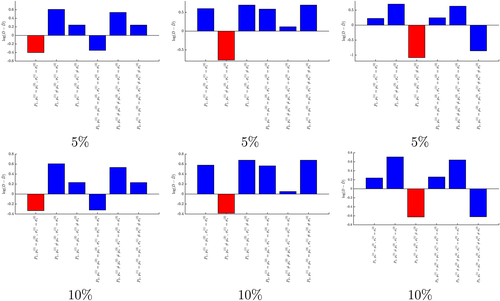
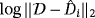 : Top row show classification with 5% noise, bottom row with 10% noise, red indicates the predicted object, which is correct in all cases [Colour figure can be viewed at wileyonlinelibrary.com]
: Top row show classification with 5% noise, bottom row with 10% noise, red indicates the predicted object, which is correct in all cases [Colour figure can be viewed at wileyonlinelibrary.com]By increasing the number of frequencies considered so that Nω = 7 with ω ∈ 2π(2,300,4 × 103,5 × 104,2 × 105,3 × 106,4 × 107)rad/s, we see in Figure 19 that the certainty of the classification is improved for both noise levels.
 : Top row show classification with 5% noise, bottom row with 10% noise, red indicates the predicted object, which is correct in all cases [Colour figure can be viewed at wileyonlinelibrary.com]
: Top row show classification with 5% noise, bottom row with 10% noise, red indicates the predicted object, which is correct in all cases [Colour figure can be viewed at wileyonlinelibrary.com]ACKNOWLEDGEMENT
The authors would like to thank Engineering and Physical Sciences U.K. (EPSRC) for the financial support received from the grants EP/R002134/1 and EP/R002177/1. The second author would like to thank the Royal Society for the financial support received from a Royal Society Wolfson Research Merit Award. All data are provided in full in Section 6 of this paper.
REFERENCES
- *
In order to simplify notation, we drop the double check on
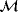 and the single check on
and the single check on
 , which was used in2 to denote two and one reduction(s) in rank, respectively. We recall that
, which was used in2 to denote two and one reduction(s) in rank, respectively. We recall that
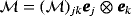 by the Einstein summation convention where we use the notation ej to denote the jth unit vector. We will denote the jth component of a vector u by u·ej = (u)j and the j,kth coefficient of a rank 2 tensor
by the Einstein summation convention where we use the notation ej to denote the jth unit vector. We will denote the jth component of a vector u by u·ej = (u)j and the j,kth coefficient of a rank 2 tensor
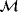 by
by
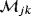 .
. - † Note no summation over n is implied.
- ‡ We use (Hα − H0)(x) instead of (Hα − H0)(x) (i.e. remove bold on the subscript α) for Theorem 3.1 throughout this section as the examples with multiple objects presented have the same object size.
- §
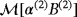 could be alternatively obtained from
could be alternatively obtained from
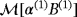 by applying 42.
by applying 42. - ¶
For (multiple) inhomogeneous objects we replace
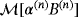 here and in the following by
here and in the following by
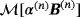 where α(n) becomes the size of the nth inhomogeneous object with configuration B(n)
where α(n) becomes the size of the nth inhomogeneous object with configuration B(n) - #
For inhomogeneous objects we require
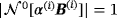 and we replace (Bα)(i) by
and we replace (Bα)(i) by
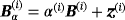 , B(i) by B(i) as well as ensuring the centre of mass coincides with the centre of mass of
, B(i) by B(i) as well as ensuring the centre of mass coincides with the centre of mass of
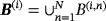 .
. - ∥ If μ∗ = μ0 we choose the object size by requiring the high conductivity limit to have unit determinant.




