Research Article
A new blowup criterion for strong solutions to the three-dimensional compressible magnetohydrodynamic equations with vacuum in a bounded domain
Yingshan Chen,
Xiaofeng Hou,
Limei Zhu,
Yingshan Chen
Department of Mathematics, South China University of Technology, Guangzhou, 510641 China
Search for more papers by this authorCorresponding Author
Xiaofeng Hou
Faculty of Applied Mathematics, Guangdong University of Technology, Guangzhou, 510006 China
Correspondence to: Xiaofeng Hou, Faculty of Applied Mathematics, Guangdong University of Technology, 510006 Guangzhou , China.
E-mail: [email protected]
Search for more papers by this authorLimei Zhu
Department of Mathematics, South China University of Technology, Guangzhou, 510641 China
Search for more papers by this authorYingshan Chen,
Xiaofeng Hou,
Limei Zhu,
Yingshan Chen
Department of Mathematics, South China University of Technology, Guangzhou, 510641 China
Search for more papers by this authorCorresponding Author
Xiaofeng Hou
Faculty of Applied Mathematics, Guangdong University of Technology, Guangzhou, 510006 China
Correspondence to: Xiaofeng Hou, Faculty of Applied Mathematics, Guangdong University of Technology, 510006 Guangzhou , China.
E-mail: [email protected]
Search for more papers by this authorLimei Zhu
Department of Mathematics, South China University of Technology, Guangzhou, 510641 China
Search for more papers by this authorAbstract
In this paper, we establish a new blowup criterions for the strong solution to the Dirichlet problem of the three-dimensional compressible MHD system with vacuum. Specifically, we obtain the blowup criterion in terms of the concentration of density in BMO norm or the concentration of the integrability of the magnetic field at the first singular time. The BMO-type estimate for the Lam
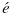system 2.6 and a variant of the Brezis-Waigner's inequality 2.3 play a critical role in the proof. Copyright © 2017 John Wiley & Sons, Ltd.
References
- 1Chen G-Q, Wang D. Global solutions of nonlinear magnetohydrodynamics with large initial data. Journal Differential Equations. 2002; 182(2): 344–376.
- 2Chen G-Q, Wang D. Existence and continuous dependence of large solutions for the magnetohydrodynamic equations. Zeitschrift für angewandte Mathematik und Physik. 2003; 54(4): 608–632.
- 3Ducomet B, Feireisl E. The equations of magnetohydrodynamics: on the interaction between matter and radiation in the evolution of gaseous stars. Communications in Mathematical Physics. 2006; 266(3): 595–629.
- 4Hu X, Wang D. Compactness of weak solutions to the three-dimensional compressible magnetohydrodynamic equations. Journal Differential Equations. 2008; 245(8): 2176–2198.
- 5Hu X, Wang D. Global solutions to the three-dimensional full compressible magnetohydrodynamic flows. Communications in Mathematical Physics. 2008; 283(1): 255–284.
- 6Hu X, Wang D. Low Mach number limit of viscous compressible magnetohydrodynamic flows. SIAM Journal on Mathematical Analysis. 2009; 41(3): 1272–1294.
- 7Hu X, Wang D. Global existence and large-time behavior of solutions to the three-dimensional equations of compressible magnetohydrodynamic flows. Archive for Rational Mechanics and Analysis. 2010; 197(1): 203–238.
- 8Jiang S, Ju Q, Li F. Incompressible limit of the nonisentropic ideal magnetohydrodynamic equations. SIAM Journal on Mathematical Analysis. 2016; 48(1): 302–319.
- 9Jiu Q, Niu D, Wu J, Xu X, Yu H. The 2D magnetohydrodynamic equations with magnetic diffusion. Nonlinearity. 2015; 28(11): 3935–3955.
- 10Kawashima S. Smooth global solutions for two-dimensional equations of electromagnetofluid dynamics. Japan Journal of Industrial and Applied Mathematics. 1984; 1(1): 207–222.
10.1007/BF03167869 Google Scholar
- 11Kawashima S, Shizuta Y. Magnetohydrodynamic approximation of the complete equations for an electromagnetic fluid. Tsukuba Journal of Mathematics. 1986; 10(1): 131–149.
10.21099/tkbjm/1496160397 Google Scholar
- 12Kawashima S, Shizuta Y. Magnetohydrodynamic approximation of the complete equations for an electromagnetic fluid. II. Proceedings of the Japan Academy Series A Mathematical Sciences. 1986; 62(5): 181–184.
- 13Landau LD, Lifshitz EM. Course of Theoretical Physics, Pergamon International Library of Science, Technology, Engineering and Social Studies, vol. 8. Pergamon Press: Oxford, 1984. Electrodynamics of continuous media, Translated from the second Russian edition by J. B. Sykes, J. S. Bell and M. J. Kearsley, Second Russian edition revised by Lifshits and L. P. Pitaevskiı̆.
- 14Li H-L, Xu X, Zhang J. Global classical solutions to 3D compressible magnetohydrodynamic equations with large oscillations and vacuum. SIAM Journal on Mathematical Analysis. 2013; 45(3): 1356–1387.
- 15Rozanova O. 2009. Blow up of smooth solutions to the barotropic compressible magnetohydrodynamic equations with finite mass and energy. In Hyperbolic Problems: Theory, Numerics and Applications, Proc. Sympos. Appl. Math., vol. 67 Amer. Math. Soc.: Providence, RI; 911–917.
10.1090/psapm/067.2/2605286 Google Scholar
- 16Wang D. Large solutions to the initial-boundary value problem for planar magnetohydrodynamics. SIAM Journal on Applied Mathematics. 2003; 63(4): 1424–1441 (electronic).
- 17Dellar PJ. A note on magnetic monopoles and the one-dimensional {MHD} riemann problem. Journal of Computational Physics. 2001; 172(1): 392–398.
- 18Fan J, Jiang S, Nakamura G. Vanishing shear viscosity limit in the magnetohydrodynamic equations. Communications in Mathematical Physics. 2007; 270(3): 691–708.
- 19Vol'pert AI, Hudjaev SI. The Cauchy problem for composite systems of nonlinear differential equations. Matematicheskii Sbornik (N.S.) 1972; 87(129): 504–528.
- 20Fan J, Yu W. Strong solution to the compressible magnetohydrodynamic equations with vacuum. Nonlinear Analysis: Real World Applications. 2009; 10(1): 392–409.
- 21He C, Xin Z. On the regularity of weak solutions to the magnetohydrodynamic equations. Journal Differential Equations. 2005; 213(2): 235–254.
- 22Xu X, Zhang J. A blow-up criterion for 3D compressible magnetohydrodynamic equations with vacuum. Mathematical Models and Methods in Applied Sciences. 2012; 22(2): 1150010, 23.
- 23Suen A. A blow-up criterion for the 3D compressible magnetohydrodynamics in terms of density. Discrete and Continuous Dynamical Systems. 2013; 33(8): 3791–3805.
- 24Wen H, Zhu C. Blow-up criterions of strong solutions to 3D compressible Navier-Stokes equations with vacuum. Advances in Mathematics. 2013; 248: 534–572.
- 25Wang Y, Li S. Global regularity for the Cauchy problem of three-dimensional compressible magnetohydrodynamics equations. Nonlinear Analysis: Real World Applications. 2014; 18: 23–33.
- 26Huang X, Li J. Serrin-type blowup criterion for viscous, compressible, and heat conducting Navier-Stokes and magnetohydrodynamic flows. Communications in Mathematical Physics. 2013; 324(1): 147–171.
- 27Du L, Wang Y. Mass concentration phenomenon in compressible magnetohydrodynamic flows. Nonlinearity. 2015; 28(8): 2959–2976.
- 28Sun Y, Wang C, Zhang Z. A Beale-Kato-Majda blow-up criterion for the 3-D compressible Navier-Stokes equations. Journal de Mathématiques Pures et Appliquées (9). 2011; 95(1): 36–47.
- 29Ladyzenskaja O-A, Solonnikov V-A, Uralceva N-N, Smith S. Linear and quasilinear equations of parabolic type, 1968.
- 30Acquistapace P. On BMO regularity for linear elliptic systems. Annali di Matematica Pura ed Applicata (4). 1992; 161: 231–269.
