Mathematical Methods in the Applied Sciences

RESEARCH ARTICLE

Open Access

Periodic Orbits of MAX and MIN Multistate Networks

Juan A. Aledo

orcid.org/0000-0003-1786-8087

Department of Mathematics, University of Castilla-La Mancha, Albacete, Spain

Contribution: Conceptualization, Methodology, Investigation, Formal analysis, Supervision, Writing - original draft, Writing - review & editing

Search for more papers by this author

Jose P. Llano,

Jose P. Llano

orcid.org/0009-0006-1115-6037

Department of Mathematics, University of Castilla-La Mancha, Albacete, Spain

Institute of Mathematics Applied to Science and Engineering, University of Castilla-La Mancha, Albacete, Spain

Contribution: Conceptualization, Methodology, Investigation, Formal analysis, Writing - original draft, Writing - review & editing

Search for more papers by this author

Leila Sharifan,

Leila Sharifan

orcid.org/0000-0003-4531-740X

Department of Mathematics and Computer Sciences, Hakim Sabzevari University, Sabzevar, Iran

Contribution: Conceptualization, Methodology, Investigation, Formal analysis, Supervision, Writing - original draft, Writing - review & editing

Search for more papers by this author

Jose C. Valverde,

Corresponding Author

Jose C. Valverde

[email protected]

orcid.org/0000-0002-3214-9606

Department of Mathematics, University of Castilla-La Mancha, Albacete, Spain

Institute of Mathematics Applied to Science and Engineering, University of Castilla-La Mancha, Albacete, Spain

Correspondence:

Jose C. Valverde ([email protected])

Contribution: Conceptualization, Methodology, Investigation, Formal analysis, Writing - original draft, Writing - review & editing, Supervision

Search for more papers by this author

Juan A. Aledo,

Juan A. Aledo

orcid.org/0000-0003-1786-8087

Department of Mathematics, University of Castilla-La Mancha, Albacete, Spain

Contribution: Conceptualization, Methodology, Investigation, Formal analysis, Supervision, Writing - original draft, Writing - review & editing

Search for more papers by this author

Jose P. Llano,

Jose P. Llano

orcid.org/0009-0006-1115-6037

Department of Mathematics, University of Castilla-La Mancha, Albacete, Spain

Institute of Mathematics Applied to Science and Engineering, University of Castilla-La Mancha, Albacete, Spain

Contribution: Conceptualization, Methodology, Investigation, Formal analysis, Writing - original draft, Writing - review & editing

Search for more papers by this author

Leila Sharifan,

Leila Sharifan

orcid.org/0000-0003-4531-740X

Department of Mathematics and Computer Sciences, Hakim Sabzevari University, Sabzevar, Iran

Contribution: Conceptualization, Methodology, Investigation, Formal analysis, Supervision, Writing - original draft, Writing - review & editing

Search for more papers by this author

Jose C. Valverde,

Corresponding Author

Jose C. Valverde

[email protected]

orcid.org/0000-0002-3214-9606

Department of Mathematics, University of Castilla-La Mancha, Albacete, Spain

Institute of Mathematics Applied to Science and Engineering, University of Castilla-La Mancha, Albacete, Spain

Correspondence:

Jose C. Valverde ([email protected])

Contribution: Conceptualization, Methodology, Investigation, Formal analysis, Writing - original draft, Writing - review & editing, Supervision

Search for more papers by this author

First published: 10 June 2025

https://doi.org/10.1002/mma.10944

Funding: Juan A. Aledo has been funded by the Government of Castilla-La Mancha and the “ERDF A way of making Europe” through the project SBPLY/21/180225/000062 and by Universidad de Castilla-La Mancha and the “ERDF A way of making Europe” through the project 2022-GRIN-34437. J.P. Llano and J.C. Valverde have been funded by the Junta de Comunidades de Castilla-La Mancha and the “ERDF A way of making Europe” within the Operational Program 2021–2027 through the project SBPLY/21/180501/000174. J.C. Valverde has been also funded by the Universidad de Castilla-La Mancha and the “ERDF A way of making Europe” within the Operational Program 2021–2027 through the project 2022-GRIN-34473.

Share a link

Email
Wechat
Bluesky

ABSTRACT

This work presents a generalization of Boolean networks to multistate networks over a complement-closed set $𝒞$ , which can be finite or infinite. Specifically, we focus on MAX (and MIN) multistate networks, whose dynamics are governed by global arbitrary $𝒞$ -maxterm (or $𝒞$ -minterm) functions, which extend the well-known maxterm (or minterm) Boolean functions. More specifically, we tackle the problem of analyzing the combinatorial dynamics of these networks. As a result, we determine the types of periodic orbits that can exist and coexist jointly, when all vertices are self-loop and the graph is undirected. In particular, we show that only fixed points and 2-periodic orbits can appear in these systems by employing tools coming from algebra and graph theory. That is, regardless of the (finite or infinite) number of elements, the types of periodic orbits remain the same as those of MAX and MIN Boolean networks. However, we demonstrate that the coexistence of fixed points and 2-periodic orbits is possible in these networks, which contrasts with the known results for the Boolean case. Moreover, we provide sufficient and necessary conditions to characterize the existence of fixed points and 2-periodic orbits, as well as their coexistence.

1 Introduction

A (deterministic) Boolean network (BN) with $n$ entities, also called Boolean finite dynamical system (see, for instance, [1, 2]), is defined by a global evolution operator $\mathbf{F}&#x0003D;\left({F}_1,\dots, {F}_n\right):{\mathcal{B}}&#x0005E;n\to {\mathcal{B}}&#x0005E;n$ , over a state space $\mathcal{B}$ that has (algebraic) structure of Boolean algebra. When $\mathcal{B}\equiv \left\{0,1\right\}$ , the system is just a standard binary BN. Given a BN, namely, $\mathbf{F}$ , the main goal is to understand its dynamics and, specifically, the limit configurations to which the remaining ones converge through iterations of $\mathbf{F}$ , that is, its periodic orbits. These features have been studied in depth from different perspectives (see, for instance, [3-7]).

BN are usually represented by a graph $G&#x0003D;\left(V,E\right)$ , where the vertices correspond to entities, and the edges represent the influence between two of them. The state variables associated with the vertices, the local functions ${F}_i$ describing the interactions, and the schedule for updating the state values over time, determine $\mathbf{F}$ . Other approaches are probabilistic, where each local function is selected based on a given probability before each iteration, introducing uncertainty into the system (see [8] and references therein).

Standard (binary) BN have been applied successfully to model countless phenomena: gene regulatory networks ([9-11]), social interactions ([12]), epidemics ([13]), physical phenomena ([14, 15]), and so forth. However, the simplicity that makes them powerful can also be a limitation. Real-world phenomena and computational processes many times require models where the entities can take more than two on-off states ([16-18]). Binary BN models are not expressive enough to capture these situations. For instance, in gene regulatory networks, genes interact in complex ways, with activation and repression occurring such that the level of activity of a gene varies depending on external factors ([18]). Therefore, to overcome this limitation, recent research has aimed to extend BN results to more general, non-binary, or multistate deterministic networks. Such networks extend those with binary state values and enable more precise modeling of complex biological and engineering systems. Since realistic models often require more than two states, these networks have already been used in mathematical modeling. Applications include biological systems such as the drifting behavior of Escherichia coli ([16]) and the denitrification process in bacteria ([19]). Other theoretical advancements include multistate versions of the Ising model ([20]), the Greenberg-Hastings model for excitable media ([21]), and other models for stock market dynamics ([22]) and epidemiology ([23]) (see also [24] and references therein).

In this sense, some works have focused on extending results related to BN to more general networks over finite sets, which are called multistate networks (MN). Specifically, in [25, 26], the authors study MN called finite dynamical systems (FDS), and in [19, 27], MN referred to as multivalued networks are analyzed. On the other hand, in [28, 29], the authors study multistate (or nonbinary) BN (MBN), in which a general Boolean algebra of ${2}&#x0005E;p$ elements, $p&gt;1$ , is employed. A suitable representation of these algebraic structures makes it possible to study such systems by analyzing independent copies of the same (binary) BN. Similarly, in [30], the author assigns a Boolean vector to each of the states in an MN. Then, the smallest $p$ such that ${2}&#x0005E;p$ exceeds the number of possible states is selected. In this setting, classifying the binary representation vectors into appropriate groups allows us to treat the state values as Boolean. Another common approach defines the values that the entities can take as elements of a finite field with $q$ elements ([31]). Other approaches focus on semilattice networks [32, 33].

In this work, we introduce a generalization of MBN by considering totally ordered sets (where the state variables take their values) that are complement-closed sets, that is, totally ordered sets in which a complement operator can be well defined. More specifically, we define a complement-closed set as a triple $(𝒞, \leq,^{'})$ , where $(𝒞, \leq)$ is a totally ordered set and $^{'} : 𝒞 \to 𝒞$ is a bijective map with the following properties: for every $a, b \in 𝒞$ , if $a&lt;b$ , then ${b}&#x0005E;{\prime }&lt;{a}&#x0005E;{\prime }$ , and for every $a \in 𝒞, a^{''} = a$ . In line with the notation MBN employed for multistate Boolean networks, we shall denote MCN to the discrete dynamical systems induced by a function on a complement-closed set $𝒞$ . We mainly focus on synchronous updated MCN, which we will denote SyMCN following the terminology used in [34]. Unlike other approaches, the set $𝒞$ does not need to be finite. However, we prove that the orbit of any given configuration is finite, allowing us to analyze the convergence to fixed points or other periodic orbits as in BN. Indeed, this approach also extends the common framework of MN over finite fields ([30, 31]), as well as other types of MN, such as the fuzzy dynamical systems presented in [35].

In the literature, synchronous BN on undirected graphs have been studied in depth. The work in [6] established the foundation for an algebraic study of the dynamics of homogeneous BN. In particular, homogeneous BN with global Boolean functions AND, OR, NAND, and NOR are studied, considering also a sequential update schedule [36]. Since then, research has expanded to the broader case where the global function is a maxterm or a minterm Boolean function.

In this sense, homogeneous BN over undirected and all self-loop graphs, where the global scalar function $F$ is a maxterm (i.e., a disjunction of direct or complemented variables) or a minterm (i.e., a conjunction of direct or complemented variables) Boolean function, are known to present only fixed points and 2-periodic orbits ([6, 37]). Moreover, fixed points and 2-periodic orbits cannot coexist in such networks ([38]). Further research has explored the exact structure of fixed points and periodic orbits in networks where all the entities are self-loop ([7, 39]) and also in generalized cases (where not all the entities are self-loop; see [40]).

Furthermore, homogeneous MBN (in which the state space is a general Boolean algebra with ${2}&#x0005E;p$ elements, $p&gt;1$ ), where the global function is a (general) maxterm or minterm have been studied ([28, 29]). Specifically, [29] shows that, similarly to the binary Boolean case, only fixed points and 2-periodic orbits can exist. Moreover, the number of periodic orbits, and the study of attractors and transient (by means of predecessors and Garden-of-Eden configurations) is also performed. Furthermore, [29] provides a similar analysis of the dynamics of such systems with a sequential update schedule.

Recently, the approach in [19] has dealt with MN with $m&#x0002B;1$ states, where the state space is $𝒞 = \{0, \frac{1}{2}, . . ., \frac{m - 1}{m}, 1\}$ , and in which all the functions consider a generalization of the Boolean disjunctive operator. The main result in the work presents an algorithm to find fixed points in such systems. However, these functions assume additive influences, as they are defined by $\odot \left(x,y\right)&#x0003D;\max \left(0,x&#x0002B;y-1\right)$ , that is, a linear summation, similar to those on MBN ([26, 27]).

In comparison with these results, we go further and consider maximum (and minimum) functions that generalize the Boolean disjunctive operator while modeling a different scenario. Specifically, we analyze network dynamics, where the strongest input determines the state value of the entity, while weaker inputs are not influential. More precisely, if the state value of each entity represents the intensity with which it exhibits a certain property, it is natural to assume that such intensity will become either the highest (resp. lowest) among the intensities of the entities that influence it. This provides the motivation for using maximum MAX (resp. minimum MIN) functions to model the updating behavior of the entities.

MAX functions preserve the specificity of the inputs by responding only to the strongest match, making them more robust to multiple stimuli. Many biological systems exhibit such non-linear summation, where strong inputs dominate weaker ones. Neurophysiological data support MAX-like mechanisms in IT neurons, where object recognition responses are driven by the strongest stimulus ([41]). Additionally, MAX functions play a key role in gene regulation where genes are activated by the strongest transcription factor input, a mechanism widely observed in regulatory networks (see [42] and the references therein). This suggests that MAX-like processing is a typical biological strategy.

Thus, the purpose of this work is to study systems modeled in that way. To define such systems, we formally extend the concept of maxterm (resp. minterm) Boolean function to $𝒞$ -maxterm (resp. $𝒞$ -minterm) on a (totally ordered) complement-closed set, which could be even infinite. Then, we use the synchronous updating scheme and determine the corresponding MCN on the complement-closed set $𝒞$ , which we denote MAX-SyMCN (resp. MIN-SyMCN)¹. The dynamics of such MAX-SyMCN (resp. MIN-SyMCN) is governed by a global (arbitrary) $𝒞$ -maxterm (resp. $𝒞$ -minterm) discrete function. Specifically, we study the case in which all the vertices are self-loop and the graph is undirected.

The main contributions of our work are the following. We prove that any configuration has a finite orbit in a MAX-SyMCN, regardless of if $𝒞$ is finite or infinite. Then, we prove that only fixed points and 2-periodic orbits can appear, preserving the known behavior from the Boolean case. This is also the case when the state space is infinite. However, when studying the coexistence of periodic orbits, we have to distinguish between two cases. If there exists a central value $c \in 𝒞$ , that is, an element such that its complementary is itself, fixed points and 2-periodic orbits can coexist, in contrast with the Boolean case. Otherwise, if there is no central value in $𝒞$ , fixed points and 2-periodic orbits cannot coexist, as occurs in the Boolean case. At this point, we completely characterize the conditions under which coexistence either occurs or does not occur.

Although throughout this paper we prove our results for MAX-SyMCN, all the results can be immediately adapted to MIN-SyMCN.

This paper is structured as follows. In Section 2, we introduce some preliminary notions needed for this study. In Section 3, we study the periodic structure of all self-loop MAX-SyMCN over undirected graphs. We prove that only fixed points and 2-periodic orbits can appear. We also characterize the existence and coexistence of fixed points and 2-periodic orbits. Section 4 provides some conclusions and future research directions of our work.

2 Preliminaries

Let

(𝒞, \leq)

be a totally ordered set. As usual, we write

a&amp;lt;b

(or

b&amp;gt;a

) meaning that

a\le b

and

a\ne b

. When

a\le b

, we also write

b\ge a

. Let

^{'} : 𝒞 \to 𝒞

be a bijective map satisfying the following:

For every $a, b \in 𝒞$ , if $a&lt;b$ then ${b}&#x0005E;{\prime }&lt;{a}&#x0005E;{\prime }$ .
For every $a \in 𝒞, a^{''} = a$ .

Then, we say that the triple $(𝒞, \leq,^{'})$ is a complement-closed set.

The previous properties have the following consequence: If there exists

c \in 𝒞

such that

{c}&amp;#x0005E;{\prime }&amp;#x0003D;c

, this element is unique. Indeed, let

c_{1}, c_{2} \in 𝒞

such that

{c}_1&amp;#x0003D;{c}_1&amp;#x0005E;{\prime },\kern0.3em {c}_2&amp;#x0003D;{c}_2&amp;#x0005E;{\prime }

and assume, for instance, that

{c}_1&amp;lt;{c}_2

. Then, we have that

{c}_2&amp;#x0003D;{c}_2&amp;#x0005E;{\prime }&amp;lt;{c}_1&amp;#x0005E;{\prime }&amp;#x0003D;{c}_1&amp;lt;{c}_2,

which contradicts our assumption, that is,

{c}_1&amp;#x0003D;{c}_2

. Such a unique element is said to be the central value of

𝒞

For the particular case in which $𝒞$ is bounded, we denote $I&#x0003D;$ sup( $𝒞$ ) and $O&#x0003D;$ inf( $𝒞$ ). An immediate consequence is that if $I, O \in 𝒞$ , then ${I}&#x0005E;{\prime }&#x0003D;O$ and ${O}&#x0005E;{\prime }&#x0003D;I$ . Notice that it may also occur that both $O$ and $I$ are not contained in $𝒞$ . Nevertheless, if one of them belongs to $𝒞$ , then the other one also does.

Remark 2.1.In general, in contrast with the particular case of BN, for a bounded complement-closed set $𝒞$ and $a \in 𝒞$ , it is $\max \left(a,{a}&#x0005E;{\prime}\right)\ne I$ and $\min \left(a,{a}&#x0005E;{\prime}\right)\ne O$ . Actually, the only elements satisfying these conditions are $I$ and $O$ , when they both belong to $𝒞$ .

We can distinguish between two classes of complement-closed sets depending on whether they have a (unique) central value or not. For simplicity, we usually denote a general complement-closed set by $𝒞 \equiv (𝒞, \leq,^{'})$ .

Example 2.2.The following are examples of complement-closed sets:

$(𝒞, \leq,^{'})$ with $𝒞 = {0, 1}, 0 \leq 1$ and ${0}&#x0005E;{\prime }&#x0003D;1$ . In this case, $O&#x0003D;0$ and $I&#x0003D;1$ .
$(𝒞, \leq,^{'})$ with $𝒞 = {α, β, γ, δ}, α < β < γ < δ$ and $^{'} : 𝒞 \to 𝒞$ defined by ${\alpha}&#x0005E;{\prime }&#x0003D;\delta$ and ${\beta}&#x0005E;{\prime }&#x0003D;\gamma$ . In this case, $O&#x0003D;\alpha$ and $I&#x0003D;\delta$ , and there is no central value.
$(𝒞, \leq,^{'})$ with $𝒞 = {x \in ℝ : - m \leq x \leq m}$ for $m\in \mathbb{R}\cup \left\{\infty \right\}$ , the standard order $\le$ in $\mathbb{R}$ , and $^{'} : 𝒞 \to 𝒞$ defined by ${x}&#x0005E;{\prime }&#x0003D;-x$ . In this case, $O&#x0003D;-m$ and $I&#x0003D;m$ , and $0 \in 𝒞$ is the central value of $𝒞$ .
$(𝒞, \leq,^{'})$ with $𝒞 = {0, 1, \dots, q} \subseteq ℤ$ , the standard order $\le$ in $\mathbb{Z}$ , and $^{'} : 𝒞 \to 𝒞$ defined by ${x}&#x0005E;{\prime }&#x0003D;q-x$ . In this case, $O&#x0003D;0$ and $I&#x0003D;q$ . In this setting, if $q$ is even, then $q / 2 \in 𝒞$ is the central value of $𝒞$ . Otherwise, there is no central value.
$(𝒞, \leq,^{'})$ with $𝒞 = [0, 1]$ , the standard order $\le$ in $\mathbb{R}$ , and $^{'} : 𝒞 \to 𝒞$ such that ${x}&#x0005E;{\prime }&#x0003D;1-x$ for $x \in 𝒞$ . In this case, $O&#x0003D;0$ and $I&#x0003D;1$ , and $1 / 2 \in 𝒞$ is the central value of $𝒞$ .

In the following, we define a multistate network over an undirected graph with values in a complement-closed set (MCN). First, we need to introduce some notation.

Let $G&#x0003D;\left(V,E\right)$ be a simple, connected, undirected graph, where $V&#x0003D;\left\{1,2,\dots, n\right\}$ is the vertex (or node) set and $E$ is the edge set, and let $(𝒞, \leq,^{'})$ be a complement-closed set. For every vertex $i \in V, x_{i} \in 𝒞$ denotes its state (variable). If $\left\{i,i\right\}\in E$ for $i\in V$ , we say that $i$ is self-loop.

For $i\in V$ , as usual, we denote ${A}_G(i)&#x0003D;\left\{j\in V:\left\{i,j\right\}\in E\right\}$ the adjacency set of $i$ . Note that $i\in {A}_G(i)$ if, and only if, $i$ is self-loop.

Definition 2.3.Let $𝒞$ be a complement-closed set and $G&#x0003D;\left(V,E\right)$ a simple, connected, undirected graph with $V&#x0003D;\left\{1,2,\dots, n\right\}$ . The map

\begin{aligned} F & = (F_{1}, \dots, F_{n}) : 𝒞^{n} \to 𝒞^{n}, \\ F & (x_{1}, x_{2}, \dots, x_{i}, \dots, x_{n}) = (y_{1}, y_{2}, \dots, y_{i}, \dots, y_{n}), \end{aligned}

where

{y}_i

is the updated state of the vertex

i

by applying the local function

{F}_i

, whose expression only depends on the state variables associated with the vertices of

{A}_G(i)

, is called a synchronous multistate network (SyMCN) (or parallel dynamical system) over

𝒞

Example 2.4.The following ones are particular examples of SyMCN:

If $𝒞 = {0, 1}, F$ is a standard synchronous binary BN.
If $𝒞 = [0, 1], F$ is a fuzzy synchronous dynamical system FDS on Zadeh operators, studied in [35].
If $𝒞 = {0, 1, . . ., q} \subseteq ℤ, F$ is a synchronous multistate network studied, for instance, in [19, 25, 31].

Remark 2.5.Observe that, for such dynamical systems on complement-closed sets, we have included the binary (Boolean) case in the definition of MCN. Indeed, the case of synchronous (multistate) BN over a general Boolean algebra $\mathcal{B}$ with ${2}&#x0005E;p$ elements and $p&gt;1$ an integer, as studied in [26, 27], can also be seen as a particular instance of SyMCN on a complement-closed set. This is because, by the Stone Representation Theorem, they can be seen as systems of the form $\mathbf{F}:{\left\{0,1\right\}}&#x0005E;{np}\to {\left\{0,1\right\}}&#x0005E;{np}$ .

In this work, we deal with homogeneous SyMCN, in which every local update function ${F}_i$ is the restriction of a global scalar function $F : 𝒞^{n} \to 𝒞$ to the set of vertices in ${A}_G(i)$ . That is, ${F}_i&#x0003D;{F}_{\mid {A}_G(i)}$ . Note that the graph $G$ and the global scalar function $F$ determine the SyMCN $\mathbf{F}$ . Due to that, we identify $F \equiv (𝒞, G, F)$ . We will omit the word homogeneous since all of the SyMCN we consider are of such type.

If $i$ is self-loop for every $i\in V$ , which means that ${x}_i$ appears in ${F}_i$ , the system is said to be all self-loop. If there exists $i\in V$ such that $i$ is not self-loop, that is, ${x}_i$ does not appear in ${F}_i$ , we say that the system is a generalized SyMCN, so following the nomenclature in [40], where the term generalized BN is introduced. In this work, we will study all self-loop MCN.

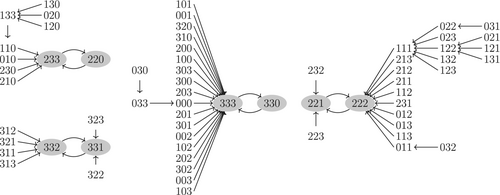
Given $a \in 𝒞^{n}$ , we write ${\mathbf{F}}&#x0005E;m\left(\mathbf{a}\right)&#x0003D;\mathbf{F}\circ \overset{m}{\cdots}\circ \mathbf{F}\left(\mathbf{a}\right)$ , where $\circ$ denotes function composition. As usual, we say that $\mathbf{a}$ is an $m$ -periodic point, $m\in \mathbb{N}$ , if ${\mathbf{F}}&#x0005E;m\left(\mathbf{a}\right)&#x0003D;\mathbf{a}$ and ${\mathbf{F}}&#x0005E;k\left(\mathbf{a}\right)\ne \mathbf{a}$ for all $k&lt;m$ . If $m&#x0003D;1$ , we say that $\mathbf{a}$ is a fixed point and denote by $\mathrm{Fix}\left(\mathbf{F}\right)$ the set of fixed points of $\mathbf{F}$ . If $m&gt;1$ , the sequence $\left\{\mathbf{a},\mathbf{F}\left(\mathbf{a}\right),\dots, {\mathbf{F}}&#x0005E;{m-1}\left(\mathbf{a}\right)\right\}$ is said to be a periodic orbit of period $m$ . We also write ${\mathbf{F}}&#x0005E;s\left(\mathbf{a}\right)\equiv {\mathbf{a}}&#x0005E;s&#x0003D;\left({a}_1&#x0005E;s,\dots, {a}_n&#x0005E;s\right)$ for $s&gt;0$ , and $\mathbf{a}&#x0003D;{\mathbf{a}}&#x0005E;0$ . Fixed points and periodic orbits are the key elements to understand the dynamics of MCN. When $𝒞$ is finite, we can use a digraph to represent the evolution of each configuration in the SyMCN, in which an arrow from $a \in 𝒞^{n}$ to $b \in 𝒞^{n}$ indicates that $\mathbf{F}\left(\mathbf{a}\right)&#x0003D;\mathbf{b}$ . Such digraph is called the phase diagram or phase portrait of the SyMCN.

As mentioned in Definition 2.3, in this paper, we consider a synchronous or parallel update scheme. This means that all the variables are updated at the same time. However, other (asynchronous) update schemes may be considered over MCN, as they are over BN. These may be either sequential or block-sequential (also known as mixed), as studied in [3, 43, 44].

In this work, we will consider generalizations of maxterms and minterms Boolean functions as global scalar functions [37]. Let

x_{1}, \dots, x_{n} \in 𝒞

. Following Boolean notation, we denote a

𝒞

-maxterm function on

n

variables MAX as

\begin{array}{cc}\hfill \operatorname{MAX}\left({x}_1,\dots, {x}_n\right)&amp;amp; &amp;#x0003D;\max \left\{{z}_1,\dots, {z}_n\right\}\equiv {z}_1\vee \cdots \vee {z}_n,\hfill \\ {}\hfill \mathrm{where}\;{z}_i&amp;amp; &amp;#x0003D;{x}_i\;\mathrm{or}\;{z}_i&amp;#x0003D;{x}_i&amp;#x0005E;{\prime }.\hfill \end{array}

Respectively, a

𝒞

-minterm function on

n

variables MIN as

\begin{array}{cc}\hfill \operatorname{MIN}\left({x}_1,\dots, {x}_n\right)&amp;amp; &amp;#x0003D;\min \left\{{z}_1,\dots, {z}_n\right\}\equiv {z}_1\wedge \cdots \wedge {z}_n,\hfill \\ {}\hfill \mathrm{where}\;{z}_i&amp;amp; &amp;#x0003D;{x}_i\;\mathrm{or}\;{z}_i&amp;#x0003D;{x}_i&amp;#x0005E;{\prime }.\hfill \end{array}

It is straightforward to check that

\wedge

and

\vee

so defined satisfy the following properties: idempotent law, commutative law, associative law, distributive law, and absorption law. Moreover, De Morgan's law holds for the complement operation

{}&amp;#x0005E;{\prime }

When the global function is a $𝒞$ -maxterm, MAX (respectively, a $𝒞$ -minterm MIN), we say that $(𝒞, G, MAX)$ is a MAX-SyMCN (resp. MIN-SyMCN). In the particular case of BN, we call these systems MAX-SyBN (resp. MIN-SyBN).

Remark 2.6.Although we will write our results for MAX-SyMCN, they can be immediately adapted for MIN-SyMCN.

3 Periodic Orbits of MAX and MIN Multistate Networks

In what follows, $F \equiv (𝒞, G, MAX)$ will stand for a (homogeneous) MAX-SyMCN, where $𝒞$ is a complement-closed set, $G&#x0003D;\left(V,E\right)$ is an undirected connected graph, and $MAX : 𝒞^{n} \to 𝒞$ is a global function expressed by means of the operators $\vee$ and ${}&#x0005E;{\prime }$ . We will also assume that all the vertices in $V$ are self-loop.

In this section, we study the dynamics of (homogeneous) MAX-SyMCN. First of all, we show that the orbit of any configuration in an $(𝒞, G, MAX)$ system is finite. This implies that every orbit is either periodic or eventually periodic (i.e., it converges to a periodic one). Thus, the periodic orbits are organizing kernels of the dynamics. Hence, we focus on periodic orbits, and we prove that only fixed points and 2-periodic orbits can appear in MAX-SyMCN. Finally, we characterize the existence and coexistence of such periodic orbits in these systems.

Lemma 3.1.Let $F \equiv (𝒞, G, MAX)$ be a MAX-SyMCN. Then $𝒪_{F} (a) = {F^{t} (a) : t \in ℕ}$ is a finite set for each $a \in 𝒞^{n}$ .

Proof.Let $a = (a_{1}, \dots, a_{n}) \in 𝒞^{n}$ and consider the finite set ${Y}_{\mathbf{a}}&#x0003D;\left\{\mathbf{z}&#x0003D;\left({z}_1,\dots, {z}_n\right):\kern0.3em \mathrm{for}\ \mathrm{every}\kern0.3em 1\le i\le n,{z}_i&#x0003D;{a}_j\kern0.3em \mathrm{or}\kern0.3em {z}_i&#x0003D;{a}_j&#x0005E;{\prime },\kern0.3em \mathrm{for}\kern0.3em 1\le j\le n\right\}$ . Observe that $\mathbf{F}\left(\mathbf{z}\right)\in {Y}_{\mathbf{a}}$ for each $\mathbf{z}\in {Y}_{\mathbf{a}}$ , and in particular $𝒪_{F} (a) \subseteq Y_{a}$ . Therefore, $𝒪_{F} (a)$ is a finite set.

Remark 3.2.Note that Lemma 3.1 is also valid for non-homogeneous SyMCN on independent local $𝒞$ -maxterms (resp. $𝒞$ -minterms) functions, so leading to extensions of the systems studied for the Boolean case in [45]. This result is also true independently of the scheme (synchronous, asynchronous, or mixed) used to update the MCN.

Remark 3.3.Although, by Lemma 3.1, the orbit of every configuration converges (in a finite number of iterations) to a periodic orbit, the number of orbits in the system, and so the number of periodic orbits, can be infinite provided that $𝒞$ is not a finite set. In other words, the phase diagram of the system is not a finite digraph if $𝒞$ is not a finite set.

Following [34] for BN, we denote the simplest $𝒞$ -maxterm as $\mathrm{OR}\left({x}_1,\dots, {x}_n\right)&#x0003D;{x}_1\vee \cdots \vee {x}_n$ , where all the variables appear in direct form (and, respectively, AND the $𝒞$ -minterm where all the variables appear in direct form). In the next result, we describe the dynamics in the particular case of an OR-SyMCN. We denote by diam $(G)$ the diameter of the graph $G$ .

Theorem 3.4.Let $F \equiv (𝒞, G, OR)$ be an OR-SyMCN. Then, all the periodic orbits of the system are fixed points. Specifically, given $a = (a_{1}, \dots, a_{n}) \in 𝒞^{n}$ and $b&#x0003D;\max \left\{{a}_1,\dots, {a}_n\right\}$ , we have that ${\mathbf{F}}&#x0005E;s\left(\mathbf{a}\right)&#x0003D;\left(b,\dots, b\right)$ for every $s\ge$ diam $(G)$ .

Proof.The result can be directly extended from its counterpart for OR synchronous (binary) BN (see, for instance, [37]).

In the following, we study the types of periodic orbits of MAX-SyMCN. The next theorem is a natural extension of [3, 37, Theorem 3], which states that all the periodic orbits of MAX synchronous (binary) BN are fixed points or have period 2. Indeed, we see that this is also the case if

F \equiv (𝒞, G, MAX)

is a MAX-SyMCN. To do that, following the notation in [38], we define the sets

W&amp;#x0003D;\left\{i\in V:{x}_i\kern0.3em \mathrm{appears}\ \mathrm{in}\ \mathrm{direct}\ \mathrm{form}\ \mathrm{in}\kern0.3em F\right\}

and

{W}&amp;#x0005E;{\prime }&amp;#x0003D;\left\{i\in V:{x}_i\kern0.3em \mathrm{appears}\ \mathrm{in}\ \mathrm{complemented}\ \mathrm{form}\ \mathrm{in}\kern0.3em F\right\}.

In this same sense, we will call direct vertices to those in

W

and complemented vertices to those in

{W}&amp;#x0005E;{\prime }

Theorem 3.5. (Periodic orbits in MAX-SyMCN)Let $F \equiv (𝒞, G, MAX)$ be a MAX-SyMCN. Then, all the periodic points of the system are fixed points or 2-periodic points.

Proof.If ${W}&#x0005E;{\prime }&#x0003D;\varnothing$ , then $\mathbf{F}$ is an OR-SyMCN, and by Theorem 3.4, all the periodic points of $\mathbf{F}$ are fixed points.

On the contrary, assume now that ${W}&#x0005E;{\prime}\ne \varnothing$ and let $a = (a_{1}, \dots, a_{n}) \in 𝒞^{n}$ be a $m$ -periodic point of $\mathbf{F}$ , with $m\ge 1$ .

Since $\mathbf{a}$ is a $m$ -periodic point, then ${a}_i&#x0005E;m&#x0003D;{a}_i$ for all $i\in V$ . Additionally, one of the following situations occurs for each $i\in V$ :

$i\in W$ . Then²
$\begin{array}{cc}\hfill {a}_i&#x0005E;1&amp; &#x0003D;{F}_i\left({a}_1,\dots, {a}_n\right)&#x0003D;{a}_i\vee \left({\bigvee}_{\ell \in {A}_G(i)\cap W}{a}_{\ell}\right)\hfill \\ {}\hfill &amp; \vee \left({\bigvee}_{k\in {A}_G(i)\cap {W}&#x0005E;{\prime }}{a}_k&#x0005E;{\prime}\right)\ge {a}_i.\hfill \end{array}$
Therefore, we have that ${a}_i&#x0003D;{a}_i&#x0005E;m\ge {a}_i&#x0005E;{m-1}\ge \cdots \ge {a}_i&#x0005E;1\ge {a}_i&#x0005E;0\equiv {a}_i$ , which leads to ${a}_i&#x0003D;{a}_i&#x0005E;s$ for each integer $s\ge 1$ . That is, the state values of all the vertices in $W$ are fixed in a periodic orbit. Moreover, it is straightforward to deduce that all the direct vertices in any connected component ${G}_{\alpha }$ of the subgraph ${G}_{\mid W}$ have the same (fixed) state value. That is,
${a}_i&#x0003D;{a}_j\kern0.3em \mathrm{for}\ \mathrm{every}\kern0.3em i,j\in {G}_{\alpha },$ (1)
where we write $i,j\in {G}_{\alpha }$ meaning that $i,j\in V\left({G}_{\alpha}\right)$ , the vertex set of ${G}_{\alpha }$ .
$i\in {W}&#x0005E;{\prime }$ and there exists $j\in {A}_G(i)\cap W$ . By the previous argument, ${a}_j&#x0003D;{a}_j&#x0005E;s$ for each integer $s\ge 1$ . We can write
$\begin{array}{cc}\hfill {F}_j\left({a}_1,\dots, {a}_n\right)&amp; &#x0003D;{a}_i&#x0005E;{\prime}\vee {a}_j\vee \left({\bigvee}_{\ell \in {A}_G(j)\cap W}{a}_{\ell}\right)\hfill \\ {}\hfill &amp; \vee \left({\bigvee}_{k\in {A}_G(j)\cap {W}&#x0005E;{\prime }}{a}_k&#x0005E;{\prime}\right),\hfill \end{array}$ (2)
and so, for every $s\ge 1$ , we have
$\begin{array}{cc}\hfill {a}_j&amp; &#x0003D;{a}_j&#x0005E;s&#x0003D;{\left({a}_i&#x0005E;{s-1}\right)}&#x0005E;{\prime}\vee {a}_j&#x0005E;{s-1}\vee \left({\bigvee}_{\ell \in {A}_G(j)\cap W}{a}_{\ell}&#x0005E;{s-1}\right)\hfill \\ {}\hfill &amp; \vee \left({\bigvee}_{k\in {A}_G(j)\cap {W}&#x0005E;{\prime }}{\left({a}_k&#x0005E;{s-1}\right)}&#x0005E;{\prime}\right)\ge {\left({a}_i&#x0005E;{s-1}\right)}&#x0005E;{\prime }.\hfill \end{array}$ (3)
Consequently,
${a}_j\ge {\left({a}_i&#x0005E;s\right)}&#x0005E;{\prime}\kern0.3em \mathrm{for}\ \mathrm{every}\kern0.3em j\in {A}_G(i)\cap W\kern0.3em \mathrm{and}\kern0.3em s\ge 0.$ (4)

On the other hand, we can write
${F}_i\left({a}_1,\dots, {a}_n\right)&#x0003D;{a}_i&#x0005E;{\prime}\vee \left({\bigvee}_{\ell \in {A}_G(i)\cap W}{a}_{\ell}\right)\vee \left({\bigvee}_{k\in {A}_G(i)\cap {W}&#x0005E;{\prime }}{a}_k&#x0005E;{\prime}\right),$
and so, for every $s\ge 1$ , we have
$\begin{array}{cc}\hfill {a}_i&#x0005E;s&amp; &#x0003D;{\left({a}_i&#x0005E;{s-1}\right)}&#x0005E;{\prime}\vee \left({\bigvee}_{\ell \in {A}_G(i)\cap W}{a}_{\ell}&#x0005E;{s-1}\right)\vee \left({\bigvee}_{k\in {A}_G(i)\cap {W}&#x0005E;{\prime }}{\left({a}_k&#x0005E;{s-1}\right)}&#x0005E;{\prime}\right)\hfill \\ {}\hfill &amp; \ge \left({\bigvee}_{\ell \in {A}_G(i)\cap W}{a}_{\ell}&#x0005E;{s-1}\right).\hfill \end{array}$ (5)
This leads to
${a}_i&#x0005E;s\ge {a}_j&#x0005E;{s-1}&#x0003D;{a}_j\kern1em \mathrm{for}\ \mathrm{every}\kern0.3em j\in {A}_G(i)\cap W\kern0.3em \mathrm{and}\kern0.3em s\ge 1.$ (6)
Since also ${a}_i&#x0005E;0\equiv {a}_i&#x0003D;{a}_i&#x0005E;m\ge {a}_j$ , we conclude that
${a}_i&#x0005E;s\ge {a}_j\kern0.3em \mathrm{for}\ \mathrm{every}\kern0.3em j\in {A}_G(i)\cap W\kern0.60em \mathrm{and}\ \mathrm{for}\ \mathrm{every}\ \mathrm{integer}\kern0.3em s\ge 0.$ (7)

Now, for every $j\in {A}_G(i)\cap {W}&#x0005E;{\prime }$ , we can apply De Morgan's law in
$\begin{array}{cc}\hfill {a}_j&#x0005E;1&amp; &#x0003D;{F}_j\left({a}_1,\dots, {a}_n\right)&#x0003D;{a}_i&#x0005E;{\prime}\vee \left({\bigvee}_{\ell \in {A}_G(j)\cap W}{a}_{\ell}\right)\hfill \\ {}\hfill &amp; \vee \left({\bigvee}_{k\in {A}_G(j)\cap {W}&#x0005E;{\prime }}{a}_k&#x0005E;{\prime}\right)\hfill \end{array}$
to obtain
${\left({a}_j&#x0005E;1\right)}&#x0005E;{\prime }&#x0003D;{a}_i\wedge \left({\bigwedge}_{\ell \in {A}_G(j)\cap W}{a}_{\ell}&#x0005E;{\prime}\right)\wedge \left({\bigwedge}_{k\in {A}_G(j)\cap {W}&#x0005E;{\prime }}{a}_k\right)\le {a}_i.$ (8)

Now, using the first equality in (5) for $s&#x0003D;1$ and $s&#x0003D;2$ , we obtain
${a}_i&#x0005E;1&#x0003D;{\left({a}_i\right)}&#x0005E;{\prime}\vee \left({\bigvee}_{\ell \in {A}_G(i)\cap W}{a}_{\ell}\right)\vee \left({\bigvee}_{k\in {A}_G(i)\cap {W}&#x0005E;{\prime }}{a}_k&#x0005E;{\prime}\right)$
and
$\begin{array}{cc}\hfill {a}_i&#x0005E;2&amp; &#x0003D;{\left({a}_i&#x0005E;1\right)}&#x0005E;{\prime}\vee \left({\bigvee}_{\ell \in {A}_G(i)\cap W}{a}_{\ell}&#x0005E;1\right)\vee \left({\bigvee}_{k\in {A}_G(i)\cap {W}&#x0005E;{\prime }}{\left({a}_k&#x0005E;1\right)}&#x0005E;{\prime}\right)\hfill \\ {}\hfill &amp; &#x0003D;\left({a}_i\wedge {\bigwedge}_{\ell \in {A}_G(i)\cap W}{a}_{\ell}&#x0005E;{\prime}\wedge {\bigwedge}_{k\in {A}_G(i)\cap {W}&#x0005E;{\prime }}{a}_k\right)\hfill \\ {}\hfill &amp; \vee \left({\bigvee}_{\ell \in {A}_G(i)\cap W}{a}_{\ell}&#x0005E;1\right)\vee \left({\bigvee}_{k\in {A}_G(i)\cap {W}&#x0005E;{\prime }}{\left({a}_k&#x0005E;1\right)}&#x0005E;{\prime}\right).\hfill \end{array}$ (9)

As the state value of the direct vertices are fixed in a periodic orbit, we have, also using (7), that ${a}_{\ell}&#x0005E;1&#x0003D;{a}_{\ell}\le {a}_i$ for every $\ell \in {A}_G(i)\cap W$ . Besides, by (8), we have that ${\left({a}_k&#x0005E;1\right)}&#x0005E;{\prime}\le {a}_i$ for every $k\in {A}_G(i)\cap {W}&#x0005E;{\prime }$ . Using these inequalities in (9), we obtain ${a}_i&#x0005E;2\le {a}_i$ . Finally, repeating the same reasoning, we conclude that
${a}_i&#x0003D;{a}_i&#x0005E;0&#x0003D;{a}_i&#x0005E;{2m}\le {a}_i&#x0005E;{2m-2}\le \cdots \le {a}_i&#x0005E;2\le {a}_i&#x0005E;0&#x0003D;{a}_i,$ (10)
which leads to ${a}_i&#x0005E;2&#x0003D;{a}_i$ .
$i\in {W}&#x0005E;{\prime }$ and ${A}_G(i)\subseteq {W}&#x0005E;{\prime }$ . Reasoning as before, using now that ${A}_G(i)\cap W&#x0003D;\varnothing$ , we also get (10) and so ${a}_i&#x0005E;2&#x0003D;{a}_i$ .

Therefore, we have that ${a}_i&#x0003D;{a}_i&#x0005E;2$ for every $i\in V$ . Hence, $\mathbf{a}$ is a fixed point or a $2$ -periodic point.

Remark 3.6.Theorem 3.5 generalizes [37, Theorems 3 and 4], which characterize the existence of periodic orbits in MAX synchronous (binary) BN. It also generalizes the results about the periodic structure of synchronous MBN given in [28, 29]. Furthermore, it extends the results presented in [35] to include general MAX and MIN fuzzy parallel dynamical systems on Zadeh operators.

Following [6], we call $\mathrm{NAND}&#x0003D;{x}_1&#x0005E;{\prime}\vee \cdots \vee {x}_n&#x0005E;{\prime }$ the $𝒞$ -maxterm where all the variables are in complemented form (and, respectively, NOR the $𝒞$ -minterm where all the variables are in complemented form).

Remark 3.7.Let $\left(\left\{0,1\right\},G,\operatorname{MAX}\right)$ be a MAX synchronous (binary) BN, with MAX $\ne$ NAND, and assume that the system presents 2-periodic orbits. Let $\mathbf{a}&#x0003D;\left({a}_1,\dots, {a}_n\right)$ be a 2-periodic point and take $j$ a complemented vertex which is adjacent to a direct one. Then, we have that ${a}_j&#x0003D;{a}_j&#x0005E;1&#x0003D;1$ (see [38]). That is, the state value of the complemented vertices adjacent to direct ones are fixed (in this setting, to the value 1).

This property does not hold in general for MAX-SyMCN over a complement-closed set. Indeed, let $𝒞 = {0, 1, 2, 3}$ and consider the MAX-SyMCN $F \equiv (𝒞, G, MAX)$ induced by $\operatorname{MAX}\left({x}_1,{x}_2,{x}_3\right)&#x0003D;{x}_1\vee {x}_2&#x0005E;{\prime}\vee {x}_3&#x0005E;{\prime }$ and the dependency graph $G&#x0003D;\left(V,E\right)$ shown in Figure 1. Then, the local functions are given by

\begin{array}{cc}\hfill {F}_1\left({x}_1,{x}_2,{x}_3\right)&amp;amp; &amp;#x0003D;{x}_1\vee {x}_2&amp;#x0005E;{\prime },\hfill \\ {}\hfill {F}_2\left({x}_1,{x}_2,{x}_3\right)&amp;amp; &amp;#x0003D;{x}_1\vee {x}_2&amp;#x0005E;{\prime}\vee {x}_3&amp;#x0005E;{\prime },\hfill \\ {}\hfill {F}_3\left({x}_1,{x}_2,{x}_3\right)&amp;amp; &amp;#x0003D;{x}_2&amp;#x0005E;{\prime}\vee {x}_3&amp;#x0005E;{\prime }.\hfill \end{array}

We have that

W&amp;#x0003D;\left\{1\right\},\kern0.3em {W}&amp;#x0005E;{\prime }&amp;#x0003D;\left\{2,3\right\}

and 2 is a complemented vertex which is adjacent to the direct vertex 1. It can be checked that

\left\{\left(2,2,0\right),\left(2,3,3\right)\right\}

is a 2-periodic orbit in which the state value of vertex 2 is not fixed (see Figure 2).

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Dependency graph $G&#x0003D;\left(V,E\right)$ of the MAX-SyMCN $F \equiv (𝒞, G, MAX)$ in Remark 3.7.

By Theorem 3.5, only fixed points and 2-periodic orbits can appear in a MAX-SyMCN. In the following result, we give a sufficient condition for such a system to only present fixed points as periodic orbits. To do that, following the notation in [38], we consider

{W}_D&amp;#x0005E;{\prime }&amp;#x0003D;\left\{i\in {W}&amp;#x0005E;{\prime }:{A}_G(i)\cap W\ne \varnothing \right\},

the set of complemented vertices adjacent to a direct vertex, and

{W}_C&amp;#x0005E;{\prime }&amp;#x0003D;\left\{i\in {W}&amp;#x0005E;{\prime }:{A}_G(i)\cap W&amp;#x0003D;\varnothing \right\},

the set of complemented vertices only adjacent to other complemented vertices. In the MAX-SyMCN of Remark 3.7, we have that

{W}_D&amp;#x0005E;{\prime }&amp;#x0003D;\left\{2\right\}

, while

{W}_C&amp;#x0005E;{\prime }&amp;#x0003D;\left\{3\right\}

, as one can easily check in Figure 1.

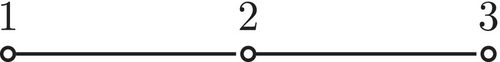
Theorem 3.8.Let $F \equiv (𝒞, G, MAX)$ be a MAX-SyMCN. Assume that ${W}_C&#x0005E;{\prime }&#x0003D;\varnothing$ . Then, all the periodic orbits of the system are fixed points.

Proof.Let $\mathbf{a}&#x0003D;\left({a}_1,\dots, {a}_n\right)$ be a periodic point of $\mathbf{F}$ . By Theorem 3.5, we have that ${\mathbf{F}}&#x0005E;2\left(\mathbf{a}\right)&#x0003D;\mathbf{a}$ , that is, ${a}_i&#x0005E;2&#x0003D;{a}_i$ for every $i\in V$ . In particular, for $i\in W$ , by the proof of Theorem 3.5, it is ${a}_i&#x0003D;{a}_i&#x0005E;1&#x0003D;{a}_i&#x0005E;2$ . On the other hand, as ${W}_C&#x0005E;{\prime }&#x0003D;\varnothing$ , we have that ${W}&#x0005E;{\prime }&#x0003D;{W}_D&#x0005E;{\prime }$ , that is, every complemented vertex is adjacent to a direct one.

Let $i\in {W}&#x0005E;{\prime }$ . Let us prove that ${a}_i&#x0005E;1&#x0003D;{a}_i$ . By Equation (4) in the proof of Theorem 3.5, we have for every $j\in {A}_G(i)\cap W$ that

{a}_j\ge {\left({a}_i&amp;#x0005E;s\right)}&amp;#x0005E;{\prime}\kern1em \mathrm{for}\ \mathrm{every}\ \mathrm{integer}\kern0.3em s\ge 0

(11)

Let us take $j\in {A}_G(i)\cap W$ such that ${a}_j&#x0003D;\max \left\{{a}_{\ell }:\ell \in {A}_G(i)\cap W\right\}$ . By (7), we have that ${a}_i&#x0005E;1\ge {a}_j$ . Let us prove that, in fact, it is ${a}_i&#x0005E;1&#x0003D;{a}_j$ .

Suppose, by contradiction, that ${a}_i&#x0005E;1&gt;{a}_j$ . Then, there exists $k\in {A}_G(i)\cap {W}&#x0005E;{\prime }$ such that ${a}_i&#x0005E;1&#x0003D;{a}_k&#x0005E;{\prime }$ . As a consequence, ${a}_k&#x0005E;{\prime }&gt;{a}_j$ . Now, let us take ${j}_k\in {A}_G(k)\cap W$ . As ${j}_k$ is a direct vertex, ${a}_{j_k}&#x0003D;{a}_{j_k}&#x0005E;1$ . Furthermore, from (6), ${a}_k&#x0005E;2\ge {a}_{\ell}&#x0005E;1$ for every $\ell \in {A}_G(k)\cap W$ , and so ${a}_k&#x0005E;2\ge {a}_{j_k}&#x0005E;1$ . Then, we have that

{a}_k&amp;#x0003D;{a}_k&amp;#x0005E;2\ge {a}_{j_k}&amp;#x0005E;1&amp;#x0003D;{a}_{j_k}\ge {a}_k&amp;#x0005E;{\prime }&amp;gt;{a}_j

(12)

where we have applied (11) for

k\in {W}&amp;#x0005E;{\prime }

and

{j}_k\in W

. Additionally, applying (11) for

i\in {W}&amp;#x0005E;{\prime }

and

j\in W

, and using also (12), we obtain

{a}_j\ge {\left({a}_i&amp;#x0005E;1\right)}&amp;#x0005E;{\prime }&amp;#x0003D;{a}_k&amp;#x0005E;{\prime \prime }&amp;#x0003D;{a}_k&amp;gt;{a}_j,

which is a contradiction. Hence,

{a}_i&amp;#x0005E;1&amp;#x0003D;{a}_j

Therefore, for every $i\in W$ it is ${F}_i\left(\mathbf{a}\right)&#x0003D;{a}_i&#x0005E;1&#x0003D;{a}_i$ , and for every $i\in {W}&#x0005E;{\prime }$ it is

\begin{array}{cc}\hfill {F}_i\left(\mathbf{a}\right)&amp;amp; &amp;#x0003D;{a}_i&amp;#x0005E;1&amp;#x0003D;\max \left\{{a}_{\ell }:\ell \in {A}_G(i)\cap W\right\}\hfill \\ {}\hfill &amp;amp; &amp;#x0003D;\max \left\{\underset{\ell }{\overset{1}{a}}:\ell \in {A}_G(i)\cap W\right\}&amp;#x0003D;{a}_i&amp;#x0005E;2&amp;#x0003D;{a}_i.\hfill \end{array}

(13)

Consequently,

\mathbf{a}

is a fixed point.

In MAX synchronous BN, the condition ${W}_C&#x0005E;{\prime }&#x0003D;\varnothing$ is a necessary and sufficient condition for the existence of fixed points. However, this is not true, in general, for MAX-SyMCN over a complement-closed set. In fact, in Corollary 3.11, we prove that systems in which there exists a central value always present (at least) one fixed point, regardless of ${W}_C&#x0005E;{\prime }$ .

On the other hand, in MAX synchronous BN, fixed points and 2-periodic orbits cannot coexist (see [38, Theorem 7]). However, this neither holds in general for MAX-SyMCN over a complement-closed set. Indeed, in Corollary 3.13, we prove that fixed points and 2-periodic orbits can coexist in systems that have a central value.

In the following result, we prove that, when $𝒞$ has no central value, the condition ${W}_C&#x0005E;{\prime}\ne \varnothing$ ensures that no fixed points appear in a MAX-SyMCN, that is, the system only presents 2-periodic orbits.

Theorem 3.9.Let $F \equiv (𝒞, G, MAX)$ be a MAX-SyMCN with no central value. Assume that ${W}_C&#x0005E;{\prime}\ne \varnothing$ . Then, all the periodic orbits of the system are 2-periodic orbits.

Proof.Recall that if $𝒞$ has no central value, then $a\ne {a}&#x0005E;{\prime }$ for every $a \in 𝒞$ .

Assume by contradiction that $\mathrm{Fix}\left(\mathbf{F}\right)\ne \varnothing$ and let $\mathbf{a}&#x0003D;\left({a}_1,\dots, {a}_n\right)$ be a fixed point of the system. Let us take $i\in {W}_C&#x0005E;{\prime }$ . Then, either ${a}_i\le {a}_j$ for every $j\in {A}_G(i)$ or there exists $j\in {A}_G(i)$ such that ${a}_i&gt;{a}_j$ .

In the first case, we have that ${a}_i&#x0005E;{\prime}\ge {a}_j&#x0005E;{\prime }$ for every $j\in {A}_G(i)\subseteq {W}&#x0005E;{\prime }$ and so

{a}_i&amp;#x0005E;1&amp;#x0003D;{\bigvee}_{j\in {A}_G(i)}{a}_j&amp;#x0005E;{\prime }&amp;#x0003D;{a}_i&amp;#x0005E;{\prime}\ne {a}_i,

which contradicts the fact that

\mathbf{a}

is a fixed point.

For the second case, let us take, without lost of generality, $j\in {A}_G(i)\subseteq {W}&#x0005E;{\prime }$ such that ${a}_j&#x0003D;\min \left\{{a}_{\ell }:\ell \in {A}_G(i)\right\}&lt;{a}_i$ . Therefore, ${a}_j&#x0005E;{\prime }&gt;{a}_i&#x0005E;{\prime }$ and ${a}_i&#x0003D;{a}_i&#x0005E;1&#x0003D;{a}_j&#x0005E;{\prime }$ . Consequently, we have that

{a}_j&amp;#x0005E;1\ge {a}_j&amp;#x0005E;{\prime }&amp;gt;{a}_i&amp;#x0005E;{\prime }&amp;#x0003D;{a}_j.

Hence,

{a}_j&amp;#x0005E;1\ne {a}_j

and so

\mathbf{a}

is not a fixed point.

Remark 3.10.Note that the assumptions in Theorem 3.9 stand for the case of the MAX-SyMCN $F \equiv (𝒞, G, MAX)$ in Remark 3.7, where the phase diagram in Figure 2 corroborates that only periodic orbits of period 2 appear.

The following result is an immediate consequence of the proof Theorem 3.9.

Corollary 3.11.Let $F \equiv (𝒞, G, MAX)$ be a MAX-SyMCN and assume that there exists a central value $c \in 𝒞$ .Suppose that ${W}_C&#x0005E;{\prime}\ne \varnothing$ .Then, the system presents fixed points and 2-periodic orbits.

Proof.The restriction of the system to the configurations in ${(𝒞 ∖ {c})}^{n}$ presents the same dynamics as the MAX-SyMCN $\mathbf{F}$ defined over $𝒞 ∖ {c}$ , which by Theorem 3.9 only presents 2-periodic orbits. On the other hand, it is easy to check that the configuration $\mathbf{c}&#x0003D;\left(c,\dots, c\right)$ is a fixed point of $\mathbf{F}$ .

Taking into account all the above results, in the following two corollaries, we characterize the periodic structure of MAX-SyMCN over complement-closed sets, which strongly depends on the existence of a central value in such sets.

Corollary 3.12.Let $F \equiv (𝒞, G, MAX)$ be a MAX-SyMCN and assume that $𝒞$ has no central value. Then, all the periodic orbits of the system are fixed points if, and only if, ${W}_C&#x0005E;{\prime }&#x0003D;\varnothing$ . On the other hand, all the periodic points of the system are 2-periodic orbits if, and only if, ${W}_C&#x0005E;{\prime}\ne \varnothing$ . That is, fixed points and 2-periodic orbits cannot coexist.

Corollary 3.13.Let $F \equiv (𝒞, G, MAX)$ be a MAX-SyMCN and assume that there exists a central value $c \in 𝒞$ . Then, the system presents fixed points. Moreover, $\mathbf{F}$ presents 2-periodic orbits if, and only if, ${W}_C&#x0005E;{\prime}\ne \varnothing$ . That is, fixed points and 2-periodic orbits coexist provided that ${W}_C&#x0005E;{\prime}\ne \varnothing$ .

Remark 3.14.In [46], it is proven that MAX-SyBN over directed dependency graphs can exhibit orbits of any period. Additionally, [47] shows that for any given integers ${n}_1,\dots, {n}_r$ , there exists a MAX-SyBN over a directed dependency graph presenting orbits with those periods. Since MAX-SyBN are a particular instance of MAX-SyMCN, these results extend to MAX-SyMCN over directed dependency graphs. Furthermore, from Lemma 3.1, they remain valid also when $| 𝒞 | > 2$ . Indeed, for a MAX-SyMCN over a directed dependency graph such that $| 𝒞 | > 2$ , taking $b \in 𝒞$ (distinct from the central value, if it exists) the restriction of the phase diagram to ${b, b^{'}}^{n} \subset 𝒞^{n}$ is isomorphic to its (binary) MAX-SyBN counterpart, with the same directed dependency graph and analogous $𝒞$ -maxterm. This allows us to construct a MAX-SyMCN over a directed dependency graph presenting periodic orbits of any given periods.

On the other hand, [46] shows that NAND-SyBN over directed dependency graphs can present orbits of whichever period, except fixed points. However, this does not hold in general for MAX-SyMCN over directed dependency graphs. Namely, when $𝒞$ has a central value, the configuration $(c, \dots, c) \in 𝒞^{n}$ is always a fixed point (as is proven in the undirected case). Therefore, in NAND-SyMCN over directed dependency graphs, since periodic orbits other than fixed points appear (by the previous arguments), fixed points and periodic orbits can coexist.

4 Conclusions and Future Research Directions

In this work, we study the types of periodic orbits of homogeneous MAX synchronous multistate networks over complement-closed sets, when the graph is undirected and all self-loop. We prove that, similarly to MAX synchronous Boolean networks, these systems only present fixed points and 2-periodic orbits. However, unlike Boolean systems, fixed points and 2-periodic orbits can coexist. All these results can be adapted immediately for MIN synchronous multistate networks over complement-closed sets.

The framework introduced in this work extends the definition of conventional finite multistate networks, considering a wide range of finite and infinite totally ordered sets where the state variables take values. In fact, these systems can be applied to real-world phenomena and computational processes in which the entities have a range of state values, rather than just two on-off states.

Future work will focus on studying the exact structure of fixed points and 2-periodic orbits, building on the work already done for the Boolean case. Additionally, this study assumes that all the entities are self-loop. More general contexts, such as generalized multistate networks, where entities may or may not depend on their own value, can also be studied. Also, the analysis of multistate networks over directed graphs appears as an interesting subject to be studied.

Author Contributions

Juan A. Aledo: conceptualization (equal), methodology (equal), formal analysis (equal), investigation (equal), writing – original draft (equal), writing – review and editing (equal), supervision (equal). Jose P. Llano: conceptualization (equal), methodology (equal), formal analysis (equal), investigation (equal), writing – original draft (equal), writing – review and editing (equal). Leila Sharifan: conceptualization (equal), methodology (equal), formal analysis (equal), investigation (equal), writing – original draft (equal), writing – review and editing (equal), supervision (equal). Jose C. Valverde: conceptualization (equal), methodology (equal), formal analysis (equal), investigation (equal), writing – original draft (equal), writing – review and editing (equal), supervision (equal).

Acknowledgments

Juan A. Aledo has been funded by the Government of Castilla-La Mancha and “ERDF A way of making Europe” through the project SBPLY/21/180225/000062 and by Universidad de Castilla-La Mancha and “ERDF A way of making Europe” through the project 2022-GRIN-34437. J.P. Llano and J.C. Valverde have been funded by the Junta de Comunidades de Castilla-La Mancha and the “ERDF A way of making Europe” within the Operational Program 2021–2027 through the project SBPLY/21/180501/000174. J.C. Valverde has been also funded by the Universidad de Castilla-La Mancha and the “ERDF A way of making Europe” within the Operational Program 2021–2027 through the project 2022-GRIN-34473.

Conflicts of Interest

The authors declare no conflicts of interest.

ENDNOTES

¹ The abbreviations BN, MN, MCN, SyMCN, MAX-SyMCN, and MIN-SyMCN will be written for the singular and plural forms of the corresponding terms, as this appears more aesthetically appropriate.
² In the expressions below, we are using the idempotent law.

Open Research

Data Availability Statement

The data used to support the findings of this study are included within the article.

References

1S. Kosub, “Dichotomy Results for Fixed-Point Existence Problems for Boolean Dynamical Systems,” Mathematics in Computer Science 1, no. 3 (2008): 487–505, https://doi.org/10.1007/s11786-007-0038-y.
10.1007/s11786-007-0038-y
Google Scholar
2M. Ogihara and K. Uchizawa, “Computational Complexity Studies of Synchronous Boolean Finite Dynamical Systems on Directed Graphs,” Information and Computation 256 (2017): 226–236, https://doi.org/10.1016/j.ic.2017.07.008.
10.1016/j.ic.2017.07.008
Web of Science® Google Scholar
3L. Pauleve and S. Sene, “ Boolean Networks and Their Dynamics: The Impact of Updates,” in Systems Biology Modelling and Analysis: Formal Bioinformatics Methods and Tools (Wiley, 2022), https://doi.org/10.1002/9781119716600.ch6.
10.1002/9781119716600.ch6
Google Scholar
4A. Veliz-Cuba and R. Laubenbacher, “On the Computation of Fixed Points in Boolean Networks,” Journal of Applied Mathematics and Computing 39 (2012): 145–153, https://doi.org/10.1007/s12190-011-0517-9.
10.1007/s12190-011-0517-9
Google Scholar
5J. Wu, Y. Liu, Q. Ruan, and J. Lou, “Robust Stability of Switched Boolean Networks With Function Perturbation,” Nonlinear Analysis: Hybrid Systems 46 (2022): 101216, https://doi.org/10.1016/j.nahs.2022.101216.
10.1016/j.nahs.2022.101216
Web of Science® Google Scholar
6C. L. Barrett, W. Y. C. Chen, and M. J. Zheng, “Discrete Dynamical Systems on Graphs and Boolean Functions,” Mathematics and Computers in Simulation 66 (2004): 487–497, https://doi.org/10.1016/j.matcom.2004.03.003.
10.1016/j.matcom.2004.03.003
Web of Science® Google Scholar
7J. A. Aledo, L. G. Diaz, S. Martinez, and J. C. Valverde, “Maximum Number of Periodic Orbits in Parallel Dynamical Systems,” Information Sciences 468 (2018): 63–71, https://doi.org/10.1016/j.ins.2018.08.041.
10.1016/j.ins.2018.08.041
Web of Science® Google Scholar
8S. Dai, B. Li, J. Lu, J. Zhong, and Y. Liu, “A Unified Transform Method for General Robust Property of Probabilistic Boolean Control Networks,” Applied Mathematics and Computation 457 (2023): 128137, https://doi.org/10.1016/j.amc.2023.128137.
10.1016/j.amc.2023.128137
Web of Science® Google Scholar
9S. A. Kauffman, “Metabolic Stability and Epigenesis in Randomly Constructed Genetic Nets,” Journal of Theoretical Biology 22 (1969): 437–467, https://doi.org/10.1016/0022-5193(69)90015-0.
10.1016/0022-5193(69)90015-0
CAS PubMed Web of Science® Google Scholar
10S. A. Kauffman, The Origins of Order: Self Organization and Selection in Evolution (Oxford University Press, 1993), https://doi.org/10.1007/978-94-015-8054-0_8.
10.1093/oso/9780195079517.001.0001
Google Scholar
11R. Thomas, “ Kinetic Logic: A Boolean Approach to the Analysis of Complex Regulatory Systems,” 1977, Proceedings of the EMBO Course Formal Analysis of Genetic Regulation, Brussels, https://doi.org/10.1007/978-3-642-49321-8.
10.1007/978?3?642?49321?8
Google Scholar
12M. Fazli, M. Ghodsi, J. Habibi, P. Jalaly, V. Mirrokni, and S. Sadeghian, “On Non-Progressive Spread of Influence Through Social Networks,” Theoretical Computer Science 550 (2014): 36–50, https://doi.org/10.1016/j.tcs.2014.07.009.
10.1016/j.tcs.2014.07.009
Web of Science® Google Scholar
13Z. Toroczkai and H. Guclu, “Proximity Networks and Epidemics,” Physica A378 (2007): 68, https://doi.org/10.1016/j.physa.2006.11.088.
10.1016/j.physa.2006.11.088
Google Scholar
14G. Cattaneo, M. Comito, and D. Bianucci, “Sand Piles: From Physics to Cellular Automata Models,” Theoretical Computer Science 436 (2012): 35–53, https://doi.org/10.1016/j.tcs.2012.02.034.
10.1016/j.tcs.2012.02.034
Web of Science® Google Scholar
15B. Chopard and M. Droz, Cellular Automata for Modeling Physics (Cambridge University Press, 1998), https://doi.org/10.1017/CBO978051154975.
10.1017/CBO9780511549755
Google Scholar
16A. Deshpande, S. Samanta, S. Govindarajan, and R. K. Layek, “Multi-Bit Boolean Model for Chemotactic Drift of Escherichia coli,” IET Systems Biology 14 (2020): 343–349, https://doi.org/10.1049/iet-syb.2020.0060.
10.1049/iet-syb.2020.0060
PubMed Web of Science® Google Scholar
17B. Luque and F. J. Ballesteros, “Random Walk Networks,” Physica A 342 (2004): 207–213, https://doi.org/10.1016/j.physa.2004.04.080.
10.1016/j.physa.2004.04.080
Web of Science® Google Scholar
18R. V. Sole, B. Luque, S. Kauffman, 1999. “ Phase Transition in Random Networks With Multiple States,” arXiv:adap-org/9907011, https://doi.org/10.48550/arXiv.adap-org/9907011.
10.48550/arXiv.adap?org/9907011
Google Scholar
19J. Garcia Galofre, M. Perez Millan, A. Galarza Rial, R. Laubenbacher, A. Dickenstein, 2024. “ Beyond Boolean Networks, a Multi-Valued Approach,” arXiv:2404.16760, https://doi.org/10.48550/arXiv.2404.16760.
10.48550/arXiv.2404.16760
Google Scholar
20F. Y. Wu, “The Potts Model,” Reviews on Modern Physics 54, no. 1 (1982): 235, https://doi.org/10.1103/RevModPhys.54.235.
10.1103/RevModPhys.54.235
Web of Science® Google Scholar
21J. M. Greenberg and S. P. Hastings, “Spatial Patterns for Discrete Models of Diffusion in Excitable Media,” SIAM Journal on Applied Mathematics 34, no. 3 (1978): 515–523, https://doi.org/10.1137/013404.
10.1137/0134040
Web of Science® Google Scholar
22M. Bartolozzi and A. W. Thomas, “Stochastic Cellular Automata Model for Stock Market Dynamics,” Physical Review E 69, no. 4 (2004): 046112, https://doi.org/10.1103/PhysRevE.69.046112.
10.1103/PhysRevE.69.046112
CAS Web of Science® Google Scholar
23G. C. Sirakoulis, I. Karafyllidis, and A. Thanailakis, “A Cellular Automaton Model for the Effects of Population Movement and Vaccination on Epidemic Propagation,” Ecological Modelling 133, no. 3 (2000): 209–223, https://doi.org/10.1016/S0304-3800(00)00294-5.
10.1016/S0304-3800(00)00294-5
Web of Science® Google Scholar
24M. Rollier, K. M. C. Zielinski, A. J. Daly, O. M. Bruno, and J. M. Baetens, “A Comprehensive Taxonomy of Cellular Automata,” Communications in Nonlinear Science and Numerical Simulation 140, no. 1 (2025): 108362, https://doi.org/10.1016/j.cnsns.2024.108362.
10.1016/j.cnsns.2024.108362
Google Scholar
25M. Gadouleau and A. Richard, “Simple Dynamics on Graphs,” Theoretical Computer Science 628, no. 15 (2016): 62–77, https://doi.org/10.1016/j.tcs.2016.03.013.
10.1016/j.tcs.2016.03.013
Google Scholar
26E. Tonello, “On the Conversion of Multivalued to Boolean Dynamics,” Discrete Applied Mathematics 259 (2019): 193–204, https://doi.org/10.1016/j.dam.2018.10.045.
10.1016/j.dam.2018.10.045
Web of Science® Google Scholar
27C. Chaouiya, A. Naldi, E. Remy, and D. Thieffry, “Petri Net Representation of Multi-Valued Logical Regulatory Graphs,” Natural Computing 10, no. 2 (2011): 727–750, https://doi.org/10.1007/s11047-010-9178-0.
10.1007/s11047-010-9178-0
Web of Science® Google Scholar
28J. A. Aledo, J. P. Llano, and J. C. Valverde, “Dynamics of Synchronous Boolean Networks With Non-Binary States,” Chaos 34, no. 7 (2024): 073124, https://doi.org/10.1063/5.0208534.
10.1063/5.0208534
PubMed Web of Science® Google Scholar
29J. A. Aledo, J. P. Llano, and J. C. Valverde, “Multi-State Sequential Boolean Networks: An Analysis of Its Combinatorial Dynamics,” Applied Mathematics and Computation 489C (2025): 129115, https://doi.org/10.1016/j.amc.2024.129115.
10.1016/j.amc.2024.129115
Google Scholar
30Y. M. Zou, “Boolean Networks With Multiexpressions and Parameters,” IEEE/ACM Transactions on Computational Biology and Bioinformatics 10 (2013): 584–592, https://doi.org/10.1109/TCBB.2013.79.
10.1109/TCBB.2013.79
PubMed Google Scholar
31O. Colon-Reyes, R. Laubenbacher, and B. Pareigis, “Boolean Monomial Dynamical Systems,” Annals of Combinatorics 8 (2004): 425–439, https://doi.org/10.1007/s00026-004-0230-6.
10.1007/s00026-004-0230-6
Google Scholar
32G. Malekbala, J. Musavizadeh, L. Sharifan, and M. Taha, “On the Dynamics of Semilattice Networks,” Journal of Symbolic Computation 113 (2022): 53–73, https://doi.org/10.1016/j.jsc.2022.02.003.
10.1016/j.jsc.2022.02.003
Web of Science® Google Scholar
33A. Veliz-Cuba and R. Laubenbacher, “Dynamics of Semilattice Networks With Strongly Connected Dependency Graph,” Automatica 99 (2019): 167–174, https://doi.org/10.1016/j.automatica.2018.10.031.
10.1016/j.automatica.2018.10.031
Web of Science® Google Scholar
34D. J. Rosenkrantz, M. Marathe, S. S. Ravi, and R. E. Stearns, “Synchronous Dynamical Systems on Directed Acyclic Graphs: Complexity and Algorithms,” Proceedings of the AAAI Conference on Artificial Intelligence 35, no. 13 (2021): 11334–11342, https://doi.org/10.1145/3653723.
10.1609/aaai.v35i13.17351
Google Scholar
35J. A. Aledo, G. Manjabacas, J. Robles, and J. C. Valverde, “Fuzzy Parallel Dynamical Systems on Zadeh Operators,” Mathematical Methods in the Applied Sciences 46, no. 9 (2023): 10260–10267, https://doi.org/10.1002/mma.9117.
10.1002/mma.9117
Web of Science® Google Scholar
36C. L. Barrett, H. S. Mortveit, and C. M. Reidys, “Elements of a Theory of Simulation II: Sequential Dynamical Systems,” Applied Mathematics and Computation 107, no. 23 (2000): 121–136, https://doi.org/10.1016/S0096-3003(98)10114-5.
10.1016/S0096-3003(98)10114-5
Google Scholar
37J. A. Aledo, S. Martinez, F. L. Pelayo, and J. C. Valverde, “Parallel Dynamical Systems on Maxterm and Minterm Boolean Functions,” Mathematical and Computer Modelling 35 (2012): 666–671.
10.1016/j.mcm.2011.08.040
Google Scholar
38J. A. Aledo, L. G. Diaz, S. Martinez, and J. C. Valverde, “On the Periods of Parallel Dynamical Systems,” Complexity 2017 (2017): 7209762, https://doi.org/10.1155/2017/7209762.
10.1155/2017/7209762
Web of Science® Google Scholar
39J. A. Aledo, A. Barzanouni, G. Malekbala, L. Sharifan, and J. C. Valverde, “Counting Periodic Points in Parallel Graph Dynamical Systems,” Complexity 2020 (2020): 9708347, https://doi.org/10.1155/2020/9708347.
10.1155/2020/9708347
Web of Science® Google Scholar
40J. A. Aledo, A. Barzanouni, G. Malekbala, L. Sharifan, and J. C. Valverde, “Fixed Points in Generalized Parallel and Sequential Dynamical Systems Induced by a Minterm or Maxterm Boolean Functions,” Journal of Computational and Applied Mathematics 408 (2022): 114070, https://doi.org/10.1016/j.cam.2021.114070.
10.1016/j.cam.2021.114070
Web of Science® Google Scholar
41M. Riesenhuber and T. Poggio, “Hierarchical Models of Object Recognition in Cortex,” Nature Neuroscience 2 (1999): 10191025, https://doi.org/10.1038/14819.
10.1038/14819
Web of Science® Google Scholar
42A. Jarrah, R. Laubenbacher, and A. Veliz-Cuba, “The Dynamics of Conjunctive and Disjunctive Boolean Network Models,” Bulletin of Mathematical Biology 72 (2010): 14251447, https://doi.org/10.1007/s11538-010-9501-z.
10.1007/s11538-010-9501-z
Web of Science® Google Scholar
43C. Gershenson, 2002, “ Classification of Random Boolean Networks,” https://doi.org/10.48550/arXiv.nlin/0408006.
10.48550/arXiv.nlin/0408006
Google Scholar
44H. S. Mortveit and C. M. Reidys, An Introduction to Sequential Dynamical Systems (Springer, 2007), https://doi.org/10.1007/978-0-387-49879-9.
Google Scholar
45J. A. Aledo, S. Martinez, and J. C. Valverde, “Parallel Discrete Dynamical Systems on Independent Local Functions,” Journal of Computational and Applied Mathematics 237, no. 1 (2013): 335–339, https://doi.org/10.1016/j.cam.2012.06.002.
10.1016/j.cam.2012.06.002
Web of Science® Google Scholar
46J. A. Aledo, S. Martinez, and J. C. Valverde, “Parallel Dynamical Systems Over Directed Dependency Graphs,” Applied Mathematics and Computation 219 (2012): 11141119, https://doi.org/10.1016/j.amc.2012.07.018.
10.1016/j.amc.2012.07.018
Web of Science® Google Scholar
47J. A. Aledo, L. G. Diaz, S. Martinez, and J. C. Valverde, “Coexistence of Periods in Parallel and Sequential Boolean Graph Dynamical Systems Over Directed Graphs,” Mathematics 8, no. 10 (2020): 1812, https://doi.org/10.3390/math8101812.
10.3390/math8101812
Web of Science® Google Scholar

Volume48, Issue12

August 2025

Pages 11620-11629

Periodic Orbits of MAX and MIN Multistate Networks

ABSTRACT

1 Introduction

2 Preliminaries

3 Periodic Orbits of MAX and MIN Multistate Networks

4 Conclusions and Future Research Directions

Author Contributions

Acknowledgments

Conflicts of Interest

ENDNOTES

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Periodic Orbits of MAX and MIN Multistate Networks

ABSTRACT

1 Introduction

2 Preliminaries

3 Periodic Orbits of MAX and MIN Multistate Networks

4 Conclusions and Future Research Directions

Author Contributions

Acknowledgments

Conflicts of Interest

ENDNOTES

Open Research

Data Availability Statement

References

Figures

References

Related

Information