Macromolecular Theory and Simulations
Volume 33, Issue 3 2400009
Perspective
Open Access

Modeling the Interface Between Phases in Dense Polymer-Carbon Black Nanoparticle Composites by Dielectric Spectroscopy: Where Are We Now and What are the Opportunities?

Christian Brosseau, 

Corresponding Author

Christian Brosseau

Université de Brest, Lab-STICC, CS 93837, 6 avenue Le Gorgeu, Brest, Cedex 3 29238 France

E-mail: [email protected]

Search for more papers by this author
First published: 07 March 2024
https://doi.org/10.1002/mats.202400009

Abstract

The macroscopic properties of polymer nanocomposites (PNC) rely largely on the interphase between the polymer chains and the filler particles. One significant difficulty to solve this issue is to quantitatively model the structure-property correlations due to the interfacial region in these complex materials. While dielectric spectroscopy (DS) measurements are routinely used to characterize the effective permittivity of filled polymers, fitting standard effective medium models and mixing equations to these data remains notoriously difficult to interpret. This is due to the absence of explicit reference to internal length scales characterizing the interfaces in the PNC. As an illustrative example, a two-level homogenization framework is proposed which enables the extraction of useful information on the impact of a thin interphase confined on a nanometer length scale based on broadband DS data. This model leads to new ways of tuning the interphase so as to optimize the material's response to electric field, a situation relevant for electromagnetic shielding. This approach provides guidance on how to observe directly and experimentally the actual properties of the interface between the phases (as opposed to model-based inference). Aside from its secure physical foundation in the theory of effective medium, a significant advantage of this approach is that a genetic algorithm (GA) technique applied to this physics-based model enables the uniqueness of the fit parameters to be considered, as the GA method is robust in terms of finding globally optimum solutions, therefore placing confidence in non-universal values of the percolation exponents. Recent work in physics-informed machine learning indicates that the effective dielectric properties of PNC with many degrees of freedom due to their complex morphology can be described by considering only a few degrees of freedom describing the interface features between the phases in these composites.

1 Introduction and Motivation

The pursuit of the physical characterization and modeling of polymer nanocomposites (PNC) is of great experimental and theoretical interest, fueled largely by the numerous technological applications such as electromagnetic shielding, structural health monitoring, high-density energy storage, static-charge dissipation, and self-regulator heater.[1-3] PNCs are structurally complex materials that offer unique properties and functions that are inaccessible in bulk materials. The manufacturability in complex shapes of the polymer matrix along with the broad choice of filler particle allows for the prospect of developing soft-polymer based nanoparticles with exciting mechanical and electric properties. These properties are strongly influenced by inherent structural disorder over length scales from molecular functional groups to crystallization scales up to sample dimensions. However, it is increasingly clear that in order to ensure the optimization of a desired multicomponent structure, specification of the bulk components is in general not sufficient. Instead, explicit account of how microscopic dynamics select assembly pathways is required. Since the early work of de Gennes, it has been understood that polymer chains adsorb from the melt onto weakly attractive surfaces, forming trains, loops, and tails.[1] Therefore, a description of the interface characteristics between the carbon black (CB) phase, for example, aggregate, agglomerate, and the polymer phase, is crucial for the understanding of the material, simply because the fraction of the overall material which is in the vicinity of an interface is high. In recent years, there have been many ideas on how such interface could be probed. For recent reviews on the subject, we refer the reader to refs. [3-9].

Since four decades, research efforts focus on two parallel approaches for characterizing the interface, depending on the characteristic length scale which is probed. One is to probe the adsorption layer of polymer chains to the surface of filler particles (e.g., CB, silica) by nuclear magnetic relaxation (NMR)[3, 10, 11] or the local electrical resistance measured through a film of the material under study by an atomic force microscopy dedicated to the electrical characterization of surfaces.[4] An alternative approach is to infer the dielectric characteristics of the interphase from effective medium analysis and its expansions via the resolution of an inverse problem. It is exemplified by the phenomenological theory proposed by Vo and Shi (VS) and Todd and Shi (TS), built on a core–shell (CS) modeling of the interphase.[5, 12] In the inceptive work of VS and TS, the authors show that the irreversibly adsorbed polymer layer forms a shell around the CB aggregates which impacts the effective complex permittivity of composite systems, for example, BaTiO3 filled trimethylolpropane triacrylate PNC.[5] They show it is possible to use trial and error to find the effective permittivity of the composite, knowing the intrinsic permittivities of the filler component, the matrix component, and the interphase region, as well as the content of each phase. Many of the engineering works for polymer heterostructures over the past decade have somewhat followed this guideline. For example, the authors of ref. [6] used VS-TS's model to show that the interphase permittivity was ≈10 vol% of the matrix phase, in good agreement with the experimental values.[3, 4] Subsequently, Liu et al. proposed a physical model to estimate the permittivity and volume of the interphase region of a composite based on the dipole polarization theory.[7] Though these studies showcase the usefulness of such CS description of the interphase, theory has thus far not developed the level of sophistication required to fully utilize the information stored in electromagnetic measurements. Even with detailed structural information in hand, the role of interface in the dielectric response of PNC is disputed, and our understanding of the role of interfacial regions lacks predictive power and remains largely descriptive. It is clear that there is a pressing need for a careful reexamination of the interfacial properties of polymer–nanoparticles mixtures. It is worth noting that in the field of thermal transport in PNC, the interpretation of the effective thermal conductivity is aided by incorporating the interface thermal resistance with a mean-field analysis.[13]

Another feature overlooked until recently in the modeling of the dielectric properties of these materials is the poor understanding of the properties of the carbonaceous phase inside the polymer matrix. This is commonly the major impediment to the inverse problem resolution mentioned above. However, over the range of frequencies explored (10–104 kHz), it was found that the intrinsic complex (relative) permittivity of the carbonaceous phase could be written as ε 2 = ε ′ 2 − j ε ′ ′ 2 ${\varepsilon }_{\mathrm{2}} = {\varepsilon ^{\prime}}_{\mathrm{2}} - j{\varepsilon ^{\prime\prime}}_{\mathrm{2}}$ with ε ′ ′ 2 > > | ε ′ 2 | ${\varepsilon ^{\prime\prime}}_{\mathrm{2}} > > | {{{\varepsilon ^{\prime}}}_{\mathrm{2}}} |$ .[2] It was also suggested that the intrinsic permittivity of the carbonaceous phase could be described by a classic free-electron-like metal (Drude form) in the case of a percolative morphology. This model provides a decent description of the intrinsic permittivity of this phase. However, contrary to the popular view of this material as a “conducting phase,” the Drude model is not effective for non-percolative morphologies in which the carbonaceous phase aggregates are dispersed in small disconnected regions.

Motivated by the conjectured importance of interphase of the electromagnetic properties of composites, the focus herein is on phenomenological approaches to reconstruct the effective permittivity of CB filled polymers measured by dielectric spectroscopy in a satisfactory way. It is meaningful to investigate the interface between the different phases in PNC. As the formation of the irreversible adsorbed polymer layer is rather general, the current model would shed new light on the impact of this interphase on the effective permittivity of polymer–nanoparticle mixtures. However, what has heretofore been lacking is a way to quantify the dielectric properties of the thin interphase confined on a nanometer length scale without the necessity of carrying out local experiments. This (theorist's) paper has intentionally not discussed the confrontation of models with experimental data because there has been considerable controversy in the literature on many dielectric studies and related morphology characterizations on PNC, for example, in some cases, authors get different results, simply because they use oriented carbon fiber filled PNC instead of randomly oriented PNC, consider semicrystalline polymer phases with different crystallite sizes and states of aggregation of the chains in the amorphous regions, or use block copolymers as templates for controlling the distributions of the filler particles. Thence, the morphology of the resulting particle dispersions cannot be related to each other in a straightforward way.

The remainder of the paper is organized as follows. We begin in Section 2 by reviewing some key features of the interface between phases in dense PNC in terms of which the problem of interphase can be approached. We try to motivate some basic results and relate them to interesting open problems. As the interphase region is likely to be pivotal in controlling the effective dielectric properties of the composite, Section 3 outlines several analytically treatable effective medium approaches to interpreting the dielectric properties of PNC. These approaches demonstrate the role of shell thickness and phase intrinsic permittivity as key parameters controlling the effective permittivity of the composite samples. A convenient way to analyze the characteristic features of the shell is by using a two-level homogenization method based on the two-exponent percolation phenomenological equation (TEPPE) that yields intuition and insight, as well as understanding.[14-18] This interplay between effective permittivity and interphase introduces complications because there is no consensus regarding the values of the two fitting parameters s ∼ $\tilde{s}$ and t ∼ $\tilde{t}$ of the TEPPE modeling Thence, assessing the relative importance of the shelled interphase requires to study a priori the TEPPE and compare predictions with experiments to infer the possible values. A genetic algorithm (GA) has been developed which allows for estimating the values for the percolation threshold, percolation exponents s ∼ $\tilde{s}$ and t ∼ $\tilde{t}$ , and the filler particle conductivity.[17] Youngs[17] showed that this GA technique enables the uniqueness of the fit parameters to be considered as the GA method is robust in terms of finding globally optimum solutions; therefore, placing confidence in non-universal values of the percolation exponents. Finally, in Section 4, we draw conclusions and propose some perspectives to develop an accurate phenomenological model for modeling the effective dielectric properties of filled PNC.

2 Characterization of the Interface Between Phases in Dense Polymer–Nanoparticle Composites

As a kind of preface to the effective macroscopic properties of dense PNC discussed below, it is useful to examine four (at least) main characteristics of filler particles, that is, the primary particle size and orientation, the particle specific surface area, the processing history, and the state of dispersion (morphology of filler aggregates and their surface chemical composition, polymer chain molecular weight distribution, and polymer crystallinity).[19-23] The reinforcing effect of CB on the polymer matrix has been extensively studied; see, for example,[24-26] controlling the interphase between the filler particles and polymer chains, for example, bound rubber in CB or carbon nanotube (CNT) filled rubber, has been a recurrent theme in the study of PNC because many observations have shown that it can significantly impact the effective mechanical properties of the samples.[27-33] As was recalled above, we can go beyond the mechanical characterization because the interfacial properties of PNC can be probed by a large variety of scattering and microscopy techniques with the aim of identifying their characteristic length and time scales, for example, NMR,[3, 10, 11, 34, 35] differential scanning calorimetry (DSC),[36] dynamic mechanical thermal analysis (DMTA),[28, 37-39] rheology,[40, 41] neutron and positron annihilation spectroscopies,[42, 43] atomic force microscopy (AFM),[26, 40] small-angle neutron (SANS),[42, 43] and small-angle X-ray scattering (SAXS).[44-46]

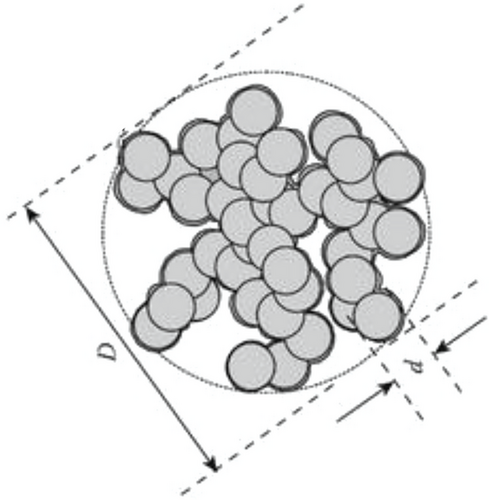
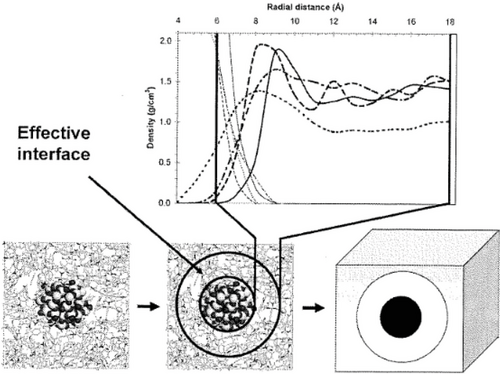
One important question in this field concerns the observed similarities amongst PNC. Transmission electron microscopy (TEM) indicated that CB exists as aggregates of spherical particles. It should perhaps be emphasized in this context that a good spatial dispersion state of individual nanoparticles (of typical particle size d) is often unlikely to be achieved but leads to the appearance of aggregates, that is, of typical size D ≈ 10 − 10 2 d $D \approx 10 - {10}^2d$ , and sometimes agglomerates, that is, > 10 3 d $ > {10}^3d$ .[20] From purely geometrical arguments, a typical aggregate volume contains typically 103–106 primary particles (Figure 1).

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Schematic picture of a nanoparticle aggregate: d and D are the primary particle size and the equivalent sphere diameter enclosing a typical aggregate. Adapted with permission.[20] Copyright 1998, John Wiley and Sons.

Many studies demonstrated that polymer chains strongly adsorb to the surface of CB particles during processing, resulting in an amorphous layer (bound polymer noted 1 in Figure 2).[47] The fundamental question of the role of polymer chain adsorption on particle aggregate (Figure 2) in determining the slow dynamics of macromolecular chains is crucial for characterizing the interfacial bonding.[2, 14, 48-51] Strong, short range attractions can trigger adsorption sites as illustrated in Figure 2. The spacing between the filler aggregates is generally larger than the dimensions of single polymer chains.[1, 19, 20]

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Schematic illustration distinguishing between the structural inhomogeneities of a PNC (not at scale). The large surface area of aggregates creates a region of altered polymer behavior (interphase): 1 denotes an adsorbed chain at localized sites that directly interacts with aggregate surface (adsorption sites), can hardly move, and can be viewed as permanent links tying individual aggregates; trains (3,4) and loop (2) are also represented; 3 and 4 show the tails (dead ends) that show high chain mobility such as free rubber chains. On a molecular scale, the crystalline (6) and amorphous (5) regions are interconnected by chains that participate in both regions. The interphase (polymer layer with reduced mobility) is responsible for the existence of flexible polymer bridges between adjacent filler aggregates and strongly impacts the transmission of stress by the filler network.

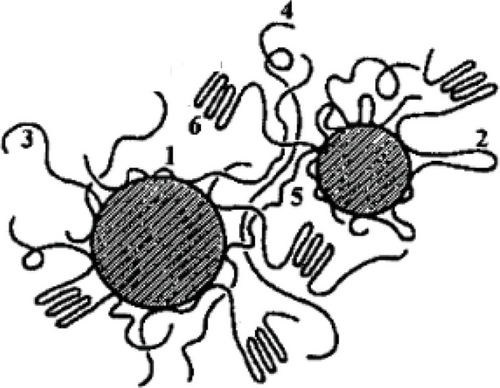
It should also be emphasized in this context that the dielectric response of CB filled PNC can change dramatically upon stretching and deformation under shear.[48-50] One natural explanation would be that that interfacial interactions have been operative, but this obvious mechanism cannot do entirely the trick. Alternatively, Huang and Schadler[50] showed that this phenomenon reflects the changes in filler aggregate connectivity due to strain.

In preparation for the next section, we will focus on physical models which can be of interest for broadband DS[50-53] for many reasons. First, the incorporation of nanoparticles has, for effect, to decrease the effective permittivity of PNC over the bare polymer.[54] Second, a reduction in space charge distribution has been documented compared to the incorporation of micron scale fillers due partly to the change of the particle–polymer interface, and also partly, due to the large surface area of particles aggregates, creating a zone of altered polymer behaviour.[27] Third, DS is a robust method to study a wide range of dynamic properties of the interphase in PNC because frequency sweeping allows to discriminate between the characteristic length scales associated with polarization and conduction phenomena.[51, 54-57] Within the linear response theory, when an ac electric field is applied to a dielectric material containing permanent dipoles, the complex permittivity ε = ε ′ − j ε ′ ′ $\varepsilon = \varepsilon ^{\prime} - j\varepsilon ^{\prime\prime}$ is related to the time correlation function of the thermal fluctuations of polarization[14] by the expression ε − ε ∞ ∝ T L [ − d d t ⟨ P ( 0 ) · P ( t ) ⟩ e q ] $\varepsilon - {\varepsilon }_\infty \propto TL[ { - \frac{d}{{dt}}{{\langle {{\bm{P}}( 0 ) \cdot {\bm{P}}( t )} \rangle }}_{eq}} ]$ , where TL is the Laplace transform (with argument jω, where ω is the angular frequency of the electric field). In this expression, the angular brackets denote an ensemble average of the fluctuations of the polarization P(t) near equilibrium and ε ∞ ${\varepsilon }_\infty $ stands for the high frequency limits of ε ′ $\varepsilon ^{\prime}$ . For simple systems (non-interacting dipoles characterized by a single relaxation time τ), we can further calculate the ensemble averaged of the fluctuating components of P(t) and obtain the Debye dielectric dispersion which reads ε − ε ∞ ε s − ε ∞ = 1 1 + j ω τ $\frac{{\varepsilon - {\varepsilon }_\infty }}{{{\varepsilon }_{\mathrm{s}} - {\varepsilon }_\infty }} = \frac{1}{{1 + j\omega \tau }}$ , where ε s ${\varepsilon }_{\mathrm{s}}$ is the low-frequency limit of ε ′ $\varepsilon ^{\prime}$ .[14] However, with respect to the dynamics on the scales shown in Figure 2, PNC are different from these simple systems, and non-ergodicity of the medium can have profound effects on the polarization dynamics. It is frequently found that the dielectric spectra of PNC can be interpreted by a broad and asymmetric distribution of relaxation times.[14, 57] A theoretical picture of the frequency dependence of the effective permittivity involves an input of the intrinsic permittivity of the different phases at the relevant frequencies together with the phase volume fractions and morphological information of the inclusions. The output is an effective complex permittivity for the heterostructure as a whole (quasi-static limit). Another thing to note is that some authors considered that the interphase is a quasi-conductive region[27] due to the formation of a double layer in the interfacial region, even if surface chemistry of the particles can strongly affect the space charge behavior.

In fact, one believes that interphase modeling proposals, if they can be fully implemented, have limiting cases that appear in various limiting cases, for example, quasi-static limit, dilute limit. Maxwell–Wagner–Sillars (MWS) polarization is often associated with interphase phenomena at radio frequency and below in heterostructures.[14, 27, 56] It manifests by an increase of polarization due to the accumulation of charges carriers at phase boundaries: first, bound charges for time less than the MWS polarization characteristic time (typically, a few µs for CB filled polymers). The mean displacement of the charge carriers is small and the conductivity is governed by a power law dependence as a function of the frequency of the ac electric field with an exponent controlled by the fractal nature of the CB aggregates. At longer times, free charges control the dc conductivity. In that case, the charge carriers follow a normal diffusion process and are forced to move over large distances, compared to the mean cluster size. Then, the effective conductivity is controlled by tunnelling or hopping between clusters.[57]

In any event, it appears that, even if the concept of interphase seems reasonable, the details thereof have not been completely disentangled. The formation and thermodynamic stability of the interphase region, the dispersion state of the interphase, and more importantly, the effect of the interphase on the macroscopic properties of PNC remain unclear. One has no rigorous calculation of the characteristic length scale of this interphase, and almost all studies on the DS characterization of the interfacial interaction between CB and polymer matrix rely on indirect evidence of the interphase (model-based inference).

3 Continuum Models and Analysis of the Interface Properties Phases in Composites

The basic objective of this section is to present different approaches for constructing a continuum model of a filled polymer material, which has been proposed in the archival literature.[10, 14-16] These models have the following advantages. They combine the convenience of dealing with the continuum description, which permits numerically analyzing complicated materials with effective characteristic parameters. In addition, these models can be implemented with specific features of interaction between filler particles and polymer chains, even if the state of the material is inhomogeneous at the scale level that is many times greater than the dimension of a primary particle. Here, we discuss different analytically soluble continuum models as well as the mutual advantages and disadvantages of various implementations. We also note that the problem of determining the effective (homogenized) characteristics of random heterostructures is still currently being investigated numerically by finite element simulations[2, 14] and by averaging over a suitable ensemble of real microscopic images.[58, 59] Here, we don't treat the opposite (scattering) limit, in which the wavelengths are short compared with inclusion sizes and distances between inclusions, by considering molecular theories of PNC such as those obtained by, for example, large scale atomistic and molecular dynamics simulation, or Monte Carlo simulations.[60-64] In many simulation studies, the CB primary particle is described by an amorphous core and a graphitized shell; while the chain–chain and chain–CB interactions are treated through two-parameter Lennard–Jones potentials, see, for example, ref. [62].

3.1 Tunneling-Percolation Model of Balberg (2002)

Among the early landmark papers using a particular combination of inter-particle tunneling conduction and non-universal percolation for explaining, at least semi-quantitively, electrical conductivity measurements of CB filled polymer composites, is the Balberg's model.[65] The key physical idea utilized in establishing this model is that the standard percolation theory (SPT)[66] is modified to consider the particular geometrical properties of CB, for example, elongated CB aggregates, and the state of dispersion (Figure 3). On the one hand, the spatial exponential decay of the tunneling conductance is introduced in the SPT. On the other hand, a distribution of the inter-particle aggregates (Figure 1) yields a distribution of resistance in the network, which in turn, determines the non-universal high values of the critical exponent describing the divergence of the effective conductivity of the PNC close to the percolation threshold. Comparison of this model with experimental results shows good agreement for dc electrical excitation.[67]

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
a) Modeling the tunneling conductance in percolation model. Black circles represent CB particles; while, the corresponding gray shells represent the effective tunneling distance. The contribution of the nearest neighbor resistors is essential to the effective conductivity of the composite. b) Different kinds of CB particles yield different kinds of conducting networks in CB-polymer composite material. For example, “high structure” CB particles form elongated structures which strongly impact the corresponding tunneling regions.

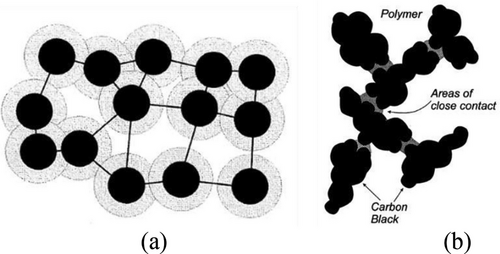
3.2 VS-TS Model (2002)

The interphase regions at polymer–filler interfaces have been also considered by VS,[12] and later used by TS.[5] In the VS-TS model, key point to be stressed here is that polymer chains that are “bonded or otherwise oriented” at the filler–particle interface result in unique electrical and physical properties. VS developed a phenomenological model[12] of the effective permittivity of a polymer filler composite material (Figure 4) and noted its nonlinearity with respect to a number of variables describing the interphase characteristics.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Schematic illustrating the principle of the VBS model, describing a polymer–ceramic composite with three phases: the filler particle, the interphase region, and the polymer matrix. Reproduced under the terms of the CC-BY license.[5] 2003, Todd and Shi, Published by AIP Publishing.

This model was used by TS to characterize the effect of chemical coupling agents on the interphase dielectric characteristics.[5] A related model was employed by Liu and coworkers,[7] for which the existence of an interfacial region between the filler particle and polymer matrix, or interphase of finite thickness, had been posited and indirectly revealed. While their findings provided further evidence that the interphase region of a polymer–ceramic composite has chemical, mechanical, and dc electrical characteristics different from that of the constituent phases, what seems to have escaped full appreciation is that no characteristic time- and length scales were suggested to understand the polarization and charge carrier relaxation mechanisms controlling this interphase region.

There are a few interesting points which merit further investigation. A continuum-based mechanical model for PNC with various interfacial conditions[18] was directly extended to the above scenario by Odegard and coworkers (OCG), where molecular dynamics (MD) simulations described the molecular structures of the nanoparticle, polymer chains, and interfacial region. Using a simulation method that involves coarse-grained and reverse-mapping techniques, OCG considered a model which included an effective interface between the polymer chains and nanoparticle with properties and dimensions that were determined using MD simulations.[18] OCG's goal was to determine which structural parameter had the most or least mechanical consequence on Young's moduli and shear moduli as a function of the effective interface (Figure 5).

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Schematic configuration of the PNC using OCG model. The bottom figures show the effective interface between the surface of the (silica) particles and the bulk polymer phase. The scheme shows how the effective interface with denser polymer phase is defined in the composite material. The top of this figure shows the radial density profile of the nanoparticle (thick lines) and polymer (thin lines) phases as a function of the radial distance from the center of a reference nanoparticle. Reproduced with permission.[18] Copyright 2005, Elsevier.

These findings highlighted the possibility of attaining a diverse set of mechanical properties and associated nanotechnological functions by tailoring its structural parameters.

3.3 Fritzsche and Klüppel Tunneling Model (2011)

Based on the pioneering work of Kawamoto's,[68, 69] Fritzsche and Klüppel (FK)[8] considered a tunneling process of charge carriers over nanoscopic gaps (Figure 6) between adjacent CB particles to interpret experimental dielectrc spectra. This model implies that charge carrier transport can take place by hopping or tunneling processes. The main assumption of this model is that CB aggregates are connected by bound rubber which can be treated as a capacitor CG and resistor RG in parallel (Figure 6).

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
CB network at the percolation threshold with nanogaps between adjacent CB aggregates modeled by resistor and capacitor in parallel. Reproduced with permission.[8] Copyright 2011, IOP Publishing.

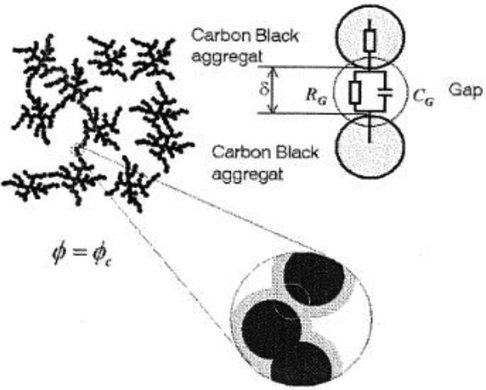
One can, therefore, argue in the framework of the quantum mechanical tunneling phenomenon that C G ∝ A / A δ δ ${C}_{\mathrm{G}} \propto {A \mathord{/ {\vphantom {A \delta }} \kern-\nulldelimiterspace} \delta }$ and R G ∝ ( A / A k δ k δ ) − 1 exp ( k δ ) ${R}_{\mathrm{G}} \propto {( {{A \mathord{/ {\vphantom {A {k\delta }}} \kern-\nulldelimiterspace} {k\delta }}} )}^{ - 1}\exp ( {k\delta } )$ , where A denotes the cross section of the gap distance δ, and k is a parameter proportional to the square root of the mean height V of the potential barrier.[70] Then, one is led to a characteristic relaxation time of the tunneling process over a CB–CB connection which scales as τ ∝ R G C G ∝ ( ε k ) exp ( k δ ) $\tau \propto {R}_{\mathrm{G}}{C}_{\mathrm{G}} \propto ( {\frac{\varepsilon }{k}} )\exp ( {k\delta } )$ , where ε is the relative permittivity of the material in the gap. The numerics are in fact straightforward. In terms of typical height of the potential barrier V = 0.2 V and a typical value ε = 3, this implies a value of the order of several nanometers for δ which can be evaluated from the dielectric spectrum and the measurement of τ. This value is consistent with that obtained by Qu[28] based on the difference between phase diagram and height diagram by AFM. Another thing to note is that FT suggested that there two relaxation transitions: one is due to the diffusion of charge carriers on CB aggregates in the low frequency range and the other due to the tunneling of charge carriers through the nanoscopic gaps at high frequency. It may be also emphasized that according to the FT model, δ decreases with increasing filler loading and specific surface area which correlates with an increase of the apparent activation energy of the filler network evaluated by DMTA.

3.4 Deng and Van Vliet Effective Medium Model (2011)

It also turns out that, as emphasized in the Introduction, PNC applications remain limited primarily due to inadequate understanding of their interface and interphase properties. To develop a comprehensive understanding of their material properties, Deng and van Vliet (DVV) investigated the mechanical behavior of a number of PNC as a function of their characteristic structural parameters under hydrostatic tension and hydrostatic compression.[28] Figure 7 shows schematically the method for estimating the effective elastic properties of PNC comprising particles encapsulated by an interphase of finite thickness and distinct elastic properties.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Schematic of the effective DVV model for estimating the effective properties of PNC comprising spherical particles surrounded by distinct interphases. The top of this figure considers, respectively: a) low volume fractions of particles (dilute limit), b) the mechanical properties are described by identical CS particles, c) effective particles are embedded in the polymer matrix, and d) the effective (homogenized) medium that is mechanically equivalent to the PNC. The bottom of this figure is concerned with: e) high particle volume fractions, or when strong intercations between particles lead to agglomeration; f) in that case, the polymer phase can surround the CS particles or the interphase-encapsulated nanoparticles can surround the polymer. The particle-interphase (or aggregate-interphase) zones are mechanically equated to effective particles and g,h) a mixture law is applied to give again the homogenized medium shown in (d). Reproduced with permission.[28] Copyright 2011, IOP Publishing.

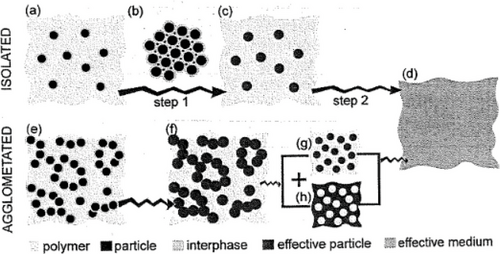
The DVV model can treat PNC that comprises either physically isolated nanoparticles (e.g., dilute limit or low volume fraction of well dispersed and spatially isolated nanoparticles) or agglomerated particles (e.g., percolating composite). Such analysis is an attempt to unravel the role of surface and volume in modulating the mechanical (electric) behavior of the PNC. This is an important investigation as surface is directly related to the chemical activity with the filler nanoparticle; while, volume is related to the weight.[50] An understanding of their role can reveal a design principle that can shed lights on what to engineer to attain a desired surface area at a reduced weight, without compromising the desired effective property of the PNC.

According to DVV, this approach provides a reliable way of interrogating the effect of different structural parameters on the mechanical properties of PNC. These authors found that the predicted elastic moduli agree with experiments for different kinds of CB filled rubber nanocomposites in which the CB particles or aggregates are well dispersed.[28] Based on the quasistatic approximation,[14] the same analysis can also be applied to model the effective permittivity of PNC and can be checked by DS.

3.5 Two-Step Effective Medium Modeling

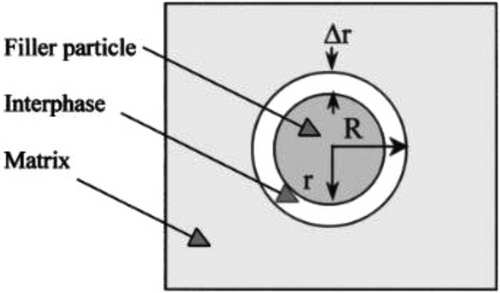
One can also consider a structurally simple representation of PNC thanks to the two-level homogenization model as depicted in Figure 8.

Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Schematic method to estimate the effective dielectric properties of a PNC comprising filler particles surrounded by interphases. a) In the first (microscale) step of this approach, each particle ‘c’ (represents the smallest discrete entity of CB, the CB aggregate in the polymer matrix 1 is surrounded by interphase 3. The dielectric properties of the effective particle ‘e’ are then estimated by a weighted volume fraction of phases 2 and 3. b) The second step of this analysis considers the macroscale heterostructure (RVE), which is represented by the effective medium representation ‘m’ of the PNC.

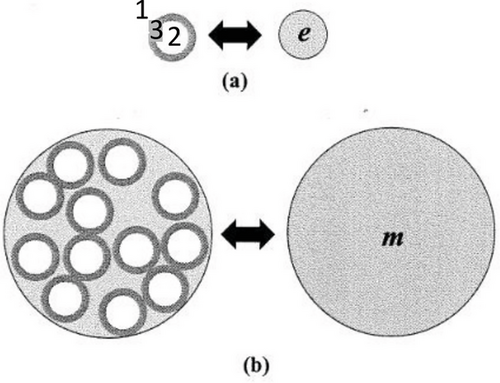
As recalled above, the assumption of homogeneous and isotropic spatially averaged electromagnetic properties is generally open to question in the theory of composites.[2, 5, 14, 15] The physical idea behind this two-step procedure is actually quite simple. The model is parameterized by three quantities: the first is the dc conductivity ε2 of the CB, the second is the relative permittivity of the interphase ε ′ 3 − j ε ′ ′ 3 ${\varepsilon ^{\prime}}_3 - j{\varepsilon ^{\prime\prime}}_3$ with volume fraction ϕ 3 ${\phi }_3$ . Although ϕ 3 ${\phi }_3$ is not entirely known, it can be estimated from refs. [5, 6]. The third is that we consider a frequency-independent permittivity, ε ′ 1 − j ε ′ ′ 1 ${\varepsilon ^{\prime}}_1 - j{\varepsilon ^{\prime\prime}}_1$ , of the polymer phase. This is what is generally observed in experimental data.[2, 7, 16, 48, 57] In the following, we estimate ε 2 = − j σ 2 / σ 2 ω ε 0 ω ε 0 ${\varepsilon }_2 = - j{{{\sigma }_2} \mathord{/ {\vphantom {{{\sigma }_2} {\omega {\varepsilon }_0}}} \kern-\nulldelimiterspace} {\omega {\varepsilon }_0}}$ , where ε 0 ≈ 8.85 ${\varepsilon }_0 \approx 8.85 $ 10−12 F m−1. In the first-step, the particle-interphase region is replaced by an effective particle e of identical size and shape. Now, a CS particle in the quasi-static limit, under plane wave excitation, responds like a homogeneous dielectric sphere with an equivalent relative permittivity given by ε c = ε 3 [ ϖ − 1 − 2 ( ε 3 − ε 2 ) / ( ε 3 − ε 2 ) ( 2 ε 3 + ε 2 ) ( 2 ε 3 + ε 2 ) ϖ − 1 + ( ε 3 − ε 2 ) / ( ε 3 − ε 2 ) ( 2 ε 3 + ε 2 ) ( 2 ε 3 + ε 2 ) ] ${\varepsilon }_{\mathrm{c}} = {\varepsilon }_3[ {\frac{{{\varpi }^{ - 1} - 2{{( {{\varepsilon }_{\mathrm{3}} - {\varepsilon }_{\mathrm{2}}} )} \mathord{/ {\vphantom {{( {{\varepsilon }_{\mathrm{3}} - {\varepsilon }_{\mathrm{2}}} )} {( {2{\varepsilon }_{\mathrm{3}} + {\varepsilon }_{\mathrm{2}}} )}}} \kern-\nulldelimiterspace} {( {2{\varepsilon }_{\mathrm{3}} + {\varepsilon }_{\mathrm{2}}} )}}}}{{{\varpi }^{ - 1} + {{( {{\varepsilon }_{\mathrm{3}} - {\varepsilon }_{\mathrm{2}}} )} \mathord{/ {\vphantom {{( {{\varepsilon }_{\mathrm{3}} - {\varepsilon }_{\mathrm{2}}} )} {( {2{\varepsilon }_{\mathrm{3}} + {\varepsilon }_{\mathrm{2}}} )}}} \kern-\nulldelimiterspace} {( {2{\varepsilon }_{\mathrm{3}} + {\varepsilon }_{\mathrm{2}}} )}}}}} ]$ , where ϖ = ( a 2 / a 2 a 3 a 3 ) 3 $\varpi = {( {{{{a}_2} \mathord{/ {\vphantom {{{a}_2} {{a}_3}}} \kern-\nulldelimiterspace} {{a}_3}}} )}^3$ , a2 denotes the radius of the core, and a3−a2 is the thickness of the coating phase of permittivity ε 3 ${\varepsilon }_3$ .[14, 71, 72] In the second step, a representative volume element (RVE), which is the smallest volume over which a calculation can be made that will yield a value representative of the whole, is considered for continuum electrostatics. In other words, we define a mesoscale of the domain of random microstructure over which smoothing (or homogenization) is being done relative to the microscale (Step 1).[14] Without losing the generality of the method, one can consider in analyzing the ϕe dependence of the effective permittivity of the Bruggeman effective medium equation for a two-phase medium (1 and e with content 1−ϕe and ϕ e = ( ϕ 2 1 3 + ϕ 3 1 3 ) 3 ${\phi }_e = {( {\phi _2^{\frac{1}{3}} + \phi _3^{\frac{1}{3}}} )}^3$ , respectively),[10] that is, ( 1 − ϕ e ) ( ε 1 − ε m ε 1 + A ε m ) + ϕ e ( ε e − ε m ε e + A ε m ) = 0 $( {1 - {\phi }_{\mathrm{e}}} )( {\frac{{{\varepsilon }_1 - {\varepsilon }_{\mathrm{m}}}}{{{\varepsilon }_1 + A{\varepsilon }_{\mathrm{m}}}}} ) + {\phi }_e( {\frac{{{\varepsilon }_e - {\varepsilon }_{\mathrm{m}}}}{{{\varepsilon }_e + A{\varepsilon }_{\mathrm{m}}}}} ) = 0$ , or the TEPPE,[14] that is, ( 1 − ϕ e ) ( ε 1 1 / 1 s ∼ s ∼ − ε m 1 / 1 s ∼ s ∼ ) ε 1 1 / 1 s ∼ s ∼ + A ε m 1 / 1 s ∼ s ∼ + ϕ e ( ε e 1 / 1 t ∼ t ∼ − ε m 1 / 1 t ∼ t ∼ ) ε e 1 / 1 t ∼ t ∼ + A ε m 1 / 1 t ∼ t ∼ = 0 $( {{\mathrm{1}} - {\phi }_{\mathrm{e}}} )\frac{{( {\mathop \varepsilon \nolimits_{\mathrm{1}}^{{1 \mathord{/ {\vphantom {1 {{\mathrm{\tilde{s}}}}}} \kern-\nulldelimiterspace} {{\mathrm{\tilde{s}}}}}} - \mathop \varepsilon \nolimits_{\mathrm{m}}^{{1 \mathord{/ {\vphantom {1 {{\mathrm{\tilde{s}}}}}} \kern-\nulldelimiterspace} {{\mathrm{\tilde{s}}}}}} } )}}{{\mathop \varepsilon \nolimits_{\mathrm{1}}^{{1 \mathord{/ {\vphantom {1 {{\mathrm{\tilde{s}}}}}} \kern-\nulldelimiterspace} {{\mathrm{\tilde{s}}}}}} {\mathrm{ + }}A\mathop \varepsilon \nolimits_{\mathrm{m}}^{{1 \mathord{/ {\vphantom {1 {{\mathrm{\tilde{s}}}}}} \kern-\nulldelimiterspace} {{\mathrm{\tilde{s}}}}}} }}{\mathrm{ + }}{\phi }_e\frac{{( {\mathop \varepsilon \nolimits_{\mathrm{e}}^{{1 \mathord{/ {\vphantom {1 {{\mathrm{\tilde{t}}}}}} \kern-\nulldelimiterspace} {{\mathrm{\tilde{t}}}}}} - \mathop \varepsilon \nolimits_{\mathrm{m}}^{{1 \mathord{/ {\vphantom {1 {{\mathrm{\tilde{t}}}}}} \kern-\nulldelimiterspace} {{\mathrm{\tilde{t}}}}}} } )}}{{\mathop \varepsilon \nolimits_{\mathrm{e}}^{{1 \mathord{/ {\vphantom {1 {{\mathrm{\tilde{t}}}}}} \kern-\nulldelimiterspace} {{\mathrm{\tilde{t}}}}}} {\mathrm{ + }}A\mathop \varepsilon \nolimits_{\mathrm{m}}^{{1 \mathord{/ {\vphantom {1 {{\mathrm{\tilde{t}}}}}} \kern-\nulldelimiterspace} {{\mathrm{\tilde{t}}}}}} }}{\mathrm{ = 0}}$ , where the exponent s ∼ $\tilde{s}$ describes the divergent behavior of the dc conductivity when the percolation threshold ϕec is approached from the insulating side (ϕe < ϕec), the exponent t ∼ $\tilde{t}$ characterizes the ac and dc conductivities for ϕe > ϕec, and A = ( 1 − ϕ e c ) / ϕ e c $A = (1 - {\phi }_{ec})/{\phi }_{ec}$ . Importantly, it is assumed that only the two phases exist and they are perfectly bonded to each other. While there has been some debate regarding the applicability of TEPPE, one attribute of this equation is that the two behaviors (mean-field Bruggeman model for ϕe << ϕec and if one sets s ∼ = t ∼ = 1 $\tilde{s} = \tilde{t} = 1$ , and critical percolation model for ϕe ϕec and if one sets s ∼ = s $\tilde{s} = s$ and t ∼ = t $\tilde{t} = t$ ) are recovered as limiting cases of the TEPPE. While a thorough discussion of the properties of these equations would be helpful, such a treatment would require a rather lengthy detour through the basic principles of effective medium theory.[14] For our purpose, we need to know that the validity of the Bruggeman equation and TEPPE rest on the long-wavelength approximation, that is the wavelength of the electromagnetic wave propagating inside the material is much larger than the intrinsic correlation length of the system. This modeling method differs from previous models. In their original work, TS used the Lichteneker and Rother formula for modeling the PNC material's effective permittivity and comparison with experimental data.[5] Liu and co-workers[7] used the Maxwell Garnett and Bruggeman equation in their modeling approach. Yet, the correct long-wavelength description of the effective permittivity of two-phase nanostructures has been subject to a lasting debate;[14, 15] that is, for nanometer-sized particles, the molecular structure of the polymer matrix can be significantly perturbed at the polymer/particle interface because the perturbed region is on a length scale that is the same at the particle size. However, these ambiguities vanish for low particle volume fraction approximating the dilute limit of physically isolated particles (ϕe << 1).

In principle, the Bruggeman equation and TEPPE have practical advantages: they are analytically soluble and can be compared to experimental data even if the core permittivity of the CS inclusions in CB filled PNC is always difficult to measure, as noted in the Introduction.

While the algorithm's primary task is to reduce the residual error between the experimental data and its fit, several studies[2, 73] have reported non-uniqueness of non-universal values of the percolation exponents, which illustrates the complexity of the TEPPE procedure very clearly. There is the presumption that non-universal exponents could be related to artefacts in the filler conductivity, for example, contact resistance effects could decrease filler conductivities below their bulk values. As a consequence, if one desires to use TEPPE in constructing an effective medium modeling of PNC comprising particles surrounded by interphases, one needs to find a more robust procedure than the standard one. Numerical simulations based on GA technique[74, 75] explain how the “most likely” set of non-universal values of percolation exponents s ∼ $\tilde{s}$ and t ∼ $\tilde{t}$ of the TEPPE-based model can be estimated.

3.6 Extending the TEPPE-Based Model by Using Genetic Algorithm

In the past decades, GA have proven to be highly effective in solving engineering and applied physics problems.[75] Random search algorithms, such as GA and simulated annealing, are becoming increasingly used in global optimization in the understanding of complex systems.[76] The key physical idea, which underlies this optimization and stochastic search problem, is in fact quite intuitive: GA is a computational model inspired by natural selection described by genetics and the Darwinian theory of evolution.[75] GA techniques have been applied to a wide variety of fields including pattern recognition, image analysis, engineering design, and electromagnetism.[17, 76] GA belongs to the larger class of evolutionary algorithms, which generates solutions to optimization problems using techniques inspired by natural evolution, such as mutation and selection. In computational physics, GA approximates the target probability distributions by a large cloud of random samples termed individuals. During the mutation transition, the individuals evolve randomly around the space independently, and to each individual, is associated a fitness weight function. During the selection transitions, such an algorithm duplicates individual with high fitness at the expense of individuals with low fitness which die. These genetic type individual samplers belong to the class of mean field methods. Each generation in the GA is composed of several individuals who form a possible solution, that is, here, the effective complex permittivity of heterostructures.[17] Then, a fitness function compares the measured and computed electromagnetic observables, and after this evaluation, a selection of individuals and mutation operations is performed in order to improve the next generation.

It should be emphasized in this context that Youngs implemented a four-step GA approach to fitting the effective complex permittivity data to the TEPPE (with reference to the workflow of the explicit method shown in ref. [17]). In the first step, trial solutions are coded as genes. The length of each gene (string of bits that is initially assigned random value within predetermined range) is determined by the range of values that the parameter defining the solution can take and the precision to which the parameter is to be determined. In a second step, the fitness, that is, a function to provide a quantitative measure of how well a trial solution meets the target specification, is calculated. Next, the selection of parents is performed. To create the next generation of trial solutions and promote optimization, sets of potential parents for new trial solutions are selected by a random process that is biased by the fitness values of the parent generation. This one-to-one competition is repeated until enough strings are obtained to fill the next population. In the final step, once a set of parents is chosen, a pair of children is created by crossover and/or mutation of the parents’ chromosomes, given a law of probability. The convergence check is performed as follows: the measure of the population convergence. If the population is still evolving, go back to the second step and continue the breeding process. If the population reaches a stationary state, go back to first step and rest the population with randomly chosen strings; while, retaining the best string from the previously converged population. The key parameters of this algorithm are the generation size, the choice of selection process, the probabilities for crossover and mutation, and the number of iterations. What is remarkable is that the use of this GA fitting process enables the uniqueness of the fit parameters to be considered for broadband permittivity data to the TEPPE analysis[17] because it is robust in terms of finding globally optimum solutions. Thus, there is solid reason to expect that GA constitutes a promising way of trying to explain certain non-universal values of the percolation exponents observed in DS data.[77]

4 Conclusions and Some Future Directions

Overall, it has been shown here on the basis of a brief review which summarizes dielectric studies and related experiments on PNC that the interphase impacts significantly their macroscopic properties. Then, we moved on to discuss constraints on analytically soluble models that attempt to explain the interface and interphase characteristics in PNC thanks to DS data. Physical arguments presented motivate the claim that the direct measurement of the local interfacial characteristics and interphase properties are generally unavailable. Given this observation, it is useful to indicate the senses in which the models reviewed in this article do or do not capture the essence of what was originally envisioned by the concept of interphase. In a certain sense, the hybrid TEPPE-GA approach described above corroborates Lewis’ idea that the “interfaces are the dominant feature of dielectrics at the nanometric level,”[27] and that, the non-universal values of the percolation exponents reflect an electric response to bulk, collective polarization effects in complex materials. Thence, interphase properties can only be deduced by inference from effective analytical and computational models. Mathematical morphology and non-linear image processing operators could provide alternatives. As we hope this paper demonstrates, there is a tremendous amount of work yet to be done before these models can get the most science out of the DS data. We conclude that generic tests of these models and the effects of systematics in all of these tests due to mismodelling are of utmost importance to extract of fundamental physics information related to interface and interphase roles in PNC. Such structural inhomogeneities would seem to be important if the physical properties of PNC are thoroughly understood.

Now, we propose a few specific questions and some general directions that appear ripe for the development of effective medium approaches to extract the poorly known interface features between the phases in these composites. First, the above discussed analytical models should be complemented with computational analysis. Regarding this issue, the most burning questions involve the multiscale multiphysics models for coupling properties including, for example, electro–mechanical and thermo–mechanical. Although some of the analytical power has been demonstrated in DS measurements when determining the geometric and electrical contributions of the interphase on the effective permittivity of PNC, we note that computational models have been proposed that best align with our understanding of PNC exhibiting an interphase. Such studies have received a great deal of attention recently. Of particular note is the development of a systematic method to discriminate between the relevant interfacial phenomena through the extraction of their characteristic time and lengths scales. For example, a simulation model was recently put forth by Albright and Hobeck (AH) based on a stochastic fractal aggregate placement algorithm (Figure 9).[78]

Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
3D CB microstructures simulated by a stochastic fractal aggregate placement algorithm: a) primary CB particle, b) aggregate of fused CB particles, and c) corresponding RVE. In this model, the resistance of electrically conductive pathways consists of intrinsic resistance between fused primary particles in aggregates and tunnelling resistance between non-fused primary particles separated by a small distance by the polymer matrix.[78] Reproduced under the terms of the CC-BY license. 2023, Albright and Hobeck, Published by MDPI.

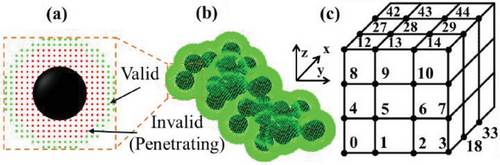
In this model, a statistical analysis was performed and compared to 2D image statistics of stochastically RVE with comparable volume properties to extract information for quantifying dispersion quality of CB filled PNC. One key advantage of this approach was that microscopy images revealed similar statistical distributions of CB agglomerates. However, one important question is how all of this is related to the problem of investigating the effective medium modelling of the physical properties of PNC that were supposed to represent the interface and interphase characteristics in the material.

Second, and as discussed in Section 3, perhaps one of the most important points is to consider AI systematics, creating a floor to our ability to test realistic and data-dependent interface and interphase models. Machine learning-driven analysis for extending a physics-based model which describes the multiscale microstructure of PNC might help to overcome the required fitting and reduce the amount of necessary DS measurements.[77] Deep learning approaches provide tools for extracting features from massive amounts of experimental data that are available on PNC with characterized multiscale microstructures. Tuning digital twins of complex heterostructures with comparable structural properties and morphological characteristics of the real material along with using efficient algorithms for estimating the quasistatic dielectric properties constitute ambitious and motivating perspectives in this field. Given all of this, it is hopefully clear that a great amount of work is still needed to extract the most fundamental physics describing the interface and interphase in PNC from DS data and to ensure such inferences are robust.

Acknowledgements

The Lab-STICC is Unité Mixte de Recherche CNRS 6285.

    Conflict of Interest

    The authors declare no conflict of interest.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.