On the fixed part of pluricanonical systems for surfaces
Abstract
We show that defines a birational map and has no fixed part for some bounded positive integer m for any -lc surface X such that is big and nef. For every positive integer , we construct a sequence of projective surfaces , such that is ample, for every i, , and for any positive integer m, there exists i such that has nonzero fixed part. These results answer the surface case of a question of Xu.
1 INTRODUCTION
We work over the field of complex numbers .
Pluricanonical systems are central objects in the study of birational geometry. More precisely, given a normal projective variety X such that is effective, we would like to study the behavior of the linear systems for any positive integer m.
It is well known that for any sufficiently divisible , the rational map given by is birationally equivalent to the Iitaka fibration of . In 2014, Hacon–McKernan–Xu proved that for any lc projective variety X of general type and of fixed dimension, there exists a uniform positive integer m such that defines a birational map [8, Theorem 1.3] (see also [7, 15, 16]). In other words, defines a birational morphism for some uniform positive integer m, where is the base locus of .
It is then natural to ask whether the behavior can be described more accurately. Since we already have a birational morphism for some uniform positive integer m, one would like to focus on the asymptotic behavior of . As the very first step, we have the following question proposed by Prof. C. Xu to the first author in 2018:
Question 1. (Xu)Assume that X is a klt projective variety of fixed dimension such that is big and nef. When will we have a uniform positive integer m, such that defines a birational map and does not have a fixed part?
Note that it is natural to assume to be nef as we can always run an MMP with scaling and reach a minimal model for varieties of general type (cf. [3, Corollary 1.4.2]).
Question 1 naturally arises as a combination of [8, Theorem 1.3] and the effective base-point-freeness theorem [9, 1.1 Theorem]. Note that when the Cartier index is bounded, not only defines a birational map but is also base-point-free for some uniform positive integer m. The interesting cases of Question 1 appear when the Cartier index of is unbounded, in which case, the uniform base-point-freeness cannot be guaranteed.
Question 1 is trivial in dimension 1 but remained widely open in dimension ≥2. In this paper, we study Question 1 when . The main theorem of this paper is the following:
Theorem 1.1.There exists a uniform positive integer m satisfying the following. Assume that X is a -lc projective surface and is big and nef. Then, defines a birational map and does not have a fixed part.
The following theorem is a complementary statement for Theorem 1.1, which shows that if the Cartier index of is not bounded and X is not -lc, then Theorem 1.1 is not expected to hold.
Theorem 1.2.For any integer , there exists a sequence of projective surfaces , such that
- 1. for each i and ,
- 2. is ample, and
- 3. if is the minimal positive integer such that defines a birational map and has no fixed part, then .
Note that the assumptions on mld(X) in Theorem 1.1 and Theorem 1.2 are natural assumptions: We are only interested in varieties such that the Cartier index of is not bounded, and if we consider a family of singularities such that the index of is unbounded, then is an infinite set (cf. [4, Proposition 7.4]) and the accumulation points of belong to (cf. [1, Corollary 3.4]). The accumulation point case is resolved by Theorem 1.1 and the remaining cases are resolved by Theorem 1.2.
It is also interesting to ask whether Question 1 has a positive answer for canonical or terminal threefolds in dimension 3, as 1 is the largest accumulation points of in dimension 3 (cf. [13, Appendix, Theorem]). We will not address this question in this paper, but we will provide a related example (cf. Theorem 5.7).
2 PRELIMINARIES
We adopt the standard notation and definitions in [11], and will freely use them.
Definition 2.1. (Pairs and singularities)A pair consists of a normal quasi-projective variety X and an -divisor such that is -Cartier. Moreover, if the coefficients of B are ⩽1, then B is called a boundary of X.
Let E be a prime divisor on X and D an -divisor on X. We define to be the multiplicity of E along D. Let be any log resolution of and let
A germ consists of a pair and a closed point . is called an lc (resp. a klt, an ε-lc) germ if is lc (resp. klt, ε-lc) near x. is called ε-lc at x if for any prime divisor D over (i.e., ).
Definition 2.2.Let be a set of real numbers. We say that satisfies the descending chain condition (DCC) if any decreasing sequence in stabilizes. We say that satisfies the ascending chain condition (ACC) if any increasing sequence in stabilizes.
Definition 2.3. (Minimal log discrepancies)Let be a pair and a closed point. The minimal log discrepancy of is defined as
Definition 2.4.Let X be a normal projective variety and D an -divisor on X. We define
- (1) for any , , and
- (2) does not contain any divisor,
We denote by the Picard number of X.
Definition 2.5.A surface is a variety of dimension 2. A rational surface is a projective surface that is birational to . For ever nonnegative integer k, the Hirzebruch surface is .
Definition 2.6.Let n be a nonnegative integer, and a collection of proper curves on a smooth surface U. The determinant of C is defined as if , and we define . We define the dual graph of C as follows.
- 1. The vertices of correspond to the curves .
- 2. For each i, is labeled by the integer . is called the weight of .
- 3. For ,the vertices and are connected by edges.
Theorem 2.7. (cf. [[1], Theorem 3.2, Corollary 3.4], [[14]])mld(2) satisfies the ACC, and the set of accumulation points of mld(2) is .
Proposition 2.8. (cf. [[4], Proposition A.5])Let be a finite set. Then, there exists a positive integer I depending only on satisfying the following. Assume that is an lc surface germ such that . Then, is Cartier near x.
Lemma 2.9.Let ε be a positive real number and an ε-lc (resp. ε-klt) surface germ. Then, for any vertex v of , the weight of v is (resp. ).
Proof.[1, Corollary 2.19] proves the ε-lc case and the ε-klt case immediately follow.
Lemma 2.10. (cf. [[1], Lemma 3.3], [[4], Lemma A.1])Let ε be a positive real number. Then, there exists a finite set of dual graphs and a finite set of positive integers, such that for any ε-lc germ , one of the following holds:
- 1. .
- 2. is of the type as in Figure 1
 FIGURE 1.Moreover, we may assume that
FIGURE 1.Moreover, we may assume that- (a) either and , or ; and
- (b) either and , or .
- 3.
is of the type as in Figure 2
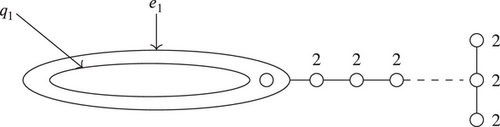 FIGURE 2.
FIGURE 2.
We remark that each oval in Figures 1 and 2 corresponds to a subdual graph, which is a chain, as shown in [1, Lemma 3.3, 2] and [4, Appendix, Notation].
Proof.The statement on the structure of the dual graphs are explained both in [1, Lemma 3.3] and in [4, Lemma A.1]. By taking the coefficient set , the inequality in (2) follows from the moreover part of [4, Lemma A.1(2)], and the inequality follows from the moreover part of [4, Lemma A.1(3)].
For the moreover part of (2), note that if , then we may add the vertex corresponding to w1 to the 2-chains and repeat this process unless this vertex is the tail of the chain. This implies (2.a), and (2.b) is similar to (2.a).
Lemma 2.11. ([[10], 3.1.11])Let be a klt surface germ such that is a chain. Then, is a cyclic quotient singularity. Moreover, if the dual graph of is
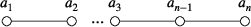
Lemma 2.12. (cf. [[12], Lemma 2.11], [[2], Theorem 1])Let be a cyclic quotient singularity of form such that . Then,
Lemma 2.13.Let and be two klt surface germs such that is a subgraph of . Then, .
Proof.Let be a partial resolution, which extracts all divisors corresponding to vertices contained in . Then, for some . Since for some , we have
Lemma 2.14.Let be a -klt surface singularity. Then, either , or , or the weight of any vertex of is ⩽3.
Proof.By Lemma 2.9, the weight of any vertex of is ⩽4. By [11, Theorem 4.7], is connected and contains no cycle. We may assume that contains a vertex of weight 4. We have the following cases.
Case 1. only contains one point. Then, and we are done.
Case 2. contains the subgraph :

Case 3. contains the subgraph :

Case 3.1. . By Lemma 2.11, is a cyclic quotient singularity of type and we are done.
Case 3.2. contains a subgraph :
Case 3.3. contains a subgraph :
Lemma 2.15.Let be a -klt surface germ and the minimal resolution of . Suppose that
Proof.By Lemma 2.14, there are three cases.
Case 1. for each i. Since for each i, for each i. Since for each i, the lemma follows.
Case 2. and . Then, and , hence . We have .
Case 3. , and possibly reordering indices, and . Then, , , , and . Thus, and , hence .
Lemma 2.16.Let be a cyclic quotient singularity of type for some positive integer k. Then, is the following graph, where there are “ 2” in the graph.
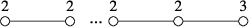
Proof.It is clear that the cyclic quotient singularity is uniquely determined by its dual graph. Since where there are “2” in the fraction, the first part of the lemma follows from Lemma 2.11. For the remaining part of the lemma, let for each i. Since for each i and for each i, when , and we are done, and when , we have
- (1) ,
- (2) for any , and
- (3) .
3 GLOBAL GEOMETRY OF SMOOTH SURFACES
3.1 Some elementary lemmas
Lemma 3.1.Let X be a smooth projective surface, D a pseudo-effective -divisor on X, and C an irreducible curve on X. If , then .
Proof.Let be the Zariski decomposition of D such that P is the positive part and N is the negative part. Since and P is nef, . Since , and .
Lemma 3.2.Let X be a smooth projective surface such that is pseudo-effective. Let C be an irreducible curve on X such that . Then, . In particular, C is a smooth rational curve.
Proof.By Lemma 3.1, . Since X is smooth, and . Thus, , which implies that , , and C is a smooth rational curve.
Lemma 3.3.Let X be a smooth projective surface such that is pseudo-effective, and C a smooth rational curve on X. Then, .
Proof.If not, then . Since , . Since is pseudo-effective, , a contradiction.
Lemma 3.4.Let X be a smooth projective surface, C an irreducible curve on X, a blow-up of a closed point, E the exceptional divisor of f, and the strict transform of C on Y. If and is a smooth rational curve, then C is a smooth rational curve.
Proof.Since X is smooth, Y is smooth. Thus, . If , then f is an isomorphism near a neighborhood of and hence C is a smooth rational curve. If , then and , and hence . Thus, C is a smooth rational curve.
Lemma 3.5.Let X be a smooth projective surface such that is pseudo-effective, and two different smooth rational curves on X such that . Then, .
Proof.Assume that , then for some positive integer n. Let be the contraction of E1 and . Then, and . Since is pseudo-effective, is pseudo-effective, which contradicts Lemma 3.1.
Lemma 3.6.Let X be a smooth projective surface such that is pseudo-effective, and three different smooth rational curves on X. If and , then either or .
Proof.Assume that and for some positive integers n1 and n3. Let be the contraction of E2. Then, Y is smooth and is pseudo-effective. Let , and . Then, , , , and . Thus, by Lemma 3.1, , which implies that and . By Lemma 3.4, and are smooth rational curves, which contradicts Lemma 3.5.
Lemma 3.7.Let X be a smooth rational surface. Then, .
Proof.We may run a -MMP such that either for some nonnegative integer k or . For any , we have and . Thus, . If for some nonnegative integer k, then . If , then . Thus, .
3.2 Zariski decomposition
Lemma 3.8.Let X be a smooth projective surface, and D, two -divisors on X, such that and is nef. Let be the Zariski decomposition of D, where P is the positive part and N is the negative part. Then, .
Proof.Assume that and , where n is a nonnegative integer, are distinct irreducible curves, , and for each i, , , and . Then, for every ,
Lemma 3.9.Let X be a smooth projective surface, D a big Weil divisor on X, an nef Weil divisor on X, and E a Weil divisor on X, such that
- (1) is the Zariski decomposition of D, where P is the positive part and is the negative part,
- (2) , and
- (3) defines a birational map.
- 1. ,
- 2. ,
- 3. defines a birational map, and
- 4. either and , or there exists at least one irreducible component F of such that .
Proof.We let , then (1) holds. Let . Since is nef and , by Lemma 3.8, . Thus, , and hence
Proposition 3.10.Let X be a smooth projective surface, D a big Weil divisor on X, and an nef Weil divisor on X, such that
- (1) is the Zariski decomposition of D, where P is the positive part and is the negative part,
- (2) , and
- (3) defines a birational map.
- 1. ,
- 2. defines a birational map, and
- 3. is big and nef.
Proof.Let , , and , and let r0 be the sum of all the coefficients of E0. Then, r0 is a nonnegative integer.
For any nonnegative integer k, assume that there exist big Weil divisors on X, Weil divisors on X, and nonnegative integers , such that for every ,
- (1) is the Zariski decomposition of , where is the positive part and is the negative part;
- (2) ;
- (3) defines a birational map;
- (4) is the sum of all the coefficients of the components of such that ; and
- (5) if , then .
Case 1. and . In this case, by our assumptions,
- (1) , hence ;
- (2) , hence ;
- (3) is big and defines a birational map; and
- (4) is nef.
Case 2. There exists a big Weil divisor on X, a Weil divisor on X, and a nonnegative integer , such that
- (1) ,
- (2) ,
- (3) defines a birational map, and
- (4) .
3.3 Effective birationality and existence of special nef -divisors
Lemma 3.11.Let X be a klt projective surface such that is big and nef, the minimal resolution of X, and the prime f-exceptional divisors. Assume that . Then, for any positive integer m, if there exist integers , such that
- 1. , and
- 2. is big and nef,
Proof.Let and . Then, L is big and nef and Cartier. In particular, is big and nef. By [6, Theorem 1.1, Remark 1.2] (see also [9, 1.1 Theorem]), 192L is base-point-free, which implies that the fixed part of is supported on . Thus, does not have a fixed part.
Theorem 3.12. (cf. [[8], Theorem 1.3])There exists a uniform positive integer m1, such that for any lc surface X such that is big, defines a birational map.
4 -KLT SURFACES
In this section, we will prove Theorem 1.1. The structure of this section is as follows. In Section 4.1, we give a detailed classification of -klt surface singularities. In Section 4.2, we consider the intersection numbers of the form where X is -klt, is big and nef, and C is a curve satisfying special properties. For some lemmas and propositions, we need to restrict ourselves to -klt surfaces. With a good description of these intersection numbers and with the help of the results on Zariski decomposition in Section 3, in Section 4.3, we will construct special nef -divisors on the minimal resolution of -klt surfaces. We will prove our main theorem in Section 4.4.
4.1 Classification of -lc singularities
Lemma 4.1.Let ε be a positive real number. Then, there exists a positive integer depending only on ε satisfying the following. Assume that is a -lc surface germ. Then,
- 1. either is Cartier near x, or
- 2. is a cyclic quotient singularity of type for some positive integer . In particular, is the following graph, where there are “ 2” in the graph.
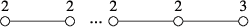
Proof.Assume that the lemma does not hold. Then, there exists a sequence of -lc surface germs , and a strictly increasing sequence of positive integer , such that
- (1) is not Cartier near for any positive integer , and
- (2) is not a cyclic quotient singularity of type for any i and any positive integer k.
We let be the finite set of dual graphs and be the finite set of real numbers as in Lemma 2.10. Then, for any such that , belongs to a finite set. Thus, possibly passing to a subsequence, by Lemma 2.10, we may assume that one of the following holds:
- (1) satisfies (2) of Lemma 2.10 for each i, and , for each i. Since is a finite set, possibly passing to a subsequence, we may assume that are constants for each i.
- (2) satisfies (3) of Lemma 2.10 for each i, and for each i. Since is a finite set, possibly passing to a subsequence, we may assume that are constants for each i.
If satisfies (2) of Lemma 2.10 for each i, and , are constants for each i, then by Lemma 2.10(2),
Case 1. . Then or 3.
Case 1.1 .
Case 1.1.1 . Then or 3.
Case 1.1.1.1 . In this case, all the weights in are 2. Thus, for every i, a contradiction.
Case 1.1.1.2 . In this case, for each i, the dual graph of is of the following form
Case 1.1.2 . In this case, there exist an integer and a nonnegative integer , such that . Thus,
Case 1.2 .
Case 1.2.1 . Then, or 3.
Case 1.2.1.1 . In this case, for each i, the dual graph of is of the following form
Case 1.2.1.2 . In this case, for each i, the dual graph of is of the following form:
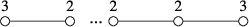
Case 1.2.2 . In this case, exactly the same argument as in Case 1.1.2 holds and we get a contradiction.
Case 2. . In this case, there exists an integer and a nonnegative integer , such that . Thus,
4.2 Intersection numbers
Lemma 4.2.Let X be a projective klt surface such that is nef and the minimal resolution of X. If X is not rational, then is pseudo-effective.
Proof.If X is not rational, Y is not rational. If is not pseudo-effective, then there exists a birational morphism to a smooth projective surface W and a -fibration . Since Y is not a rational surface, . Thus, for any exceptional curve F of f, F does not dominate R. Pick a general h-vertical curve Σ and let , be the strict transforms of Σ on Y and X, respectively. Then,
Lemma 4.3.Let X be a -klt surface such that is big and nef, C an irreducible curve on X, a closed point, the minimal resolution of X, and the strict transform of C on Y. Assume that
- X is not a rational surface,
- ,
- is a cyclic quotient singularity of type for some integer , and
- are prime f-exceptional divisors over , such that
- 1. when ,
- 2. , and
- 3. if and only if .
- 1. when , and
- 2. .
Proof.By Lemma 4.2, is pseudo-effective. By Lemma 3.2, and . Moreover, each is a smooth rational curve. Let be the contraction of and for each i. Then, W is smooth and is pseudo-effective.
Claim 4.4. for every .
Proof of Claim 4.4.Suppose this is not the case, then there exists an integer and an integer , such that . We have
Claim 4.5. are smooth rational curves for every i.
Claim 4.6. for every .
Proof of Claim 4.6.Suppose that the claim does not hold. Then, by Claim 4.4, there exists such that . There are three cases:
Case 1. . In this case, and . By Claim 4.5, and are smooth rational curves. Since is pseudo-effective, this contradicts Lemma 3.5.
Case 2. . We get a contradiction by the same arguments as Case 1 except that we replace with .
Case 3. . In this case, , , , which contradicts Lemma 3.6.
Claim 4.7..
Proof of Claim 4.7.Suppose that the claim does not hold. Then, by Claim 4.4, . By Claim 4.6, for every . There are two cases:
Case 1. . In this case, , , , , and . This contradicts Lemma 3.6.
Case 2. . In this case, , , , and for every , if and if .
Let be the contraction of and for any . Then, Z is smooth and is pseudo-effective. By Lemma 3.4, , and are smooth rational curves. Moreover, , , and . This contradicts Lemma 3.6.
Claim 4.8..
Proof of Claim 4.8.Suppose that the claim does not hold. Then, by Claim 4.4, . By Claim 4.6 and Claim 4.7, for every . By Claim 4.4, there are two cases:
Case 1. . In this case, , , , which contradicts Lemma 3.6.
Case 2. . The are two subcases:
Case 2.1. For any closed point such that , X is smooth near y. In this case, let . Since is big and nef,
Case 2.2. There exists a closed point such that and X is not smooth near y. Then, there exists a prime divisor F on Y that is over , such that . Moreover, F is a smooth rational curve. Since X is -klt, by Lemma 2.9, . Let .
We have for every , , , and for every , when and when .
There are two subcases:
Case 2.2.1. . In this case, by Lemma 3.4, is a smooth rational curve. Moreover, and ,
Let be the contraction of , for each , and . Then, Z is smooth and is pseudo-effective. By Lemma 3.4, , and are smooth rational curves. Moreover, , , , , and .
Let be the contraction of , for each , and . Then, T is smooth and is pseudo-effective. By Lemma 3.4, , and are smooth rational curves. Moreover, , , , and .
By Lemma 3.3, . By Lemma 3.5, . But this contradicts Lemma 3.6.
Case 2.2.2. . In this case, we let and . Then, , , and .
Let be the contraction of and . Then, Z is smooth and is pseudo-effective. Moreover, , and . Since and , and , which contradicts Lemma 3.1.
Proof of Lemma 4.3 continued.By Claim 4.6, Claim 4.7, and Claim 4.8, we get (1). Since , intersects , which implies that intersects . Thus, . (2) follows from Claim 4.4.
Lemma 4.9.Let X be a rational -klt surface such that is big and nef and an integer. Then, X does not contain a cyclic quotient singularity of type .
Proof.Assume not. Then, there exists a closed point such that x is a cyclic quotient singularity of type . By Lemma 2.16, we may let be the minimal resolution of X and write
- (1) are the prime f-exceptional divisors over such that when and , and
- (2) for every , for some closed point , such that .
Lemma 4.10.Then, there exists a positive integer n1, a DCC set of nonnegative real numbers, and a positive real number γ0 satisfying the following. Assume the following:
- X is a -klt surface such that is big and nef,
- C is an irreducible curve on X,
- is the minimal resolution of X,
- is the strict transform of C on Y, and
- ,
- 1. ,
- 2. if , then is Cartier near C, and
- 3. if , then .
Proof.By Lemma 4.1, there exists a positive integer , such that for any closed point , either is Cartier near x, or x is a cyclic quotient singularity of type for some positive integer . Now we let
Consider the equation
We show that , and γ0 satisfy our requirements. For any curve C as in the assumption, there exists a nonnegative integer s, such that
- (1) there are closed points on X, such that and is a cyclic quotient singularity of type for some positive integer for each i, and
- (2) for any closed point , is Cartier near y.
- (1) and are distinct prime f-exceptional divisors for every ,
- (2) for any , ,
- (3) are positive integers,
- (4) for each i, and
- (5) and for every .
4.3 Construction of nef -divisors
Proposition 4.11.There exists a positive integer m0 satisfying the following. Assume the following:
- (1) X a -klt surface such that is big and nef,
- (2) is the minimal resolution of X, and
- (3) , where are the prime f-exceptional divisors,
Proof.Let n1 and γ0 be the numbers given by Lemma 4.10, n0 the number given by Lemma 4.1, , and
We classify the singularities on X into three classes:
Class 1. Cyclic quotient singularities of type where . Let these singularities be for some nonnegative integer s. We may assume that is a cyclic quotient singularity of type for some integer for every .
Class 2. Singularities of type where . Let these singularities be for some integer . In particular, by the definition of m0. is Cartier near for every .
Class 3. Other singularities. Let these singularities be for some integer . In particular, by Lemma 4.1, and the definition of m0, is Cartier near for every .
Now we may write
- (1) for every and , ;
- (2) for every and , ;
- (3) for every , ;
- (4) is a f-exceptional Weil divisor, such that for every .
Case 1. is not pseudo-effective. In this case, by Lemma 4.2, X is rational. By Lemma 4.9, . Thus, and
Case 2. is pseudo-effective.
Case 2.1. is not exceptional over X. Let .
Case 2.1.1. . In this case, and , hence .
Case 2.1.2. . By Lemma 3.2, . By Lemma 4.3, for every i and every , and for every i. By Lemma 4.10, there are two possibilities.
Case 2.1.2.1. is Cartier near C. In this case, since , we have for every i. Since the Cartier index of near is and is Cartier near C, C does not pass through . Thus, does not intersect for any , and hence
Case 2.1.2.2. . Possibly reordering indices, we may assume that there exists an integer , such that when and when . There are two cases:
Case 2.1.2.2.1. . In this case, since , . Thus,
Case 2.1.2.2.2. . In this case, we have
Case 2.2. is exceptional over X. Then, .
Case 2.2.1 . In this case, for every , and hence
Case 2.2.2 . We may assume that for some i and some . In this case,
Case 2.2.2.1 . In this case, .
Case 2.2.2.2 . In this case,
Case 2.2.2.3 . In this case, .
Case 2.2.2.4 . In this case, .
Proposition 4.12.There exists a uniform positive integer m2 satisfying the following. Assume that
- 1. X a -klt surface such that is big and nef,
- 2. is the minimal resolution of X, and
- 3. , where are the prime f-exceptional divisors,
Proof.By Proposition 4.11, there exist a positive integer which does not depend on X, and non-negative integers , such that is nef and for each i. By Theorem 3.12, there exists a uniform positive integer m1 such that defines a birational map. Let . Then, defines a birational map, and hence
Let and . Since ,
4.4 Proof of the main theorem
Proof of Theorem 1.1.Let be the minimal resolution of X such that , where are the prime exceptional divisors of f. By Proposition 4.12, there exists a uniform positive integer m2, such that is big and nef for some integers such that for each i. By Lemma 3.11, defines a birational map and we may let .
5 EXAMPLES
In this section, we will provide two theorems where we construct some interesting examples. The first one is Theorem 5.3 (= Theorem 1.2), which shows that the -lc assumption in Theorem 1.1 is necessary. The second one is Theorem 5.7. It shows that, even if we only have a very strong control on mld(X) (i.e., when X is a terminal threefold), “ has no fixed part” is the best we may expect, as we cannot expect to be free in codimension 2 for any bounded m.
Lemma 5.1.Let X be an lc projective surface such that is big and nef, the minimal resolution of X, and the prime f-exceptional divisors of X. Assume that , where . Let m be a positive integer and nonnegative integers, such that
- ,
- ,
- the fixed part of is supported on , and
- is big but not nef,
- 1. for each i,
- 2. there exists such that ,
- 3. , and
- 4. the fixed part of is supported on ,
Proof.Since , is lc. Thus, we may run a -MMP . Since the fixed part of is supported on , h only contracts divisors supported on . Let , then we have
Theorem 5.2.Let X be an lc projective surface such that is big and nef, the minimal resolution of X, and the prime f-exceptional divisors of X. Assume that , where . Then, for any positive integer m, if defines a birational map and does not have fixed part, then there exist positive integers , such that
- 1. , and
- 2. is big and nef.
Proof.The fixed part of
We inductively define integers for every for nonnegative integers j in the following way: Let for every i. If is big and nef, then we let for every i and we are done. Otherwise, by Lemma 5.1, there exist integers for every i, such that , for some , , and the fixed part of is supported on . This process must terminate after finitely many steps, and we get the desired for every i.
Theorem 5.3. (= Theorem 1.2)There exist normal projective surfaces , such that
- 1. and has a nonzero fixed part for any positive integers , and ,
- 2. is ample for every , and
- 3. for any n.
Proof.Step 1. In this step, we construct for every and .
For any positive integer and positive integer , we let be a general hypersurface of degree in the weighted projective space . Since and
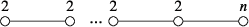
- (1) when ,
- (2) , and
- (3) if and only if .
Step 2. In this step, we show the following:
Claim 5.4.For any positive integers m, and , if and is big, then has nonzero fixed part.
Proof.We let and . Then, o1 is a cyclic quotient singularity of type with dual graph
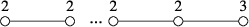
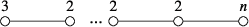
- (1) when , and
- (2) when .
- (1) if is not nef, then has nonzero fixed part, and
- (2) if is nef, then by Theorem 5.2, has nonzero fixed part.
Step 3. In this step, we show that is ample.
Claim 5.5.For any integers and , is ample, defines a birational map, and and has no fixed part. In particular, defines a birational map.
Proof.Let . Then,
Let be the coordinates of and since . Let and . Then, and . We only need to show that . This is the same as saying that does not contain the line in . Suppose that is defined by the homogeneous weighted polynomial . Since is general, . Thus, does not contain the line and we are done.
Claim 5.6.For any integers and , is ample.
Proof.For any , by Claim 5.5, the fixed part of is supported on . Since
Since is nef and big, . Since is nef and big, is nef and big and . In particular, .
For any irreducible curve on such that , if , we have that
Step 4. Claim 5.4 and Claim 5.6 imply (1)(2). Since
Theorem 5.7.For any positive integer m0, there exists a terminal threefold X such that is ample but is not free in codimension 2.
Proof.Step 1. We start with a local construction by using the language of toric varieties.
Let , , , , . Let and , where are positive integers such that and . Then, all these vectors above are primitive in N.
Let Σ1 be the fan determined by the single maximal . Let be the corresponding toric variety. Then, is affine and the cyclic quotient singularity is of the form . Notice that has an isolated singularity.
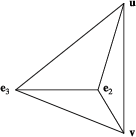
Let be the star subdivision of Σ1 at e2 as above (see [5, Chapter 11]) and be the corresponding toric variety, then is a birational morphism, which is an isomorphism outside the unique torus-invariant point . Since is smooth, has only two isolated singularities, which are of type and . In particular, is terminal. We use to denote the corresponding torus-invariant divisors. We can see that is the only exceptional divisor. Let R denote the proper curve in that corresponds to . Then, . By [5, Proposition 6.4.4], , , , and . Therefore,
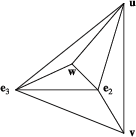
Let be the star subdivision of Σ2 at w as above and be the corresponding toric variety, then is a birational morphism, which is an isomorphism outside the torus-invariant point that corresponds to the maximal . We use to denote the corresponding torus-invariant divisors. Notice that is the only exceptional divisor of f and are the birational transforms of on . Let denote the birational transform of R on X3, then corresponds to .
Since , we have , hence
By [5, Lemma 6.4.2], . Thus, for any positive integer k,
Step 2. Next, we will use covering trick to make the canonical divisor ample.
Choose a projective threefold Z with the isolated quotient singularity of type at P, after resolving singularities away from P, we may assume that P is the only singular point on Z. By abuse of notation we continue to use and to denote the corresponding toric blow-ups defined in Step 1. Let E be the exceptional divisor of g and be the proper curve defined in Step 1. Then, is g-ample and we have , where
Let L be a sufficiently ample Cartier divisor on Z such that is ample on X. We can find an effective that is smooth and avoids P. Let be the double cover ramified along A. Then, by Hurwitz's Formula, we have and h is étale around P. Let be the corresponding base change of h. Then, is ample, where is the canonical projection. Since R is a proper curve in one of the components of as in Step 1 and its birational transform in , we have
Now we can choose such that , then
ACKNOWLEDGMENTS
The authors would like to thank Christopher D. Hacon for useful discussions and encouragements. They would like to thank Chenyang Xu for proposing Question 1 to them and sharing useful comments to this question. The authors would like to thank useful discussions with Paolo Cascini, Guodu Chen, Jingjun Han, Junpeng Jiao, Yuchen Liu, Yujie Luo, and Qingyuan Xue. They would like to thank the referees for useful suggestions.




